Received 25 March 2014; revised 25 April 2014; accepted 2 May 2014

ABSTRACT

Short-term memory allows individuals to recall stimuli, such as numbers or words, for several seconds to several minutes without rehearsal. Although the capacity of short-term memory is considered to be 7 ± 2 items, this can be increased through a process called chunking. For example, in Japan, 11-digit cellular phone numbers and 10-digit toll free numbers are chunked into three groups of three or four digits: 090-XXXX-XXXX and 0120-XXX-XXX, respectively. We use probability theory to predict that the most effective chunking involves groups of three or four items, such as in phone numbers. However, a 16-digit credit card number exceeds the capacity of short-term memory, even when chunked into groups of four digits, such as XXXX-XXXX-XXXX-XXXX. Based on these data, 16-digit credit card numbers should be sufficient for security purposes.

Keywords:

Short-term Memory, Chunking, Probabilistic Model, Credit Card Number

1. Introduction

Short-term memory allows stimuli, such as numbers or words, to be recalled for several seconds to several minutes without rehearsal. Miller (1956) reported that the storage capacity of short-term memory was 7 ± 2 items, naming this “the magical number” [1] . He concluded that human “channel capacity” does not exceed a few bits and that unambiguous judgment of one-dimensional stimuli (i.e., all numbers) can be made from 7 ± 2 categories. Recently, Cowan (2001) reported that the capacity of short-term memory is 4 - 5 items [2] . Baddeley (1994) thought highly of “magical number seven”, saying that it gives a beautifully clear account of information theory [3] , and several mathematical models investigating the origin of the magical number seven have been reported [4] [5] . Whether the capacity of short-term memory is 4 - 5 or 7 ± 2 items, it is clearly limited. However, memory capacity can be increased through a process called chunking [1] . For example, in Japan, 11-digit cellular phone numbers and 10-digit toll free numbers are chunked into groups of three or four digits: 090-XXXX- XXXX and 0120-XXX-XXX, respectively. Phone numbers in many other countries are similarly chunked. It is unclear how many items per group provide the most efficient chunking, and the current study used probability theory to investigate this.

In probability theory, there is a problem entitled “the tourist with a short memory” [6] . For example, if a tourist wants to visit four capitals A, B, C, and D, he travels first to one capital chosen at random. If he visits A, the next time, he should choose among B, C, and D with the same probability. However, in this problem, the tourist quickly forgets that he has already visited A. Therefore, if he visits B second, the next time, he would choose among A, C, and D with the same probability. The problem is to find the expected number, E(N), of trips required until the tourist has visited all four capitals. To address this question, the problem is transformed into a problem of short-term memory based on some hypotheses and assumptions described below. In the present paper these capitals correspond to items which are recalled. We study a case without chunking (Procedure 1), a case in which items are chunked in order into groups containing the same number of items (Procedure 2), and a case in which items are chunked in order into groups containing the different number of items (Procedure 3). The novelty of this study is that the most effective chunking involves groups of three or four items, such as in phone numbers, and that 23 trips may be the critical number, beyond which some items will be forgotten. A 16-digit credit card number exceeds the capacity of short-term memory, even when chunked into groups of four digits, such as XXXX-XXXX-XXXX-XXXX. Based on these data, 16-digit credit card numbers should be sufficient for security purposes.

2. Model

When a subject responds to an event involving several stimuli, those stimuli must be processed in such a way to distinguish among them while still associating them with the entire set of items. According to Miller’s and Cowan’s hypotheses (7 ± 2 or 4 - 5 items, respectively) [1] [2] , the capacity of short-term memory is between 4 - 9 items. Stimuli are often processed in order of dominance. The simplest way to order n items is to compare two items, retain the more dominant of the pair, then compare that with another item, again retaining the dominant one, and repeating this process until the entire collection has been ordered [5] . Although this process may be considered fundamental, it is assumed for simplicity that input items are one-dimensional categories, for example, strings of digits, letters, or words. The following assumptions were made:

Assumption 1: Input items (or stimuli) are assumed to be labeled as A₁, A₂, …, and A_n in order.

Assumption 2: Items are remembered equally with no one item being more dominant. The probability to recall any A_j except A_i next after A_i is recalled is equal.

Assumption 3: The subject can only recall n items in order after he recalls every item at least once.

Applying these assumptions to the problem of “the tourist with a short memory”, the problem is to find the expected number, E(N), of trips required until the tourist has visited all capitals. The process that any A_j except A_i is recalled after A_i is represented as a way: W(A_i→A_j). This can be calculated without chunking (Procedure 1) and with chunking into same-sized or different-sized groups (Procedures 2 and 3) as follows:

Procedure 1: To find the expected number, E(N), of ways required until all A_i’s are recalled (Figure 1(a)).

Procedure 2: Items are chunked in order into groups, which have the same number of items (Figure 1(b)). For example, (A₁, A₂, A₃), (A₄, A₅, A₆), (A₇, A₈, A₉), …, and (A_n−2, A_n−1, A_n). Groups are denoted in order as B₁, B₂, B₃, … (Figure 1(b)). There is equal probability to recall any B_j except B_i immediately after B_i is recalled. When any B_j is recalled for the first time, all items in B_j are recalled at least once, which assumes that the relationship among the items in B_j has already been confirmed. Hence, all visits within B_j are remembered from the second visit of B_j onwards. When all B_i’s are recalled, all A_i’s are also recalled, confirming the relationship among all A_i’s.

Procedure 3: Items are chunked into groups with different numbers of items. For example, in Japan, 11-digit cellular phone numbers and 10-digit toll free numbers are displayed as 090-XXXX-XXXX and 0120-XXX- XXX, respectively. The 11-digit phone number is chunked into three groups, B₁, B₂, B₃, one of which consists of three digits, B₁ = (A₁, A₂, A₃), and two of which consist of four digits, B₂ = (A₄, A₅, A₆, A₇), B₃ = (A₈, A₉, A₁₀, A₁₁). Similarly, the 10-digit toll free number is chunked into three groups, B₁, B₂, B₃, one of which consists of four

digits, B₁ = (A₁, A₂, A₃, A₄), and two of which consist of three digits, B₂ = (A₅, A₆, A₇), B₃ = (A₈, A₉, A₁₀).

3. Results of Calculation

3.1. Procedure 1

When the number of all items is n, the expected number, E(N), of ways, W(A_i→A_j), required until all A_i’s are recalled can be calculated.

In the case of n = 3, a subject wants to recall three items, A₁, A₂, A₃.

Set N as follows:

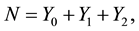
where Y_m is the number of ways required for recalling one more item when m items have already been recalled. Therefore, Y_m’s are independent stochastic variables. Y₀ and Y₁ are always 1. Y₀ = 1 indicates the first way of recalling one of the items. For example, it corresponds to the first way of Figure 1(a). In case of Y₂, one item has yet not been recalled, but it is recalled the k^th time with a geometric probability of

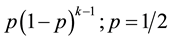
for k = 1, 2, …. The expected distribution is 1/p. Therefore, E(Y₂) = 2. Since Y_m’s are mutually independent random variables,

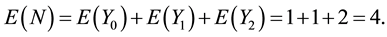
This equation is transformed into

When Y₂ = y₂, the probability of N; P(N: Y₂ = y₂), is expressed as

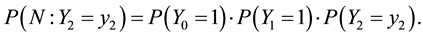
P(Y₀ =1) and P(Y₁ = 1) are always 1.

Therefore,

As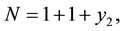

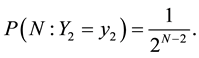
Hence,

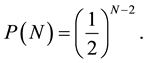
In the case of n = 4, a subject wants to recall four items, A₁, A₂, A₃, A₄.

Set N as follows:

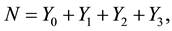
where Y_i is the number of ways required for recalling one more item when i items have already been recalled. Therefore, Y_i’s are mutually independent random variables. Y₀ and Y₁ are always 1. In the case of Y₂, two items have not yet been recalled, so one of these two items is recalled the k^th time with a geometric probability of

for k = 1, 2, …. Similarly, has a geometric probability function with p = 1/3. The expected distribution of a geometric probability function is 1/p. Therefore, E(Y₂) = 3/2 and E(Y₃) = 3. Since Y_i’s are mutually independent random variables,

This equation is transformed into

Therefore, the expression for a general number, n, of items is:

This can be easily proven.

When Y₂ = y₂ and Y₃ = y₃, the probability of N; P(N: Y₂ = y₂, Y₃ =y₃), is expressed as

P(Y₀ = 1) and P(Y₁ = 1) are always 1.

Therefore,

As

Hence,

In the case of n = 5,

For a general number, n (≥3), of items,

The equation is proved (Appendix). Specifically, in the case of n = 2, E(N) = 2 with a probability of 1; in the

case of n = 3, E(N) = 4, and the cumulative probability that N is smaller than or equal to E(N), ,

is 0.75; in the case of n = 4, E(N) = 13/2 and.

In the case of n = 5, which corresponds to one of Miller’s magical numbers, , E(N) = 28/3 ? 10 and in case of n = 9, which corresponds to the other of Miller’s magical numbers, , E(N) = 796/35 ? 23. In the case of n = 10, E(N) = 7409/280 ? 27. Clearly, as n increases, E(N) increases exponentially (Figure 2(a)). Hence, the greater the number, n, of items, the greater the difficulty to recall all items. Although the

cumulative probability of decreases steadily, it is larger than 0.5 until n = 40 (Figure 2(b)).

3.2. Procedure 2

Items are chunked in order into groups with all groups containing the same number of items. The number of all items is denoted as n, and the number of items in each group is denoted as m. For an example of m = 3, the groups are (A₁, A₂, A₃), (A₄, A₅, A₆), (A₇, A₈, A₉), … (A_n−2, A_n−1, A_n). These groups are denoted in order as B₁, B₂, B₃, … (Figure 1(b)). Similar to Procedure 1, there is equal probability to recall any B_j except B_i immediately after B_i. When any B_j is recalled for the first time, all items in B_j are recalled at least once, so it is assumed that the relationship among the items in B_j has already been confirmed. Hence, all visits within B_j are saved from the second visit of B_j onwards. When all B_i’s are recalled, it means that all A_i’s are recalled, confirming the relationship among all A_i’s.

The number of B_i’s is, which is replaced by the nearest integer above, , if is not an integer.

The expected number, E(N_n,m), of ways required until all A_i’s are recalled can be calculated. For the example of n = 12 and m = 3, a subject wants to recall 12 items, A₁, A₂, A₃, … ,A₁₂. Then, B₁ = (A₁, A₂, A₃), B₂ = (A₄, A₅, A₆), B₃ = (A₇, A₈, A₉), and B₄ = (A₁₀, A₁₁, A₁₂).

Set N_12,3 as follows:

where Z_i is the number of ways required for recalling one more group when i groups have been recalled, and Y_j is the number of ways required for recalling one more item of any group when j items of this group have been recalled. Therefore, Z_i’s and Y_j’s are mutually independent random variables. Z₀, Z₁, and Y₁ are always 1. Specifically, Z₀ = 1 indicates the first way going to one of the groups. For example, it corresponds to the first way of Figure 1(b). Hence,

Using the case of four items in Procedure 1, we can regard the four groups in Procedure 2 as four items,

Using the case of three items from Procedure 1,

Hence,

As another practical example, the expected number of ways required to recall 16 digits, E(N_16,4), corresponding to a credit card account number, XXXX-XXXX-XXXX-XXXX, can be calculated.

Using the case of four items in Procedure 1 and regarding the four groups as four items,

Using the case of four items in Procedure 1,

Hence,

Generally,

Then, if is an integer, , otherwise stands for the nearest integer above. E(N_n,m) ca-

nonly be calculated precisely when n is a multiple of m. However, even if n is not a multiple of m, E(N_n,m) is calculated to observe the relationship between m and E(N_n,m). This calculation will be justified when n is larger than m, for example and. When, E(N_n,m) is calculated only when n is a multiple of m. E(N_n,m) is calculated for n = 10, 11, …, 100, and m = 1, 2, …, 10. Figure 3 shows the results for n = 20, 30, 40, …, 100 and m = 1, 2, …, 10. When m = 3 and 4, E(N_n,m) is the smallest and the second smallest for any. When m = 2 or 5, E(N_n,m) is the third smallest. It is interesting to note that the case of m = 1 corresponds to any case without chunking from Procedure 1.

3.3. Procedure 3

The expected number E(N_n,*) of ways required until all A_i’s are recalled can be calculated in the same manner as Procedure 2 for special cases of items chunked into groups of different lengths. When lengths of chunked groups, m = 2, 3, or 4, E(N_n,m) is the smallest. All integers are expressed by a sum of 2’s, 3’s, and 4’s. For example, Hence, items of any length can be chunked into groups, the lengths of which are 2, 3, or 4.

The 11-digit phone number 090-XXXX-XXXX is chunked into three groups, B₁, B₂, B₃, one of which consists of three digits, B₁ = (A₁, A₂, A₃), and two of which consist of four digits, B₂ = (A₄, A₅, A₆, A₇), B₃ = (A₈, A₉, A₁₀, A₁₁).

Hence,

The 10-digit phone number 0120-XXX-XXX is chunked into three groups, B₁, B₂, B₃, one of which consists of four digits, B₁ = (A₁, A₂, A₃, A₄), and two of which consist of three digits, B₂ = (A₅, A₆, A₇), B₃ = (A₈, A₉, A₁₀).

Hence,

A 10-digit phone number of 03-XXXX-XXXX (for example, in Tokyo) is chunked into three groups, B₁, B₂, B₃, one of which consists of two digits, B₁ = (A₁, A₂), and two of which consist of four digits, B₂ = (A₃, A₄, A₅, A₆), B₃ = (A₇, A₈, A₉, A₁₀).

Hence,

4. Discussion

4.1. Findings Obtained from the Mathematical Model

4.1.1. Without chunking

As the number of the items, n, increases, the expected number, E(N), of ways required until all items are recalled

increases exponentially. The cumulative probability that N is smaller than or equal to E(N), P(N ≤ E(N)), decreases steadily. Hence, the greater the number, n, of items, the greater the difficulty to recall all items. In the case of five items, which corresponds to one of Miller’s magical numbers (7 − 2 = 5), E(N) = 28/3 ? 10, and in the case of nine items, which corresponds to the other of Miller’s magical numbers (7 + 2 = 9), E(N) = 796/35 ? 23. In the case of n = 10, E(N) = 7409/280 ? 27.

4.1.2. With chunking

E(N_n,m) is the expected number of ways required until all items are recalled. Hence, a smaller value for E(N_n,m) indicates more efficient recall. For example, the expected number of ways required until 12 items chunked into three groups are recalled, E(N_12,3), is 37/2 ? 19. In the case of a 16-digit credit card number, XXXX-XXXX- XXXX-XXXX, E(N_16,4) = 57/2 ? 29. From the results for n = 10, 11, …, 100, and m = 1, 2, …, 10, E(N_n,m) is the smallest for any n (10 ≤ n ≤ 100), when m = 3 or 4. Hence, when m = 3 or 4, all items can be recalled most quickly.

4.1.3. Special cases of items chunked into groups of different lengths

The expected number of ways required to recall all 11 digits (e.g., in the phone number 090-XXXX-XXXX), E(N_11,*), is 18. For a 10-digit phone number in the format 0120-XXX-XXX, E(N_10,*) = 31/2 ? 16. For a 10-digit phone number in the format 03-XXXX-XXXX, E(N_10,*) = 16.

4.2. Interpretation of the findings

4.2.1. Without chunking

Short-term memory lasts from several seconds to several minutes. Based on the current data, we conclude that an individual can follow the 23 ways required to recall nine items within several minutes, but it takes longer to follow the 27 ways required to recall 10 items, so some one of the items are forgotten. These results suggest that 23 ways may be the critical number, beyond which some items will be forgotten.

4.2.2. With chunking

A smaller number of E(N_n,m) indicates more efficient recall. From the results for n = 10, 11, …, 100, and m = 1, 2, …, 10, E(N_n,m) is the smallest for any n, (10 ≤ n ≤ 100) when m = 3 or 4. Each group has 3 or 4 items (m = 3 or 4) without chunking. From Procedure 1, P(N ≤ E(N)) is 0.75 in the case of three items, and P(N ≤ E(N)) is 0.7407 in the case of four items. P(N ≤ E(N)) decreases steadily with more items. Hence, when m = 3 or 4, all items of each group can be recalled most quickly and with the greatest confidence. E(N₁₂,₃) = 37/2 ? 19 is less than 23, the critical number for recall. Hence, chunking will be effective: B₁ = (A₁, A₂, A₃), B₂ = (A₄, A₅, A₆), B₃ = (A₇, A₈, A₉), B₄ = (A₁₀, A₁₁, A₁₂). However, for 16 digits, such as in a credit card number, XXXX-XXXX- XXXX-XXXX, E(N_16,4) = 57/2 ? 29, which is larger than the critical number for recall. Thus chunking will not benefit short-term memory recall of a 16-digit credit card number. Based on these findings, a 16-digit credit card number of XXXX-XXXX-XXXX-XXXX should have greater security than a 12-digit number of XXX-XXX- XXX-XXX.

4.2.3. Special cases of items chunked into groups of different sizes

The expected numbers, E(N), of ways for 090-XXXX-XXXX, 0120-XXX-XXX, and 03-XXXX-XXXX, are less than 23, the critical number for recall. Hence, chunking into groups of two to four items is truly effective for recalling 11 or 10-digit phone numbers.

4.3. Study Limitations

The current findings were obtained using a model based on certain assumptions. The validity of these assumptions should be investigated in the future.

5. Conclusion

We use probability theory to predict that the most effective chunking involves groups of three or four items, such as in phone numbers, and conclude that an individual can follow the 23 ways required to recall nine items within several minutes, but it takes longer to follow the 27 ways required to recall 10 items, so some of the items are forgotten. These results suggest that 23 ways may be the critical number, beyond which some items will be forgotten. A 16-digit credit card number exceeds the capacity of short-term memory, even when chunked into groups of four digits, such as XXXX-XXXX-XXXX-XXXX. Based on these data, 16-digit credit card numbers should be sufficient for security purposes.

References

Appendix

The equation,

,

for a general number, n (≥3), of items, represents the probability, P(N), that all A_i’s are not visited until the N-th way W (A_j→A_i). Then A_i is visited lastly and only once. This equation is proved below.

Proof: Let see Figure 1(a). Then, A₁ is visited first, A₂ is visited second, and thereafter these may be visited several times. It is assumed that the first visit is A₁andthe second visit is A₂ without loss of generality. It is assumed that the last visit is A_i (i = 3, 4, …,n). When the present visit is A_j (j ≠ i), the probability that A_i is visited is

and A_i is one of A₃, A₄, …, A_n except A_j (j ≠ i). The probability that the items except A_i are visited totally

N ? 3 times is Hence, the probability C(0) that the items except A_i are visited totally N ? 3

times and A_i is visited lastly is

However, some events that at least k (1 ≤ k ≤ n ? 3) items except A₁, A₂, and A_i are not visited should be excluded. This probability C(k) is

Moreover, some events that at least m (≤ n ? 3 ? k) items except A₁, A₂, A_i, and those excluded k items are not visited should be excluded. This probability C(k, m) is

D(0) is defined as C(0). D(k), (1 ≤ k ≤ n ? 3), is defined as D(k ? 1) + (?1)^k C(k). D(p, p), (0 ≤ p ≤ n ? 3), is defined as the probability that at least p items except A₁, A₂, and A_i are not visited within D(p).

1) Since D(1) is also defined as D(0) ? C(1), D(1,1) = 0.

2) D(2) is also defined as D(0) ? C(1) + C(2).

.

3) D(k) = D(k?1)+ (?1)^kC(k): 1 ≤ k ≤ n?3.

Hence, D(k, k) = 0 (1 ≤ k ≤ n ? 3). Hence, the probability that at least q, (1 ≤ q ≤ n ? 3), items except A₁, A₂, and A_i are not visited within D(k) is equal to 0. In other words, D(n ? 3) represents the probability that all items except A_i are visited totally N ? 1 times and A_i is visited lastly.

The equation has been proved.