Received 15 April 2014; revised 25 May 2014; accepted 6 June 2014

ABSTRACT

In this paper, a hybrid dividend strategy in the compound Poisson risk model is considered. In the absence of dividends, the surplus of an insurance company is modelled by a compound Poisson process. Dividends are paid at a constant rate whenever the modified surplus is in a interval; the premium income no longer goes into the surplus but is paid out as dividends whenever the modified surplus exceeds the upper bound of the interval, otherwise no dividends are paid. Integro- differential equations with boundary conditions satisfied by the expected total discounted dividends until ruin are derived; for example, closed-form solutions are given when claims are exponentially distributed. Accordingly, the moments and moment-generating functions of total discounted dividends until ruin are considered. Finally, the Gerber-Shiu function and Laplace transform of the ruin time are discussed.

Keywords:

Hybrid Dividend Strategy, Compound Poisson Risk Model, Moment-Generating Function, Gerber-Shiu Function

1. Introduction

The dividends problem was first proposed by Finetti [1] , who considered a discrete time risk model and found that the optimal dividend strategy is a barrier strategy, that is, any surplus above a certain level would be paid as dividend. Nowadays, this problem still attracts a lot of research interest. For example, [2] [3] considered the compound Poisson risk model. [4] studied the continuous counterpart of Finetti [1] , and it is assumed that the surplus is a Brownian motion with a positive drift. Jeanblanc-Picque and Shiryaev [5] and Asmussen and Taksar [6] postulated a modified version of barrier strategy called threshold strategy, that is, dividends are paid at a constant rate whenever the surplus is above a threshold level; however, when the surplus is below the threshold level, no dividends are paid. Some calculations for the classical risk model and Brownian motion model are given in [7] [8] . For recent publications on this topic, see, for example, [9] -[14] .

Recently, the multi-layer dividend strategy as an extension of the threshold dividend strategy has drawn many authors’ attention. Under such a dividend strategy, premiums will be collected at different rates whenever the surplus is in different layers. The modified surplus process is obtained from the original surplus process by refraction at each threshold level. Within this framework, many authors have studied the Gerber-Shiu expected discounted penalty function, see, for instance, [15] -[17] and the references therein.

Under such framework, Ng [18] combined barrier strategy and threshold strategy for the first time and then proposed a hybrid dividend strategy, who considered a dual risk model with phase-type gains under a hybrid dividend strategy and derived the explicit formula for the expected total discounted dividends until ruin and the Laplace transform of the time of ruin. In this paper, we consider the hybrid dividend strategy for the classical risk model. Let 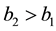be two positive constants, under a hybrid strategy, no dividends are paid whenever the modified surplus is below the level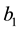; dividends are paid at a constant rate whenever the modified surplus is in interval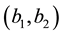; the premium income no longer goes into the surplus but is paid out as dividends whenever the modified surplus exceeds the level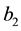. The modified surplus is obtained from the original surplus process by refraction at the level 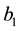and reflection at the level. The hybrid dividend strategy introduced above is a generalization of a pure barrier strategy and a pure threshold strategy. Apparently the hybrid strategy is more realistic than a pure barrier strategy, because it is inflexible for companies to use a switching mechanism of either paying nothing or paying all excess surplus as dividends. In the meantime, it is more practical than a pure threshold, because it is the ideal for a surplus of a company to be allowed to grow infinitely.

The rest of the paper is organized as follows. In Section 2, we find the integro-differential equations and boundary conditions for the expected discounted dividend payments until ruin. The integro-differential equations with boundary conditions satisfied by the moments and the moment-generating function are given in Section 3. Section 4 discussed the integro-differential equations with boundary conditions for the Gerber-Shiu function, and Section 5 presents the integro-differential equations with boundary conditions satisfied by the Laplace transform of ruin time.

2. The Model

We consider the compound Poisson model of risk theory with initial surplus. In the absence of dividends, the surplus process 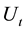at time t is given by

where 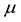is the premium rate, and representing the aggregate claims up to time t, is a Poisson process with intensity, and independent of, are positive i.i.d. random variables with distribution function and density function.

Unlike the dividend strategies in [4] [8] , we assume the company will pay dividends to its shareholders according to a hybrid dividend strategy with parameters. The dividends consists of two parts. The first part of dividends are paid at a constant rate whenever the modified surplus between the level and the level. The second part, whenever the modified surplus reaches the level, the overflow will be paid as dividends. For, let denote the aggregate dividends paid by time t, where and caused by the two parts of dividends, respectively. Thus

(2.1)

is the company’s modified surplus at time t.

Let T be the ruin time of, namely

and let be the force of interest for valuation, we denote

We use the symbols to denote the expectations of, i.e.

Define the moment-generating function of D by

and kth moment by

with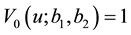, and the Gerber-Shiu functions by

(2.2)

where is the surplus immediately before ruin, is the deficit at ruin and the penalty is a nonnegative bounded measurable function of, and the Laplace transform of ruin time by

(2.3)

3. Expected Discounted Dividend Payments

In this section, we consider the hybrid dividend strategy for dividend payments in a compound Poisson risk model. We write

Then, we have

In the following, we first derive the integro-differential equations and boundary conditions satisfied by and.

Theorem 3.1 Assume that is continuously differentiable in u on. Then, satisfies the following integro-differential equations, when,

(3.1)

and, when,

(3.2)

with boundary conditions

(3.3)

(3.4)

(3.5)

Proof. When, consider such that the modified surplus can not reach level by time t, i.e.. In view of the strong Markov property of the surplus process, we have

(3.6)

where is the shift operator. By conditioning on the time and amount of the first claim and whether the claim causes ruin or not, and using (3.6), we get

(3.7)

By Taylor’s expansion,

Substituting the above expressions into (3.7), and dividing both sides of (3.7) by t and letting, we can get (3.1).

When, we still consider a small time interval, with being sufficiently small so that the modified surplus will not reach in the time interval. In view of the strong Markov property of the surplus process, we have

(3.8)

By conditioning on the time and amount of the first claim and whether the claim causes ruin or not, and using (3.8), we get

(3.9)

By Taylor’s expansion,

Substituting the above expressions into (3.9), and dividing both sides of (3.9) by t and letting, we can get (3.2).

Next we prove the condition (3.3). It follows from

let, we have

Similarly,

let, we obtain

So we get (3.3).

Furthermore, when the initial surplus is, we can mimic the derivation of (3.9) to obtain

(3.10)

Dividing both sides of (3.10) by t and letting, we can obtain

(3.11)

Letting in (3.2) and comparing it to (3.11), we obtain

When, we have

thus,

So we get (3.4).

Finally, letting in (3.1) and in (3.2), we can get (3.5). This completes the proof of Theorem 3.1.

Remark 3.1 Letting in Theorem 3.1, then (3.1) and (3.2) reduce, respectively, to (5.1) and (5.2) of [7] .

Theorem 3.2 Assume that is continuously differentiable in u on. Then, satisfies the following integro-differential equations, when,

(3.12)

and, when,

(3.13)

with boundary conditions

(3.14)

(3.15)

(3.16)

Proof. In view of the strong Markov property of the surplus process, we have

(3.17)

When, we consider a small time interval, with being sufficiently small so that the modified surplus will not reach in the interval. By conditioning on the time and amount of the first claim and whether the claim causes ruin or not, and using (3.17), we get

(3.18)

By Taylor’s expansion,

Substituting the above expression into (3.18), and dividing both sides of (3.18) by t and letting, we can get (12).

When, we still consider a small time interval, with being sufficiently small so that the modified surplus will not reach in the interval. Similar to the derivation of (3.12), we can obtain Equation (3.13).

The condition (3.14) can be obtained similar to (3.3).

When the initial surplus is, we have

(3.19)

Dividing both sides of (3.19) by t and letting, we can obtain

(3.20)

Letting in (3.13) and comparing it to (3.20), we obtain

When, we have

thus,

So we get (3.15).

Finally, letting in (3.12) and in (3.13), we can get (3.16). This completes the proof of Theorem 3.2.

According to the definition of, from Theorems 3.1 and 3.2, we can lead to the integro-differential equations and the boundary conditions satisfied by.

Theorem 3.3 Assume that is continuously differentiable in u on. Then, satisfies the following integro-differential equations, when,

(3.21)

and, when,

(3.22)

with boundary conditions

(3.23)

(3.24)

(3.25)

Example 3.1. Now we assume that the individual claim amounts are exponentially distributed with mean, i.e.

Then, we have

(3.26)

Applying the operator on (3.21) and (3.22) respectively, and using (3.26) and rearranging them, we get

(3.27)

for, and for

(3.28)

We can obtain the solutions of Equation (3.27) as follows

(3.29)

with the coefficients A and B being independent of u, and r and s being the roots of the characteristic equation

We let r denote the positive root and s the negative root, i.e.

Substituting (3.29) in Equation (3.21) and equating the coefficient of with 0, we have

(3.30)

From (3.29) and (3.30), we can rewrite

(3.31)

where dose not depend on. A particular solution of (3.28) is. Hence, the solutions of Equation (3.28) are given by

(3.32)

where the coefficients C and G are independent of u, and and are the roots of the characteristic equation

namely,

From (3.31) and (3.32), we observe that the convolution integral in Equation (3.22) is

By setting the coefficient of to 0, we have

(3.33)

From (23) and (24), we have the conditions

(3.34)

and

(3.35)

It follows from (33) and (34) that

(3.36)

(3.37)

Substitution of (3.36) and (3.37) into (3.35), thus we get the closed-form solution of as follows,

(3.38)

where

(3.39)

We can get C and G by substituting into (3.36) and (3.37).

Hence

(3.40)

and

(3.41)

Remark 3.2 Let us compare our results with known results.

1) When, the hybrid dividend becomes a barrier dividend strategy, the condition (3.25) is the same as (3.24), from (3.31) and (3.24), we have

which agrees with formula (7.8) in [2] .

2) Letting, the hybrid dividend strategy becomes a threshold dividend strategy, we get

(3.42)

From (3.36), (3.37) and (3.42), we have

(3.43)

(3.44)

It follows from (3.40) to (3.44) that

and

which are (6.14) and (6.15) in [7] .

4. The Moment-Generating Function

In this section, we study the moment-generating function which has been discussed in various models, for example, see [8] [19] . We can analyze the moments of D through. Since has different paths for and, we define

We first derive the integro-differential equations and boundary conditions for.

Theorem 4.1 Assume that is continuously differentiable in u on and in. Then, satisfies the following integro-differential equations, when,

(4.1)

and, when,

(4.2)

with boundary conditions

(4.3)

(4.4)

(4.5)

Proof. In view of the strong Markov property of the surplus process, we have

(4.6)

when, consider being sufficiently small so that the modified surplus can not reach level by time. By conditioning on the time and amount of the first claim and whether the claim causes ruin or not, and using (4.6), we get

(4.7)

By Taylor’s expansion,

Substituting the above expression into (4.7), and dividing both sides of (4.7) by and letting, we can get (4.1).

When, we still consider a small time interval, with being sufficiently small so that the modified surplus will not reach in the interval. In view of the strong Markov property of the surplus process, we have

(4.8)

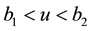
By conditioning on the time and amount of the first claim and whether the claim causes ruin or not, and using (4.8), we yield

(4.9)

Since

using the similar arguments as above, we get (4.2) from (4.9).

Next we prove the condition (4.3). For, let, and is the time that the modified surplus reaches for the first time from with no claims, i.e.. Then is a stopping time, and by the strong Markov property, we have

(4.10)

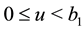
On the other hand, we have

(4.11)

where is the first time that the claim happens. When, and both go into zero, and , letting in (4.10) and (4.11), we obtain

When, we consider an infinitesimal time interval, then

From this formula we get

and

Let, we obtain

So we obtain (4.3).

Furthermore, when the initial surplus is, we can mimic the derivation of (4.9) to obtain

(4.12)

Using

Substituting the above expression into (4.12), and dividing both sides of (4.12) by and letting, we can obtain

(4.13)

Letting in (4.2) and comparing it to (4.13), we obtain

Finally, letting in (4.1) and in (4.2), we can get (4.5). This completes the proof of Theorem 4.1.

Remark 4.1 1) In the case of, (4.1) is corresponding to (3.1) of [20] by letting, and substitute c there.

2) In the case of, (4.1) and (4.2) are corresponding to (2.10) and (2.11) of [21] by letting, and substitute c there.

By the definitions of and, we obtain

(4.14)

We denote

Substituting (4.14) into (4.1) and (4.2) respectively and comparing the coefficients of yields the following integro-differential equations and corresponding boundary conditions.

Theorem 4.2 For each, we assume that is continuously differentiable in u on . Then, satisfies the following integro-differential equations:

and

with boundary conditions

(4.15)

Remark 4.2 Letting, we have, Theorem 3.3 can be reduced by Theorem 4.2. From (4.15).

is an obvious result since.

5. The Gerber-Shiu Functions

In the following we will discuss the famous Gerber-Shiu expected discounted penalty function. We also write

By a similar derivation to Theorem 4.1, we get the integro-differential equations and boundary conditions for.

Theorem 5.1 Assume that is continuously differentiable in on. Then, satisfies the following integro-differential equations, when,

(5.1)

and, when,

(5.2)

where and with boundary conditions

(5.3)

(5.4)

(5.5)

Proof. We can mimic the derivation of (4.1), (4.2), (4.3) and (4.5) to obtain (5.1), (5.2), (5.3) and (5.5).

Next we prove the condition (5.4). In view of the strong Markov property of the surplus process, we have

(5.6)

When the initial surplus is,

dividing t on both sides of the above expression, letting, we can obtain

(5.7)

Letting in (5.2) and comparing it to (5.7), we obtain

When, we have

thus,

So we get (5.4).

This completes the proof of Theorem 5.1.

Remark 5.1 1) In the case of, (5.1) is corresponding to (2.6) of [3] by letting substitute.

2) Letting, (5.1) and (5.2) are corresponding to (3.1) of [9] by letting substitute.

6. Explicit Expressions of the Laplace Transform of Ruin Time

In this section, we give the closed form expression for the Laplace transform of ruin time when claim size has exponential distribution with mean, i.e.. We also write

By setting in (5.1) and (5.2) and letting substitute, we obtain the integro-differential equations and the boundary conditions satisfied by from Theorem 5.1.

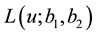
Theorem 6.1 satisfies the following integro-differential equations, when,

(6.1)

and, when,

(6.2)

with boundary conditions

(6.3)

(6.4)

(6.5)

Remark 6.1 In the case of, (6.1) and (6.2) are corresponding to equations (10.2) and (10.3) in [7] .

Applying to (6.1) and (6.2) in the case of respectively, and using (3.26) and rearranging them, we have that for

(6.6)

and for

(6.7)

We can obtain the solutions of Equation (6.6) and (6.7) as follows

(6.8)

(6.9)

with the coefficients, , and being independent of, and, , and are the same as in Example 3.1. Substituting (5.8) in Equation (5.1) and equating the coefficient of with 0, we have

(6.10)

Substitute (5.8) and (5.9) in Equation (5.2) and equating the coefficient of with 0, we have

(6.11)

From (5.3) and (5.4), we have the conditions

(6.12)

and

(6.13)

It follows from (6.11) and (6.12) that

(6.14)

(6.15)

and from (6.13), we get

(6.16)

Substituting (6.14), (6.15) into (6.10) and then using (6.16), the constants and can be given by

(6.17)

(6.18)

where

(6.19)

Substituting (6.17) and (6.18) into (6.14) and (6.15), the constants and can be given by

(6.20)

(6.21)

From (6.17)-(6.21), we have

(6.22)

(6.23)

Remark 6.2 Letting, from (6.17) to (6.21), we have

Thus,

which are (10.17) and (10.19) of [7] .

Acknowledgements

The authors are grateful to the anonymous referee’s careful reading and detailed helpful comments and constructive suggestions, which have led to a significant improvement of the paper. The research was supported by the National Natural Science Foundation of China (No. 11171179), the Research Fund for the Doctoral Program of Higher Education of China (No. 20133705110002) and the Program for Scientific Research Innovation Team in Colleges and Universities of Shandong Province.

References

NOTES

^*Corresponding author.