Applied Mathematics
Vol.5 No.15(2014), Article
ID:48642,7
pages
DOI:10.4236/am.2014.515220
Countably Many Positive Solutions for Nonlinear Singular n-Point Boundary Value Problems
Zhenguo Li, Youlin Shang*
Department of Mathematics and Statistics, Henan University of Science and Technology, Luoyang, China
Email: *mathshang@sina.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()


Received 18 May 2014; revised 22 June 2014; accepted 5 July 2014
ABSTRACT
In this paper, a fixed-point theorem has been used to investigate the existence of countable positive solutions of n-point boundary value problem. As an application, we also give an example to demonstrate our results.
Keywords:Boundary Value Problem, Existence of Positive Solutions, Fixed-Point Theorem

1. Introduction
The multi-point boundary value problems arising from applied mathematics and physics have received a great deal of attention in the literature (for instance, [1] -[4] and references therein). But, by so far, few results are about the existence of more than five solutions. To the author’s knowledge, there are very few papers concerned with the existence of countable positive solutions for multiple point BVPS (for instance, [5] and references therein). In [5] , the authors discussed the existence of countable positive solutions of n-point boundary value problems for a p-Laplace operator on the half-line. Directly inspired by [5] , in this paper, by using a fixed-point theorem, we study the existence of countable positive solutions of the following n-point boundary value problems.
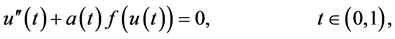 (1.1)
(1.1)
 (1.2)
(1.2)
where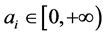 ,
, 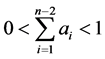 ,
, 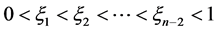 ,
, .
. 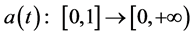 and
and 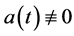 has countable many singularities in
has countable many singularities in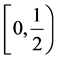 .
.
This kind of problem arises in the study of a number of chemotherapy, population dynamics, ecology, industrial robotics and physics phenomena. Moreover, many problems in optimal control system, neural network (for example in BAM neural network) and information systems for computational science and engineering (especially in Internet-based computing) can be established as differential equation models with boundary condition (see, for instance, [6] and references therein).
At the end of this section, we state some definitions and lemmas which will be used in Section 2 and Section 3.
Definition 1.1 A map ![]() is said to be a nonnegative, continuous, concave function on a cone
is said to be a nonnegative, continuous, concave function on a cone 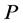 of a real Banach space
of a real Banach space , if
, if 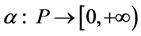 is continuous, and
is continuous, and
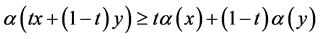
for all  and
and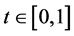 .
.
Definition 1.2 Given a nonnegative continuous function 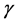 on a cone
on a cone , for each
, for each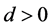 , we define the set
, we define the set 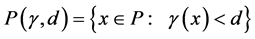
Lemma 1.1 [7] Let 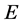 be a Banach space and
be a Banach space and 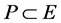 be a cone in
be a cone in . Let
. Let , be three increasing, nonnegative and continuous functions on
, be three increasing, nonnegative and continuous functions on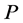 , satisfying for some
, satisfying for some 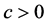 and
and 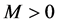 such that
such that
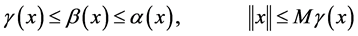
for all . Suppose that there exists a completely continuous operator
. Suppose that there exists a completely continuous operator 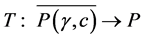 and
and 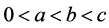 such that 1)
such that 1)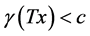 , for
, for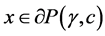 .
.
2)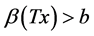 , for
, for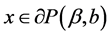 .
.
3)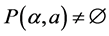 , and
, and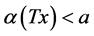 , for
, for .
.
Then ![]() has at least three fixed points
has at least three fixed points 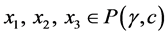 such that
such that
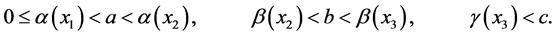
This paper is organized as follows: The preliminary lemmas are in Section 2. The main results are given in Section 3. Finally, in Section 4, we give an example to demonstrate our results.
2. The Preliminary Lemmas
In this paper, we will use the following space 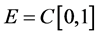 and
and 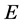 is a Banach space with the norm
is a Banach space with the norm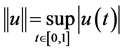 . Let
. Let , we define a cone
, we define a cone 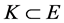 by
by
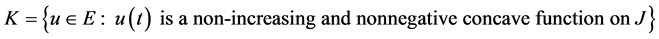 .
.
For convenience, let us list some conditions.
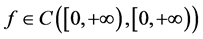
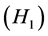 and on any subinterval of
and on any subinterval of ![]() and when
and when ![]() is bounded,
is bounded, 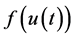 is bounded on
is bounded on![]() .
.
 There exists a sequence
There exists a sequence  such that
such that ,
, 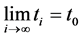 ,
,  ,
,  , and
, and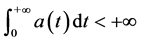 .
.
Lemma 2.1. Let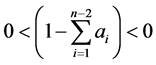 ,
, 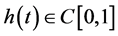 and
and 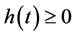 on
on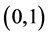 , then the boundary value problem
, then the boundary value problem
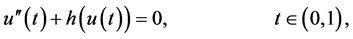 (2.1)
(2.1)
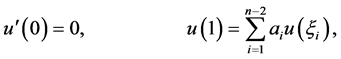 (2.2)
(2.2)
has a unique solution
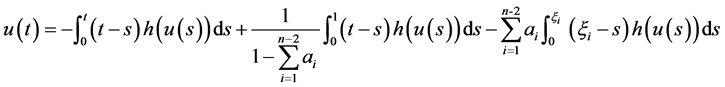
Proof. The proof is easy, so we omit it.
By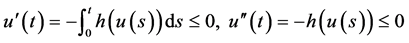 , we know
, we know  is decreasing and concave on
is decreasing and concave on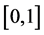 . Then we have
. Then we have
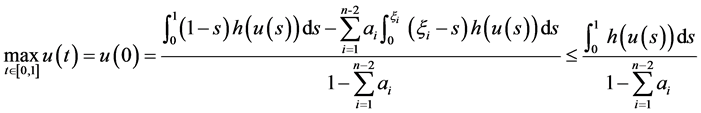 (2.3)
(2.3)
 (2.4)
(2.4)
From (2.3), (2.4) and the concavity of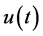 , we can easily get the following lemma.
, we can easily get the following lemma.
Lemma 2.2. Let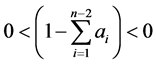 , if
, if 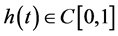 and
and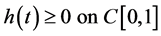 , then the unique solution
, then the unique solution 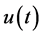 of (2.1)-(2.2) satisfies
of (2.1)-(2.2) satisfies 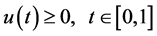 and
and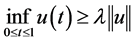 , where
, where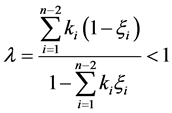 .
.
For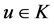 , we define an operator
, we define an operator 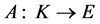 by
by
 (2.5)
(2.5)
For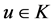 , then
, then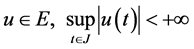 , by
, by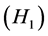 , we know
, we know 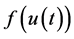 is bounded on
is bounded on![]() .
.
So there exists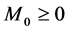 , such that
, such that
 . (2.6)
. (2.6)
It is easy to see that 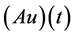 is decreasing and concave on
is decreasing and concave on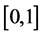 . Then for
. Then for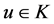 , we have
, we have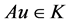 , that is
, that is
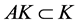 . (2.7)
. (2.7)
From , (2.3) and (2.6), we have
, (2.3) and (2.6), we have
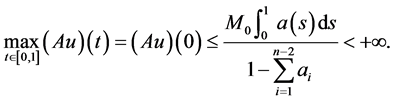 (2.8)
(2.8)
From (2.7), (2.8), we can get the following lemma.
Lemma 2.3. Suppose 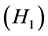 and
and 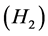 are satisfied. Then
are satisfied. Then 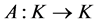 is bounded.
is bounded.
Lemma 2.4. Assume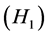 ,
,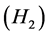 are satisfied, then
are satisfied, then 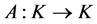 is completely continuous.
is completely continuous.
Proof. From Lemma 2.2, we know  is bounded. If
is bounded. If 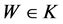 is a bounded subset of
is a bounded subset of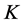 , then
, then 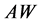 is uniformly bounded on
is uniformly bounded on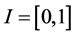 .
.
For any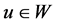 ,
,  , without loss generality, we may assume
, without loss generality, we may assume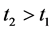 , by (2.5), (2.6),
, by (2.5), (2.6), 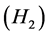 , we have
, we have
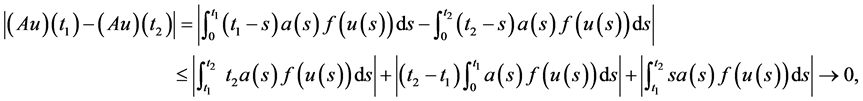
uniformly as .
.
So  is equi-continuous on
is equi-continuous on .
.
At last, by (2.5),  , the Lebesgue dominated convergence theorem and continuity of
, the Lebesgue dominated convergence theorem and continuity of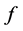 , we know
, we know 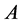 is continuous. Then by the Arzela-Ascoli theorem, we can get that
is continuous. Then by the Arzela-Ascoli theorem, we can get that  is completely continuous.
is completely continuous.
3. Main Results
Let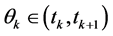 ,
, 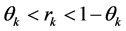 and
and 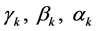 be three nonnegative, decreasing and continuous functions with
be three nonnegative, decreasing and continuous functions with
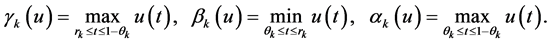
Obviously, for 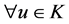 we have
we have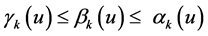 .
.
In the following, we let

Then it is easy to see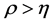 .
.
The main result of this paper is as follows.
Theorem 3.1. Assume that 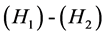 hold. Let
hold. Let 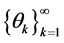 be such that
be such that 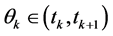
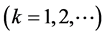 ,
,  be such that
be such that 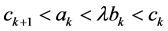 and
and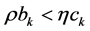
 .
.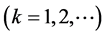 .
.
Furthermore for each natural number 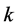 we assume that
we assume that  satisfies:
satisfies:
 for all
for all 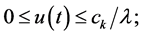
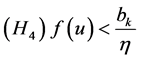 for all
for all 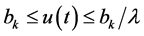
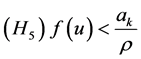 for all
for all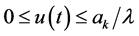 .
.
Then the BVP (1.1)-(1.2) has at least three infinite families of positive solutions
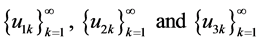 with
with
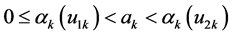 ,
, 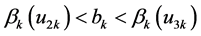 ,
, 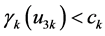 , for
, for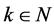 .
.
Proof. From the definition of , (2.7) and Lemma 2.4, it is easy to see that
, (2.7) and Lemma 2.4, it is easy to see that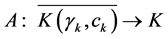 , for
, for 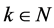 is completely continuous.
is completely continuous.
Next we show all the conditions of Lemma 1.2 hold.
For any , it is easy to see
, it is easy to see . From Lemma 2.2, we have
. From Lemma 2.2, we have
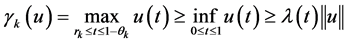 , so
, so 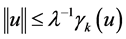 (3.1)
(3.1)
First, we choose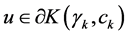 , then we have
, then we have . From
. From 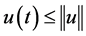 and (3.1), we can get
and (3.1), we can get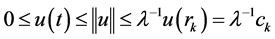 , for
, for . Then with
. Then with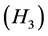 , it implies that
, it implies that , for
, for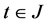 .
.
So 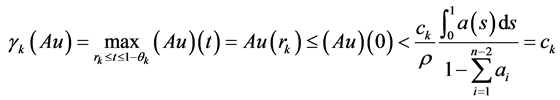
Therefore, the first condition of Lemma 1.2 satisfies.
Next, we select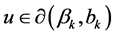 . Then
. Then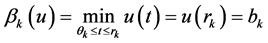 , we have
, we have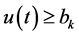 , for
, for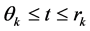 .
.
Again from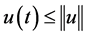 , and Lemma (2.2) we can get that
, and Lemma (2.2) we can get that

Then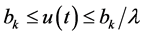 , for
, for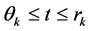 . By
. By , we have
, we have , for
, for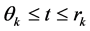 .
.
So, there has
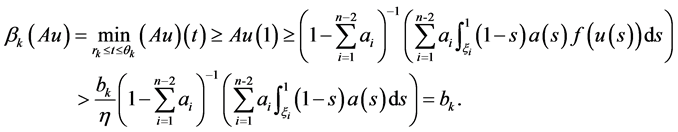
This implies the second condition of Lemma 1.2 is satisfied.
Finally, we only need to show the third condition of Lemma 1.2 is also satisfied.
We select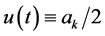 , for
, for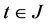 . Obviously,
. Obviously,  , hence
, hence 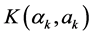 is nonempty.
is nonempty.
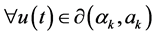 , we have
, we have . Also from
. Also from 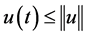 and Lemma (2.4), we can get
and Lemma (2.4), we can get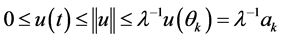 , for
, for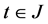 . Then from
. Then from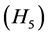 , we have
, we have .
.
So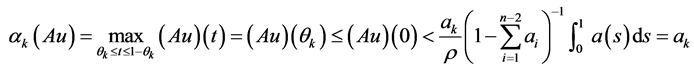 .
.
Then all the conditions of Lemma 1.2 are satisfied. From Lemma 1.2, we get the conclusion in Theorem 3.1.
4. Example
Now we consider an example to illustrate our results.
Example 4.1. Consider the boundary value problem
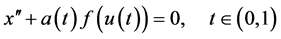 , (4.1)
, (4.1)
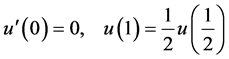 , (4.2)
, (4.2)
Then the BVP (4.1)-(4.2) can be regarded as a BVP of the form (1.1)-(1.2) in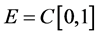 . In this situation,
. In this situation,
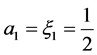 .
.
Let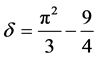 ,
, 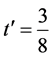 ,
,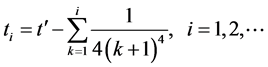 .
.
Consider the function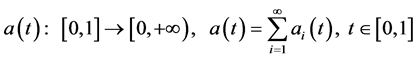 , where
, where
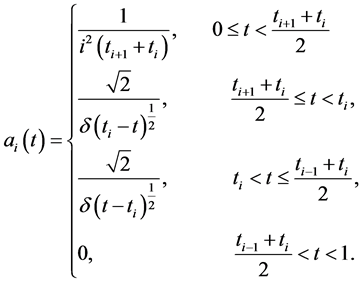

It is easy to know 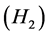 satisfies.
satisfies.
Let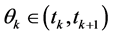 ,
, 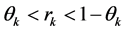 ,
, 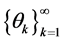 be such that
be such that 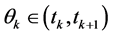
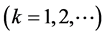 ,
, 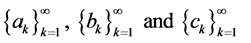 be such that
be such that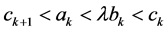 , and
, and 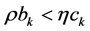
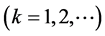 .
.
This with 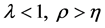 implies that
implies that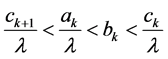 ,
, 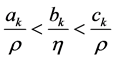 ,
,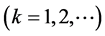 .
.
Let 
Obviously, 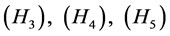 are satisfied, and it is easy to prove that
are satisfied, and it is easy to prove that 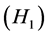 is also satisfied. So all the conditions of Theorem 3.1 are satisfied, thus the BVP (4.1)-(4.2) has at least three infinite families of positive solutions
is also satisfied. So all the conditions of Theorem 3.1 are satisfied, thus the BVP (4.1)-(4.2) has at least three infinite families of positive solutions 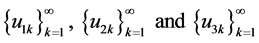 satisfying
satisfying
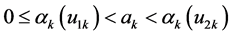 ,
, 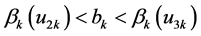 ,
,  , for
, for .
.
References
- Ma, R. (1999) Positive Solutions for a Nonlinear Three-Point Boundary Value Problem. Electronic Journal of Differential Equations, 34, 1-8.
- Liu, B. (2004) Positive Solutions of Nonlinear Four-Point Boundary Value Problem. Applied Mathematics and Computation, 155, 179-203. http://dx.doi.org/10.1016/S0096-3003(03)00770-7
- Chen, S.H., Hu, T., Chen, L., et al. (2005) Existence Results for n-Point Boundary Value Problem of Second Order Ordinary Differential Equations. Journal of Computational and Applied Mathematics, 180, 425-432.http://dx.doi.org/10.1016/j.cam.2004.11.010
- Ma, R. (2001) Existence of Solutions of Nonlinear m-Point Boundary Value Problem. Journal of Mathematical Analysis and Applications, 256, 556-567. http://dx.doi.org/10.1006/jmaa.2000.7320
- Liang, S.H. and Zhang, J.H. (2008) The Existence of Countably Many Positive Solutions for One-Dimensional p-Laplacian with Infinitely Many Singularities on the Half-Line. Applied Mathematics and Computation, 201, 210-220.http://dx.doi.org/10.1016/j.amc.2007.12.016
- Xu, C., He, X. and Li, P. (2011) Global Existence of Periodic Solutions in a Six-Neuron BAM Neural Network Model with Discrete Delays. Neurocomputing, 74, 3257-3267. http://dx.doi.org/10.1016/j.neucom.2011.05.007
- Ren, J., Ge, W. and Ren, X. (2005) Existence of Positive Solutions for Quasi-Linear Boundary Value Problems. Acta Mathematicae Applicatae Sinica, 21, 353-358. (in Chinese) http://dx.doi.org/10.1007/s10255-005-0242-y
NOTES

*Corresponding author.

