Applied Mathematics
Vol.5 No.8(2014), Article ID:45697,6 pages DOI:10.4236/am.2014.58112
The Exp-Function Method for Solving Two Dimensional Sine-Bratu Type Equations
Eslam Moradi1, Hamidreza Varasteh2, Abolfazl Abdollahzadeh3, Mojtaba Mostafaei-Malekshah1
1Faculty of Mathematical Sciences and Computer, Kharazmi University, Tehran, Iran
2Department of Mathematics, Payamenoor University, Tehran, Iran
3Department of Mathematics, Faculty of Mathematical Sciences and Statistics, Birjand University, Birjand, Iran
Email: eslam.moradi@gmail.com, varastehhamid@gmail.com, aboalfazl.zadeh@yahoo.com, m.mostafaei.m@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 January 2014; revised 25 February 2014; accepted 4 March 2014
ABSTRACT
In this paper, we apply Exp-function method to give traveling wave solutions of second order sineBratu type equations. This method is straightforward, concise and effective.
Keywords:Exp-Function Method, Sine-Bratu Type Equation

1. Introduction
Nonlinear differential equations have an important role in the study of nonlinear physical phenomena in science and technology. This paper investigates the exact solutions of nonlinear second order sine-Bratu type equations using the Exp-function method. Recently, several direct methods such as 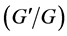 -expansion method [1] -[3] , sine-cosine method [4] [5] , tanh-coth method [6] [7] , He’s homotopy perturbation method [8] [9] , F-expansion method [10] [11] and others have been proposed to obtain exact solutions of nonlinear partial differential equations. Using these methods many exact solutions, including the solitary wave solutions, shock wave solutions and periodic wave solutions are obtained for some kinds of nonlinear evolution equations. The application of Exp-function method to obtain more explicit traveling wave solutions to many nonlinear differential equations has been developed by many researchers [12] -[15] . The Exp-function method is based on the assumption that the travelling wave solutions can be expressed by a polynomial in Exp-function. It has been shown that this method is direct, concise, basic and effective. The solution procedure of this method, by the help of Maple, Matlab, or any mathematical package, is of utter simplicity.
-expansion method [1] -[3] , sine-cosine method [4] [5] , tanh-coth method [6] [7] , He’s homotopy perturbation method [8] [9] , F-expansion method [10] [11] and others have been proposed to obtain exact solutions of nonlinear partial differential equations. Using these methods many exact solutions, including the solitary wave solutions, shock wave solutions and periodic wave solutions are obtained for some kinds of nonlinear evolution equations. The application of Exp-function method to obtain more explicit traveling wave solutions to many nonlinear differential equations has been developed by many researchers [12] -[15] . The Exp-function method is based on the assumption that the travelling wave solutions can be expressed by a polynomial in Exp-function. It has been shown that this method is direct, concise, basic and effective. The solution procedure of this method, by the help of Maple, Matlab, or any mathematical package, is of utter simplicity.
2. Exp-Function Method
We suppose that the given nonlinear differential  to be in the form
to be in the form
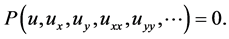 (2.1)
(2.1)
where P is a multivariate polynomial in its arguments. In the following, it is explained the basic for implementing Exp-function method. Taking the change of variable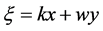 , gives
, gives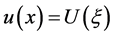 , where k and w are constants parameter to be determined later. Substituting
, where k and w are constants parameter to be determined later. Substituting  into the Equation (2.1) yields an ODEs for
into the Equation (2.1) yields an ODEs for  of the form
of the form
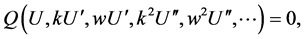 (2.2)
(2.2)
where 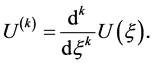 So, if possible, integrate Equation (2.2), term by term one or more times. This introduces one or more constants of integration.
So, if possible, integrate Equation (2.2), term by term one or more times. This introduces one or more constants of integration.
According to this method, we introduce the approach
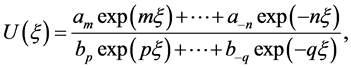 (2.3)
(2.3)
where m, n, p, and q are positive integers, which could be freely chosen,  for
for 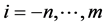 and
and 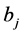 for
for  are unknown constants to be determined. Substituting Equation (2.3) into Equation (2.2) yields an algebraic equation in powers of the Exp-function. Then, to determine the values of m and p, we balance the linear and nonlinear terms of the highest order in the resulting algebraic equation. Similarly, to determine the values of n and q, we balance the linear terms of the lowest order in Equation (2.2) with the lowest order nonlinear terms.
are unknown constants to be determined. Substituting Equation (2.3) into Equation (2.2) yields an algebraic equation in powers of the Exp-function. Then, to determine the values of m and p, we balance the linear and nonlinear terms of the highest order in the resulting algebraic equation. Similarly, to determine the values of n and q, we balance the linear terms of the lowest order in Equation (2.2) with the lowest order nonlinear terms.
3. Application of the Exp-Function Method
Consider the following sine-Bratu type equation
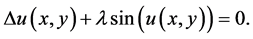 (3.1)
(3.1)
In order to apply the  method, we use the transformation
method, we use the transformation 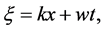 and change Equation (3.1) into the form
and change Equation (3.1) into the form
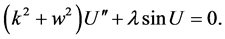 (3.2)
(3.2)
And then we use the transformation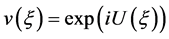 , so that
, so that
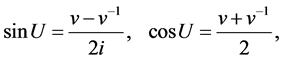
which gives

This transformation will change Equation (3.2) into the ODE in the form
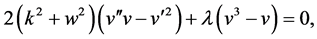 (3.3)
(3.3)
where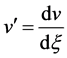 ,
, . Now, we assume that the solution of Equation (3.3) can be expressed in the form shown in Equation (2.3). To determine the constants m and p, we balance
. Now, we assume that the solution of Equation (3.3) can be expressed in the form shown in Equation (2.3). To determine the constants m and p, we balance 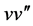 with
with , by simple calculation, we have
, by simple calculation, we have
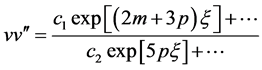 (3.4)
(3.4)
and
 (3.5)
(3.5)
then we get 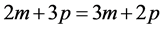 which yields the leading term order
which yields the leading term order![]() . Similarly, we balance the lowest order terms in Equations (3.4) and (3.5), to determine the values of n and q, we obtain
. Similarly, we balance the lowest order terms in Equations (3.4) and (3.5), to determine the values of n and q, we obtain  which leads to the result
which leads to the result![]() .
.
It is possible to choose the difference values of m, n, p and q. It is seen that when the equation has multiple solutions (like solitons) the Exp-function method is able to give us these solutions with the aid of using different m, n, p and q. Although it worth mentioning that different parameters may lead to equivalent solutions.
Case 1:  and
and 
For simplicity, we choose  and
and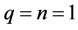 , the trial function, Equation (2.3) becomes as
, the trial function, Equation (2.3) becomes as
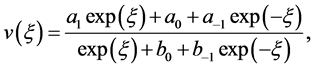 (3.6)
(3.6)
Substituting Equation (3.6) into Equation (3.3) and taking the coefficients of  in each term zero yield a set of algebraic equations for
in each term zero yield a set of algebraic equations for , and k. Solving this system of algebraic equations with the aid of Maple, we obtain
, and k. Solving this system of algebraic equations with the aid of Maple, we obtain
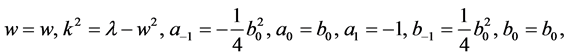 (3.7)
(3.7)
where w and 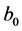 are free parameters. Substituting Equation (3.7) into Equation (3.6), it is obtained the following exact solution
are free parameters. Substituting Equation (3.7) into Equation (3.6), it is obtained the following exact solution
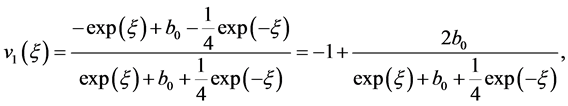 (3.8)
(3.8)
so
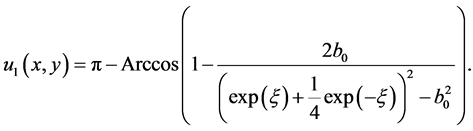
Case 2: 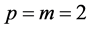 and
and 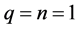
When the parameters p, m, q and n are chosen 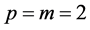 and
and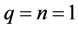 , the solution is of the following form:
, the solution is of the following form:
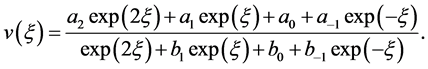 (3.9)
(3.9)
Proceeding in a similar way as illustrated in case 1, we can identify parameters, 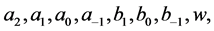 and k in Equation (3.9) as follows:
and k in Equation (3.9) as follows:
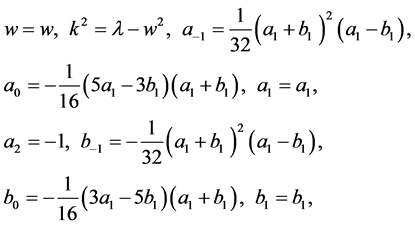 (3.10)
(3.10)
where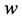 ,
,  and
and 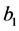 are free parameters. Similarly
are free parameters. Similarly
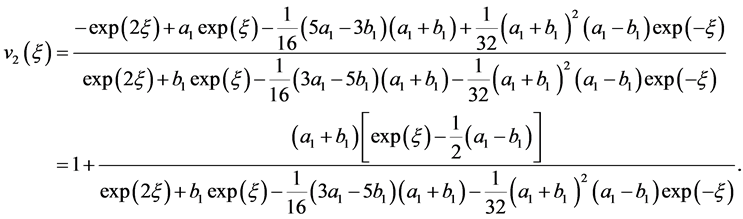 (3.11)
(3.11)
So,
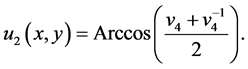
Case 3: 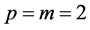 and
and 
As mentioned earlier, the values of m and n can be freely chosen, now we set 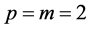 and
and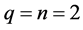 , Equation (2.3) turns to the following form:
, Equation (2.3) turns to the following form:
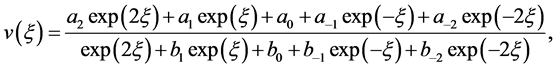 (3.12)
(3.12)
By the same manipulation as illustrated earlier, the following relations is obtained
 (3.13)
(3.13)
where 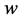 and
and 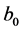 are free parameters. By substituting Equation (3.13) into Equation (3.12), the following exact solution is obtained
are free parameters. By substituting Equation (3.13) into Equation (3.12), the following exact solution is obtained
 (3.14)
(3.14)
So

or
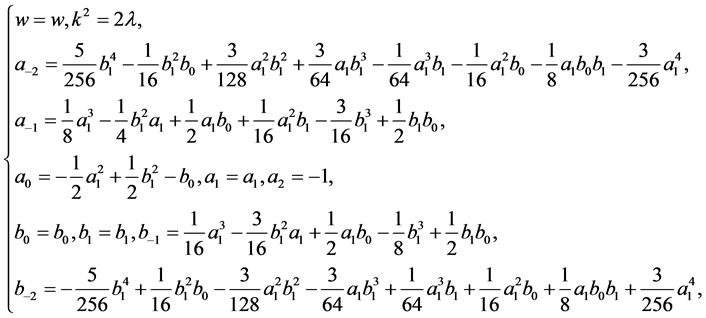 (3.15)
(3.15)
where 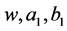 and
and  are free parameters. Substituting Equation (3.15) into Equation (3.14), we obtain the following exact solution
are free parameters. Substituting Equation (3.15) into Equation (3.14), we obtain the following exact solution
 (3.16)
(3.16)
So

4. Conclusion
In this paper, we have obtained the exact solution of sine-Bratu type equation. We achieved the solution by applying Exp-function method. The results show that Exp-function method is a powerful tool for obtaining solitary solution. It may be concluded that the Exp-function method can be easily extended to all kinds of nonlinear equations. The advantage of this method over other methods is that we can obtain the exact solution by using a simple computer program. The computations associated in this work were performed by using Maple 15.
References
- Kutluay, S., Esen, A. and Tasbozan, O. (2010) The
 -Expansion Method for Some Nonlinear Evolution Equations. Applied Mathematics and Computation, 217, 384-391. http://dx.doi.org/10.1016/j.amc.2010.05.073
-Expansion Method for Some Nonlinear Evolution Equations. Applied Mathematics and Computation, 217, 384-391. http://dx.doi.org/10.1016/j.amc.2010.05.073 - Aslan, I. and Ozis, T. (2009) On the Validity and Reliability of the
 -Expansion Method by Using Higher-Order Nonlinear Equations. Applied Mathematics and Computation, 211, 531-536. http://dx.doi.org/10.1016/j.amc.2009.01.075
-Expansion Method by Using Higher-Order Nonlinear Equations. Applied Mathematics and Computation, 211, 531-536. http://dx.doi.org/10.1016/j.amc.2009.01.075 - Wang, M., Zhang, J. and Li, X. (2008) Application of the
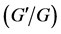 -Expansion to Travelling Wave Solutions of the Broer-Kaup and the Approximate Long Water Wave Equations. Applied Mathematics and Computation, 206, 321-326. http://dx.doi.org/10.1016/j.amc.2008.08.045
-Expansion to Travelling Wave Solutions of the Broer-Kaup and the Approximate Long Water Wave Equations. Applied Mathematics and Computation, 206, 321-326. http://dx.doi.org/10.1016/j.amc.2008.08.045 - Wazwaz, A.M. (2006) The tanh and the sine-cosine Methods for a Reliable Treatment of the Modified Equal Width Equation and Its Variants. Communications in Nonlinear Science and Numerical Simulation, 11, 148-160. http://dx.doi.org/10.1016/j.cnsns.2004.07.001
- Yan, C.T. (1996) A Simple Transformation for Nonlinear Waves. Physics Letters A, 224, 77-84. http://dx.doi.org/10.1016/S0375-9601(96)00770-0
- Parkes, E.J. (2010) Observations on the tanh-coth Expansion Method for Finding Solutions to Nonlinear Evolution Equations. Applied Mathematics and Computation, 217, 1749-1754. http://dx.doi.org/10.1016/j.amc.2009.11.037
- Wazwaz, A.M. (2005) The tanh Method: Exact Solutions of the Sine-Gordon and Sinh-Gordon Equations. Applied Mathematics and Computation, 167, 1196-1210. http://dx.doi.org/10.1016/j.amc.2004.08.005
- Biazar, J. and Ghazvini, H. (2007) Exact Solutions for Non-Linear Schrödinger Equations by He’s Homotopy Perturbation Method. Physics Letters A, 366, 79-84. http://dx.doi.org/10.1016/j.physleta.2007.01.060
- He, J.H. (2005) Application of Homotopy Perturbation Method to Nonlinear Wave Equations. Chaos, Solitons & Fractals, 26, 695-700. http://dx.doi.org/10.1016/j.chaos.2005.03.006
- Wang, M.L. and Li, X.Z. (2005) Extended F-Expansion Method and Periodic Wave Solutions for the Generalized Zakharov Equations. Physics Letters A, 343, 48-54. http://dx.doi.org/10.1016/j.physleta.2005.05.085
- Wang, M.L. and Li, X.Z. (2005) Applications of F-Expansion to Periodic Wave Solutions for a New Hamiltonian Amplitude Equation. Chaos, Solitons & Fractals, 24, 1257-1268. http://dx.doi.org/10.1016/j.chaos.2004.09.044
- Bekir, A. and Boz, A. (2008) Exact Solutions for Nonlinear Evolution Equations Using Exp-Function Method. Physics Letters A, 372, 1619-1625. http://dx.doi.org/10.1016/j.physleta.2007.10.018
- Ebaid, A. (2007) Exact Solitary Wave Solutions for Some Nonlinear Evolution Equations via Exp-Function Method. Physics Letters A, 365, 213-219. http://dx.doi.org/10.1016/j.physleta.2007.01.009
- Abdou, M.A., Solimanm, A.A. and El-Basyony, S.T. (2007) New Application of Exp-Function Method for Improved Boussinesq Equation. Physics Letters A, 369, 469-475. http://dx.doi.org/10.1016/j.physleta.2007.05.039
- Zhu, S.D. (2007) Exp-Function Method for the Discrete mKdV Lattice. International Journal of Nonlinear Sciences and Numerical Simulation, 8, 465-469.

