Applied Mathematics
Vol.4 No.7(2013), Article ID:34315,7 pages DOI:10.4236/am.2013.47142
New Practical Algebraic Public-Key Cryptosystem and Some Related Algebraic and Computational Aspects
Faculty of Mathematics and Mechanics, Tomsk State University, Tomsk, Russia
Email: rososhek@list.ru
Copyright © 2013 S. K. Rososhek. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 26, 2013; revised May 26, 2013; accepted June 6, 2013
Keywords: Public-Key Cryptosystem; Modular Matrix Ring
ABSTRACT
The most popular present-day public-key cryptosystems are RSA and ElGamal cryptosystems. Some practical algebraic generalization of the ElGamal cryptosystem is considered-basic modular matrix cryptosystem (BMMC) over the modular matrix ring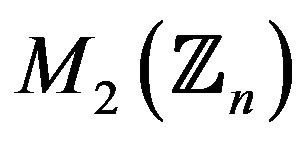 . An example of computation for an artificially small number n is presented. Some possible attacks on the cryptosystem and mathematical problems, the solution of which are necessary for implementing these attacks, are studied. For a small number n, computational time for compromising some present-day public-key cryptosystems such as RSA, ElGamal, and Rabin, is compared with the corresponding time for the ВММС. Finally, some open mathematical and computational problems are formulated.
. An example of computation for an artificially small number n is presented. Some possible attacks on the cryptosystem and mathematical problems, the solution of which are necessary for implementing these attacks, are studied. For a small number n, computational time for compromising some present-day public-key cryptosystems such as RSA, ElGamal, and Rabin, is compared with the corresponding time for the ВММС. Finally, some open mathematical and computational problems are formulated.
1. Introduction
Security of some present-day public-key cryptosystems is based on computational complexity of some numbertheoretical problems. Two of these problems are used most often: the integer factorization problem and the discrete logarithm problem. These problems ensure the security of the RSA and ElGamal cryptosystems, as well as of the corresponding digital signature schemes [1].
However, the true level of the computational complexity of these problems is unknown. That is to say, they are widely believed to be intractable, although no proof of this fact is known.
In [2], randomized polynomial-time algorithms for computing discrete logarithms and integer factoring were presented for the quantum computer.
Nevertheless, some alternatives should be proposed. One of possible approaches is to replace number-theoretical cryptosystems by such algebraic cryptosystems that would be resistant to an attack on a quantum computer.
Let us now consider some scheme of cryptosystems, namely, cryptosystems of group rings.
In the author’s work [3,4], a scheme of group ring cryptosystems was proposed. The idea to apply group rings in cryptography is based on the fact that if we fix the cardinality of a finite ring R, the cardinality of the group ring RG for a finite group G is an exponent of the cardinality of the group G. Then, a legal user can perform cryptographic transformations separately in the ring R and in the group G using polynomial algorithms and the illegal user has to solve computationally difficult problems in the group ring RG.
Let us consider the standardization problem in the group ring and two its aspects. The direct standardization problem is to construct a standard automorphism g of the group ring RG from an automorphism a of the group G and automorphism b of the ring R in the following way: if an element х of the group ring RG is represented as a formal linear combination of elements 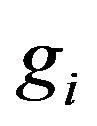 of the group G with coefficients ri from the ring R, then the image of the element х under the action of g is a formal linear combination of images of the elements gi of the group G under the action of a with coefficients that are images of the coefficients ri under the action of b.
of the group G with coefficients ri from the ring R, then the image of the element х under the action of g is a formal linear combination of images of the elements gi of the group G under the action of a with coefficients that are images of the coefficients ri under the action of b.
The inverse standardization problem is formulated as follows. For a given automorphism g of a group ring RG, find an automorphism a of the group G and an automorphism b of the ring R such that g can be constructed from a and b by the way that was mentioned in the direct standardization problem or prove that such automorphisms a and b do not exist.
It is easy to see that, in the case of an efficient specification of the automorphism a in the group G and of the automorphism b in the ring R, one can efficiently compute the action of the automorphism g on any element of the group ring RG, i.e., efficiently specify the automorphism g of the ring RG.
As for the inverse standardization problem, there are some reasons to believe that this problem is computationally difficult. However, there is no proof for this statement.
In [5] some generalization of group ring cryptosystem is considered in the case of quasigroup ring.
The question “For which finite commutative rings R and finite groups G all automorphisms of the group ring RG are standard automorphisms?” was partially answered in [6-8]. It should be noted that an inner automorphism of an integral group ring of a finite group is not a standard automorphism as a rule. This is why, together with the standard automorphisms of the group ring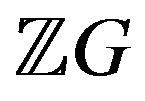 , where G is a finite group, we use inner automorphisms. In [9] the group ring
, where G is a finite group, we use inner automorphisms. In [9] the group ring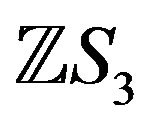 , where
, where 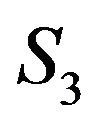 is the permutation group for three symbols, is represented in a matrix form as block diagonal matrices of the fourth degree with two one-dimensional blocks and one two-dimensional block. In [9,10] it is shown that the unit group of the group ring
is the permutation group for three symbols, is represented in a matrix form as block diagonal matrices of the fourth degree with two one-dimensional blocks and one two-dimensional block. In [9,10] it is shown that the unit group of the group ring 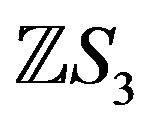 is a semi-direct product of trivial units
is a semi-direct product of trivial units 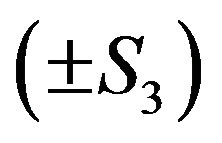 and a free subgroup of rank 3. Since matrices of the fourth degree from this subgroup contain two identity one-dimensional blocks, we can restrict ourselves by a free group of matrices of the second degree with the free generators [9]:
and a free subgroup of rank 3. Since matrices of the fourth degree from this subgroup contain two identity one-dimensional blocks, we can restrict ourselves by a free group of matrices of the second degree with the free generators [9]:
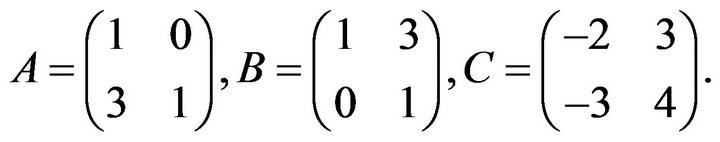
If we fall outside the limits of the matrix representation of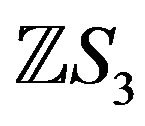 , we consider arbitrary matrices of the second degree from the ring
, we consider arbitrary matrices of the second degree from the ring 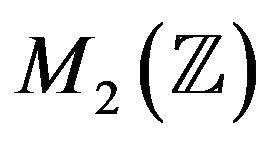 and its unit group
and its unit group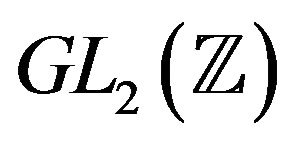 , which contains free rank 3 subgroups
, which contains free rank 3 subgroups 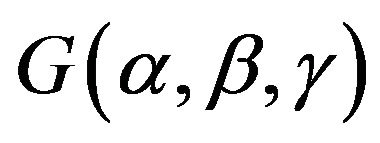 with the free generators
with the free generators
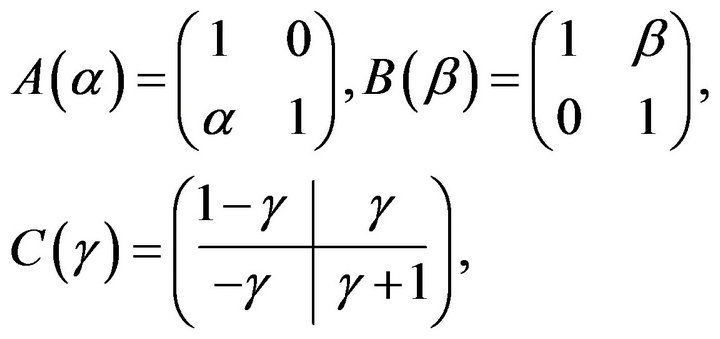
where 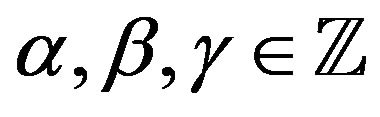 and
and 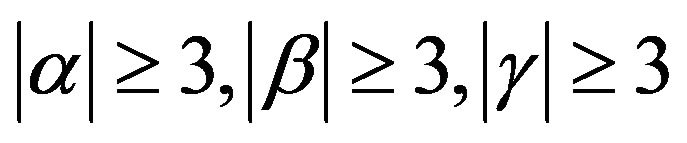 [11]. For example, if
[11]. For example, if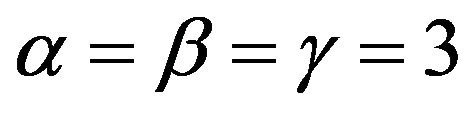 , we obtain a free rank 3 subgroup
, we obtain a free rank 3 subgroup 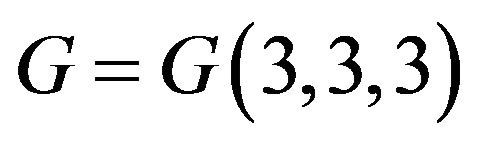 with the aforesaid free generators А, В, and С.
with the aforesaid free generators А, В, and С.
It should be also noted that all automorphisms of the group ring 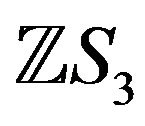 are inner [12].
are inner [12].
New practical algebraic generalization of the ElGamal cryptosystem will be given in the Section 2, some attacks on this cryptosystem—in the Section 4, new hard computational problems—in the Section 5, comparison of the security level of classical RSA, ElGamal and Rabin cryptosystems with security level of this cryptosystem for the same small number—in the Section 7, some related open mathematical and computational problems— in the Section 8. It should be noted, that some other theoretical algebraic generalizations of the ElGamal cryptosystem are given in [13,14].
2. Basic Modular Matrix Cryptosystem (BMMC)
2.1. Key Generation
User А does the following:
1) picks large random positive integer n;
2) picks the random words 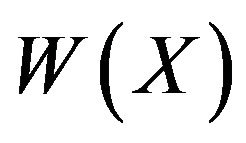 and
and 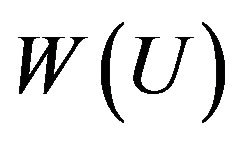 in the alphabet
in the alphabet 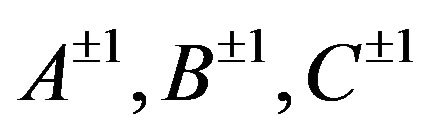 in a free rank 3 group with free generators А, В, and С;
in a free rank 3 group with free generators А, В, and С;
3) computes the noncommuting matrices 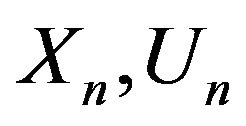 by replacing the symbols А, В, and С in the words
by replacing the symbols А, В, and С in the words 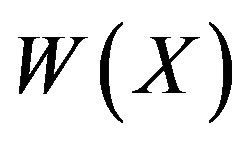 and
and 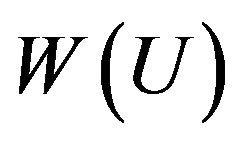 by the corresponding matrices
by the corresponding matrices
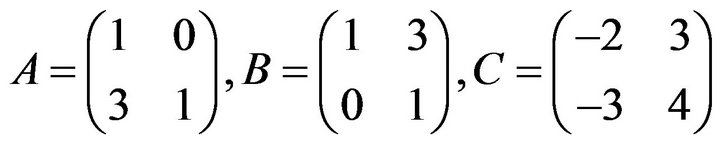
and performing matrix computations modulo n, i.e.,
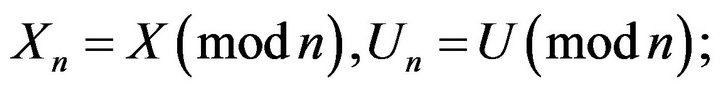
If 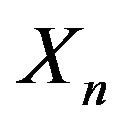 and
and 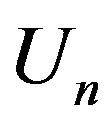 commute, then return to 2);
commute, then return to 2);
4) let 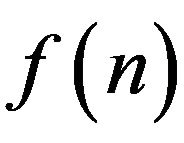 be the cardinality of the group
be the cardinality of the group 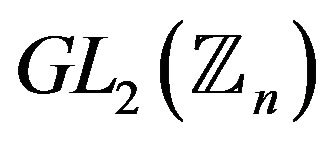 over
over 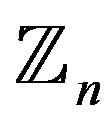 -residue ring modulo n, then user A picks the random integers
-residue ring modulo n, then user A picks the random integers
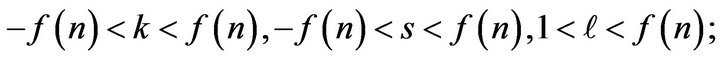
5) public key of user А is
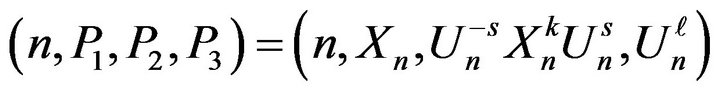
and its private key is
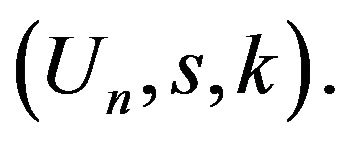
Remark 1. Orders of matrices
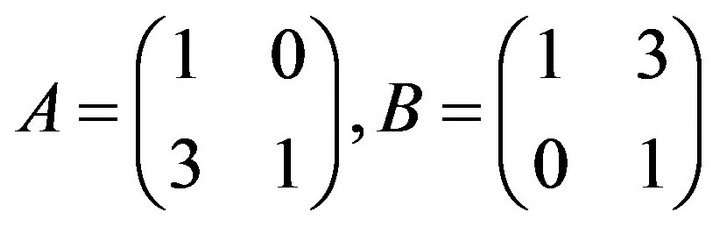
in the group  are equal to n;
are equal to n;
Remark 2. The cardinality of the group 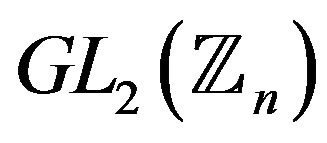 in the case
in the case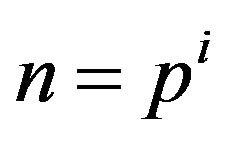 , p is a prime number, i is a positive integer, is equals to
, p is a prime number, i is a positive integer, is equals to
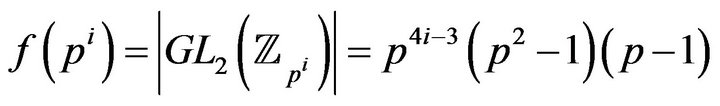 [15].
[15].
As consequence in the case 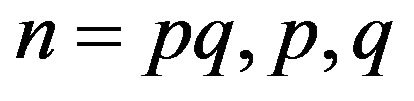 are primes, we have
are primes, we have
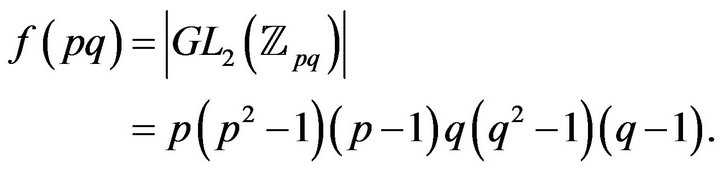
2.2. Encryption
User В does the following:
1) writes the plaintext as a sequence of N numbers from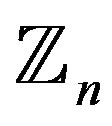 , where N is a multiple of 4,
, where N is a multiple of 4,  , adding, if necessary, numbers from the first quadruple by a cyclic permutation at the end of the sequence;
, adding, if necessary, numbers from the first quadruple by a cyclic permutation at the end of the sequence;
2) writes each quadruple of numbers of the obtained sequence similarly as matrix:
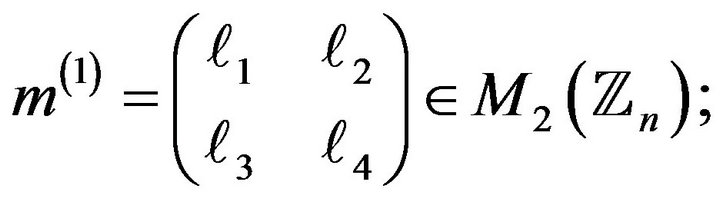
3) picks session keys-random integers
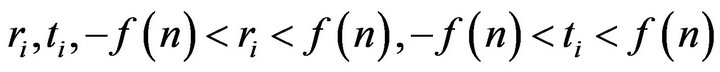 for each of
for each of 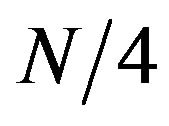 obtained matrices
obtained matrices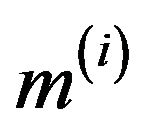 ;
;
4) computes the ciphertext block for each matrix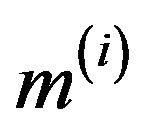 :
:
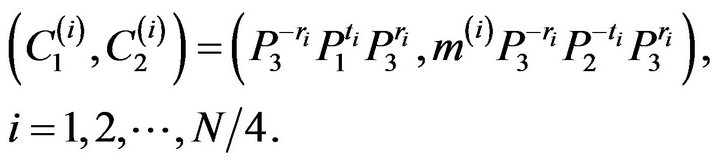
2.3. Decryption
Using the private key, user А computes for each ciphertext block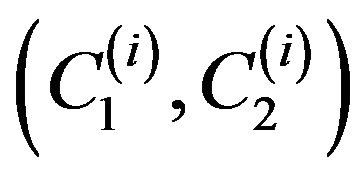 :
:
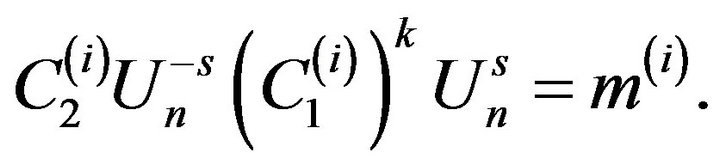
After obtaining the sequence of matrices
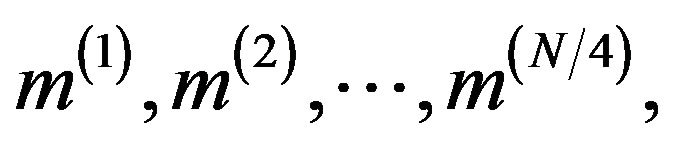
the sequence of numbers 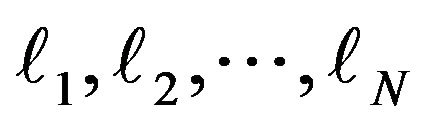 and hence the plaintext can be reconstructed uniquely.
and hence the plaintext can be reconstructed uniquely.
Theorem. Decryption in the ВММС is correct.
Proof. It is sufficiently to consider a case of one block of the ciphertext:
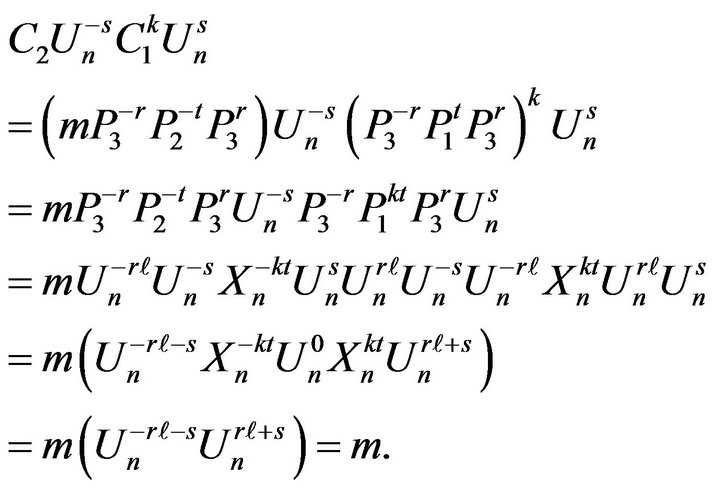
It should be noted that algorithms of the BMMC are implemented using the algorithm of matrix modular exponentiation similar to the usual modular exponentiation algorithm in which multiplication of integers is replaced by multiplication of matrices with reduction of their elements modulo n. In addition parallel computations may be used in matrix multiplications to increase the computational efficiency of the cryptosystem.
Let n be a large 256 bit integer, then the cardinality bit length of the group 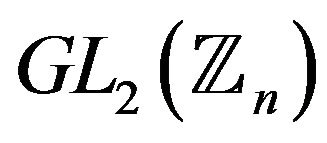 would be near 800 bits or more. For comparing in the case of the ElGamal cryptosystem the bit lengths of p and the cardinality of corresponding multiplicative group of residue field
would be near 800 bits or more. For comparing in the case of the ElGamal cryptosystem the bit lengths of p and the cardinality of corresponding multiplicative group of residue field 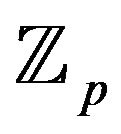 are equal. But one reduction modulo 1024 bit number in the ElGamal cryptosystem costs as some reductions modulo 256 bit number in the BMMC. Therefore, under corresponding choice of parameters the BMMC may be faster than the ElGamal cryptosystem with the same security level, because the gybrid problem and the transformation problem are harder than the discrete logarithm problem in the groups of the same cardinality.
are equal. But one reduction modulo 1024 bit number in the ElGamal cryptosystem costs as some reductions modulo 256 bit number in the BMMC. Therefore, under corresponding choice of parameters the BMMC may be faster than the ElGamal cryptosystem with the same security level, because the gybrid problem and the transformation problem are harder than the discrete logarithm problem in the groups of the same cardinality.
3. Example
3.1. Key Generation
User А does the following:
1) picks two prime numbers 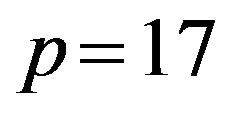 and
and 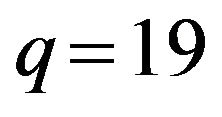 and computes
and computes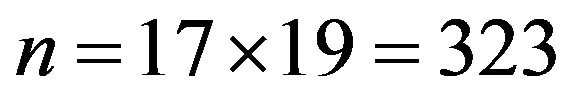 ;
;
2) picks the words in the free group:
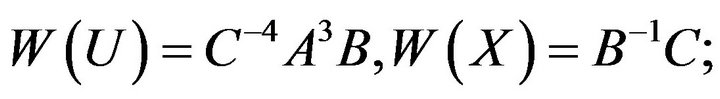
3) computes matrices modulo n:
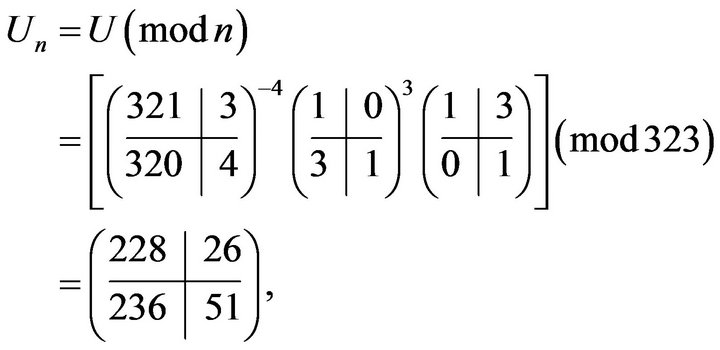
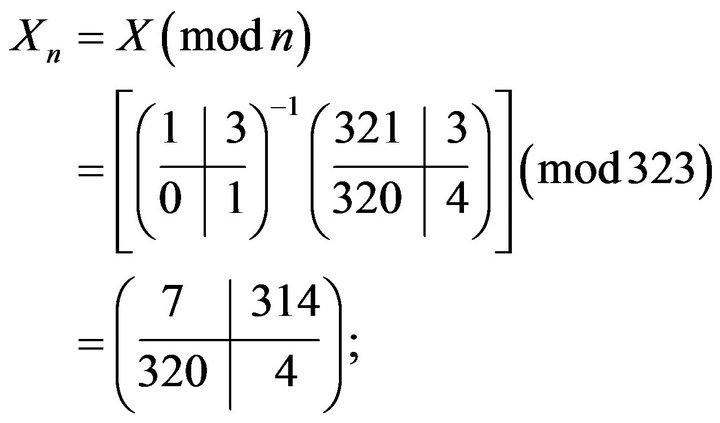
matrices  and
and  do not commute and, therefore, the user passes to the next step;
do not commute and, therefore, the user passes to the next step;
4) picks the integers 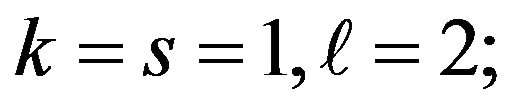
5) the public key is
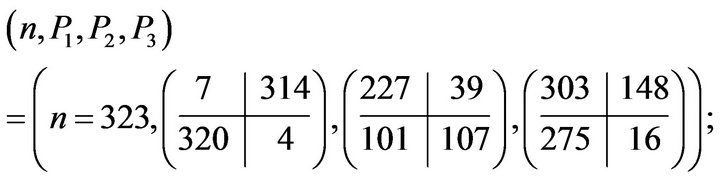
the private key is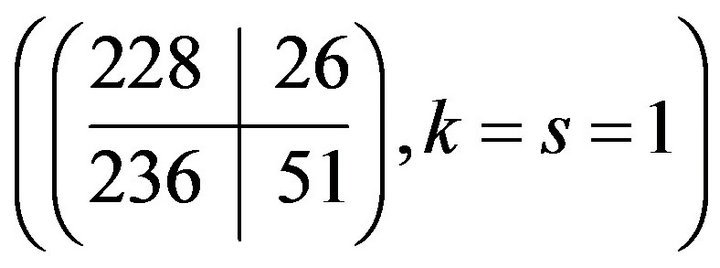 .
.
3.2. Encryption
User В does the following:
1) writes the plaintext as a sequence of numbers from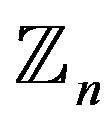 . The length of this sequence is multiple of 4. If necessary, some numbers are added. For example, let the plaintext be
. The length of this sequence is multiple of 4. If necessary, some numbers are added. For example, let the plaintext be
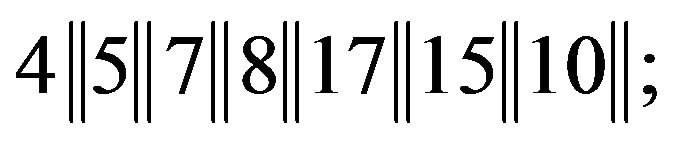
here, a number should be added to the last block by shifting the first number cyclically, the user obtains two quadruples of numbers from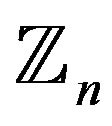 :
:
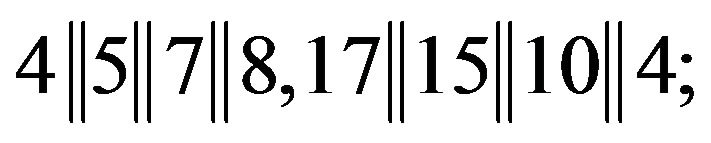
2) writes the plaintext as two matrices from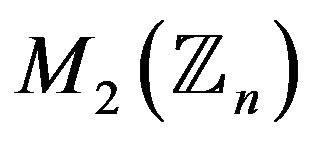 :
:
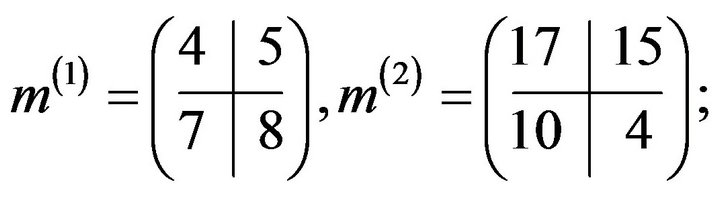
3) encrypts each block (matrix) separately choosing different session keys. For example, the first block is encrypted as follows;
4) picks the session key for the first block r1 = 2, t1 = 1;
5) computes the ciphertext of the first block modulo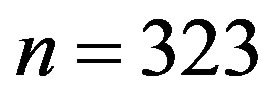 :
:

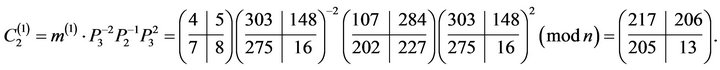
The ciphertext of the second block 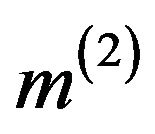 is computed similarly with the choice of another session key
is computed similarly with the choice of another session key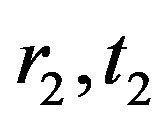 .
.
3.3. Decryption
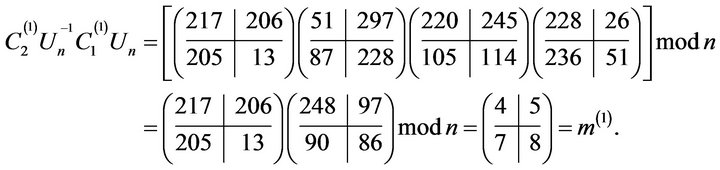
User А, having obtained the ciphertext from user В, does the following: using its private key, for each ith block, computes
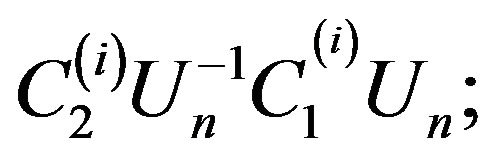
in particular, for the first block, he obtains
4. Some Attacks on ВММС
4.1. Find the Private Key 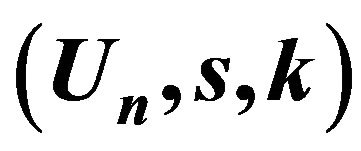 by the Public Key
by the Public Key 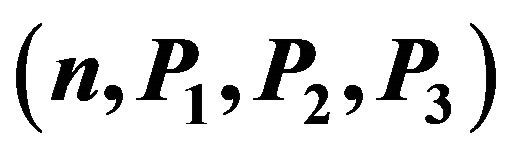
1) Let the cardinality of the group 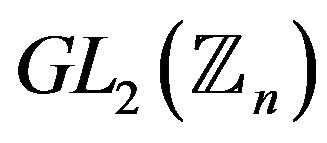 be
be
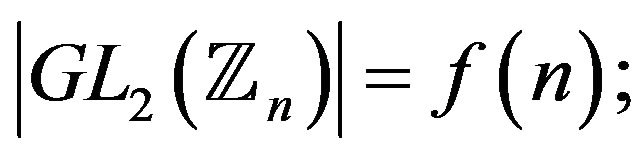
Since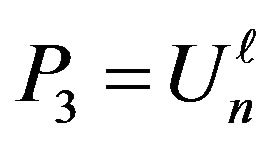 , the cryptanalyst can try to solve the equation with two unknowns Y and х:
, the cryptanalyst can try to solve the equation with two unknowns Y and х:
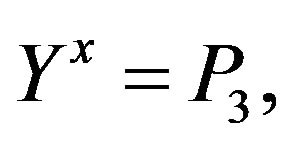
where 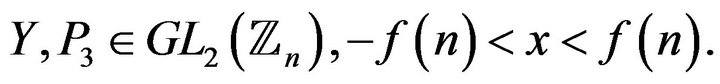
2) Since
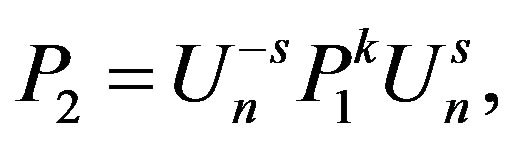
the cryptanalyst can try to solve the equation with two unknowns Z and х:
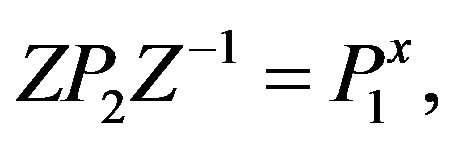
where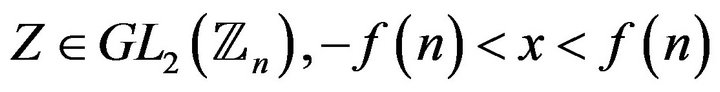 , what leads to the private key by applying 1) to each solution
, what leads to the private key by applying 1) to each solution 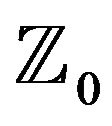 (which we call the transforming matrix).
(which we call the transforming matrix).
4.2. Find the Private Key 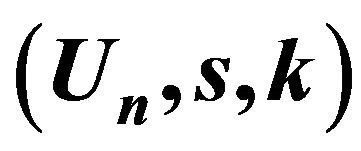 by the Ciphertext
by the Ciphertext 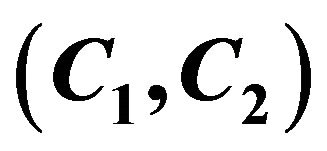
Since the private key is applied in the ciphertext 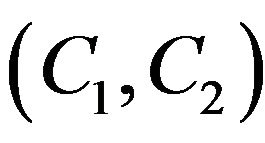 not directly but only via the public key, the knowing of only the ciphertext does not yield additional possibilities to the attacks from 4.1 for the attack on the private key.
not directly but only via the public key, the knowing of only the ciphertext does not yield additional possibilities to the attacks from 4.1 for the attack on the private key.
4.3. Find the Session Key 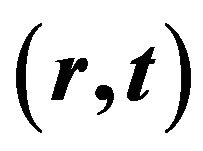 by the Ciphertext
by the Ciphertext 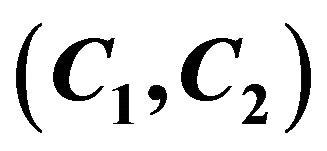
1) Since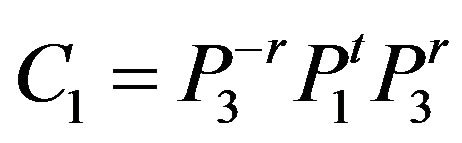 , the cryptanalyst can try to solve the equation with two unknowns Z and у:
, the cryptanalyst can try to solve the equation with two unknowns Z and у:
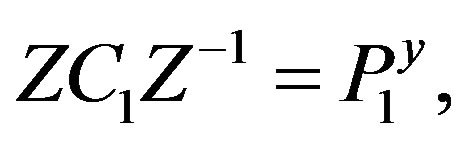
where 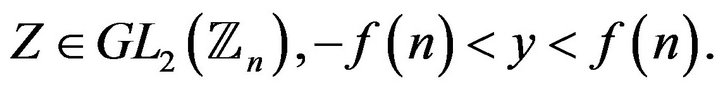
2) For any solution 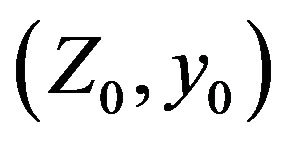 of the equation from 1), the cryptanalyst can try to solve the equation with two unknowns Y and х:
of the equation from 1), the cryptanalyst can try to solve the equation with two unknowns Y and х:
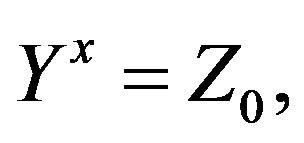
where 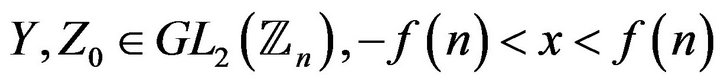
4.4. Find the Corresponding Plaintext m or the Session Key 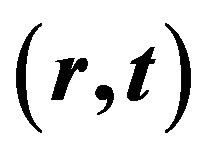 by a Chosen Ciphertext
by a Chosen Ciphertext 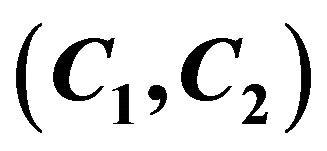
Cryptanalyst chooses the random 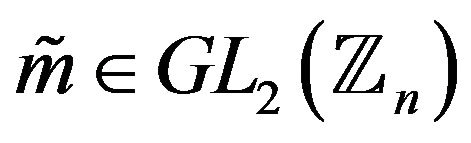 and computes
and computes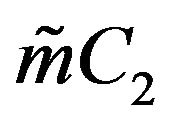 , then send it to user A for decryption. User A computes:
, then send it to user A for decryption. User A computes:
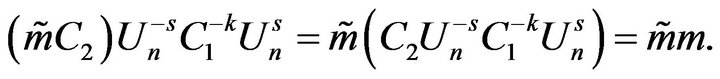
and send the result to cryptanalyst, which computes the plaintext:
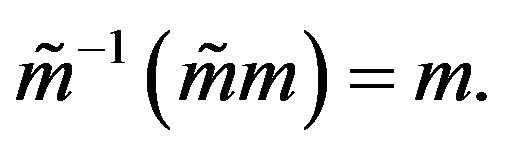
Hence for protecting cryptosystem the modification of encryption algorithm is:
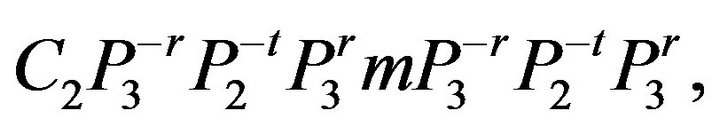
the modification of decryption algorithm is:
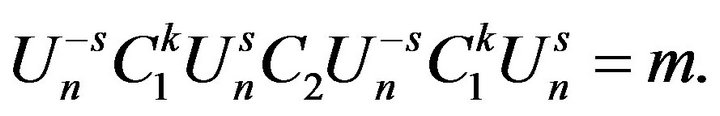
5. Computational Problems in Ensuring ВММС Security
From the consideration of attacks 4.1-4.4 one can formulate some problems, the solution of which is necessary to implement the corresponding attacks.
5.1. The Transformation Problem
Let a matrix 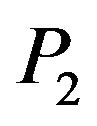 be conjugated with an unknown integral power of a matrix
be conjugated with an unknown integral power of a matrix 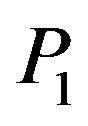 for two given matrices
for two given matrices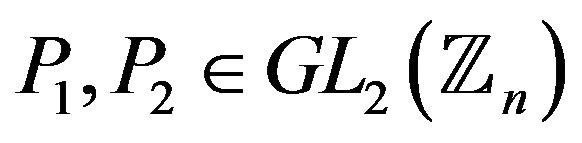 . Find all solutions of the equation with two unknowns Z and у:
. Find all solutions of the equation with two unknowns Z and у:
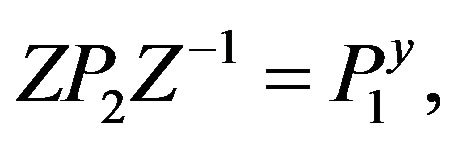
where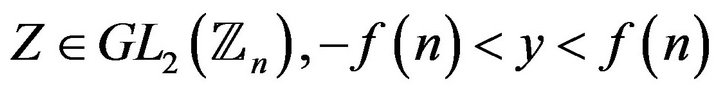 .
.
Let us consider a particular case of Problem 5.1.
1) The conjugation problem.
For two given conjugated matrices 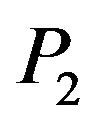 and
and 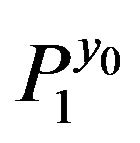 from the group
from the group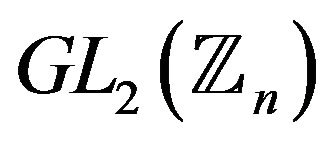 , find a transforming matrix
, find a transforming matrix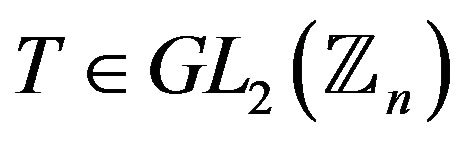 , i.e., matrix Т such that
, i.e., matrix Т such that
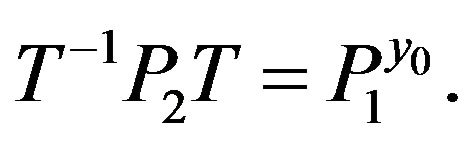
5.2. The Hybrid Problem
Find all solutions of the equation with two unknowns Y and х
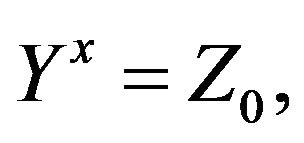
where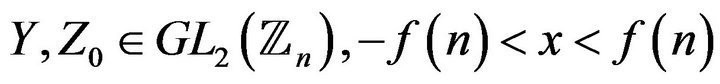 in the group
in the group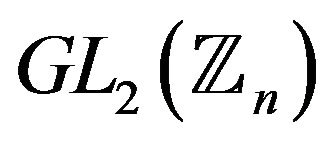 .
.
Let us also consider two particular cases of Problem 5.2.
1) The discrete logarithm problem in a cyclic subgroup of the group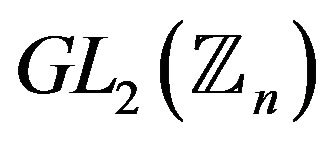 .
.
Let 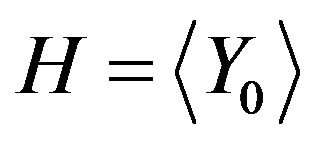 be a fixed cyclic subgroup of order j of the group
be a fixed cyclic subgroup of order j of the group 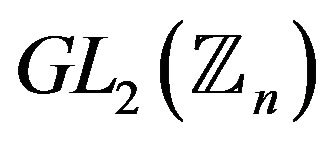 with the generator
with the generator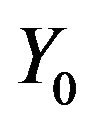 ,
, 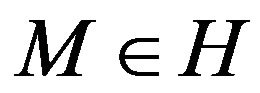 be an arbitrary element. Find the unique solution
be an arbitrary element. Find the unique solution 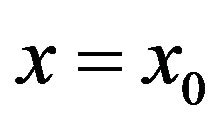 of the equation
of the equation
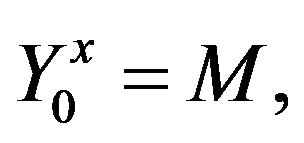
where х is an integer such that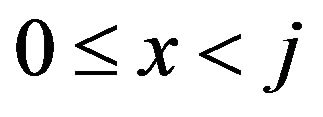 .
.
2) The problem of extracting a root of the ith power in the group 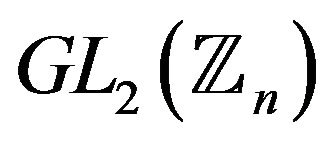 (the matrix RSA problem).
(the matrix RSA problem).
Let 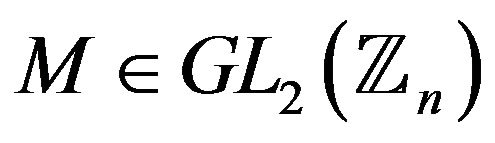 be an arbitrary element,
be an arbitrary element, 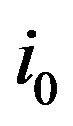 be a fixed integer satisfying the condition
be a fixed integer satisfying the condition 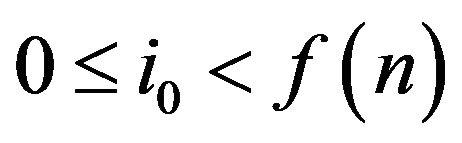 and
and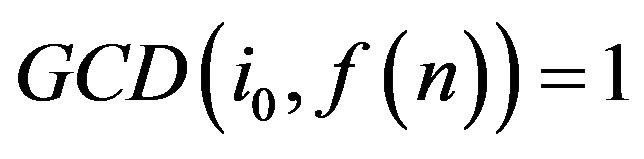 .
.
Find all solutions of the equation with a single unknown Y:
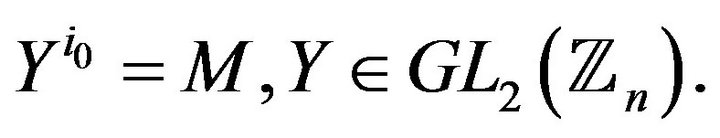
According to the Problem 2), in turn, one can also discern the following problem.
The problem of square-root extraction in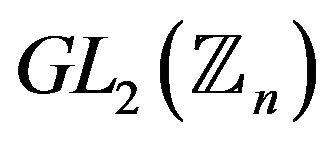 .
.
Find all solutions of the equation with a single unknown Y:
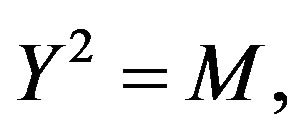
where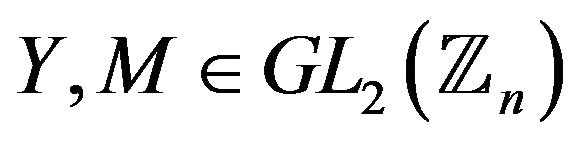 .
.
6. Computational Complexity of Problems 5.1, 5.2
If the order 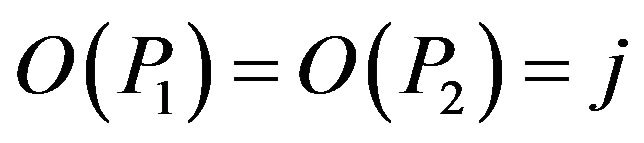 is a large number, then, the fact that the generators in a cyclic group are indistinguishable and random choice of k in the key generation show, on the one hand, that the identification of matrices
is a large number, then, the fact that the generators in a cyclic group are indistinguishable and random choice of k in the key generation show, on the one hand, that the identification of matrices 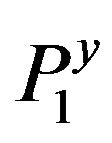 in Problem 5.1 is a hard problem and, on the other hand, the impossibility to implement the exhausting search in practice for a large number j.
in Problem 5.1 is a hard problem and, on the other hand, the impossibility to implement the exhausting search in practice for a large number j.
Considering Problem 5.1 1), it should be noted that this problem is solvable in the free subgroup 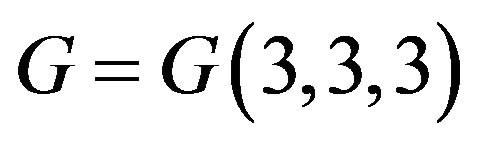 of the group
of the group 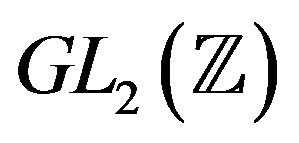 (see [16]). The possibility to extend this algorithm for a subgroup of the group
(see [16]). The possibility to extend this algorithm for a subgroup of the group  depends on the solution of the following problem: for a given matrix
depends on the solution of the following problem: for a given matrix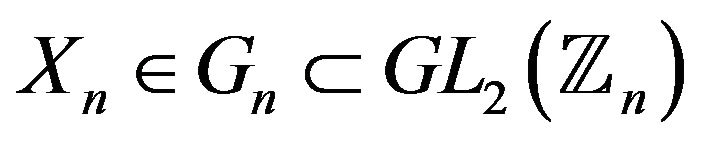 , find the word
, find the word 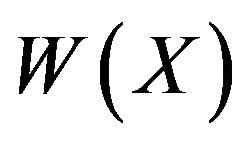 and matrix
and matrix 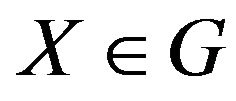 whose reduction modulo n yields the matrix
whose reduction modulo n yields the matrix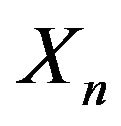 .
.
Nevertheless, even in the case of a solved problem of extension, the problem about the existence of an efficient algorithm for solving Problem 5.1 1) remains open.
Let us now consider Problem 5.2. As it is a problem with two unknowns, this problem is more complicated in the general case than its particular cases, the discrete logarithm problem and the problem of extracting a matrix root modulo n. It is worth to note that the square-root extracting problem is computationally difficult for large number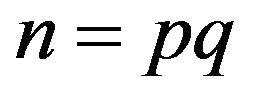 , p and q are primes.
, p and q are primes.
Let us now turn to the discussion of the cardinality of the set of secret keys for ВMМС. Note that, for classical cryptosystems, the uniqueness of the secret key can be reached by fitting of parameters. For BMMC, the situation is other. Indeed, if a matrix 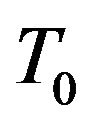 transforms the matrix
transforms the matrix 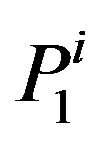 into the matrix
into the matrix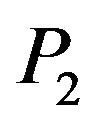 , i.e.,
, i.e.,
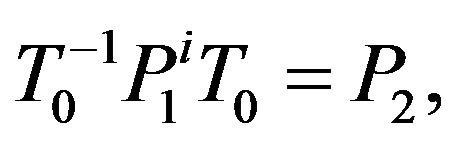
then the matrix 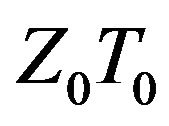 also transforms
also transforms 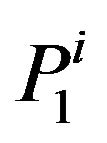 into
into 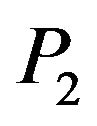 for any matrix
for any matrix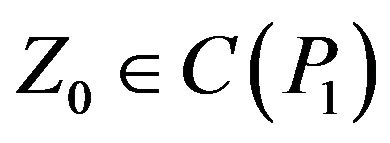 , where
, where 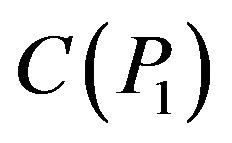 is a centralizer of
is a centralizer of 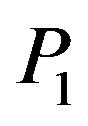 in
in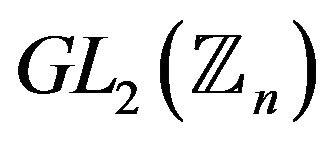 , because
, because
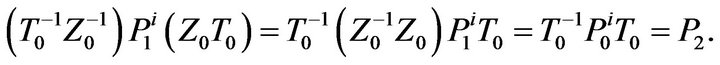
Thus, if the secret key 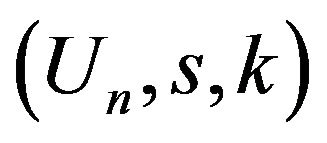 is considered as initial, the cryptanalyst can compromise the BMMC by any real key of the form
is considered as initial, the cryptanalyst can compromise the BMMC by any real key of the form , where
, where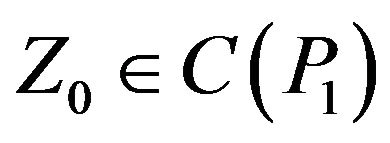 . Then, for the cardinality of the set of real keys
. Then, for the cardinality of the set of real keys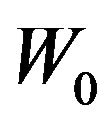 , we have
, we have
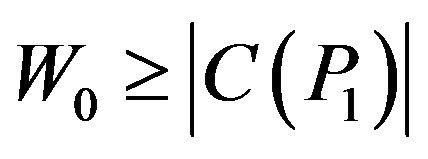
and when generating a key it is necessary to choose matrix 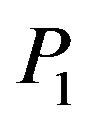 so that
so that
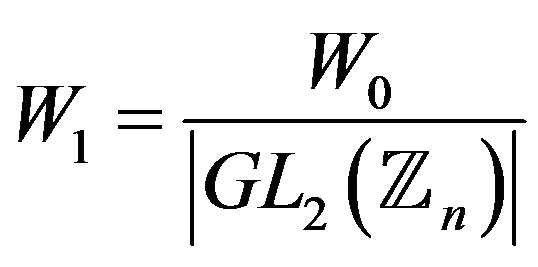
was negligibly small, e.g.,
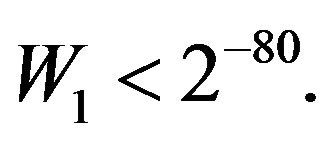
This protects from random guessing of the private key.
7. Comparison of Computational Security of Classical RSA, ElGamal, and Rabin Cryptosystems with ВММС
For demonstrativeness, we compare the cryptosystems for a very small number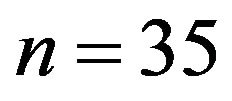 .
.
7.1. RSA Cryptosystem
Let the public key be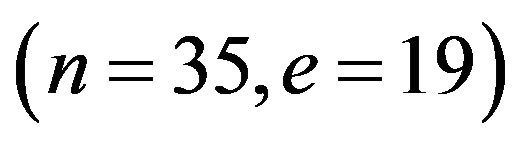 .
.
In this case, the cryptanalyst instantaneously compromises RSA by factorization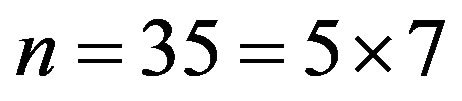 , from which finds
, from which finds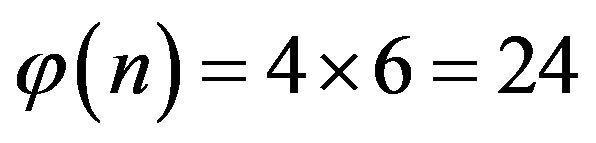 , and computation of the secret key
, and computation of the secret key 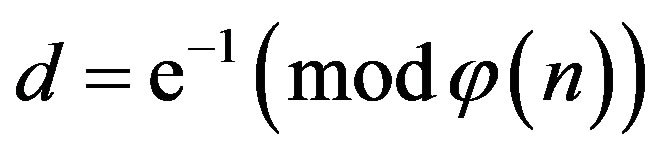 either by the extended Euclid’s algorithm or by exhaustive search. Then the cryptanalyst finds the secret key:
either by the extended Euclid’s algorithm or by exhaustive search. Then the cryptanalyst finds the secret key:

7.2. Modified ElGamal Cryptosystem
In the unit group 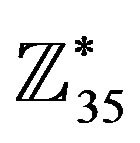 of the ring
of the ring 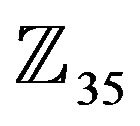 one has to choose an element of the maximal order. For this purpose,
one has to choose an element of the maximal order. For this purpose, 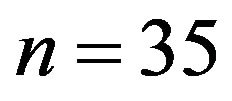 is factorized as
is factorized as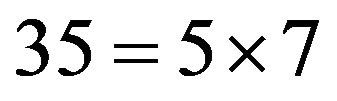 , and the generators are chosen in the groups
, and the generators are chosen in the groups 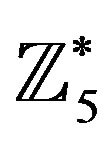 and
and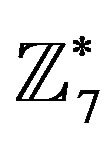 , e.g.,
, e.g.,
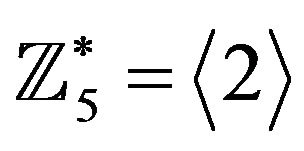 and
and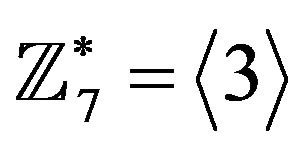 .
.
Then the element of maximal order in 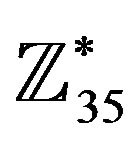 is obtained from the solution of the following simultaneous congruences either by inspection or by the Chinese reminder theorem:
is obtained from the solution of the following simultaneous congruences either by inspection or by the Chinese reminder theorem:
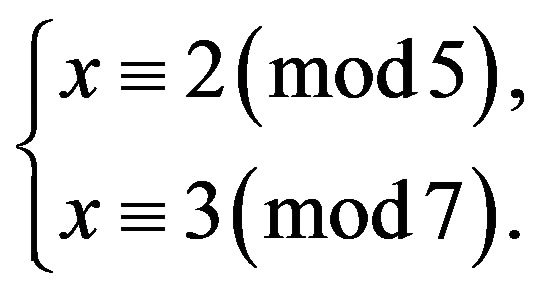
It follows that 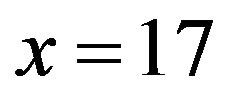 and its order is
and its order is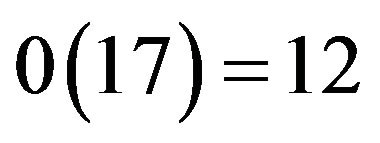 .
.
Let one of cyclic subgroups of order 12, for example, 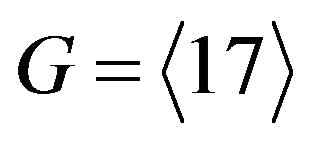 be chosen in the group
be chosen in the group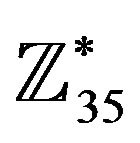 . In the group G, another generator may be chosen, e.g.,
. In the group G, another generator may be chosen, e.g.,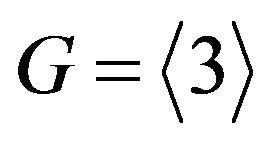 .
.
Let the modified ElGamal cryptosystem be considered in a cyclic group G of order 12 with a generator 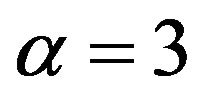 and let the public key be
and let the public key be
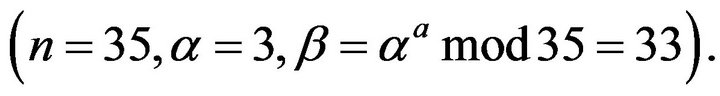
In this case, the cryptanalyst instantaneously compromises the modified ElGamal cryptosystem using exhaustive search in the cyclic group of order 12 finding the secret key а = 5 since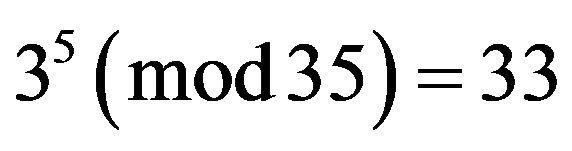 .
.
Remark. In the case of choice n as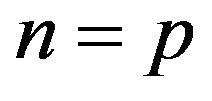 , where p is a prime number, we compare BMMC with classical ElGamal cryptosystem.
, where p is a prime number, we compare BMMC with classical ElGamal cryptosystem.
7.3. Rabin Cryptosystem
Let the public key be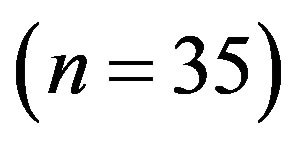 , then the cryptanalyst instantaneously compromises the Rabin cryptosystem in this case by factorizing the number by prime multipliers
, then the cryptanalyst instantaneously compromises the Rabin cryptosystem in this case by factorizing the number by prime multipliers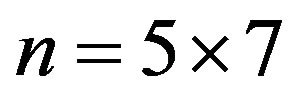 .
.
One can see that, in all three cases, the cryptanalyst instantaneously compromises these classical cryptosystems for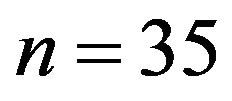 . Let us now the case of the BMMC cryptosystem for
. Let us now the case of the BMMC cryptosystem for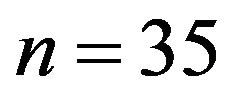 .
.
7.4. BMMC
Let the public key be
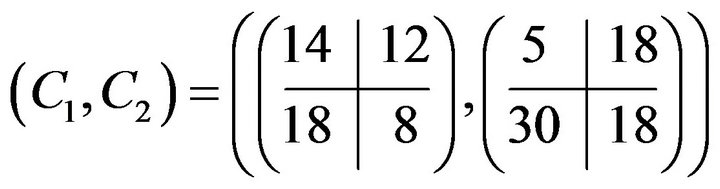
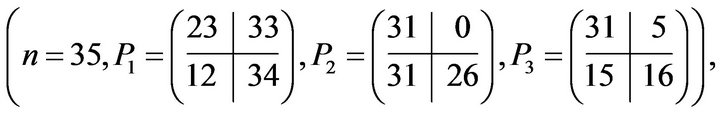
be the ciphertext of a certain matrix m.
Compromising BMMC in this case needs essentially more efforts than for the classical cryptosystems and exhausting search in the space of the search containing 775,760 matrices gives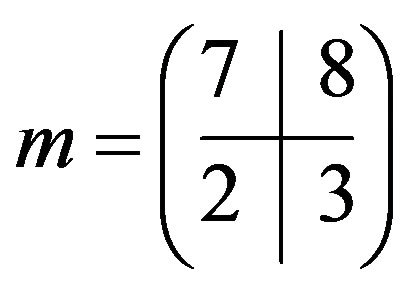 ; secret key—
; secret key—
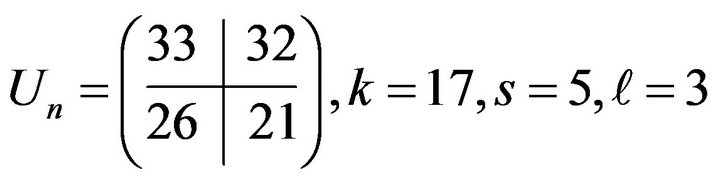 ; session key—
; session key—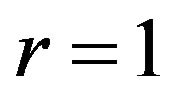 ,
,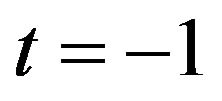 .
.
8. Some Open Mathematical and Computational Problems
1) For which finite groups G and rings R the unit group of group ring RG is a semi-direct product of trivial units and a free subgroup of a finite rank?
2) For which groups G and rings R every automorphism of the group ring RG has a standard form?
3) For which subgroups of the group 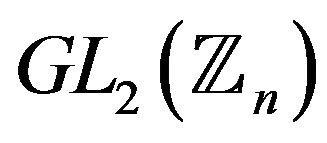 it takes place the property of small centralizers i.e. every element has a cyclic centralizer?
it takes place the property of small centralizers i.e. every element has a cyclic centralizer?
Remark. It is well-known [16] that in the free group of finite rank centralizer of any element is a cyclic subgroup.
4) Is there a polynomial-time algorithm for constructing cyclic centralizer of any element in a free group of finite rank?
5) Is there a polynomial-time algorithm for solving the membership problem for cyclic subgroup of the a) free group of finite rank, b) subgroup 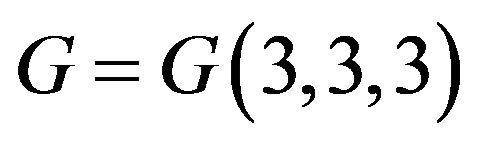 by modulo n in a group
by modulo n in a group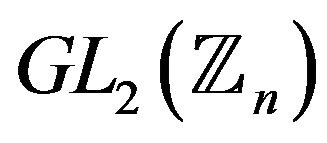 ?
?
6) Is there a polynomial-time algorithm for solving the modular factorization problem, i.e. to represent every matrix from the subgroup 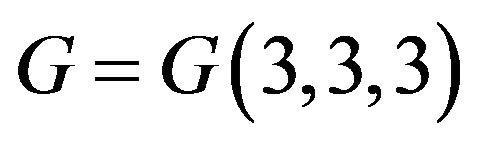 by modulo n in a group
by modulo n in a group 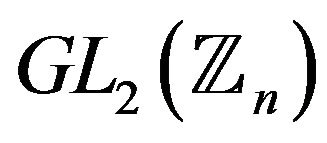 as a word in an alphabet of
as a word in an alphabet of 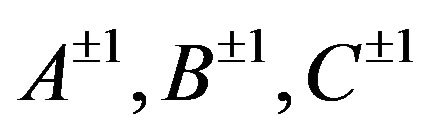 by modulo n?
by modulo n?
7) How to compute the number 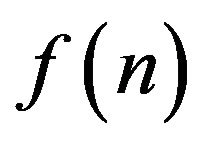 for arbitrary positive integers n? More exactly, is there a polynomialtime algorithm for computing
for arbitrary positive integers n? More exactly, is there a polynomialtime algorithm for computing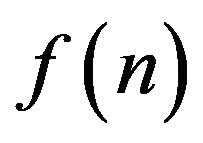 ?
?
8) Is there a polynomial-time algorithm for computing maximal order elements in a subgroup 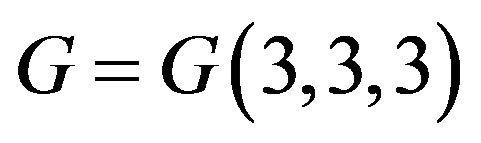 by modulo n in the group
by modulo n in the group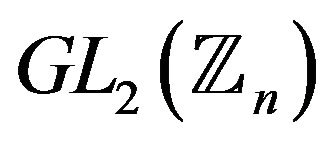 ? What is a cardinality of this subgroup
? What is a cardinality of this subgroup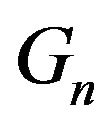 ?
?
9. Conclusion
The practicality of the BMMC is provided by the absence of the necessity in the computer algebra systems used for computer realization of cryptosystem algorithms and efficient matrix computations by modulo number of essentially less bit length than that are usually used in classical cryptosystems under the same security level.
REFERENCES
- A. Menezes, P. van Ooshot and S. Vanstone, “Handbook of Applied Cryptography,” CRC Press, Waterloo, 1996. doi:10.1201/9781439821916
- P. W. Shor, “Algorithms for Quantum Computation: Discrete Logarithm and Factoring,” Proceedings of the IEEE 35th Communications Annual Symposium on Foundations of Computer Science, Santa Fe, 20-22 November 1994, pp. 124-134.
- S. K. Rososhek, “Cryptosystems in Automorphism Groups of Group Rings of Abelian Groups,” Fundamentalnaya I prikladnaya matematica, Vol. 13, No. 8, 2007, pp. 157- 164 (in Russian).
- S. K. Rososhek, “Cryptosystems in Automorphism Groups of Group Rings of Abelian Groups,” Journal of Mathematical Sciences, Vol. 154, No. 3, 2008, pp. 386-391. doi:10.1007/s10958-008-9168-2
- A. N. Gribov, P. A. Zolotykh and A. V. Mikhalev, “A Construction of Algebraic Cryptosystem over the Quasigroup Ring,” Mathematical Aspects of Cryptography, Vol. 1, No. 4, 2010, pp. 23-32 (in Russian).
- K. N. Ponomarev, “Automorphically Rigid Group Algebras I. Semisimple Algebras,” Algebra and Logic, Vol. 48, No. 5, 2009, pp. 654-674. doi:10.1007/s10469-009-9064-y
- K. N. Ponomarev, “Automorphically Rigid Group Algebras II. Modular Algebras,” Algebra and Logic, Vol. 49, No. 2, 2010, pp. 216-237.
- K. N. Ponomarev, “Rigid Group Rings,” In: A. G. Pinus and K. N. Ponomarev, Eds., Algebra and Model Theory, 6, Novosobirsk Technical University Press, Novosibirsk, 2007, pp. 73-83 (in Russian). doi:10.1007/s10469-010-9086-5
- A. Popova and E. Poroshenko, “Units Group of Integral Group Rings of Finite Groups,” In: A. G. Pinus and K. N. Ponomarev, Eds., Algebra and Model Theory, 4, Novosibirsk Technical University Press, Novosibirsk, 2003, pp. 99-106 (in Russian).
- A. Dooms and E. Jespers, “Normal Complements of the Trivial Units in the Unit Group of Some Integral Group Rings,” Communications in Algebra, Vol. 31, No. 1, 2003, pp. 475-482. doi:10.1081/AGB-120016770
- Y. I. Merzlyakov, “Matrix Representations of Free Groups,” Doklady Akademii Nauk, Vol. 238, No. 3, 1978, pp. 527-533 (in Russian).
- A. Popova, “Group of Automorphisms of the Ring
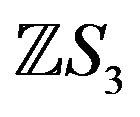 ,” In: A. G. Pinus and K. N. Ponomarev, Eds., Algebra and Model Theory, 6, Novosibirsk Technical University Press, Novosibirsk, 2007, pp. 84-90 (in Russian).
,” In: A. G. Pinus and K. N. Ponomarev, Eds., Algebra and Model Theory, 6, Novosibirsk Technical University Press, Novosibirsk, 2007, pp. 84-90 (in Russian). - A. Mahalanobis, “A Simple Generalization of the ElGamal Cryptosystem to Non-Abelian Groups,” Communications in Algebra, Vol. 36, No. 10, 2008, pp. 3878-3889. doi:10.1080/00927870802160883
- S.-H. Paeng, K.-C. Ha, J. N. Kim, S. Chee and C. Park, “New Public Key Cryptosystem Using Finite Non-Abelian Groups,” Proceedings of the Crypto 2001, Lecture Notes in Computer Sciences, Santa Barbara, 19-23 August 2001, pp. 470-485.
- M. I. Kargapolov and Y. I. Merzlyakov, “Foundations of Group Theory,” Nauka, Moscow, 1977 (in Russian).
- R. C. Lyndon and P. E. Schupp, “Combinatorial Group Theory,” Springer-Verlag, Berlin, Heidelberg, New York, 1977.

