ABSTRACT

The paper deals with cluster analysis and comparison of clustering methods. Cluster analysis belongs to multivariate statistical methods. Cluster analysis is defined as general logical technique, procedure, which allows clustering variable objects into groups-clusters on the basis of similarity or dissimilarity. Cluster analysis involves computational procedures, of which purpose is to reduce a set of data on several relatively homogenous groups-clusters, while the condition of reduction is maximal and simultaneously minimal similarity of clusters. Similarity of objects is studied by the degree of similarity (correlation coefficient and association coefficient) or the degree of dissimilarity-degree of distance (distance coefficient). Methods of cluster analysis are on the basis of clustering classified as hierarchical or non-hierarchical methods.

1. Introduction

“Cluster analysis is a general logic process, formulated as a procedure by which groups together objects into groups based on their similarities and differences.” [1]

Having a data matrix X type n × p, where n is the number of objects and p is the number of variables (features, characteristics). Next there is a decomposition S(k) of set n objects to k certain groups (clusters), i.e.

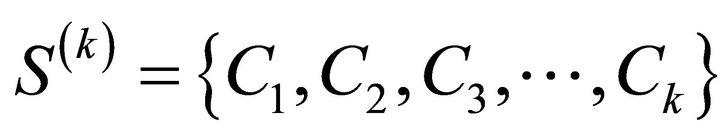, [2]:

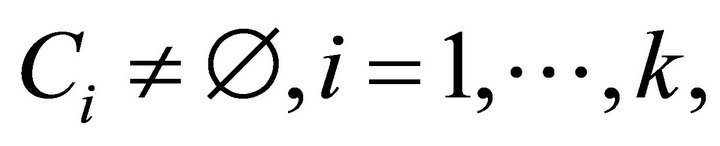
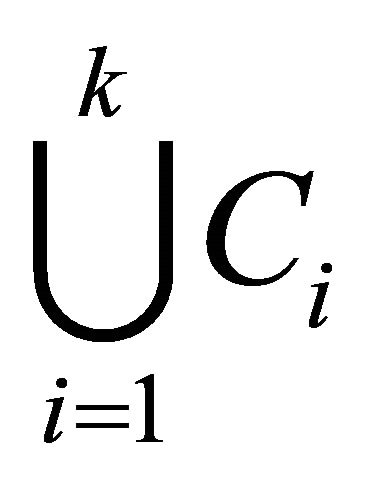comprises all the space.

If that set of objects and any dissimilarity coefficient of objects D, then a cluster is called a subset of p sets of objects o to which it applies [2]:

where and. This means that the maximum distance of objects belonging to the cluster must always be less than the minimum distance any object from the cluster and object outside cluster.

The input for the clustering of the input data matrix and output are specific identification of clusters. The input matrix X of size n × p contains the i-th row of characters x_ij object A_i, where 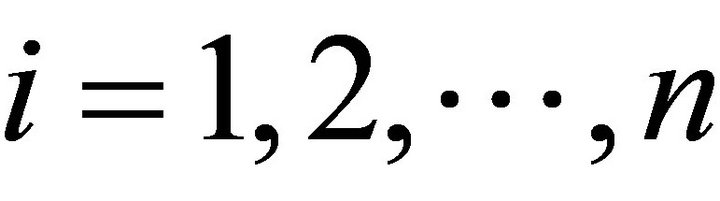and. Therefore

.

2. Cluster Analysis Methods

Classification of cluster analysis methods is shown in Figure 1.

2.1. Hierarchical Cluster Analysis Methods

Hierarchical cluster analysis methods included of the analyzed objects into a hierarchical system of clusters. This system is defined as a system of mutually distinct non-empty subsets of the original set of objects. The main characteristic of hierarchical methods of cluster analysis is creating a decomposition of the original set of objects, in which each of the partial decomposition refines next or previous decomposition.

According to the way of creating decompositions (Figure 2) the hierarchical clustering methods are divided into several groups:

• Agglomerative clustering—at the beginning of clustering are considered individual objects as separate

clusters. The next steps will then be the most similar clusters combine into larger clusters until the specified criteria of quality decomposition is fulfilled.

• Divisional clustering—at the beginning of the clustering process all objects are in one cluster. This cluster is then divided into smaller clusters.

Agglomerative hierarchical clustering methods assign to set of objects O the sequence of its decomposition 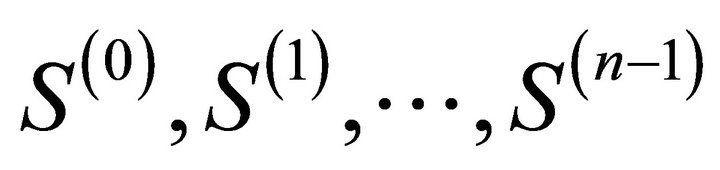to clusters and hereby the real nonnegative number is assigned to each cluster.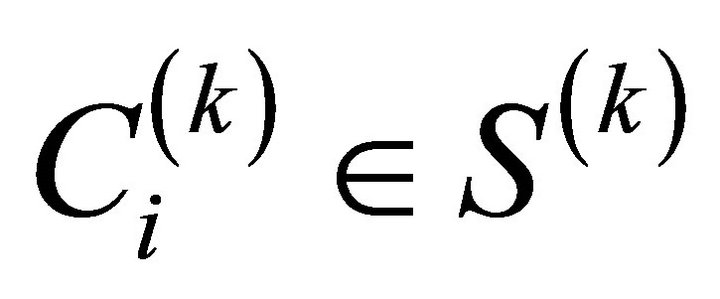

1) The decomposition of the set of objects 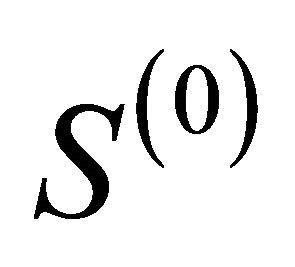are its individual objects, i.e., single element clusters whereby the numbe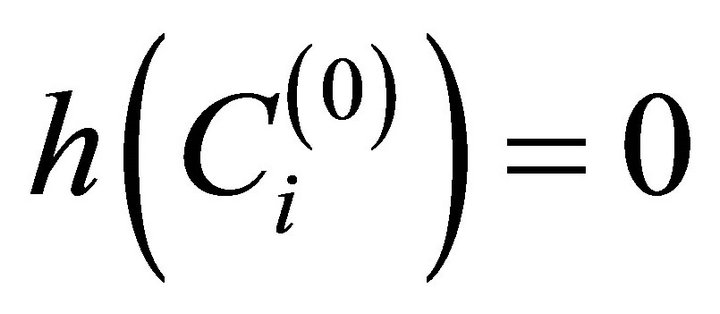r for belongs to each single element cluster.

2) There is a decomposition 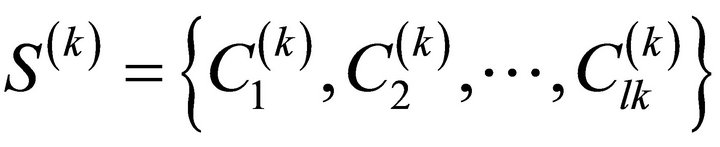and the numbers 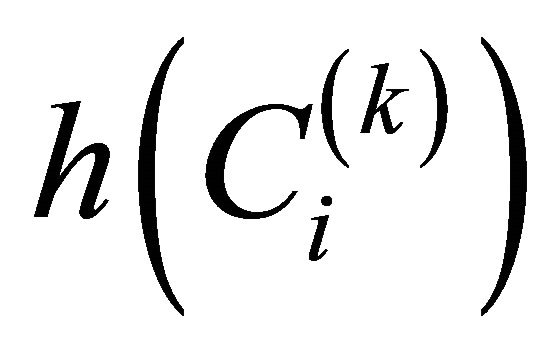for 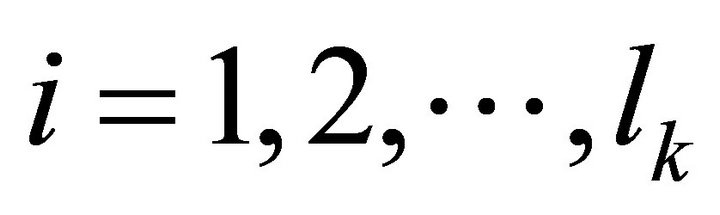are assigned to clusters. A pair of cluster which has the minimal dissimilarity of coefficient D is chosen, it means, they are the most similar. These clusters are combined to form one cluster. Other clusters stay unchanged and they pass to next decomposition.

2.1.1. Simple Linkage Method

The simple linkage method can be defined as follows: if D is a random coefficient of dissimilarity, symbols C₁, C₂ are two different clusters, A_i object belongs to a cluster C₁ and object A_j belongs to cluster C₂ then

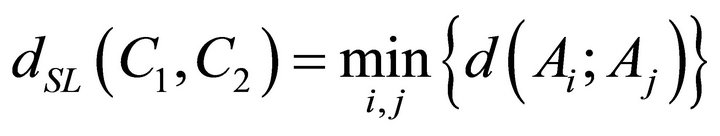
determines the distance of clusters for the Simple linkage method [3].

2.1.2. Complete Linkage Method

The complete linkage method is a dual method to the simple linkage method its principle is following [3]:

If D is a random coefficient of dissimilarity, symbols C₁, C₂ are two different clusters, A_i object belongs to a cluster C₁ and object A_j belongs to cluster C₂ then

determines the distance of clusters for the complete linkage method.

2.1.3. Average Linkage Method

The distance between the clusters for the average linkage method is defined as follows [3]:

If D is a random coefficient of dissimilarity, symbols C₁, C₂ are two different clusters, A_i object belongs to a cluster C₁ and object A_j belongs to cluster C₂ then

determines the distance of clusters for the average linkage method, where n₁ and n₂ are the number of objects in clusters C₁ and C₂.

2.1.4. Centroid’s Method

In Centroid’s method the dissimilarity of 2 clusters is expressed as the distance of centroids of these clusters. Each cluster is represented by the average of its elements, which is called the centroid. The distance between clusters is determined by the Lance-William correlation:

where n₁, n₂ and n₃ are the number of objects in clusters C₁, C₂ and C₃.

2.1.5. The Median Method

If the size of the clusters is different, the centroid of new cluster may lie within a larger cluster or near the larger cluster. The median method tries to reduce this deficiency in that way that it does not reflect the size of clusters, but it reflects its average. The distance between newly-formed clusters and other clusters is calculated by equation [3]:

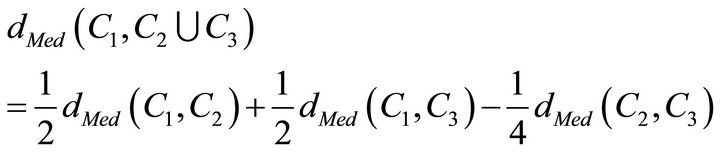
2.1.6. Ward’s Method

Ward’s method is also marked as a method of minimizing the increases of errors of sum squares. It is based on optimizing the homogeneity of clusters according to certain criteria, which is minimizing the increase of errors of sum squares of deviation points from centroid. This is the reason why this method is different from previous methods of hierarchical clustering, which are based on optimization of the distance between clusters [4].

The loss of information is determined at each level of clustering, which is expressed as the increase of total sum of aberrance square of each cluster point from the average ESS value. Then it comes to a connection of clusters where there is a minimal increase in the errors of sum of squares [5].

The accruement of ESS function is calculated according to [5]:

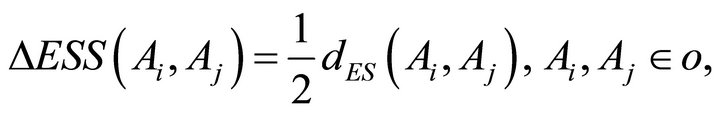
where.

2.2. Non-Hierarchical Cluster Analysis Methods

For non-hierarchical cluster analysis methods is the typical classification of objects into a predetermined number of disjunctive clusters. These clustering methods can be divided into 2 groups [6]:

• Hard clustering methods—assignment an object to a cluster is clear;

• Fuzzy cluster analysis—it calculates the rate of relevancy of objects to clusters.

3. Conclusion

In recent years, many companies, institutions and organizations collect a full range of database. The process of accumulation of data has an explosive character, that it’s why it is important to find one’s way in these data and extract some relevant information. The importance of clustering methods increases for that reason.

REFERENCES

NOTES

^*This article was created by implementation of the grant project VEGA no. 1/0102/11 Experimental methods and modeling techniques in-house manufacturing and non-manufacturing processes.