Applied Mathematics
Vol.4 No.1(2013), Article ID:27131,6 pages DOI:10.4236/am.2013.41010
MHD Free Convective Flow of Water near 4˚C past a Vertical Moving Plate with Constant Suction
1Department of Mathematics, University of Ioannina, Ioannina, Greece
2Instituto de Matemática, Estatística e Computação Científica, Universidade Estadual de Campinas, Campinas, Brasil
Email: *mxenos@cc.uoi.gr, spawn@math.upatras.gr, araptis@uoi.gr
Received November 9, 2012; revised December 9, 2012; accepted December 16, 2012
Keywords: Free Convection; Water near 4˚C; Constant Magnetic Field; Finite Volume Method
ABSTRACT
The aim of this work is the study of the magnetohydrodynamic (MHD) unsteady free convective flow of water near 4˚C past an infinitely vertical plate moving with constant velocity. The influence of constant uniform suction was also considered. The partial differential equations (PDEs) and their initial and boundary conditions, describing the problem under consideration, are dimensionalized and the numerical solution is obtained by using the finite volume discretization methodology which is suitable for Fluid Mechanics applications. The numerical results for the velocity and temperature fields are shown in figures for different dimensionless parameters entering in the problem under consideration, such as the magnetic parameter, M and the Grashof number, Gr. This study predicts the effects of a constant magnetic field and uniform suction on the free convective flow of water near 4˚C, when the water is electrically conductive. Analysis of the results showed that the velocity and temperature profiles are noticeably influenced by these parameters.
1. Introduction
Free convection flow past an infinite vertical plate is an important application from a technological point of view. It becomes a more attractive problem when the fluid is water near 4˚C, electrically conductive, and the flow is subjected to a transverse and constant magnetic field.
It is known that for a fluid like air or water at ordinary temperature and atmospheric pressure the variation 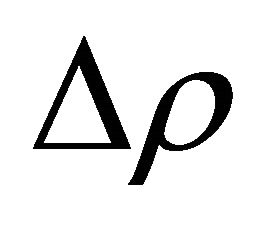 of the density with the variation
of the density with the variation  of the temperature is given by
of the temperature is given by
 (1)
(1)
where  at 20˚C. However, for temperature variations of magnitude ±4˚C away from 4˚C, the variations in density are very closely given by
at 20˚C. However, for temperature variations of magnitude ±4˚C away from 4˚C, the variations in density are very closely given by
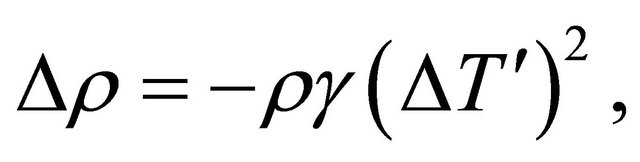 (2)
(2)
with  equal to
equal to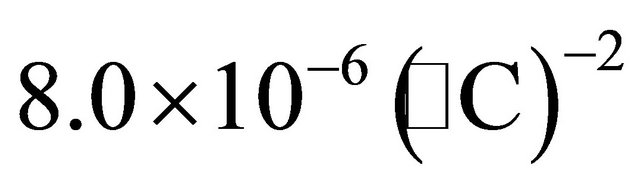 . From the above it is apparent that for small temperature variations, free convection in water near 4˚C would be different from that at 20˚C [1].
. From the above it is apparent that for small temperature variations, free convection in water near 4˚C would be different from that at 20˚C [1].
Many researchers have studied the steady free convective flow of water near 4˚C past a vertical plate. Govindarajulu [2] has studied the steady free convection flow of water near 4˚C on vertical and horizontal plates when the temperature of the plate is varying as a power of the distance along the plate from the leading edge. Soundalgekar [3] has investigated the free convection effects on oscillatory flow of water near 4˚C past an infinite vertical and porous plate with constant suction. The transient free convection of water near 4˚C over a doubly infinite vertical porous plate was studied by Pop and Raptis [4].
The combined convection flow of water near 4˚C through a porous medium bounded by a vertical plate was studied by Raptis and Pop [5]. Raptis and Perdikis also studied the free convection flow of water near 4˚C past an infinite porous plate with constant suction and free stream-velocity [6]. Singh and Raptis, further investigated the free-convection flow of water near 4˚C past an infinite vertical porous plate with constant heatflux [7]. The steady mixed convective water flow over a vertical plate in a porous medium near 4˚C when the wall temperature and surface heat flux vary, were studied by Ling et al. [8,9]. Oztop et al. [10], studied the natural convection in a triangular enclosure filled with porous media saturated with water near 4˚C. Recently, the free convection stagnation-point boundary-layer flow in a porous medium with density maximum was studied by Merkin and Kumaran [11]. The mixed convection of water near 4˚C along a wedge with variable surface temperature in porous medium was studied by Khan and Gorla [12]. They also studied the nonsimilar solutions for mixed convection of water near 4˚C in a porous medium [13].
The MHD free-convection effects on the oscillatory flow of water near 4˚C past an infinite porous plate was studied by Georgantopoulos et al. [14]. The steady Magnetohydrodynamic (MHD) free convective flow of water near 4˚C past a semi-infinite porous plate was studied by Perdikis and Takhar [15]. Recently, Guedda et al. [16], used the Chebyshev pseudospectral differentiation matrix (ChPDM) approach for studying the MHD mixed convection of a vertical plate embedded in a porous medium filled with water near 4˚C.
In this work we consider the unsteady free convective flow of water near 4˚C in the laminar boundary layer over a vertically moving permeable plate, under the influence of a constant transverse magnetic field. The presented results were obtained after dimensionalization of the PDEs using a numerical approach. This approach is based on the finite volume (FV) discretization scheme which is suitable for Fluid Mechanics applications. The discretization was performed with the help of a specialized symbolic package created by the authors in Mathematica.
2. Mathematical Analysis
We consider the unsteady free convective and MHD flow of water near 4˚C past an infinite vertical moving plate with uniform suction. The  -axis is taken along the plate in the vertical upward direction and the
-axis is taken along the plate in the vertical upward direction and the 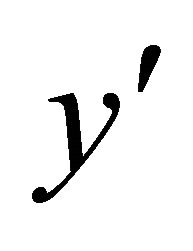 -axis normal to the plate, Figure 1. The equations governing the problem are:
-axis normal to the plate, Figure 1. The equations governing the problem are:
Continuity equation
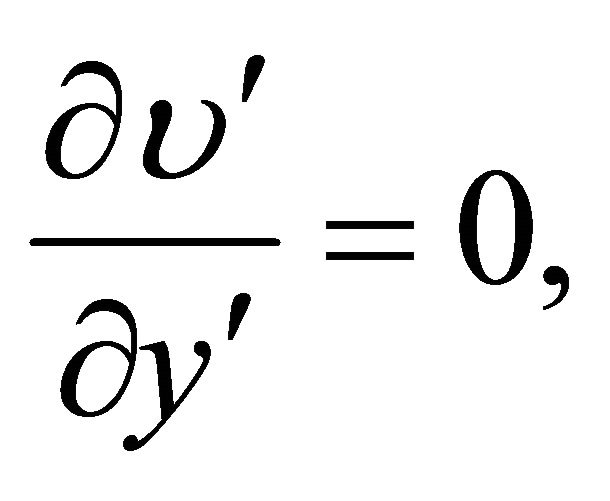 (3)
(3)
Equation of motion
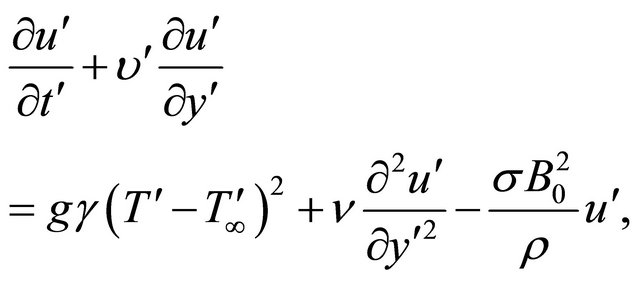 (4)
(4)
Energy equation
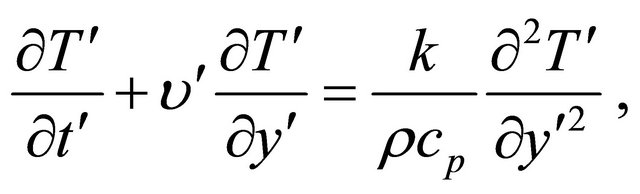 (5)
(5)
where  is the velocity component at the
is the velocity component at the 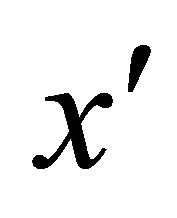 -direction,
-direction, 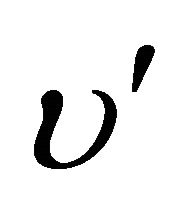 is the normal velocity at the plate,
is the normal velocity at the plate,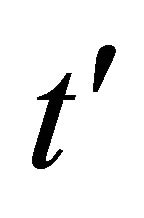 : the time;
: the time;![]() : the acceleration due to gravity;
: the acceleration due to gravity; : the coefficient of thermal expansion;
: the coefficient of thermal expansion;![]() : the kinematic viscosity;
: the kinematic viscosity;![]() : the electrical conductivity;
: the electrical conductivity; : the magnetic induction;
: the magnetic induction;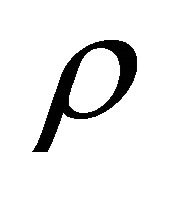 : the fluid density;
: the fluid density;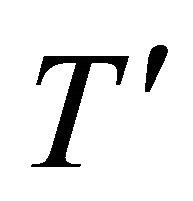 : the fluid temperature;
: the fluid temperature;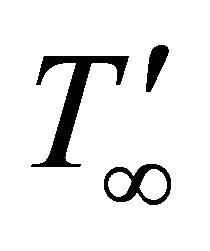 : the
: the
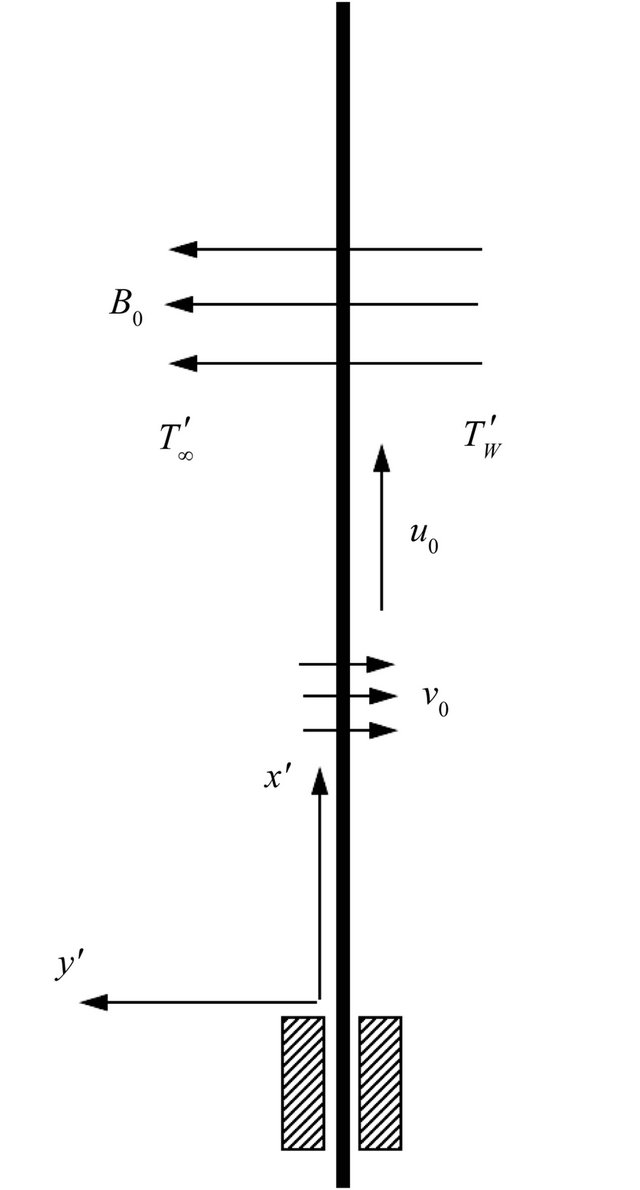
Figure 1. Physical model and coordinate system of the problem.
fluid temperature at infinity;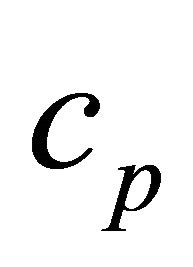 : the specific heat at constant pressure and
: the specific heat at constant pressure and : the thermal conductivity.
: the thermal conductivity.
The initial and the boundary conditions are
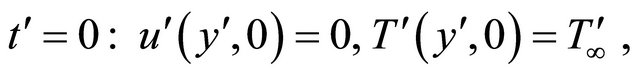 (6)
(6)
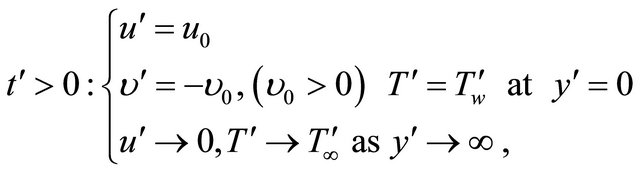 (7)
(7)
where u0 is the velocity of the plate, 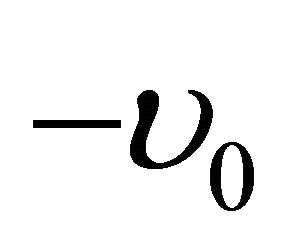 is the constant normal suction and
is the constant normal suction and 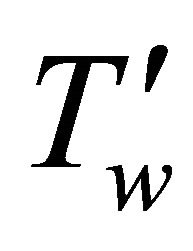 is the temperature of the plate. From (3) it is obtained that
is the temperature of the plate. From (3) it is obtained that , for every
, for every .
.
We introduce the dimensionless quantities
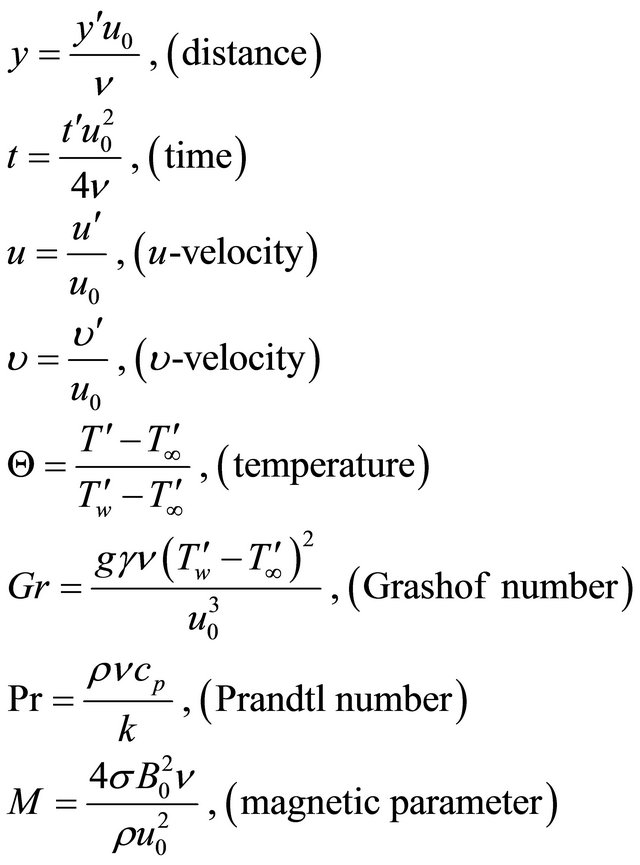 (8)
(8)
Using the dimensionless quantities in (8), Equations (4) and (5) become respectively:
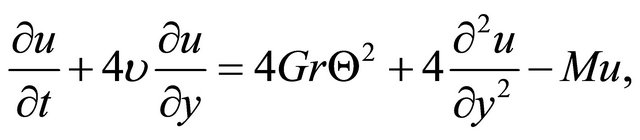 (9)
(9)
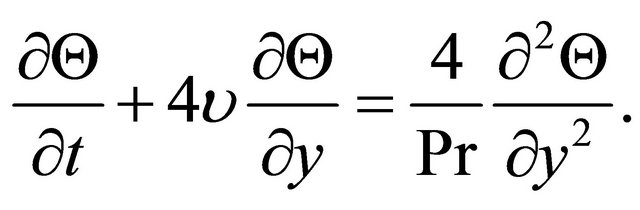 (10)
(10)
The initial and boundary conditions in dimensionless form are as follows:
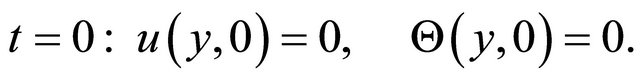 (11)
(11)
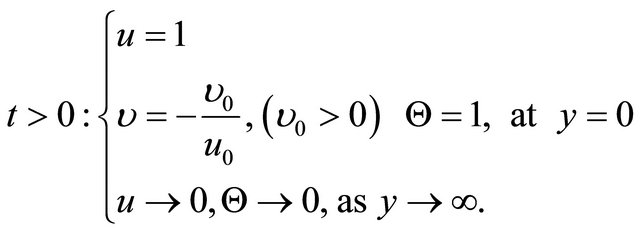 (12)
(12)
Finally, the problem under consideration is described by the system of Equations (9) and (10), subjected to the initial and boundary conditions (11) and (12).
3. Numerical Solution
Contrary to the technique used in previous works of the authors for numerically solving the problem at hand [17], in the present paper we follow a more symbolic approach. For this purpose we have used the Computer Algebra System (CAS) Mathematica [18].
The analysis begins by obtaining the discretized form of the system of Equations (9)-(10) by using a symbolic package developed by the authors for that purpose. To discretize the coupled set of PDEs the finite volume method on a collocated grid is used (all variables are discretized at the center of the control volume, Figure 2) [19]. The result of this discretization is given below:
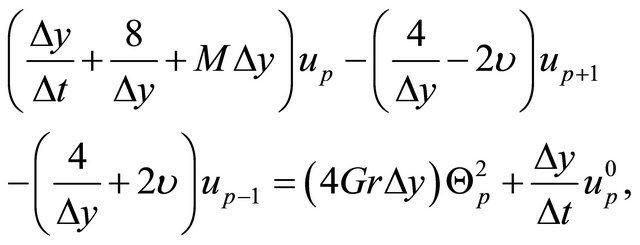 (13)
(13)
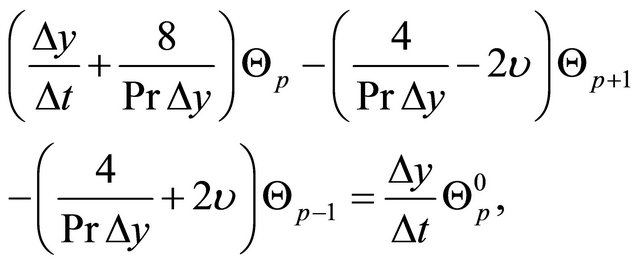 (14)
(14)
where 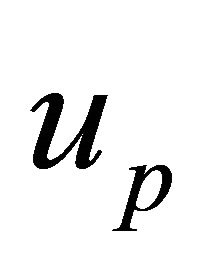 and
and  are the unknown quantities at the center of the control volume as shown in Figure 2,
are the unknown quantities at the center of the control volume as shown in Figure 2,  and
and 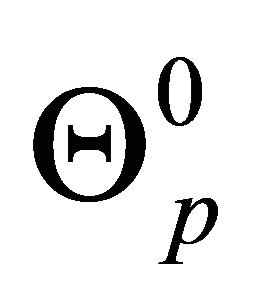 are the unknown quantities at the center of the control volume at the previous time, and where all the parameters,
are the unknown quantities at the center of the control volume at the previous time, and where all the parameters,  ,
, 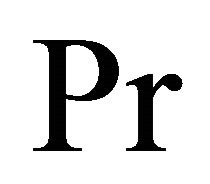 and
and 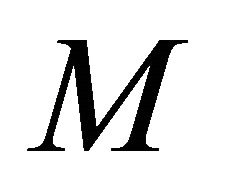 are introduced in (8).
are introduced in (8).
Having obtained the discretized systems (13)-(14), we construct the system of algebraic equations that constitute the grid for each time step. By grid and time in-
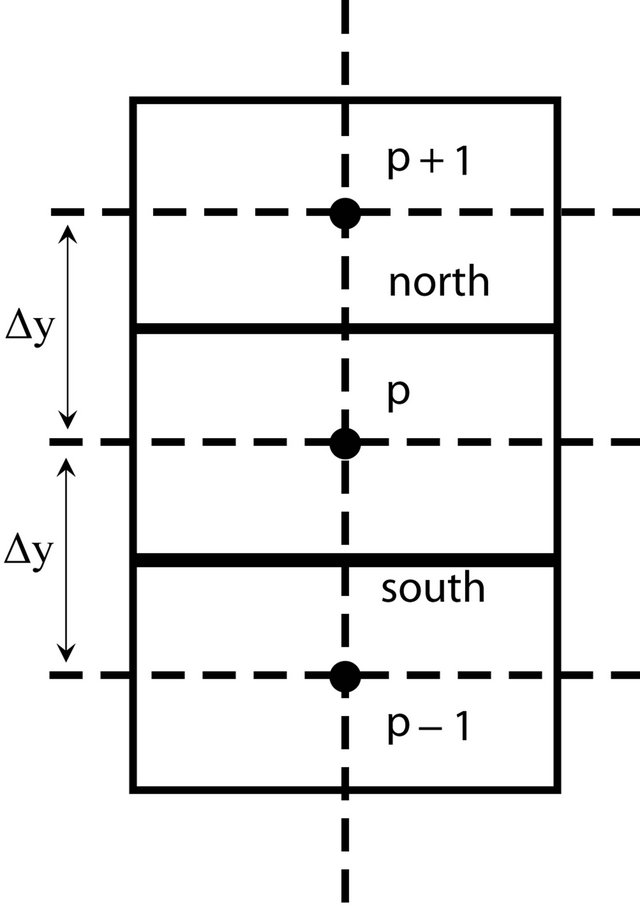
Figure 2. Finite Volume discretization scheme, collocated approach.
dependence studies with different grid sizes, it is established that the results are time and space independent for 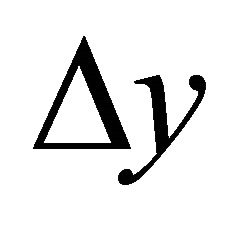 equal to 0.05 and
equal to 0.05 and 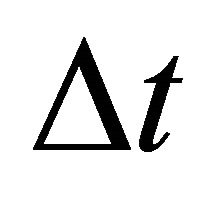 equal to
equal to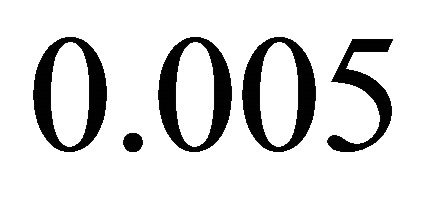 .
.
Then, for each time step, the system is solved algebraically by Mathematica’s function Solve in respect to the grid values of the functions![]() , after first substituting the values of the previous time steps to the system. The procedure is optimized for speed by keeping all the grid values for all the time steps in memory.
, after first substituting the values of the previous time steps to the system. The procedure is optimized for speed by keeping all the grid values for all the time steps in memory.
4. Results and Discussion
The system of equations under consideration is a highly coupled system of two nonlinear equations, whose solution can be tedious. However, with the advancement of numerical techniques such as the finite volume (FV) methodology, which is suitable for Fluid Mechanics applications, problems like this can be solved. A thorough analysis of the problem under consideration includes the study of the velocity and temperature fields under the influence of the dimensionless parameters entering in the problem, such as the magnetic parameter, 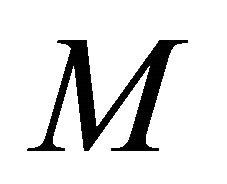 and the Grashof number,
and the Grashof number, . The Prandtl number was the same for all cases and equal to 11.4.
. The Prandtl number was the same for all cases and equal to 11.4.
Initially, the suction velocity was considered equal to zero, 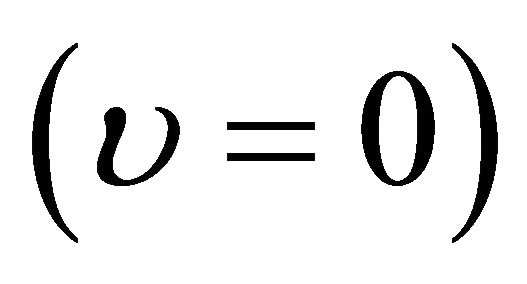 and the influence of the dimensionless parameters entering in the problem was studied. Next, the effect of a constant suction velocity,
and the influence of the dimensionless parameters entering in the problem was studied. Next, the effect of a constant suction velocity, ![]() , on the velocity and temperature profiles under the influence of a constant transverse magnetic field was investigated.
, on the velocity and temperature profiles under the influence of a constant transverse magnetic field was investigated.
4.1. Case I, Suction Velocity, 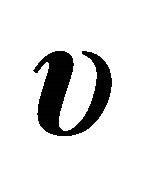 , Is Zero
, Is Zero
The velocity and temperature distributions for different dimensionless times 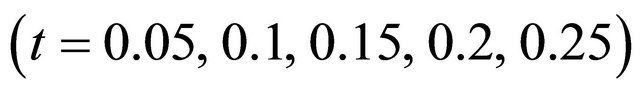 are shown in Figure 3. In this case, the velocity and temperature fields increase away from the flat plate, as time increases.
are shown in Figure 3. In this case, the velocity and temperature fields increase away from the flat plate, as time increases.
The effect of the magnetic parameter, M, on the
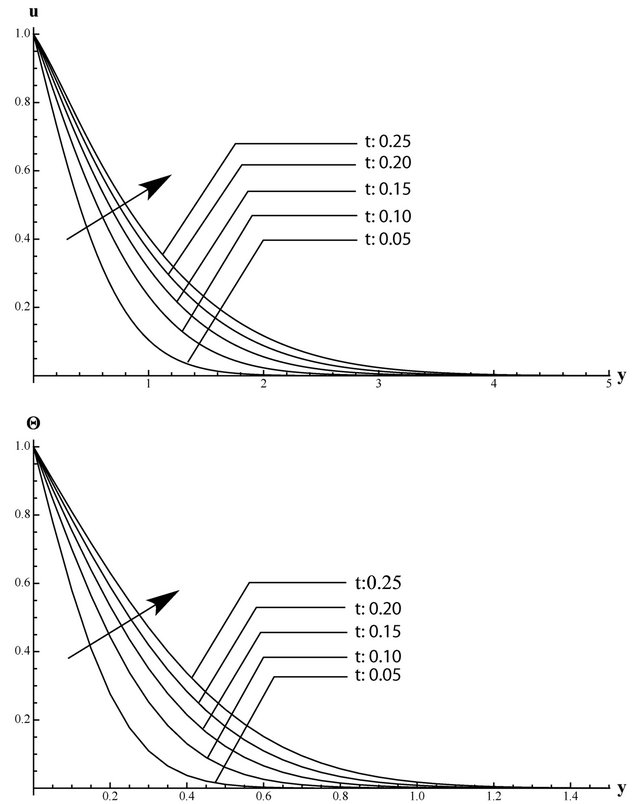
Figure 3. Dimensionless velocity and temperature distributions for different dimensionless time (t = 0.05, 0.1, 0.15, 0.2, 0.25).
velocity field for different times , (
, ( and
and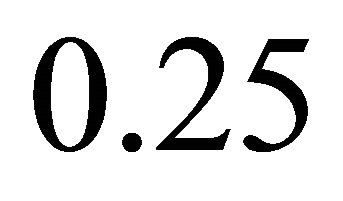 ) are shown in Figures 4 and 5. For
) are shown in Figures 4 and 5. For 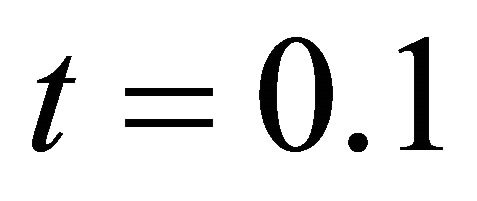 the magnetic parameter, M, decreases the velocity, Figure 4. Similarly, for t = 0.25 the velocity decreased throughout the boundary layer when the magnetic parameter was increased, Figure 5. This is because the presence of a magnetic field introduces a force (Lorentz force) that acts on the fluid (water) creating a drag-like effect that slows down the flow in the boundary layer.
the magnetic parameter, M, decreases the velocity, Figure 4. Similarly, for t = 0.25 the velocity decreased throughout the boundary layer when the magnetic parameter was increased, Figure 5. This is because the presence of a magnetic field introduces a force (Lorentz force) that acts on the fluid (water) creating a drag-like effect that slows down the flow in the boundary layer.
Figures 6 and 7 show the effect of Grashof number,  , on the velocity profiles for
, on the velocity profiles for 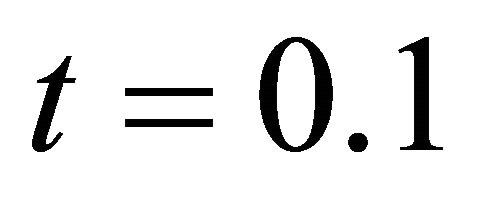 and
and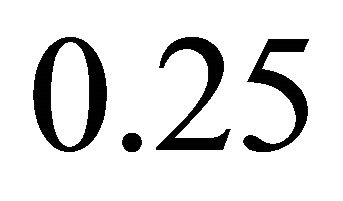 . The velocity increased noticeably near the plate as the Grashof number increased, due to the increase of the buoyancy forces compared to the viscous forces acting on the fluid (water) near 4˚C.
. The velocity increased noticeably near the plate as the Grashof number increased, due to the increase of the buoyancy forces compared to the viscous forces acting on the fluid (water) near 4˚C.
4.2. Case II, Suction Velocity, 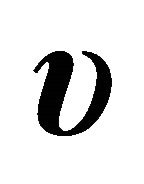 , Is Constant
, Is Constant
The effect of a constant suction velocity on the velocity and temperature fields under the influence of a constant transverse magnetic field was also studied. The effects of suction velocity upon the velocity and temperature fields for dimensionless time t = 0.25 are shown in Figures 8

Figure 4. The effect of the magnetic parameter, M, on the dimensionless velocity distribution for t = 0.1.
and 9. It is evident from the figures that as the absolute value of suction velocity increases, the profiles of the velocity and temperature decrease. These findings are in accordance with previously published results [20]. It is also worth noting that the suction velocity has a more profound effect on the temperature field, Figure 9.
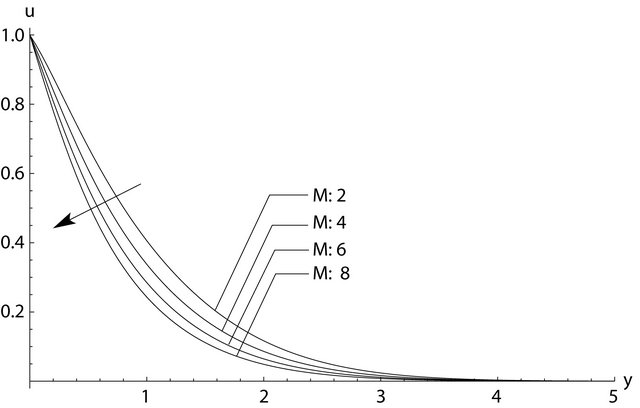
Figure 5. The effect of the magnetic parameter, M, on the dimensionless velocity distribution for t = 0.25.
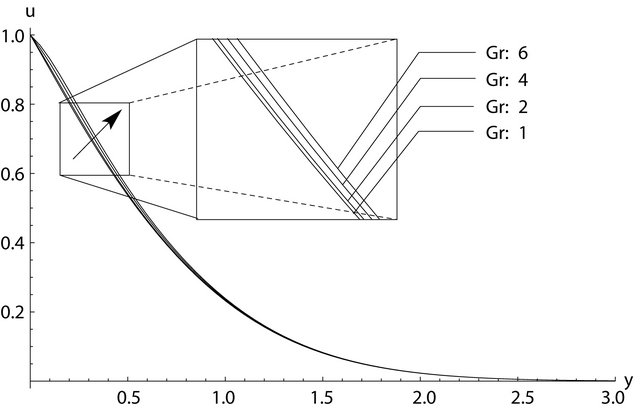
Figure 6. The effect of Grashof number, Gr, on the dimensionless velocity profiles for t = 0.1.
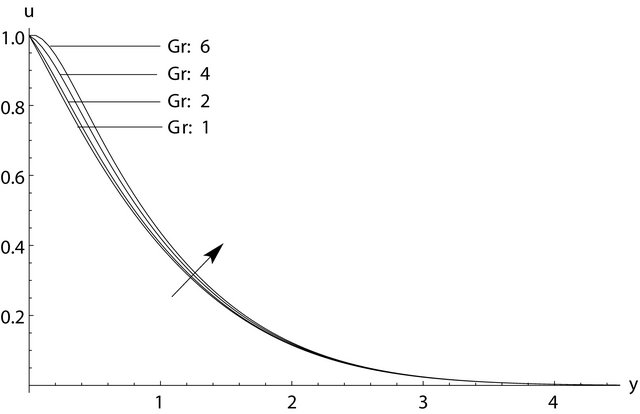
Figure 7. The effect of Grashof number, Gr, on the dimensionless velocity profiles for t = 0.25.
5. Conclusions
The unsteady free convective flow of water near 4˚C, past a vertical plate, moving with constant velocity, and subjected to a transverse magnetic field and constant suction velocity was numerically studied.
In the present paper an analytic/symbolic approach was chosen for solving the system of Equations (9) and (10), subjected to the initial and boundary conditions (11)
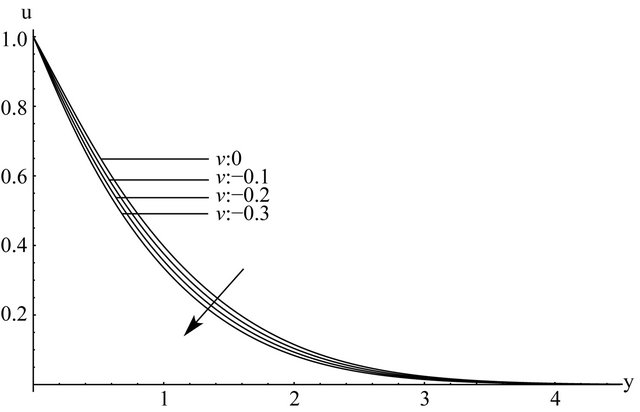
Figure 8. The effect of constant dimensionless suction on the dimensionless velocity profiles for Pr = 11.4, Gr = 1, M = 2, and t = 0.25.

Figure 9. The effect of constant dimensionless suction on the dimensionless temperature profiles for Pr = 11.4, Gr = 1, M = 2, and t = 0.25.
and (12). A symbolic package developed in Mathematica is used for obtaining the discretization of the problem and for constructing the algebraic system to be solved for each grid point. Then, for each time step the system was solved analytically using the numerical data of the previous time step, hence avoiding errors in accuracy due to the use of a numerical solver such as a Newton-like method. As a consequence, the obtained solution is more accurate for greater values of t.
Moreover, further development of the symbolic package for the fast and accurate discretization of dynamical systems using the Finite Volume approach (with the option of different grid choices available to the user) will be an invaluable tool for any researcher using the Finite Volumes discretization scheme, especially for systems in multi-dimensions where the calculations by hand are not only time consuming but also error prone.
The results of this study showed that the velocity and temperature fields increase away from the flat plate, as time increases. For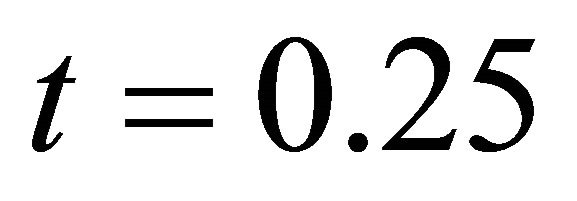 , the velocity decreased throughout the boundary layer when the magnetic parameter was increased while it increased noticeably near the plate when the Grashof number was increased. Finally, as the value of the suction velocity increased, the profiles of velocity and temperature decreased.
, the velocity decreased throughout the boundary layer when the magnetic parameter was increased while it increased noticeably near the plate when the Grashof number was increased. Finally, as the value of the suction velocity increased, the profiles of velocity and temperature decreased.
REFERENCES
- S. Goren, “On Free Convection in Water at 4˚C,” Chemical Engineering Science, Vol. 21, No. 6-7, 1966, pp. 515- 518. doi:10.1016/0009-2509(66)85065-0
- T. Govindarajulu, “Free Convection Flow of Water at 4˚C on Vertical and Horizontal Plates,” Chemical Engineering Science, Vol. 25, No. 11, 1970, pp. 1827-1828. doi:10.1016/0009-2509(70)80076-8
- V. Soundalgekar, “Free Convection Effects on the Oscillatory Flow of Water at 4˚C past an Infinite Vertical, Porous Plate with Constant Suction,” Heat and Mass Transfer, Vol. 9, 1976, pp. 111-115.
- I. Pop and A. Raptis, “A Note on Transient Free Convection of Water at 4˚C over a Doubly Infinite Vertical Porous Plate,” Journal of Heat Transfer-Transactions of the ASME, Vol. 104, 1982, pp. 800-802. doi:10.1115/1.3245206
- A. Raptis and I. Pop, “Combined Convection Flow of Water at 4˚C through a Porous Medium Bounded by a Vertical Surface,” Letters in Heat and Mass Transfer, Vol. 9, 1982, pp. 309-318. doi:10.1016/0094-4548(82)90039-X
- A. Raptis and C. Perdikis, “Free Convection Flow of Water at 4˚C past an Infinite Porous Plate with Constant Suction and Free Stream Velocity,” Bulletin de la Classe des Sciences Academie Royale de Belgique, 5th Series— Tome LXVIII, 1982-1984, pp. 259-266.
- A. Singh and A. Raptis, “Free-Convection Flow of Water at 4˚C past an Infinite Vertical Porous Plate with Constant Heat Flux,” Astrophysics and Space Science, Vol. 104, 1984, pp. 399-404. doi:10.1007/BF00650312
- S. Ling, R. Nazar and I. Pop, “Steady Mixed Convection Boundary Layer Flow over a Vertical Flat Plate in a Porous Medium Filled with Water at 4˚C: Case of Variable Wall Temperature,” Transport in Porous Media, Vol. 69, No. 3, 2007, pp. 359-372. doi:10.1007/s11242-006-9077-0
- S. Ling, R. Nazar and J. Merkin, “Steady Mixed Convection Boundary-Layer Flow over a Vertical Flat Surface in a Porous Medium Filled with Water at 4˚C: Variable Surface Heat Flux,” Transport in Porous Media, Vol. 70, No. 3, 2007, pp. 307-321. doi:10.1007/s11242-007-9101-z
- H. Oztop, Y. Varol and I. Pop, “Investigation of Natural Convection in Triangular Enclosure Filled with Porous Media Saturated with Water near 4˚C,” Energy Conversion and Management, Vol. 50, No. 6, 2009, pp. 1473- 1480. doi:10.1016/j.enconman.2009.02.023
- J. Merkin and V. Kumaran, “Free Convection Stagnation-Point Boundary-Layer Flow in a Porous Medium with a Density Maximum,” International Journal of Thermal Sciences, Vol. 50, No. 11, 2011, pp. 2176-2183. doi:10.1016/j.ijthermalsci.2011.05.012
- W. Khan and R. Gorla, “Mixed Convection of Water at 4˚C along a Wedge with Variable Surface Temperature in a Porous Medium,” International Journal of Thermophysics, Vol. 32, No. 10, 2011, pp. 2079-2091. doi:10.1007/s10765-011-1069-9
- W. Khan and R. Gorla, “Nonsimilar Solutions for Mixed Convection of Water at 4˚C over a Vertical Surface with Prescribed Surface Heat Flux in a Porous Medium,” Journal of Porous Media, Vol. 13, 2010, pp. 1025-1032. doi:10.1615/JPorMedia.v13.i11.90
- G. Georgantopoulos, N. Nanousis and C. Douskos, “Hydromagnetic Free Convection Effects on the Oscillatory Flow of Water at 4˚C past an Infinite Porous Plate,” Revue Roumaine de Physique, Vol. 26, 1982, pp. 39-58.
- C. Perdikis and H. Takhar, “MHD Free Convective Flow of Water at 4˚C past a Semi-Infinite Porous Plate,” Bulletin De la Classe des Sciences, 6th serie—Tome V, 1994, pp. 67-70.
- M. Guedda, E. Aly and A. Quahsine, “Analytical and ChPDM Analysis of MHD Mixed Convection over a Vertical Flat Plate Embedded in a Porous Medium Filled with Water at 4˚C,” Applied Mathematical Modelling, Vol. 35, No. 10, 2011, pp. 5182-5197. doi:10.1016/j.apm.2011.04.014
- M. Xenos, S. Dimas and A. Raptis, “MHD and Thermal Radiation of an Optically Thin Gray Fluid in the Presence of an Induced Magnetic Field,” Advances and Applications in Fluid Mechanics, Vol. 11, No. 2, 2012, pp. 73-85.
- Wolfram-Reasearch, Inc., “Mathematica Edition: Version 8.0,” Wolfram Research, Inc., Champaign, 2010.
- S. Patankar, “Numerical Heat Transfer and Fluid Flow,” McGraw-Hill, New York, 1980.
- A. Raptis and C. Perdikis, “Free Convection Flow of Water near 4˚C past a Moving Plate,” Forschung im Ingenieurwesen, Vol. 67, 2002, pp. 206-208. doi:10.1007/s10010-002-0093-0
NOTES
*Corresponding author.

