Applied Mathematics
Vol. 3 No. 11A (2012) , Article ID: 24763 , 6 pages DOI:10.4236/am.2012.331249
Improve the Nonparametric Image Segmentation with Narrowband Levelset and Fast Gauss Transformation*
School of Information Science and Engineering, Yunnan University, Kunming, China
Email: jiangmr@ynu.edu.cn
Received August 8, 2012; revised September 8, 2012; accepted September 16, 2012
Keywords: Nonparametric Image Segmentation; Mutual Information; Narrowband Levelset; Fast Gauss Transformation
ABSTRACT
Nonparametric method based on the mutual information is an efficient technique for the image segmentation. In this method, the image is divided into the internal and external labeled regions, and the segmentation problem constrained by the total length of the region boundaries will be changed into the maximization of the mutual information between the region labels and the image pixel intensities. The maximization problem can be solved by deriving the associated gradient flows and the curve evolutions. One of the advantages for this method does not need to choose the segmentation parameter; another is not sensitive to the noise. By employing the narrowband levelset and Fast Gauss Transformation, the computation time is reduced clearly and the algorithm efficiency is greatly improved.
1. Introduction
In recent years, the image segmentation technology has been made the great progress with many mathematical analytic methods like Partial Differential Equation widely used in it. Among these methods, the non-edge profile model (short as CV model) raised by Chan and Vese [1] is the most famous curve evolution combing with Mumford-Shah function and the levelset method. In addition, Caselles and Catte et al. [2] discussed geometric model based on the geodetic active contours, it can extract the smooth shape target and test a few outlines at the same time. Caselles, Kimmel et al. [3] and N. Paragios, R. Deriche et al. [4] promoted the geodetic active contour model based on the active contours can evolve the outline splitting and merging naturally along with the time changes and detect the internal and external boundaries for many objects according to the image internal geometry measures. These methods are efficiently, but there still exist some difficulties in the computation. The main reason is the parameter selection. For the different style image, choosing the different parameters will obtain the different qualities, and the parameter should be computed for many times in order to get the needed result, and the suitable parameter values usually depend on someone’s experiences. There are some researches using the information theory into the curve evolution. For example, Unal [5] used the information theoretic active polygons to produce the texture segmentation, the carve evolution is based on the image region information with simply statistics such as the mean or the variance. Sun Da et al. [6] estimated the probability density gradient to detect the image edge according to the field edge point’s gradient located in the opposite directions. F. Liu [7] improved the traditional segmentation method with combining the largest mutual information theory and the image histogram.
In this paper, we focus on the implementation of the nonparametric method based on the mutual information developed by J. Kim et al. [8]. In this method, the segmentation problem is developed as the maximization of the mutual information between the region label and the image pixel intensities, subject to a constraint on the total length of the region boundaries. During the iterations, the segmentation result is approached by deriving the associated gradient flow and the curve evolution techniques, extract the target without any parameter given first. But estimating the mutual information between the whole region labels and all the image pixel values in each iteration leads a large amount of calculation. Therefore, we use the narrowband levelset to reduce the computation pixels and use the Fast Gauss Transformation to reduce the time consumption for estimating the mutual information. Compared with some popular methods include boundary-based, region-based segmentation, this method does not have the parameter selection problem, and it is also not sensitive to the noise in the image. The algorithm efficiency is greatly improved, and it is more suitable to be used in solving the practical problem.
2. Nonparametric Method Based on the Mutual Information
2.1. Mutual Information between the Image Intensity and the Label
We review the mutual information between the image intensity and the label which provided by J. Kim et al. [8].
Given an image 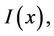
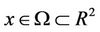 ,
, 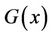 denotes the image intensity at pixel
denotes the image intensity at pixel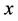 ,
,  and
and 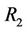 denote the two regions which are unknown. Assume that the pixel intensities in each region are independent, identically and distributed (i.i.d), the associated densities
denote the two regions which are unknown. Assume that the pixel intensities in each region are independent, identically and distributed (i.i.d), the associated densities  if
if  and
and 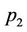 if
if 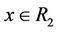 as follows:
as follows:

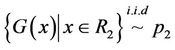
where 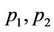 are also unknown.
are also unknown.
Given an initial evolution curve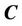 , then
, then 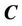 may divide the image into two regions,
may divide the image into two regions, 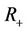 is the region inside the curve and
is the region inside the curve and 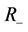 is the region outside the curve. Suppose that
is the region outside the curve. Suppose that 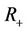 corresponds to
corresponds to 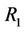 (object region) and
(object region) and  corresponds to
corresponds to 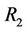 (background region), then the segmentation problem is to move the curve
(background region), then the segmentation problem is to move the curve 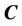 such that
such that  and
and 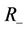 converge to
converge to 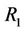 and
and 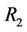 respectively (see Figure 1).
respectively (see Figure 1).
Define the label as follows

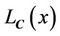 is a binary random variable which depends on the curve
is a binary random variable which depends on the curve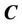 . According to the probability, we have
. According to the probability, we have

Figure 1. Initial the evolution curve.
 (1)
(1)
where 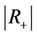 denotes the area of the region
denotes the area of the region 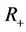 and
and 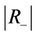 the area of the region
the area of the region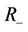 . Therefore, the more accurately the label
. Therefore, the more accurately the label 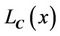 is, the less uncertainty
is, the less uncertainty 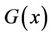 has. Choose an arbitrary point
has. Choose an arbitrary point 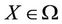 and
and 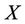 being in
being in  or
or  is uncertain, then the mutual information
is uncertain, then the mutual information 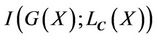 is given by
is given by
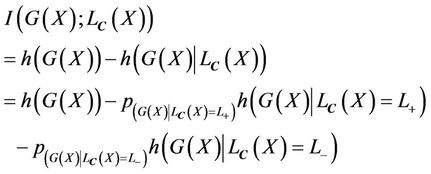 (2)
(2)
where 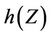 is the differential entropy of a continuous random variable
is the differential entropy of a continuous random variable 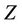 with support
with support  defined by
defined by
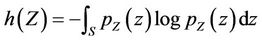
and
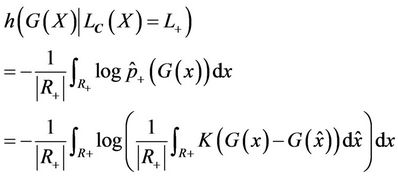 (3)
(3)
 (4)
(4)
where 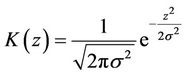 is the kernel and
is the kernel and 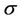 is given. The two conditional distributions are given by
is given. The two conditional distributions are given by
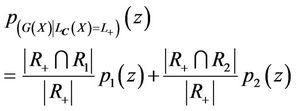 (5)
(5)
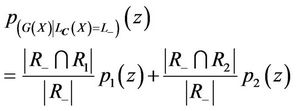 (6)
(6)
Since the mutual information 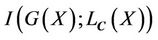 describes the correlation between
describes the correlation between 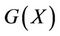 and
and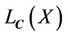 , when
, when 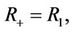
 , then
, then 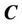 is the correct segmentation, and
is the correct segmentation, and 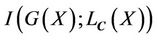 is the maximized.
is the maximized.
2.2. Energy Functional and Its Computation
In order to compute the maximum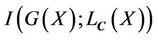 , we use the energy functional given as [8]
, we use the energy functional given as [8]
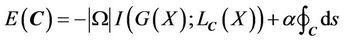 (7)
(7)
where 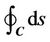 is the length of the curve
is the length of the curve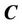 ,
, 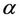 is a scalar parameter. Therefore, the maximization problem of the mutual information
is a scalar parameter. Therefore, the maximization problem of the mutual information 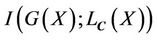 subject to a constraint on the total length of the region boundaries
subject to a constraint on the total length of the region boundaries 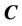 may be changed into the minimization of the energy functional
may be changed into the minimization of the energy functional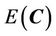 .
.
Let 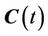 denotes the curve evolution at time
denotes the curve evolution at time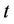 , rewrite the energy functional
, rewrite the energy functional 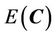 as
as

where 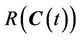 is the region inside the curve
is the region inside the curve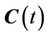 . By using the variation principle and employing Equations (3) and (4), we have the gradient flow equation for
. By using the variation principle and employing Equations (3) and (4), we have the gradient flow equation for 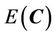 as [8]
as [8]
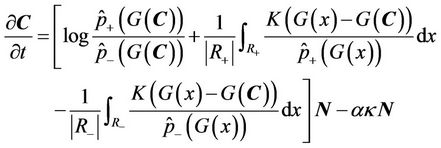 (8)
(8)
where 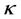 is the curvature of the curve,
is the curvature of the curve, 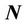 is the outward unit normal vector,
is the outward unit normal vector, 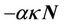 is the gradient flow for the curve length penalty, and
is the gradient flow for the curve length penalty, and

is the density estimate at pixel  inside the curve
inside the curve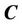 .
.
We compute the gradient flow Equation (8) with the levelset method. The steps are shown as following:
Step 1. Input an image 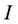 and set the initialize curve
and set the initialize curve 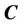 according to the image size.
according to the image size.
Step 2. Compute the signed distance function 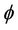 as the levelset function with
as the levelset function with
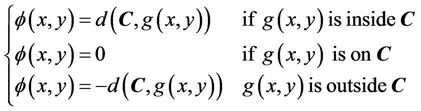
where 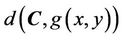 is the Euclidean distance between
is the Euclidean distance between 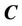 and the point
and the point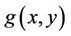 .
.
Step 3. Save the points on the curve 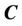 into
into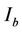 , the points inside the curve
, the points inside the curve 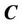 into
into 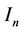 and outside
and outside 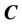 into
into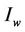 .
.
Step 4. Compute the second term 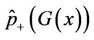 noted as
noted as 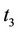 and the third term
and the third term 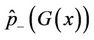 noted as
noted as 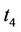 with
with
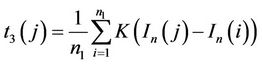
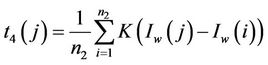
where 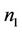 is the pixel number of
is the pixel number of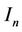 ,
, 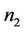 is the pixel number of
is the pixel number of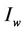 , and
, and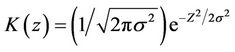 .
.
Step 5. Compute the first term 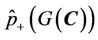 noted as
noted as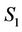 , and
, and  noted as
noted as 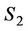 with
with
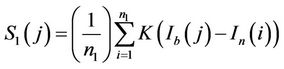
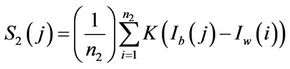
Step 6. Compute the term 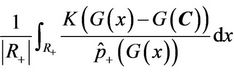 noted as
noted as 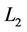
and  noted as
noted as 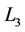 with
with
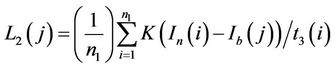
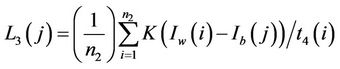
Step 7. Calculate the curvature 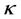 and save it in
and save it in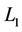 .
.
Step 8. Renew the levelset function 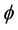 with
with
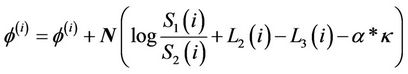
If 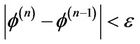 holds, then stop the computation, else return to Step 3.
holds, then stop the computation, else return to Step 3.
Figure 2 shows the result for the noisy image segmentation implemented on Matlab2009a.
3. Using the Narrowband Levelset and Fast Gauss Transformation to Improve the Computation Efficiency
Direct to compute the gradient flow Equation (8) is more expensive. During the iteration, compute 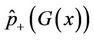 and
and 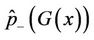 at each pixel
at each pixel 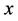 on the curve will take
on the curve will take 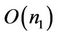 and
and 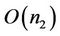 times, compute the density
times, compute the density
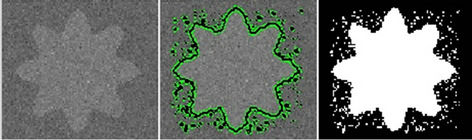
Figure 2. Noisy image segmentation.
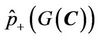 and
and  at all the points on the curve will take
at all the points on the curve will take  time, where
time, where 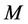 is the number of pixels along the curve. Therefore, compute the gradient flow equation to get the mutual information between the whole region labels and all the image pixel values needs a large amount of calculation. Then, we consider about the narrowband levelset which makes the levelset function update only in the narrowband. Similarly, we use the Fast Gauss Transformation to reduce the time consumption.
is the number of pixels along the curve. Therefore, compute the gradient flow equation to get the mutual information between the whole region labels and all the image pixel values needs a large amount of calculation. Then, we consider about the narrowband levelset which makes the levelset function update only in the narrowband. Similarly, we use the Fast Gauss Transformation to reduce the time consumption.
3.1. Narrowband Levelset Method
Narrowband is a ring surrounding the curve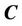 . Narrowband levelset [9,10] is to set the narrowband by choosing a width
. Narrowband levelset [9,10] is to set the narrowband by choosing a width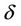 , contracting and expanding the zero levelset curve
, contracting and expanding the zero levelset curve 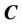 with
with 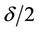 respectively to get the curve
respectively to get the curve  and
and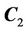 , then the narrowband region is located between the curve
, then the narrowband region is located between the curve 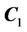 and
and 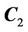 shown as Figure 3. In each iteration, the computation only be produced on the points in the narrowband, the amount for the renew points is reduced, and the computation quantities is also descend obviously.
shown as Figure 3. In each iteration, the computation only be produced on the points in the narrowband, the amount for the renew points is reduced, and the computation quantities is also descend obviously.
Using the narrowband to renew the levelset function is detailed as follows:
1) Initiate the narrowband. Assume the width of the narrowband is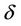 , then initial the label region, assign a larger negative number to the points inside the curve and a larger positive number to the points outside the curve.
, then initial the label region, assign a larger negative number to the points inside the curve and a larger positive number to the points outside the curve.
2) Iterate to renew the levelset. After one iteration, set the new function  to the curve
to the curve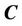 , check if the curve
, check if the curve 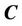 is exceed the bounds of the narrowband. If
is exceed the bounds of the narrowband. If 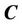 is cross out of the bound, then reinitialize the narrowband, and compute the levelset function
is cross out of the bound, then reinitialize the narrowband, and compute the levelset function 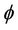 such that the evolution curve
such that the evolution curve  is inside the narrowband. When the computation finished, check whether the terminal condition is satisfied. Once the iteration stops,
is inside the narrowband. When the computation finished, check whether the terminal condition is satisfied. Once the iteration stops, 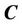 is the needed segmentation boundary.
is the needed segmentation boundary.
It is easy to see that, different width of the narrowband
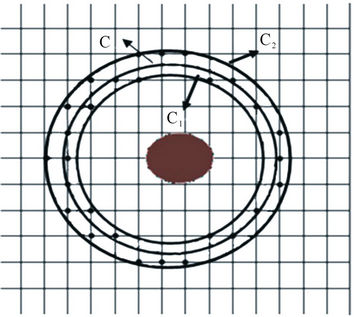
Figure 3. Narrowband.
will lead the different efficiency. If the width is too small, the initialization of the narrowband and levelset function need to be replaced many times; and if the width is too large, the number of points will be increased. Both of them will increase the time consumption. Usually, the better width is 7 - 10.
3.2. Fast Gauss Transformation
Fast Gauss Transformation [11] is using the following weighted Gauss function
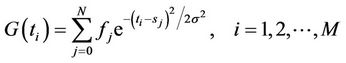
where 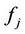 is the weights,
is the weights, 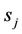 ,
, is the center of the Gauss function,
is the center of the Gauss function, 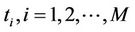 are the goal points. By using the Hermite function:
are the goal points. By using the Hermite function: ,
, 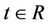 , where
, where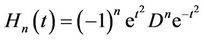 ,
,  , we have
, we have

where 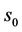 is the center of the expanding Hermite function. Exchange
is the center of the expanding Hermite function. Exchange 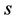 and
and , we also have
, we also have
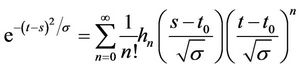
Then the Fast Gauss Transformation is

Because of the series drop fast and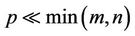 , the computation amount is also reduced obviously.
, the computation amount is also reduced obviously.
Table 1 shows the computation time comparison using four methods for the noisy image (see Figure 4).
From Table 1, we see that the time produced by the levelset is the biggest, and the time for the improved algorithm with the narrowband levelset and Fast Gauss Transformation is the lowest, which means the efficiency of the improved algorithm.
4. Experimental Results
4.1. Compare with Other Segmentation Methods
Threshold segmentation is a simple but effective solution for most segmentation problems. If the image has some


Figure 4. Noisy image segmentation.

Table 1. Computation time using four methods.
noise, it is difficulty to choose a suitable threshold, one need to produce many experiments to get a better threshold. Region-based segmentation is also sensitive to the noise. Figure 5 shows the results for the noisy image segmentation by using the threshold, region-based and nonparametric methods.
Obviously, for the noisy image, due to the noises located randomly in the whole region, the threshold method can remove some noise but blur the object, and the region-based method can not find the accurately object boundary, but the nonparametric method can get the needed result, although there are some small noisy points in the result image.
4.2. Several Experiments
We present some experiment results on the synthetic images.
First, we perform an experiment on an image sized 128 × 128 with four synthetic objects. It’s difficult for the traditional methods to deal with the noisy image, as they have to filter noisy to get smooth image, which will also filter out some useful information, so the errors are inevitable exist. However, seen from experimental result, nonparametric method can get better segmentation result for noisy image. As shown in Figure 6, it costs 170.601 seconds.
Second, we select another noisy image sized 128 × 128. This image is representative for three reasons: first, the noise is on the object boundary; second, there is a narrow concave part in the middle of the object; third, the image contains three dispersive parts. Traditional methods can do little on the image with such features. However, nonparametric method also can get good segmentation results but the time consumption is higher with 2647.57 seconds shown in Figure 7.

Figure 5. Noisy image segmentation with different methods.
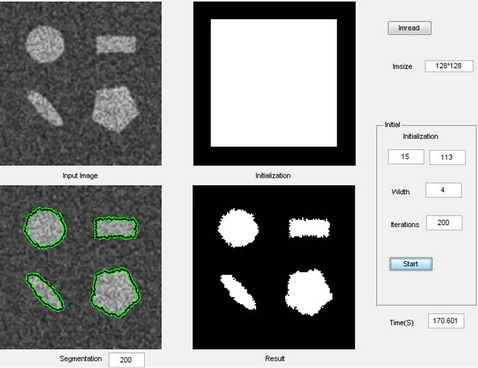
Figure 6. Noisy image segmentation.

Figure 7. Image with noisy boundary.
Furthermore, we carry out another experiment on a noisy image sized 172 × 172 with a narrow gap in the object region. The object likes a character “O” sloped down to the left, and a small break is on the right side. Many traditional methods hardly cross the gap and converge into the inner region. Nonparametric method can separate the object easily, although there are some noisy points left. The segmentation result is better shown in Figure 8.
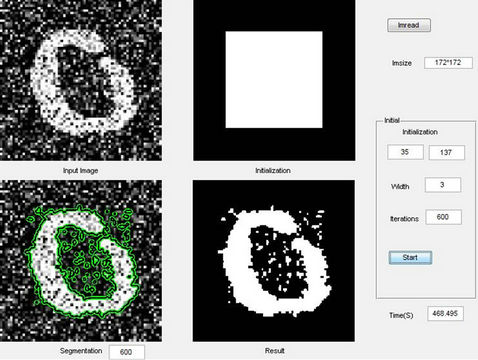
Figure 8. Noisy image segmentation.
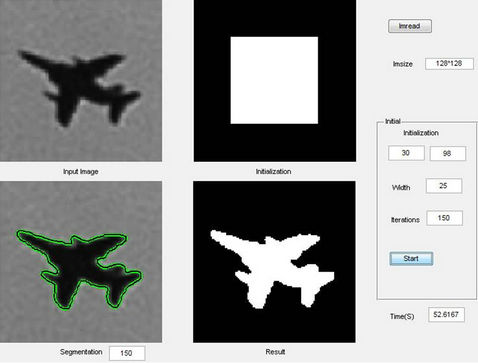
Figure 9. Image segmentation.
The computation time is 468.495 seconds.
Finally, we select a plane image sized 128 × 128, the computation time is 52.6167 seconds (see Figure 9).
From the results shown in Figures 6-9, we see that the improved nonparametric method can process many segmentations with different types, include the larger noisy image, lower contrast gray image, rough boundary image, etc. When the object boundary is smooth, the computing time is shorter; else it will take longer at a reasonable level.
5. Conclusion
In this paper, we discuss the nonparametric segmentation method based on the mutual information and its implementation. This method can solve a variety of different types of the image segmentation, and it can get very good results for processing the noise image. However, due to the estimation on the whole image probability density, it makes the calculation increasing greatly. Thus, we discuss an improved method by using the narrowband levelset which only update in the narrow-band, and Fast Gauss Transformation to reduce the iterations. Some experiment show that our improvement can reduce the amount of computation and greatly improve the calculation efficiency. Furthermore, if the implementation can be produced by the parallel computing on the multi-core or cluster computers, the improvement will be upgraded more efficiently.
REFERENCES
- T. Chan and L. Vese, “Active Contours without Edges,” IEEE Transactions on Image Processing, Vol. 10, No. 2, 2001, pp. 266-277. doi:10.1109/83.902291
- V. Caselles, F. Catte, T. Col and F. Dibos, “A Geometric Model for Active Contours in Image Processing,” Numerische Mathematik, Vol. 66, 1993, pp. 1-31. doi:10.1007/BF01385685
- V. Caselles, R. Kimmel and G. Sapiro, “Geodesic Active Contours,” International Journal of Computer Vision, Vol. 22, No. 1, 1997, pp. 61-79. doi:10.1023/A:1007979827043
- N. Paragios and R. Deriche, “Geodesic Active Regions and Level Set Methods for Supervised Texture Segmentation,” International Journal of Computer Vision, Vol. 46, No. 3, 2002, pp. 223-247. doi:10.1023/A:1014080923068
- G. Unal, A. Yezzi Jr. and H. Krim, “Information-Theoretic Active Polygons for Unsupervised Texture Segmentation,” International Journal of Computer Vision, Vol. 62, No. 3, 2002, pp. 199-220. doi:10.1007/s11263-005-4880-6
- D. Sun, J. Liu and X. Tang, “Edge Detection Based on Density Gradient,” Chinese Journal of Computers, Vol. 32, No. 2, 2009, pp. 299-307.
- F. Liu, “Medical Image Fine Segmentation Based on the Mutual Information,” China Foreign Medical Treatment, No. 2, 2010, pp. 186-187.
- J. Kim, J. W. Fisher, A. Yezzi, M. Cetin and A. S. Willsky, “A Nonparametric Statistical Method for Image Segmentation Using Information Theory and Curve Evolution,” IEEE Transactions on Image Processing, Vol. 14, No. 10, 2005, pp. 1486-1502. doi:10.1109/TIP.2005.854442
- J. A. Sethian, “Level Set Methods: Evolving Interfaces in Geometry, Fluid Mechanics, Computer Vision, and Material Science,” Cambridge University Press, Cambridge, 1996.
- D. Adalsteinsson and J. A. Sethian, “A Fast Level Set Method for Propagating Interfaces,” Journal of Computer Physics, Vol. 118, No. 2, 1995, pp. 269-277. doi:10.1006/jcph.1995.1098
- L. Greengard and J. Sethian, “The Fast Gauss Transform,” SIAM Journal on Scientific and Statistical Computing, Vol. 12, No. 1, 1991, pp. 79-94. doi:10.1137/0912004
NOTES
*This work has been supported by Chinese NSF Grant No. 11161055 and Yunnan NSF Grant No. 2008PY034.

