Applied Mathematics
Vol.3 No.9(2012), Article ID:23006,7 pages DOI:10.4236/am.2012.39151
Fritz John Duality in the Presence of Equality and Inequality Constraints
Department of Mathematics, Jaypee University of Engineering and Technology, Guna, India
Email: ihusain11@yahoo.com, santosh_00147@rediffmail.com
Received June 10, 2012; revised August 3, 2012; accepted August 10, 2012
Keywords: Second-Order Invexity; Second-Order Pseudoinvexity; Second-Order Quasi-Invexity; Nonlinear Programming; Fritz John Type Dual
ABSTRACT
A dual for a nonlinear programming problem in the presence of equality and inequality constraints which represent many realistic situation, is formulated which uses Fritz John optimality conditions instead of the Karush-Kuhn-Tucker optimality conditions and does not require a constraint qualification. Various duality results, namely, weak, strong, strict-converse and converse duality theorems are established under suitable generalized convexity. A generalized Fritz John type dual to the problem is also formulated and usual duality results are proved. In essence, the duality results do not require any regularity condition if the formulations of dual problems uses Fritz John optimality conditions.
1. Introduction
Consider the following mathematical programming problems.
(NP): Minimize 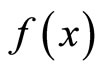
Subject to

(NEP): Minimize 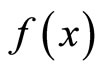
Subject to
 (1)
(1)
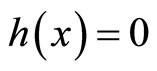 (2)
(2)
where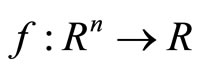 ,
, 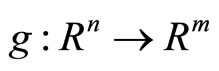 and
and 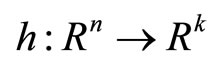 are differentiable functions. The best-known necessary optimality conditions for the mathematical programming problem (NP) and (NEP) are Fritz John necessary optimality conditions and Karush-Kuhn-Tucker type optimality conditions. The Fritz John type [1] optimality condition which predates the Karush-Kuhn-Tucker type optimality conditions by a few years are more general in a sense. In order for Karush-Kuhn-Tucker type optimality conditions to hold, a constraint qualification or regularity condition on the constraint is required. On the other hand, no such constraint qualification is needed for Fritz John optimality conditions to hold.
are differentiable functions. The best-known necessary optimality conditions for the mathematical programming problem (NP) and (NEP) are Fritz John necessary optimality conditions and Karush-Kuhn-Tucker type optimality conditions. The Fritz John type [1] optimality condition which predates the Karush-Kuhn-Tucker type optimality conditions by a few years are more general in a sense. In order for Karush-Kuhn-Tucker type optimality conditions to hold, a constraint qualification or regularity condition on the constraint is required. On the other hand, no such constraint qualification is needed for Fritz John optimality conditions to hold.
Fritz John [2] established the following optimality conditions for (NP):
Proposition 1. (Fritz John type necessary conditions). If 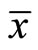 is an optimal solution of (NP), then there exist
is an optimal solution of (NP), then there exist  and a vector
and a vector 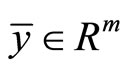 such that
such that
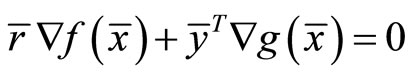

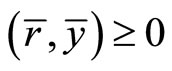
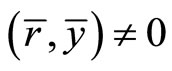
Using these optimality conditions, Weir and Mond [3] formulated the for Fritz John type dual  to (NP) and established usual duality theorems, this eliminating the requirement of a constraint qualification:
to (NP) and established usual duality theorems, this eliminating the requirement of a constraint qualification:
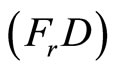 : Maximize
: Maximize 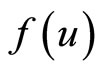
Subject to
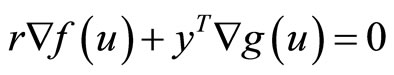
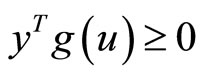
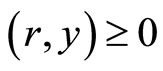
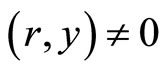 .
.
Originally, Fritz John derived his optimality condition for the case of inequality constraint alone. If equality constraint are present in a mathematical programming problem and they are converted into two inequality constraints, then the Fritz John optimality conditions become useless because every feasible point satisfying them. Later Mangasarian and Fromovitz [4] derived necessary optimality condition for (NEP) without replacing an equality constraint by two inequalities and hence making it possible to handle equalities and inequalities together as many realistic problems contain both equality and inequality constraint. Mangasarian and Fromovitz [4] established the following Fritz John type optimality condition given in the following propositions:
Proposition 2.(Generalized Fritz John necessary optimality Conditions [4]):
If 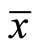 is an optimal solution of (NEP), then there exist
is an optimal solution of (NEP), then there exist ,
,  and
and 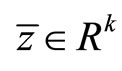 such that
such that
 (3)
(3)
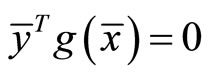 (4)
(4)
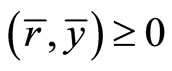 (5)
(5)
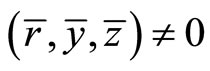 (6)
(6)
2. Sufficiency of Fritz John Optimality Conditions
Before proceeding to the main results of our analysis we give the following definitions which are required for their validation.
1) The function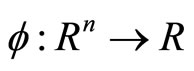 is strictly pseudoconvex on
is strictly pseudoconvex on 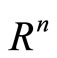 for all
for all 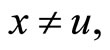
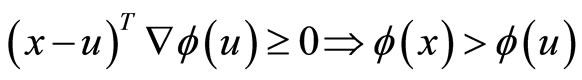
Equivalently

2) For 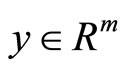 and
and  is said to be semi-strictly pseudoconvex if
is said to be semi-strictly pseudoconvex if 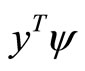 is strictly pseudoconvex for all
is strictly pseudoconvex for all 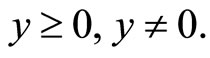
Theorem 1. (Sufficient Optimality Conditions):
Assume that
1) 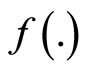 is pseudoconvex2)
is pseudoconvex2) 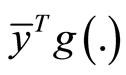 is semi strictly pseudoconvex and 3)
is semi strictly pseudoconvex and 3) 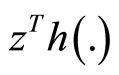 is quasiconvexIf there exist
is quasiconvexIf there exist ,
,  ,
, 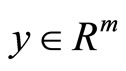 and
and 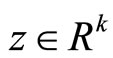 such that (3)-(8) are satisfied, then
such that (3)-(8) are satisfied, then 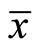 is an optimal solution of (NEP).
is an optimal solution of (NEP).
Proof: Suppose 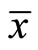 is not optimal, i.e., and then there exists
is not optimal, i.e., and then there exists 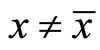 Such that
Such that
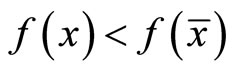
Since  is pseudoconvex, this implies
is pseudoconvex, this implies

and
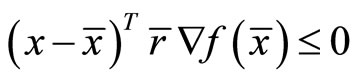 (7)
(7)
with strict-inequality in the above if 
Since 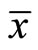 is feasible for (NEP) we have
is feasible for (NEP) we have
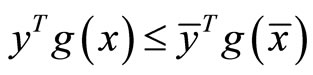
Because of semi strict pseudoconvexity of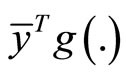 , This implies
, This implies
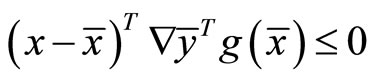 (8)
(8)
With strict inequality with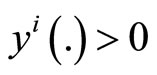 ,
, .
.
Also 
Because of quasi-convexity of 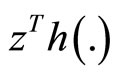 at
at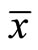 ,
,
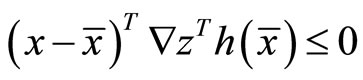 (9)
(9)
Combining (7), (8) and (9), we have
 Contradicting (3). Hence
Contradicting (3). Hence 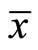 is an optimal solution of (NEP).
is an optimal solution of (NEP).
3. Fritz John Type Duality
We propose the following dual (FrED) to (NEP), using Fritz John optimality conditions stated in the preceding section instead of Karush-Kuhn-Tucker conditions [5,6] and established duality results, thus the requirement of a constraint qualification [4] is eliminated:
Dual Problem:
(FrED): Maximize 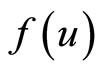
Subject to
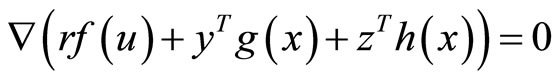 (10)
(10)
 (11)
(11)
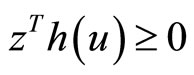 (12)
(12)
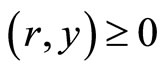 (13)
(13)
 (14)
(14)
Theorem 2. (Weak Duality):Assume that
 : x is feasible for (NEP) and
: x is feasible for (NEP) and  is feasible for
is feasible for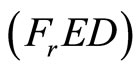 .
.
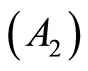 : For all feasible
: For all feasible ,
, 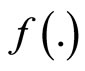 is pseudoconvex,
is pseudoconvex, 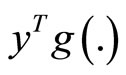 is semi-strictly pseudoconvex and
is semi-strictly pseudoconvex and  is quasiconvex.
is quasiconvex.
Then
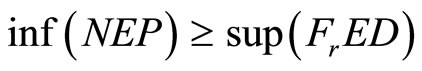
Proof: Suppose 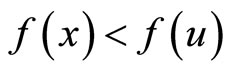 this, because of pseudoconvexity of
this, because of pseudoconvexity of 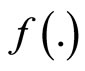 yields
yields , Multiplying this, by
, Multiplying this, by 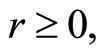 We have
We have
 (15)
(15)
With strict inequality in (15) if 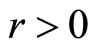
From the Constraints of  and
and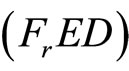 , we have
, we have
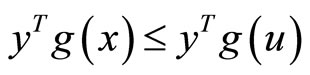
which by semi-strictly pseudoconvexity of 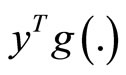 implies
implies
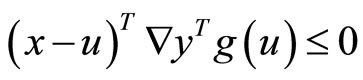 (16)
(16)
with strict inequality in (16) if 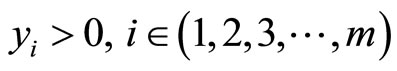
As earlier 
This along with quasiconvexity of 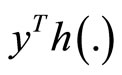 implies
implies
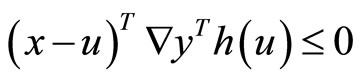 (17)
(17)
Combining (15), (16), (17), we have
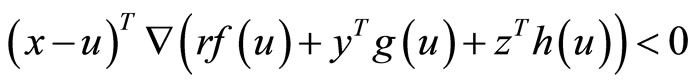
Contradicting

Hence 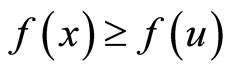
This implies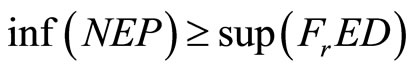 .
.
Theorem 3. (Strong Duality):
If  is an optimal solution of
is an optimal solution of  then there exist
then there exist ,
, 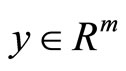 and
and 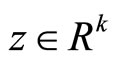 such that
such that  is feasible for
is feasible for  and the corresponding values of
and the corresponding values of 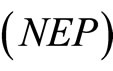 and
and 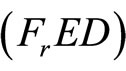 are equal. If, also f is pseudoconvex,
are equal. If, also f is pseudoconvex, 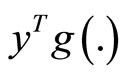 is semi-strictly pseudoconvex and
is semi-strictly pseudoconvex and 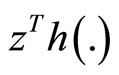 is quasi-convex, then
is quasi-convex, then 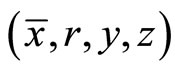 is an optimal solution of
is an optimal solution of .
.
Proof: Since 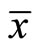 is an optimal solution of
is an optimal solution of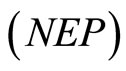 , by Proposition 2. There exist
, by Proposition 2. There exist ,
, 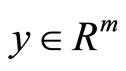 and
and 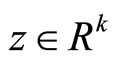 such that
such that
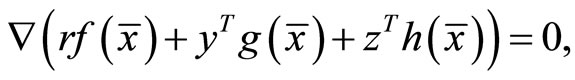
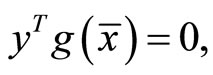
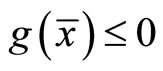
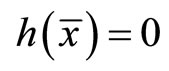
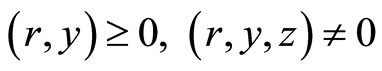
This implies 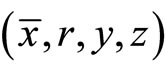 is feasible for
is feasible for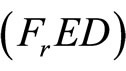 . Equality of objective function of
. Equality of objective function of 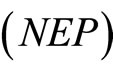 and
and  is abovious optimality follows, in view of the hypothesis of the theorem1.
is abovious optimality follows, in view of the hypothesis of the theorem1.
Theorem 4. (Strict Converse Duality): Assume that
1) 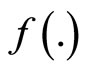 is strictly pseudoconvex,
is strictly pseudoconvex, 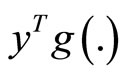 is semistrictly pseudoconvex and as
is semistrictly pseudoconvex and as 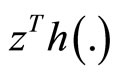 is quasiconvex and 2) The problem
is quasiconvex and 2) The problem 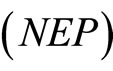 has an optimal solution
has an optimal solution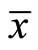 .
.
If 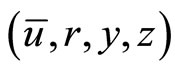 is an optimal solution of
is an optimal solution of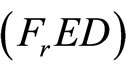 , Then
, Then 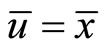 i.e.
i.e. 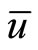 is an optimal solution of
is an optimal solution of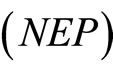 .
.
Proof: We assume that 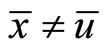 and exhibit a contradiction, it follows from Proposition 2 that there exist
and exhibit a contradiction, it follows from Proposition 2 that there exist ,
, 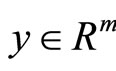 and
and 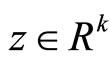 such that
such that  is optimal solution of
is optimal solution of , since
, since  is also an optimal solution for
is also an optimal solution for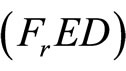 , It follows that
, It follows that

by strict pseudoconvexity of 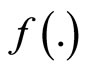 we have
we have
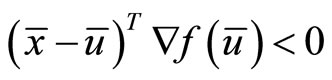 (18)
(18)
Also from the constraints of  and
and 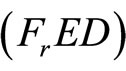 we have
we have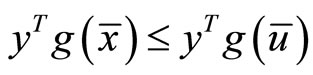 .
.
By the semi strictly convexity of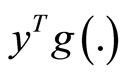 , this implies
, this implies
 (19)
(19)
with strict inequality in the above, if 
Also  which by quasi-convexity of
which by quasi-convexity of 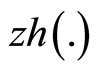 at
at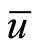 , implies
, implies
 (20)
(20)
Combining (18), (19), and (20), we have
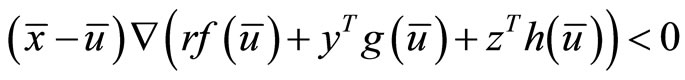
which contradicts
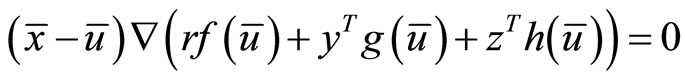
Hence 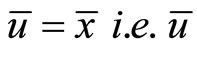 is an optimal solution.
is an optimal solution.
Theorem 5. (Converse Duality): If 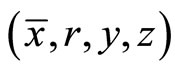 is an optimal solution of
is an optimal solution of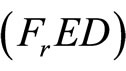 . Assume that
. Assume that
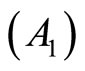 :
: 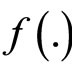 is pseudoconvex,
is pseudoconvex, 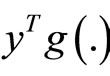 is semi strictlypseudoconvex and
is semi strictlypseudoconvex and 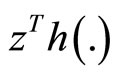 is quasiconvex.
is quasiconvex.
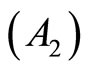 : Hessian matrix
: Hessian matrix  is positive or negative definite, and
is positive or negative definite, and
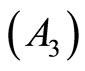 : the set
: the set 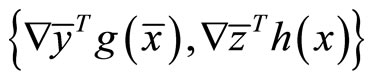 is linearly independent, and Then
is linearly independent, and Then 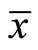 is an optimal solution of
is an optimal solution of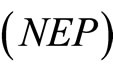 .
.
Proof: By Preposition 2, there exist ,
, 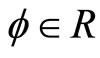
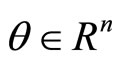 ,
,  ,
, 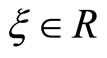 and
and 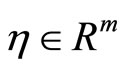 such that
such that
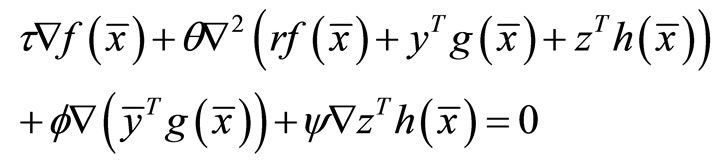 (21)
(21)
 (22)
(22)
 (23)
(23)
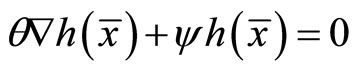 (24)
(24)
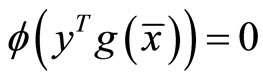 (25)
(25)
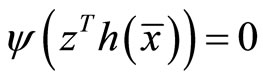 (26)
(26)
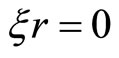 (27)
(27)
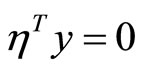 (28)
(28)
 (29)
(29)
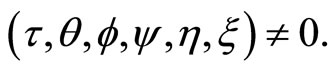 (30)
(30)
Multiplying (23) by y ≥ 0 and using (25) and (28), we obtain
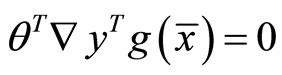 (31)
(31)
Multiplying (24) by  and
and  we have
we have
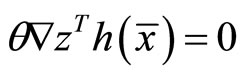 (32)
(32)
Multiplying equality constraint of 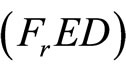 by
by 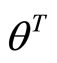 and using (31) and (32) We have
and using (31) and (32) We have 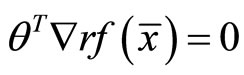
Multiplying (21) by 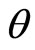 and using (31) and (32), we have
and using (31) and (32), we have

Multiplying the above equation by r and using (33), we have

This because of hypothesis (A2) implies rθ = 0. In view of (A3) the equality constraint of 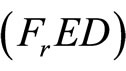 implies r ≠ 0, i.e., r > 0.consequently θ = 0.
implies r ≠ 0, i.e., r > 0.consequently θ = 0.
Multiplying (21) by r and using θ = 0, we have
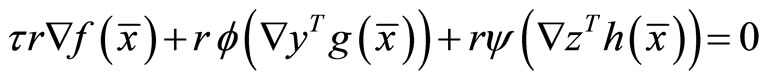
Using the equality constraint (10) in the above, we have
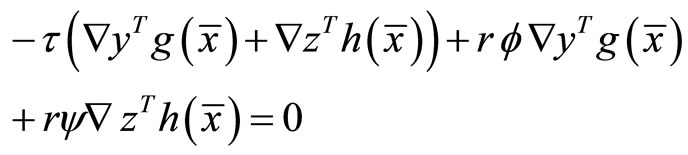
This reduces to
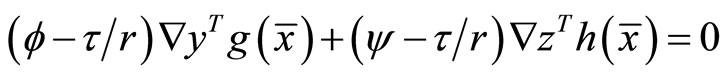
By the linear independence hypothesis (A3). this implies
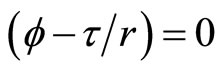 and
and 
Now if τ = 0, then from above, we have ϕ = 0, ψ = 0 and from (22) and (23), We have ξ = 0, η = 0, consequently we have 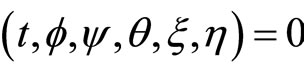 contradicting to (30).
contradicting to (30).
Hence t > 0, ϕ > 0, and ψ > 0.
Using  in (23) and (24), we have
in (23) and (24), we have
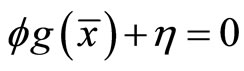 ,
, 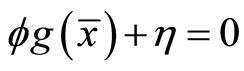
This implies 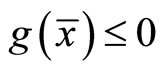 and
and 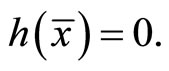
Thus 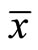 is feasible for
is feasible for 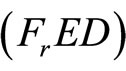 and the objective functions of
and the objective functions of  and
and 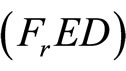 are equal in their formulations. Under, the state generalized Convexity, Theorem 1 implies that,
are equal in their formulations. Under, the state generalized Convexity, Theorem 1 implies that, 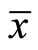 is an optimal solution of
is an optimal solution of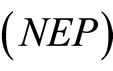 .
.
4. Generalized Fritz John Duality
Let 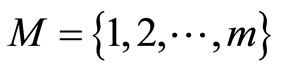 and
and 

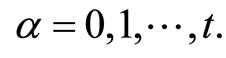 with
with 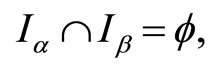
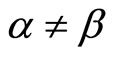 and
and
 . and
. and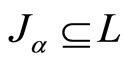 with
with ,
,  and
and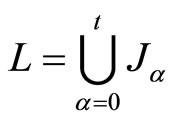 . Let
. Let 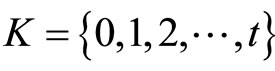 and
and 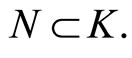 The following is the generalized Fritz John type dual to
The following is the generalized Fritz John type dual to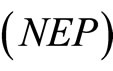 .
.
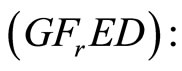 Maximize
Maximize 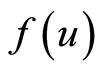
Subject to

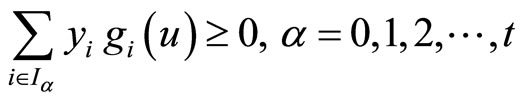

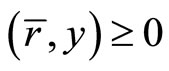
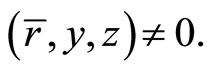
Theorem 6: If 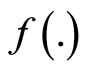 is pseudoconvex,
is pseudoconvex, 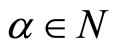
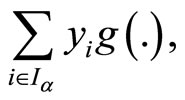 is semi-strictly pseudoconvex,
is semi-strictly pseudoconvex, 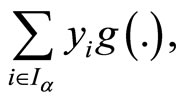
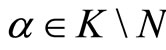 and
and  is quasiconvexThen
is quasiconvexThen 
Proof: Let 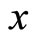 be feasible for
be feasible for 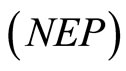 and
and  feasible for
feasible for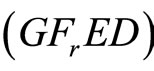 . Suppose
. Suppose 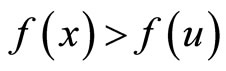 This by pseudoconvexity of
This by pseudoconvexity of 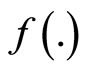 yields
yields
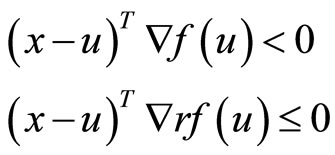 (34)
(34)
with strict inequality in (34) if 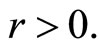
From the constraint of  and
and , we have
, we have
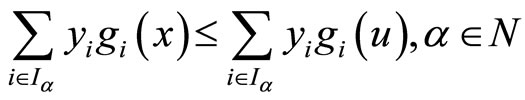 (35)
(35)
Which because of semistrictly pseudoconvexity of  implies
implies
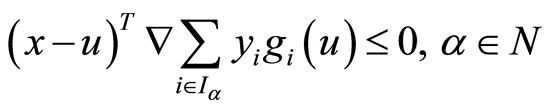 (36)
(36)
with strict inequality in (36) if some 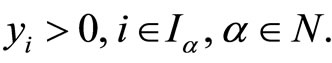
Also
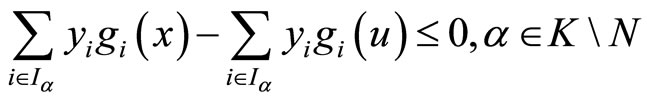
And

Which by quasiconvex of 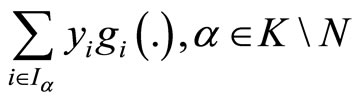 and
and
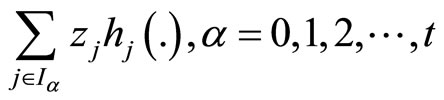
respectively imply

and
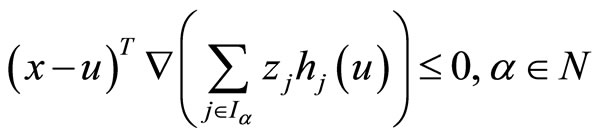
combining (34), (35), (36) and above equation we have
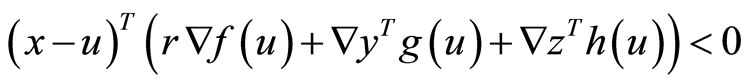
contradicting the equality constraint of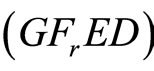 . Hence
. Hence 
Implying 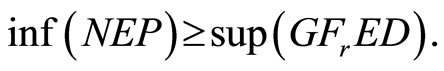
Theorem 7. (Strong Duality):
If 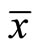 is an optimal solution of
is an optimal solution of 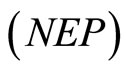 and there exist
and there exist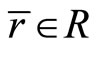 ,
,  and
and 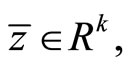 such that
such that 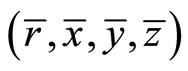 is feasible for
is feasible for 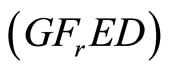 and the corresponding value of
and the corresponding value of  and
and 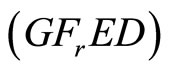 are equal. If, the hypotheses of Theorem 1 hold, then
are equal. If, the hypotheses of Theorem 1 hold, then 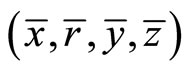 is an optimal solution of
is an optimal solution of .
.
Proof: By Proposition 2, there exist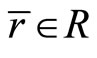 ,
, 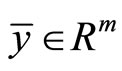 and
and 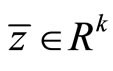 such that
such that
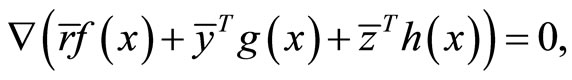
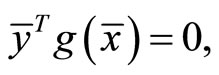
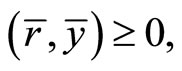
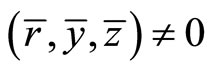
Since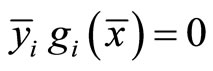 ,
, 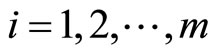 and
and 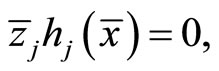 feasibility of
feasibility of 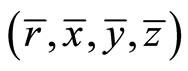 for
for 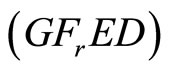 is obvious. Optimality follows, give the pseudoconvexity of
is obvious. Optimality follows, give the pseudoconvexity of 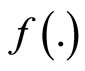
and semi-strict pseudoconvexity of 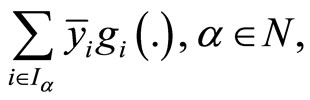 quasiconvexity of
quasiconvexity of  and quasiconvexity of
and quasiconvexity of 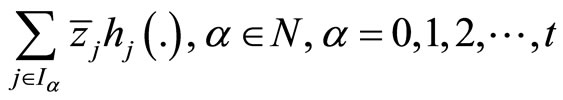 from Theorem 1.
from Theorem 1.
Theorem 8: (Mangasarian [4] Type Strict Converse Duality): Assume that

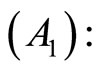 is strictly pseudoconvex,
is strictly pseudoconvex,

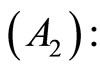 is semi-strictly pseudoconvex and
is semi-strictly pseudoconvex and
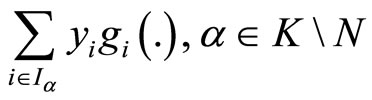
 and
and 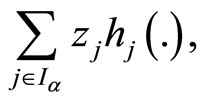
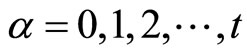 are quasiconvex.
are quasiconvex.
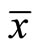
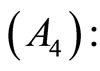 is an optimal solution of
is an optimal solution of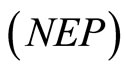 .
.
If 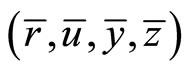 is an optimal solution of
is an optimal solution of  then
then 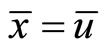 i.e.
i.e.  is an optimal solution of
is an optimal solution of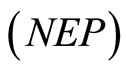 .
.
Proof: Assume that  and exhibit a contradiction. Since
and exhibit a contradiction. Since 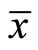 is an optimal solution of
is an optimal solution of , by Proposition 2, it implies that there exist
, by Proposition 2, it implies that there exist ,
, 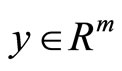 and
and  such that
such that 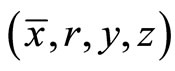 is an optimal solution of
is an optimal solution of .
.
Since 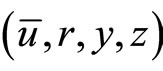 is an optimal solution for
is an optimal solution for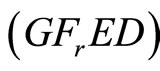 , it follows that
, it follows that 
This, in view of strict pseudoconvexity of 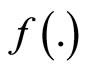 implies
implies
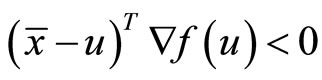 (37)
(37)
From the constraint of 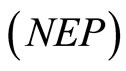 and
and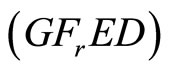 , we have
, we have
 (38)
(38)
and
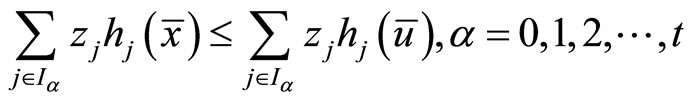 (39)
(39)
The inequality (38), in view of semi-strict pseudo convexity of 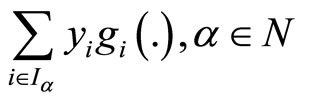 implies
implies
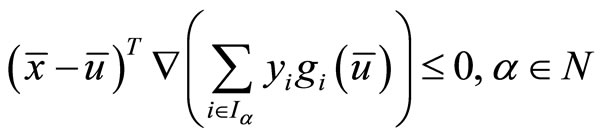 (40)
(40)
with strict inequality in (40) if .
.
By quasiconvexity of 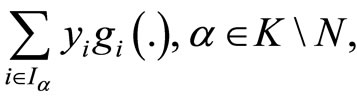 (38) implies
(38) implies
 (41)
(41)
The inequality (39), because of quasiconvexity of 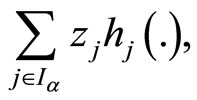
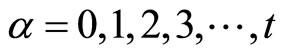 yields,
yields,
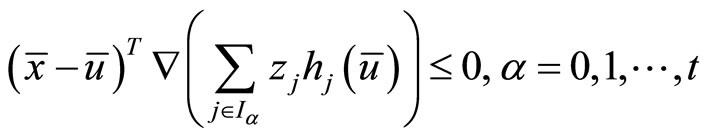 (42)
(42)
Combining (37), (40), (41) and (42), we have
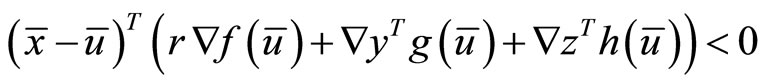
which contradicts the feasibility of 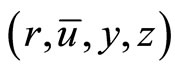 for
for 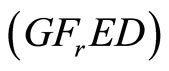 . Hence
. Hence 
Theorem 9 (Converse Duality): Let
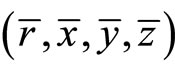
 be an optimal solution of
be an optimal solution of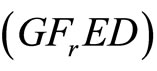 .
.

 be pseudoconvex,
be pseudoconvex, 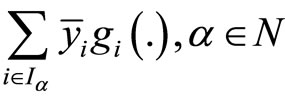 semistrictly pseudoconvex,
semistrictly pseudoconvex, 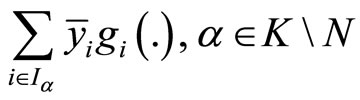 quasiconvex.
quasiconvex.
 The Hessian matrix
The Hessian matrix
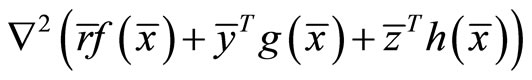
is positive or negative definite, and
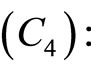 The set
The set
is linearly independent. Then  is feasible for
is feasible for .
.
Proof: By Proposition 2, there exist 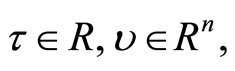

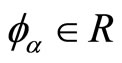 ,
, 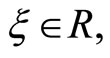
 and
and 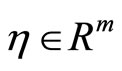 such that
such that
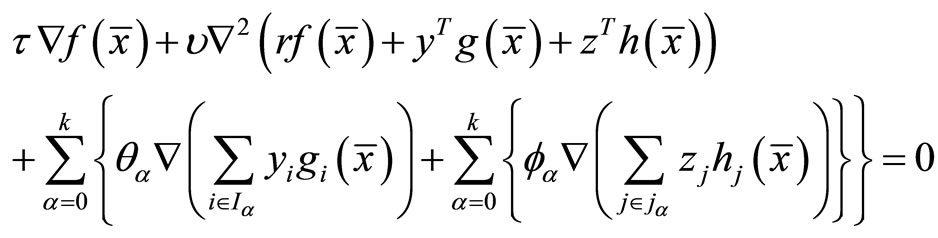 (43)
(43)
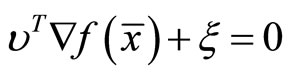 (44)
(44)
 (45)
(45)
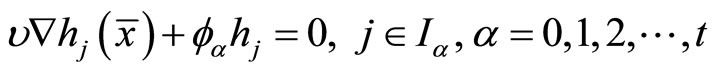 (46)
(46)
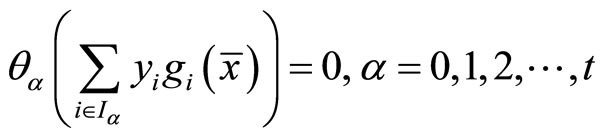 (47)
(47)
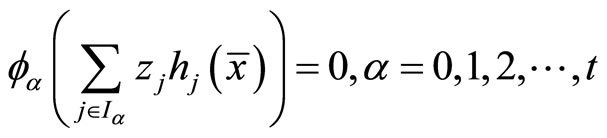 (48)
(48)
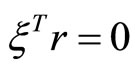 (49)
(49)
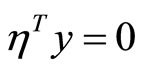 (50)
(50)
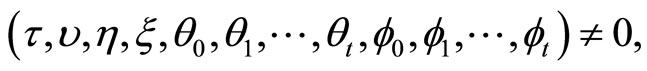 (51)
(51)
 (52)
(52)
Multiplying (45) and (46) by 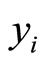 and
and  respectively and using (47) and (48), we have
respectively and using (47) and (48), we have
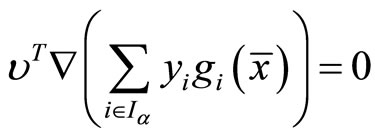 (53)
(53)
 (54)
(54)
Multiplying (44) by r, we have
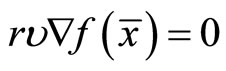 (55)
(55)
Multiplying (43) by  and using (53), (54) and (53), we have
and using (53), (54) and (53), we have
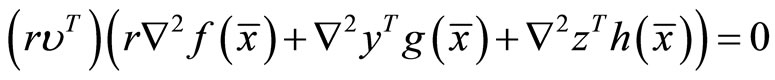
By positive or negative definite and by hypothesis , we have
, we have 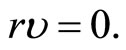
In view of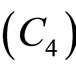 , equality constraint of
, equality constraint of 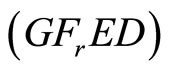 implies that
implies that 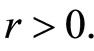 Hence
Hence 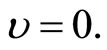 using
using  we have
we have

which in view of the hypothesis 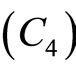 gives
gives 
 ,
, . From (44) and (45), we have
. From (44) and (45), we have  and
and 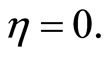 consequently we have
consequently we have
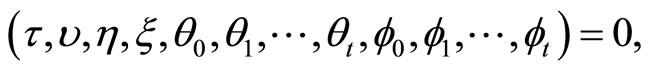
Contradicting Fritz John Condition (51). Hence 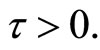 since
since 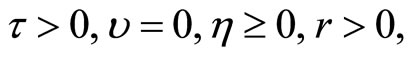 The Equations (45) and (46), implies
The Equations (45) and (46), implies 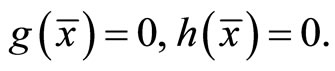
Thus 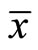 is feasible for
is feasible for 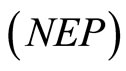 and optimality follows as earlier.
and optimality follows as earlier.
5. Conclusion
In this exposition, we have formulated a dual and generalized dual by Fritz John optimality conditions instead of the Karush-Kuhn-Tucker optimality conditions. Consequently no constraint qualification is required and hence such formulations enjoy computational advantage over those formulated by using Karush-Kuhn-Tucker. The problems of these results can be revisited in multiobjective and dynamic setting.
REFERENCES
- R. W. Cottle, “A Theorem of Fritz John in Mathematical Programming,” RAND Memorandum RM-3538-PR, 1963.
- F. John, “Extremum Problems with Inequalities as Side Condition,” In: K. O. Frierichs, O. E. Neugebaur and J. J. Stoker, Eds., Studies and Essays, Courant Anniversary Volume, Wiley (Interscience), New York, 1984, pp. 187- 204.
- T. Weir and B. Mond, “Sufficient Fritz John Optimality Conditions and Duality for Nonlinear Programming Problems,” OPSEARCH, Vol. 23, No. 3, 1986, pp. 129-141.
- O. L. Mangasarian and S. Fromovitz, “The Fritz John Necessary Optimality Conditions in the Presence of Equality and Inequality Constraints,” Journal of Mathematical Analysis and Applications, Vol. 17, No. 1, 1967, pp. 37-47. doi:10.1016/0022-247X(67)90163-1
- H. W. Kuhn and A. W. Tucker, “Nonlinear Programming,” Proceeding of the Second Berkeley Symposium on Mathematical Statistics and Probability, University of California Press, Berkeley, 1951, pp. 481-492.
- O. L. Mangasarian, “Nonlinear Programming,” McGrawHill, New York, 1969.

