Applied Mathematics
Vol.4 No.2(2013), Article ID:28204,8 pages DOI:10.4236/am.2013.42050
Exact Solutions of a Power Law Fluid Model in Posttreatment Analysis of Wire Coating with Linearly Varying Boundary Temperature
1Department of Basic Sciences and Islamiat, University of Engineering and Technology, Peshawar, Pakistan
2Department of Mathematics, Abdul Wali Khan University, Mardan, Pakistan
3Department of Mathematics, Pennsylvania State University, York Campus, York, USA
4Department of Mathematics, COMSATS Institute of Information Technology, Islamabad, Pakistan
Email: *mmrehan79@yahoo.com
Received April 19, 2012; revised January 11, 2013; accepted January 18, 2013
Keywords: Exact Solution; Wire Coating; Power Law Fluid Model; Linearly Varying Temperature at Boundaries
ABSTRACT
In this paper, analysis of post-treatment of wire coating is presented. Coating material satisfies power law fluid model. Exact solutions for the velocity field, volume flow rate and average velocity are obtained. Moreover, the heat transfer results are presented for different cases of linearly varying on the boundaries. The variations of velocity, volume flow rate, radius of coated wire, shear rate and the force on the total wire are presented graphically and discussed.
1. Introduction
The wire coating process is basically an extrusion operation in which either the molten polymer, in the form of tubing, is extruded continuously over axially moving wire, or the wire is pulled through the extruded molten polymer. Polymer extrudate is an important industrial process used for coating a wire for primary insulation of conducting wires with molten polymers for mechanical strength and environmental protection purposes. Wire coating have many application in the field of chemical and industrial engineering. Many authors have studied the wire coating phenomena.
The basic concept of modeling the wire coating for viscous fluid is given in the books by Denn and middleman [1,2]. McKelvey [3] and Paton et al. [4] have analyzed the flow of Newtonian and power law fluid model in wire coating process, and obtained expressions for the flow rate, shear rate and the velocity distribution along the radial direction. Gagley and storey [5] provided numerical simulations for a Newtonian fluid in the form of dimensionless parameters characterizing the wire speed, die dimensions, radial position, shear rate, and melt viscosity. Akhter and Hashmi [6,7] have developed the mathematical model for wire coating using power law model and investigated the effect of the change in viscosity. A.M Siddiqui, T.Haroon and H. Khan [8] studied the wire coating extrusion in a pressure-type die in flow of third grade fluid. Fenner and Williams [9] carried out an analysis of the flow in the tapering section of a pressure type die. They obtained the numerical solutions for the pressure and velocity profiles in the die. M. Sajjid et al. [10] studied the wire coating with Oldroyd 8-constant fluid and gave the solution for velocity field in the series form.
The coated wire after leaving the die is effected by the quality of the material used in coating process, the wire drawing velocity and the temperature. There are very few disclosures presenting theoretical analysis of flow in the posttreatment process subsequent to the die.
The analysis of the drag flow of the coated polymer outside pressure die was carried out by Kasajima and Katsuhiko Ito [11]. They derived the expression for velocity and temperature field. Moreover, they found the volume flow rate, average velocity and discussed some cases for constant velocity and constant temperature on the boundaries. We work under the same geometry as by Masayuki Kasajima and Katsuhiko with the assumption that the polymer obeys the power law fluid model and derived the velocity field, volume flow rate, thickness of coated wire, average velocity, the force on the total wire surface and linearly varying temperature distribution in the direction of flow. As the posttreatment problem is mainly concern with temperature for cooling the coated wire therefore due to its importance and realization of physical problem we discussed some cases of linearly varying temperature for analysis of temperature distribution as follows:
• Temperature of the wire is constant while it is varying linearly on the surface of the coated wire.
• Temperature of the wire varying linearly while it is constant on the surface of the coated wire.
• Temperature of the wire and the surface of coated wire are varying linearly at the same temperature gradient.
The non-linear differential equations governing the model are made dimensionless and solved for velocity and temperature distribution. Theoretical analysis on the drag flow mechanism of polymer extrudate, in the heat treatment process, is presented.
2. Basic Governing Equations
The basic equations governing the flow of an incompressible fluid with thermal effects are:
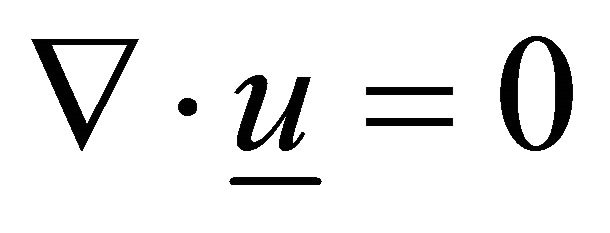 , (1)
, (1)
 , (2)
, (2)
 (3)
(3)
where 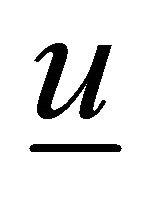 is the velocity vector,
is the velocity vector, 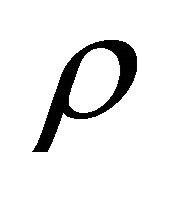 is the constant density,
is the constant density, 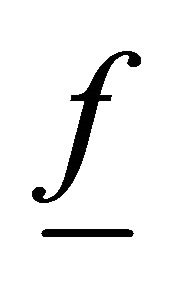 is the body force,
is the body force, ![]() is the Cauchy stress tensor,
is the Cauchy stress tensor, 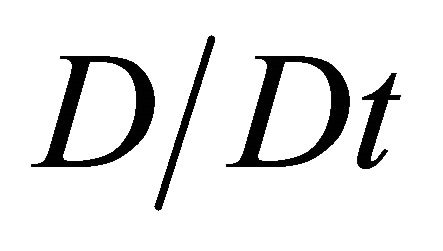 denote the material derivative,
denote the material derivative,  is the fluid temperature,
is the fluid temperature,  is the thermal conductivity,
is the thermal conductivity, 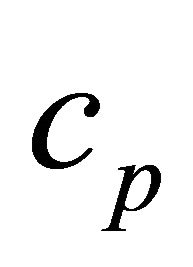 is the specific heat and
is the specific heat and ![]() is the gradient of velocity vector
is the gradient of velocity vector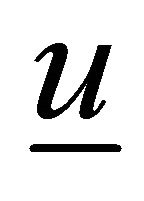 .
.
The Cauchy stress tensor ![]() is defined as
is defined as
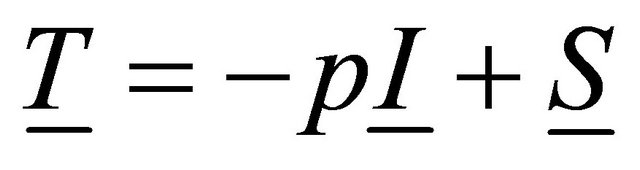 , (4)
, (4)
In which ![]() is the pressure,
is the pressure,  is the identity tensor and
is the identity tensor and ![]() is the extra stress tensor. For power law fluid model
is the extra stress tensor. For power law fluid model ![]() is defined as
is defined as
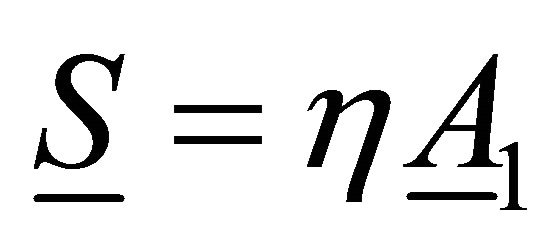
 , (5)
, (5)
where
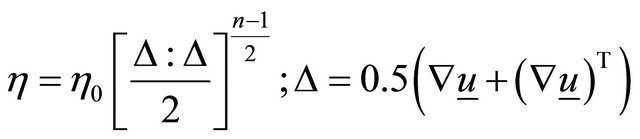 (6)
(6)
where 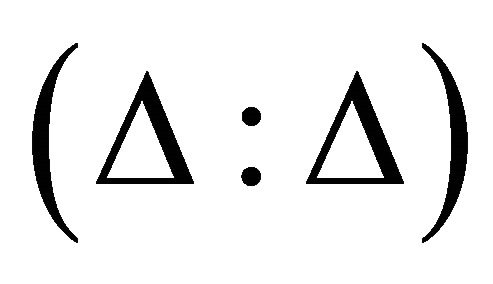 is the scalar invariant,
is the scalar invariant, 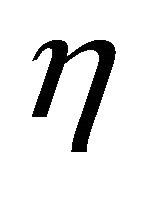 is the coefficient of viscosity of the fluid,
is the coefficient of viscosity of the fluid, ![]() in superscript denotes the transpose of the matrix
in superscript denotes the transpose of the matrix ,
, 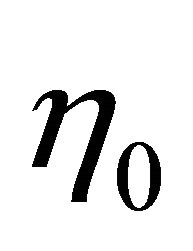 is the consistency index and
is the consistency index and ![]() is the power law index. The index
is the power law index. The index ![]() is non-dimensional and the dimension of
is non-dimensional and the dimension of 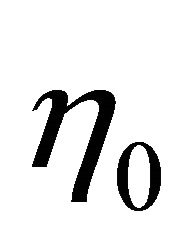 depends on the value of
depends on the value of![]() . The parameter
. The parameter ![]() subdivide fluids into pseudoplastic fluids
subdivide fluids into pseudoplastic fluids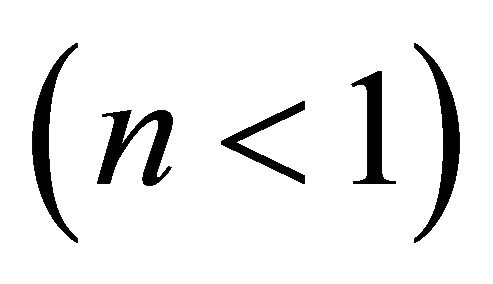 , dilatant fluids
, dilatant fluids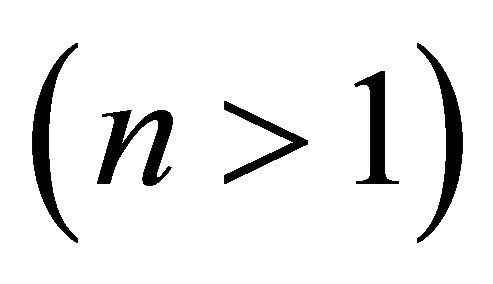 and Newtonian fluid For
and Newtonian fluid For . Therefore the deviation of
. Therefore the deviation of ![]() from unity indicates the degree of deviation from Newtonian behavior [12].
from unity indicates the degree of deviation from Newtonian behavior [12].
3. Formulation and Solution of the Problem
In wire coating process, the quality of the polymer and wire drawing velocity are important within the die, after leaving the die temperature and the shape of the transverse sectioning is also very important. Consider the flow of the polymer extrudate given in Figure 1, denoted by the solid line. To analyze the flow behavior of a polymer used in wire coating, it is convenient to divide the flow transversely into many short sections as shown by broken lines in Figure 1 with the assumption that each section has almost the same shape, we analyze only one section because each section can be assumed to be approximately of the shape shown in Figure 2 and readily analyzable.
Consider the wire of radius 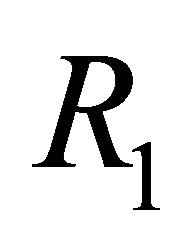 is dragged in the
is dragged in the  direction with velocity
direction with velocity  through an incompressible polymer satisfying power law fluid model (II) and the gas (III) surrounding the polymer (II) is flowing with a velocity
through an incompressible polymer satisfying power law fluid model (II) and the gas (III) surrounding the polymer (II) is flowing with a velocity  in the
in the  direction.
direction.
Consider the cylindrical coordinates  such that
such that 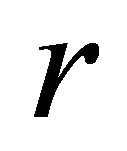 is perpendicular to the direction of flow.
is perpendicular to the direction of flow.
Assume that:
1) The flow is incompressible due to the high viscosity of the polymer.
2) Polymer II holds the power law fluid model for shear rate.
3) In Figure 2 the wire I, the polymer II and gas III are in contact with each other and consider no slippage occurs along the contacting surfaces of the wire, polymer, and the gas.
Also assume that the flow is steady, laminar, unidirectional and axisymmetric:
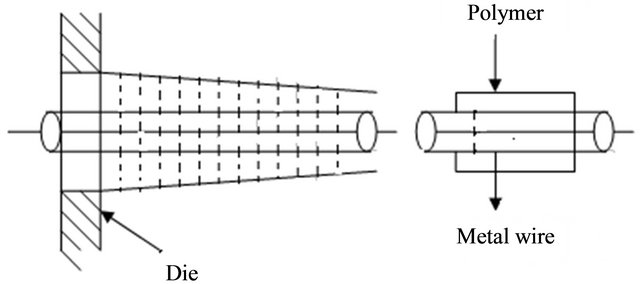
Figure 1. Schematic profile of polymer extrudate in wire coating.
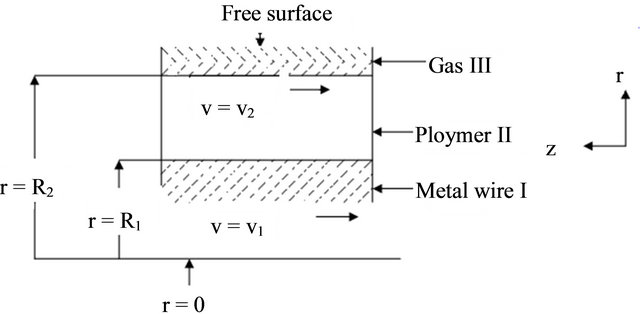
Figure 2. Drag flow in wire coating.
We seek the velocity field of the form
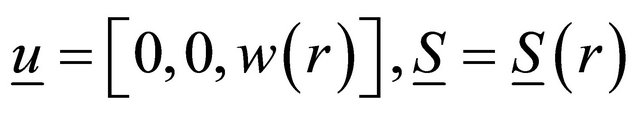 . (7)
. (7)
then the boundary conditions for the problem become
 (8)
(8)
In the flow through the tube, the scalar invariant is:
 (9)
(9)
Substituting Equation (9) into Equation (6) one obtains:
 . (10)
. (10)
Using the velocity field (7) the continuity Equation (1) is satisfied identically, and the non zero components of Equation (5) with the help of Equation (10) become:
 (11)
(11)
Substituting the velocity field and Equation (11) in the momentum Equation (2) neglecting the body force take the form:
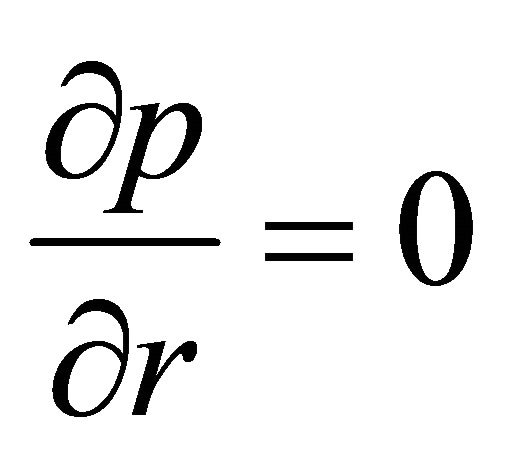 (12)
(12)
 (13)
(13)
 (14)
(14)
If the z-axis is chosen correspond to the direction of increasing pressure, polymer (II) moves in the minus direction of the z-axis and the shear rate becomes plus for all value of
becomes plus for all value of ![]() Therefore, the absolute value of Equation (5) can be discarded.
Therefore, the absolute value of Equation (5) can be discarded.
Equation (14) represents the flow due to pressure gradient. After leaving the die, there is only drag flow. Hence, we consider
 (15)
(15)
and the energy Equation (3) becomes:
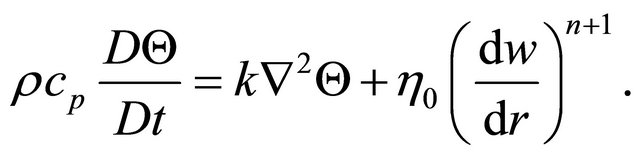 (16)
(16)
For linearly varying temperature, consider
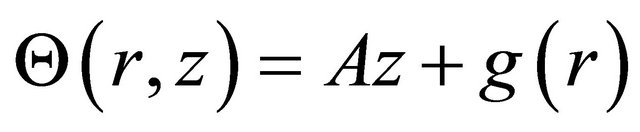 , (17)
, (17)
where  is the temperature gradient.
is the temperature gradient.
Substituting Equation (17) into Equation (16), we have
 (18)
(18)
Now first the velocity field is determined from Equation (15) and then the temperature distribution can be easily calculated using Equation (18).
The average velocity is
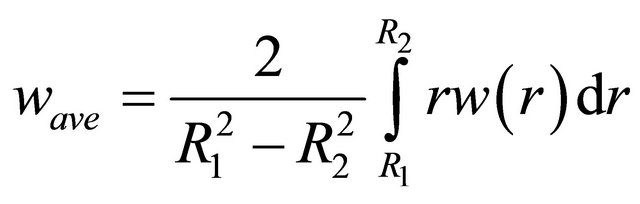 (19)
(19)
At some control surface downstream, the volume flow rate of coating is
 (20)
(20)
where 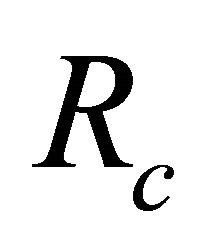 is the radius of the coated wire.
is the radius of the coated wire.
The volume flow rate of the polymer is
 (21)
(21)
The thickness of the coated wire can be obtained from Equations (16) and (17) as
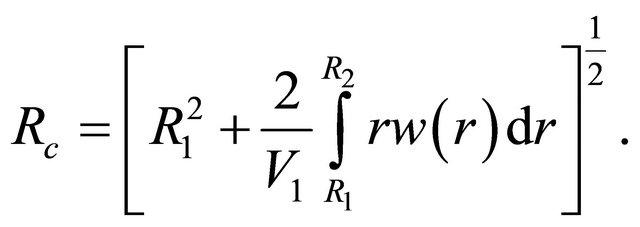 (22)
(22)
The force on the wire is computed by determining the shear stress at the wire surface. This is given by
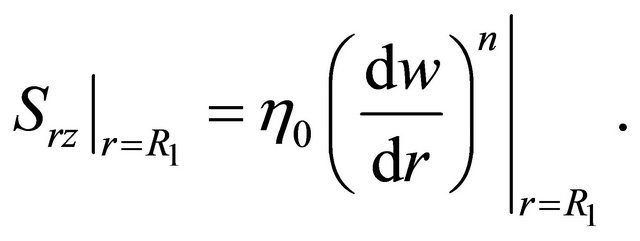 (23)
(23)
The force on the total wire surface is
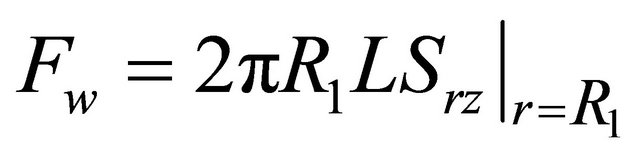 (24)
(24)
Introduce the dimensionless parameters
 (25)
(25)
Equations (8), (15) and (18)-(25) after dropping the “![]() ” take the following form:
” take the following form:
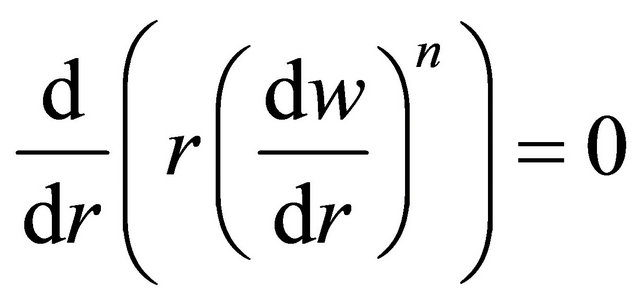 , (26)
, (26)
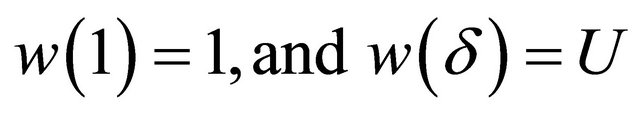 , (27)
, (27)
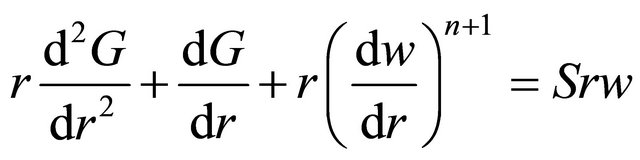 , (28)
, (28)
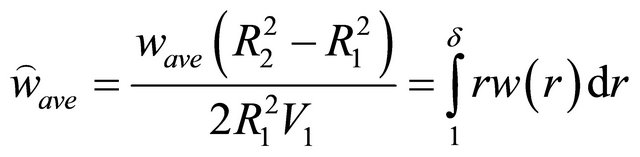 , (29)
, (29)
 , (30)
, (30)
 (31)
(31)
 (32)
(32)
 (33)
(33)
The solution to (26) corresponding to the boundary conditions (27) are:
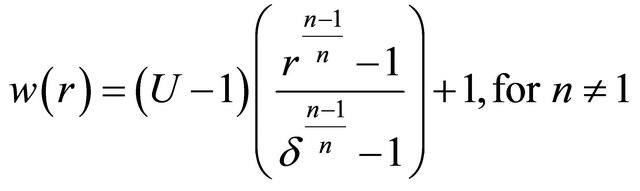 (34)
(34)
For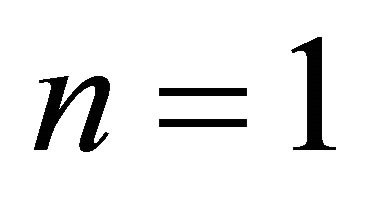 , the velocity field can be obtain from Equation (26).
, the velocity field can be obtain from Equation (26).
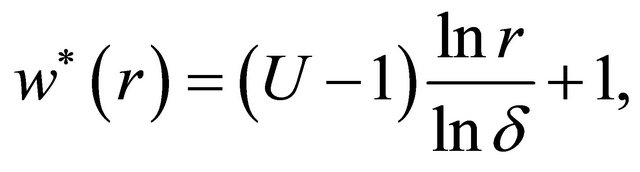 (35)
(35)
where the superscript “![]() ” means the case of
” means the case of .
.
For 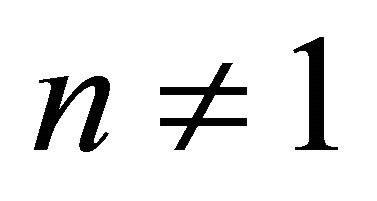 the average velocity is obtained from Equations (29) and (34):
the average velocity is obtained from Equations (29) and (34):
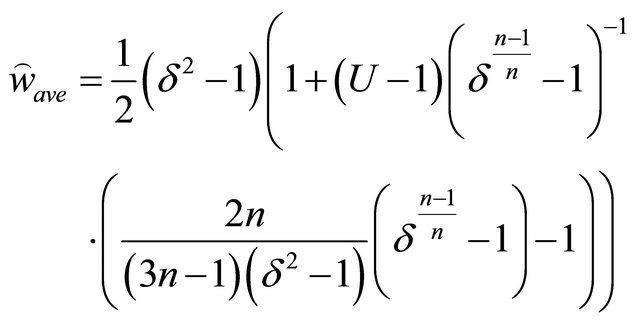 (36)
(36)
For 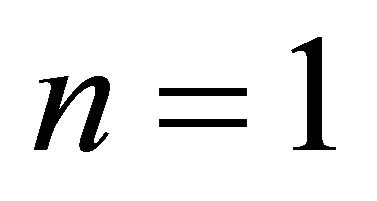 the average velocity is obtained from Equations (29) and (35):
the average velocity is obtained from Equations (29) and (35):
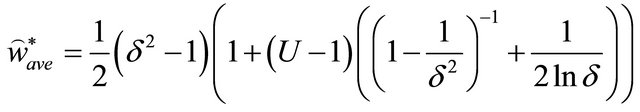 (37)
(37)
For 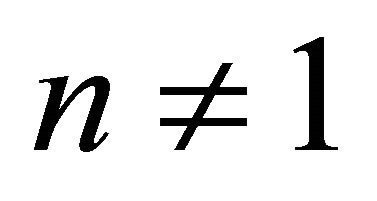 the shear rate can be obtained from Equation (34):
the shear rate can be obtained from Equation (34):
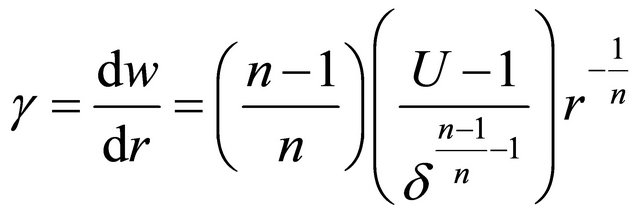 (38)
(38)
For 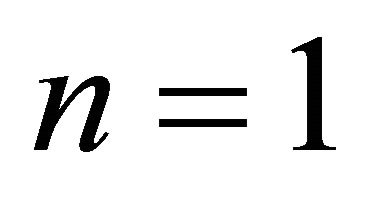 the shear rate is obtained from Equation (35) as:
the shear rate is obtained from Equation (35) as:
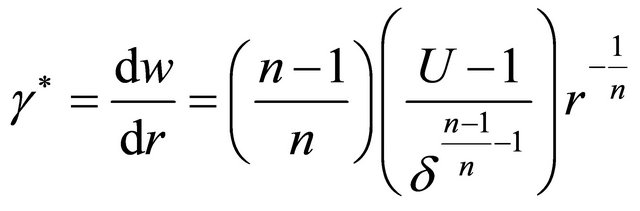 (39)
(39)
The thickness of the coated wire for 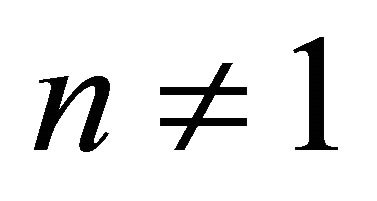 is obtained from Equations (31) and (34):
is obtained from Equations (31) and (34):
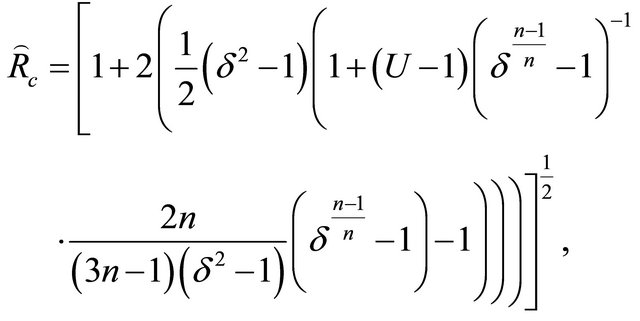 (40)
(40)
Similarly, the thickness of the coated wire for 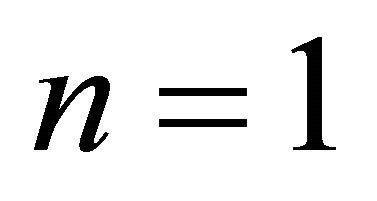 is obtained from Equations (31) and (35):
is obtained from Equations (31) and (35):
 (41)
(41)
In a similar manner, the force on the total wire surface for power law index ![]() is not equal to 1 is
is not equal to 1 is
 , (42)
, (42)
and the force on the total wire surface for the case when the power law index ![]() is equal to 1 is given by
is equal to 1 is given by
 . (43)
. (43)
In dimensionless form the volume flow rate for ![]() is or is not equal to 1are the same as the average velocity in Equations (37) and (36) respectively.
is or is not equal to 1are the same as the average velocity in Equations (37) and (36) respectively.
In case of transformation of our problem to original parameters the results of velocity field, volume flow rate, average velocity and rate of shear stress are transformed to the results of Kasajima and Katsuhiko Ito [11] for ![]() is or is not equal to 1.
is or is not equal to 1.
Figure 3 illustrates the well known effect of ![]() on the velocity profile; i.e. for pseudoplastic the profile becomes progressively flatter; and for dilatant fluids the profile becomes progressively linear.
on the velocity profile; i.e. for pseudoplastic the profile becomes progressively flatter; and for dilatant fluids the profile becomes progressively linear.
Keeping the importance of temperature in our problem we are seeking the temperature distribution with different cases.
Case 1. Temperature of the wire is constant while it is varying linearly on the surface of the coated wire:
Here, consider the temperature of the wire is , and it is
, and it is 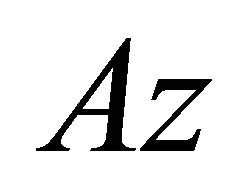 on the surface of the coated wire, so from Equation (17) we have
on the surface of the coated wire, so from Equation (17) we have
 (44)
(44)

Figure 3. The velocity profile for different index ![]() taking
taking 
After transformation we obtain
 (45)
(45)
where
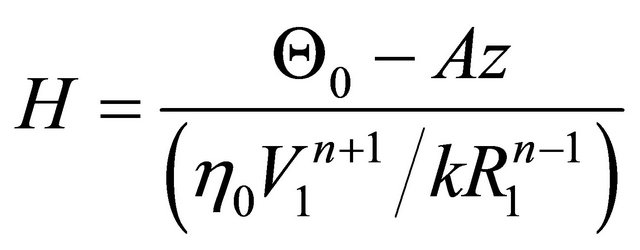 .
.
For 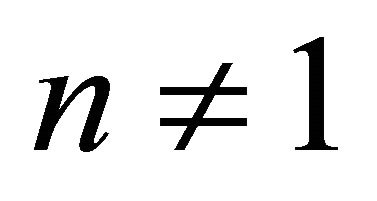 the velocity field from Equation (23) is substitute in Equation (22) and solved corresponding to the boundary conditions (45), we obtain the expression for temperature distribution in form of
the velocity field from Equation (23) is substitute in Equation (22) and solved corresponding to the boundary conditions (45), we obtain the expression for temperature distribution in form of 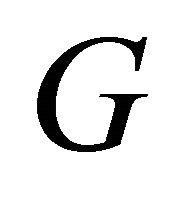 as:
as:
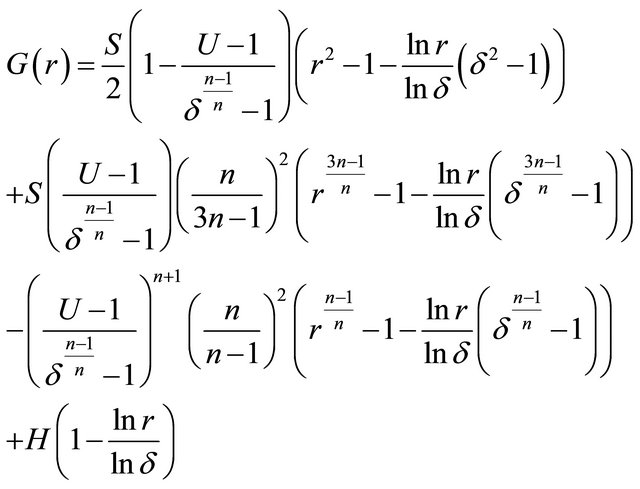 (46)
(46)
For  the velocity field from Equation (24) is substitute in Equation (22) and solved corresponding to the boundary conditions (45), the explicit function for
the velocity field from Equation (24) is substitute in Equation (22) and solved corresponding to the boundary conditions (45), the explicit function for  is obtained for temperature field as:
is obtained for temperature field as:
 (47)
(47)
Case 2. Temperature of the wire varying linearly while it is constant on the surface of the coated wire:
In this case, consider the temperature at the surface of wire is , and
, and 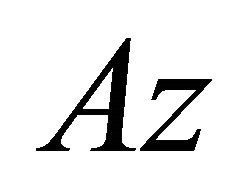 on the surface of continuum.
on the surface of continuum.
Under the above consideration Equation (17) gives
 (48)
(48)
After transformation of the boundary conditions (48) for the non-dimensional temperature distribution 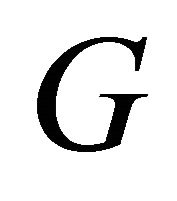 takes the following form
takes the following form
 (49)
(49)
where
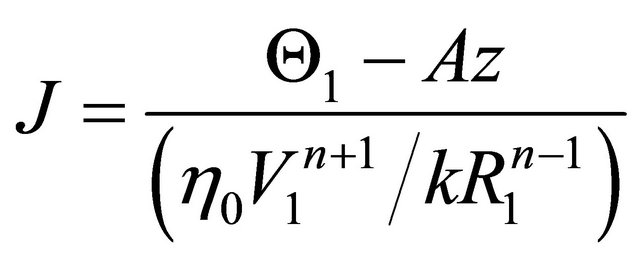 .
.
For  the velocity field from Equation (22) is substitute in Equation (22) and solved corresponding to the boundary conditions (49), we have
the velocity field from Equation (22) is substitute in Equation (22) and solved corresponding to the boundary conditions (49), we have
 (50)
(50)
For 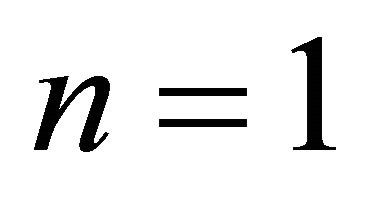 the velocity field from Equation (24) is substitute in Equation (22) and solved corresponding to the boundary conditions (49), we have
the velocity field from Equation (24) is substitute in Equation (22) and solved corresponding to the boundary conditions (49), we have
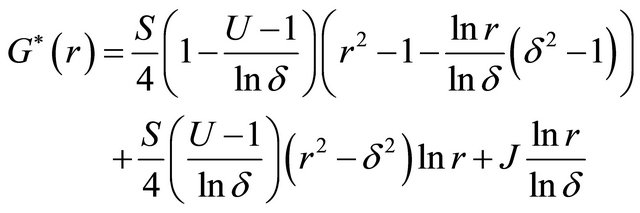 (51)
(51)
Case 3. Temperature of the wire and the surface of coated wire are varying linearly at the same temperature gradient:
Consider the temperatures at the surface of wire and on the surface of continuum are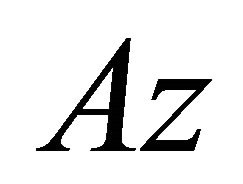 .
.
From Equation (17), we have
 (52)
(52)
After simplification according to demand of our problem, we obtain
 (53)
(53)
For  the velocity field from Equation (22) is substitute in Equation (22) and solved corresponding to the boundary conditions (53), we have
the velocity field from Equation (22) is substitute in Equation (22) and solved corresponding to the boundary conditions (53), we have
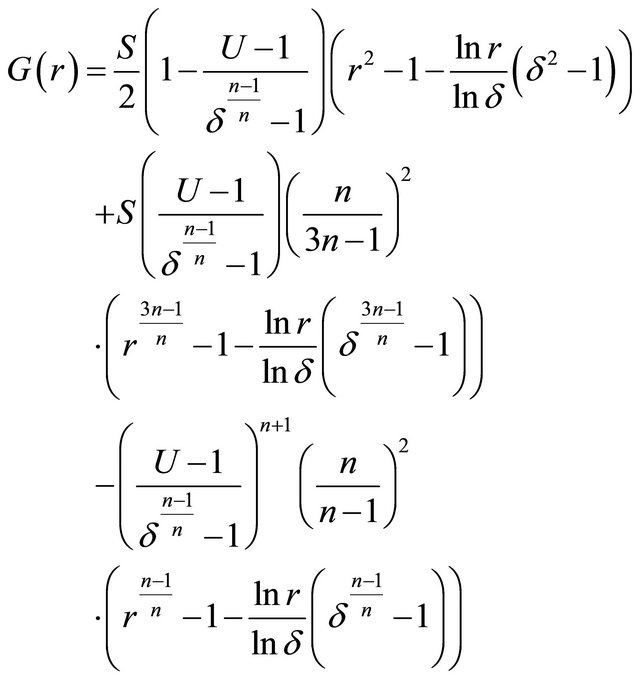 (54)
(54)
For 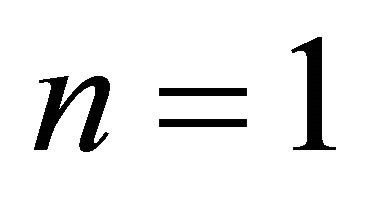 the velocity field from Equation (24) is substitute in Equation (22) and solved corresponding to the boundary conditions (53), after simplification we have
the velocity field from Equation (24) is substitute in Equation (22) and solved corresponding to the boundary conditions (53), after simplification we have
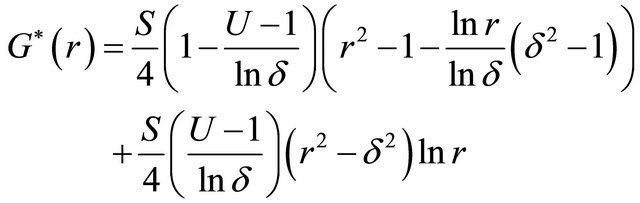 (55)
(55)
4. Conclusion
The posttreatment of wire coating analysis are carried out for power law model fluid. The velocity field, volume flow rate, average velocity, force on the total wire, thickness of coated wire and shear rate have been derived for ![]() is or is not equal to 1. In posttreatment problem the temperature is extremely important for cooling the wire. Therefore, regarding the importance of temperature we have discussed three cases for linearly varying temperature. Expression for temperature distributions in non-dimensional form are obtained for
is or is not equal to 1. In posttreatment problem the temperature is extremely important for cooling the wire. Therefore, regarding the importance of temperature we have discussed three cases for linearly varying temperature. Expression for temperature distributions in non-dimensional form are obtained for 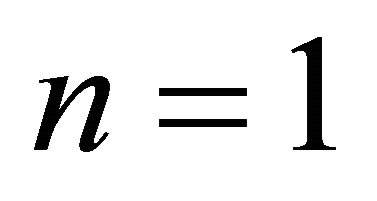 and
and . The interpretations of the results are carried out under the influence of non-dimensional parameters. It is concluded that the velocity decreases as the power law index
. The interpretations of the results are carried out under the influence of non-dimensional parameters. It is concluded that the velocity decreases as the power law index ![]() increases. In addition, the non-Newtonian parameter
increases. In addition, the non-Newtonian parameter![]() decrease the fluid velocity. Also, it is concluded that the force on the coated wire increases as the velocity ratio increases and decreases while increases
decrease the fluid velocity. Also, it is concluded that the force on the coated wire increases as the velocity ratio increases and decreases while increases![]() . It is observed that for
. It is observed that for  the thickness of coated wire increases. Moreover, with a linearly varying wall temperature along the direction of flow the highest temperature rise in the centre of the channel depends on the dimensionless number
the thickness of coated wire increases. Moreover, with a linearly varying wall temperature along the direction of flow the highest temperature rise in the centre of the channel depends on the dimensionless number![]() . One can see the behavior of the physical quantities such as velocity function, non-dimensional function of temperature profile and the differential form of these functions from Figures 3-15.
. One can see the behavior of the physical quantities such as velocity function, non-dimensional function of temperature profile and the differential form of these functions from Figures 3-15.

Figure 4. The velocity profile for different values of velocity ratio  taking index
taking index  and
and 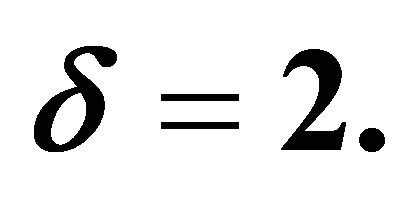

Figure 5. The shear rate for different values of velocity ratio  taking index
taking index 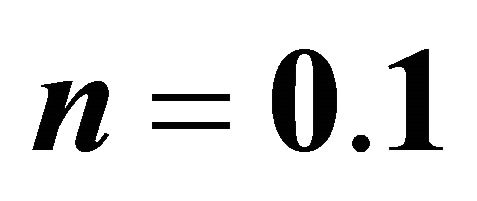 and
and 

Figure 6. Force 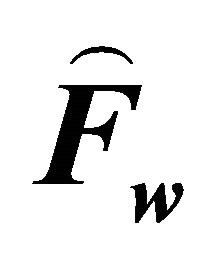 is plotted against U for different values of
is plotted against U for different values of ![]() by taking
by taking 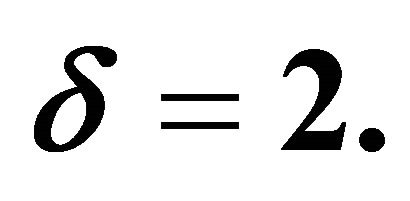

Figure 7. Radius of coated wire 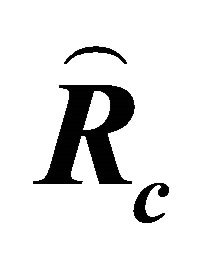 is plotted against
is plotted against ![]() for different values of
for different values of ![]() by taking
by taking 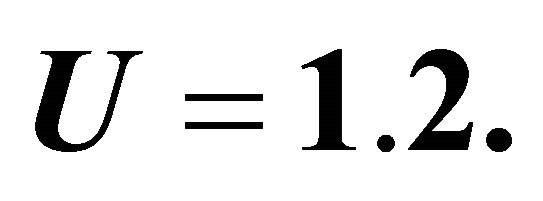
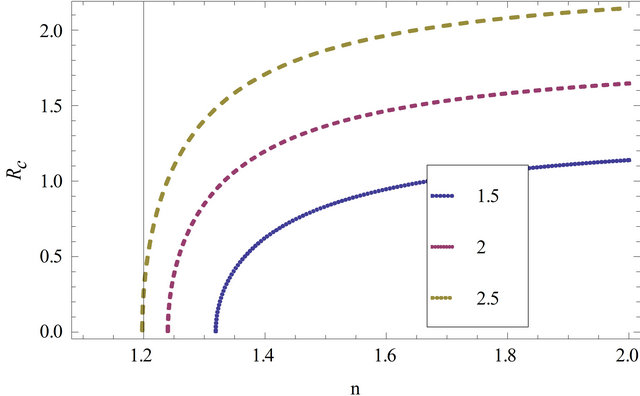
Figure 8. Radius of coated wire  is plotted against
is plotted against ![]() for different values of
for different values of ![]() by taking
by taking 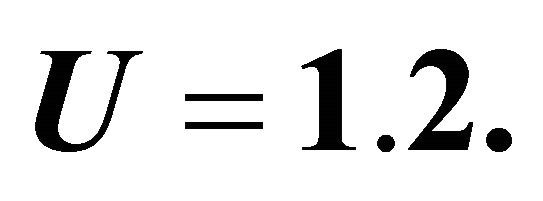

Figure 9. Volume flow rate is plotted against 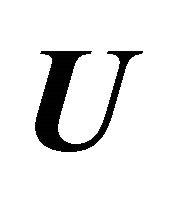 for different values of power law index
for different values of power law index ![]() by taking
by taking 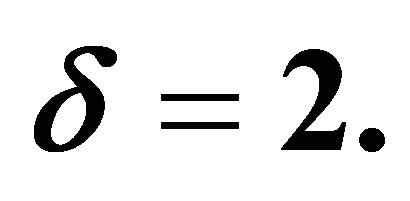
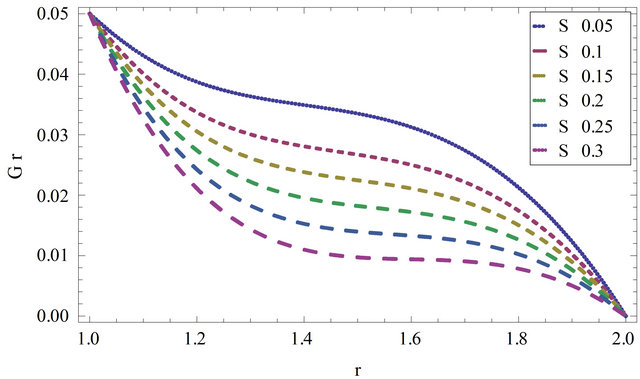
Figure 10. The non-dimensional function  for different values of non-dimensional parameter
for different values of non-dimensional parameter ![]() taking
taking 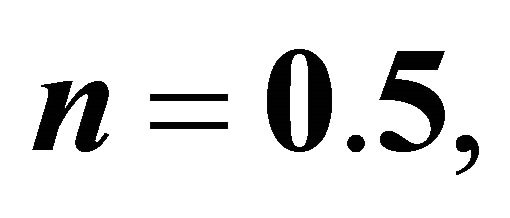
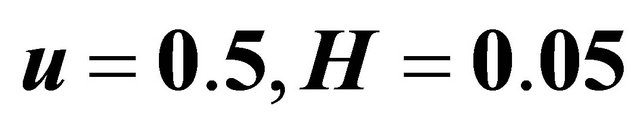 and
and 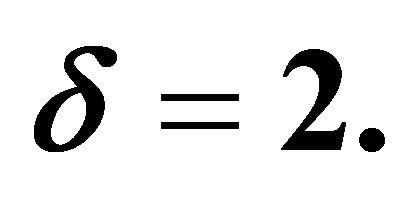
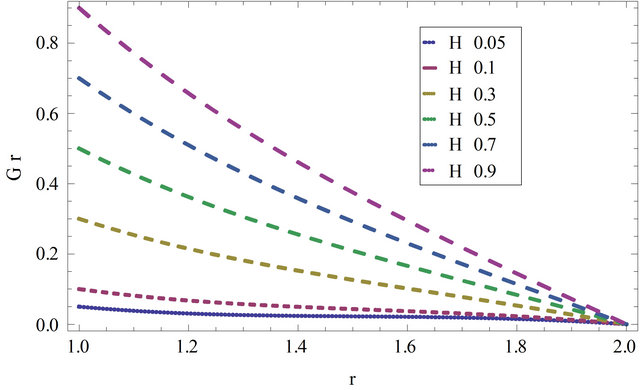
Figure 11. The non-dimensional function  for different values of
for different values of  taking
taking 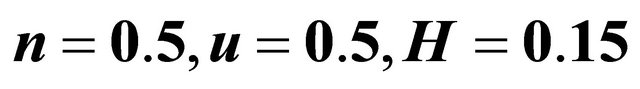 and
and 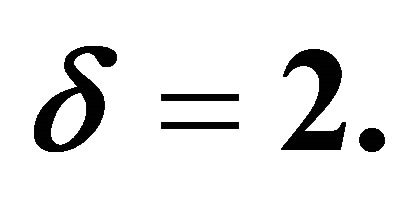
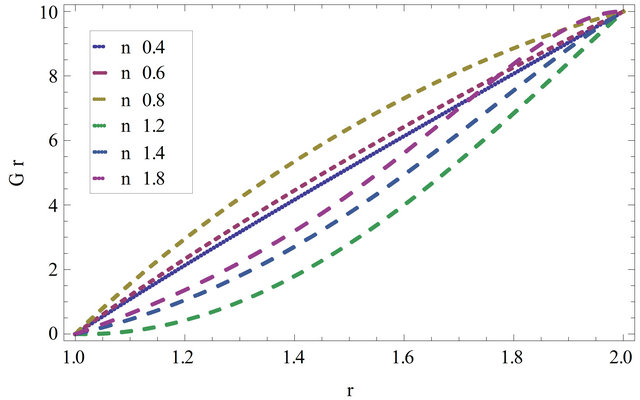
Figure 12. The non-dimensional function  for different values of
for different values of ![]() taking
taking 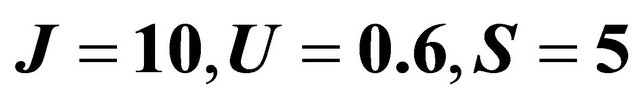 and
and 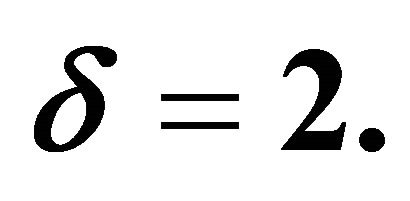

Figure 13. The non-dimensional function  for different values of H taking J = 4, U = 0.6, S = 25, n = 0.5 and
for different values of H taking J = 4, U = 0.6, S = 25, n = 0.5 and 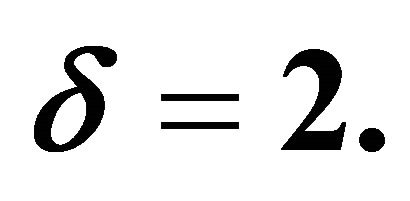

Figure 14. The non-dimensional function  for different values of
for different values of ![]() taking
taking  and
and 
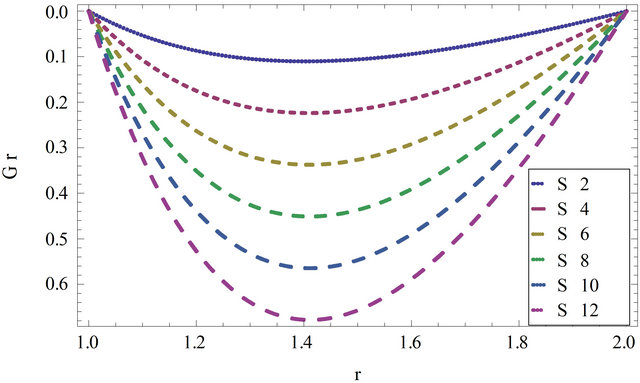
Figure 15. The non-dimensional function  for different values of non-dimensional parameter
for different values of non-dimensional parameter ![]() taking
taking 
 and
and 
5. Acknowledgements
The first author is thankful to higher education commission of Pakistan for funding in MS leading to PhD studies under the 5000 indigenous scholarship scheme BatchIV.
REFERENCES
- M. M. Denn, “Process Fluid Mechanics,” Prentice-Hall, Upper Saddle River, 1980.
- S. Middleman, “Fundamentals of Polymer Processing,” McGraw-Hill, New York, 1977.
- J. M. McKelvey, “Polymer Processing,” John Wiley and Sons, New York, 1962.
- J. B. Paton, P. H. Squire, W. H. Darnell, F. M. Cash and J. F. Carley, “Processing of Thermoplastic Materials,” Reinhold Pub. Corp., New York, 1959, pp. 269-299.
- E. B. Bagley and S. H. Storey, Wire and Wire Products, Vol. 38, No. 7, 1963, pp. 1104-1122.
- S. Akter and M. S. J. Hashmi, “Analysis of Polymer Flow in a Canonical Coating Unit: Power Law Approach,” Progress in Organic Coatings, Vol. 37, No. 1-2, 1999, pp. 15-22. doi:10.1016/S0300-9440(99)00045-4
- S. Akter and M. S. J. Hashmi, “Plasto-Hydrodynamic Pressure Distribution in a Tepered Geometry Wire Coating Unit,” Proceedings of the 14th Conference of the Irish Manufacturing Committee Dublin, Vol. 37, No. 3, 1997, pp. 331-340.
- A. M. Siddiqui, T. Haroon and H. Khan, “Wire Coating Extrusion in a Pressure-Type Die in Flow of a Third Grade Fluid,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 10. No. 2, 2009, pp. 247-257.
- R. T. Fenner and J. G. Williams, “Rheological Analysis of Stabilizing Forces in Wire Coating Analysis,” Trans. Plastic Inst. London, Vol. 35, 1967, pp. 701-706.
- M. Sajjid, A. M. Siddiqui and T. Hayat, “Wire Coating Analysis Using MHD Oldroyd 8-Constant Fluid,” International Journal of Engineering Science, Vol. 45, No. 2-8, 2007, pp. 381-392.
- M. Kasajima and K. Ito, “Posttreatment of Polymer Extrudate in Wire Coating,” Applied Polymer Symposium, No. 20, 1973, pp. 221-235.
- H. I. Andersson and F. Irgens, “Film Flow of Power-Law Fluids,” Encyclopedia of Fluid Mechanics, Polymer Flow Engineering, Vol. 9, 1990.
NOTES
*Corresponding author.

