Applied Mathematics
Vol. 3 No. 2 (2012) , Article ID: 17395 , 5 pages DOI:10.4236/am.2012.32027
Spatial Inhomogenity Due to Turing Instability in a Capital-Labour Model
1Department of Mathematics, Faculty of Science, King Khalid University, Abha, Saudi Arabia
2Department of Mathematics, Faculty of Science, Al-Azhar University, Assiut, Egypt
Email: shhaly70@yahoo.com
Received November 26, 2011; revised December 26, 2011; accepted January 3, 2012
Keywords: Cross-Diffusion; Diffusive Instability; Turing Bifurcation
ABSTRACT
A cross-diffusion system is set up modelling the distribution of capital and labour over the land of two identical patches (cites, markets or countries) in which the per capita migration rate of each species (investment capital or labour force) is influenced not only by its own but also by the other one’s density, i.e. there is cross-diffusion present. Numerical studies show that at a critical value of the bifurcation parameter the system undergoes a Turing bifurcation and the cross-migration response is an important factor that should not be ignored when pattern emerges.
1. Introduction
Mathematically this paper is about a two dimensional reaction diffusion system in which the per capita migration rate of each substance is influenced not only by its own but also by the other one’s density, i.e. there is crossdiffusion present. The Turing bifurcation (see [1]) is the basic bifurcation generating spatial pattern, wherein an equilibrium of a nonlinear system is asymptotically stable in the absence of diffusion but unstable in the presence of diffusion. This lies at the heart of almost all mathematical models for patterning in ecology, embryology, economy and elsewhere in biology and chemistry (see [2-5]).
To formulate a spatio-temporal model, one has to make some basic choices about space, time, and state variables. Each of them may be continuous or discrete (see [6-9]). Classical theories, such as diffusion driven instability and meta-population dynamics which are developed via simple spatial population models, have profoundly increased our understanding of the issue.
In this paper I scrutinize these theories by considering more complicated processes of spatial interaction of populations. In its economic interpretation the model to be constructed describes, the dynamics of capital and labour force in an economy (see [10]). For this purpose I consider the economy of a two countries, two cites or a two larger common markets are not concentrated in a point at the physical space but is distributed in a bounded spatial domain which is the territory of the given two country or two common market. It is assumed that capital and labour force is moving around freely in the given domain and that the domain provides homogeneous, equal conditions to investment and life everywhere. The basic assumptions concerning the movement of capital and labour in the spatial domain are that both investment capital and labour are moving away places where their respective densities are high but the movement of both substances is influenced also by the density of the other: capital is moving towards places where (cheap) labour is abundant and the labour force is moving towards place where there are free jobs, i.e. investment takes place.
This paper is organized as follows: In Section 2 the model is built, in Section 3 its linearization is treated and the conditions for the Turing bifurcation are established (these are the main results of this paper), in Section 4 we consider an example to illustrate what can be expected, in Section 5 we summarize the main conclusions of the study.
2. The Model
Denote the quantity of free jobs (prey) in patch, that is, jobs available at time 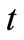 by
by . This quantity will be considered proportional or positively correlated, at least, to investment capital. Denote the total labour force (predator), i.e. the number of those employed and unemployed at time
. This quantity will be considered proportional or positively correlated, at least, to investment capital. Denote the total labour force (predator), i.e. the number of those employed and unemployed at time  by
by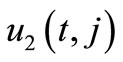 ,
,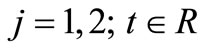 . We assume that the quantity of free jobs would grow according to the logistic law if there was no labour force available. The latter decreases the
. We assume that the quantity of free jobs would grow according to the logistic law if there was no labour force available. The latter decreases the 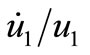 of free jobs proportionally to the quantity of labour force
of free jobs proportionally to the quantity of labour force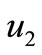 . The labour force is increasing by the logistic law provided that there is no capital investment. If there is the per capita growth rate of working force is increased by a quantity proportional to the number of free jobs. The interaction between two species (capital-labour Model) living in a habitat of two identical patches (cites) linked by migration is described as a system of differential equations as follows:
. The labour force is increasing by the logistic law provided that there is no capital investment. If there is the per capita growth rate of working force is increased by a quantity proportional to the number of free jobs. The interaction between two species (capital-labour Model) living in a habitat of two identical patches (cites) linked by migration is described as a system of differential equations as follows:
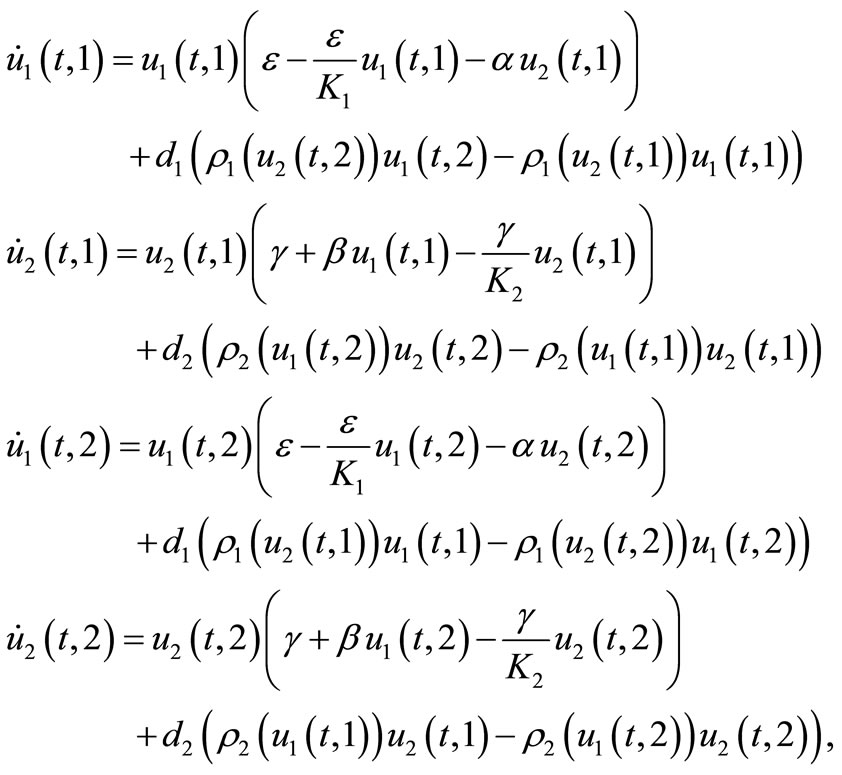 (1)
(1)
where 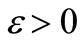 is the natural per capita growth rate of free jobs, and
is the natural per capita growth rate of free jobs, and 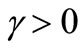 is the natural per capita growth rate of the working force,
is the natural per capita growth rate of the working force, 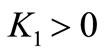 is the theoretical eventual maximum of the number of free jobs (related to the theoretical maximum of investment capital), and
is the theoretical eventual maximum of the number of free jobs (related to the theoretical maximum of investment capital), and 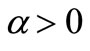 is the rate by which the labour force is filling in the free jobs,
is the rate by which the labour force is filling in the free jobs, 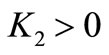 is the theoretical eventual maximum (in fact the lim sup) of the total labour force in absence of investment, and
is the theoretical eventual maximum (in fact the lim sup) of the total labour force in absence of investment, and 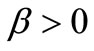 is the rate by which available jobs increase the per capita growth rate of the labour force.
is the rate by which available jobs increase the per capita growth rate of the labour force. 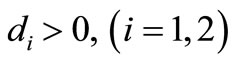 are the diffusion coefficients and
are the diffusion coefficients and 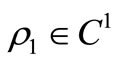 is a positive decreasing function of
is a positive decreasing function of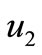 , the density of the predator,
, the density of the predator, 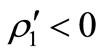 and
and 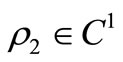 is a positive decreasing function of
is a positive decreasing function of  the density of the prey,
the density of the prey,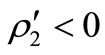 .
.
First we consider the kinetic system without migration, i.e. 
 (2)
(2)
System (2) has a positive equilibrium point 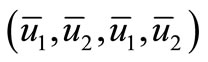 where
where
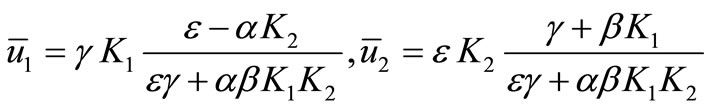 . (3)
. (3)
If
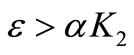 . (4)
. (4)
This result is intuitive: if the growth of investment capital is slow, labour force is abundant and free jobs are filled in fast then we have a stable equilibrium with practically no free jobs available. In this case this is the only eqilibrium with non-negative, i.e. meaningful coordinates.
The Jacobian matrix of the system without diffusion linearized at 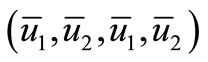 is
is
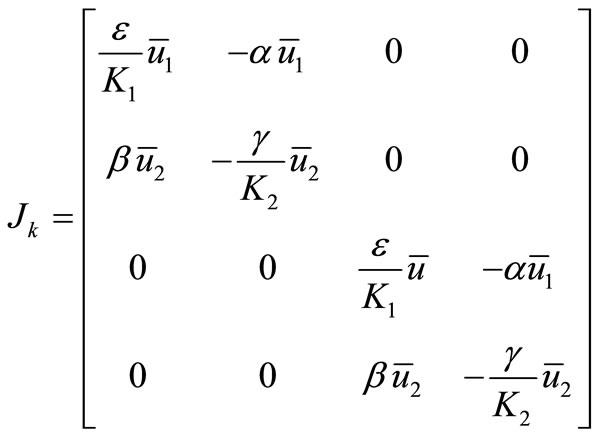 , (5)
, (5)
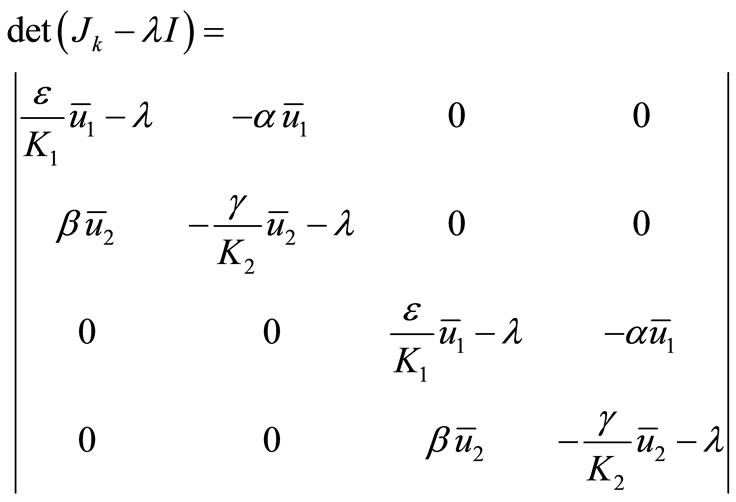 . (6)
. (6)
The characteristic polynomial is
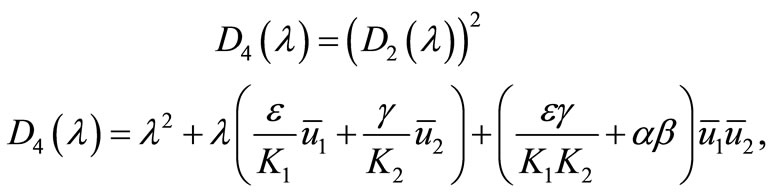 (7)
(7)
hence, the positive equilibrium point 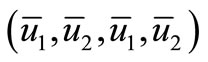 is linearly asymptotically stable.
is linearly asymptotically stable.
3. The Linearized Problem
Returning to system (1), we see that 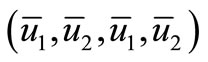 is also a spatially homogeneous equilibrium of the system with diffusion. The Jacobian matrix of the system with diffusion at
is also a spatially homogeneous equilibrium of the system with diffusion. The Jacobian matrix of the system with diffusion at 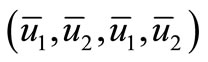 can be written as:
can be written as:
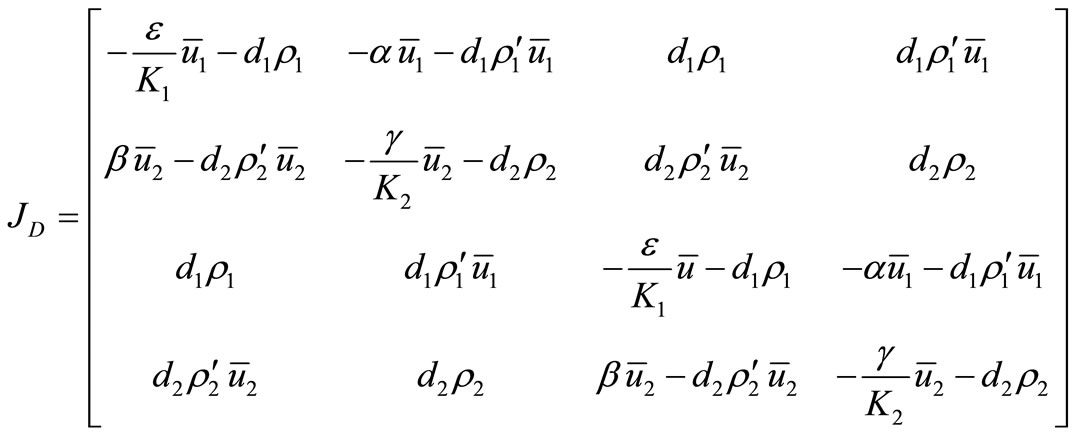 , (8)
, (8)
where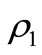 ,
, 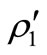 re to be taken at
re to be taken at 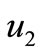 and
and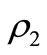 ,
, 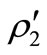 at
at .
.
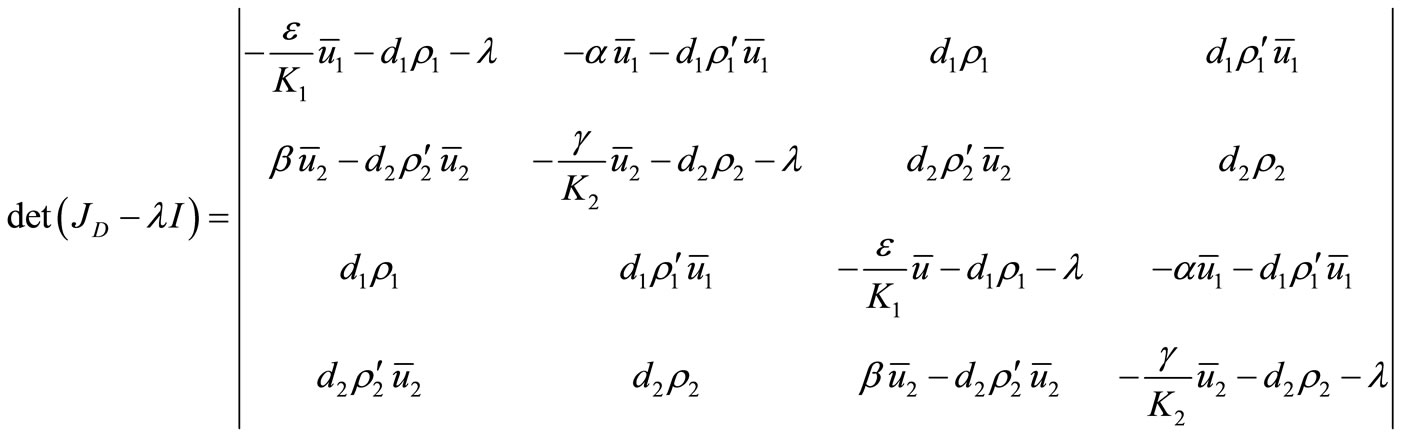 . (9)
. (9)
Using the properties of determinant we get
 , (10)
, (10)
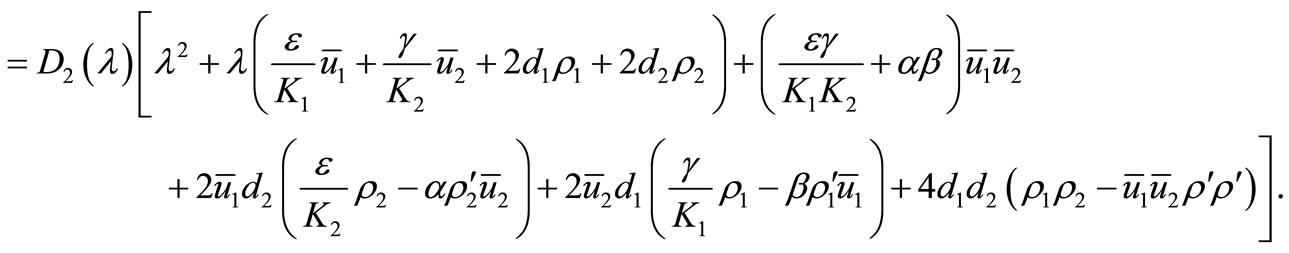 (11)
(11)
We know that  has two roots with negative real parts. The other polynomial will have a negative and a positive root if the constant term is negative. Clearly,
has two roots with negative real parts. The other polynomial will have a negative and a positive root if the constant term is negative. Clearly, 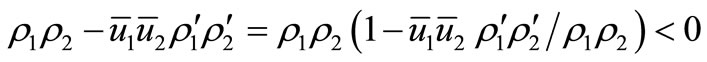 is
is 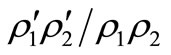 big enough. If we have achieved this we may increase
big enough. If we have achieved this we may increase 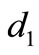 and/or
and/or 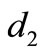 and the constant term becomes negative. These calculations lead to the following Theorem.
and the constant term becomes negative. These calculations lead to the following Theorem.
Theorem: The equilibrium 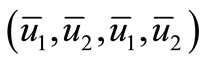 of system (1) is asymptotically stable if
of system (1) is asymptotically stable if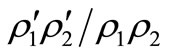 ,
, 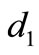 and
and 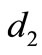 are sufficiently small; if
are sufficiently small; if 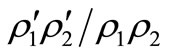 and either
and either 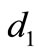 and
and 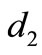 are sufficiently big then
are sufficiently big then 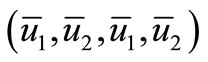 loses its stability by a Turing bifurcation.
loses its stability by a Turing bifurcation.
4. Numerical Investigations
We apply our analytical approach to the following example of migration function and we are looking for conditions which imply Turing instability (diffusion driven instability).
Example: We choose
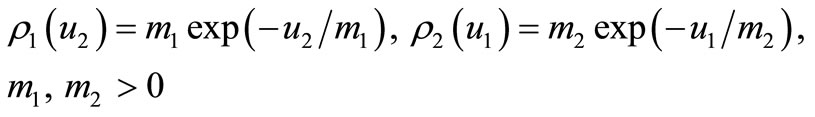 (12)
(12)
If 
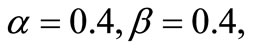

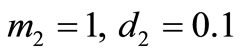
then 
At 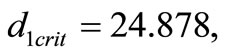 we have four eigenvalues
we have four eigenvalues 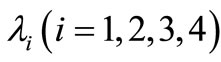 such that
such that 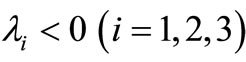 and
and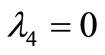 .
.
If , then
, then 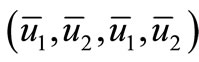 is asymptotically stable.
is asymptotically stable.
If 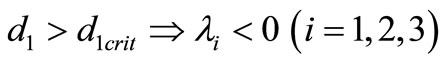 and
and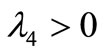 , then
, then 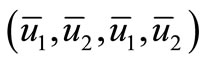 is unstable.
is unstable.
Thus as 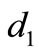 is increased through
is increased through 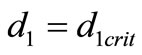 then the spatially homogeneous equilibrium loses its stability. Numerical calculations show that two new spatially nonconstant equilibria emerge (see the just Table 1 and Figures 1-4), and these equilibria are asymptotically stable; so that this is a pitchfork bifurcation.
then the spatially homogeneous equilibrium loses its stability. Numerical calculations show that two new spatially nonconstant equilibria emerge (see the just Table 1 and Figures 1-4), and these equilibria are asymptotically stable; so that this is a pitchfork bifurcation.
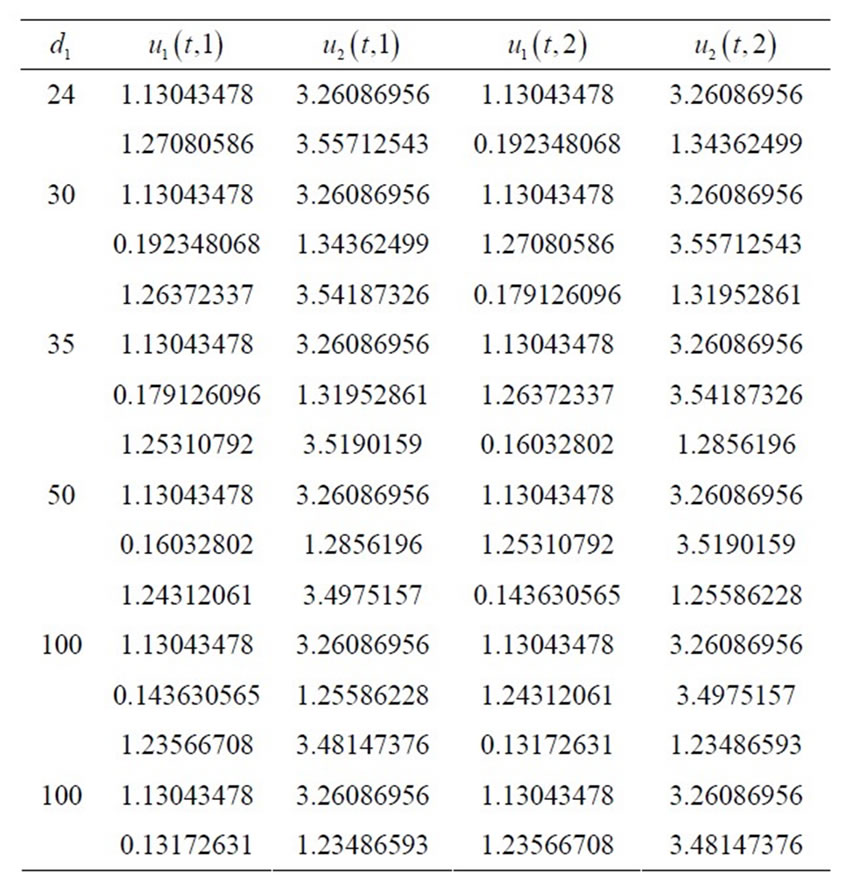
Table 1. Equilibria of the example before and after bifurcation.
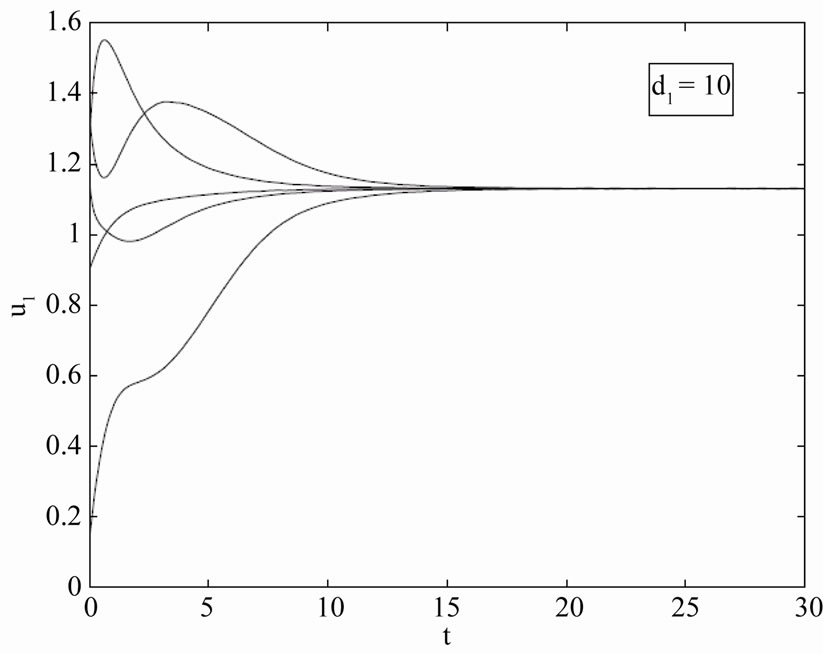
Figure 1. Graphs of the coordinate u1(t,1) before bifurcation at d1 = 10 (see the Table) (Figure produced by applying MATLAB).

Figure 2. Graphs of the coordinate u1(t,1) after bifurcation at d1 = 30 (see the Table) (Figure produced by applying MATLAB).
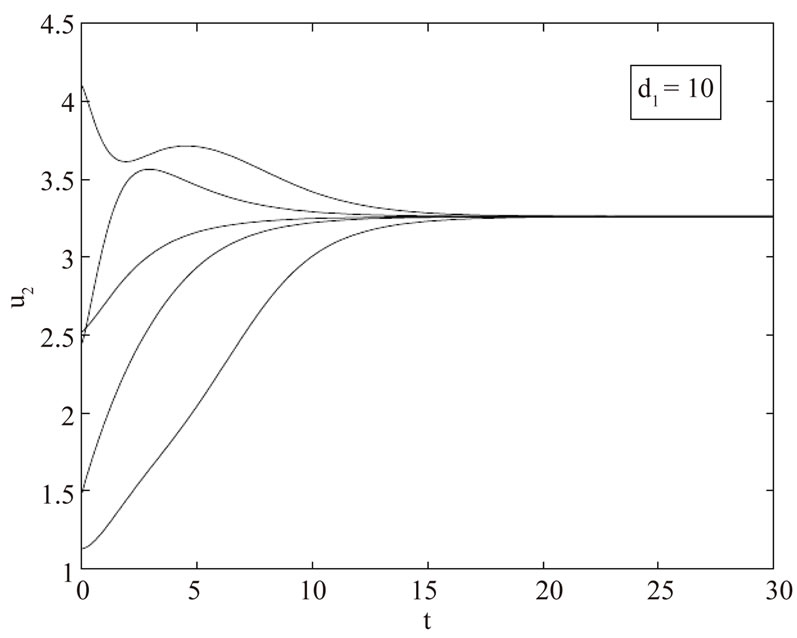
Figure 3. Graphs of the coordinate u2(t,1) before bifurcation at d1 = 10 (see the Table) (Figure produced by applying MATLAB).

Figure 4. Graphs of the coordinate u2(t,1) before bifurcation at d1 = 30 (see the Table) (Figure produced by applying MATLAB).
5. Conclusion
In the present article our interest is to study a preypredator (free jobs or investment capital-labour force) system in two patches (cites, markets or countries) in which the per capita migration rate of each species is influenced not only by its own but also by the other one’s density, i.e. there is cross diffusion present. We show that at a critical value of the bifurcation parameter the system undergoes a Turing bifurcation and the cross migration response is an important factor that should not be ignored when pattern emerges, also as  is increased through
is increased through 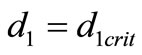 the spatially homogeneous equilibrium loses its stability and two new stable equilibria emerge.
the spatially homogeneous equilibrium loses its stability and two new stable equilibria emerge.
6. Acknowledgements
We thank Prof. Gamal M. Mahmoud (Assiut University, Faculty of science, Department of Mathematics) for valuable comments on an earlier version of this paper and dedicated to the memory of Farkas Miklos. The Research partially supported by the Deanship of Scientific Research, King Khalid University, KSA (KKU-SCI-11-025).
REFERENCES
- A. M. Turing, “The Chemical Basis of Morphogensis,” Philosophical Transactions of the Royal Society B, Vol. 237, No. 641, 1953, pp. 37-72. doi:10.1098/rstb.1952.0012
- M. Farkas, “Two Ways of Modeling cross Diffusion,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 30, No. 2, 1997, pp. 1225-1233. doi:10.1016/S0362-546X(96)00161-7
- M. Farkas, “Dynamical Models in Biology,” Academic Press, Cambridge, 2001.
- Y. Huang and O. Diekmann, “Interspecific Influence on Mobility and Turing Instability,” Bulletin of athematical Biology, Vol. 65, No. 1, 2003, pp. 143-156. doi:10.1006/bulm.2002.0328
- J. D. Murray, “Mathematical Biology,” Springer-Verlag, Berlin, 1989.
- S. Aly and M. Farkas, “Competition in Patchy Environment with cross Diffusion,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 5, No. 4, 2004, pp. 589-595. doi:10.1016/j.nonrwa.2003.10.001
- S. Aly and M. Farkas, “Bifurcation in a Predator-Prey Model in Patchy Environment with Diffusion,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 5, No. 3, 2004, pp. 519-526. doi:10.1016/j.nonrwa.2003.11.004
- S. Aly, “Bifurcations in a Predator-Prey Model with Diffusion and Memory,” International Journal of Bifurcation and Chaos, Vol. 16 No. 6, 2006, pp. 1855-1863. doi:10.1142/S0218127406015751
- Y. Takeuchi, “Global Dynamical Properties of LotkaVolterra System,” World Scientific, Hackensack, 1996.
- M. Farkas, “On the Distribution of Capital and Labour in a Closed Economy,” Southeast Asian Bulletin of Mathematics, Vol. 19 No. 2, 1995, pp. 27-37.

