Applied Mathematics
Vol. 3 No. 1 (2012) , Article ID: 16754 , 8 pages DOI:10.4236/am.2012.31010
Generalized Quasi Variational-Type Inequalities
Department of Mathematics, Aligarh Muslim University, Aligarh, India
Email: ahmad_kalimuddin@yahoo.co.in, salahuddin12@mailcity.com
Received September 9, 2011; revised November 4, 2011; accepted November 12, 2011
Keywords: Generalized quasi variational type inequalities (GQVTI); (η,h)-quasi pseudo-monotone operator; locally convex Hausdorff topological vector spaces; compact sets; bilinear functional; lower semicontinuous; upper semicontinuous
ABSTRACT
In this paper, we define the concepts of (η,h)-quasi pseudo-monotone operators on compact set in locally convex Hausdorff topological vector spaces and prove the existence results of solutions for a class of generalized quasi variational type inequalities in locally convex Hausdorff topological vector spaces.
1. Introduction
Variational inequality theory has appeared as an effective and powerful tool to study and investigate a wide class of problems arising in pure and applied sciences including elasticity, optimization, economics, transportation, and structural analysis, see for instance [1,2]. In 1966, Browdev [3] first formulated and proved the basic existence theorems of solutions to a class of nonlinear variational inequalities. In 1980, Giannessi [1] introduced the vector variational inequality in a finite dimensional Euclidean space. Since then Chen et al. [4] have intensively studied vector variational inequalities in abstract spaces and have obtained existence theorems for their inequalities.
The pseudo-monotone type operators was first introduced in [5] with a slight variation in the name of this operator. Later these operators were renamed as pseudomonotone operators in [6]. The pseudomonotone operators are set-valued generalization of the classical pseudomonotone operator with slight variations. The classical definition of a single-valued pseudo-monotone operator was introduced by Brezis, Nirenberg and Stampacchia [7].
In this paper we obtained some general theorems on solutions for a new class of generalized quasi variational type inequalities for (η,h)-quasi-pseudo-monotone operators defined as compact sets in topological vector spaces. We have used the generalized version of Ky Fan’s minimax inequality [8] due to Chowdhury and Tan [9].
Let 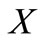 and
and 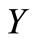 be the topological spaces,
be the topological spaces, 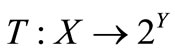 be the mapping and the graph of
be the mapping and the graph of 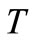 is the set
is the set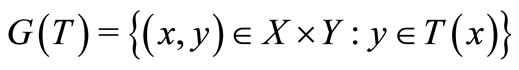 . In this paper,
. In this paper, 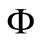 denotes either the real field
denotes either the real field 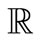 or the complex field
or the complex field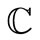 . Let
. Let 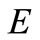 be a topological vector space over
be a topological vector space over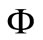 ,
, 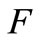 be a vector space over
be a vector space over 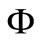 and
and 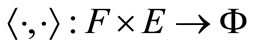 be a bilinear functional.
be a bilinear functional.
For each nonempty subset 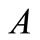 of
of 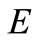 and
and 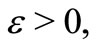 let
let 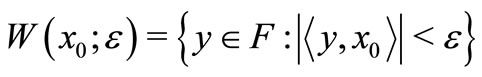 and
and
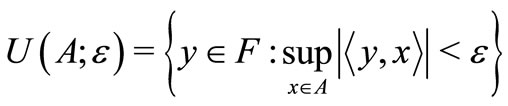 for
for . Let
. Let  be the (weak) topology on
be the (weak) topology on 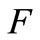 generated by the family
generated by the family 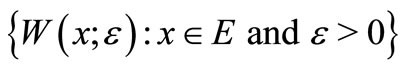 as a subbase for the neighbourhood system at 0 and
as a subbase for the neighbourhood system at 0 and 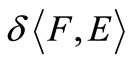 be the (strong) topology on
be the (strong) topology on 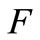 generated by the family {
generated by the family {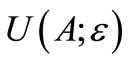 :
: 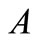 is a nonempty bounded subset of
is a nonempty bounded subset of 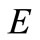 and
and 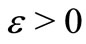 } as a base for the neighbourhood system at 0. The bilinear functional
} as a base for the neighbourhood system at 0. The bilinear functional 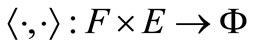 separates points in
separates points in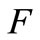 , i.e., for each
, i.e., for each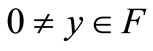 , there exists
, there exists 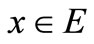 such that
such that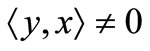 , then
, then 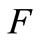 also becomes Hausdorff. Furthermore, for a net
also becomes Hausdorff. Furthermore, for a net 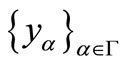 in
in 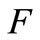 and for
and for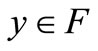 1)
1) 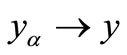 in
in 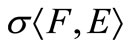 if and only if
if and only if 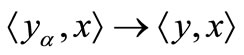 for each
for each 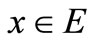 and 2)
and 2) 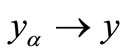 in
in 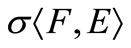 if and only if
if and only if 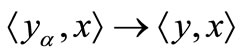 uniformaly for
uniformaly for 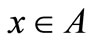 for each nonempty bounded subset
for each nonempty bounded subset 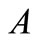 of
of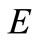 .
.
Given a set-valued map 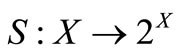 and two set valued maps
and two set valued maps 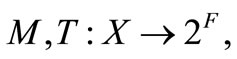 the generalized quasi variational type inequality (GQVTI) problem is to find
the generalized quasi variational type inequality (GQVTI) problem is to find 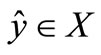 and
and 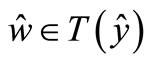 such that
such that 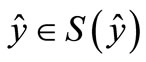 and
and
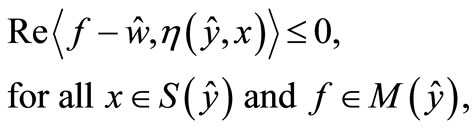
where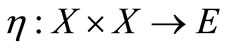 .
.
If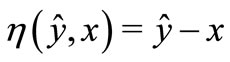 , then generalized quasi variational type inequality (GQVTI) is equivalent to generalized quasi variational inequality (GQVI).
, then generalized quasi variational type inequality (GQVTI) is equivalent to generalized quasi variational inequality (GQVI).
Find  and
and 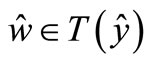 such that
such that 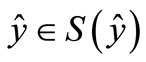 and
and
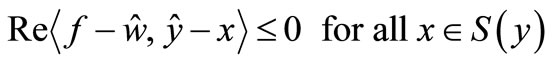
and 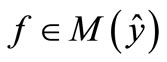 was introduced by Shih and Tan [10] in 1989 and later was stated by Chowdhury and Tan in [11].
was introduced by Shih and Tan [10] in 1989 and later was stated by Chowdhury and Tan in [11].
Definition 1. Let 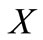 be a nonempty subset of a topological vector space
be a nonempty subset of a topological vector space 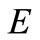 over
over 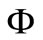 and
and 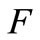 be a topological vector space over
be a topological vector space over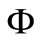 , which is equipped with the
, which is equipped with the 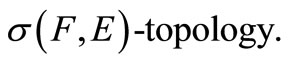 Let
Let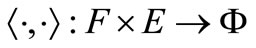 be a bilinear functional. Suppose we have the following four maps.
be a bilinear functional. Suppose we have the following four maps.
1) 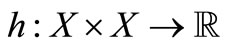
2) 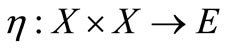
3) 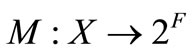
4)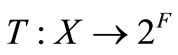 .
.
1) Then 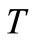 is said to be an (η,h)-quasi pseudo-monotone type operator if for each
is said to be an (η,h)-quasi pseudo-monotone type operator if for each 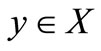 and every net
and every net 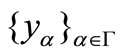 in
in 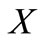 converging to y (or weakly to y) with
converging to y (or weakly to y) with
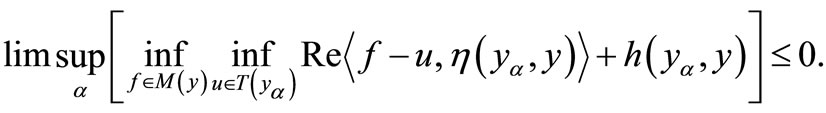
We have
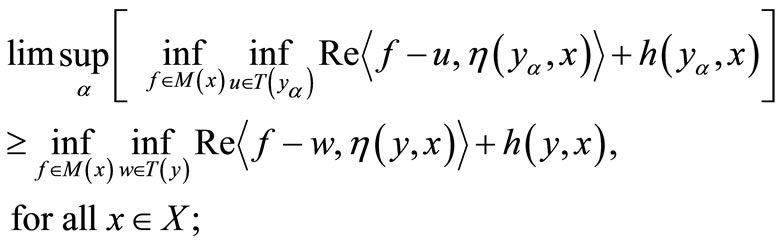
2) 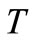 is said to be h-quasi-pseudomonotone operator if
is said to be h-quasi-pseudomonotone operator if 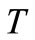 is (η,h)-quasi-pseudomonotone operator with
is (η,h)-quasi-pseudomonotone operator with 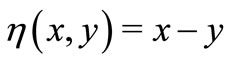 and for some
and for some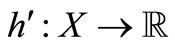 ,
,
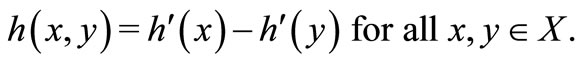
3) a quasi-pseudo monotone operator if 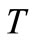 is an h-quasi pseudo-monotone operator with
is an h-quasi pseudo-monotone operator with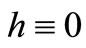 .
.
Remark 1. If 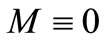 and
and 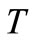 is replaced by
is replaced by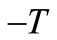 , then h-quasi-pseudo monotone operator reduces to the h-pseudo monotone operator, see for example [5]. The h-pseudo monotone operator defined in [5] is slightly more general than the definition of h-pseudo monotone operator given in [12]. Also we can find the generalization of quasi-pseudo monotone operator in [11] and for more detail see [13].
, then h-quasi-pseudo monotone operator reduces to the h-pseudo monotone operator, see for example [5]. The h-pseudo monotone operator defined in [5] is slightly more general than the definition of h-pseudo monotone operator given in [12]. Also we can find the generalization of quasi-pseudo monotone operator in [11] and for more detail see [13].
Theorem 1. [8] Let 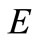 be a topological vector space,
be a topological vector space, 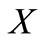 be a nonempty convex subset of
be a nonempty convex subset of 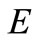 and
and 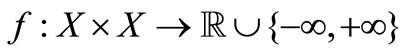 be such that 1) For each
be such that 1) For each 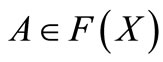 and each fixed
and each fixed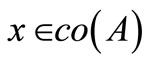 ,
, 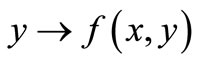 is lower semicontinuous on
is lower semicontinuous on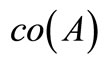 ;
;
2) For each 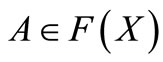 and each
and each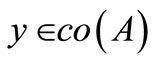 ,
, 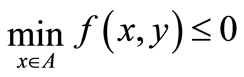 ;
;
3) For each 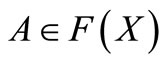 and each
and each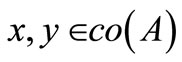 , every net
, every net 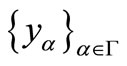 in
in  converging to
converging to 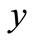 with
with
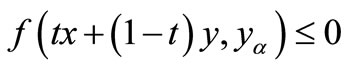 for all
for all 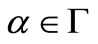 and all
and all 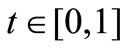 we have
we have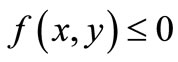 ;
;
4) There exist a nonempty closed compact subset 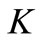 of
of 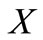 and
and 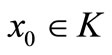 such that
such that
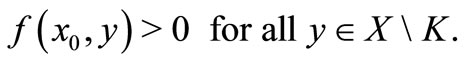
Then there exists 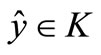 such that
such that
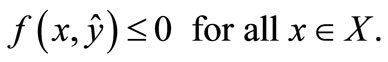
2. Preliminaries
In this section, we shall mainly state some earlier work which will be needed in proving our main results.
Lemma 1. [14] Let 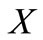 be a nonempty subset of a Hausdorff topological vector space
be a nonempty subset of a Hausdorff topological vector space 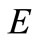 and
and 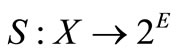 be an upper semicontinuous map such that
be an upper semicontinuous map such that 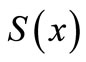 is a bounded subset of
is a bounded subset of 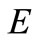 for each
for each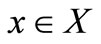 . Then for each continuous linear functional
. Then for each continuous linear functional 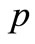 on
on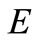 , the map
, the map 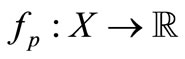 defined by
defined by
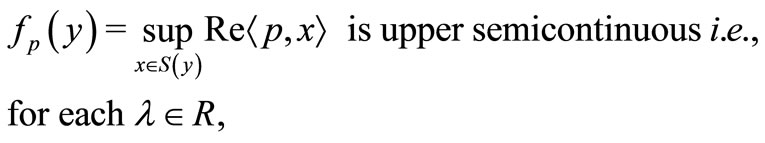
the set 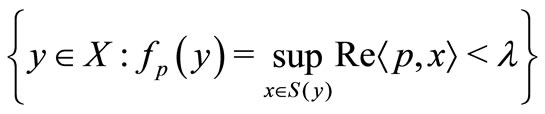 is open in
is open in  .
.
Lemma 2. [15] Let 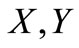 be topological spaces,
be topological spaces, 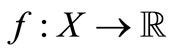 be non-negative and continuous and
be non-negative and continuous and 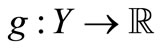 be lower semicontinuous. Then the map
be lower semicontinuous. Then the map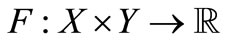 , defined by
, defined by 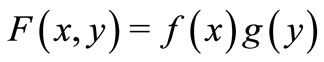 for all
for all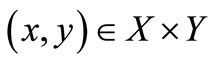 , is lower semicontinuous.
, is lower semicontinuous.
Lemma 3. [11] Let 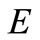 be a topological vector space over
be a topological vector space over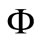 ,
, 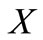 be a nonempty compact subset of
be a nonempty compact subset of 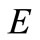 and
and 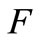 be a Hausdorff topological vector space over
be a Hausdorff topological vector space over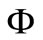 . Let
. Let 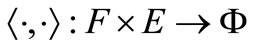 be a bilinear functional and
be a bilinear functional and 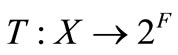 be an upper semicontinuous map such that each
be an upper semicontinuous map such that each 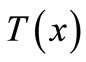 is compact. Let
is compact. Let 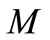 be a nonempty compact subset of
be a nonempty compact subset of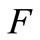 ,
, 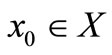 and
and 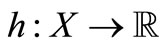 be continuous. Define
be continuous. Define 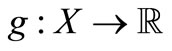 by
by
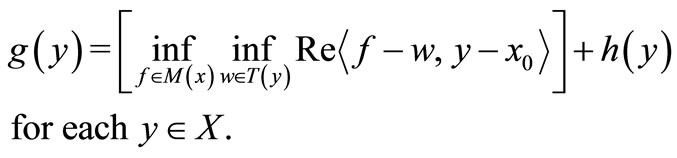
Suppose that 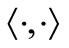 is continuous on the (compact)
is continuous on the (compact)
subset 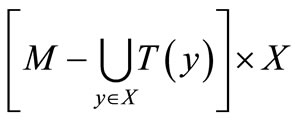 of
of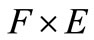 . Then
. Then 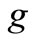 is lower semicontinuous on
is lower semicontinuous on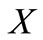 .
.
Lemma 4. [11] Let 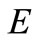 be a topological vector space over
be a topological vector space over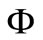 ,
, 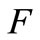 be a vector space over
be a vector space over 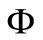 and
and 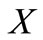 be a nonempty convex subset of
be a nonempty convex subset of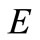 . Let
. Let 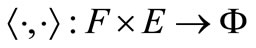 be a bilinear functional, equip
be a bilinear functional, equip 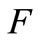 with the
with the 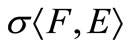 topology. Let
topology. Let 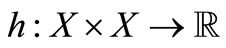 be convex with second argument and
be convex with second argument and 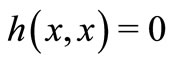 for all
for all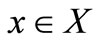 . Let
. Let 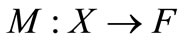 be lower semicontinuous along line segments in
be lower semicontinuous along line segments in 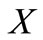 to the
to the 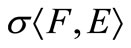 -topology on
-topology on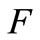 . Let
. Let 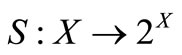 and
and 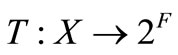 be two maps. Let the continuous map
be two maps. Let the continuous map 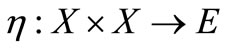 be convex with second argument,
be convex with second argument, 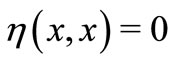 for every
for every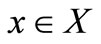 . Suppose that there exists
. Suppose that there exists 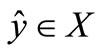 such that
such that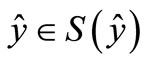 ,
, 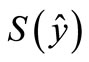 is convex and
is convex and
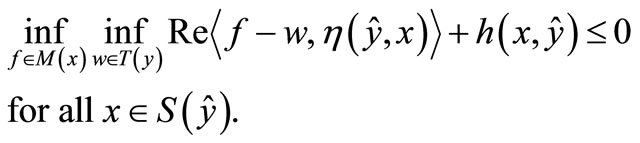
Then
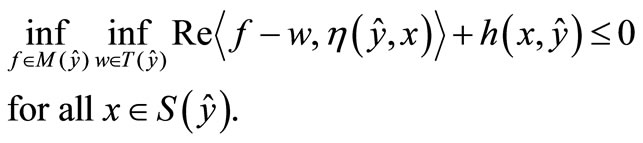
Theorem 2. [16] Let 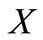 be a nonempty convex subset of a vector space and
be a nonempty convex subset of a vector space and 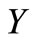 be a nonempty compact convex subset of a Hausdorff topological vector space. Suppose that
be a nonempty compact convex subset of a Hausdorff topological vector space. Suppose that 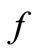 is a real-valued function on
is a real-valued function on 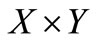 such that for each fixed
such that for each fixed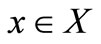 , the map
, the map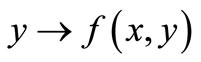 , i.e.,
, i.e., 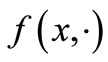 is lower semicontinuous and convex on Y and for each fixed
is lower semicontinuous and convex on Y and for each fixed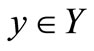 , the map
, the map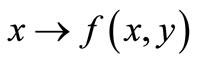 , i.e.,
, i.e., 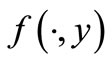 is concave on
is concave on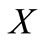 . Then
. Then
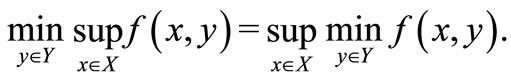
3. Existence Result
In this section, we prove the existence theorem for the solutions to the generalized quasi variational type inequalities for (η,h)-quasi-pseudo monotone operator with compact domain in locally convex Hausdorff topological vector spaces.
Theorem 3. Let 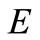 be a locally convex Hausdorff topological vector space over
be a locally convex Hausdorff topological vector space over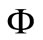 ,
, 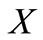 be a nonempty compact convex subset of
be a nonempty compact convex subset of 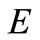 and
and 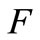 a Hausdorff topological vector space over
a Hausdorff topological vector space over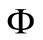 . Let
. Let 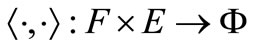 be a bilinear continuous functional on compact subset of
be a bilinear continuous functional on compact subset of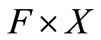 . Suppose that 1)
. Suppose that 1) 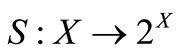 is upper semicontinuous such that each
is upper semicontinuous such that each 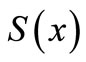 is closed and convex;
is closed and convex;
2) 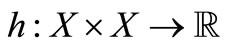 is convex with second argument,
is convex with second argument, 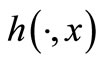 is lower semicontinuous and
is lower semicontinuous and 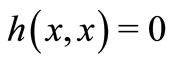 for
for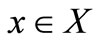 ;
;
3) 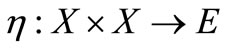 is convex with second argument,
is convex with second argument, 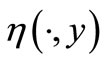 is continuous and
is continuous and 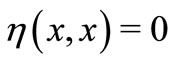 for all
for all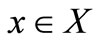 ;
;
4) 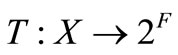 is an (η,h)-quasi-pseudo-monotone operator and is upper semicontinuous such that each
is an (η,h)-quasi-pseudo-monotone operator and is upper semicontinuous such that each 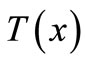 is compact, convex and
is compact, convex and 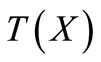 is strongly bounded;
is strongly bounded;
5) 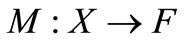 is a linear and upper semicontinuous map in
is a linear and upper semicontinuous map in 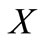 such that each
such that each 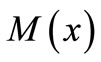 is (weakly) compact convex;
is (weakly) compact convex;
6) the set
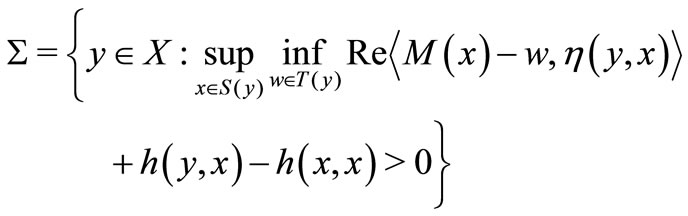
is open in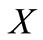 .
.
Then there exists 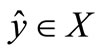 such that a)
such that a)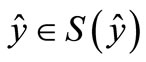 and b) there exists
and b) there exists 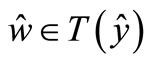 with
with
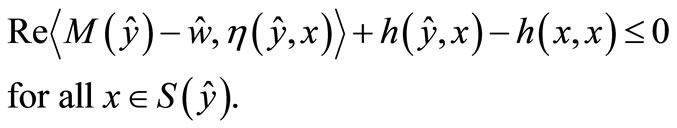
Moreover if 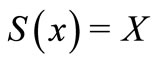 for all
for all ,
, 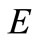 is not required to be locally convex and if
is not required to be locally convex and if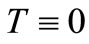 , the continuity assumption on
, the continuity assumption on 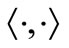 can be weakened to the assumption that for each
can be weakened to the assumption that for each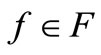 , the map
, the map 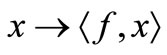 is continuous on
is continuous on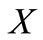 .
.
Proof. We divide the proof into three steps.
Step 1. There exists 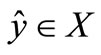 such that
such that 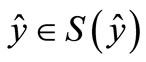 and
and
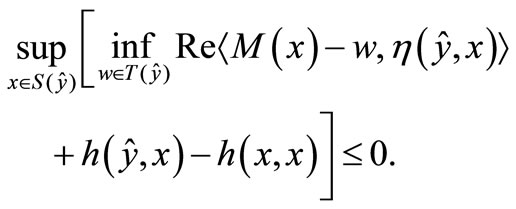
Contrary suppose that for each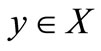 , either
, either 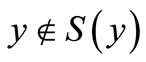 or there exists
or there exists 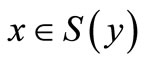 such that
such that
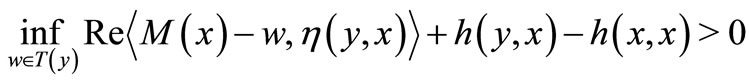 that is for each
that is for each 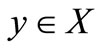 either
either 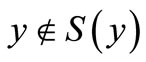 or
or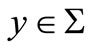 . If
. If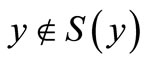 , then by a Hahn-Banach separation theorem for convex sets is locally convex Hausdorff topological vector spaces, there exists
, then by a Hahn-Banach separation theorem for convex sets is locally convex Hausdorff topological vector spaces, there exists 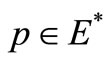 such that
such that
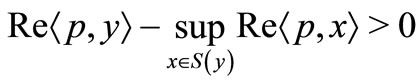 .
.
For each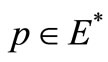 , set
, set
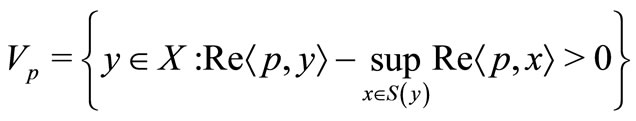 .
.
Then  is open in
is open in  by Lemma 1 and
by Lemma 1 and  is open in
is open in
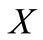 by hypothesis. Now
by hypothesis. Now 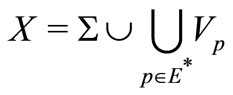 and
and
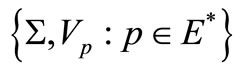 is an open covering for
is an open covering for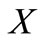 . Since
. Since 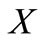
is compact subset of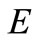 , there exists
, there exists 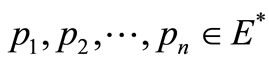
such that 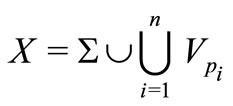 for
for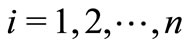 . Let
. Let
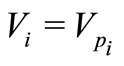 for
for 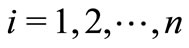 and
and 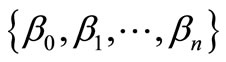 be a continuous partition of unity on
be a continuous partition of unity on 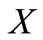 subordinated to the covering
subordinated to the covering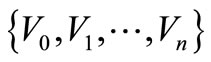 . Then
. Then 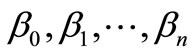 are continuous non-negative real valued functions on
are continuous non-negative real valued functions on 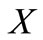 such that
such that 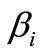 vanishes on
vanishes on 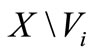 for each
for each 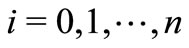
and 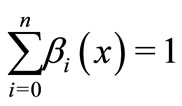 for all
for all 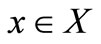 (see [17] p. 83).
(see [17] p. 83).
Define 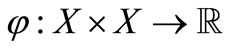 by
by
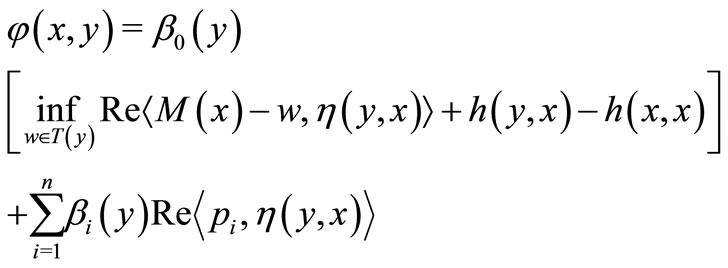
for each . Then we have 1)
. Then we have 1) 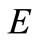 is Hausdorff for each
is Hausdorff for each 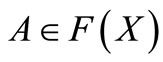 and each fixed
and each fixed 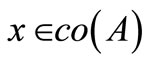 the map
the map
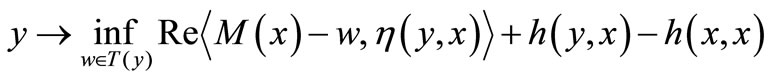
is lower semicontinuous on 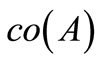 by Lemma 3 and the fact that
by Lemma 3 and the fact that 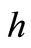 is continuous on
is continuous on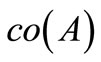 , therefore the map
, therefore the map
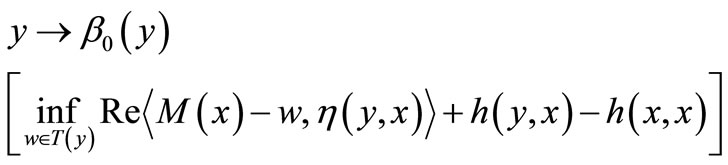
is lower semicontinuous on 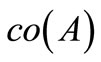 by Lemma 2. Also for each fixed
by Lemma 2. Also for each fixed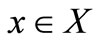 ,
,
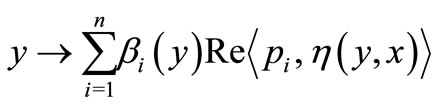
is continuous on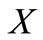 . Hence for each
. Hence for each 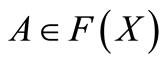 and each fixed
and each fixed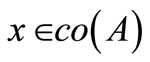 , the map
, the map 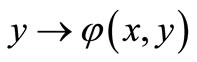 is lower semicontinuous on
is lower semicontinuous on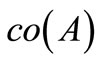 .
.
2) for each 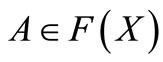 and each
and each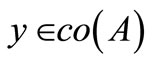 ,
,
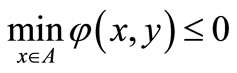 . Indeed, if these were false then for some
. Indeed, if these were false then for some
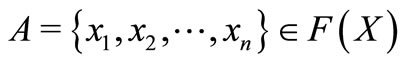 and some
and some 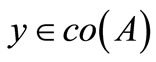 (say
(say
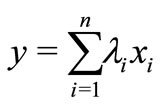 , where
, where 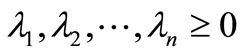 with
with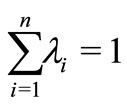 ), we have
), we have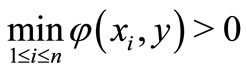 . Then for each
. Then for each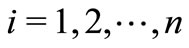 ,
,
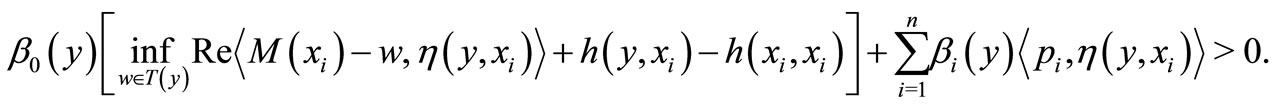
So that
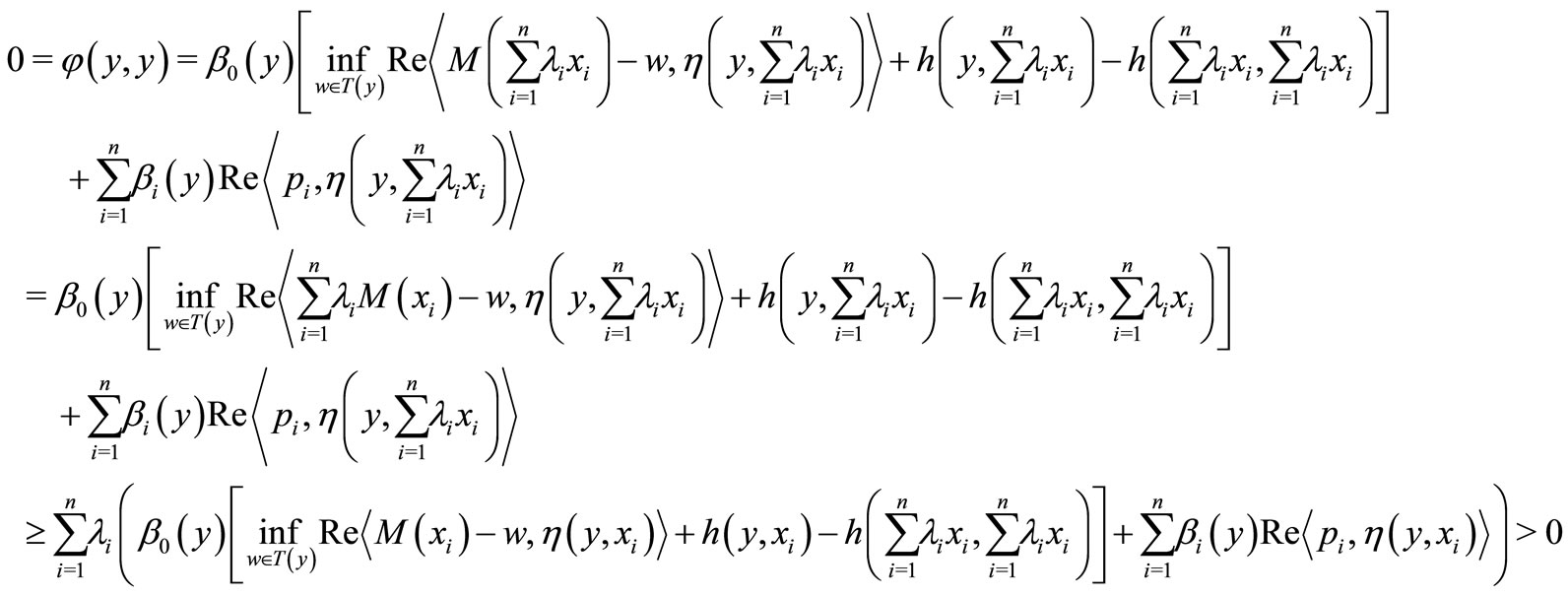
which is a contradiction.
Thus we have 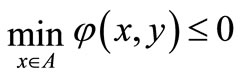 for each
for each 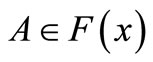 and each
and each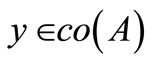 .
.
3) Suppose that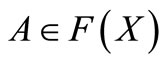 ,
, 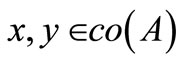 and
and 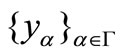 is a net in
is a net in 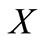 converging to
converging to 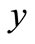 with
with 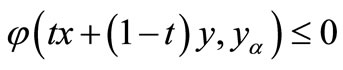 for all
for all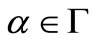 ,
,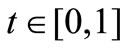 .
.
Case 1.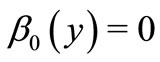 .
.
Note that 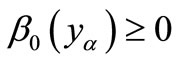 for each
for each 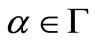 and
and 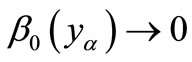 . Since
. Since 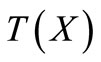 is strongly bounded and
is strongly bounded and 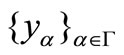 is a bounded net, therefore
is a bounded net, therefore
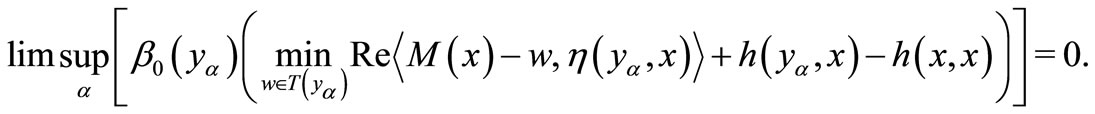 (1)
(1)
Also
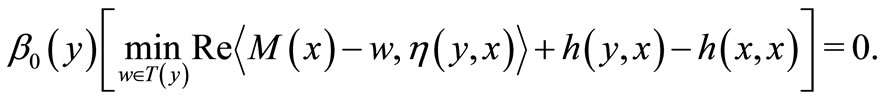
Thus
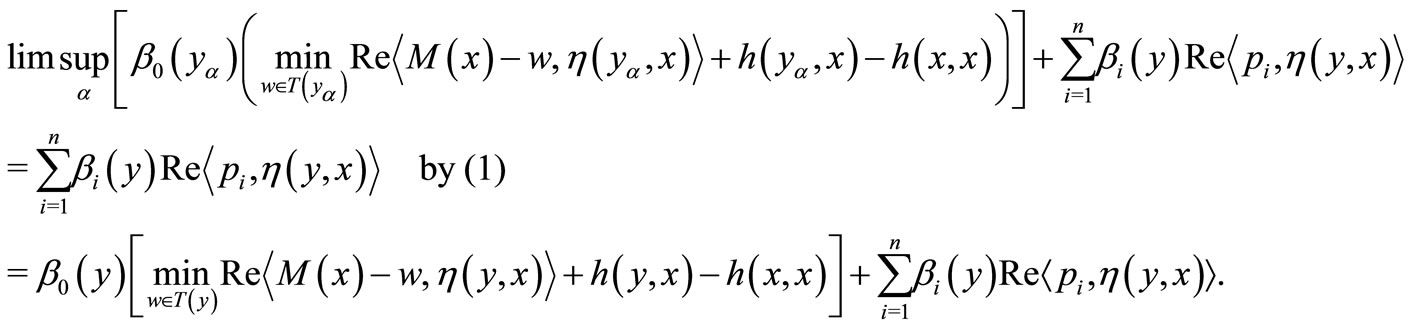 (2)
(2)
When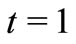 , we have
, we have 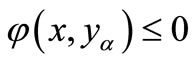 for all
for all 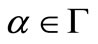 i.e.,
i.e.,
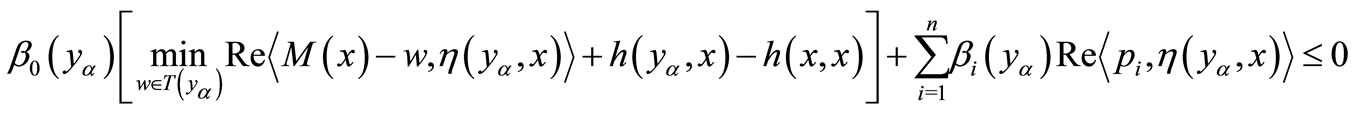 (3)
(3)
for all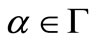 .
.
Therefore by (3), we have
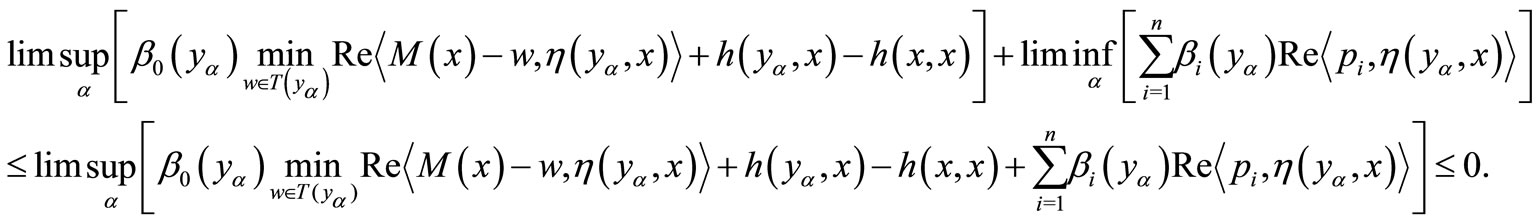
Thus
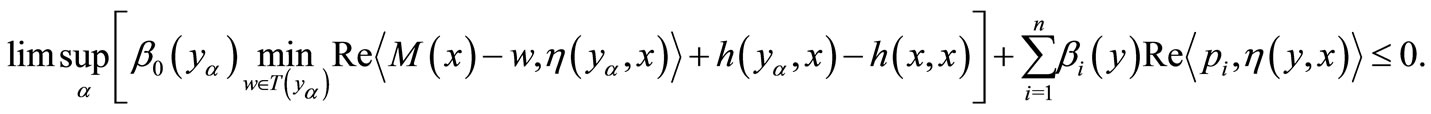 (4)
(4)
Hence by (2) and (4), we have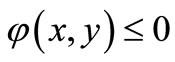 .
.
Case 2.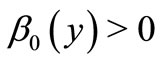 .
.
Since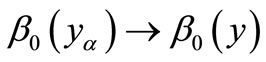 , there exists
, there exists  such that
such that 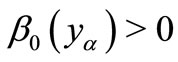 for all
for all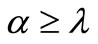 . When
. When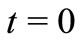 , we have
, we have 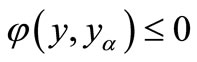 for all
for all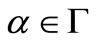 , i.e.,
, i.e.,
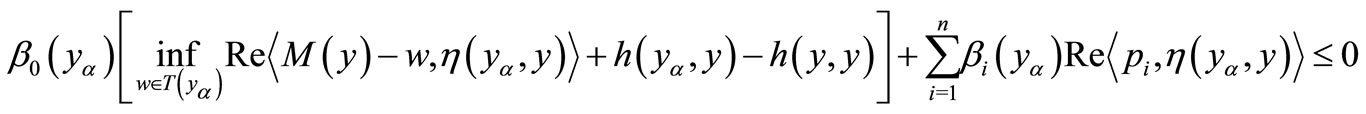
for all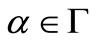 .
.
Thus
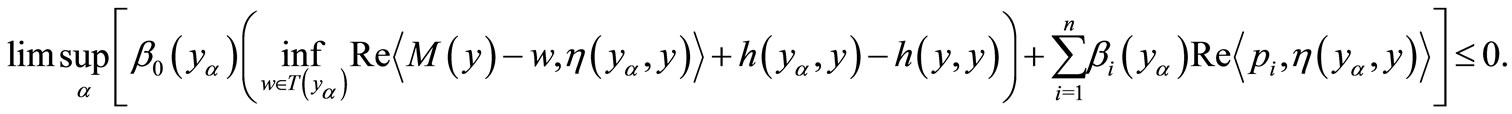 (5)
(5)
Hence
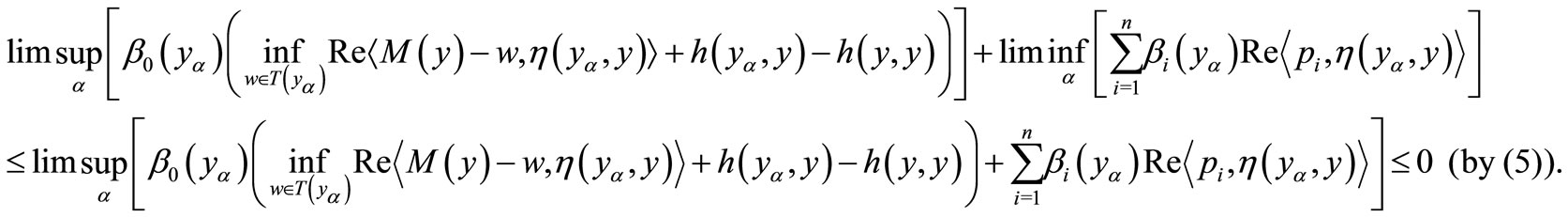
Since
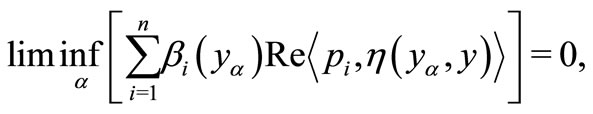
we have
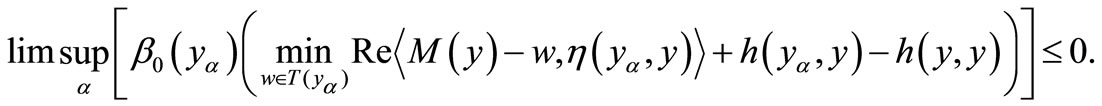 (6)
(6)
Since 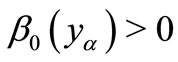 for all
for all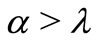 . It follows that
. It follows that
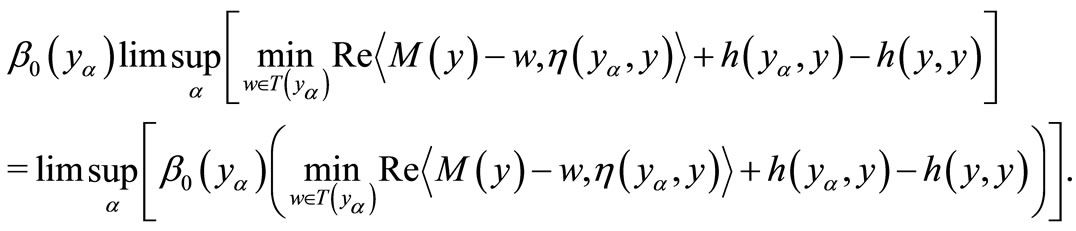 (7)
(7)
Since 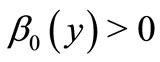 by (6) and (7), we have
by (6) and (7), we have
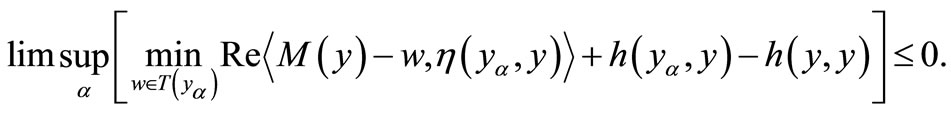
Since  is (η,h)-quasi pseudomonotone operator, we have
is (η,h)-quasi pseudomonotone operator, we have
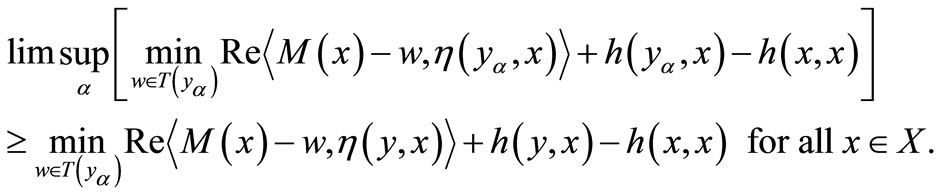
Since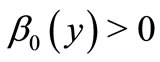 , we have
, we have
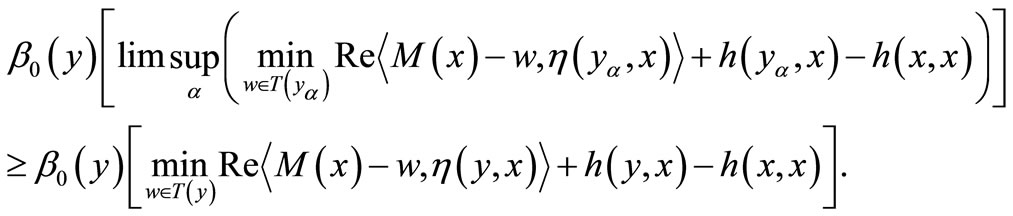
Thus
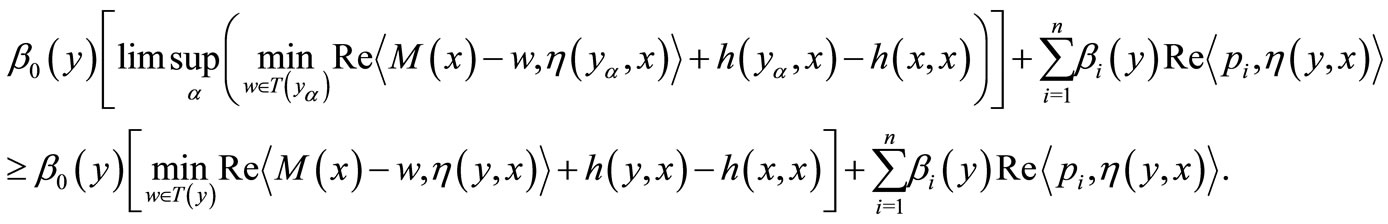 (8)
(8)
When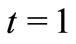 , we have
, we have 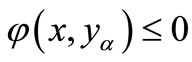 for all
for all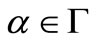 , i.e.,
, i.e.,
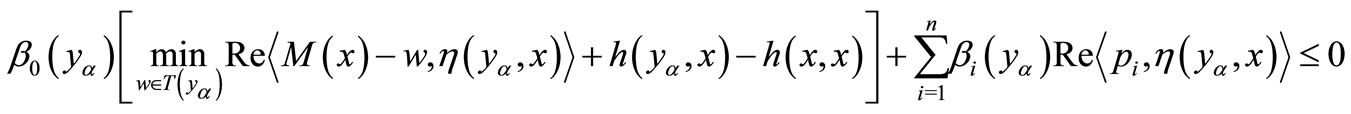
for all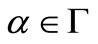 .
.
Thus
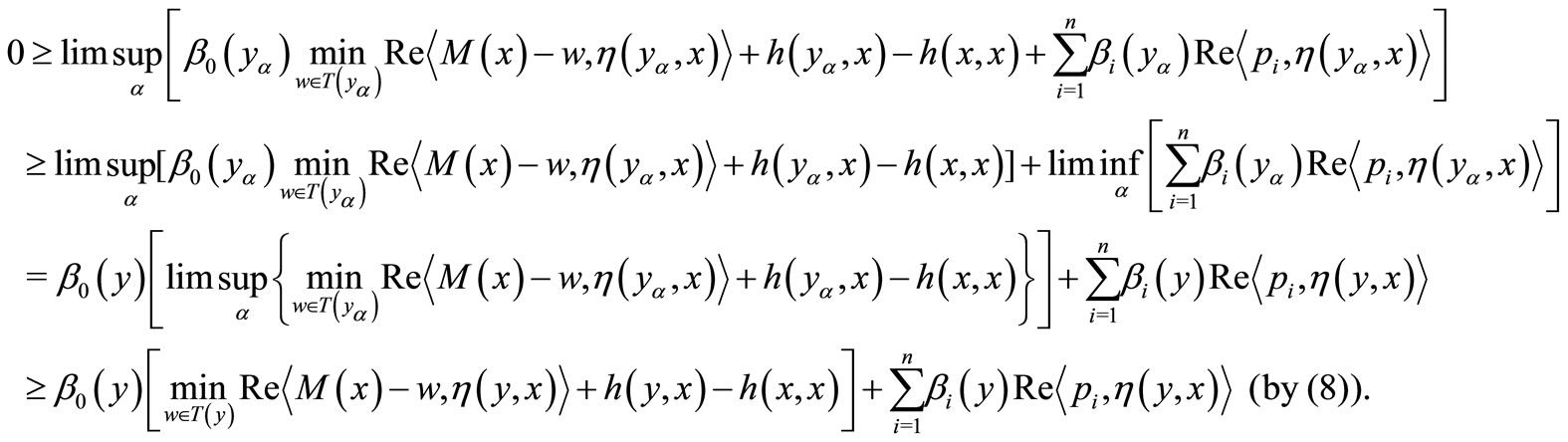 (9)
(9)
Hence, we have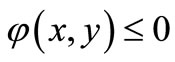 .
.
Since 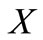 is a compact subset of the Hausdorff topological vector space
is a compact subset of the Hausdorff topological vector space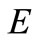 , it is also closed. Now if we take
, it is also closed. Now if we take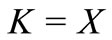 , then for any
, then for any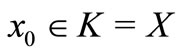 , we have
, we have
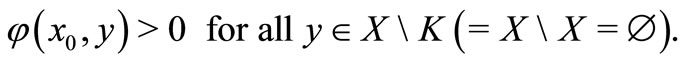
Thus 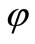 satisfies all the hypothesis of Theorem 1. Hence by Theorem 1, there exists
satisfies all the hypothesis of Theorem 1. Hence by Theorem 1, there exists 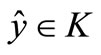 such that
such that
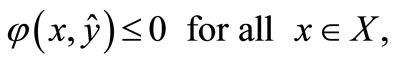
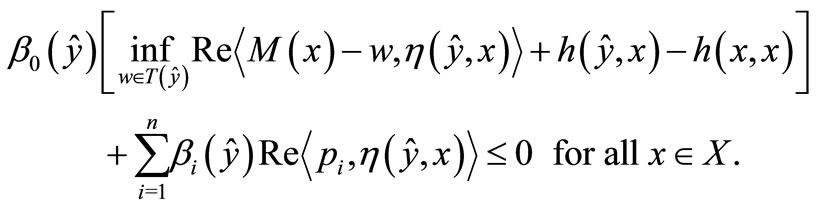 (10)
(10)
Now the rest of the proof of Step 1 is similar to the proof in Step 1 of Theorem 1 in [11]. Hence Step 1 is proved.
Step 2.
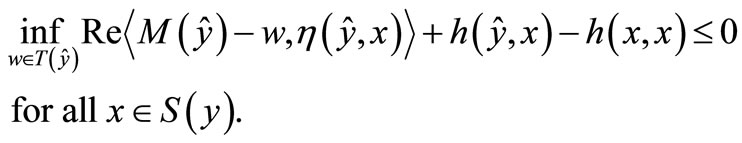
From Step 1, we have 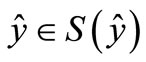 and
and
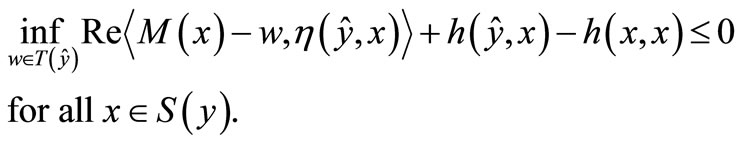
Since 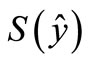 is a convex subset of
is a convex subset of 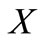 and
and 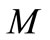 is linear, continuous along line segments in
is linear, continuous along line segments in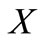 , by Lemma 4 we have
, by Lemma 4 we have
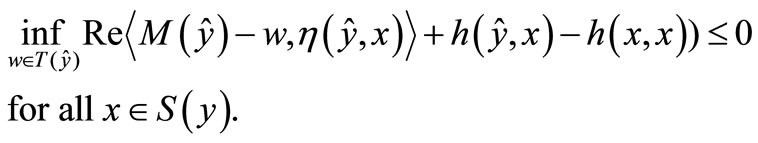
Step 3. There exists 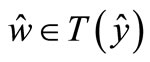 with
with
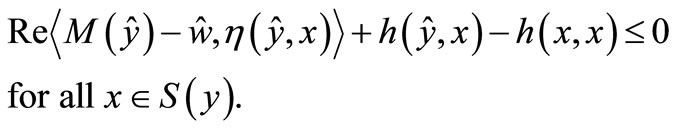
By Step 2 and applying Theorem 2 as proved in Step 3 of Theorem 1 in [11], we can show that there exists 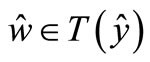 such that
such that
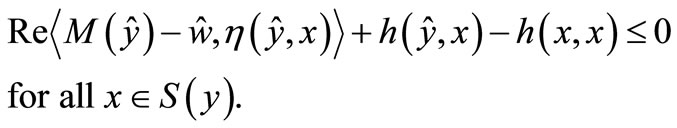
We observe from the above proof that the requirement that 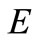 be locally convex is needed when and only when the separation theorem is applied to the case
be locally convex is needed when and only when the separation theorem is applied to the case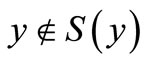 . Thus if
. Thus if 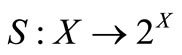 is the constant map
is the constant map 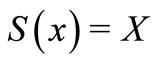 for all
for all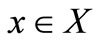 ,
, 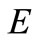 is not required to be locally convex.
is not required to be locally convex.
Finally, if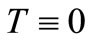 , in order to show that for each
, in order to show that for each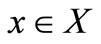 ,
, 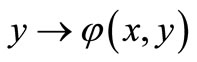 is lower semicontinuous, Lemma 3 is no longer needed and the weaker continuity assumption as
is lower semicontinuous, Lemma 3 is no longer needed and the weaker continuity assumption as 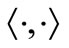 that for each
that for each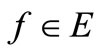 , the map
, the map 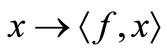 is continuous on
is continuous on 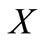 is sufficient. This completes the proof.
is sufficient. This completes the proof.
REFERENCES
- F. Giannessi, “Theorems of Alternative Quadratic Programs and Complementarity Problems,” In: R. W. Cottle, F. Gianessi and J. L. Lions, Eds., Variational Inequalities and Complementarity Problems, John Wiley and Sons, Chichester, 1980.
- D. Kinderlehrer and G. Stampacchia, “An Introduction to Variational Inequalities and Their Applications in Pure and Applied Mathematics,” Vol. 88, Academic Press, New York, 1980.
- F. E. Browdev, “Existence and Approximation of Solutions of Nonlinear Variational Inequalities,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 56, No. 4, 1966, pp. 1080-1086.
- G. Y. Chen and G. M. Cheng, “Vector Variational Inequality and Vector Optimizations,” Lecture Notes in Economics and Mathematical Systems, Vol. 285, 1967, pp. 408-456.
- M. S. R. Chowdhury and K. K. Tan, “Generalization of Ky Fan’s Minimax Inequality with Applications to Generalized Variational Inequalities for Pseudomonotone Operators and Fixed Point Theorems,” Journal of Mathematical Analysis and Applications, Vol. 204, No. 3, 1996, pp. 910-929. doi:10.1006/jmaa.1996.0476
- M. S. R. Chowdhury, “The Surjectivity of Upper Hemicontinuous and Pseudomonotone Type II Operators in Reflexive Banach Ppaces,” Journal Bangladesh Mathematical Society, Vol. 20, 2000, pp. 45-53.
- H. Brezis, L. Nirenberg and G. Stampacchia, “A Remark on Ky Fan’s Minimax Principle,” Bollettino Unione Matematica Italiana, Vol. 6, No. 4, 1972, pp. 293-300.
- K. Fan, “A Minimax Inequality and Applications,” In: O. Shisha, Ed., Inequalities III, Academic Press, San Diego, 1972, pp. 103-113.
- M. S. R. Chowdhury and K. K. Tan, “Generalized Variational Inequalities for Quasimonotone Operators and Applications,” Bulletin of Polish Academy of Science, Vol. 45, No. 1, 1997, pp. 25-54.
- M. H. Shih and K. K. Tan, “Generalized Bi-Quasi Variational Inequalities,” Journal of Mathematical Analysis and Applications, Vol. 143, No. 1, 1989, pp. 66-85. doi:10.1016/0022-247X(89)90029-2
- M. S. R. Chowdhury and K. K. Tan, “Applications of Upper Hemicontinuous Operators on Generalized Bi-Quasi Variational Inequalities in Locally Convex Topological Vector Spaces,” Positivity, Vol. 3, No. 4, 1999, pp. 333- 344. doi:10.1023/A:1009849400516
- M. S. R. Chowdhury and K. K. Tan, “Applications of Pseudomonotone Operators with Some Kind of Upper Semicontinuity in Generalized Quasi Variational Inequalities on Noncompact Sets,” Proceeding of American Mathematica Society, Vol. 126, No. 10, 1998, pp. 2957- 2968. doi:10.1090/S0002-9939-98-04436-0
- X. P. Ding and E. Tarafdar, “Generalized Variational Like Inequalities with Pseudomonotone Setvalued Mappings,” Archieve Journal of Mathematics, Vol. 74, No. 4, 2000, pp. 302-313. doi:10.1007/s000130050447
- M. H. Shih and K. K. Tan, “Generalized Quasi Variational Inequalities in Locally Convex Topological Vector Spaces,” Journal of Mathematical Analysis and Applications, Vol. 108, No. 2, 1985, pp. 333-343. doi:10.1016/0022-247X(85)90029-0
- W. Takahashi, “Nonlinear Variational Inequalities and Fixed Point Theorem,” Journal of Mathematical Society of Japan, Vol. 28, No. 1, 1976, pp. 168-181. doi:10.2969/jmsj/02810168
- H. Kneser, “Sur un Theoreme Fundamental de la Theorie des Jeux,” CRAS Paris, Vol. 234, 1952, pp. 2418-2420.
- R. T. Rockafeller, “Convex Analysis,” Princeton University Press, Princeton, 1970.

