Modern Economy
Vol.07 No.02(2016), Article ID:63724,10 pages
10.4236/me.2016.72021
Can Business Firms Have Too Much Leverage? M&M, RJR 1990, and the Crisis of 2008
William Carlson, Conway Lackman
School of Business, Duquesne University (ret.), Pittsburgh, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 November 2015; accepted 21 February 2016; published 24 February 2016
ABSTRACT
In 1958 Modigliani and Miller published one of the most significant papers in finance on the cost of capital. It presented the capital structure irrelevance theorem which states that the cost of capital is independent of capital structure. It implies that there is no optimal structure and consequently denies the existence of non-optimal structures. If there are no non-optimal structures then there is no such thing as a business firm having too much leverage or debt. We disagree with that conclusion on both theoretical and empirical grounds supported by the evidence provided by the Financial Crisis Inquiry Commission plus the basic logic behind Basel III. The model of this paper comes from Brigham and Houston’s Bigbee case using beta, the Hamada transformation and an interest rate function which is crucial, concepts not available to M&M in 1958. We show how the minimization of WACC (weighted average cost of capital) and maximization of stock price give identical solutions and their similarity to M&M Propositions I and II. It also shows the simple mechanism that causes non-optimality. M&M missed non optimal structures partly because their data base from 1948 and 1953 had only low and moderate debt/equity ratios. Non-optimal behavior appears at high (double digit) D/E ratios. We have examples of the consequences of excessive leverage not available to M&M, including RJR, Houdaille Industries, the casualties of the 2008 crisis and others. The RJR LBO is examined in detail because it is as close to a laboratory experiment as can be expected in economics. The analysis shows how extremely high leverage put RJR on the path to bankruptcy and how the Roberts-Gerstner plan restored profitability following the logic of Brigham’s Bigbee model.
Keywords:
Corporate Finance, Leveraged Buyouts

1. Introduction
Flashback to July 1990. RJR Nabisco’s debt is $22.90 billion and equity $0.80 billion, a debt/equity ratio of 28.6. This is an extremely high ratio. Table B.102 in the historical statistics of Release z.1 of the Federal Reserve [1] on the web contains data for calculating historical cost D/Es from 1945-2012 (line 21 divided by line 44) for Non-Financial Corporate Business xD/E for 1945-2012 was 1.719 in 1989. Quarterly operating earnings before interest and taxes are about $600 million with interest expenses of $830 million causing a quarterly loss of $230 million. At that burn rate RJR will become bankrupt in about 10 months. George Roberts of Kohlberg, Kravis and Roberts (KKR) and CEO Louis V. Gerstner saved RJR from bankruptcy and brought it back to prosperity. How did they do it with no gain in operating earnings?
Brigham’s Bigbee Electronics Company case ([2] , p. 437) was constructed with the intent of showing students how to use the ideas of minimizing the weighted average cost of capital (Min WACC) and maximizing the stock price (Max P) and the optimal capital structure or leverage for the rm. The RJR Nabisco leveraged buyout (LBO) analyzed in this paper shows the principles of the Bigbee model in a real world setting and the danger of too much debt. In these two cases, one academic and the other real world context with the capital structure irrelevance theorem of Modigliani and Miller [3] which denies that an optimum exists, or that non-optimal structures exist is put to a validity test. The theorem implies that there is no such thing as too much debt. It implies that 96% debt and 4% equity is as good (or bad) as 96% equity and 4% debt. A question is: Is the irrelevance theorem correct? Have events that have happened since 1958 such as LBOs, particularly that of RJR Nabisco, and the disasters of 2008 called the irrelevance theorem into question?
Modigliani and Miller actually had the modern WACC function in their 1958 paper. It is Equation (19) of footnote 27. The equation was formed as they modeled the “classic” theory of the cost of capital. They rejected Equation (19) because their empirical analysis did not fit the required curvature for optimality (and non-optimality). Unfortunately their pre LBO 1948 and 1953 data bases, which they described as skimpy and of rather limited scope (p. 281), did not contain double digit D/Es at which non-optimal effects tend to appear. Their 1953 sample of 42 oil companies had an average D/E of 0.41 with a maximum of 1.70, and their1947-8 sample of 43 electricutilities had an average D/E of 1.62 with a maximum of 3.76. In 1958 M&M did not have the advantage of observing the results of the LBO era nor the disasters of 2008.They also did not have the concepts of beta, the Hamada transformation [4] , and an interest rate function in 1958. All of these tools are used in the Bigbee model.
Modern theory says that the firm should minimize the weighted average cost of capital (Min WACC) and maximize the common stock price (Max P) and that the two solutions should be identical. The Bigbee model in Brigham and Houston [2] is in a discrete format for instructional simplicity. The interest rate function in the model follows a simple quadratic function over the relevant range of values so that function was used to form a continuous WACC function. Then, a continuous stock price function was formed. To find optimum calculus derivatives were taken and set to zero. Unfortunately, while the answers were close, they were not identical. When we changed the pricing procedure in the Max P function to an ex-ante basis from an ex-post basis the Min WACC and Max P derivatives and solutions became identical.
Other investigators have had a difficult time trying to find an optimal capital structure. This is because the optimal structure is not a well defined point but a rather broad shallow range. Accordingly, we have taken the reversed approach of trying to find non-optimal structures. It is easier to find non-optimal structures than to find an optimum.
2. The Classical M&M and Modern Approaches
Three approaches summarize the nature of the capital structure debate. According to classical theory the graph of WACC versus the debt ratio has a U shape. See Modigliani and Miller, (1958, p. 278). This led to an attempt to find an optimal capital structure at the bottom of the U. Then, in 1958, Modigliani and Miller (M&M) wrote their famous and controversial paper: The Cost of Capital, Corporation Finance, and the Theory of Investment.
Their key proposition was the average cost of capital to any firm is “completely independent” of its capital structure and is equal to the capitalization rate of a pure equity stream of its class. The words “completely independent” indicate that the WACC-debt ratio graph is perfectly flat and that there is no optimal structure. This is the capital structure irrelevance theorem. M&M’s theorem has another interesting conclusion: not only is there no optimum there can be no non-optimum either, because if a non-optimum exists there must be some better point. This means that there is no such thing as too much leverage. 96% debt and 4% equity is as good (or bad) as 4% debt and 96% equity. The Financial Crisis Inquiry Commission investigation [5] of the debacle of 2008-9 including testimony from executives from the largest US banks (Jamie Dimon, Lloyd Blankfein, John Mack, Brian Moynihan, and Kyle Bass) disagrees as does the Basel III Commission.
The third version of the capital structure problem is the modern Min WACC-Max P model. Here we are not so concerned with an optimal structure because we believe the WACC function is relatively at low and moderate levels of debt and the optimum is actually a rather wide range. But, as the debt ratio approaches extreme levels around and above 90% the WACC curve increases rapidly and becomes non-optimal. See Figure 1 for the typical pattern which is neither a U nor flat. Our main concern here is finding and analyzing the consequences of high and extreme levels of leverage. There is a clear difference between this model and that of M&M. This model indicates that there is such a thing as too much debt contrary to the irrelevance theorem. The large dots in Figure 1 show WACC-debt ratio values for RJR Nabisco before and during the LBO but before the Roberts- Gerstner rescue operation. See Table 2 and Table 3 for RJR WACC data and derivation. The small dots are hand plotted points from M&M’s 43 company utility sample. The equation of Figure 1 is M&M’s Equation (19) with different symbols: their D/V is ourd. A regression estimate without the RJR points reproduces M&M’s regression result (a horizontal at line) but when the RJR Points are added the curve shown is the result, essentially at until d = 0.78 and then turns sharply upward sloping. As mentioned above M&M admitted that their database was skimpy and of limited scope. If they had had observations of debt ratios above 0.90 perhaps they might have come to a different conclusion. They did have the correct equation format (which we borrowed).
3. Why Too Much Debt Causes Trouble: The Interest Expense Effect
Clearly debt and the associated interest is a problem as any household with large debt would confirm as it experiences rising interest expense with rising debt. Lawrence Fisher (1959) found a significant (t-statistic = 17.32) quantitative relation between the debt/equity ratio and the interest rate risk premium. Using a very simple example supposes debt doubles and as a result the interest rate also doubles. Then interest expense (IEX) will go up four times since IEX = debt D times the interest rate, id. Let us look at the interest expense effect in the Bigbee case. See Table 1 which has income statement data for various levels of debt. At a debt ratio of 0.50, debt D = $100,000 and the interest rate is 0.12 giving an interest expense IEX of $12,000. With an EBIT (earnings before interest and taxes) of $40,000 EBT (earnings before taxes) are $28,000. Now suppose debt is used to buy back common stock so that the new level of debt is $160,000 (debt ratio 0.80) and the interest rate goes to 0.24. Now IEX is $38,400 and EBT only $1600. A formula that calculates the new IEX is $12,000 × (160,000/100,000) × (0.24/0.12) = $38,400. Note that at a debt ratio of 0.90. Bigbee runs a substantial loss of $14,000. A possible benchmark: at what debt ratio and debt/equity ratio would Bigbee break even to the nearest basis point? It would seem that LBOs should not go above this level. A later assignment will be to determine how far KKR went beyond the breakeven point in its LBO of RJR.
Table 2 has data for checking the interest expense effect for the real world example of the RJR LBO. In 1989 debt averaged $23,998 for the whole year (the LBO was on Feb.9, 1989) compared to $5518 at the end of
Figure 1. WACC vs. d (debt ratio) RJR observations.
Table 1. The 1EX effect-Bigbee.
*res = rRF + mrp [1 + (1 − T) d/1 − d] Bu = 0.06 + 0.06 (1 + 0.6d/1 − d).
1988, up 4.35 times. 23,998 = 0.11 × 5518 + 0.14 × 29,100 + 0.25 × (26,420 + 25,690 + 25,159). From the rd% column the interest rate on debt averaged 15.57% adjusting for the Feb. 9 date) compared to 11.12% in December 1988, up 40%. 15.57 = 0.11 × 11.12 + 0.14 × 13.71 + 0.25 × (14.0 + 17.3 + 18.4). IEX in 1988 was $549. Using the quick formula: IEX = $549 × 4.35 × 1.40 = $3343 which is close to the actual IEX of $3384. In 1989 RJR’s interest expense rose more than six times to $3384 million from $549 million, far exceeding EBIT and causing a $1.3 billion loss before taxes.
M&M do not have the interest expense effect in their model. The reason is given in the fourth paragraph of their paper. This attempt typically takes the form of superimposing on the results of the certainty analysis the notion of a risk “discount” to be subtracted from the expected yield (or a “risk premium” to be added to the market rate of interest). Investment decisions are then supposed to be based on a comparison of this “risk adjusted” or “certainty equivalent” yield with the market rate of interest. No satisfactory explanation has yet been provided, however, as to what determines the size of the risk discount and how it varies in response to changes in other variables. This last sentence gives the reason why M&M did not have an interest expense effect in their analysis. They could not find a function relating the risk premium (they call it the risk discount) to capital structure and other variables. An interest rate function is a crucial part of the modern WACC function. This may be a second reason M&M rejected their Equation (19). As a substitute for the missing interest rate function they used an “arbitrage” type of argument discussed below. Fisher interest rate function appeared after M&M hence it was not available for them to include in their model.
4. Comparing Min WACC and Max P to Propositions I and II
Ignoring preferred stock as do M&M, the WACC function is:
 (1)
(1)
Table 2. From profit to loss-RJR.
Source: 10Ks, 10Qs, Annual Reports, Wall Street Journal bond tables. More details in Part 2.
where d is the debt ratio (debt/debt plus equity or D/(D + E)), rd is the interest rate on debt, (1 − d) is the equity ratio, and rcs is the return on equity. T is the tax rate assumed to be 0.40 in the Bigbee case, and (1 − T) converts the before tax interest rate on debt to an after tax measure. Sometimes the debt/equity ratio or D/E is used in formulas; D/E is equal to d/(1 − d). Proposition II is:
 (2)
(2)
Solving this equation for WACC yields:
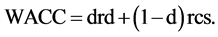 (3)
(3)
Hence Proposition II is the modern WACC function missing the (1 − T) factor, a minor omission. There is no conflict at this point. The models differ when it comes to specifying the behavior of rcs and particularly rd.
The equation for finding the stock price P developed below is:
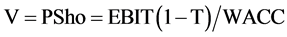 (4)
(4)
where V is the value of the company, P the price of a share of common stock, Sho the unlevered number of shares outstanding, and EBIT earnings before interest and taxes or operating earnings. Proposition I is:
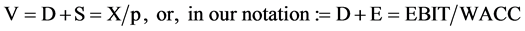 (5)
(5)
Later it will be shown that D + E = P Sho so the P function and Proposition I are the same except for the missing (1 − T) factor. Again there is no conflict at this point with M&M. The process of finding Min WACC and Max P in the Bigbee case is a classical calculus problem. The first task is to find the equations for rcs and rd to be substituted into the WACC function. Then take the derivatives which should be identical. Indeed, the corrected version of the P function is the inverse of the WACC function so that which minimizes WACC maximizes P.
Substituting for rcs: Step 1, the WACC function is:
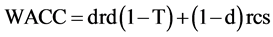 (6)
(6)
where T = 0.40. The capital asset pricing model CAPM provides an equation for rcs:
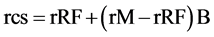 (7)
(7)
where rRF is the risk free interest rate (0.06 in Bigbee), rM the stock market rate of return (0.10 in Bigbee), and B is beta. A shorter form is
 (8)
(8)
where rMP is the market risk premium equal to rM − rRF (rMP = 0.04 in Bigbee).
Next, the Hamada transformation is used to relate beta to unlevered beta and capital structure: 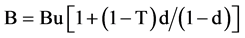 where Bu is unlevered beta (Bu = 1.50 in Bigbee). Then,
where Bu is unlevered beta (Bu = 1.50 in Bigbee). Then,
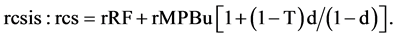 (9)
(9)
With d = 0.40 rcs = 0.144. Substituting rcs into the WACC function yields:

At this point assume rd is a constant. Since rRF (0.06), rMP (0.04), Bu (1.50), and T (0.40) also are constants, WACC is a linear function of d and there is neither interior optimum nor non-optimum. M&M contend that the slope is zero. If the slope is positive the optimal d is zero (a clean balance sheet). If the slope is negative (due to the tax deductibility of debt then the optimal d is 0.99999―(it cannot be 1 because there must be at least one share of stock otherwise no one would own the company). Given that the rcs effect in WACC is linear, if the WACC function is curved and in the Bigbee data, Table 3, the effect will have to come from the rd function.
With respect to the tax advantage of debt Professor Michael Jensen in 1976 asked [6] why we don’t observe large corporations individually owned, with a tiny fraction of the capital supplied by the entrepreneur in return for 100 percent of the equity, and the rest simply borrowed. Two years later Kohlberg, Kravis, and Roberts (KKR) began the LBO of Houdaille Industries, the first Fortune 500 LBO [7] -[10] . That started a decade of LBOs that culminated in the huge 1990 LBO of RJR Nabisco which nearly failed and Federated Department Stores which did fail.
Substituting for rd: Step 2
There are four alternatives. First, as noted in the interest expense section above, a year after the Cost of Capital article Lawrence Fisher [11] published Determinants of Risk Premiums on Corporate Bonds “M&M closed
Table 3. Bigbee WACC results.
their fourth paragraph with this sentence, “No satisfactory explanation has yet been provided, however, as to what determines the size of the risk discount and how it varies in response to changes in other variables.” The Fisher regressions provide exactly what M&M said was missing. The key regression is:

where all variables are in common logarithms: Xo is the risk premium, X1 the coefficient of variation of after tax earnings (should have been EBIT, earnings before interest and taxes), X2 the time of solvency, X3 the D/E ratio (Fisher did the E/D ratio), and X4 size. The numbers in parentheses are standard errors. The t-statistic of D/E is 17.32. Altman’s (1968) Z-Score also found D/E to be extremely significant but it is not in a directly usable format. Using the Hamada transformation to adjust earnings variability to EBIT from earnings after taxes yields a function and converting back from logarithms yields:

The second solution is to not have an rd function. In 1958 the Fisher and Altman studies had not been done. Accordingly, M&M could not find any quantitative relation of rd to capital structure so they did not include an interest rate function in their model. Suppose rd is a linear function of

Inserting Equation (13) into the WACC function yields:

Now look at M&M’s footnote 27 Equation (19) with our notation for the debt ratio d and the equity ratio (1 − d) and capital letters for Greek letters:

They have the same form and the d2/(1 − d) terms which cause curvature are the same, except again the (1 − T) factor is missing in Equation (19). This is the form of equation used in Figure 1. An interesting feature of the curvature term in Equation (19) is that it does not come from an assumption about rd. Rather; it comes from M&M’s Equation (15) in footnote (25). Equation (15) is a quadratic form of the rcs function. This means that M&M were looking in the wrong place for possible curvature. They assumed that curvature would come from the rcs function rather than the rd function. In turn this explains why they missed the interest expense effect discussed in the introductory section.
The Brigham-Houston Bigbee case rd assumption. For instructional simplicity the rd function was presented in Table 1 and Table 3 at d intervals of 0.10. The optimum d is in between 0.30 and 0.40. We need a continuous function which can be differentiated. It turns out that the function rd = 0.12 − 0.25d + 0.50d2 ts the points d = 0.00, 0.30, 0.40, 0.50, and 0.60 perfectly (values for d = 0.10 and 0.20 which are not of concern can be found by using a piecewise quadratic approach or a6th order polynomial. We extend the quadratic trend to higher d values to see what happens at d ratios higher than 0.60. This extension has no effect on the search for an optimum but does show the interest expense effect more fully. Substituting the Brigham rd quadratic function into WACC yields:

Substituting rRF = 0.06, rMP = 0.04, Bu = 1.50, T = 0.40 yields:

This equation reproduces WACC values for Bigbee exactly for d = 0.00, 0.30, 0.40, 0.50, and 0.60 (WACCs are 0.1200, 0.1110, 0.1104, 0.1140, and 0.1236).
5. Finding the Optimal WACC and Non-Optimality
The optimal WACC cited from Brigham’s discrete table is 0.1104 from a d of 0.40.
Solving for the first order condition of Equation (4) yields:

The positive root of this quadratic is d = 0.36942542 giving a minimum WACC of 0.110221.
A feature of the Bigbee case is that the WACC function is relatively at around the minimum. The RJR Nabisco WACC function is even fatter in the optimal range. This fatness around the minimum may account partly for the difficulty in overturning the irrelevance theorem. In pre LBO days most rms had conservative debt ratios way below d = 0.90 where non-optimality begins to appear. Hence most observations come from the at range so that the irrelevance theory appears to be valid. The next task is to find out if the Max P function gives the same result. It does not meaning that the Bigbee model has to be fixed.
6. The Max P Function: Generating Bigbee Results
The Brigham analysis that determines the stock price P begins with Line 1 of Table 1, Bigbee with no debt. The price of the shares is Po = $20 and the number of shares outstanding Sho is 10,000 and the total capitalization is $200,000. Now assume that the company issues $80,000 of debt and buys back 4000 shares at the price of $20 each. The repurchase price of the shares is a crucial assumption. At this point d = 0.40 ($80,000/$200,000).
The new stock price P is: P = EPS/rcs, where EPS is earnings per share (also, dividends per share equal earnings per share for simplicity). EPS = (EBIT − rdD) (1T)/Sh, where EBIT = $40,000 which is fixed for all situations), rd is 0.10 (from
As Bigbee issues debt and uses the proceeds to buy back shares, the debt D is dPoSho and shares outstanding Sh equal (1 − d) Sho. Substituting yields the P function:

With EBIT = 40,000, Po = 20, Sho = 10,000, 


The derivative is a mess so Function Grapher Online by walterzorn.com was used to nd the maximum P at $22.2241 and d = 0.39358. This is incorrect because the correct optimal d found by minimizing WACC is 0.36943.
7. Fixing the Max P Function
The reason that the optimal d for Max P is different than the d that minimizes WACC is the assumption that as the company levers itself the stock price P remains at $20/share regardless of the amount of debt undertaken. But if investors are informed they may not want to sell their shares back to the company if restructuring generates a higher price. The efficient markets solution is to assume that the shares are sold back to the company at the equilibrium price P instead of Po = $20. Replacing Po with P in Equation (20) yields:

Now P is on both sides of the equation. To solve for P cross multiply, divide by Sho, add Pdrd (1 − T) to both sides and then factor out P:

The term in brackets, 

Since EBIT, Sho, and T are constants, P is a reciprocal function of WACC. What minimizes WACC maximizes P which is what is supposed to happen. Since EBIT = 40,000, Sho = 10,000, T = 0.40, and Min WACC = 0.110221, the Maximum price is 21.7744. The reason why this value is lower than the Brigham answer of $22.2222 is because Bigbee is repurchasing shares at a price of $21.77 rather than the bargain price of $20.00.
Now Equation (23), can be converted into M&M’s Proposition. Multiply both sides of Equation (23) by Sho. Debt D = dPSho and equity E = (1 − d) PSho so that D + E = PSho. Hence,

which is Proposition I (including the tax adjustment factor)?
8. Why Didn’t M&M Find the Min WACC Max P Solution in 1958?
M&M’s Proposition II is the WACC function in a different algebraic form. Proposition I is the stock price function as shown by Equations ((23) and (24)). M&M had the modern curved WACC function with their Equation 19 but did not believe it a problem with their admittedly “skimpy database of rather limited scope” was that it did not have any high D/E observations th attend to show non-optimal behavior. They did not have the benefit of seeing the LBO era in 1958 nor the excesses of 2008.
The most important theoretical reason was that M&M did not have an interest rate function relating the interest rate on corporate debt through the default risk premium to capital structure. In 1958 M&M did not have the 1959 Fisher interest model or the Altman model [12] that showed that such a link was statistically extremely significant. Missing the interest rate function and writing before the 1980s decade of LBOs and the debacle of 2008 they did not find that interest expense could exceed EBIT at double digit D/Es which is non-optimal to the point of leading to bankruptcy. Also, the Min WACC analysis above shows that curvature of the WACC function comes from the interest rate function, not from the rcs function as hypothesized by M&M in their Equation 15 of footnote 25.
9. Conclusion
In 1958 Modigliani and Miller published one of the most significant papers in finance on the cost of capital. It presented the capital structure irrelevance theorem which states that the cost of capital is independent of capital structure. It implies that there is no optimal structure and consequently denies the existence of non-optimal structures. If there are no non-optimal structures then there is no such thing as a business firm having too much leverage or debt. We disagree with that conclusion on both theoretical and empirical grounds supported by the evidence provided by the Financial Crisis Inquiry Commission plus the basic logic behind Basel III. The model of this paper comes from Brigham and Houston’s Bigbee case using beta, the Hamada transformation, and an interest rate function which is crucial, concepts not available to M&M in 1958.to show how the minimization of WACC (weighted average cost of capital) and maximization of stock price give identical solutions and their similarity to M&M Propositions I and II. It also shows the simple mechanism that causes non-optimality. M&M missed non optimal structures partly because their data base from 1948 and 1953 had only low and moderate debt/equity ratios and the lacked the interest function provided later by Fisher. Non-optimal behavior appears at high (double digit) D/E ratios. We have examples of the consequences of excessive leverage not available to M&M, including RJR, Houdaille industries, the casualties of the 2008 crisis and others.
Cite this paper
WilliamCarlson,ConwayLackman, (2016) Can Business Firms Have Too Much Leverage? M&M, RJR 1990, and the Crisis of 2008. Modern Economy,07,194-203. doi: 10.4236/me.2016.72021
References
- 1. “Board of Governors of the Federal Reserve System”, Release 1 Historical Statistics. Table B 102, 2015.
- 2. Brigham, E. and Houston, J. (2007) Fundamentals of Financial Management. Thomson Southwestern, Cincinnati.
- 3. Modigliani, F. and Miller, M. (1958) The Cost of Capital, Corporation Finance and the Theory of Investment. American Economic Review, 48, 261-297.
- 4. Hamada, R. (1969) Portfolio Analysis, Market Equilibrium and Corporation Finance. Journal of Finance, 24, 13-31.
http://dx.doi.org/10.1111/j.1540-6261.1969.tb00339.x - 5. Financial Crisis Inquiry Commission (2010) Hearings and Testimony. First Public Hearings.
http://fcic.law.stanford.edu/hearings - 6. Anders, G. (1992) Merchants of Debt: KKR and the Mortgaging of American Business. Basic Books Harper Collins, New York, 22.
- 7. Holland, D. (1989) An Industry Dies in Gardena: When the Machine Stopped, A Cautionary Tale From Industrial America. Harvard Business School Press, Cambridge, MA, 1989.
- 8. Kosman, J. (2009) The Buyout of America. Penguin Group, New York, 28.
- 9. Holson, L. (1999) Investing: A Goodbye to the Weight of Leveraging. New York Times Business Section, 14 March 1999.
- 10. Thornton, M. (2011) The Biggest Private Buyouts in History. Business Insider, 18 April 2011.
- 11. Fisher, L. (1959) Determinants of Risk Premiums on Corporate Bonds. Journal of Political Economy, 67, 217-287.
http://dx.doi.org/10.1086/258172 - 12. Altman, E. (1968) Financial Ratios, Discriminant Analysis and the Prediction of Default. Journal of Finance, 2, 189-209.



