Modern Economy
Vol.06 No.04(2015), Article ID:56057,11 pages
10.4236/me.2015.64049
Fuzzy Comprehensive Evaluation of Service Agent Based on Large-Scale Products of New Technology
Jianhui Kong1,2, Fengying Zhang3, Zongfang Zhou1
1School of Economics and Management, University of Electronic Science and Technology, Chengdu, China
2School of Law, Southwest University for Nationalities, Chengdu, China
3West China School of Nursing, Sichuan University, Chengdu, China
Email: 1531123491@qq.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 March 2015; accepted 26 April 2015; published 30 April 2015
ABSTRACT
For new-tech products manufacturing enterprises, good after-sale service plays an important role in the marketing of new-tech products and promoting the sustainable development. Therefore, how to select and evaluate the service agent will be an inevitable and important job for new-tech manufacturing enterprises. However, the evaluation process and results of the service agent always show fuzziness because of the uncertain evaluation factors. In order to solve this problem, the dissertation firstly introduced methods of fuzzy comprehensive evaluation and multiple attri- bute decision making from quantitative and qualitative views respectively. Secondly, a method of evaluation on “important” service agent based on fuzzy Borda method was constructed. By the numerical experiment, results show that the fuzzy comprehensive evaluation methods of service agent proposed in this paper are feasible and effective, which provides a new idea to address the problem of evaluating the service agent for new-tech products manufacturing enterprises.
Keywords:
New-Tech Products, Service Agent, Fuzzy Comprehensive Evaluation, Multiple Attribute Decision Making, Fuzzy Borda Method

1. Introduction
Service agent arrangement, which means manufacturers (the principal) entrust the independent third-party (service agent) to do the after-sale service job, is an organization form of after-sale service [1] . Agency relation is a stable contractual relationship in the long term. Service agents operate and gain profits by commission. The commission is paid by the manufacturers (the principal) in the amount of a certain percentage of service profits. The three types of service agent arrangements can be classified as: 1) sole agent, generic agent and general agent according to the scope of the power of agency; 2) maintenance agent, marketing agent and purchasing agent of products or equipment according to the content of agency; 3) service agents in cross region or multiple products and in designated region or products according to the scope of the service agency.
High-tech products are the leading technology products, which use advanced and high-tech fields of science and technology tools and technology, with high technological content and market competitiveness [2] . In China, high-tech products mainly contain new-tech equipment or components that are used in the fields such as aerospace and defense. Compared with traditional enterprises, high-tech enterprises have higher uncertainty during the technological achievements period [3] . Therefore, high-tech products are faced with a changeable market environment in the era of rapid development in modern science and technology. On the one hand, when new-tech products are promoted to the market, the imperfect technology or improper use of them can cause unstable performance or failure because of their attributes. On the other hand, the new-tech products manufacturers expect to devote the limited energy and resources to the development and manufacture of new products. So the demand for service agent of after-sale service of new-tech products appears objectively. Good after-sale service plays an important role in both the marketing of new-tech products and promoting the sustainable development of enterprises. For new-tech products manufacturing enterprises, choosing an improper service agent can not only cause the failure of the new-tech products but also huge losses or even devastating disasters in the enterprise.
The existing literature mainly evaluates the logistics service agent in the aspects of cost, quality and reputation of service. In contrast, there is little research on service agent [4] - [8] . It asks for a service agent to have strong operation efficiency and financial capability to do the after-sale service on certain products with high technology and value. The operational and financial indicators of this type of service agent are usually complete. They are of strong competitiveness. In this dissertation, we call this type of service agent as “important” service agent for new-tech manufacturing enterprises. Because different service agents differ greatly in essence, the manufacturing enterprises of large-scale products of new technology are faced with two problems: how to evaluate the alternative service agents and how to choose the best “important” service agent based on the evaluation.
Because the efficiency and capability of service agent of large-scale new-tech products are fuzzy and often restricted by its comprehensive strength, they can be considered as an important aspect which reflects the efficiency and capability of the “important” service agent. In the process of evaluation on “important” service agent, if the valuator is influenced greatly by his conceptual knowledge or the evaluation method is not scientifically reasonable, inferior “important” service agents may enter into the service agent library or even establish a strategic partnership with enterprises. In this consideration, the method of fuzzy comprehensive evaluation is adopted in this dissertation. In the beginning, fuzzy evaluation method of three types of service agents are put forward. Then, we use quantitative and qualitative assessment indexes to establish a kind of method to evaluate service agents of large-scale products (equipment) of new technology based on the method of fuzzy Borda.
2. The Fuzzy Evaluation Based on Quantitative Indexes
According to the attributes of “important” service agent and main factors that influence its comprehensive strength, the process of fuzzy comprehensive evaluation based on quantitative indexes is as follows:
1) The rating levels of “important” service agent
In this part, we divide the service agent into five rating levels according to the comprehensive strength of “important” service agent. The result is shown in Table 1.
2) Normalization processing of raw data in evaluation index system
In the following, we use fifteen “important” service agents of one manufacturing enterprise of new-tech products (represented by letters a, b, c,…, m, n, o) as empirical sample. According to article [1] , eight indexes which reflect the operational and financial condition of the fifteen “important” service agents in one year are chosen as main evaluation indexes (Table 2).
Table 1. Different rating levels of “important” service agent.
Table 2. Evaluation indexes of “important” service agent.
The raw data is shown in Table 3.
We need to normalize the raw data of evaluation indexes in order to eliminate the dimension of indexes and unify the variation range and direction of the indexes. For positive and negative indexes1, we can use the following equation to carry out the normalization processing [9] .
Equation (1) is used when the index is positive (benefit-contribute)
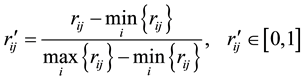 (1)
(1)
Equation (2) is used when the index is negative (cost-contribute)
 (2)
(2)
In the two equations, 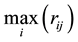 and
and 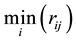 represent the maximum and minimum of the jth index respectively.
represent the maximum and minimum of the jth index respectively.
By exploiting the above equations, the normalization processing on raw index data can be conducted. The result is shown in Table 4.
3) Determine the membership function of the indexes
To facilitate discussion, supposing the membership function of each evaluation index which belongs to the five levels is fuzzy normal distribution:
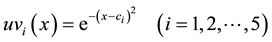 (3)
(3)
In the equation, x represents the index value; 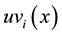 represents the membership degree of
represents the membership degree of to Level
to Level ;
; 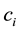 is the constant when the membership degree of
is the constant when the membership degree of 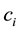 to Level
to Level 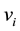 equals one
equals one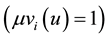 . The membership function of indexes in each level is shown in Table 5.
. The membership function of indexes in each level is shown in Table 5.
Table 3. Raw data of evaluation indexes of “important” service agents.
Table 4. The index data after normalization processing.
Table 5. The membership function in each level.
In Table 5, we gained the membership function of indexes in each level, and the corresponding relationship is as follows. First, we divided the levels into {very good, good, average, bad, very bad} 5 grades; then according to the membership function, we set 1, 0.8, 0.6, 0.4, 0.2 as the parameters, in order to correspond to the 5 grades.
4) Compute the weighted membership degree and determine the level each service agent belongs to.
Firstly, we compute the membership degree of different levels of each corresponding index by using the membership function in Table 4. The index belongs to each corresponding “important” service agent. Then the level each “important” service agent belongs to is determined according to the maximum membership degree principle. The results are shown in Table 6.
From Table 5, we can see j is the best service agent, c and f are the good service agents; e and l are service agents in average level; a, b, d, g and n are bad service agents and the worst service agents are h, i, k, m, o among the fifteen service agents. The above evaluation results offer effective decision-making basis for choosing “important” service agent to a certain degree.
3. The Fuzzy Multiple Attribute Decision Making (MADM) Based on Qualitative Indexes
The above evaluation system based on quantitative indexes makes a quantitative assessment on “important” service agents. Revaluation which combines some key qualitative indexes should be made on condition that quantitative evaluation meets the requirement. The key qualitative indexes should include the following five aspects. They are quality of service, level of technology, satisfaction of users, relationship of cooperation and capacity to coordinate. The fuzzy multiple attribute decision making method is used to qualitatively evaluate “important” service agents in the following part.
3.1. The Theory of Fuzzy Multiple Attribute Decision Making
Let the attribute value of the “important” service agent Xi under evaluation attribute Gj is interval fuzzy number

According to the ideology of Grey Relational Analysis, the process of interval fuzzy number multiple attri- bute decision making on the condition that the information of attribute weight is not complete is presented as follows:
1) Normalize the decision-making matrix
Define the matrix after normalization as

Table 6. Table of membership degree and the level each service agent belongs to.
When the attribute index is positive

When the attribute index is negative (cost-contribute):

2) Determine the positive and negative ideal points
Positive ideal point:
Negative ideal point:
3) Compute the grey relational coefficient of the attribute value from interval fuzzy number to positive ideal point
The grey relational coefficient of the attribute value of those “important” service agents from interval fuzzy number to positive ideal point is

And the grey relational coefficient of the attribute value of those “important” service agents from interval fuzzy number to negative ideal point is

In addition, the equation to calculate the distance between the interval numbers is
The alphabet 


4) Compute the correlation ship between the positive and negative ideal points:
As the attribute weight 



The above multi-objective optimization model can be transformed into single-objective optimization problem2 in case that all the schemes are in fair competition which means that there do not exist any preference relations.

In this way, the weight vector can be worked out.
5) Evaluate the results

Rank 

3.2. Analysis of Examples
Define the five attributes: quality of service (G1), level of technology (G2), satisfaction of users (G3), relationship of cooperation (G4) and capacity to coordinate (G5) as qualitative attributes to evaluate the “important” service agents. Make qualitative evaluation of the first five “important” service agents (j, c, f, e, l) selected by the method of fuzzy comprehensive evaluation. The incomplete hypothesis of weight information is as follows:
After the grading by some experts in this field, the fuzzy decision-making matrix X is as follows:
The fuzzy decision-making matrix after normalization processing is:
1) Determine the positive and negative ideal points
2) Compute the grey relational coefficient of the fuzzy number between the “important” service agents.
3) Solve the single-objective optimization problem listed below
The weight vector is
4) The correlation degree of each service agent to positive and negative ideal points is:
5) Results evaluation.
It can be seen that the five “important” service agents can be ranked as: f > j > c > l > e. In other words, the result of qualitative evaluation of service agent f is the best, and the agent j takes the second place…The result of e is the worst.
4. Comprehensive Evaluation Based on Fuzzy Borda Method
Fuzzy Borda method based on quantitative and qualitative evaluation is utilized to combine the evaluation results in which way optimization of “important” service agents can be ultimately achieved.
4.1. Principle of Fuzzy Borda Method
Fuzzy Borda Method is put forward by C. de Borda [10] [11] , which was firstly used in combination evaluation of election. It is designed to get the Borda scores by collecting the evaluation results of the n objects that are evaluated by m assessors. And then, the objects being evaluated will be ranked according to the value of the Borda scores. It is considered by some scholars that the ordering relation which is gained via the Borda method is a qualitative result itself. Therefore, it cannot embody the comprehensive evaluation of the quantitative and qualitative results. To settle the problem, the quantitative conclusion in the third part and the qualitative conclusion in the fourth part are integrated in this part. Some improvements are made on the basis of Borda method, which is known as fuzzy Borda method [12] [13] .
The computational steps of fuzzy Borda method are listed in the following part.
First: calculate the degree of membership:

In the above equation, 





Second: Calculate the fuzzy frequency

In the above equation, 

Third: Transform the rank of objects being evaluated into scores to expand the difference. The equation can be shown as

In the above equation, Qk represents the score of xi under the number kth method when it ranks number hth in optimum order.
Fourth: Calculate the Fuzzy Borda Number

4.2. Analysis of Examples
According to the conclusion of qualitative analysis mentioned above, select five superior service agents (j, c, f, e, l) and integrate the conclusion of quantitative analysis in the third part to calculate. To begin with, do uniformization with the conclusion of fuzzy comprehensive evaluation in the third part (shown in Table 5). As it is shown in the classification, grade I to grade V represent that the results are from very good to very bad. Therefore, we can give weight to grade I to V in a descending order, namely, 0.3, 0.25, 0.2, 0.15, 0.1. Furthermore, calculate the degree of membership of each service agent under fuzzy comprehensive evaluation and fuzzy multiple attribute decision making method through Equation (3) and Equation (13). The following are the results.
According to Table 7, compute the fuzzy frequency of each service agent through Equation (14). The results are listed in the following Table 8.
Replace the ranks of service agents under fuzzy comprehensive evaluation and fuzzy multiple attribute decision making method with scores through Equation (15) and compute the Borda number according to Equation (16). The results are listed in the following Table 9.
Table 7. Membership of service agents.
Table 8. Fuzzy frequencies of service agents.
Table 9. Fuzzy Borda number and ranking results.
Therefore, the ranking results based on fuzzy Borda method can be attained:
j > c > f > e > l
According to the previous result, agent j is the best, c and f are in the second class while e and l are not so good, which is in accordance with the results of quantitative fuzzy evaluation. The ranking results of service agents based on qualitative evaluation is f >j > c > l > e. That is to say, agent f receives the highest qualitative evaluation from experts. As a result, enterprises can adjust the rating level of agent according to their own conditions (in this example, agent f and c get the same level II in quantitative evaluation, shown in Table 5).
5. Conclusions
Focusing on the attributes of “important” service agents, based on the theory of fuzzy evaluation and multiple attribute decision making, this paper discussed how to deal with the uncertainty and fuzziness in the process of evaluating the service agents. Furthermore, methods of comprehensive evaluation and multiple attribute decision making are adopted to evaluate “important” service agents from quantitative and qualitative views respectively. On this basis, fuzzy Borda method was used to combine the results of quantitative and qualitative evaluations to rank the “important” service agents.
As is shown in the examples presented, the evaluation results which are gained from the three methods mentioned have good consistency3. Since the fuzzy Borda method combines the quantitative results with the qualitative results, the ranking results based on this method can embody the final evaluation results of “important” service agents. Methods involved in this dissertation are simple, reasonable and operable. It is convenient to make evaluation and selection of “important” service agents of new-tech products.
Funding
Funding Project: National Natural Science Foundation of China (71271043; 71473031); the Special Research Fund for the Doctor Program of Higher Education (20110185110021) and the Projects Supported by Science and Technology of Sichuan Province (2012SZ0001).
References
- Zhou, Z.F. and Ren, J.F. (2011) Research on Selection of Service Providers and Inventory Management of Spare Parts. Economic Science Press, Beijing.
- Wang, H.Q. and Hu, Y.Q. (2002) A Study on the Definitions of High & New Technology and Its Industry as Well as Their Standardized Use. Science of Science and Management of S. & T, 23, 8-11.
- Xiong, B. and Chen, L. (2007) Study on Financing in Transforming Technology Achievements of High-Tech Firms and Institutional Investors under Asymmetric Information. Chinese Journal of Management Science, 15, 136-141.
- Shao, X.F., Ji, J.H. and Huang, P.Q. (2001) Research on Methods of Suppliers Selection in Supply Chain. Quantitative & Technical Economics, 12, 80-83.
- Bao, Z.Q. and Yang, B. (2010) The Model of Outsourcing Service Providers Selection for Enterprise under the Asymmetric Information. Logistics Technology, 12, 51-54.
- Liu, J. (2009) Research on Incentive Mechanism of Logistics Outsourcing Based on Principal-Agent Theory. Tsinghua University, Beijing.
- Yao, Z.S. and Lu, Y.P. (2010) Selection of Third-Part Logistics Based on Logistics Outsourcing. Science Technology and Industry, 10, 89-95.
- Huang, D.S. and Zhang, X.P. (2005) A Dynamic Decision Approach for Long-Term Vendor Selection Based on AHP & BSC[C], LNCS 3645.
- Zhao, X.H. and Zhao, X.M. (2002) Selection of Suppliers Based on Fuzzy Decision Making. Industrial Engineering and Management, 4, 27-29.
- Guo, X.G. (1995) A New Comprehensive Evaluation Method―A Combination Evaluation Methods. Statistical Research, 15, 56-58
- Su, W.H. and Chen J. (2006) Development Ideas of Comprehensive Evaluation Method. Statistical Research, 26, 32-37.
- Su, W.H. and Chen, J. (2007) The Defects of Fuzzy Borda Method and Its Improvement. Statistical Research, 24, 58- 64.
- Zhang, M. and Zhou, Z.F. (2010) Credit Rating of High-Tech Enterprise Based on Fuzzy Borda Method. Value Engineering, 29, 43-44.
NOTES
1Positive index means that the bigger the index is, the better the service agent will be and negative index has the opposite meaning.
2If there are preference relations, the weighting processing is needed to do only.
3In many cases, there will be differences among the evaluation results of the three methods. However, due to the fact that fuzzy comprehensive evaluation method and fuzzy multi-attribute decision-making method evaluate service agents from quantitative and qualitative views respectively while fuzzy Borda method combines the quantitative and qualitative results, the latter conclusion is more reasonable.





















