Modern Economy
Vol. 3 No. 3 (2012) , Article ID: 19170 , 8 pages DOI:10.4236/me.2012.33044
Strategic Interaction and Charitable Fundraising
1School of Development Economics, National Institute of Development Administration, Bangkok, Thailand
2Department of Economics, University of Ottawa, Ottawa, Canada
Email: amornrat.a@nida.ac.th, vbarham@uottawa.ca
Received February 23, 2012; revised March 5, 2012; accepted March 29, 2012
Keywords: Non-Profit; Charities; Strategic Interaction
ABSTRACT
This paper studies strategic interaction between rival charities providing multiple public goods, highlighting the role of fundraising campaigns in influencing donor decision-making. The analysis suggests that, even when charities honor donor designation, social welfare may be higher in equilibrium when charities solicit donors sequentially, rather than simultaneously or through a United Fund.
1. Introduction
Non-profit organizations or charities provide a large number of public goods and services including health and medical services, education, museum exhibits, shelters for battered spouses and runaway teenagers, wildlife and environmental protection and research, sports programs, and religious services. With such an enormous number of organizations seeking to contribute to the common weal, and with financial resources often inversely proportional to the grandeur of their goals, many charities have become extremely inventive and determined in the pursuit of fundraising strategies, which range from phone call solicitation, to running lotteries, rummage sales, auctions and concerts. Larger charities often undertake significant fundraising campaigns, through which they seek both to inform donors about their activities and plead for new contributions. Since the competition for donor dollars is intense, many charities spend a significant proportion of their donation income on fundraising expenses, a reality that is a source of concern to many contributors since this means that a smaller proportion of their gift ends up being used for charitable activity.
Given the highly competitive nature of the environment in which charitable organizations operate it is somewhat surprising that there is a relative paucity of existing research focusing on the nature and consequences of strategic interaction between rival charities. One issue which has attracted attention is that of the desirability of collecting funds via a single United Fund versus specialized separate charities. Rose-Ackerman [1] studies a United Fund, which collects money and subsequently disburses it to specialized charities. Fundraising via a United Fund is considered to be advantageous because it allows for a reduction in the cost of running a fundraising campaign. As well, a United Fund provides a solution to the agency problem arising between donors and charities, because the United Fund can take on the role of auditing and monitoring the specialized charities which are the ultimate recipients of the funds donated, and in that role can assure donors that their money is being well spent. However, Rose-Ackerman [1] argues that in reality United Funds actually have very limited power to appeal to donors to funnel donations through the United Fund, since by giving directly to specialized charities donors can ensure that 100% of their contributions are used to support those organizations whose goals they wish to promote. Additionally, those specialized charities which have acquired good reputations amongst givers have strong bargaining power, enabling them to negotiate a greater share of the total funds collected, since they can creditably threaten to leave the United Charity to run their own campaigns.
Relatedly, Bilodeau [2] considers a non-cooperative game in which consumers choose to donate their money either to specific charities or to the United Fund. From the standpoint of consumers it is typically utility-maximizing to donate their money directly to their favorite charities rather than to the United Fund; this result is due largely to Bilodeau’s assumption that there is typically a fixed attribution rule determining how funds collected are to be split amongst the member charities, and this attribution rule may not reflect consumer preferences. When the United Fund is the last mover, it may be able to offset individual donations by reallocating funds amongst charities to ensure that no charity receives too much or too little. However, if the United Fund’s earmarked contribution rule contrasts distinctly with individual preferences, there will be a lower overall level of contributionsand thus the overall impact of the United Fund’s activity on social welfare is uncertain. (This may be the reason for which United Funds now typically allow donors to designate which organization will be the ultimate beneficiary of their contributions.) In subsequent work Bilodeau and Slivinski [3] consider consumers’ contribution decisions when there is competition between specialized charities and the diversified charity and where, additionally, the individual donor can influence the allocation of donations by founding a charity himself. The authors predict that the level of public good should be higher with two specialized charities rather than one single diversified charity. This result is consistent with Bilodeau [2] in the sense that the diversified charity can increase the overall level of contributions by honoring donors’ wishes about the way in which their contributions are to be used.
A number of papers explicitly explore the issue of the cost of fundraising, and whether or not these costs are influenced by the competitive environment in which charities must operate. Rose-Ackerman [4] presents a model to explain charities’ fundraising behavior. She concludes that fundraising is not only excessive in the absence of barriers to entry, but also that charities with heavy fundraising will become larger while charities which do less fundraising will contract. She argues that a monopoly United Fund will be superior to a system of rival charities if and only if 1) the demand for public goods is inelastic and charities are different in terms of services and costs of provision, or 2) demand is elastic but the costs of provision are similar, and fundraising expenses are high for individual charities. Andreoni [5] considers the role of “development directors”, who launch fundraising campaigns only once they have first secured large initial contributions from “leadership givers”. He considers an economy in which the cost function for the provision of public good is characterized by both fixed and variable costs, and in which fundraising is costly. Andreoni finds that a relatively small amount of initial seed money typically generates an enormous increase in subsequent donation income. More recently Andreoni and Payne [6] consider a model with two charities and two public goods, in which consumers donate only when asked, and donate to at most one charity. The authors show that an increase in fundraising effort by one charity always decreases the effort and consequently the level of the public good provided by the rival charity.
Like Andreoni and Payne [6], the model examined here features multiple public goods, and highlights the strategic dimensions of the rivalry between the charities. The analysis presented here departs significantly from the approach taken by Andreoni and Payne in that it views charities as producing two public goods: a physical good or service (for example, cancer research), and an informational public good (for example, information about how research funded by the Cancer Society has led to increased survival rates for those struck by cancer). The informational public good can be interpreted as the good which is generated by the charity’s fundraising campaign. Many factors influence donor decisions, but the bedrock on which successful fundraising campaigns are built is “the case”: charities have to demonstrate to donors both that there is a need for donor dollars, and that there are real benefits generated from the provision of the public good which the charity produces. Throughout the month of November, billboards throughout North America ask consumers “Not to forget those who cannot remember.” When canvassers for the Alzheimer Society knock on the door later in the month and ask for a contribution, donors choose to give because they know what the Alzheimer Society does, and that the Society needs their support. By modeling the output of the fundraising campaign as an informational public good it is possible to explicitly investigate the impact that the fundraising campaign undertaken by one charity has on the level donations received by other charities. For example, the campaign promoting the Heart and Stoke Research Foundation Lottery may have a negative impact on the General Hospital Lottery (since consumers may take the view that they have “already given”) but have a positive impact on the fundraising campaign of the Cancer Society (by increasing donor awareness of the benefits of medical research).
The outline of this paper is as follows. Section Two describes the model. Section Three considers the planning problem, and establishes a benchmark for efficient provision of the public goods. Section Four examines equilibrium outcomes when provision of the public goods is assured by a benevolent United Charity which respects donor preferences with respect to the attribution of donations. This institutional framework can be contrasted with that considered in Section Five, in which each public good is provided by a specialized charitable organization. Section Six concludes.
2. The Model
We consider an economy with N consumers, indexed by i, and two charities, indexed by j. The work of the charities is funded by donations solicited from consumers. We use 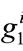 and
and 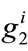 to denote the amount of money that individual i contributes to each of the charities. Each charity produces two public goods: information about its activeties (Ij, j = 1, 2), and a physical good or service (Gj, j = 1, 2). Donations received finance the production of both of these public goods. We denote by Aj, j = 1, 2, the resources allocated to producing the information goods; we interpret Aj as representing fundraising expenses. The production technology for the informational public good is assumed to depend only on fundraising expenses incurred as follows:
to denote the amount of money that individual i contributes to each of the charities. Each charity produces two public goods: information about its activeties (Ij, j = 1, 2), and a physical good or service (Gj, j = 1, 2). Donations received finance the production of both of these public goods. We denote by Aj, j = 1, 2, the resources allocated to producing the information goods; we interpret Aj as representing fundraising expenses. The production technology for the informational public good is assumed to depend only on fundraising expenses incurred as follows:

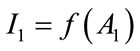
It is assumed that both f and h are concave functions. Charities produce the physical good Gj using net donation income:
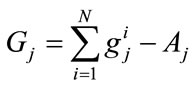 ; j = 1, 2 where
; j = 1, 2 where 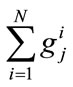 is the gross donation income received by Charity j. Note that there are constant returns to scale in the production of Gj.
is the gross donation income received by Charity j. Note that there are constant returns to scale in the production of Gj.
Consumers have an initial endowment of the private good, ωi, which they allocate either to donations or to their own private consumption (xi). Since the goods provided by the charities are pure public goods, free-riding is of course an option, and non-contributors will therefore obtain the same level of the informational public goods I1 and I2 and of the physical public goods G1 and G2 as do contributors. Consumer i’s budget constraint can be represented as follows:
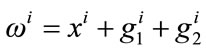 (1)
(1)
where the level of contributions must be non-negative, i.e.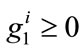 ,
,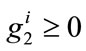 .
.
Consumer utility functions are assumed to be additively separable in the private good and the public goods as follows:
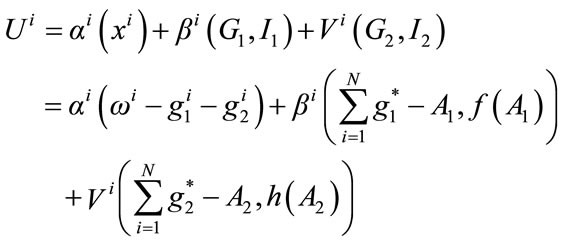 (2)
(2)
bi(×) and Vi(×) measure the utility consumer i derives from the consumption of two pairs of public goods (G1, I1) and (G2, I2) respectively. We assume that αi(×), βi(×) and Vi(×) are strictly concave in xi, Gj, Ij, for j = 1, 2. Since the information Ij helps consumers to be more aware of the benefits to be derived from higher levels of provision of the public goods Gj (j = 1, 2), we therefore assume that an increase in Ij will increase consumers’ marginal benefit from the consumption of Gj, i.e., both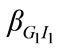 , and
, and  are positive.
are positive.
3. Establishing a Benchmark: The Planner’s Problem
In this section, we study the solution to the optimization problem faced by a Benthamite social planner; this allocation acts as the benchmark for our subsequent analysis. In order to facilitate comparisons with the decentralized outcome, it is useful to express the Planner’s problem as the choice of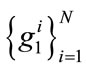 ,
,  , A1, A2. Specifically, the Planner solves:
, A1, A2. Specifically, the Planner solves:

Subject to 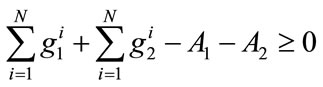 (3)
(3)
The Planner obtains the following first-order necessary conditions:
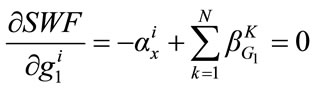 ;
;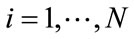 (4)
(4)
 ;
;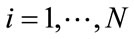 (5)
(5)
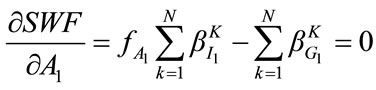 (6)
(6)
and, (7)
(7)
The system of Equations (4)-(7) implicitly defines the optimal levels of each of the choice variables. We denote by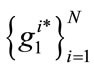 ,
, 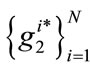 ,
, 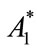 ,
,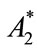 , the solution to this system of equations. Re-arranging these expressions we obtain, as expected, that:
, the solution to this system of equations. Re-arranging these expressions we obtain, as expected, that:
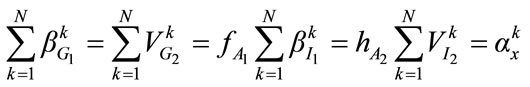 for all k (8)
for all k (8)
which means that the social marginal benefit of an additional unit of provision of any of the public goods must be equal to the marginal benefit of additional private consumption forgone for all consumers. This may be rewritten as the appropriate Samuelson’s [7] condition for each of the public goods:
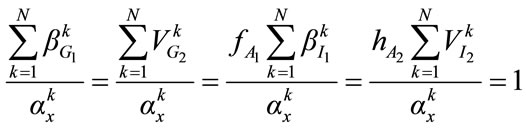 (9)
(9)
4. Benevolent United Charity
In this section we examine the level of donations elicited and the levels of fundraising expenditure chosen when production of the public goods is the responsibility of a single charitable organization—in effect, a United Fund. These outcomes are compared to the benchmark model above to investigate whether the United Fund will choose the same level of fundraising expenditure and, therefore, the same levels of I1, I2, G1 and G2 as does the social planner. It is reasonable to anticipate that strategic interaction between donors may affect the fundraising effort of the United Fund: since the charitable contributions sub-game is liable to be characterized by free-riding, the United Fund may seek to compensate for this inefficiency by over-investing in A1, A2.
It is assumed that the United Fund is a benevolent charity. That is, in choosing its level of fundraising expenditure for each of its charitable activities, the United Fund seeks to maximize social welfare, and thus has exactly the same objective as the Planner. Obviously, alternative objective functions could have been considered—for example, maximizing the output of the charity, maximizing the benefit-cost ratio, minimizing cost, maximizeing revenue, etc. In this section, however, we consider a truly benevolent charity because we wish to establish whether or not outcomes will be efficient in the “best of all” possible decentralized worlds. We also give consumers the right to control how their donations are allocated to each of the United Fund’s charitable activities; i.e., the United Fund cannot arbitrarily divide total donations received between the two charities.
We model the interaction between the single benevolent charity and consumers as a two-stage non-cooperative game. In the first stage, the United Fund runs a campaign informing consumers about the public goods funded by the United Fund and asking them to contribute to this year’s campaign. In the second stage, consumers decide how much to contribute to each of the physical public goods produced by the charity; the United Fund collects the donations and uses all donations  (less fundraising expenses incurred for that good) for production of Gj. Everyone then receives their payoff and the game ends. The equilibrium concept used is that of subgame perfect Nash equilibrium, and so the game is solved using backward induction.
(less fundraising expenses incurred for that good) for production of Gj. Everyone then receives their payoff and the game ends. The equilibrium concept used is that of subgame perfect Nash equilibrium, and so the game is solved using backward induction.
4.1. Consumer I Chooses the Optimal Level of Donations
In stage two, consumers must choose how much to donate to each of the charitable activities funded by the United Fund. This decision is taken after the United Fund has run its fundraising campaign, and thus A1, A2 are parameters of the consumer’s decision problem. Maximizing consumer i’s utility function with respect to  and
and  yields the following first-order necessary conditions:
yields the following first-order necessary conditions:
 ,
, (10)
(10)
 ,
, (11)
(11)
We define 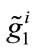 and
and  as the implicit solutions for consumers i’s strategic choice variables derived from solving the preceding first-order conditions given the levels of fundraising expenditure A1, A2 chosen by the United Fund in stage one. Note that the optimal level of contri-butions-
as the implicit solutions for consumers i’s strategic choice variables derived from solving the preceding first-order conditions given the levels of fundraising expenditure A1, A2 chosen by the United Fund in stage one. Note that the optimal level of contri-butions-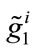 and
and 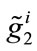 are functions of
are functions of
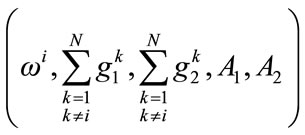
where  and
and 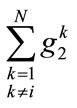 represent total contributions by all consumers except i. This is just the standard voluntary contributions game (e.g., Bergstrom, Blume and Varian (BBV [8])), and as usual it is the case that consumers under-contribute, as they equalize their personal marginal benefit from the provision of each of the public goods to their personal marginal cost, and neglect the benefit of increased public good provision to other members of the community:
represent total contributions by all consumers except i. This is just the standard voluntary contributions game (e.g., Bergstrom, Blume and Varian (BBV [8])), and as usual it is the case that consumers under-contribute, as they equalize their personal marginal benefit from the provision of each of the public goods to their personal marginal cost, and neglect the benefit of increased public good provision to other members of the community:
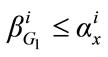 ,
,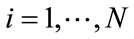 (12)
(12)
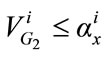 ,
,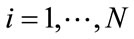 (13)
(13)
It is immediately evident that the Nash equilibrium of the contributions subgame is not unique: for any allocation of 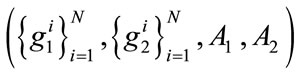 it is possible to define another equilibrium which maintains the total amount donated to each charity, but redistributes the actual amounts contributed by each donor. Since the total level of provision of each public good, and the total amount donated, remains the same, this alternative configuration of donor contributions must also be equilibrium. Note, however, a sufficient condition for the total level of provision of each public good to be unique is that all goods are normal goods (BBV [8]). Uniqueness in levels is all that is required for the charity’s decision problem to be well-defined.
it is possible to define another equilibrium which maintains the total amount donated to each charity, but redistributes the actual amounts contributed by each donor. Since the total level of provision of each public good, and the total amount donated, remains the same, this alternative configuration of donor contributions must also be equilibrium. Note, however, a sufficient condition for the total level of provision of each public good to be unique is that all goods are normal goods (BBV [8]). Uniqueness in levels is all that is required for the charity’s decision problem to be well-defined.
For the subsequent analysis it is useful to study the sensitivity of consumer donation decisions to the changes in the level of fundraising for each good. If consumer’s preferences and incomes differ, then calculation of comparative statics results requires the analysis of 2N × 2N matrices, which is only feasible when undertaking numerical simulation. Consequently, for the remainder of the analysis we assume that consumers are identical, and study the symmetric Nash equilibrium. In view of the above proposition, the symmetric Nash equilibrium is unique. It is straightforward to show that:
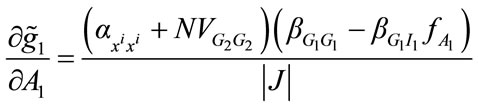 (14)
(14)
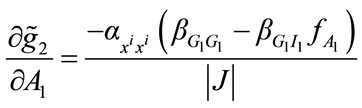 (15)
(15)
 (16)
(16)
 (17)
(17)
where  is the Jacobian term. Recall that ai(×), bi(×), and Vi(×), are strictly concave in xi, G1, G2, therefore,
is the Jacobian term. Recall that ai(×), bi(×), and Vi(×), are strictly concave in xi, G1, G2, therefore, 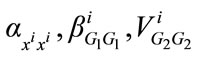 are negative. The Jacobian term is indeed positive.
are negative. The Jacobian term is indeed positive.
The comparative statics results have the expected signs:
 , and
, and . The fundraising campaign by charity i therefore crowds out donations to its rival. It is also straightforward to check that both
. The fundraising campaign by charity i therefore crowds out donations to its rival. It is also straightforward to check that both
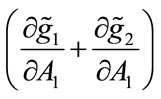 and
and 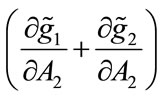 are positive: increasing expenditure on fundraising will increase total donations.
are positive: increasing expenditure on fundraising will increase total donations.
4.2. The United Fund Choose the Level of Fundraising for Each Public Good
Since we assume that the United Fund seeks to maximize social welfare, and recalling that we are treating the case of identical individuals, the decision problem for the United Fund can be expressed as:

Subject to 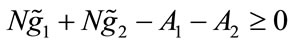
The first-order conditions are:
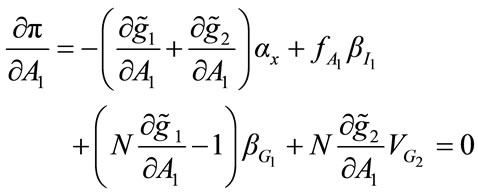 (18)
(18)
 (19)
(19)
And using (10) and (11), we can rewrite (18) and (19) as:
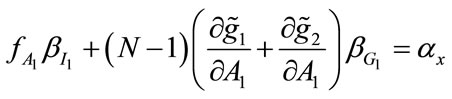 (20)
(20)
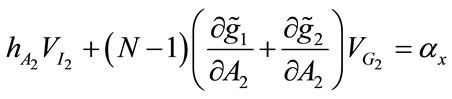 (21)
(21)
We denote the solution to (20) and (21) by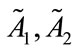 . The right-hand side of Equations (20) and (21) measures the marginal cost of the foregone private good consumption that is required to finance an incremental increase in fundraising expenditure, whereas the left-hand side measures the net marginal benefits of increased fundraising. As compared with the solution to the Planner’s problem, the key difference is that the United Fund must take account of the strategic interaction between donors in the contributions game, which means that there are two additional terms i.e.,
. The right-hand side of Equations (20) and (21) measures the marginal cost of the foregone private good consumption that is required to finance an incremental increase in fundraising expenditure, whereas the left-hand side measures the net marginal benefits of increased fundraising. As compared with the solution to the Planner’s problem, the key difference is that the United Fund must take account of the strategic interaction between donors in the contributions game, which means that there are two additional terms i.e., 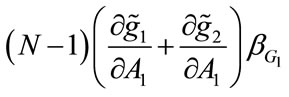 and
and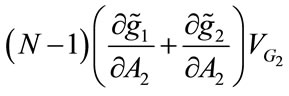 . Both of which are positive. It is easy to verify that
. Both of which are positive. It is easy to verify that , and,
, and,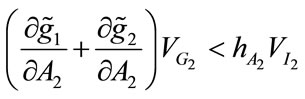 . Consequently, if
. Consequently, if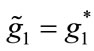 ,
,
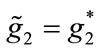 then
then 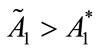 and
and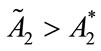 : the United Fund would overspend on fundraising, as compared to the Planner’s solution, because it cannot be expected that
: the United Fund would overspend on fundraising, as compared to the Planner’s solution, because it cannot be expected that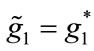 ,
,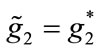 at a sub-game perfect Nash equilibrium. In fact, the possibility exists that the benevolent charity over provides I1 or I2 in order to crowd in donations, and/or that the total level of provision of G1 or G2 at the Nash equilibrium could be greater than at the first best. However, it can be shown that at the Nash equilibrium, all of the public goods cannot be overprovided relative to the social welfare optimum.
at a sub-game perfect Nash equilibrium. In fact, the possibility exists that the benevolent charity over provides I1 or I2 in order to crowd in donations, and/or that the total level of provision of G1 or G2 at the Nash equilibrium could be greater than at the first best. However, it can be shown that at the Nash equilibrium, all of the public goods cannot be overprovided relative to the social welfare optimum.
Proposition 1 At a sub-game perfect Nash equilibrium with a benevolent United Charity, it cannot be true that all public goods are overprovided relative to the social welfare optimum. Furthermore, G1 and/or G2 are not both provided at levels exceeding the first-best levels.
Proof: When all consumers are identical, the Planner’s first order conditions Equations (7) and (8) can be rewritten as follow.
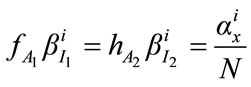 (22)
(22)
Recall also that when the United Charity chooses its fundraising expenditure optimally, it must be true that:
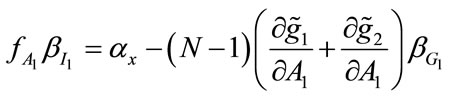 (23)
(23)
 (24)
(24)
Using the expressions calculated earlier for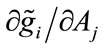 , it is straightforward to check that
, it is straightforward to check that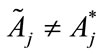 : the fact that donors engage in free-riding behavior in the second-stage means that a benevolent United Charity can never implement the first-best outcome.
: the fact that donors engage in free-riding behavior in the second-stage means that a benevolent United Charity can never implement the first-best outcome.
It remains to show that we will never observe ,
, 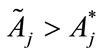 , for all j = 1, 2. Suppose the contrary that when a benevolent United Charity chooses fundraising expenses optimally, all public goods are overprovided. Recall from the analysis of the consumer’s giving decision that
, for all j = 1, 2. Suppose the contrary that when a benevolent United Charity chooses fundraising expenses optimally, all public goods are overprovided. Recall from the analysis of the consumer’s giving decision that
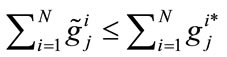 when
when , j = 1, 2. Moreover, it is trivial to check that
, j = 1, 2. Moreover, it is trivial to check that  if
if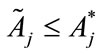 , j = 1, 2. By continuity, we then know that there exists a pair of fund raising expenditures
, j = 1, 2. By continuity, we then know that there exists a pair of fund raising expenditures 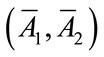 where
where ,
, 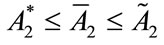 such that
such that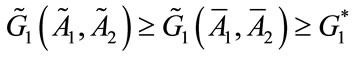 ,
,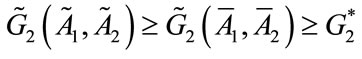 . But from the concavity of consumers’ utility functions, it must be true that
. But from the concavity of consumers’ utility functions, it must be true that
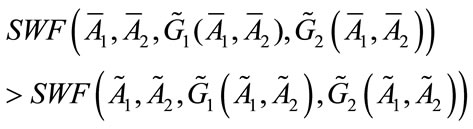
which contradicts the initial assumption that the benevolent United Charity has chosen fundraising expenditures to maximize welfare. It follows immediately that at most one of the physical public good can be overprovided.
As compared to the first-best allocation, the benevolent charity is obliged to try and “undo” the inefficiencies generated by free-riding behavior in the contributions sub-game. This may lead to a situation where it is appropriate to overinvest in fundraising, in order to strategically distort the incentives facing donors: donors are in fact grateful to the charity for the constant solicitation, because it helps them to make a larger donation. This result is comparable to results on possible overprovision of public goods when there is distortionary taxation (e.g., Atkinson and Stern [9]), and to Lipsey and Lancaster’s [10] pioneering work on the general theory of second-best.
5. Benevolent Stand-Alone Charities
In the real world, United Funds are never solely responsible for the provision of public goods in a given community. Typically, many charities run their fundraising campaigns independently (the Alzheimer’s Society in February, the Cancer Society in March, etc.). It is therefore of interest to examine whether or not equilibrium outcomes are affected by the institutional separation that typically exists between public goods providers. However, once there is more than one player in the game, it is natural to suspect that the order of play may matter, and in particular that equilibrium outcomes when charities undertake their fundraising campaigns simultaneously may differ from those that arise when they advertise sequentially.
The analysis below demonstrates that the timing of play does in fact matter: and that it is better for the charities to solicit funds sequentially rather than simultaneously. This result is striking, as it suggests that a system of stand-alone charities will actually achieve a better outcome than can be achieved when a United Fund solicits donors to contribute simultaneously towards both charitable organizations. Before analyzing the sequential model, however, we first present a proposition regarding the equivalence of a system of stand-alone benevolent charities which simultaneously undertake their fundraising programs, and the United Fund.
Proposition 2 Any sub-game perfect Nash equilibrium of the United Charity game is also a sub-game perfect Nash equilibrium of the benevolent stand-alone charity model when both charities solicit donors simultaneously.
Proof: If both stand-alone charities in this model are benevolent, and thus seek to maximize social welfare, then they each have the same objective function as the Planner (and thus also of the benevolent United Fund). The first-order necessary conditions of this game are essentially identical to that of the benevolent United Charity examined above. In effect, since charities share the same objectives, there are no costs and no benefits to working collaboratively through a United Fund, versus independently-sponsored fundraising campaigns.
This result is worth underscoring in the context of debate with respect to the desirability of using United Funds to raise dollars for charitable purposes, versus a system of independent charities. Clearly, advocates of the United Fund approach must believe that member charities are not truly benevolent, and in fact must have a more limited vision of what constitutes the public interest. If charities were indeed truly benevolent, and took account of the impact of their own fundraising efforts on the success of their rivals, then there would be no need to coordinate fundraising effort through a United Fund.
Rather than assuming that charities approach donors simultaneously, it seems worthwhile to consider a sequential framework in which charities decide in turn on their level of fundraising effort. Different approaches to timing could be considered, each of which might potentially have different equilibrium outcomes. Below, we consider a specific sequential game in which, in stage one, Charity 1 first chooses its level of fundraising expenditure A1 and then, in stage two, Charity 2 chooses A2. In stage three, consumers decide how much to donate to both charities. The appropriate equilibrium concept for this game is again sub-game perfect Nash equilibrium. Notice that since consumers choose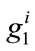 , and
, and  after the charities have chosen A1 and A2, the consumer’s decision problem is identical to that analyzed above with respect to the benevolent United Fund: the consumer’s donation decision is thus not directly affected by the change in the institutional environment. For it to be argued that “institutions matter” it is therefore necessary to show that the change in the institutional environment affects the behavior of the charities.
after the charities have chosen A1 and A2, the consumer’s decision problem is identical to that analyzed above with respect to the benevolent United Fund: the consumer’s donation decision is thus not directly affected by the change in the institutional environment. For it to be argued that “institutions matter” it is therefore necessary to show that the change in the institutional environment affects the behavior of the charities.
5.1. Choosing A2
Recall that Charity 2 is the “second mover”, and chooses its fundraising expenditure only after Charity 1 has run its campaign. Since it is assumed that each charity is benevolent, and can fully anticipate how consumers will react in stage three, Charity 2’s decision problem can be expressed as
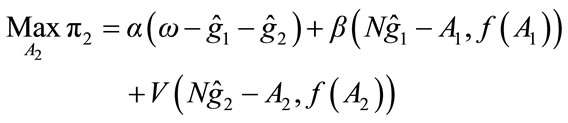
Subject to 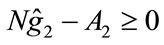
where  is the solution for the consumer’s utility maximizing problem in stage three. The first-order necessary condition for Charity 2 is identical to that of the United Fund in Equation (20), that is:
is the solution for the consumer’s utility maximizing problem in stage three. The first-order necessary condition for Charity 2 is identical to that of the United Fund in Equation (20), that is:
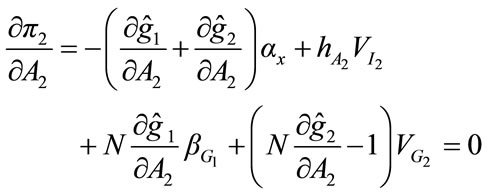 (25)
(25)
We define 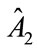 as the level of fundraising expenditure chosen by Charity 2. Notice that for a given G1, the level of A2 chosen by Charity 2 is the same as would be chosen by the United Fund. Using (10) and (11), Equation (25) can be re-written as follow:
as the level of fundraising expenditure chosen by Charity 2. Notice that for a given G1, the level of A2 chosen by Charity 2 is the same as would be chosen by the United Fund. Using (10) and (11), Equation (25) can be re-written as follow:
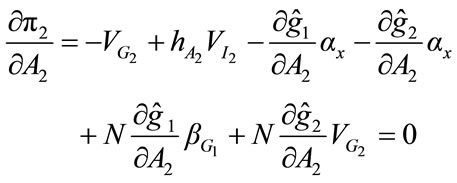 (26)
(26)
It would obviously be useful to be able to determine how the level of fundraising expenditure chosen by Charity 2,  , responds to the changes in the level of fundraising expenditure chosen by Charity 1, A1. However, although an expression for
, responds to the changes in the level of fundraising expenditure chosen by Charity 1, A1. However, although an expression for 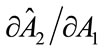 can be calculated, the sign is indeterminate: this means that increased fundraising efforts by Charity 1 may crowd in or crowd out fundraising effort on the part of Charity 2.
can be calculated, the sign is indeterminate: this means that increased fundraising efforts by Charity 1 may crowd in or crowd out fundraising effort on the part of Charity 2.
5.2. Choosing A1
Charity 1 chooses its level of fundraising effort in the first period of the game taking into account the impact of its choice both on Charity 2’s choice of A2 as well as on donor behavior. Since the charity is benevolent, its decision problem can be expressed as:

subject to 
The optimal level of fundraising expenditure is thus found as a solution to

which (using (10) and (11)) can be rewritten as:
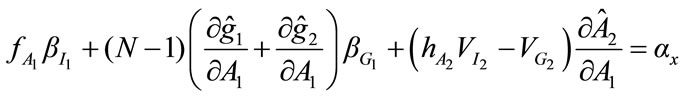 (27)
(27)
Denote the optimal level of fundraising for Charity 1, as implicitly defined by the above first-order condition, by A1. Comparing (27) to (20), it is evident that the fundraising effort of Charity 1 will generally differ from that chosen by a benevolent United Charity. From (10) (11), and (25), we can show that
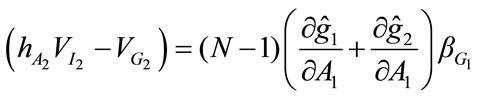
is negative. Therefore if 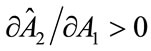 the last term on the left hand side of (27) must be negative, which implies that if in equilibrium it were the case that
the last term on the left hand side of (27) must be negative, which implies that if in equilibrium it were the case that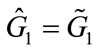 ,then
,then : Charity 1 would choose a lower level of A1 than does the United Fund. If
: Charity 1 would choose a lower level of A1 than does the United Fund. If 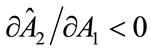 then the opposite is true.
then the opposite is true.
The interpretation of this result is straightforward: since 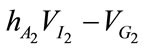 measures the net social marginal benefit of an increase in A2, and this is negative in any sub-game perfect Nash equilibrium, then if fundraising expenditure by Charity 1 crowds in fundraising effort by Charity 2 (that is,
measures the net social marginal benefit of an increase in A2, and this is negative in any sub-game perfect Nash equilibrium, then if fundraising expenditure by Charity 1 crowds in fundraising effort by Charity 2 (that is,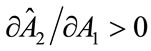 ), then it is desirable for Charity 1 to decrease its fundraising efforts, below the level that would be chosen by a United Fund, in order to discourage fundraising effort by its sister charity, which decreases the negative net social marginal benefit created by A2. In contrast, if
), then it is desirable for Charity 1 to decrease its fundraising efforts, below the level that would be chosen by a United Fund, in order to discourage fundraising effort by its sister charity, which decreases the negative net social marginal benefit created by A2. In contrast, if 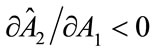 then Charity 1 will expands its own fundraising effort to crowd-out the fundraising efforts of Charity 2. This discussion is summarized in the proposition below.
then Charity 1 will expands its own fundraising effort to crowd-out the fundraising efforts of Charity 2. This discussion is summarized in the proposition below.
Proposition 3 Ceteris paribus, when charities choose fundraising effort sequentially, fundraising expenditure by Charity 1 is smaller (respectively, greater) than the level chosen by the United Fund if 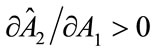 (respectively, if
(respectively, if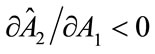 ). Furthermore, the level of social welfare obtained when charities move sequentially is greater than when all fundraising is undertaken by a United Fund.
). Furthermore, the level of social welfare obtained when charities move sequentially is greater than when all fundraising is undertaken by a United Fund.
Proof: As the first mover in the sequential game, Charity 1 can always choose  in Stage One, in which case Charity 2 will choose
in Stage One, in which case Charity 2 will choose  in stage Two. So if
in stage Two. So if 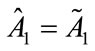 the level of public goods provided under the sequential contribution game will be identical to that which would be provided by the benevolent United Charity, in another words
the level of public goods provided under the sequential contribution game will be identical to that which would be provided by the benevolent United Charity, in another words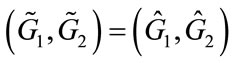 . As a benevolent charity, Charity 1 chooses
. As a benevolent charity, Charity 1 chooses 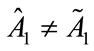 if and only if
if and only if , generate a higher level of social welfare. From (27), it is evident that generically
, generate a higher level of social welfare. From (27), it is evident that generically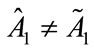 , and so social welfare must be higher with sequential fundraising rather when there is a benevolent United Charity.
, and so social welfare must be higher with sequential fundraising rather when there is a benevolent United Charity.
This result is interesting for two reasons. Firstly, it clearly demonstrates that institutions matter: even in an economic environment in which all parties are equally committed to promoting the general good, economic outcomes are not the same when decision-makers choose sequentially and when they choose simultaneously. Secondly, if one takes the view that charities are genuinely interested in promoting social welfare then not only is there no need for a United Fund, but in fact society is (weakly) better off when each charity sequentially undertakes its fundraising campaign.
6. Conclusions
The analysis above examines strategic interaction between rival charities in a variety of institutional settings. The model features four pure public goods, and one private good. Two charities undertake fundraising campaigns to solicit donations of the private good from consumers. Donations are used to finance fundraising, and to produce a physical public good. The fundraising activeties generate information, which is also a public good: in effect, potential donors need to not only be asked to contribute to the cause, but must also be convinced that the cause is worthy and that funds will be used effectively. The results obtained clearly illustrate the importance of institutions, even when charities are truly benevolent. In particular, a weakly higher level of social welfare is achieved when solicitation is undertaken sequentially by benevolent charities, rather than by a United Fund which respects donor designation. Also, a sub-game perfect Nash equilibrium (with either a United Fund or sequential solicitation of donors) may feature levels of provision of some of the public goods that are higher than the levels observed at a first-best allocation; however, at least one of the physical public goods must be undersupplied.
We believe that there is much opportunity to generate important insights into the behavior of non-profits through the thoughtful analysis of strategic interaction between charities in undertaking fundraising campaigns. A natural direction for future research is to explore in greater depth issues related to the timing of fundraising campaigns, and to develop a model of endogenous timing, possibly in the spirit of Hamilton and Slutsky [11]. In particular, if sequential fundraising campaigns are weakly welfare superior to a United Fund, is it reasonable to anticipate that charities will in fact choose to solicit donors at different times of the year, as would seem to be desirable, or will strategic considerations lead them to all launch a Christmas appeal? Also, it would be interesting to incorporate considerations of imperfect information, e.g., the notion that a United Fund may have access to superior technology for monitoring charity behavior as compared to individual donors.
REFERENCES
- S. Rose-Ackerman, “United Charities,” Public Policy, Vol. 28, No. 3, 1980, pp. 323-350.
- M. Bilodeau, “Voluntary Contributions to United Charities,” Journal of Public Economics, Vol. 48, No. 1, 1992, pp. 119- 133. doi:10.1016/0047-2727(92)90044-G
- M. Bilodeau and A. Slivinski, “Rival Charities,” Journal of Public Economics, Vol. 66, No. 3, 1997, pp. 449-467. doi:10.1016/S0047-2727(97)00046-7
- S. Rose-Ackerman, “Charitable Giving and Excessive Fundraising,” The Quarterly Journal of Economics, Vol. 97, No. 2, 1982, pp. 193-212. doi:10.2307/1880754
- J. Andreoni, “Toward a Theory of Charitable Fun-Draising,” Journal of Political Economy, Vol. 106, No. 6, 1998, pp. 1186-1213. doi:10.1086/250044
- J. Andreoni and A. A. Payne, “Do Government Grants to Private Charities Crowd out Giving or Fund-Raising?” American Economic Review, Vol. 93, No. 3, 2003, pp. 792- 812. doi:10.1257/000282803322157098
- P. A. Samuelson, “The Pure Theory of Public Expenditure” Review of Economics and Statistics, Vol. 36, No. 4, 1954, pp. 387-389. doi:10.2307/1925895
- T. Bergstrom, L. Blume and R. H. Varian, “On the Private Provision of Public Goods,” Journal of Public Economics, Vol. 29, No. 1, 1986, pp. 25-49.
- Atkinson and Stern, “Pigou, Taxation and Public Goods” Review of Economic Studies, Vol. 41, No. 1, pp. 1974, pp. 119-128. doi:10.2307/2296403
- R. G. Lipsey and K. Lancaster, “The General Theory of Second Best,” Review of Economic Studies, Vol. 24, No. 1, 1956, pp. 11-32. doi:10.2307/2296233
- J. Hamilton and S. Slutsky, “Endogenous Timing in Duopoly Games: Stackelberg or Cournot Equilibria,” Games and Economic Behavior, Vol. 2, No. 1, 1990, pp. 29-46. doi:10.1016/0899-8256(90)90012-J

