Journal of Environmental Protection
Vol.5 No.11(2014), Article
ID:49353,16
pages
DOI:10.4236/jep.2014.511103
The Use of SF6 and GIS to Study Farfield Modeling of Ocean Outfall Plumes in Florida
Frederick Bloetscher1*, Fernando J. Pleitez1, Thomas Romah1, Ahmed Albasri1, Chase Dickinson1, Husayn El Sharif1, Kevin Matthews1, Trung-Duong Nguyen1, Lucrece Riche1, Frank Youngman1, Thomas P. Carsey2, Jack Stamates2, John R. Proni3
1Florida Atlantic University, Civil Engineering Department, Boca Raton, FL, USA
2Atlantic Oceanographic and Meteorological Laboratory, Ocean Chemistry Division, Miami, FL, USA
3Applied Research Center (ARC), Florida International University, Miami, FL, USA
Email: *h2o_man@bellsouth.net
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 May 2014; revised 8 June 2014; accepted 1 July 2014
ABSTRACT
In June, 2004 and February, 2007, in field tracer studies were conducted on the Hollywood and South Central outfalls, using sulfur hexafluoride (SF6) as a tracer. The objective of these studies was to determine if the tracer could be detected in the farfield at significant distance, and if so, could this data be used to construct a model of the farfield plume. Prior models for farfield plume movement do not appear to comport well with the conditions in southeast Florida. Extensive research was conducted in southeast Florida on 4 outfalls, which led to the development of nearfield dilution equations for same. However farfield modeling of outfall plumes was difficult to accomplish because the tracers used are not detectable for significant distances. The SF6 resolved that problem and as a result the Hollywood outfall was used to construct a model. Two methods were investigated for modeling the plume, 1) the Eureqa formulation method and 2) the Gamma-Curve method. The concentrations in the x-y plane were first found by using the Eureqa formulation to calculate the concentration at each grid point given its depth and the concentration of the centerline at the same latitude. The plume models were generated using MATLAB that matched with the results actually seen in the field.
Keywords:Ocean Outfall, Treated Sewage, Effluent Disposal, Farfield Modeling, Sulfur Hexafluoride

1. Introduction
Six utilities in Palm Beach, Broward and Miami-Dade counties were discharging 396 million gallons per day (MGD) of wastewater in 2005. In 2009, the Florida Legislature passed a bill to cease outfall operations by 2025. In 2011 this deadline was modified slightly. The proposed solution was to reuse the wastewater. However how over 300 MGD of brackish water was to be reused was not answered. Instead more questions have been raised about the actual impact of the outfalls as the impact of policies implemented for the coastal ocean may have profound impacts on other activities as such decisions are closely linked to actions to be undertaken with respect to water and energy supplies to the rapidly growing population of southeast Florida. These costs are expected to excel $20 billion dollars and require over 2 Giga Watts of new power (proposed as nuclear reactors on Biscayne Bay [1] ).
The State of Florida is presently faced with critical decisions regarding the future of its coastal environment as a result of terrestrial activities. Coastal ecosystems, including both inshore estuaries and offshore reefs, sustain the State of Florida’s natural resource driven economy [2] . Both must be protected to continue providing economic opportunities critical to the State. Increased nutrient loads could promote the growth of algae on the reefs, harming their habitat, their dependent wildlife and affecting tourist and commercial activities. Implication of anthropogenic causation have been suggested in the overgrowth of macroalgae and/or benthic cyanobacteria blooms which cause loss of coral and sponge cover and changes in reef fish demographics [3] . In 1994-1995, a blooms of codium ishmocladum were reported in reefs off of Broward and Palm Beach Counties [4] , and Caulerpa brachypus C. brachypus var. parvifolia in 2001 [5] [6] . Lyngbya spp blooms were observed off of Broward County in 2003 [7] . Blooms of Cladophora liniformis, Enteromorpha prolifera, and Centroceras clavulatum were observed in the spring of 2007 [8] .
While it is asserted that a significant fraction of the nutrients impacting the coastal ecosystem are anthropogenic [9] [10] , the current state of understanding concerning point and non-point sources of pollution, as well as natural process such as upwelling, is incomplete [11] . Prior efforts by the authors has indicated that the canals and upwelling are significant courses of nutrient deposition [12] -[19] , but other sources could include such far-field processes as coastal pollutants from the Florida Keys, the Caribbean, the Mississippi River, the southwest Florida shelf and atmospheric deposition, depending on the prevailing oceanographic conditions and location. Differentiating which, if any of these discharges may be the source(s) of nutrients is nearly impossible. Despite these numerous sources of nutrients, the outfalls have long been a target of divers as the cause of the algal blooms, despite the lack of data to implicate the outfalls [18] [20] .
South Florida has six outfalls discharge (see Figure 1). Each of these outfalls discharges secondary treated wastewater at a depth of 100 feet below the surface (see Table 1). Prior researchers have developed equations to describe the nearfield dilution characteristics through the efforts from the Southeast Florida Ocean Outfall Experiments (SEFLOE) conducted from 1984-1994 [20] -[22] . As a result, the southern four outfalls are among the most studied outfalls in the world.
Among the findings of SEFLOE were that the secondary treated wastewater is less dense than seawater and hence rises as a buoyant jet above the outfall (see Figure 2—acoustic photograph of the Broward outfall). The region of the rising plume where mixing is caused predominantly by buoyancy effects, is known as the nearfield region. Dilution exceeds 20:1 for all four outfalls before reaching the surface during the 10th percentile current condition [20] . Once the plume reaches the surface, it spreads out at the sea surface (top 1/3) as a less salty plume above the denser seawater as predicted by Richardson [23] . The surface region is termed the farfield, which is the result of further mixing that occurs due to ambient ocean currents [24] . Vertical transport is usually considered to be small, as diffusion effects are orders of magnitude smaller than advective horizontal transport [25] .
Tracking nutrients from the ocean outfalls in the farfield is difficult as the nutrient concentrations are very low. For example, the total nitrogen concentration is typically less than 20 mg/L in the discharge. If it receives a 20:1 or more dilution in the rise of the plume to the surface, the total nitrogen concentration will be below 1 mg/L which is hard to track for any distance on the surface. During the SEFLOE effort, only entorocuccus was detectable at 800 m, while no other parameter was detectable at 400 m [20] . Given that the plume rise to the surface, and tracking nutrients is difficult at the surface due to dilution, impacts to the reefs on the bottom are not anticipated in the nearfield vicinity of the outfalls.
A variety of investigators have made suggestions on modeling outfall plumes. Koh and Brooks [26] equated

Figure 1. Location of ocean outfalls in SE Florida.
outfalls to underwater chimneys with an emphasis on particulate deposition. They note that “it is practically never feasible to provide such complete treatment that an outfall is not necessary, nor is it common to depend entirely on an outfall with no treatment.” As a result, modeling the fate and transport is assumed to follow a Gaussian dispersion which continually deforms under applied shear stress to generate a time-averaged pollutant concentration relationship between that can be modeled using a normal, Gaussian, distribution curve along its longitudinal axis [26] [27] .
There has been much work on nearfield dilution, but far less on the far field. Initial plume models were developed for the nearfield rise based on thermal principles by Trent and Welty (1973), and subsequently improved on by others using buoyancy. Eulerian integral models simulate buoyant jets based on a set of control volumes fixed in space [28] -[33] . Lagrangian models have also been used by treating buoyant jets as a series of non-interfering moving elements [34] -[36] . Other efforts have been undertaken by Grace [37] and Carvalho et al. [38] . Economopoulou and Economopoulou [39] [40] developed a graphical solution for outfalls that are useful in the nearfield Others developed or used software: VISJET [41] , Delft3D and the Cornell mixing zone expert system (CORMIX [42] ) and Visual Plumes [43] [44] , Huang et al. [21] [22] presented a probabilistic approach to develop initial dilution criteria or standards for ocean outfall design in the nearfield as a part of SEFLOE, while. Lye and Sharp [45] used a Monte Carlo Simulation to predict the ability of outfall to meet compliance requirements in the nearfield.
With respect to farfield outfall studies, a series of investigators attempted to model the farfield without tracers [46] [47] . Several found tracers to be not viable in Florida [48] -[52] . Gray [53] investigated the impact on Australia’s outfalls on fish populations, but detected no numerical impacts on fish larvae, which is not inconsistent with the finding of Bloetscher et al. [18] for Florida’s outfalls. Outfall plumes that do not follow the flow regime of the Florida outfalls or their currents include plumes modeled by many others [54] -[66] . As a result, there are no prior studies that occur in conditions similar to SE Florida, and due to cost to conduct tracer experiments, a limited data sample was available for this effort, fully acknowledging that studying the dispersion of effluent from coastal ocean sewage outfalls has continued to be a difficult problem to study in situ because the conditions are constantly changing as Jones, et al. [67] noted.
2. Methods
Given highly diluted environments in the nearfield, defining farfield effects requires the ability to measure very small quantities of highly diluted contributions on the bottom of the ocean floor. Therefore, to resolve the problem of detecting plume movement in the farfield, NOAA proposed a conservative tracer to prevent impacts on the reef community whenever the terrestrial plume touched the bottom. The indicator chemical that could be detected in-situ at very low levels was sulfur hexafluoride (SF6). SF6 was suggested as the tracer due to NOAA’s success in using it in the open ocean. Its usefulness in the coastal ocean had not been tested until the Hollywood experiment discussed here in 2004 [68] . The detection limit of SF6 is less than 1 part per trillion by volume (pptv) using headspace analysis, and two orders of magnitude lower still using trap and purge techniques [69] which has made it possible to perform tracer studies over large space scales and long time scales. The continuous release was performed to create a quasi-stationary tracer field in the ocean. Wannikhof et al. [68] notes this application adds to the utility of the tracer, which had only previously been used as a tracer of gas exchange processes in the ocean [70] -[72] , lakes [73] [74] , and in rivers [75] ; as a surface water dispersion tracer [76] , as a tag for surface water in Lagrangian studies ([77] -[79] ; and to determine mixing in the deep ocean [80] [81] . Because Wannikhof et al. [68] noted success with the Hollywood tracer in June 2004, a second tracer study of the Boynton outfall was conducted in 2007. The intention was to use these data points to develop a model of the farfield plume to evaluate the potential effects of the outfalls on benthic communities.
The Hollywood outfall is located approximately 2.5 km offshore and approximately 8.5 km south of Port Everglades. The outfall terminates at a depth of approximately 30 m and discharges roughly 46 MGD of treated waste water through a 60 inch diameter armored concrete pipe. A conservative tracer sulfur hexafluoride gas (SF6) was injected via bubbling into the wastewater stream. SF6 was used because it is a good tracer to study point source releases as it has low background levels in the environment. It is nontoxic, stable, and measurable at low concentrations [68] . The injection of SF6 began on June 4, 2004 (10 a.m. EDT) and ended on June 9, 2004 (3 p.m. EDT) as described in Wannikhof et al. [68] .
The ambient current velocity of the ocean during the sampling, data was available from two different locations. One was a current profiler located 5 km downstream of the outfall at 11 m depth. Here, the current was predominantly northward with little vertical shear and with a flow of about 20 cm∙s−1. Another measurement of northward velocity was taken 12 km offshore just north (downstream) of the study region with a flow of 80 cm∙s−1. For the development of this model 20 cm∙s−1 was used. In the offshore, there is no noticeable difference in salinity [82] [83] .
The continuous injection of SF6 into the outfall pipes was performed to create an environment of elevated SF6 concentrations along the predominant flow path of the plume to facilitate tracking of the farfield SF6 levels. The sampling survey of the ocean waters commenced on three days after initial dosing commenced on the Hollywood outfall in a continuous mode using a towed “fish” containing a Seabird Micro Cat C (onductivity)-T (emperature) recorder and submersible water pump and samples as described in Wannikhof et al. [68] . The same basic procedures were used in February 2007 for the second SF6 tracer experiment conducted by NOAA and Florida Atlantic University (FAU).
Garvine [84] suggests that the plumes may be modeled and characterized by using averaged conditions to develop a simpler model as opposed to partial or stochastic differential equations or may be specified only probabilistically. Using this theory, the constituent was assumed effluent be released in steady state to the ocean surface at a rate (M) and at a location (x0, y0, z0) as defined by Huang et al. (1996), where the effects of advection are assumed to be significantly larger than the amount of dispersion in the x direction. Pire-Schmidt et al. [13] used limited data to develop a useful predictive model of an inlet plume, based on the same tracer study methods using the 2007 data. The plume was successfully modeled with a Gaussian plume model that appears to mimic the response. It was noted that the tracer concentrated in a series of boluses that migrated north of the inlet [13] , which is not expected because the inlet pulses with the tidal cycle.
The dispersion coefficients σy and σz are the standard deviations of the horizontal and vertical Gaussian distribution respectively [27] . As such, the dispersion coefficients represent the area under a Gaussian curve that encompasses 68% of the variance present in the distribution. The most common procedure for estimating the dispersion coefficients was introduced by Pasquill [85] and modified by Gifford [86] . In ocean plume modeling, dispersion coefficients are the driving force behind the advection-dispersion equation. This equation can be solved using a finite element method that is forward in time and central in space for dispersion. Using finite elements, the solution of a 2D diffusion equation for an instantaneous point source of mass per unit length M/L released at time t = t0 and location (x, y) = (xo, yo) in an unbounded domain is:
 (1)
(1)
The value of σy and σz are based on units of (m2∙s−1). Equation (1) can be used to predict the concentration at a distance x, y, and z away from the point source given all parameters. Finding these parameters however, is an art of its own requiring professional expertise, mathematical formulation, and computer modeling. Shear and horizontal dispersion as discussed by Okubo [87] -[91] were reviewed, but the conditions did not appear to be replicated for the outfalls. This work will therefore only use the principles of ADE to model the plume equation in the x-z plane. The x-y plane will be modeled using data-fitting software to derive an empirical equation based on the Hollywood outfall data
2.1. Creating the Base Map of Measured Concentrations
Using the same assumptions as Pire-Schmidt et al. [13] , and Pire-Schmidt [12] , the process involved taking the data sets, and mining them for information. As noted during the 2007 SF6 event [13] two sources of bias exist in the sample data: the SF6 adhering to sampling hardware on eastward (outbound) sampling tracks which results in artificially increased SF6 concentrations on eastward tracks and reflection of the SF6 pollutant from the southeast Florida coast which lies to the west of the outfall location. Pire-Schmidt [12] outlined how this bias was addressed, but generally the following assumptions were used:
• The SF6 adherence issue biases maximum SF6 concentrations towards the east.
• The coastal reflection issue biases maximum SF6 concentrations towards the west.
• The biases are generally of equal magnitude.
• Rotating east-biased sample points westward and west-biased sample points eastward will sufficiently remove biases.
• A coordinate of the centerline of the SF6 tracer plume in the Hollywood outfall experiment is generally located at the point of highest concentration along a given latitude (after sample points are bias-corrected).
• The centerline of the SF6 tracer plume in the Hollywood outfall experiment has its origin (passes through) the actual Hollywood outfall location (i.e. the origin of the Hollywood tracer centerline is not significantly affected by the hydrodynamic phenomena at Port Everglades).
• Beyond 13 kilometers north of the Hollywood outfall origin, the tracer plume is completely mixed in the water column.
2.2. Spatial Mapping of Experimental Data
The primary tool for generating spatial interpolation maps was ESRI Arc Map v.10.0 software using its Geostatistical Analyst Tool. Data sets originally provided in a spreadsheet form were imported as points into the ArcMap software environment. Spatial data sets were also projected to the NAD 1983 HARN State Plane Florida East FIPS 0901 coordinate system.
To map the SF6 concentrations, the Kernel Smoothing interpolation with barriers method under the ArcMap Geostatistical Analyst tool was used. The Kernel Smoothing method is a variant of a first-order local polynomial interpolation [92] [93] and allows for the incorporation of barrier features (i.e. the Florida coastline) into the interpolation. This interpolation method was selected as results appeared to capture the theoretical north-south anisotropy of the tracer plume better than other available interpolation methods. The biases noted above were corrected by separated the incoming (west biased) and outgoing (east biased) data sets and rotating them through a common origin. Initial interpolation algorithms were applied to the rotated concentration data using Inverse Distance Weighting (IDW) and Kriging, with Kriging being the most typically used algorithm for plume modeling as determined during the literature review. The predictions created by the IDW algorithms produced results that when viewed using a dozen classifications bins highly indicated the presence of the tent pole effect around the data points Kernel smoothing was the applied to achieve the best Root Square Mean Error (RSME).
To map the seafloor depths in the Hollywood outfall study area, the Ordinary Kriging interpolation under the ArcMap Geostatistical Analyst tool was used. Bathymetry is an important factor due to the reflection caused by the seabed. After the generation of interpolation maps for SF6 concentrations and seafloor depths in the Hollywood region, results were exported to a rectangular grid of 2368 data points, covering an area of approximately 8.5 × 108 square meters that reflected the actual data gathered during the experiment.
2.3. Creating a Model
Data on current velocity was gathered from bottom instruments. Coastal inlets also were investigated to see if tidal periods had an effect on determining the centerline equation from interpolation. The reason why inlets are of concern is that during tidal periods large quantities of water are channeled through the inlet as a gradient change. Specifically the velocity component of the tide is of concern to this project. The underlying assumption is that advection which is driven by velocity will cause the spread of the tracer in the direction of the velocity. When considering South Florida, the initial velocity travels parallel to the coast in a northern direction. When peak tide periods are present the possibility of an additional velocity component acting transversely to primary advection current can significantly alter the direction of the centerline plume. To determine if tidal influence could be an influencing factor on the centerline and concentrations an evaluation of the location of test sites to proximity of inlets were made.
2.4. Model in the X-Plane
As noted above, it was suggested that under perfect conditions, the behavior of the plume is such that it can be characterized as having a Gaussian distribution in respect to its longitudinal axis with the highest peak at the centerline, while exponentially decaying along that same axis. The first step was to develop the centerline, taking into account the reflection is caused by the plume being trapped at the surface, hitting the shallow ground and/or the westbound coast and reflecting off those surfaces creating a higher concentration than what is actually present. The highest concentrations were mapped by the latitude and longitude. Ultimately, the coastline reflection effect was handled by deleting the westbound samples, and assuming that the concentration west of the centerline (towards the shoreline) would have a concentration equal to or greater than that of the centerline for the same reasons as outlined in Pire-Schmidt [12] and Pire-Schmidt et al. [13] . This implies that the effects of the reflection sources are proportional to depth; hence, depth is a parameter in the model. To determine the magnitude of the effects due to image sources, one can simply reflect the left side of the Gaussian distribution to generate a graph that would exponentially increase the concentration at shallower depths.
2.5. X-Y Plane
Conceptually, the concentrations in the x-y plane were found by modifying the “ideal” plume to account for the different factors that alter the dispersion/diffusion of it. In practice, concentrations were found by calculating the concentration, using the data-fitting modeling software Eureqa v.0.95 at each grid point given the depth and the centerline concentration associated with the grid point. The Eureqa v.0.95 application was developed by the Cornell Creative Machines Lab [94] as a tool that searches mathematical relationships between input and output variables. Assumptions used for modeling purposes were as follows:
• The initial dilution S, is the dilution (So) found at the end of the near-field regime (Lb), which is assumed to be 40:1 based prior modeling using and average current speed of 0.2 m/s.
• The average current velocity ua, was 20 cm/s or 0.2 m/s (based on estimated, average, current meter data).
• Vertical diffusion has minimal affect on the plume until the plume and ambient waters are nearly identical, and therefore can be ignored in the initial phases of the farfield. For purposes on the analysis this will be assumed to occur when S >100:1 and beyond 13 km from the outfall discharge point.
• Initial plume thickness remains a thickness of 0.3 of the total depth for some undefined distance (<13 km), but becomes a complete mix system after that point.
• Results of SEFLOE II are used where applicable.
The actual data points were used in Eureqa. Identification of a mathematical relationship between these variables assisted with the characterization of pollutant plume dispersion in the lateral (east-west) direction without the need for determining horizontal dispersion coefficients directly. The relationship search was simplified by allowing seafloor depth to serve as a surrogate for east-west distance of a point from the Florida coast, based on the high positive correlation between the shallowness of seafloor depth and nearness to the southeast Florida coast. The ideal equation minimizes complexity while still exhibiting optimal performance in various statistical error and correlation measures, which obfuscates the need to determine the exact relationship between a variable and the system. The concentration at a point (x,y) on the grid changed by Cx,y – Cxo,yo regardless of the mechanism.
2.6. X-Z Plane
Evaluating the x-z plane of the outfall plume requires information about the general behavior of an effluent under buoyancy-dominated conditions. At the outfall pipe, the jet stream will bend upwards within a short distance from the outlet due to the difference in buoyancy between the effluent and the surrounding environment. Once it hits the surface, the plume is advected with the ambient velocity field at the speed u of the surface plume layer [21] . The subsequent dilution/dispersion of outfall plumes is essentially governed by buoyant spreading and oceanic turbulent diffusion. Results from the SEFLOE field tests indicated that the dilution/dispersion of the Hollywood outfall plume was dominated by buoyant spreading over a range of several hundred meters from the outfall [20] [21] . It is also known that the plume will continue to spread in 2D in the x-z plane until it is fully mixed along its water column. Based on cast data during the 2007 experiment, 13 km downstream of the outfall the water column appears to be completely mixed. Since the concentration at 13 km is known at the centerline (y = 0), the z-dispersion coefficient can be back calculated.
3. Results and Discussion
3.1. Hollywood Model
The centerline model was developed as follows based on the data shown in Figure 3:
 (2)
(2)
Figure 3 shows the plot of this equation versus the data points.
Figure 4 shows the Eureqa plot for the equation to describe the horizontal diffusion:

Figure 3. Exponential regression line of CL values for Hollywood outfall.

Figure 4. Predicted vs. observed plot.
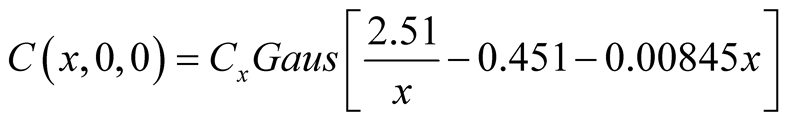 (3)
(3)
Both predicted and observed values of SF6 concentrations were plotted along a 45 degree line to provide a graphical illustration of how the model is performing. A review of the graph indicates that the plotted points generally follow the path of the 45 degree line. This suggests that the model is performing relatively well. More points appear on the left of the 45 degree line which is an indication that the model is slightly overestimating SF6 concentrations.
A line plot was also done for the analysis (see Figure 5). The graph shows how the predicted values (red), matches those of the observed values (blue), indicating a good fit.
The software program MATLAB was used to generate a boxplot of the residual errors (see Figure 6). The plot showed four (4) points which could be considered as outliers. Removing these 4 points reduces the RSME value from 27.77 to 13.13 and the MAE value from 17.08 to 10.70. The statistical performance measures asso-
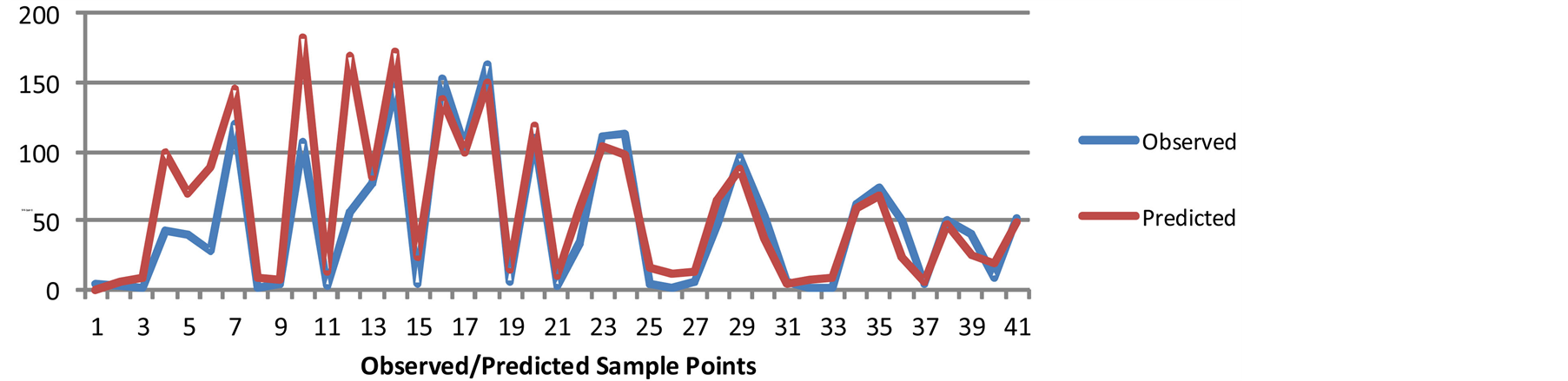
Figure 5. Line plot of predicted and observed values for Hollywood outfall.
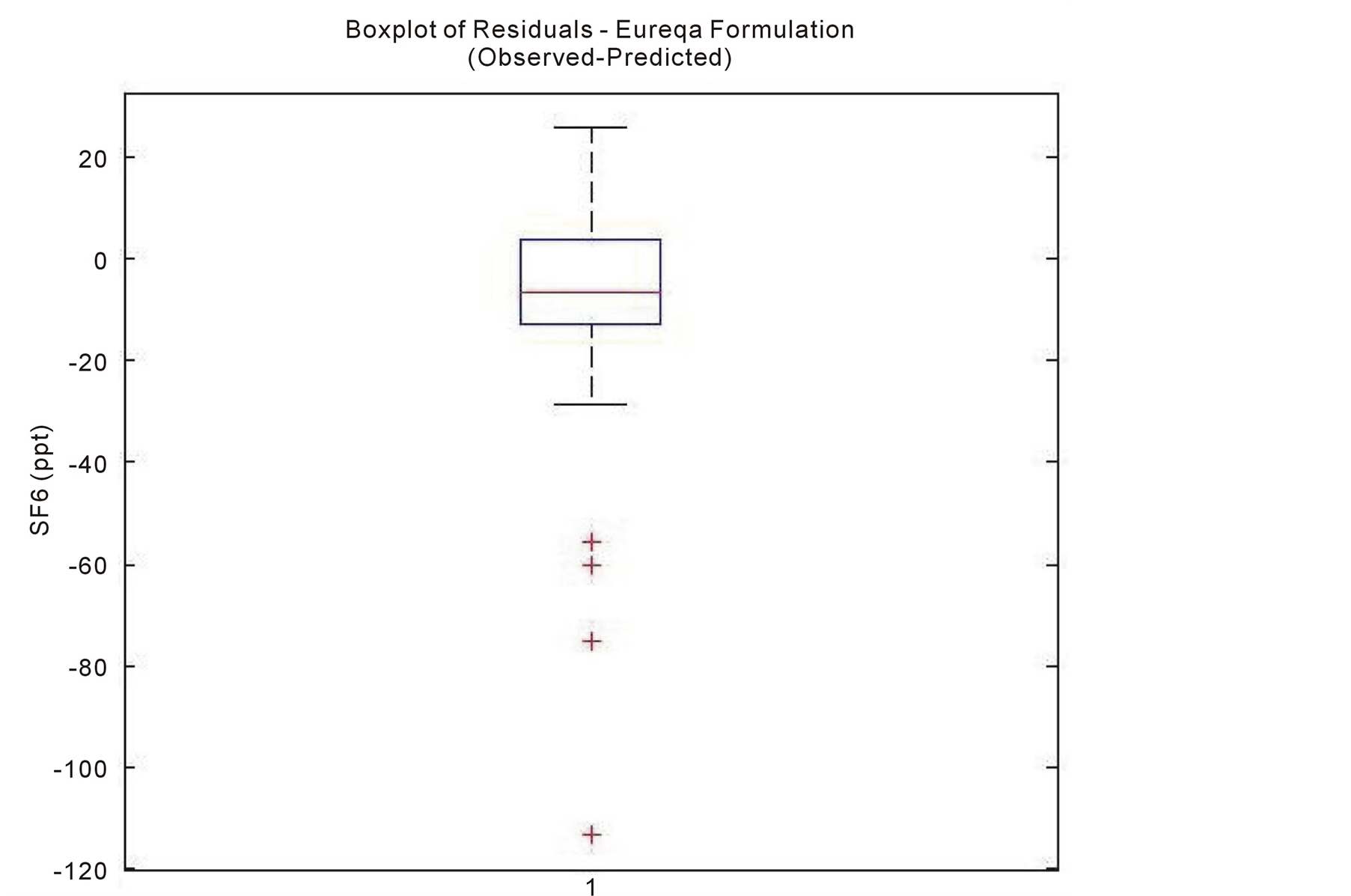
Figure 6. Boxplot of residuals.
ciated with this formulation are presented in Table2
3.2. X-Z Plane
Using the fact that based on the Hollywood cast samples, at 13 kilometers north of the Hollywood outfall the ocean plume the SF6 had completely mixed along the water column, the dispersion coefficient in the z direction was back calculated. Additionally, the concentration values at the centerline were plotted against distance and an exponential regression line of best fit was drawn. A trial and error method was employed to find the dispersion coefficient in the z direction because it was known that at 13 km, the ocean plume was completely mixed in the water column. These centerline concentrations were the inputs to obtain the following expression for the x-z plane:
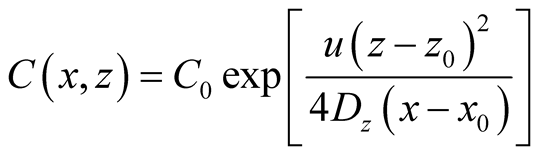 (4)
(4)
Figure 7 shows a comparison of the SF6 concentrations from the Hollywood outfall plume obtained using two

Figure 7. Kernal data smoothing vs. mathematical relationship.
different methods: the Kernel Smoothing method and the mathematical model. Both tend to follow the same pattern as far as surface concentration distribution is concerned. Additionally, the magnitudes of the concentrations seem to be consistent with one another. The mathematical model however displays series of boluses that appear along the longitudinal axis with decreasing magnitude. It is uncertain what the cause to these boluses but they may be caused by the different depths present at the ocean bed since the Kriging method does not take depth into account when formulating its graph. The stars represent the location of the ocean outfall.
An error analysis was performed for the calculation of the concentration plume for the Hollywood outfall in the x and y directions. No error analysis was done for the z direction due to limited sampled data points. A grid system was used for comparison. Table 3 summarizes how the model correlates to the raw data points.
Table 3. Summary statistics for model: Hollywood model (Eureqa) error analysis.
4. Conclusions
The objective of the plume modeling study was to 1) determine if a farfield tracer could used for data gathering and 2 ) if that data would permit modeling and calibration of a farfield, coastal ocean plume that adequately describes the advection and dispersion of a near-coastal conservative pollutant plume in the southeast Florida region. The following are the conclusions that can be gleaned from the experiment:
1) SF6 can successfully be used for monitoring terrestrial discharges to the coastal ocean in the farfield. The tracer captured data ≈ 10 to 60 km downstream.
2) From 20 to 60 km northward of the outfall maximum concentrations decreased less than twofold.
3) To track the far, farfield, the SF6 that may be required may overwhelm detection instruments in the nearfield.
4) Complete mix of terrestrial discharges occur less than 13 km downstream of the discharge terminus.
5) Terrestrial activities such as the port is a complicating factor for coastal ocean discharges, especially if they are less than 13 km from the terminus as their impact on complete mixing is unclear.
The development of the plume model in this study used data gathered from the experiment conducted by Wanninkh of et al. [68] on the Hollywood outfall as well as data other NOAA operations [83] [95] .
The results of the modeling showed that the data could be translated into a model. The magnitudes of the concentrations seem to be consistent with one another. The error analysis performed on the Hollywood model (Eureqa method) indicated that the model is performing exceptionally well for that region. Four performance measures were used to evaluate the model; Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Absolute Error (AE) and Correlation Coefficient (ρ). An analysis was also done of the gamma-curve method using the same procedures. The models showed a slight inclination towards overestimating the SF6 concentrations.
There were several issues that were discovered through the experiment that need to be dealt with in the future. A complicating factor was Port Everglades. The tidal considerations create the potential for the change from a continuous flow stream to become a pulsed stream as a result of SF6 moving to the port during incoming tides. Hence the boluses. No samples were taken to identify the variation in SF6 in the port, but a repeated experiment should be undertaken to study this issue.
The impact of trapping as a result of the Florida Current being east of the outfall discharge, differential current velocities below the plume and the complete mix assumptions. A predictive Bayesian exercise would appear to be worthwhile.
Finally wind is an issue not addressed during the experiment. The wind was shoreward. As a result, the off-gassing SF6 could have been reincorporated into the surface waves, creating a false footprint of the plume, which is one reason the west side of the data was ignored. Hence the SF6 should not be used as the only tracer in future studies intended to trace a specific point source.
Varying physical conditions in the ocean mean that the experiments should be repeated to demonstrate veracity and robustness of the model. A future experiment, under different current speeds is suggested. However if such an experiment is conducted, the following should be addressed:
1) For quantitative interpretation, current (ADCP) measurements and wind data must be collected in conjunction with the SF6 injection to determine the coastal current conditions.
2) A second, conservative, non-gaseous tracer should be included along with the SF6 to get an additional confirmation of the nutrient sources.
3) Reconnaissance of discharge pipelines should be undertaken to insure that there are no leaks and that appurtenances do not leak SF6 gas.
4) Background information on significant current regime disruptors, like Port Everglades, should be gathered and characterized along with other discharges.
One major finding was that dilution in the farfield (60 km) was extensive (greater than 10,000:1), and within 5 km was well over 1000:1. Therefore the outfalls are unlikely to be a major source of contaminants to the coast ecosystem. As a result, the bill passed by Florida Legislature to cease outfall operations by 2025 is unlikely to cause any significant change in the nutrient impacts in the coastal environment. However despite the modification of the deadline, the cost to the residents of SE Florida are considerable, as are the new energy demands.
References
- Bloetscher, F. and Muniz, A. (2012) Where Is the Power to Treat All the Water? Potential Utility Driven Solutions to the Coming Power-Water Conflict. Florida Water Resource Journal, 64, 32-46.
- Johns, G., Leeworthy, V.R., Bell, F.W. and Bonn, M.A. (2003) Socioeconomic Study of Reefs in Southeast Florida. Final Report. Hazen and Sawyer, Hollywood.
- Lapointe, B.E. and Bedford, B.J. (2010) Ecology and Nutrition of Invasive Caulerpa brachypus f. parvifolia blOoms on Coral Reefs off Southeast Florida, USA. Harmful Algae, 9, 1-12. http://dx.doi.org/10.1016/j.hal.2009.06.001
- Lapointe, B.E. (1997) Nutrient Thresholds for Bottom-Up Control of Macroalgal Blooms on Coral Reefs in Jamaica and Southeast Florida. Limnol. Oceanogr, 42, 1119-1131. http://dx.doi.org/10.4319/lo.1997.42.5_part_2.1119
- Lapointe, B.E., Barile, P.J., Littler, M.M., Littler, D.S., Bedford, B.J. and Gasque, C. (2005) Macroalgal Blooms on Southeast Florida Coral Reefs. I. Nutrient Stoichiometry of the Invasive Green Alga Codium isthmocladum in the Wider Caribbean Indicates Nutrient Enrichment. Harmful Algae, 4, 1092-1105. http://dx.doi.org/10.1016/j.hal.2005.06.004
- LaPointe, B.E., Barile, P.J., Littler, M.M. and Littler, D.S. (2005) Macroalgal Blooms on Southeast Florida Coral Reefs II. Cross-shelf Discrimination of Nitrogen Sources Indicates Widespread Assimilation of Sewage Nitrogen. Harmful Algae, 4, 1106-1122. http://dx.doi.org/10.1016/j.hal.2005.06.002
- Paul, V.J., Thacker, R., Banks, K. and Golubic, S. (2005) Benthic Cyanobacterial Bloom Impacts on the Reefs of South Florida (Broward County, USA). Coral Reefs, 24, 693-697. http://dx.doi.org/10.1007/s00338-005-0061-x
- Banks, K.W., Riegl, B.M., Shinn, E.A., Piller, W.E. and Dodge, R.E. (2007) Geomorphology of the Southeast Florida Continental Reef Track (Miami-Dade, Broward, and Palm Beach Counties, USA). Coral Reefs, 26, 617-633. http://dx.doi.org/10.1007/s00338-007-0231-0
- Lapointe B.E. and Bedford, B.J. (2010) Ecology and Nutrition of Invasive Caulerpa brachypus f. parvifolia Blooms on Coral Reefs off Southeast Florida, USA. Harmful Algae, 9, 1-12. http://dx.doi.org/10.1016/j.hal.2009.06.001
- Zhang, J-Z., Kelble, C.R., Fischer, C.J. and Moore, L. (2008) Hurricane Katrina Induced Nutrient Runoff from an Agricultural Area to Coastal Waters in Biscayne Bay, Florida. Estuarine, Coastal and Shelf Science, 84, 209-218. http://www.sciencedirect.com/science/article/pii/S0272771409002960
- Collier, C., Ruzicka, R., Banks, K., Barbieri, L., Beal, J., Bingham, D., Bohnsack, J., Brooke, S., Nancy, C., Dodge, R., Fisher, L., Gadbois, N., Gilliam, D., Gregg, L., Kellison, T. and Kosmynin, V. (2008) The State of Coral Reef Ecosystems of Southeast Florida. In The State If Coral Reef Ecosystems of the United States and Pacific Freely Associated States: 2008. NOAA. http://ccmaserver.nos.noaa.gov/ecosystems/coralreef/coral2008/welcome.html
- Pire-Schmidt, J., Bloetscher, F., Meeroff, D.M., Carsey, T., Stamates, J., Sullivan, K. and Proni, J.R. (2012) Farfield Modeling of the Boynton Inlet Plume. Environmental Management and Sustainable Development, 1, 74-89.
- Pire-Schmidt, J. (2009) Farfield Modeling of the Boynton Inlet Plume Using Sulfur Hexafluoride as Tracer. A Thesis Submitted to the Faculty of the College of Engineering and Computer Science in Partial Fulfillment of the Requirements for the Degree of Master of Science, Florida Atlantic University, Boca Raton.
- Carsey, T., Stamates, J., Amornthammarong, N., Bishop, J., Bloetscher, F., Brown, C., Craynock, J., Cummings, S., Dammann, P., Davis, J., Featherstone, C., Fischer, C., Goodwin, K., Meeroff, D., Proni, J.R., Sinigalliano, C., Swart, P. and Zhang, J-Z. (2012) Boynton Inlet 48 Hou Sampling Intensives: June and September, 2007. Ocean Chemistry Division, Atlantic Oceanographic and Meteorological Laboratory, Miami.
- Carsey, T., Casanova, H., Drayer, C., Featherstone, C., Fischer, C., Goodwin, K., Proni, J.R., Saied, A., Sinigalliano, C., Stamates, J., Swart, P. and Zhang, J.Z. (2010) FACE Outfalls Survey Cruise—October 6-19, 2006, NOAA Technical Report, OAR AOML-38. AOML, Miami.
- Stamates, S.J. (2013) Boynton Inlet Flow Measurement Study. NOAA Technical Report, OAR-AOML-43, 13 p.
- Fergen, R.E., Davis, P.A. and Bloetscher, F. (2004) Ammonia Dynamics on the Ocean Environment. Florida Water Resource Journal, 56, 33-36.
- Bloetscher, F., Meeroff, D.E. and Plummer, J.D. (2010) Environmental Reviews and Case Studies: Evaluation of Costal Ocean Discharges, Environmental Impacts, and Regional Solutions in Southeast Florida. Environmental Practice, 12, 285-303. http://dx.doi.org/10.1017/S1466046610000360
- Bloetscher, F. and Meeroff, D.E. (Florida Atlantic University) (2007) Boynton Inlet Sampling Event; NOAA Dye Study Coordination. FAU, Boca Raton.
- Hazen, S. (1994) SEFLOE II Final Report: Broward County Office of Environmental Services North Regional Wastewater Treatment Plant, City of Hollywood Utilities Department Southern Region Wastewater Treatment Plant, Miami-Dade Water and Sewer Department North District Wastewater Treatment Plant, Miami-Date Water and Sewer Department Central District Wastewater Treatment Plant. Hollywood. Submitted to National Oceanic and Atmospheric Administration.
- Huang, H., Proni, J.R. and Tsai, J.J. (1994) Probabilistic Approach to Initial Dilution of Ocean Outfalls. Water Environment Research, 66, 787-793.
- Huang, H., Fergen, R.E., Proni, J.R. and Tsai, J.J. (1998) Initial Dilution Equations for Buoyancy-Dominated Jets in Currents. Journal of Hydraulic Engineering, 124, 105-108. http://dx.doi.org/10.1061/(ASCE)0733-9429(1998)124:1(105)
- Richardson, L.F. (1926) Atmospheric Diffusion Shown on a Distance-Neighbor Graph. Proceedings of the Royal Society A, 110, 709-737. http://dx.doi.org/10.1098/rspa.1926.0043
- Proni, J., Adler, M., Amornthammarong, N., Bishop, J., Bloetscher, F., Carsey, T., Craynock, J., Cummings, S., Dammann, P., Drayer, C., Featherstone, C., Goodwin, K., Meeroff, D., Peltola, E., Pierrot, D., Sinigalliano, C., Swart, P., Stamates, J., Sullivan, K., Wanninkhof, R. and Zhang, J.Z. (2011) Final Report: An Investigation of the South Central Regional Wastewater Treatment Plan Ocean Outfall and Coastal Environment. Ocean Chemistry Division, Atlantic Oceanographic and Meteorological Laboratory, Miami, 58 p.
- Chin, D.A. (2000) Water Resources Engineering. Prentice-Hall, Upper Saddle River.
- Koh, R.C.Y. and Brooks, N.H. (1975) Fluid Mechanics of Waste-Water Disposal in the Ocean. Annual Review of Fluid Mechanics, 7, 187-211. http://www.annualreviews.org/aronline
- Lewis, R. (1997) Dispersion in Estuaries and Coastal Water. John Wiley & Sons, New York.
- Hirst, E. (1971) Buoyant Jets Discharged to Quiescent Stratified Ambient. Journal of Geophysical Research, 76, 7375-7384. http://dx.doi.org/10.1029/JC076i030p07375
- Schatzmann, M. (1979) An Integral Model of Plume Rise. Atmospheric Environment, 13, 721-731. http://dx.doi.org/10.1016/0004-6981(79)90202-6
- Delvigne, G.A.L. (1980) Round Buoyant Jet with Three-Dimensional Trajectory in Ambient Flow. Pub. No. 22H, Delft.
- Gu, R. and Stefan, H.G. (1988) Analysis of Turbulent Buoyant Jet in Density-Stratified Water. Journal of Environmental Engineering, 114, 878-897.
- Bemporad, G.A. (1994) Simulation of Round Buoyant Jet in Stratified Flowing Environment. Journal of Hydraulic Engineering, 120, 529-543. http://dx.doi.org/10.1061/(ASCE)0733-9429(1994)120:5(529)
- Chu, V.H. and Lee, J.H.W. (1996) General Integral Formulation of Turbulent Buoyant Jets in Cross-Flow. Journal of Hydraulic Engineering, 122, 27-34. http://dx.doi.org/10.1061/(ASCE)0733-9429(1996)122:1(27)
- Frick, W.E. (1984) Non-Empirical Closure of the Plume Equations. Atmospheric Environment, 18, 653-662.http://dx.doi.org/10.1016/0004-6981(84)90252-X
- Lee, J.H.W. and Cheung, V. (1990) Generalized Lagrangian Model for Buoyant Jets in Current. Journal of Environmental Engineering, 116, 1085-1105. http://dx.doi.org/10.1061/(ASCE)0733-9372(1990)116:6(1085)
- Frick, W.E., Baumgartner, D.J. and Fox, C.G. (1994) Improved Prediction of Bending Plumes. Journal of Hydraulic Research, 32, 935-950.
- Grace, R.A. (2005) Marine Outfall Performance. I: Introduction and Flow Restoration. Journal of Performance of Constructed Facilities, 19,347-358.
- Carvalho, J.L.B., Feitosa, R.C., Rosman, P.C.C. and Roberts, P.J.W. (2004) Bacterial Decay Model for Coastal Outfall Plumes. Journal of Coastal Research, 1524-1528.
- Economopoulou, M.A. and Economopoulos, A.P. (2001) Graphical Sizing and Analysis of Ocean Outfalls with Buoyant Plumes. Journal of Environmental Engineering, 127, 3-12.http://dx.doi.org/10.1061/(ASCE)0733-9372(2001)127:1(3)
- Economopoulou, M.A., Economopoulos, A.A. and Economopoulos, A.P. (2003) Sensitivity Analysis and Comparative Performance of Outfalls with Single Buoyant Plumes. Journal of Environmental Engineering, 129, 168-178.
- Cheung, S.K.B., Leung, D.Y.L., Wang, W., Lee, J.H.W. and Cheung, V. (2000) VISJET—A Computer Ocean Outfall Modelling System. 2000 Proceedings of Computer Graphics International, Geneva, 19-24 June 2000, 75-80.
- Bleninger, T. and Jirka, G.H. (2004) Nearand Far-Field Model Coupling Methodology for Wastewater Discharges. In: Lee, J.H.W. and Lam K.L., Eds., Proccedings of 4th International Symposium on Environmental Hydraulics and 14th Congress of Asia and Pacific Division, International Association of Hydraulic Engineering and Research, Hong Kong, China, 15-18 December 2004, . http://outfalls.ifh.uni-karlsruhe.de/download/near-far-field-coupling-final.pdf
- Frick, W.E., Roberts, P.J.W., Davis, L.R., Keyes, J., Baumgartner, D.J. and George, K.P. (2003) Dilution Models for Effluent Discharges, 4th Edition (Visual Plumes), United States National Exposure EPA/600/R-03/025, Environmental Protection Agency Research Laboratory, Research Triangle Park NC 27709.
- Frick, W.E. (2004) Visual Plumes Mixing Zone Modeling Software. Environmental Modeling & Software, 19, 645-654. http://dx.doi.org/10.1016/j.envsoft.2003.08.018
- Lye, L.M. and Sharp, J.J. (2002) Methods of Compliance Evaluation for Ocean Outfall Design and Analysis. Environmental Management, 30, 536-546. http://dx.doi.org/10.1007/s00267-002-2642-6
- Bogle, G.V., Volioulis, I.A. and Meiorin, L. (1993) Estimation of Far-Field Dilution in Ocean Waste Discharges. Journal of Waterway, Port, Coastal, and Ocean Engineering, 119, 15-29. http://dx.doi.org/10.1061/(ASCE)0733-950X(1993)119:1(15)
- Roberts, P. (1999) Modeling Mamala Bay Outfall Plumes. II: Farfield. Journal of Hydraulic Engineering, 125, 574-583. http://dx.doi.org/10.1061/(ASCE)0733-9429(1999)125:6(574)
- Loh, P.C., Fujioka, R.S. and Lau, L.S. (1979) Recovery, Survival and Dissemination of Human Enteric Viruses in Ocean Waters Receiving Sewage in Hawaii. Water, Air, and Soil Pollution, 12, 197-217.
- Lin, J., Xie, L., Pietrafesa, L.J., Ramus, J.S. and Paerl, H.W. (2007) Water Quality Gradients across Albemarle-Pamlico Estuarine System: Seasonal Variations and Model Applications. Journal of Coastal Research, 23, 213-229. http://dx.doi.org/10.2112/05-0507.1
- Elliott, A.H. (1998) Prediction of Illness Risk near Ocean Outfalls Using Frequency Distributions of Bacterial Concentrations. Water Research, 32, 3182-3187.
- Chang, N.B., Yeh, S.C. and Chang, C.H. (2011) Optimal Expansion of a Coastal Wastewater Treatment and Ocean Outfall System under Uncertainty (II): Optimisation Analysis. Civil Engineering and Environmental Systems, 28, 39-59. http://dx.doi.org/10.1080/10286600903243138
- Washburn, L., Stone, S. and MacIntyre, S. (1999) Dispersion of Produced Water in a Coastal Environment and Its Biological Implications. Continental Shelf Research, 19, 57-78. http://dx.doi.org/10.1016/S0278-4343(98)00068-5
- Gray, C.A. (1997) Field Assessment of Numerical Impacts of Coastal Sewage Disposal on Fish Larvae Relative to Natural Variability. Environmental Biology of Fishes, 50, 415-434. http://dx.doi.org/10.1023/A:1007365232465
- Ozgokmen, T.M., Fischer, P.F., Duan, J. and Iliescu, T. (2006) Three-Dimensional Turbulent Bottom Density Currents from a High-Order Nonhydrostatic Spectral Element Model. Journal of Physical Oceanography, 34, 2006-2026.
- Nageswara, S.V. (2006) Identification of Simple Product-Form Plumes Using Networks of Sensors with Random Errors. Computer Science and Mathematics Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831.raons@ornl.gov
- Yapa, P.D. and Li, Z. (1997) Simulation of Oil Spills from Underwater Accidents I: Model Development. Journal of Hydraulic Research, 35, 673-688. http://dx.doi.org/10.1080/00221689709498401
- Koh, R.C.Y. (1982) Initial Sedimentation of Waste Particulates Discharged from Ocean Outfalls. Environmental Science & Technology, 16, 757-763. http://dx.doi.org/10.1021/es00105a006
- Thomassin, B.A., Gourbesville, P., Gout, B. and Arnoux, A. (1998) Impact of Industrial and Urban Sewage Outflows off Tropical High Islands Is an Important Environmental Problem for Many Developing Countries of the Indopacific and Caribbean Regions. OCEANS ’98 Conference Proceedings, 28 September-1 October 1998.
- Frick, W.E., Khangaonkar, T., Sigleo, A.C. and Yang, Z. (2007) Estuarine-Ocean Exchange in a North Pacific Estuary: Comparison of Steady State and Dynamic Models. Estuarine, Coastal and Shelf Science, 74, 1-11.
- Blumberg, A.F. (1993) Modeling Transport Processed in the Coastal Ocean. Journal of Marine Environmental Engineering, 1, 31-52.
- Blumberg, A.F., Ji, Z.G. and Ziegler, C.K. (1996) Modeling Outfall Plume Behavior Using Farfield Circulation Model. Journal of Hydraulic Engineering, 122, 610-616. http://dx.doi.org/10.1061/(ASCE)0733-9429(1996)122:11(610)
- Hunt, C.D., Mansfield, A.D., Mickelson, M.J., Albro, C.S., Geyer, W.R. and Roberts, P.J.W. (2010) Plume Tracking and Dilution of Effluent from the Boston Sewage Outfall. Marine Environmental Research, 70, 150-161. http://dx.doi.org/10.1016/j.marenvres.2010.04.005
- Purnama, A. and Al-Barwani, H.H. (2006) Spreading of Brine Waste Discharges into the Gulf of Oman. Desalination, 195, 26-31.
- Al-Barwani, H.H. and Purnama, A. (2007) Simulating Brine Plumes Discharged into the Seawaters. Desalination, 221, 608-613. http://dx.doi.org/10.1016/j.desal.2007.02.060
- Bleninger, T. and Jirka, G.H. (2008) Modeling and Environmentally Sound Management of Brine Discharges from Desalination Plants. Desalination, 221, 585-597. http://dx.doi.org/10.1016/j.desal.2007.02.059
- Ahmed, M., Shayyab, W.H., Hoey, D. and Al-Handaly, J. (2001) Brine Disposal from Reverse Osmosis Desalination Plants in Oman and the United Arab Emirates. Desalination, 133, 135-147.http://dx.doi.org/10.1016/S0011-9164(01)80004-7
- Jones, B.H., Barnett, A. and Robertson, G.L. (2001) Towed Mapping of the Effluent Plume from a Coastal Ocean Outfall. Proceedings of MTS/IEEE International Conference Oceans 2001, MTS 0-933957-29-7, Biloxi, 5-8 November 2001, 1985-1989.
- Wanninkhof, R., Sullivan, K.F., Dammann, W.P., Proni, J.R., Bloetscher, F., Soloviev, A.V. and Carsey, T. (2005) Farfield Tracing of a Point Source Discharge Plume in the Coastal Ocean Using Sulfur Hexafluoride. Environmental Science Technology, 39, 8883-8890. http://dx.doi.org/10.1021/es048126+
- Wanninkhof, R., Ledwell, J.R. and Watson, A.J. (1991) Analysis of Sulfur Hexafluoride in Seawater. Journal of Geophysical Research: Oceans, 96, 8733-8740. http://dx.doi.org/10.1029/91JC00104
- Wanninkhof, R., Asher, W., Weppernig, R., Chen, H., Schlosser, P., Langdon, C. and Sambrotto, R. (1993) Gas Transfer Experiment on Georges Bank Using Two Volatile Deliberate Tracers. Journal of Geophysical Research: Oceans, 98, 20237-20248. http://dx.doi.org/10.1029/93JC01844
- Nightingale, P.D., Liss, P.S. and Schlosser, P. (2000) Measurements of Air-Sea Gas Transfer during an Open Ocean Algal Bloom. Geophysical Research Letters, 27, 2117-2120. http://dx.doi.org/10.1029/2000GL011541
- Watson, A.J., Upstill-Goddard, R.C. and Liss, P.S. (1991) Air-Sea Exchange in Rough and Stormy Seas Measured by a Dual Tracer Technique. Nature, 349, 145-147. http://dx.doi.org/10.1038/349145a0
- Wanninkhof, R., Ledwell, J.R. and Broecker, W.S. (1985) Gas Exchange-Wind Speed Relationship Measured with Sulfur Hexafluoride on a Lake. Science, 227, 1224-1226. http://dx.doi.org/10.1126/science.227.4691.1224
- Clark, J.F., Schlosser, P., Wanninkhof, R., Simpson, H.J., Schuster, W.S.F. and Ho, D.T. (1995) Gas Transfer Velocities for SF6 and 3He in a Small Pond at Low Wind Speeds. Geophysical Research Letters, 22, 93-96.http://dx.doi.org/10.1029/94GL02410
- Caplow, T., Schlosser, P., Ho, D.T. and Enriquez, R. (2004) Effect of Tides on Solute Flushing from a Strait: Imaging Flow and Transport in the East River with SF6. Environmental Science & Technology, 38, 4562-4571.http://dx.doi.org/10.1021/es035248d
- Ho, D., Schlosser, P. and Caplow, T. (2002) Determination of Longitudinal Dispersion Coefficient and Net Advection in the Tidal Hudson River with a Large-Scale, High Resolution SF6 Tracer Release Experiment. Environmental Science & Technology, 36, 3234-3241.
- Coale, K.H., Johnson, K.S., Chavez, F.P., Buesseler, K.O., Barber, R.T., Brzezinski, M.A., Cochlan, W.P., Millero, F.J., Falkowski, P.G., Bauer, J.E., Wanninkhof, R.H., Kudela, R.M., Altabet, M.A., Hales, B.E., Takahashi, T., Landry, M.R., Bidigare, R.R., Chase, Z., Strutton, P.G., Friederich, G., Gorbunov, M.Y., Lance, V.P., Hilting, A.K., Hiscock, M.R., Demerest, M., Hiscock, W.T., Sullivan, K.A., Tanner, S.J., Gordon, R.M., Hunter, C.L., Elrod, V.A., Fitzwater, S.E., Tozzi, S., Koblizek, M., Roberts, A.E., Herndon, J., Timothy, D., Brown, S.L., Selph, K.E., Sheridan, C.C., Twining, B.S. and Johnson, Z.I. (2004) Southern Ocean Iron Enrichment Experiment: Carbon Cycling in Highand Low-Si Waters. Science, 304, 408-414. http://dx.doi.org/10.1126/science.1089778
- Martin, J.H., Coale, K.H., Johnson, K.S., Fitzwater, S.E., Gordon, R.M., Tanner, S.J., et al. (1994) Testing the Iron Hypothesis in Ecosystems of the Equatorial Pacific Ocean. Nature, 371, 123-129. http://dx.doi.org/10.1038/371123a0
- Jahne, B., Heinz, G. and Dietrich, W. (1987) Measurement of the Diffusion Coefficients of Sparingly Soluble Gases in Water. Journal of Geophysical Research: Oceans, 92, 10767-10776. http://dx.doi.org/10.1029/JC092iC10p10767
- Ledwell, J.R., Watson, A.J. and Law, C.S. (1998) Mixing of a Tracer in the Pycnocline. Journal of Geophysical Research: Oceans, 103, 21499-21529. http://dx.doi.org/10.1029/98JC01738
- Watson, A.J., Messias, M.J., Fogelqvist, E., Van Scoy, K.A., Johannessen, T., Oliver, K.I.C., Stevens, D.P., Rey, F., Tanhua, T., Olsson, K.A., Carse, F., Simonsen, K., Ledwell, J.R., Jansen, E., Cooper, D.J., Kruepke, J.A. and Guilyardi, E. (1999) Mixing and Convection in the Greenland Sea from a Tracer-Release Experiment. Nature, 40, 902-904. http://dx.doi.org/10.1038/44807
- Bloetscher, F. and Meeroff, D.E. (2007) Implications of Nutrients in Coastal Environments. NAEP Conference Proceedings, Orlando.
- Carsey, T., Featherstone, C., Goodwin, K., Sinigalliano, C., Stamates, J., Zhang, J.Z., Proni, J.R., Bishop, J., Brown, C., Adler, M., Blackwelder, P. and Alsayegh, H. (2011) Boynton-Delray Coastal Water Quality Monitoring Program, NOAA Technical Report, OAR AOML-39. Atlantic Oceanographic and Meteorological Laboratory, Miami.
- Garvine, R.W. (1998) Penetration of Buoyant Coastal Discharge onto the Continental Shelf: A Numerical Model Experiment. Journal of Physical Oceanography, 29, 1892-1909.
- Pasquill, F. (1961) The Estimation of the Dispersion of Windborne Material. Meteorological Magazin, 90, 33-49.
- Gifford Jr., F.A. (1961) Use of Routine Observations for Estimating Atmospheric Dispersion. Nuclear Safety, 2, 47-57.
- Okubo, A. (1969) Ocean Mixing. Management Information Services, Detroit.
- Okubo, A. (1971) Ocean Diffusion Diagrams. Deep-Sea Research, 18, 789-802
- Okubo, A. and Karweit, M. (1964) Diffusion from a Continuous Source in a Uniform Shear Flow. Limnology and Oceanography, 14, 514-520. http://dx.doi.org/10.4319/lo.1969.14.4.0514
- Okubo, A. (1966) A Note on Horizontal Diffusion from an Instantaneous Source in a Nonuniform Flow. Journal of the Oceanographical Society of Japan, 22, 35-40.
- Okubo, A. (1968) Some Remarks on the Importance of the “Shear Effect” on Horizontal Diffusion. Journal of the Oceanographical Society of Japan, 24, 60-69
- ESRI (2008) Transcript: Understanding the ArcGIS Desktop Applications: What Is ArcMap? ESRI.
- ESRI (2010) ArcGIS 10 Help. ArcGIS ArcMap Version 10. ESRI.
- Cornell Creative Machine Lab (2012) Eureqa. http://creativemachines.cornell.edu/eureqa
- NOAA: National Oceanographic and Atmospheric Agency (2008) Interim Report South Central Regional Waste Water Treatment Plant. Florida Area Coast Environment (FACE) NOAA-AOML, Miami.
NOTES
![]()
*Corresponding author.



