Creative Education
Vol.08 No.04(2017), Article ID:75783,20 pages
10.4236/ce.2017.84047
Mathematics in the Initial Years of Fundamental Teaching in Brazil: An Experience with Teachers in Training in the Pedagogy Course
Raimundo Luna Neres1,2, Eliziane Rocha Castro3, José Carlos Miguel4
¹CEUMA University-UNICEUMA, São Luís, MA, Brazil
2Graduate Program in Basic Education Teaching Management-UFMA, São Luís, MA, Brazil
3Public Teaching Network, MA, Brazil
4Department of Didactics, Postgraduate Education Program, UNESP, Marilia, SP, Brazil
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 20, 2017; Accepted: April 23, 2017; Published: April 28, 2017
ABSTRACT
This article presents the research carried out with a focus on didactic-peda- gogical experience developed on the four fundamental operations of Arithmetic with contribution in Duval’s Theory of Semiotic Representation Registers. Mackinder Box was used as didactic material and records of semiotic representation in natural, numerical and geometric languages. This is a qualitative research carried out with students of Pedagogy course, from a Public University of Fortaleza, CE, Brazil, with the purpose of analyzing the appropriation of the didactic-pedagogical use of the Mackinder Box and the semiotic representations in the operationalization of the Four operations by these students. The investigation revealed that the students learned the methodological use of the Mackinder box in the application of the fundamental operations and recognized that the methodology used allows using different strategies of resolution for the same mathematical activity. However, the research also showed that students had difficulty working with the conversion between records of semiotic representation.
Keywords:
Mathematics Teaching, Arithmetic Fundamental Operations, Registers of Semiotic Representation, Mackinder Box

1. Introduction
This article discusses the initial formation of the teacher of the initial years of Elementary Education, specifically of the training for the teaching of Mathematics. We assume that such training implies the formal preparation of the pedagogical professional in order to become aware of a set of theoretical and practical knowledge to be used in the classroom. Thus, during the initial formation the teacher should experience formative experiences that serve as support to face the challenges that are present in his day to day in the classes of Mathematics.
In classes, in general, reference is made to theoretical and pedagogical approaches to teaching and learning, such as, for example, interactionist appro- aches, which promulgate that in class, the teacher, when guiding the students’ learning process, becomes the Mediator between them and knowledge, thus undertaking actions in a systematic way with a view to achieving the proposed educational objectives. In this direction, it is the knowledge acquired in the initial formation that propitiates the conceptual and didactic competences of the teachers in their pedagogical practices. It seems to be a consensus among the authors (Libaneo, 2010; Mello, 2000; Pimenta, 2005; Rios, 2010) that the initial training focuses on the quality of education, constituting as a guarantee of quality in institutionalized education.
In Brazil, according to Resolution CNE/CP no. 01 of May 15, 2006, of the National Council of Education, the graduates of Pedagogy courses should be able to teach Mathematics (Brazil, 2006) . However, information from Gatti’s research (2010) states that Pedagogy courses do not significantly prepare professionals to act in the initial years of Elementary School, because their knowledge is presented in a fragmented way, with a predominance of descriptive approaches in which theory and practice are dissociated. Gatti (2010) warns that there is little or no deepening regarding the specific contents of subjects that are taught in Basic Education. Generally, these contents are approached sporadically and, in most of the courses, they are treated superficially, evidencing the fragility of the pedagogue’s formation for the teaching of mathematics in the initial years.
In general, the teachers of the final years of Elementary School, during the course of graduation specialize in an area of knowledge, in which they intend to practice teaching. However, according to (Gatti, 2010; Libaneo, 2010) , with teachers of the initial years, graduated in Pedagogy, this does not happen, because they are trained to work with the different knowledge and methodologies of the different disciplines that make up this level of education.
Based on these assumptions, the aim of the research was to analyze the appropriation of the didactic-pedagogical process inherent to the use of the Mackinder box by undergraduates of the Pedagogy Course with a view to the constitution of elementary arithmetic operations, as well as the pedagogical implications for the development of the registers of semiotic representation in natural languages, numerical and geometric.
2. Theoretical and Methodological Bases
The research1 addressed in this article focused on the formation of pedagogues for the teaching of Mathematics with respect to the learning of concepts mediated by the didactic pedagogical use of the didactic material Mackinder box with theoretical contribution in the registers of semiotic representation of Duval. It is a qualitative research with pedagogical didactic intervention in mathematics classes of a Pedagogy course. The research information consists of both the written records of the students who participated and those of the researchers who did the didactic intervention.
The methodology consisted of experiencing in the classroom how the appropriation and abilities of the students would occur when performing the addition, subtraction, multiplication and division operations using the Mackinder2 box, as well as the use of semiotic representation registers. The data of this observation were recorded in logbook for later analysis.
Thus, the context of the research consisted of a didactic process3 in which the teaching decisions were problematized and began to provide theoretical and methodological knowledge to the students of a course of Pedagogy in what concerns the teaching of the fundamental operations of Arithmetic with contribution In the Theory of Semiotic Representation Registers.
Duval (2007) argues that one cannot have understanding in Mathematics if one does not distinguish an object from its representation. For this author it is essential that the student does not confuse mathematical objects, such as numbers, with their representations, since the same mathematical object can be re- presented through different registers. The various semiotic representations used in fundamental operations, according to Duval (2009) , are necessary for the development of mathematical learning. The possibility of working with a variety of registers of mathematical objects depends directly on the semiotic representation system used.
Duval (2007: pp. 11-33) states that when mathematical operations are perfor- med in the very record by which they were enunciated, it is “Record Process- ing.” For example, calculate the value of the numeric expression. And the Con- version it defines as being the transformation of a representation record into another record, and must retain all or only part of the given record as a starting point. As for example, to represent through a graph the information: Joseph has four marbles, won five of his aunt, played with his colleagues and lost two. How many are left?
According to Godino (2007) , we can consider as mathematical object everything that can be indicated, that can be signaled or to which we can refer. For Peirce (2005) , an object is the real representation of a sign, it can be perceptible or only imaginable (abstract), a purely mental or imaginary entity. In this direction, the present research covered the thematic of the teaching method of the specific content of the four fundamental operations of Arithmetic, problematized in the question: How the methodological use of the Mackinder box and of the registers of semiotic representation allow the students’ understanding of Pedagogy related to the concepts Of the four fundamental operations of Arithmetic and a way of teaching them?
The teaching experience considered in the context of the research was carried out in the mathematics discipline of a class of 21 students of the 5th period of the graduation in Pedagogy, in September 2015. The focus on mathematics teaching is justified on the assumption that students of Pedagogy can be considered future teachers of the early years of Elementary School, and consequently teachers of Mathematics.
Thus, the appropriation of the concepts related to the four fundamental operations of Arithmetic and the teaching practices of these concepts is a necessary condition in the initial formation of these future teachers. In this way, it is justified to search as the didactic material the box Mackinder, together with the records of semiotic representation mobilize the learning of the future teachers regarding the fundamental operations of Arithmetic and how to teach them through this material.
We believe that non-appropriation of concepts and relationships in addition, subtraction, multiplication, and division operations will significantly interfere with their professional practices and possibly their students' learning. Although it cannot be guaranteed that these future teachers, when in action in their classrooms, can reproduce the practice mobilized in the research, likewise it cannot be said that a good student will be a good teacher.
On the other hand, when we look at the results of the National Assessment of School Income, Prova Brazil, of the National System of Evaluation of Basic Education, SAEB, published by the National Institute of Educational Studies and Research Anísio Teixeira, INEP, we found that the average proficiency in Mathematics did not evolve in the initial and final years of Elementary School, from 211 points in 2013 to only 219 points in 2015 (DAEP/INEP, 2015) and we have to accept the thesis that teachers, especially in the initial years, are not being well prepared to teach mathematics.
It should be noted that, according to Vergnaud (2008, p. 5), “some students learn, even if poorly taught. But others, even if well taught, fail when the teacher does not master the didactics”. In the task of teaching and promoting learning, according to Ponte, Brocardo and Oliveira (2015: p. 48) , “the teacher must follow the way students develop the activities that guide the teaching and learning process.”
It is a fact that the mastery of these skills by the teachers is not enough for success in school indexes to occur. Other factors challenge the teacher's didactic-pedagogical competence, linked to the teacher’s working conditions: overcrowded classrooms, lacking physical conditions to promote concentration and motivation of the student, students without school meals, poor socioeconomic conditions, lacking in incentive Cultural, among others unfavorable to a psychological disposition to learn.
2.1. The Informational Principle in the Development of Mathematical Activity
As Ponte, Brocardo and Oliveira (2015) , “the active development of the student” is a fundamental condition of learning, that is, the student learns when he mobilizes his cognitive and affective resources in order to reach a goal.
Bruner (1978) considers that mediation allows the teacher to teach certain strategies of solving mathematical activities to his students in order to lead them to the learning that allows them to use them in another situation of teaching. In general, when a student is able to solve a mathematical activity, satisfaction of the achievement may encourage him to seek out new experiences and to enable him to make new discoveries.
The specific problems of understanding that students face in learning math in general.
They have their origin in the particular epistemological situation of mathematical knowledge, and not only in the questions of pedagogical organization of the activities, since the way of access to mathematical objects is radically different from the way of access to the objects of knowledge in other scientific disciplines. Here lies the challenge, and also reason, of mathematics teaching. Therefore, in order for students to effectively understand mathematics or to contribute to their formation, it is necessary to develop another type of cognitive functioning than that practiced in other disciplines. In order to see and teach Mathematics in another way, it is necessary to be aware of the specific cognitive processes required by mathematical thought (Duval, 2011: pp. 8-9) .
We call attention to the fact that the teaching and learning of Mathematics require, according to VALE; PIMENTEL and BARBOSA, (2015), a clear relation between the development of the understanding of the mathematical concepts and the development of the competences in working with daily situations of the student. This practice may become a powerful mechanism for developing more substantive mathematical concepts.
Thus, for the construction of mathematical knowledge between teacher and student, student and student, one must work in the perspective of the student to be the one responsible for the decision making, not only being bound by the rules and models presented in the textbooks, since according to Gontijo (2015) , by providing students with the opportunity to construct their own mathematical models, creativity, flexibility and originality are stimulated.
The Indicators of Achievement of Elementary School students published in recent years, especially the Basic Education Development Index, IDEB (2015) , show the low performance of students in Primary and Secondary Education in Mathematics and also in reading and interpretation. These results point to the imperative of working with conceptions of teaching that mobilize the teacher in the stimulation of students.
For Brousseau (2008) this can be done by selecting mathematical activities (problems, exercises) that propose the desired adaptations that the case requires. These activities should be chosen in such a way that the student agrees to participate, to reflect, and to develop his or her cognitive skills.
For Freitas (2008) the mathematical knowledge for the student is strongly ingrained and influenced by the methodological way in which the contents are taught. The participation of the students involves their involvement with the different learning activities that are presented and taught to them.
We corroborate with the idea that the teacher, in teaching certain solving techniques to his students, through a Mathematical activity, as in this case, aims at these students to apprehend the knowledge and to use them in other types of problems. According to Silver and Smith (2008) , the student needs not only to understand what the technique means, but also to believe that the teacher's suggestions can be useful.
Thus, it is believed that the teaching of the four fundamental operations of Arithmetic using the Mackinder box and the semiotic representation registers is another alternative for the teacher and for the student to develop arithmetic knowledge. According to Duval (2007) , in order to develop an understanding of Mathematics in the initial grades of Elementary School, a cognitive approach is necessary, given that at this level of Mathematics teaching, we seek to develop skills and competences that may contribute to the development of reasoning and analysis skills.
Peirce (2005) defined Semiotics as the task of determining what must be true of the representation used by all scientific intelligence, so that it may incorporate any meaning. Thus, the use of semiotic representations in the study and analysis of resolution of activities involving the fundamental operations of arithmetic is necessary, because of these representations allow easy communication between the various forms of records, besides the possibility of facilitating the treatment of objects Mathematicians In general, the evolution of mathematical learning is associated with the development of new semiotic systems related to those already existing and known to the students.
2.2. Dialogues and Teaching
Professional teaching practice, academic trajectory, and dialogues with Basic Education co-workers are informal, unregistered sources, but they support the view that the Mathematics discipline is marked by pre-conceived discourses that echo and propagate the idea that this discipline is extremely difficult, creating a halo4 effect related to it.
Throughout their professional practices, the teachers who conducted this research witnessed some testimonies of Pedagogy students emphasizing their repulsion for the Mathematics discipline. It is observed that this aversion trans- cends the theoretical training space and is reflected in the practice of some professionals, producing not always satisfactory results in the cognitive development of the students of these teachers and in the perception about the learning of school mathematics. However, this does not characterize a definition, or a norm.
When a professional does not have the skills and competences of a certain subject or theory, in general, he/she abstains from teaching such a concept; At least that’s what is expected of this professional.
In this research the testimonies were also present, because at the time, in September 2015, when the students were asked to introduce themselves to the other students and teachers, the questioning about their impressions about Mathematics was also launched. In this aspect, inspiration, affinity, blockages and traumas were pointed out as part of the life trajectory that composes the relationship of those students with Mathematics, being more frequent the statements emphasizing the repulsion by this discipline.
Walking through the contents of Mathematics is seen as “a terror”5. Their formulas and rules, which for some are frightening, have led us to consider the discipline with a high degree of difficulty and as a consequence “the immediate withdrawal from all that asks for Mathematics” (Danyluk, 1993: p. 289) . Nonetheless, Mathematics, equips human beings for the battles of life in society.
This observation emphasizes the importance of the discipline of Mathematics in Early Childhood Education and Early Years of Primary Education I in the formative flow of the Pedagogy Course, because through this discipline the students had access to a set of theoretical and practical knowledge that serve as support to face the challenges that are present within the classroom and also serve to restructure their didactic-pedagogical knowledge and their perception and appreciation of the Mathematics discipline.
Researches such as Curi (2006) , Barreto (2007) and Nacarato (2010) deal with the different aspects of the mathematical formation of pedagogues, converging to the understanding that there are several obstacles to be faced, which highlights the need to Reflections, discussions and research on teacher education for the teaching of Mathematics in the Early Years of Elementary School.
Directing the look at Mathematics education in the Early Years of Elementary School, space of action of the Pedagogue, one can see that traditionally one confuses the rigor of Mathematics itself with the rigor of its teaching. According to Curi (2006) , this is due to the fragility of the pedagogues about the contents of Mathematics as well as the related didactic and curricular knowledge. The author says: “...it is possible to consider that future teachers complete training courses without knowledge of mathematical contents with which they will work both in terms of concepts and procedures...” (CURI, 2005: p. 69) .
The lack of deepening in the content also compromises relevant aspects since “nobody learns from the one who teaches about what he does not know, because nobody can teach what he does not know”. (Lorenzato, 2006: p. 3) .
It becomes commonplace to label that the pedagogues do not know math; If this is fact, it may be, however, that the guilt in part is not only theirs. Are educators trained to have investigative autonomy in Mathematics? How many degrees are there also forming mathematics teachers without the proper knowledge and autonomy of their practice?
The Bachelor’s Courses need to better prepare future teachers to work in the field of work. Are there sufficient continuing education courses to cater for the range of licensed teachers working in the labor market?
In this sense, the reflection of a fragile formation is observed in the indicators of performance of the national evaluations such as the National Assessment of School Income (ANRESC) also designated (PROVA BRAZIL, 2015), an integral part of the National System for the Evaluation of Basic Education (SAEB, 2015). These performance indicators promote the fight against conformism and disbelief in the face of the problems that beset the Brazilian educational scene, especially in what concerns Mathematics Education.
Thus, it is pointed out the relevance of this research in social scope, in contrast to the evaluations carried out that assess the performance of students focusing on learning, disregarding the didactic process of learning.
The template is used to format your paper and style the text. All margins, column widths, line spaces, and text fonts are prescribed; please do not alter them. You may note peculiarities. For example, the head margin in this template measures proportionately more than is customary.
This measurement and others are deliberate, using specifications that anticipate your paper as one part of the entire journals, and not as an independent document. Please do not revise any of the current designations.
3. Development: The Didactic Process Using the Mackinder Box in the Light of Semiotic Representation Registers
The 21 students, who participated in the mathematics classes, were divided into four working groups, each of them assuming the study of one of the four fundamental operations: addition, subtraction, multiplication and division. The analyzes of the treatments of the numerical representation registers in each operation were made in light of the Theory of Semiotic Representation Registers. The data collected were recorded in the logbook, because if there was any doubt about a group participant in the mathematical operation performed, the process would be repeated until all were appropriated the way to perform each operation. In this way, it would make it easier for the researcher to express opinions about the procedure and about learning, since it could already be verified in loco if the students learned or not to operate with Mackinder’s box the arithmetic operation destined to each group.
It should be noted that Mackinder teaching material was unknown to all students in the 5th period of Pedagogy. This finding was obtained through discussions with the class in the first meeting, September 2015, of the discipline of Mathematics in Early Childhood and Early Years of Elementary School I, when future teachers were invited to list the didactic resources, knowledge of them, used in the teaching and learning of Mathematics in the early years of Elementary School.
It was recorded in the logbook of one of the students of the class who said6: “[...] It would be interesting that we had classes on this subject to know this resource, because it is the first time I see talk about him and what I realized my colleagues too”.
Faced with this fact and in response to the request of the students, who promptly agreed with the student, some classes were planned to reveal the potential of this didactic material and thus to extend the students’ theoretical and methodological knowledge through the use of the Mackinder box.
The research was guided by the articulation between content and didactics, followed by an exploratory approach in the classroom that involved contents, concepts, tasks, debates and analysis of situations inherent to the teaching of the fundamental operations of arithmetic mediated by the use of the Mackinder box, with contribution in the Theory of Semiotic Representation Registers.
According to this theory, the resolution of mathematical activities requires the conversion of at least two registers of representation, i.e.: that the student moves from the text to the writing (numerical and figural) or vice versa of the operation to be performed. According to Damm (2009) , in order to perform the conversion, it is necessary to select, in the enunciation, the data pertinent to the resolution, that is, the numbers indicated, the values that are assigned to them lexically and to organize this data in such a way that the Mathematical operation can Be executed.
Groups were rotated so that all groups worked with the four core operations. We then distributed xerocopy texts containing information on how to use the Mackinder box.
The informative material was elaborated from readings and debates around didactic mentioned above. After the distribution of the texts, there was a time for discussion among the members of the working groups, as well as for them to or- ganize themselves to present their impressions on the material under discussion.
Each group was responsible for presenting to the class an arithmetic operation and its considerations on the Mackinder box.
We work several activities involving the fundamental operations of Arithmetic using the Mackinder box; here are some of these activities.
As Table 1, in the proposed activities it was required that students from each group initially make the conversion of the given record into natural language for the numerical record and then carry out the processing operations of the records obtained through the use of the Mackinder box.
This activity is shown in Figure 1, in which we illustrate, in the Mackinder box, the addition operation: 4 + 6 =? For the work with the addition operation, we initially use the small boxes, placing in each of them the quantity of tokens stated in each parcel.
Then you begin by withdrawing and counting the chips from one of the small boxes, placing them in the large box. When you finish the chips of the first box, continue to remove the chips from the second small box, and continue counting the chips, always putting them in the big box; After the withdrawal of all the to-
Table 1. Activity 1.
Source: Researchers archive.
Figure 1. Representation of addition operation. Source: Researchers archive.
kens from the two small boxes, the total number of tokens placed in the large box is counted, which will be the result of the sum of the parcels (of the two small boxes). This is the result of addition.
There are other ways of adding numbers, in ancient times the way the addition was conceptualized still remains undefined, for until more recent times few written records were written describing the process. According to Wall (2014) , much of what we know about the first practices of addition comes from speculations for the use of the first calculating devices and the analysis of historical financial accounts.
Addition from a developmental perspective goes from counting to addition in a kind of natural progression. In this direction the children most often go from counting a set of blocks to counting two sets of blocks, physically forming the union of sets, according to Wall (2014) , combining, counting “one, two, three, four, five, six , seven eight nine”.
As they become more comfortable with the notion of cardinality, that is, when they can understand that the last number counted within a set is the total number of objects in that set, children then begin to include a quantity in the other, and can continue counting a new set of objects. For Cardoso (2007) , cardinality means the number of elements in a set. As expressed in Table 2, we also worked with students to use the Mackinder box in open-ended addition problems such as:
Based on the Theory of Semiotic Records students are required to convert the natural language record to the numerical record, and then treat that record as constructed. It is observed that several combinations can be made with the hypotheses given in the statement of the problem to arrive at the result.
All groups showed insecurity to work with this type of problem and realized that in this case the Mackinder box is limited to carry out such operations. However, after discussions of the construction of some answers, the students observed that they could construct several answers to the same problem, and this sharpened them enough to think mathematically.
3.1. Using the Mackinder Box in the Subtraction Operation
By involving the subtraction operation using the Mackinder box, we also work on various activities. Among them, we highlight Table 3. Here’s one of these activities, performed in a 50-minute class with prospective teachers.
In the case of the subtraction operation, the inverse of the addition occurs. The large carton is first used, placing in it tokens corresponding to the amount indicated by the minuend; then some reference is made to the quantity of the sub-path (in this specific example, the number of tokens corresponding to the sub-path has been circulated).
Then, the chips indicated by the subtracting are removed from the big box, one at a time, placing them in a small box. After you have removed all the chips corresponding to the subtracting, what is left in the large box corresponds to the result of the subtraction, which can be checked by counting the remaining chips in the large box. In Figure 2 we present the subtraction operation: 10 − 6 =?
As with the addition, according to Wall (2014) , the first practices of subtraction come from speculations on the use of the first calculation devices and analysis of historical judicial and financial accounts. We also worked on the possibility of using the Mackinder box in subtraction problems, using the algebraic/nu- meric register to convert it into natural language as described below as Table 4.
Table 2. Activity 2.
Source: Researchers archive.
Table 3. Activity 3.
Source: Researchers archive.
In this activity an algebraic/numeric record was given and students were required to convert to a natural language record and through the Mackinder box to perform the necessary operations to find the minuend. This situation is expressed in Figure 3.
This type of activity leads the student to think of subtraction as an inverse addition operation, and contributes to the student's cognitive development.
3.2. Using the Mackinder Box in the Multiplication Operation
We worked several activities that involved multiplication operations, using the Mackinder box. Following is one of these activities developed with students.
Figure 2. Representation of subtraction operation. Source: Researchers archive.
Figure 3. Resolution using the Mackinder Box. Source: Researchers archive.
Table 4. Activity 4.
Source: Researchers archive.
Table 5 express this operation.
With the Mackinder box, the multiplication operation is worked as follows: the multiplicand indicates how many small boxes will be used in the multiplicative process and the multiplier indicates the number of tokens that will be placed in each small box.
In Figure 4, we present the multiplication operation referring to the proposed activity, involving multiplication; the numerical record is given by: 2 × 5 =? In this multiplication it is observed that the multiplicand is equal to 2; therefore, two small boxes will be used to place the chips, and since the multiplier is equal to 5, will be placed 5 chips in each small box.
After the chips are distributed in the small boxes, they are removed and the chips of one of the boxes are counted, placing them in the large box; then the same process of removing the chips from the other box is repeated, also placing it in the large box. Then, count the total of chips that have been placed in the big box; this amount of chips corresponds to the multiplication result, i.e.: ten chips.
Multiplication, in the mathematical sense, is a repeated addition, so the notion probably appeared very early in mankind, according to Wall (2014) , only around 1650 bc, is that methods of multiplication began to appear in the historical record.
3.3. Using the Mackinder Box in the Split Operation
Activities involving the division operation were also worked using the Mackinder box. Following is one of these activities developed with students, as Table 6.
Using the Mackinder box, in the split operation, you enter the amount indicated by the dividend in the large box. The divider indicates how many small boxes will be used. Is the numerical record 11:3 =?
Figure 4. Multiplication operation. Source: Researchers archive.
Table 5. Activity 5.
Source: Researchers archive
Therefore, 11 chips are placed in the large box, and 3 small boxes will be used to distribute the chips in the large box. One chip at a time will be removed from the large box and distributed in each small box so that each small box has the same amount of chips. In this particular example 3 chips are placed in each small box, as can be seen from the Figure 5, and since there are two tokens in the large box, it is concluded that the division is not exact; In addition, it is observed that, because there are two chips remaining in the large box, these two chips represent the rest; So the rest of the 11 by 3 division is 2.
If the division is accurate there will be no tokens left in the big box; therefore, the rest will be zero. If not exact, corresponds to the process shown in Figure 5. When using the Mackinder box, in order to carry out the division operation, one can work on the concept of exact and not exact division.
The division probably has its historical roots from the Papyrus of Rhind, in it was found the problem of dividing; in a developmental perspective, one of the first contexts in which the child finds the division, according to Wall (2014) is in sharing, that is, in the process of distributing various objects, among several people.
We also work with future pedagogues to use the Mackinder’s box in open division problems such as Table 7.
In this activity we had as objectives to make the students to think mathematically and to develop their abilities in the dealing with the operations of division, since the student needed to know and to use with competences the algorithm of Euclides and its properties.
Table 6. Activity 6.
Source: Researchers archive.
Figure 5. Representation of the operation of the division. Source: Researchers archive.
Table 7. Activity 7.
Source: Researchers archive.
The students revealed some difficulties in understanding the proposed mathematical proposition, they knew Euclid’s algorithm, but presented difficulties in using it. They completely denied the use of the Mackinder box because they could not find ways to put the data in the box and solve the problem situation.
4. Analysis of Student Reports
All groups, of addition, subtraction, multiplication and division, have made good use of the conversion of the natural language register to the numerical registers; in the same way in the operations of treatment of the registries constructed through the Mackinder box.
In the treatment of the operations of addition to the student Jacimara7, on behalf of the group of addition, highlighted “[...] this box is interesting because it can be worked with children of different ages, enables the construction of operative thinking from concrete material [...]”. This team considers one of the aspects that gave origin to this material, thought to attend the cognitive development, according to the piagetian stages. In fact, its creator, Jesse Mackinder, when creating the box bearing his name aimed at its application with children from 4 to 8 years of age. Considering the piagetian stages, children between 4 and 8 years of age are in the preoperative stage (2 to 7 years) and beginning of the concrete operative stage (7 to 11 years). In this sense, the placement of the group that the Mackinder box makes possible the construction of operative thinking is theoretically sound.
The students were asked about the importance of binary addition, that is, on the two base that is used as the language of computers. Can addition in base two be made using the Mackinder’s box? Having said nothing, we said that it could be done perfectly, and we exemplified the addition of 15 to 47, in base 10, translated to (1111)2 + (101111)2.
It was also questioned whether with the Mackinder box it was possible to add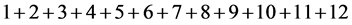 . It was observed that the students did not present a sum equal to what Gauss performed at age seven, as shown in the table below.
. It was observed that the students did not present a sum equal to what Gauss performed at age seven, as shown in the table below.

In a similar way to the placement of the Jacimara student, the Glacimara8 student who presented the subtraction operation on behalf of her group (2015) highlighted: “[...] the box is easy to make. We can see that it can be constructed with different materials, such as: with boxes of matches, disposable cups, and also allows the construction of operative thinking from concrete material, etc. [...]”.
We agree with the addition group on the aspect that the Mackinder box enables the construction of operative thinking, which is theoretically sound. We believe that for children in the preoperative period (2 to 7 years) the use of the Mackinder box will greatly help the teacher and the student in the subtraction learning process.
The group of the multiplication represented by the student Josefa9, emphasized: “...we of the group enjoy the ease that this box gives us when making multiplicative calculations, because it makes visible the multiplication as the sum of equal parcels [...]”, (Sep. 2015). However, there were no comments from the group that with the Mackinder box it becomes more difficult to work the multiplication with the idea of combining possibilities, such as discovering the amount of different ways of dressing by combining three trousers with five shirts. Or, the multiplication by decomposition, in which one of the parcels of the multiplication decomposes.
For example, multiplying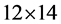 , making the decomposition of the parcels, that is, proceeding as follows: 12 = 10 + 2 and 14 = 10 + 4 Or yet (10 + 2) × (10 + 4) =10 × 10 + 10 × 4 + 2 × 10 + 2 × 4.
, making the decomposition of the parcels, that is, proceeding as follows: 12 = 10 + 2 and 14 = 10 + 4 Or yet (10 + 2) × (10 + 4) =10 × 10 + 10 × 4 + 2 × 10 + 2 × 4.
Nor was the group aware of another limitation of the Mackinder box, that of multiplying two plots using geometry, such as the 10 by 18 product, as an area.
12
18
Dividing the rectangle in half, we have two rectangles:
6

18 18
Again dividing each rectangle in the middle, we will now have 4 rectangles, that is:
3
18 18 18 18
The product of 12 by 18 was taken as the area of the first rectangle. Then the first rectangle was divided in the middle, obtaining two rectangles, that is, (6 + 6) × 8 Again, dividing in the middle, we obtain 4 rectangles, that is to say, (3 + 3 + 3 + 3) × 8 Continuing the division of each rectangle we have the result of the multiplication, according to Wall (2014) .
Although addition and multiplication can be operably related, as future teachers have identified through the Mackinder box handling, there is a difference between such operations. In addition the whole is the sum of its parts and in multiplication it is a fixed relation (frequency) between two quantities. Thus, the researchers who conducted didactic experience clarified the conceptual differences between addition and multiplication by referring to Vergnaud’s Conceptual Field Theory (2009) that multiplication must be worked in the operative sense of proportionality and not only from the successive sum.
The student who represented the group in the division highlighted: “[...] the box helps students visualize the rest, which is important in the division [...]” (September 2015), in this sense, the Mackinder box pedagogic allowed the students to perceive in the division the quotient and the rest, and the rest may be null or not. It helped in the reflection on the meaning of the rest and its relation with the other terms of the division. That is, with the division using the Euclid algorithm in which the dividend is equal to the quotient times the divisor plus the remainder.
We draw the students’ attention to the fact that the Mackinder box was not designed to calculate the quotient and the rest of the division by applying successive differences. For example, calculate the division using successive differences: (20 ? 1.3 = 17); (20 ? 2.3 = 14); (20 ? 3.3 = 11); (20 ? 4.3 = 8); (20 ? 5.3 = 5); (20 ? 6.3 = 2).
In this division we have the quotient equal to 6 and the rest equal to 2. However, it is important to note that this type of division is not usually presented in the books of Mathematics of elementary school I, and consequently it is not taught in most Brazilian schools, according to Neres (2015) .
5. Conclusions
It is considered that this research contributed to the development of the conceptual and didactic knowledge of the students who participated in it, also pointing out the relevance of the use of the Mackinder box in the school context. In addition, the exploration of this didactic material favored the understanding that the use of different representations of the mathematical object of the four operations favors the conceptual understanding of these operations.
The use of the Mackinder box in the research enabled the transformation of operations indicated in three types of language such as the natural, formal and figurative language used here in the sense of physical representation; It allowed future teachers to expand their knowledge of addition and multiplication operations and their respective reverse operations, subtraction and division beyond the usual algorithms that they brought from their training in Basic Education.
In addition, in the research process, exploring the use of the Mackinder box to solve activities that require more mathematical skills from students enabled them to discover new resolution heuristics. On the other hand, to use the Mackinder box it is necessary, first, to select the relevant data of the problem and organize it in order to obtain the addition or subtraction operation to be performed. According to Damm (2007) this is because a semiotic representation is available. In the problems involving multiplication and division occurs in a similar way.
Usually in textbooks, at this level of education, the fundamental operations of Arithmetic are treated, as it were, in the traditional way, that is, in adding natural numbers, the plots are placed one below the other, or one after the other, and the student is asked to perform the addition operation. Similarly, it occurs with subtraction and multiplication. The division is usually done using Euclid's algorithm, although most of the teachers we work with do not know this denomination.
It should be noted that, in general, mathematics teachers who work with children aged 7 to 10 only mobilize in mathematics teaching a single semiotic representation, since they were not prepared to work also with the conversion between semiotic registers. This fact, according to Duval (2007) , can hamper the cognitive development of the student and consequently in the non-streng- thening of learning in mathematics.
It was possible to observe from the data of this research that there was learning, which confirms Duval (2011) that if the student can mobilize at least two semiotic registers and operate them is because there was learning.
On the other hand, although the student is able to mobilize different registers, it is necessary to consider what Almouloud (2007) says about learning, “several of the problems of teaching and learning, in some content, may not just be just mathematics In itself, but of didactic and linguistic origin” (pp. 125-147).
The data show that all students were able to make the conversion of the natural register to the numerical register with skill, or vice versa, and with some of the activities they used the Mackinder box, which gave them the knowledge and Understanding of a new didactic material, hitherto unknown to them.
We also observe that in the bibliographies consulted, in general, no resolution of exercises and problems is done through the Semiotic Representation Registers. However, we recognize that teaching based on the mobilization of a diversity of registers cannot and should not be considered as the solution to the teaching of Mathematics, it is understood that it is another tool, an alternative to develop skills and competences in mathematical activities, thus contributing to the student’s cognitive development.
Cite this paper
Neres, R. L., Castro, E. R., & Miguel, J. C. (2017). Mathematics in the Initial Years of Fundamental Teaching in Brazil: An Experience with Teachers in Training in the Pedagogy Course. Creative Education, 8, 607-626. https://doi.org/10.4236/ce.2017.84047
References
- 1. Almouloud, S. A. (2007). Registers of Semiotic Representation and Understanding of Geometric Concepts. In S. D. A. Machado (Ed.), Learning in Mathematics: Records of Semiotic Representation (3rd ed., pp. 125-147). Campinas, SP: Papirus. [Paper reference 1]
- 2. Barreto, M. C. (2007). Challenges to Pedagogues in the Teaching of Mathematics. In J. A. M. de Sales et al. (Orgs.), Training and Teaching Practices (pp. 243-254). Fortaleza, CE: EdUECE. [Paper reference 1]
- 3. Brazil (2006). Resolution of the National Council of Education CNE/CP1/2006. Official Journal of the Union, Brasília/Brazil, Section 1, 11. [Paper reference 1]
- 4. Brousseau, G. (2008). Introduction to the Study of Didactic Situations: Content and Teaching Methods (Trans. by Camila Bogéa). Sao Paulo, SP: Atica. [Paper reference 1]
- 5. Bruner, J. S. (1978). The Process of Education. Sao Paulo, SP: Nacional. [Paper reference 1]
- 6. Cardoso, L. F. (2007). Dictionary of Mathematics (53 2p). Rio de Janeiro, RJ: Lexikon. [Paper reference 1]
- 7. CURI (2005). The Mathematics and Teachers of the Early Years. Sao Paulo, SP: Musa Editora. [Paper reference 1]
- 8. Curi, E. (2006). The Mathematical Formation of Teachers from the Initial Years of Elementary Education in Face of the New Brazilian Demands. Revista Iberoamericana de Educación (Online), No. 37/4. [Paper reference 2]
- 9. DAEP/INEP (2015). RESULT SAEB, National Institute of Educational Studies and Research Anízio Teixeira. Inep, 2015.
www.inep.gov.br/resultados [Paper reference 1] - 10. Damm, R. F. (2007). Additive Representation, Understanding and Problem Solving. In S. D. A. Machado (Ed.), Learning in Mathematics: Records of Semiotic Representation (3rd ed., pp. 35-47). Campinas, SP: Papirus. [Paper reference 1]
- 11. Damm, R. F. (2009). Mathematical Education: A (New) Introduction. In S. D. A. Machado (Ed.), Representation Registers (3rd ed., pp. 167-188). Sao Paulo, SP EDUC. [Paper reference 1]
- 12. Danyluk, O. S. (1993). Mathematical Literacy: The Everyday Life of School (3rd ed.). Passo Fundo, RS: UFP. [Paper reference 1]
- 13. Duval, R. (2007). Record of Semiotic Representation and Cognitive Functioning of Comprehension in Mathematics. In S. D. A. Machado (Ed.), Learning in Mathematics: Records of Semiotic Representation (3rd ed., pp. 11-33). Campinas, SP: Papirus. [Paper reference 4]
- 14. Duval, R. (2009). Semósis and Human Thought: Semiotic Records and Intellectual Learning (Transl. by L. F. Levy & M. R. da Silva, 1st ed., 115 p.). Sao Paulo, SP: Publisher Livraria da Física. [Paper reference 1]
- 15. Duval, R. (2011). See and Teach Mathematics in Another Form—Enter into the Mathematical Mode of Thinking: The Records of Semiotic Representations (Organization: Tania M. M. Campos, Translation: Marlene Alves Dias, 1st ed., 160 p). Sao Paulo, SP: PROEM. [Paper reference 2]
- 16. Freitas, J. L. M. de. (2008). Theory of Didactic Situations. In S. D. A. Machado (Ed.), Mathematical Education: A (New) Introduction (3rd ed. revised, pp. 77-111). Sao Paulo, SP: EDUC. [Paper reference 1]
- 17. Gatti, B. A. (2010). Teacher Training in Brazil: Characteristics and Problems. Education and Society, Campinas/SP/Brazil, 31, 1355-1379. [Paper reference 3]
- 18. Godino, J. D. (2007). The Onto-Semiotic Approach to Research in Mathematics Education. ZDM: The International Journal on Mathematics Education, 39, 127-135. [Paper reference 1]
- 19. Gontijo, C. H. (2015). Creativity Techniques to Stimulate Mathematical Thinking. Education and Mathematics, Journal of the Association of Teachers of Mathematics, No. 135. [Paper reference 1]
- 20. IDEB (2015). Results of the Basic Education Development Index (IDEB).
www.inep.gov.br/resultados [Paper reference 1] - 21. Libaneo, J. C. (2010). Goodbye Teacher, Goodbye Teacher: New Educational Requirements and Teaching Profession (12th ed.). Sao Paulo, SP: Cortez. [Paper reference 2]
- 22. Lorenzato, S. (2006). To Learn Mathematics. Campinas, SP: Autores Associados. [Paper reference 1]
- 23. Mello, G. (2000). Initial Teacher Education for Basic Education: A Radical (Re)vision. Perspectiva, 14, 98-110. [Paper reference 1]
- 24. Nacarato, A. M. (2010). The Mathematical Formation of the Teachers of the Initial Series: Self-Writing as a Training Practice. Bolema, Rio Claro/SP/Brazil, 23, 905-930. [Paper reference 1]
- 25. Neres, R. L. (2015). Learning with Numbers (90 p). Rio de Janeiro, RJ: Editora Ciência Moderna Ltd. [Paper reference 1]
- 26. Peirce, C. S. (2005). Semiotics (Translation: José Teixeira Coelho Neto, 3rd ed., 337 p). Sao Paulo, SP: Perspectivas. [Paper reference 2]
- 27. Pimenta, S. G. (2005). Teacher Training: Identity and Knowledge of Teaching. In S. G. Pimenta (Org.), Pedagogical Knowledge and Teaching Activity. Sao Paulo, SP: Cortez. [Paper reference 1]
- 28. Ponte, J. P., Brocardo, J., & Oliveira, H. (2015). Mathematical Investigations in the Classroom (159 p). Belo Horizonte, MG: Authentic. [Paper reference 2]
- 29. Rios, T. A. (2010). Understand and Teach: for Better Teaching of the Best Quality. Sao Paulo, SP: Cortez. [Paper reference 1]
- 30. Rosenzweig, P. M. (2008). Overthrowing Myths: How to Avoid the Nine Basic Misconceptions in Business (Translation: Ricardo Gouveia). Sao Paulo, SP: Globo. [Paper reference null]
- 31. Silver, E. A., & Smith, J. P. (2008). Imagine a Related Problem. In S. Krulik, & R. E. Reys (Orgs.), The Problem Solving in School Mathematics (No. 215, pp. 32-36). Sao Paulo, SP, Interview with Gabriel Grossi. [Paper reference 2]
- 32. Wall, E. S. (2014). Theory of Numbers for Elementary School Teachers (Translation: Roberto Cataldo Costa, 179 p). Porto Alegre, RS: AMGH. [Paper reference 6]
NOTES
1Research carried out in the first semester of 2015, in the didactic process of the discipline “Mathematics in Early Childhood and in the Early Years of Elementary School” of a course in Pedagogy.
2The Mackinder box is a didactic material that allows the understanding, in a playful and concrete way, of how to develop with children the basic operations of addition, subtraction, multiplication and division (CARDOSO; CASTRO; NERES, 2016).
3According to Veiga (2004), the didactic process is the path between the selection of contents and the strategies of teaching in favor of the objectives established considering in this selection, the psycho-pedagogical characteristics of the students so that they can develop their intellectual capacities in the face Of the complexity of the modern world.
4Propensity to impute negative characteristics to those who have negative results and vice versa. According to Rosenzweig, Philip M., 1955. Breaking Myths: How to Avoid the Nine Basic Misconceptions in Business/ Phil Rosenzweig, São Paulo: Globo, 2008 .
5Verbal information from one of the students.
6The student’s speech was recorded in the logbook on September 14, 2015.
7Fictitious name.
8Fictitious name.
9Fictitious name.















