Energy and Power Engineering
Vol. 4 No. 3 (2012) , Article ID: 19023 , 5 pages DOI:10.4236/epe.2012.43024
Wear Predictions of Metal Matrix Composite in Presence of Greasing Material
1Mechanical Engineering Department, Pune Vidhyarthi Griha’s College of Engineering and Technology, Pune, India
2Production Engineering Department, Shri Guru Gobind Singhji Institute Of Engineering & Technology, Nanded, India
Email: svgawali@yahoo.com
Received February 13, 2012; revised March 15, 2012; accepted March 29, 2012
Keywords: Centrifugal Casting; Al-4cu-xTiB2; Mathematical Regression Analysis
ABSTRACT
Aluminum-copper titanium di-boride [Al-4Cu-xTiB2] composite (x = 1%, 1.75%, 2.5%) is prepared successfully by centrifugal casting. Samples pin of diameter 8 mm, 10 mm, & 12 mm are prepared with help of special purpose die. An experimental parameter analysis is obtained for various load and speed combinations on pinon wear disc testing machine. A larger volume fraction of particles can be attained near the wear surface via centrifugal casting. The volume fraction of the heavier titanium di-boride is controlled by inertial forces upon centrifugal processing the semisolid composite. Mathematical Regression Analysis is carried out to calculate wear. Greasy material facilitates heat transfer on the counter side material. Comparative study facilitates wear predictions of Al-4Cu-xTiB2 metal matrix composite for various practical applications.
1. Introduction
The difficulties in the development of particulate metal matrix such as poor wettability, inhomogeneous distribution of reinforcement particles, formation of unwanted reaction products at the interface between the matrix and reinforcement, etc. have led to attempts to synthesis new generation in composites. Among the composites metal matrix composites have become popular in the recent years. Functionally graded materials (FGMs) are spatial composites that display discrete or continuously varying composition over a definable geometrical length [1]. A number of processes are proposed to fabricate the FGMs such as adhesive bonding, sintering, thermal spray, reaction infiltration and so on. Centrifugal casting is a special type of casting process in which the melt fills into the mould and solidifies under a centrifugal force field. Major applications of centrifugal walled castings are pipes, piston rings, cylinder liners, rollers, pulleys etc. The features involved in centrifugal casting are fluid flow, thermal properties and solidification. The casting parameters that influence solidification structures includs the mold rotation velocity, the pouring temperature of the molten metal and the alloy composition the mould dimension and the mould preheating temperature etc. [2]. The extent of segregation depends on various above process parameters. The moving direction of the solid particles in the molten matrix is determined by the densities differences between the molten metal and reinforcement particles.High density reinforcement particles move far away in the radial direction compared to the molten matrix particles [3]. Some previous work considers a hollow cylinder rotating vertically around the central axis under the effect of gravity [4]. Experimentation is carried to prepare the samples of 12mm diameter. Various constants are calculated from the wear equation. Mathematical Regression Analysis is used to calculate wear.
2. Experimentation
An Experimental set up used to prepare Al-TiB2 metal matrix composite is shown is Figure 1. A 3 HP, 1440 rpm, motor is used to drive the cantilever die with the help of belt drive. A stepped pulley is mounted on one end of shaft and to other end cantilever die is fitted. The speed of the casting is varied using stepped pulley drive. Crucible kept in the furnace for melting the base metal and the reinforcing material is shown in Figure 2. Special purpose die used to prepare samples as per ASTM G99 standards is shown in Figure 3, while Figure 4 shows cut section of special purpose die. Figure 5 shows sample pin.
3. Result and Discussions
Wear and friction testing machine is shown in Figure 6. The wear and friction monitor consist of machine, controller, data acquisition system, sensors and cables. It

Figure 1. Experimental set up showing the drive arrangement for cantilever die.

Figure 2. Furnace with crucible.

Figure 3. Special purpose die.
Figure 4. Cut section of special purpose die.

Figure 5. Sample pin.

Figure 6. Wear and friction test rig.
facilitates study of friction and wear characteristics in sliding contact under desired conditions. Sliding occurs between the stationary pin and a rotating disc. Normal load, rotational speed and wear track diameter can be varied to suit the test conditions. Tangential frictional force and wear are monitored with electronic sensors and recorded on computer .These parameters are available as function of load and speed. Reading of wear are taken after making all the necessary connections and Sliding speed is calculated as follows Sliding speed = π × D × N/60,000.
Cross section Area of rod = π × d2/4 where, D = Diameter of wear track in mm. N = Disc speed in rpm. T = Test duration in sec, d = diameter of specimen rod.
3.1. Calculation of Constants [5,6]
Let, W = Wear in micron, L = Load in N, V = Sliding Speed in m/s, T = Test duration in sec.
K = Proportionality Constant, a, b, & c are the index of load, speed & time respectively,W1 and W2 are wears corresponding to loads L1, L2; Sliding speeds V1, V2 and testing time T1, T2
Equation of wear is –W = K × La × Vb × Tc
3.1.1. Calculation of “a”
Table 1 shows Calculation of “a” by considering V & T Constant i.e. (k × Vb × Tc = Cont).
W1/W2 = (L1/L2)a
ln(W1/W2) =a × ln(L1/L2)
a = ln(W1/W2)/ln(L1/L2)
Regression Analysis: WEAR versus LOAD
The regression equation is
WEAR = –1.77 + 0.437 LOAD
Predictor Coef SE Coef T P VIF
Constant –1.7670 0.6073 –2.91 0.101
LOAD 0.43750 0.01685 25.97 0.001 1.000
S = 0.370355 R-Sq = 99.7% R-Sq(adj) = 99.6%
3.1.2. Calculation of “b”
Similarly, b is
b= ln (W1/W2) / ln(V1/V2)
where, k × La × Tc = Constant
Table 2 shows calculations of b by considering L &T constant.
Regression Analysis: WEAR versus SLIDING SPEED
The regression equation is
WEAR = –52.0 + 33.4 SLIDING SPEED
Predictor Coef SE Coef T P VIF
Constant –52.0010 0.0022 –23758.06 0.000
SLIDING SPEED 33.4093 0.0005 73904.47 0.000 1.000
S = 0.000423587 R-Sq = 100.0% R-Sq(adj) = 100.0%
3.1.3. Calculations of “c”
c = ln (W1/W2)/ln (T1/T2) where k × La × Vb = Constant.
Table 3 shows calculations of “c” by considering L & V Constant.
Regression Analysis: WEAR versus TEST TIME
The regression equation is
WEAR = 11.5 + 0.0800 TEST TIME
Predictor Coef SE Coef T P
Constant 11.5000 0.8660 13.28 0.006
TEST TIME 0.080000 0.003162 25.30 0.002
S = 0.707107 R-Sq = 99.7% R-Sq(adj) = 99.5%
3.1.4. Calculations of “k”
Table 4 shows calculations of “k”.
3.1.5. Wear Equation
In the preceding calculation of constants a, b, c and k with help of wear, friction monitor and regression analysis
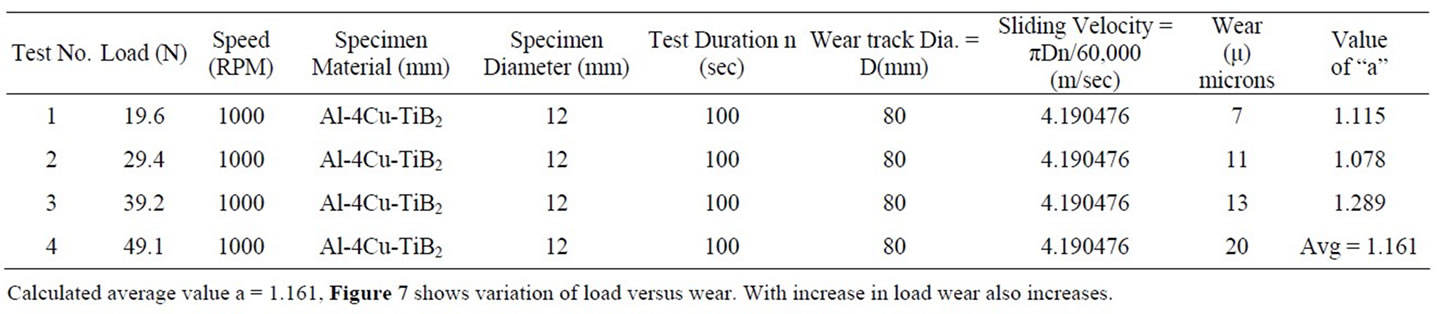
Table 1. Calculation of “a”.

Table 2. Calculation of “b” (L & T constant).
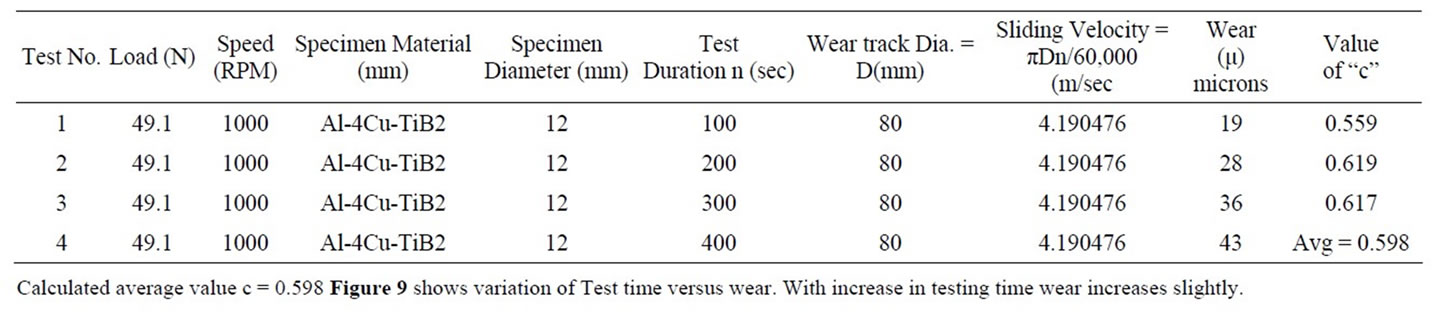
Table 3. Calculation of “c” (L &V constant).

Table 4. Calculation of “k”.

Figure 7. Load vs wear.
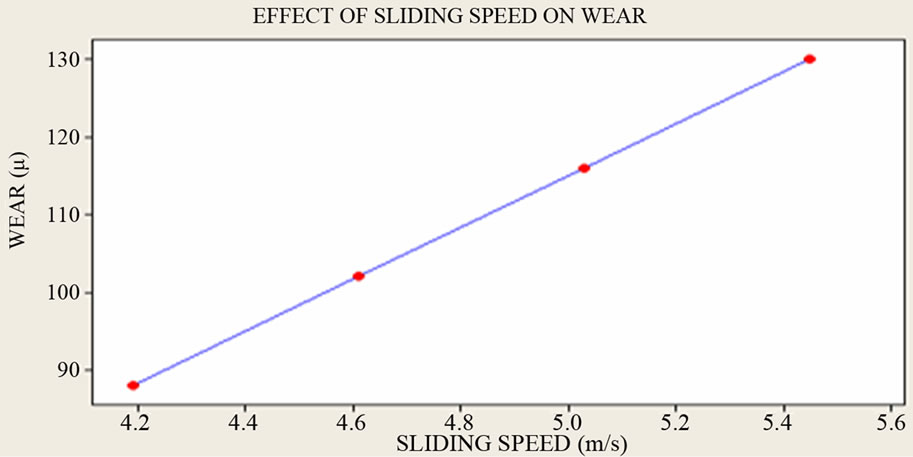
Figure 8. Sliding speed vs wear.
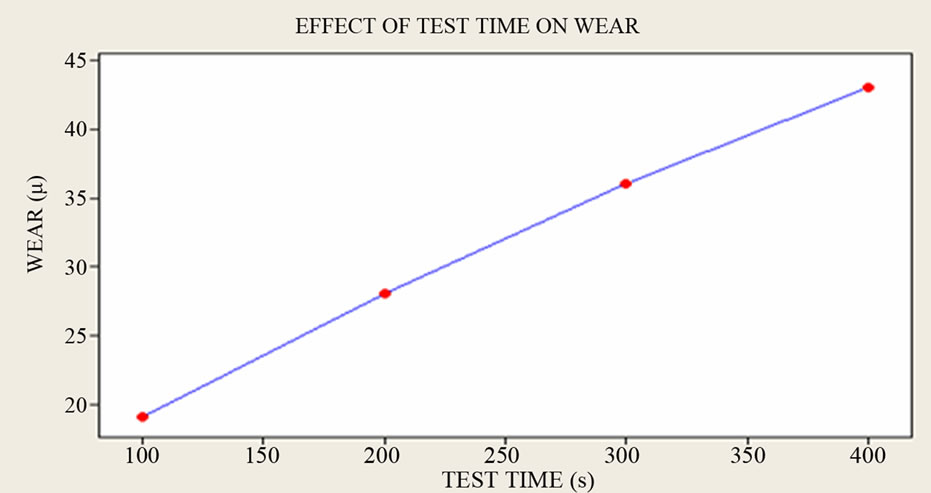
Figure 9. Test time vs wear.
we get
For Al-4cu-TiB2
a = 1.161, b = 1.484, c = 0.598, K = 0.019
Substituting these values in the wear equation (1), the wear at different load, speed & time can be calculated as
W= 0.019 × L1.161 × V1.484 × T0.598
This wear equation is useful for predicting wear at different load, speed & time ranges described in above tables.
4. Conclusion
A mathematical Regression analysis is used to calculate wear. Wear influencing parameters like load, sliding speed, and testing time are studied comparatively. Experimental and theoretical wear results for Al-4cu-TiB2 are in good comparision.The study facilitates the predictions of wear rate parameters for various applications like clutch plate, brake shoe etc. The presence of greasy material facilitates heat transfer where good amount of heat conduction is also a criteria and an optimum wear of counter side material is required.
REFERENCES
- A. Mandal, R. Maiti, M. Chakraborty and B. S. Murty, “Effect of TiB2 Particles on Aging Response of Al-4Cu alloy,” Material Science and Engineering: A, Vol. 386, No. 1-2, 2004, pp. 296-300. doi:10.1016/j.msea.2004.07.026
- T. Ogawa, Y. Watanabe, H. Sato, I.-S. Kim and Y. Fukui, “Theoretical Study on Fabrication of Functionally Graded Material with Density Gradient by Centrifugal Solid-Particle Mathod,” Composites Part A: Applied Science and Manufacturing, Vol. 37, No. 12, 2006, pp. 2194-2200. doi:10.1016/j.compositesa.2005.10.002
- S. Narendranaath, G. C. Mohankumar and P. G. Mukunda, “Effect of Mould Wall Thickness on rate of Solidification of Centrifugal Casting,” International Journal of Engineering Science and Technology, Vol. 2, No. 11, 2010, pp. 6092-6096.
- J. K. Kim and P. K. Rohatgi, “Interaction between moving Cellular Solidification front and Graphite Particles during Centrifugal Casting”, Materials Science and Engineering: A, Vol. 244, No. 2, 1998, pp. 168-177. doi:10.1016/S0921-5093(97)00539-X
- S. Bahadur, “Fundamentals of Friction and Wear of Automobile Brake Materials”, Ph.D. Thesis, University Professor and Professor of Mechanical Engineering, Ames.
- I. G. Waston, M. F. Forster, P. D. Lee and R. J. Dashwood, “Investigation of the Clustering Behaviour of Titanium Diboride Particles in Aluminium,” Composites Part A: Applied Science and Manufacturing, Vol. 36, No. 9, 2005, pp. 1177-1187. doi:10.1016/j.compositesa.2005.02.003

