Communications and Network
Vol. 5 No. 1 (2013) , Article ID: 28259 , 12 pages DOI:10.4236/cn.2013.51010
Three-Dimensional Dynamic Based Borrowing Scheme for Wireless Cellular Networks
Department of Computer Science, Amman, Jordan
Email: mshridah@ju.edu.jo
Received December 4, 2012; revised January 5, 2013; accepted February 8, 2013
Keywords: Wireless Networks; QoS; Multimedia Services; 3-D Structure; Call Blocking Probability; Call Dropping Probability
ABSTRACT
Mobility metrics of wireless networks such as link availability, number of neighboring nodes, link duration, link state, and link stability make it difficult to provide a node with quality of services guarantee. In previous research on Quality of Service (QoS) for cellular networks especially for handling handoff connections, the design was based on a flat 2D hexagon cells. However, in reality Base Station antenna coverage is in a 3D space and there exists a blind spot; the area which is just above and bellow the radiated antenna. In this paper we introduce the concept of Blind Spot (BS) in which there is no signals to initiate a call or accepting a handoff one. In BS, the signal power equal zero. Even if there is enough bandwidth to initiate or accept a handoff call, it will be blocked or dropped respectively. We present an implementation of Static Borrowing Scheme (SBS) and we extend the dynamic-rate based borrowing scheme [1] into 3-Dimentional structure and call it 3-Dimensional Dynamic Based Borrowing Scheme (3D DBBS). The proposed new technique for resource sharing is to ensure the continuity for both originating and handoff connections in 3-D cellular networks based on Dynamic-Based Borrowing Scheme (3D BBS). This technique aims to minimize the blocking probability of the originating calls by minimizing the dropping probability of the handoff requests and maximizing the channel utilization. The results revealed that 3D DBBS outperformed the static based schemes by 5% on average even when the blind spot of the base station antenna is taken into consideration. When moving to a 3D space, the results of the simulation showed the 3D DBBS outperformed the static scheme by 2% on average. As a result, considering nodes in a 3D space will have better QoS guarantee as the blocking and dropping probabilities are decreased. Thus, the bandwidth utilization is increased.
1. Introduction
With the increasing demand for wireless networks, QoS “Quality of Service” and multimedia (audio, video and data) services (audio, video and data) especially in the last two decades, many researchers made proposals that provide enhancements and developments on the structure and resource utilization techniques used in those networks [2-6].
Admission control is the task of determining whether a network is capable of admitting and supporting a given connection. For real time multimedia traffic, Call Admission Scheme (CAS) is not an easy task. Most CAS algorithms work by organizing the total utilized bandwidth, calls, and the number of packets. A new call may be blocked by the network when a defined limit is reached until at least one of the current calls terminates [7-8].
Many schemes were proposed to ensure QoS in wireless networks [9-12]. The proposed schemes are based on statistical, dynamic techniques or a combination of both. Some of these schemes used the resources reserved in each cell in order to reduce handoff failure due to the lack of resources in adjacent cells. As a result the bandwidth utilization was dropped significantly. The Guard Channel Scheme (GCS) [7] is based on reservation technique in which a specific number of channels are reserved in each cell only for handoffs calls. The GCS is optimal for minimizing call blocking probability (BP), but not for call dropping probability (CDP) and utilization.
The Shadow Cluster Scheme (SCS) is proposed in [8] to improve the resource allocation and the call admission control in wireless networks. Based on a call’s requirements and local traffic conditions, SCS can be used to allocate resources that are needed for call handoffs, and to determine whether a new call should be admitted to a wireless network. Furthermore, the base station maintains status of each ongoing call and delivers it to each cell in the shadow cluster. This scheme depends on the degree of accuracy of guessing the movement of mobile hosts.
The Distributed Call Admission Scheme (DCAS) proposed in [9] makes the admission decision by depending on the number of active calls in each cell and its neighboring cells. DCAS requires exchanging periodically and not during each call, rather it requires that periodically. Measurement-based Pre-assignment (MPr) technique [10], which employs a dynamic allocation of bandwidth to prevent handoff failure, allows the handoff calls to share a pre-reserved channel before the new calls compete for the shared channels. An adaptive QoS management scheme used to meet dynamic differences in network resources due to the mobility of mobile hosts and location-dependant errors.
Due to the dynamic movement of nodes, it is possible for a mobile node to move from one cell to another, during the lifetime of a connection, which is called handoff operation. It is possible to initiate a new connection in a certain cell, which is called originating call operation. A cell may drop the handoff call or block the originating call because the base station controller can not allocate sufficient bandwidth.
Two important metrics in evaluating the performance of any call admission scheme are (1) CDP the Call Dropping Probability (CDP) the Call Blocking Probability (CBP). CDP is the probability of an existing call being terminated due to the lack of bandwidth resources and CBP is the probability of a call being denied resources of bandwidth due to the lack of such resources [12].
To resolve the handoff calls (e.g., blocked or dropped), three approaches were proposed in the literature. The first approach is the Static Based Scheme (SBS) [7]. In this scheme a certain percentage of available resources in a cell are reserved for handoff connections such as the guard channel scheme and the statistical reservation scheme. In the statistical reservation scheme, the cell resources (bandwidth) are statistically reserved. The previous two schemes help in minimizing the CDP and CBP. However, a degradation in the utilization performance metric was noted. This is because the pre-reserved bandwidth might not be fully used by the handoff calls [1]. Al-Sharaeh in [1] proposed a dynamic based borrowing scheme.
E Mona et al. [12] proposed the borrowing scheme and the results shows that it outperformed the approaches presented in [8-10] in terms of CBP, CDP, and Utilization of bandwidth resources. However, the proposed approach outperforms the approach presented in [1].
We present in this paper an approach that helps in reducing the call dropping and call blocking probabilities while increasing the amount of bandwidth utilization in a more realistic simulation environment which mimic real life scenarios. In order to conduct our experiments (simulation), a java simulator was created to simulate a set of Borrowing Schemes, using different structures of wireless networks—As illustrated in Section 4. The rest of the paper is organized as follows: in Section 2 we give a brief discussion of 3-D Cellular network structure. In Section 3 we present our approach (Give it a meaningful name). A simulation model and the experimental results are presented in Section 4. A concluding remark is presented in Section 5.
2. 3D Cellular Wireless Networks
The idea of extending the standard concept of planar cellular networks into space is discussed in [1]. Figure 1 shows an Antenna Radiated Pattern in order to illustrate the need for a 3-D cellular network structure. Note that the largest coverage area is in the circular pattern and the energy level directly above or below the antenna will be lower. In our simulation we shall call the area the area in which there is no coverage the blind spot (BS).
In Omni directional antenna [12], radio frequency waves travel in two-dimensional plane in planner circle. The average power received at a distance 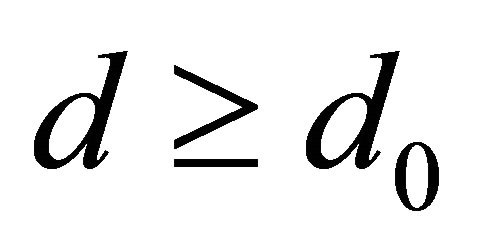 is
is

where 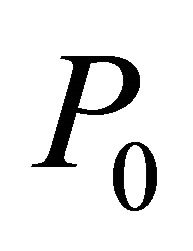 is the power that is received at small distance
is the power that is received at small distance  from the receiver and
from the receiver and 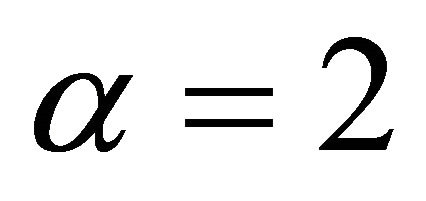 for free-space environment.
for free-space environment.
In fact, RF signals travel in 3D space rather than 2D. Thus, for the proposed simulation to be closer to reallife environment, it is natural to use three-dimensional transmission and to take into account the movement of the mobile node. For more realistic results, the blind spot of the base station should also be taken into consideration [12].
In our simulation model, we examine different structures of the cellular networks in order to emulate real-life environment. Theoretically, cellular networks are divided into hexagonal cells. Each cell contains one or more tower/antenna that covers a specific range where nodes can receive an acceptable signal-to-noise ratio. Research interests that concern the Effective Isotropic Radiated Power (EIRP) of the antenna which represents the
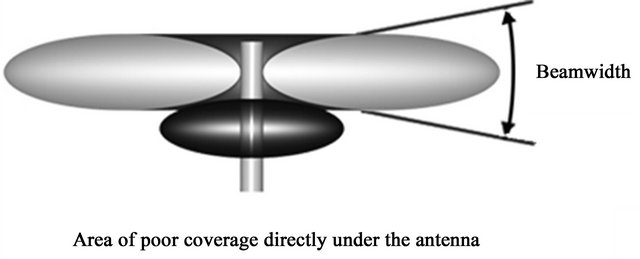
Figure 1. Antenna radiated pattern.
maximum radiated power available from a transmitter in the direction of maximum antenna gain (cf. Figure 2) have decreased lately.
Since we are interested in 3D propagation, emphasis will be EIRP and BS (cf. Figure 1) and the Effective Radiated Power (ERP) which denotes the maximum radiated power as compared to a half-wave dipole antenna (cf. Figure 3) where in this area the signal power is almost zero. Thus, a node that exists in this spot can not receive any signal and considered to be BS. For example, if we have an ongoing connection, it will in this spot be dropped by the handling Mobile Switching Center (MSC). As far as we know, there is no research work that considers the dropping and blocking probabilities in BS. These properties are embedded into the simulation that we designed for this reported work.

Figure 2. Effective isotropic radiated power “EIRP” of the antenna.

Figure 3. Effective radiated power “ERP” of the antenna.
For a fair comparison with previous research work, we shall suppose that the area of this spot to be a 10% of the cell’s area in a 2-D structure and the volume to be to be a 10% of the cell’s volume in a 3D structure. We shall also assume that in this spot any new call that is generated will be blocked, even if there is enough bandwidth, and any handoff request will be dropped.
3. The Proposed Technique
As mentioned above in Section 1, in SBS [7] a specific amount of bandwidth, from the total quantity available to the cell, is reserved for the handoff connections and the remaining is used for the new connections.
In this paper we present an implementation of SBS as (cf. Figure 4). For each new or handoff call, the static scheme will give the maximum, average or minimum bandwidth according to the available free bandwidth from the reserved amount for either the handoff or the new calls. Any call which is initiated during the time when there is no enough free bandwidth in the cell (i.e. less than the minimum) will be blocked and thus, the handoff connection will be dropped. Since there is no borrowing technique used in this scheme many calls will be blocked or dropped. This explains why CBP and CDP in this scheme are higher than those of other schemes that depend on borrowing bandwidth from other existing connections.
In this paper we extend the dynamic-rate based borrowing scheme [1] into 3-Dimentional structure and call it 3-Dimensional Dynamic Based Borrowing Scheme (3D DBBS). The pre-allocation of the bandwidth for the handoff requests, employed in SBS, exists in this scheme. The main difference between the RBBS and the SBS is the division of the bandwidth taken by a new call into a number of shares “lambda”, depending on a fairness factor “f” as displayed in Figure 5. In this scheme, the technique for handling the new calls is similar to that described in the Static Scheme. However, dealing with the handoff requests is different because keeping the calls enduring is an important issue from the end-user point of view. If a handoff call occurs, RBBS will give the maximum, average or minimum bandwidth according to the available free bandwidth reserved for the handoff calls.
If a handoff request occurs and there is not enough free bandwidth in the cell, then it will take one share from an number of ongoing “originating calls”, which have already taken maximum bandwidth, so that the amount is greater than or equal the to minimum required bandwidth. An ongoing call that only has minimum bandwidth does not give bandwidth shares. Needed share are usually taken from calls that are working at average level rather than those that are working at maximum level if all ongoing calls have reached the minimum
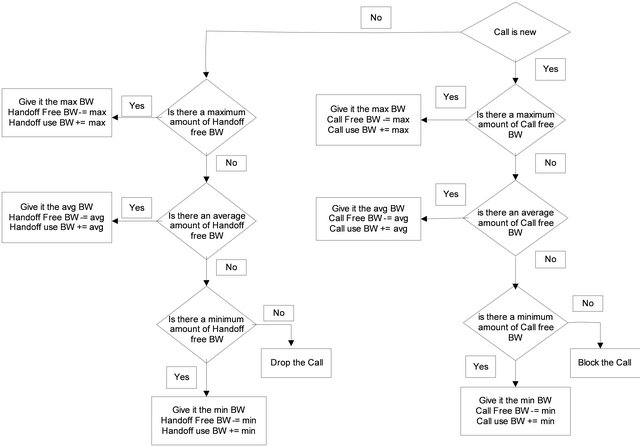
Figure 4. Static based scheme.

Figure 5. The division of the new call’s bandwidth into set of shares.
bandwidth. At the end, when there are no calls working at the maximum or average levels, the handoff request will be dropped. Figure 6 presents the flow diagram for the RBBS.
The proposed scheme, 3DBBS, presents a technique for call admission in three-Dimensional wireless cellular networks that decreases CBP and CDP while increasing the bandwidth utilization. This scheme (cf. Figure 7) is
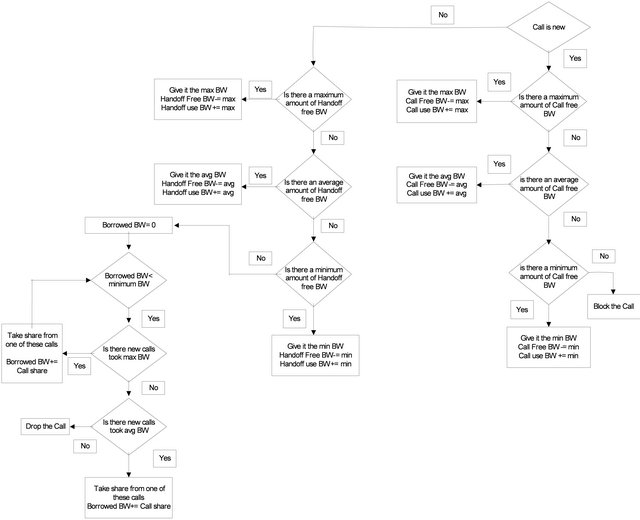
Figure 6. Rate based borrowing scheme flow chart.
based on borrowing bandwidth temporarily from ongoing connections in order to decrease dropping and blocking probability. 3DBBS is purely dynamic and does not make pre-allocation for bandwidth for incoming calls or handoffs where some bandwidth will be wasted. Therefore, the degree of bandwidth utilization will be increased. Any new or handoff call will be given the maximum, average or minimum bandwidth, depending on the available amount. Finally, when there is no available bandwidth left, it will borrow bandwidth (e.g., take shares) from the new calls working on the maximum level, then from the average ones as described in RBBS. At the end when there are no calls working on either the maximum or average levels, the new call will be blocked and the handoff call will eventually be dropped. The main difference between the proposed scheme and the RBBS, other than the pre-allocation, is in the treatment of the handoff requests. In RBBS, there is no bandwidth borrowing from existing calls; if the all free bandwidth is used, the request will be dropped.
There are two classes for the traffic offered to the cellular system.
Class Ι traffic: real-time multimedia traffic, such as interactive voice and video applications.
Class ΙΙ traffic: non real-time data traffic such as email or FTP.
When a mobile host requests a new connection within a cell, it provides the following parameters:
The desired class of traffic (either Ι or ΙΙ). We assume that all calls are from the class I.
The desired amount of bandwidth for the connection; maximum bandwidth.
The average amount of bandwidth.
The minimal acceptable amount of bandwidth, i.e. the minimum amount of bandwidth needed to guarantee the quality. An ongoing connection of class Ι will be dropped if its minimum requirement of bandwidth cannot be met during a handoff. Class ΙΙ connections have no minimum
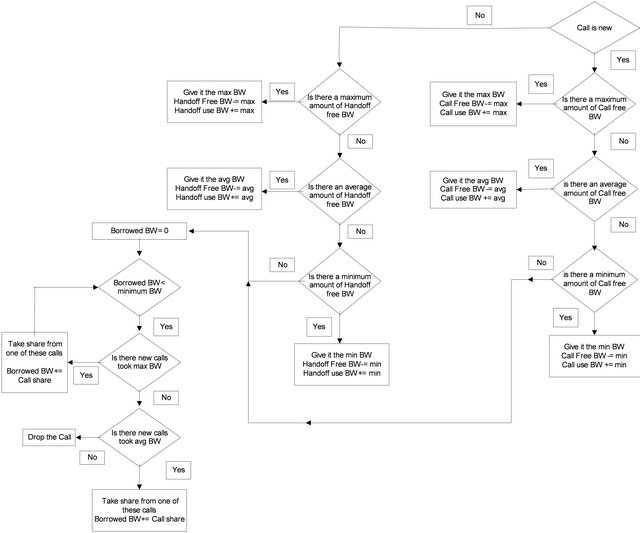
Figure 7. Three-dimensional dynamic based borrowing scheme.
bandwidth requirement and they can be continued even when the bandwidth is less than the minimum level.
3.1. Cell and Connection Parameters
In our approach, we will use the same parameters and functions that have been used in [1]. Initially, each cell specifies a maximum (desired) bandwidth (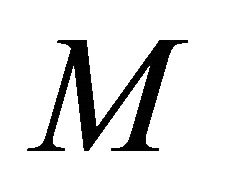 ), an average bandwidth (Avg) and a minimum bandwidth (
), an average bandwidth (Avg) and a minimum bandwidth (![]() ). The difference between M and m is called bandwidth loss tolerance. Each cell maintains a local parameter
). The difference between M and m is called bandwidth loss tolerance. Each cell maintains a local parameter 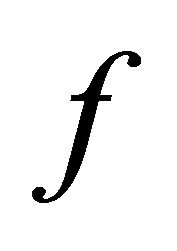 (where
(where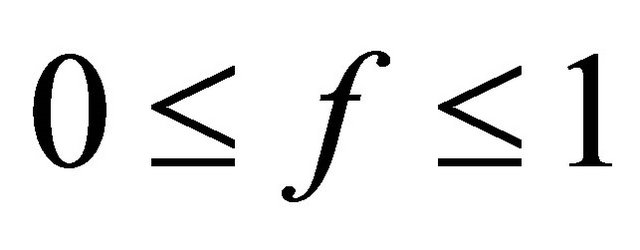 ) which represents the fraction of the bandwidth loss tolerance that a connection may tolerate in the worst case. If a cell accepts a new call, it guarantees that the supplied bandwidth will not be less than a certain level which is called the minimum expected bandwidth (MEX) where,
) which represents the fraction of the bandwidth loss tolerance that a connection may tolerate in the worst case. If a cell accepts a new call, it guarantees that the supplied bandwidth will not be less than a certain level which is called the minimum expected bandwidth (MEX) where,
 (1)
(1)
The bandwidth loss tolerance is divided into shares, each share is equal to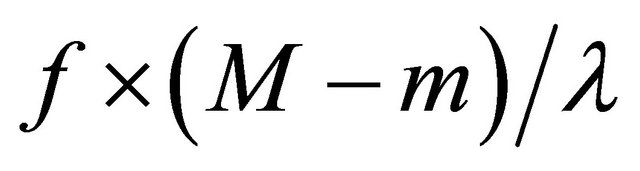 . as illustrated in Figure 5 where
. as illustrated in Figure 5 where ![]() is cell parameter (cf. [1,12]).
is cell parameter (cf. [1,12]).
3.2. Fair Factor Effect
When the value of the fair factor “f”, is small, the values of the blocking and dropping probabilities will be expected to increase. This is due to the fact that the value of “f” will determine the amount of BW that can be borrowed by other calls. That is, if “f” is small then the amount of BW is small. Thus, higher number of calls will be dropped or blocked. As a result, blocking and dropping probabilities will increase. On the contrary, the bandwidth utilization will increase as “f” increases.
4. Experimental Results and Analysis
4.1. System Model
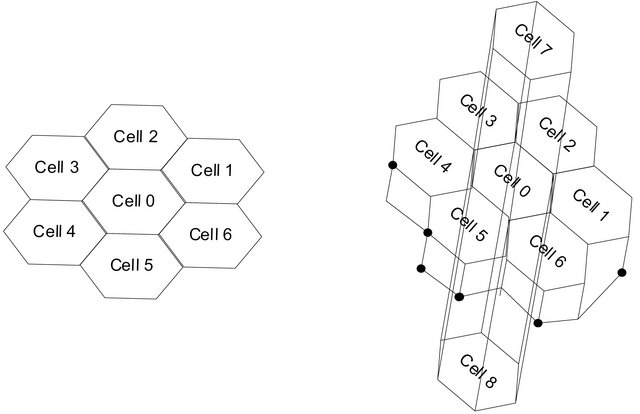
The structure of a 2-D Cellular wireless network consists of seven hexagonal cells that have equal probability of receiving new calls or handoff requests. We have implemented our system using a Java simulation model. It creates seven cells with one in the centre and the remaining six cells are its neighbors as illustrated in Figure 8, with maximum bandwidth of 30,000 kbps. Each cell accepts a new or handoff connection if it can support a bandwidth that is grater than the minimum bandwidth. We use the parameter values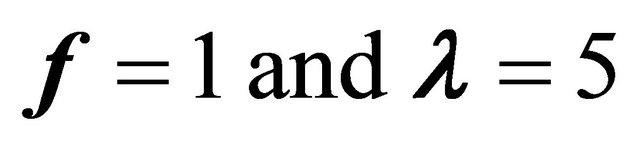 , which means a connection can give maximum 5 shares, and the radius of the cell is 3000.
, which means a connection can give maximum 5 shares, and the radius of the cell is 3000.
In our simulation, we assume that we have class Ι traffic with a maximum bandwidth 8000 kbps, a minimum bandwidth of 2500 kbps and an average bandwidth of 5000 kbps.
As we mentioned previously, we extend a 2-D structure (Figure 8(a)) of the cellular wireless network into 3D (Figure 8(b)). Our goal is to compare the system behavior in the two structures and study the effects of 3D structure on the CBP and the CDP and Bandwidth Utilization.
4.2. Simulation Results
The simulation considers 2D and 3D cellular networks. The simulated area is partitioned into 7 cells in the 2D structure and 9 cells in the 3D. In a 2D structure, we enter the radius of the cell in order to compute the BS radius (e.g., 10% from the whole cell area). To determine whether a call is within the vicinity of BS, we generate a random point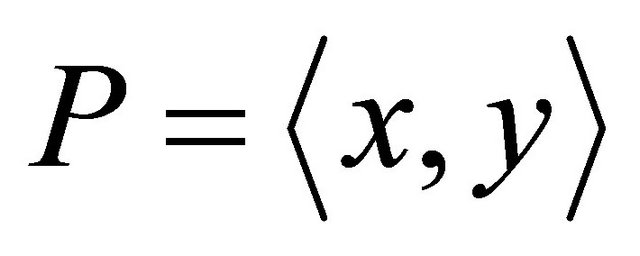 , where
, where![]() ,
, ![]() are the Cartesian coordinates of P, and compute the new radius according to the following equation: [Match names
are the Cartesian coordinates of P, and compute the new radius according to the following equation: [Match names  and Radius3Dnew with that in the flowchart Figure 9].
and Radius3Dnew with that in the flowchart Figure 9].
 (2)
(2)
In a 3D structure the computation is the same except we randomly generate a point 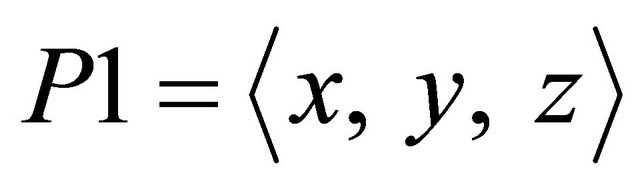 in order to compute the new radius according to the following equation:
in order to compute the new radius according to the following equation:
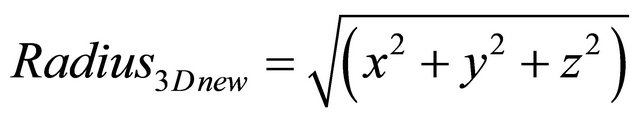 (3)
(3)
The flowchart in Figure 9 describes the process, IN-BS, by which we determine whether, or not, a node is within BS.
In the first experiment we compare between SBS and DBBS in terms of Blocking, Dropping probabilities and Bandwidth Utilization in 2D and 3D structures.
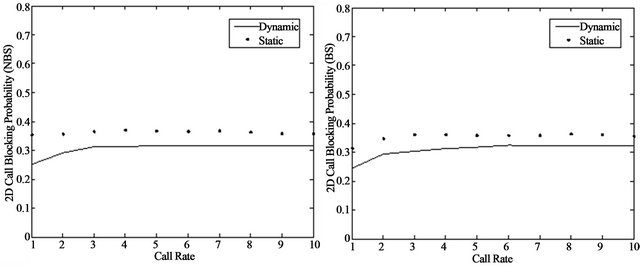
Figure 10 illustrates the results of the simulation for both Blocking Probabilities (BP) in 2D space for both Non BS (NBS) as in Figure 10(a) and with BS as in Figure 10(b). As expected, BP is less in the case of BS in comparison with that of NBS for both schemes. This is due to an increase in the probability of nodes that cross the BS region. The experiment shows that DDBS outperform the static scheme by almost 6% on average for the NBS case and by almost 5% for the BS case on average.
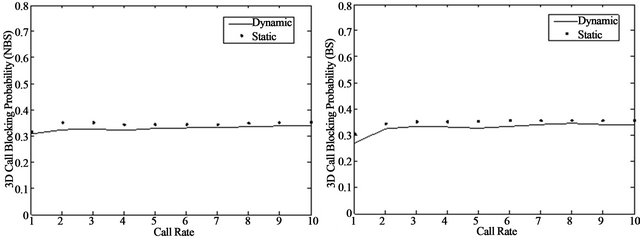
For 3D space, the area of the covered cell gets increased. Thus, the movement space is as well getting increased. As a node moves freely, the probability of a call being dropped in a 3D space is more when compared with 2D space. As a result, BP in 3D increases by 2% on average (cf. Figure 11).
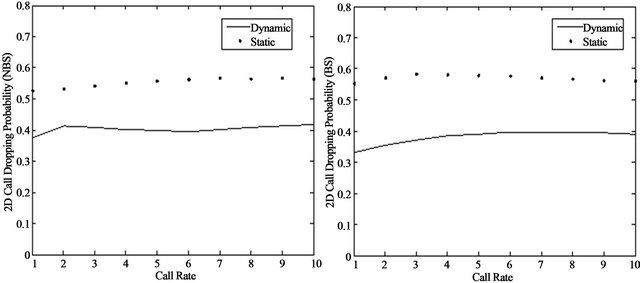
The results of the simulation for both 2D and 3D dropping probabilities respectively are shown in Figures 12 and 13. As expected, DP outperforms the static scheme in both cases with BS and with NBS. Further-
 (a) (b)
(a) (b)
Figure 8. (a) The structure of a 2D cellular wireless network; (b) 3D model.

Figure 9. IN-BS.
 (a) (b)
(a) (b)
Figure 10. (a) 2D BP with NBS; (b) 2D BP BS.
 (a) (b)
(a) (b)
Figure 11. (a) 3D BP with NBS; (b) 3D BP with BS.
 (a) (b)
(a) (b)
Figure 12. (a) 2D DP with NBS; (b) DP with BS.
 (a) (b)
(a) (b)
Figure 13. (a) 3D DP with NBS; (b) 3D DP with BS.
more, taking into consideration the increase of the dimension from 2 to 3, the comparison shows that the DP increases on average by almost 2%.
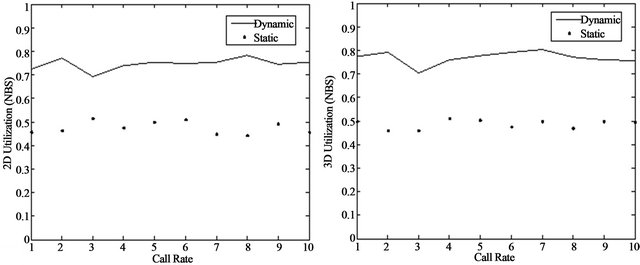
Figure 14 shows the results of bandwidth utilization with no BS for both cases 2D and 3D. We note that the BW utilization in the 3D case is on average more by 2.3%. This is due to an increase in the area of coverage.
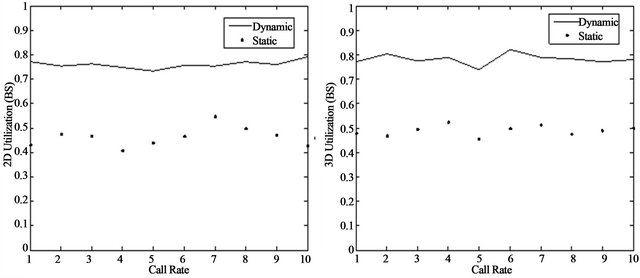
Figure 15 shows the results of bandwidth utilization with the existence of BS region for both cases 2D and 3D. We note that the BW utilization for the 3D case is on average is more by 2.1% which is 0.2% less with NBS. This is due to the fact that when the area of coverage is less, the utilization decreases. The 3D structure has higher bandwidth utilization than 2D due to the fact that there are 8 cells in a 3D structure while there are 6 cells in a 2D structure only. As a result, the probability for any new or handoff call will be 1/6 in 2D and 1/8 in 3D. In other words, the bandwidth utilization decreases since the distribution of calls will be over 8 cells instead of 6.
To show the effect of “f” on both DP and BP, we run the simulation for different values of “f” that range from 0.1 to 1. Figure 16 shows the results: as “f” increases, both BP and DP decrease. This is due to the fact that the value “f” determines the amount of BW that can be borrowed by other calls. That is, if “f” is small then the amount of borrowed BW is small hence higher number
 (a) (b)
(a) (b)
Figure 14. (a) 2D bandwidth utilization with NBS; (b) 3D bandwidth utilization with NBS.
 (a) (b)
(a) (b)
Figure 15. (a) 2D bandwidth utilization with BS; (b) 3D bandwidth utilization with BS.
of calls will be dropped or blocked. As a result, BP and DP increase. On the contrary, the bandwidth utilization will increase as “f” increases. This is due to the fact that when the value of “f” is as large of 1, then larger amount of bandwidth will be utilized (cf. Figure 17).
5. Conclusion
Having a QoS guarantee in wireless cellular networks is not an easy task, due to the mobility of nodes and the scarcity of resources. Two different techniques Static and Dynamic Borrowing schemes (both in 2D and extended to 3D) were presented in this paper. A java code simulator was used to implement the two proposed techniques.
We have employed three important performance metrics: BP, DP and bandwidth utilization. We have also studied the effect of fair factor “f” and the three-dimensional motion effect on the performance metrics. The experiments have shown that, on average for BP, DBBS outperforms the static scheme by 5.5% in a 2D structure, and 2% in a 3D structure. DP has increased by 2% on average in 3D in comparison with 2D. The effect of moving from 2D to 3D space on BW utilization has also proved to be positive: the utilization have increased by 2.3% due to an increase on the area of coverage. The utilization with BS was less by 0.2% in a 3D space. With regard to “f”, an increase in the value of “f” has led to a decrease in the values of both BP and DP. This is due to the fact that the
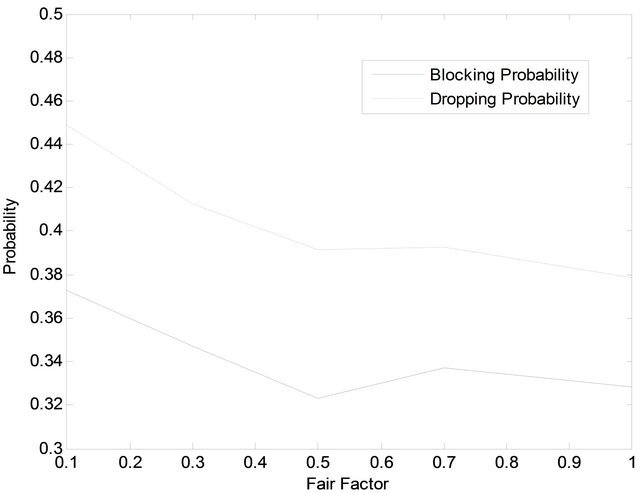
Figure 16. Fair factor effect on the blocking and dropping probabilities.
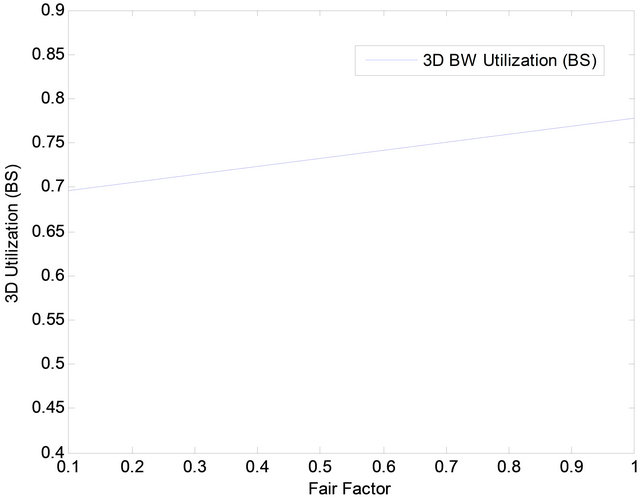
Figure 17. Fair factor effect on utilization with blind spot in three-dimensional space.
value “f” determines the amount of BW that can be borrowed by other calls.
REFERENCES
- S. H. Al-Sharaeh, “Dynamic Rate-Based Borrowing Scheme for QoS Provisioning in High Speed Multimedia Wireless Cellular Networks,” Applied Mathematics and Computation, Vol. 179, No. 2, 2006, pp. 714-724.
- C.-J. Huang, Y.-T. Chuang and D.-X. Yang, “Implementation of Call Admission Control Scheme in Next Generation Mobile Communication Networks Using Particle Swarm Optimization and Fuzzy Logic Systems,” Expert Systems with Applications, Vol. 35, No. 3, 2008, pp. 1246- 1251.
- H.-Y. Hsieh, C.-W. Li, S.-W. Liao, Y.-W. Chen, T.-L. Tsai and H.-P. Lin, “Moving toward End-to-End Support for Handoffs across Heterogeneous Telephony Systems on Dual-Mode Mobile Devices,” Computer Communications, Vol. 31, No. 11, 2008, pp. 2726-2738.
- P. V. Krishna, N. C. S. N. Iyengar and S. Misra, “An Efficient Hash Table-Based Node Identification Method for Bandwidth Reservation in Hybrid Cellular and AdHoc Networks,” Computer Communications, Vol. 31, No. 4, 2008, pp. 722-733. doi:10.1016/j.comcom.2007.10.018
- N. Hu and W.-L. Wu, “Call Admission Control Scheme for Real-Time Services in Packet-Switched OFDM Wireless Networks,” The Journal of China Universities of Posts and Telecommunications, Vol. 15, No. 1, 2008, pp. 80- 84.
- S. A. AlQahtani and A. S. Mahmoud, “Performance Analysis of Two Throughput-Based Call Admission Control Schemes for 3G WCDMA Wireless Networks Supporting Multiservices,” Computer Communications, Vol. 31, No. 1, 2008, pp. 49-57.
- D. A. Levine, I. F. Akyildiz and M. Naghshineh, “The Shadow Cluster Concept for Resource Allocation and Call Admission in ATM-Based Wireless Networks,” Proceedings of the 1st Annual International Conference on Mobile Computing and Networking, 1995, pp. 142- 150.
- S. Valaee and B. Li, “Distributed Call Admission Control for Ad Hoc Networks”.
- Y. B. Lin and I. Chlamtac, “Wireless and Mobile Network Architecture,” Wiley, New York, 2001, pp. 60-65.
- X. Y. Luo, I. L.-J. Thng, B. Li and S. M. Jiang, “Measurement-Based Pre-assignment Scheme with Connection-Level QoS Support for Multiservice Mobile Networks,” Lecture Notes in Computer Science, Vol. 1815, 2000, pp. 932-944.
- J. Carle, J.-F. Myoupo and D. Sem, “A Basis for 3-D Cellular Networks,” Proceedings of the 15 International Conference on Information Networking (ICOIN.01), Beppu City, 31 January-2 February 2001, pp. 631-636.
- E. Mona, O. Stephan and A. Hussein, “A Rate-Based Borrowing Scheme for QoS Provisioning in Multimedia Wireless Networks,” IEEE Transactions on Parallel and Distributed Systems, Vol. 13, No. 2, 2002, pp. 156-166.

