Advances in Pure Mathematics
Vol.4 No.6(2014), Article ID:47285,7 pages
DOI:10.4236/apm.2014.46039
On Some Properties of Digital Roots
Ilhan M. Izmirli
Department of Statistics, George Mason University, Fairfax, USA
Email: iizmirl2@gmu.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 March 2014; revised 24 April 2014; accepted 9 May 2014
ABSTRACT
Digital roots of numbers have several interesting properties, most of which are well-known. In this paper, our goal is to prove some lesser known results concerning the digital roots of powers of numbers in an arithmetic progression. We will also state some theorems concerning the digital roots of Fermat numbers and star numbers. We will conclude our paper by an interesting application.
Keywords:Digital Roots, Additive Persistence, Perfect Numbers, Mersenne Primes, Fermat Numbers, Star Numbers

1. Introduction
The part of mathematics that deals with the properties of specific types of numbers and their uses in puzzles and recreational mathematics has always fascinated scientists and mathematicians (O’Beirne 1961 [1] , Gardner 1987 [2] ).
In this short paper, we will talk about digital roots—a well-established and useful part of recreational mathematics which materializes in as diverse applications as computer programming (Trott 2004) [3] and numerology (Ghannam 2012 [4] ). As will see, digital roots are equivalent to modulo 9 arithmetic (Property 1.6) and hence can be thought of as a special case of modular arithmetic of Gauss (Dudley, 1978) [5] .
Let us start out by the following existence theorem:
Theorem 1.1. Let
![]() be a natural number and let
be a natural number and let
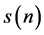 denote the sum of the digits of
denote the sum of the digits of![]() . In a finite number of steps, the sequence
. In a finite number of steps, the sequence
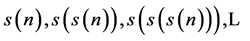 becomes a constant.
becomes a constant.
Proof. Let , where for any
, where for any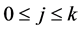 ,
,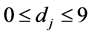 . This implies that
. This implies that

If
![]() is a one digit number, that is if
is a one digit number, that is if , then,
, then,
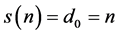 is the required constant. Else, at least one of
is the required constant. Else, at least one of
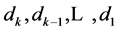 is positive and,
is positive and,
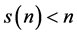
Thus, repeatedly applying the s operator, we will get a decreasing sequence of numbers. Once a term of this sequence becomes a single digit number, from then on the sequence will remain a constant.
Definition 1.1. Let
 denote the constant value the sequence
denote the constant value the sequence
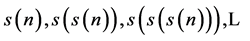 converges to. We call
converges to. We call
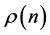 the digital root of
the digital root of![]() .
.
Here are some simple properties that follow immediately from this definition:
Property 1.1.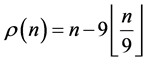 , where
, where
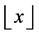 stands for the geatest integer less than or equal to
stands for the geatest integer less than or equal to![]() .
.
Property 1.2.
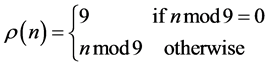
Property 1.3.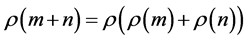 .
.
Property 1.4.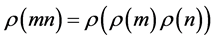 .
.
Property 1.5. .
.
Property 1.6.
This
![]() symmetric matrix Table 1, which is formed by replacing
the numbers in a regular
symmetric matrix Table 1, which is formed by replacing
the numbers in a regular
![]() multiplication table by their digital roots, is referred to as a Vedic square. Vedic
squares have been used extensively to create geometric patterns and symmetries,
and even musical compositions by highlighting specific numbers. For more information
see Pritchard (2003) [6] .
multiplication table by their digital roots, is referred to as a Vedic square. Vedic
squares have been used extensively to create geometric patterns and symmetries,
and even musical compositions by highlighting specific numbers. For more information
see Pritchard (2003) [6] .
Closely related to the concept of digital roots is that of additive persistence,
which is defined as the number of (additive) steps required to obtain its digital
root. We will denote the additive persistence of a nonnegative integer n by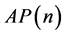 . Clearly, for any single digit number
n the additive persistence is 1.
. Clearly, for any single digit number
n the additive persistence is 1.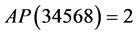 , because we need two steps to obtain
, because we need two steps to obtain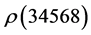 :
:
Step 1.
![]()
Step 2.
![]()
The smallest number with additive persistence of
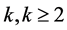 is
is
![]()
1 followed by ’s. For more information on additive
persistence see Hinden (1974) [7] .
’s. For more information on additive
persistence see Hinden (1974) [7] .
Some Well-Known Results
Proposition 1.1. Digital root of a square is 1, 4, 7, or 9.
By Property 1.2, the digital root of
![]() is
is
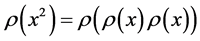
which can only be
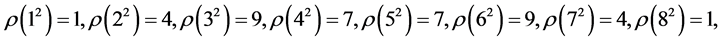
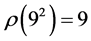 .
.
Proposition 1.2. Digital root of a perfect cube is 1, 8 or 9.
Proof is similar to the one given above.
Proposition 1.3. Digital roots of the powers of a natural number x form a cyclical
sequence. This cycle is the same for all numbers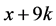 , where k is any natural number:
, where k is any natural number:
This follows because for any![]() ,
,
![]() and for any two natural numbers
and for any two natural numbers
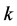 and
and
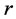
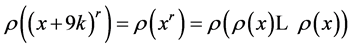
We can use Table 2 to compute digital roots of powers of large numbers. For example,

Proposition 1.5. Digital root of an even perfect number (except 6) is 1.
Proof. Every even perfect number
![]() is of the form
is of the form
Table 1 . The multiplication table for digital roots is the familiar modulo 9 multiplication table with 0 replaced by 9.
Table 2. Digital roots of the powers of a natural number x form a cyclical sequence.

where
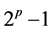 is a Mersenne prime. By putting
is a Mersenne prime. By putting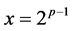 , we have
, we have

Here, the last equality follows from properties 1, 2, and 3 above.
By proposition 1.2,
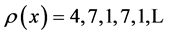
and
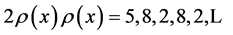
Hence the result follows.
To generalize the concept of digital roots to any other base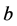 , one should simply change the 9 in the
formulas to
, one should simply change the 9 in the
formulas to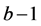 . For more information on digital roots
see Averbach and Chein (2000) [8] .
. For more information on digital roots
see Averbach and Chein (2000) [8] .
In the following sections, we will prove some results on digital roots of powers of numbers in an arithmetic progression as well as digital roots of Fermat numbers and star numbers.
2. Digital Roots of Powers of Numbers in an Arithmetic Progression
We start with the following Proposition 2.1. Let k, m and n be three consecutive
terms in an arithmetic progression with common difference![]() . Let
. Let
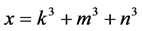
If d is not a multiple of 3, then .
.
Proof. Let
 and
and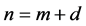 . Then
. Then
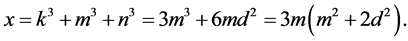
Consequently, to prove the proposition, we must prove
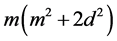 is divisible 3 by for any natural number m and for any natural number d that is
not a multiple of three.
is divisible 3 by for any natural number m and for any natural number d that is
not a multiple of three.
If m is divisible by 3, the result follows. So, let us consider the two cases:
Case 1.![]() . In this case
. In this case
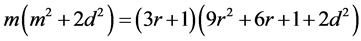
Since ,
,
Thus,
Case 2.![]() . In this case
. In this case
Again,
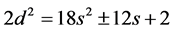
Thus,
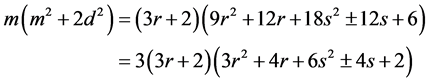
Remark. The restriction on
![]() is necessary. For example, let
is necessary. For example, let
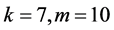 and
and![]() .
.
Then,
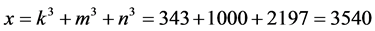
and
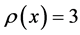
Using the fact that a sum is divisible by a positive integer if all terms are divisible
by a positive integer we get Theorem 2.1. Let q be a multiple of three. Let
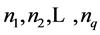 be any q consecutive terms of an arithmetic progression whose common difference
d is not a multiple of three. Let
be any q consecutive terms of an arithmetic progression whose common difference
d is not a multiple of three. Let
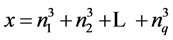
Then,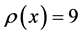 .
.
For example, let
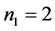 ,
,
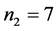 ,
,
 ,
,
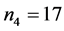 ,
,
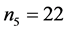 and
and

Then,

and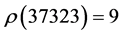 .
.
Again if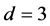 , this does not hold. As a counterexample,
, this does not hold. As a counterexample,
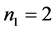 ,
,
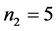 ,
,
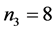 ,
,
 ,
,
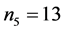 and
and

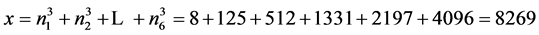
and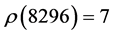 .
.
Corollary 2.1. Let q be a multiple of three. Putting , we get that the sum of the cubes of
q consecutive integers is divisible by 9. Putting
, we get that the sum of the cubes of
q consecutive integers is divisible by 9. Putting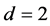 , we get that the sum of the cubes of
q consecutive odd integers (even integers) is divisible by 9.
, we get that the sum of the cubes of
q consecutive odd integers (even integers) is divisible by 9.
Although similar results do not necessarily hold for sixth powers, we show that they do for ninth powers. In fact, we find out that the restriction on d is not needed for ninth powers.
Proposition 2.2. Let
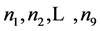 be nine consecutive terms in an arithmetic progression with common difference d.
Let
be nine consecutive terms in an arithmetic progression with common difference d.
Let
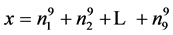
Then,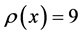 .
.
Proof. This follows by writing
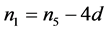
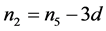
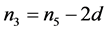
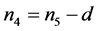

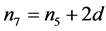

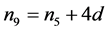
and noting that
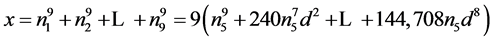
Using the fact that a sum is divisible by a positive integer if all terms are divisible
by a positive integer we get Theorem 2.2. Let
![]() be a multiple of nine. Let
be a multiple of nine. Let
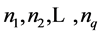 be any
be any
![]() consecutive terms of an arithmetic progression whose common difference d. Let
consecutive terms of an arithmetic progression whose common difference d. Let
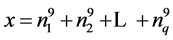
Then, .
.
Corollary 2.2. Let
![]() be a multiple of nine. Putting
be a multiple of nine. Putting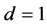 , we get that the sum of the ninth powers
of
, we get that the sum of the ninth powers
of
![]() consecutive integers is divisible by 9. Putting
consecutive integers is divisible by 9. Putting , we get that the sum of the ninth powers
of
, we get that the sum of the ninth powers
of
![]() consecutive odd integers (even integers) is divisible by 9.
consecutive odd integers (even integers) is divisible by 9.
3. Digital Roots of Fermat Numbers
As is well-known, a Fermat number
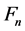 is defined as
is defined as
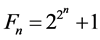
For computational purposes the following recursion formula is useful:
Theorem 3.1. For![]() ,
,

Proof. Since
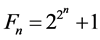
and for![]() ,
,
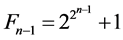

Thus,
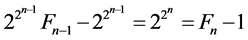
Thus,
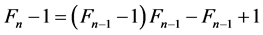
and the formula follows.
Inspection of the first few Fermat numbers F0 = 3, F1 = 5,
F2 = 17, F3 = 257, F4 = 655373, F5 =
4294967297…shows that for![]() ,
,
 is 5 if
is 5 if
![]() is odd and 8 if
is odd and 8 if
![]() is even. In fact, this is indeed true for all
is even. In fact, this is indeed true for all![]() :
:
Theorem 3.1. Let
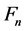 be the
be the
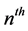 Fermat number. Then,
Fermat number. Then,
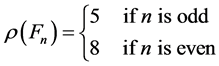
Proof. Proof is by induction. Clearly, the claim is true for![]() . Assume it is true for
. Assume it is true for![]() . Then,
. Then,
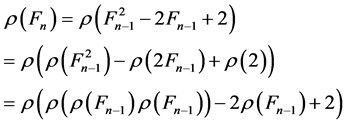
Suppose
![]() is odd. Then
is odd. Then

Suppose
![]() is even. Then
is even. Then
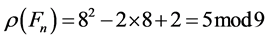
4. Digital Roots of Star Numbers
The
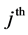 star number (so called because geometrically these numbers can be arranged to represent
hexagrams) is denoted as
star number (so called because geometrically these numbers can be arranged to represent
hexagrams) is denoted as
![]() and is of the form
and is of the form

for
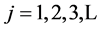
So,
 ,
,
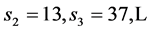 and so on. It is easy to show that
and so on. It is easy to show that

for
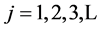
Pictorially,
![]() can be represented as
can be represented as
•
and
![]() as
as
•
••••
•••
••••
•
depicting the six-cornered star shape.
Clearly,
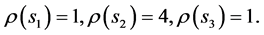 In factLemma 4.1. The digital root of a star number is
always 1 or 4. In fact, the progression of digital roots of star numbers is
In factLemma 4.1. The digital root of a star number is
always 1 or 4. In fact, the progression of digital roots of star numbers is

Proof. Since the digital root of any integer is one of , the digital root of a product of the
form
, the digital root of a product of the
form
 is
is
 (0 represented as 9). Consequently, the digital root of a product of the form
(0 represented as 9). Consequently, the digital root of a product of the form
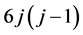 is one of
is one of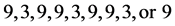 . Hence the digital roots of star numbers
are
. Hence the digital roots of star numbers
are
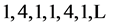
5. An Application
Here is a problem simple problem.
Prove that
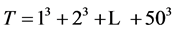
is divisible by 9.
Here we will apply Proposition 2.1. We write
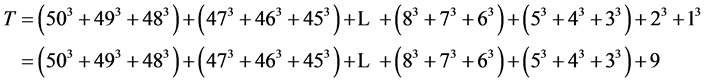
But by Proposition 2.1 the sum in each parenthesis is divisible by 9, and hence so is their sum, and their sum plus 9.
Here is another problem that can be solved using digital roots. Problems similar to this one can be found in Polya (1957) [9] and (Noller, et al. 1978) [10] .
Suppose we have a five-digit number. We are given that this number is divisible by 72. Starting with the first one, how many digits of this number must be disclosed before we can uniquely determine it?
Assume we are given the first digit, say 4. Obviously, more information will be
needed before a unique solution is found. For example,
 ,
,
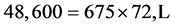 all fit the bill. So, assume now the second digit is
also given, say 8. Again, we cannot find a unique solution based on this information:
all fit the bill. So, assume now the second digit is
also given, say 8. Again, we cannot find a unique solution based on this information: ,
,
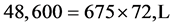 are all possible solutions. So, assume one more digit
is given, say 9. We claim this would be enough to solve the problem.
are all possible solutions. So, assume one more digit
is given, say 9. We claim this would be enough to solve the problem.
If a number is divisible by 72, it must be divisible by both 8 and 9. But a number
is divisible by 8 only if one of the two conditions holds: The hundreds digit is
even and the last two digits are a multiple of 8 or the hundreds digit is odd and
the last two digits are a multiple of 4 but not 8. Since in our example the hundreds
digit is odd, the last two digits of the number we are looking for must be a multiple
of 4 but not 8, that is, the last two digits must be one of
![]()
On the other hand, to be divisible by 9, the digital root of the number must be 9.
Since
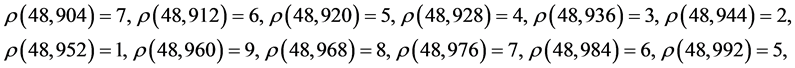
we know that the number must be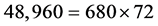 .
.
References
- O’Beirne, T.H. (1961) Puzzles and Paradoxes. New Scientist, No. 230, 53-54
- Gardner, M. (1987) The Second Scientific American Book of Puzzles and Diversions. University of Chicago Press, Chicago.
- Trott, M. (2004) The Mahematica Guide Book for Programming. Springer-Verlag, New York.http://dx.doi.org/10.1007/978-1-4419-8503-3
- Ghannam, T. (2012) The Mystery of Numbers: Revealed through Their Digital Roots. 2nd Edition, Create Space Publications, Seattle.
- Dudley, U. (1978) Elementary Number Theory. Dover, New York.
- Pritchard, C. (2003) The Changing Shape of Geometry: Celebrating a Century of Geometry and Geometry Teaching. Cambridge University Press, Cambridge.
- Hinden, H.J. (1974) The Additive Persistence of a Number. Journal of Recreational Mathematics, 7, 134-135.
- Averbach, B. and Orin, C. (2000) Problem Solving through Recreational Mathematics. Dover Publications, Mineola.
- Polya, G. (1957) How to Solve It: A New Aspect of Mathematical Method. 2nd Edition, Princeton University Press, Princeton.
- Noller, R.B., Ruth, E.H. and David, A.B. (1978) Creative Problem Solving in Mathematics . State University College at Buffalo, Buffalo.


