Advances in Pure Mathematics
Vol.3 No.1(2013), Article ID:27357,5 pages DOI:10.4236/apm.2013.31010
Hyperbolic Coxeter Pyramids
Department of Mathematical Sciences, University of Durham, Durham, England
Email: j.a.mcleod@durham.ac.uk
Received August 11, 2012; revised October 10, 2012; accepted October 21, 2012
Keywords: Hyperbolic; Coxeter; Polytope; Pyramid
ABSTRACT
Hyperbolic Coxeter polytopes are defined precisely by combinatorial type. Polytopes in hyperbolic n-space with n + p faces that have the combinatorial type of a pyramid over a product of simplices were classified by Tumarkin for small p. In this article we generalise Tumarkin’s methods and find the remaining hyperbolic Coxeter pyramids.
1. Introduction
The polytopes in n dimensions that have 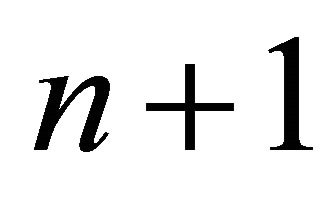 faces are referred to collectively as the simplices of the geometric space they inhabit. A simplex may always be thought of as a pyramid, although every face may be considered to be the “base” of the pyramid. In this article we consider only Coxeter polytopes, which are precisely those that are the fundamental domains of reflection groups. The Coxeter simplices are well known in Euclidean, Spherical and Hyperbolic space. These lists illustrate an important distinction that separates Hyperbolic space from the first two spaces in this list, namely that there is an upper bound on the dimension above which there are no simplices.
faces are referred to collectively as the simplices of the geometric space they inhabit. A simplex may always be thought of as a pyramid, although every face may be considered to be the “base” of the pyramid. In this article we consider only Coxeter polytopes, which are precisely those that are the fundamental domains of reflection groups. The Coxeter simplices are well known in Euclidean, Spherical and Hyperbolic space. These lists illustrate an important distinction that separates Hyperbolic space from the first two spaces in this list, namely that there is an upper bound on the dimension above which there are no simplices.
This distinction is much stronger than the example illustrates. The proof due to Vinberg that there are no co-compact hyperbolic reflection groups for 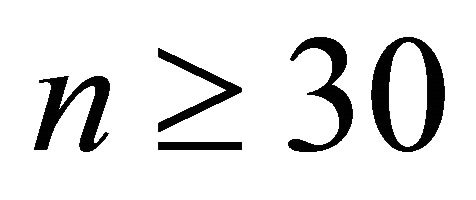 is principally a combinatorial proof demonstrating that there are no hyperbolic Coxeter polytopes for large enough dimension (c.f. [1]).
is principally a combinatorial proof demonstrating that there are no hyperbolic Coxeter polytopes for large enough dimension (c.f. [1]).
The bounded hyperbolic Coxeter simplices were classified by Lannér [2] in 1950. The non-compact hyperbolic Coxeter simplices can be enumerated using similar methods to Lannér. These have been well studied (c.f. [3-6]).
Let 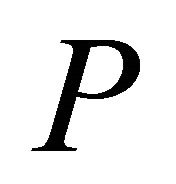 be a Coxeter polytope in hyperbolic space
be a Coxeter polytope in hyperbolic space 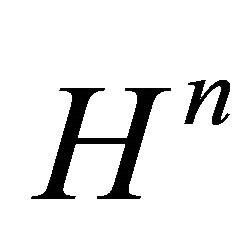 with
with  faces. For
faces. For  complete lists of hyperbolic Coxeter polytopes have been published by Tumarkin:
complete lists of hyperbolic Coxeter polytopes have been published by Tumarkin: 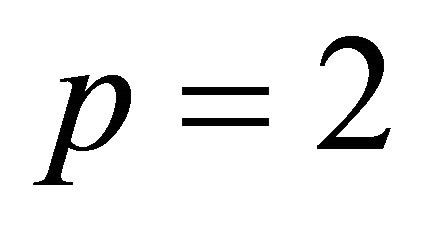 in [7]; and
in [7]; and 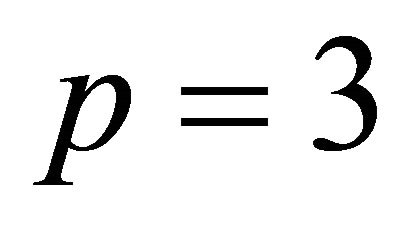 in [8]. These lists are complete, and contain in their number many examples of hyperbolic Coxeter polytopes with the combinatorial type of a pyramid. Tumarkin’s technique made use of the Gale diagram (c.f. [9]) which has quantitatively different characteristics when it describes a pyramid, as compared to other configurations. This distinction led to pyramids being classified using separate methods originally due to Vinberg.
in [8]. These lists are complete, and contain in their number many examples of hyperbolic Coxeter polytopes with the combinatorial type of a pyramid. Tumarkin’s technique made use of the Gale diagram (c.f. [9]) which has quantitatively different characteristics when it describes a pyramid, as compared to other configurations. This distinction led to pyramids being classified using separate methods originally due to Vinberg.
In this article we generalise Tumarkin’s classification of Hyperbolic Coxeter pyramids in terms of the Coxeter diagram, and then find all remaining examples of such polytopes using simple combinatorial arguments. The relevant background about Coxeter diagrams and the polytopes they represent is presented in Section 2. In Section 3 we generalise the appropriate results of Tumarkin, and complete the classification of hyperbolic Coxeter polytopes whose combinatorial type is a pyramid over a product of simplices.
2. Coxeter Diagrams
An acute-angled polytope is called a Coxeter polytope if all the dihedral angles at the intersections of pairs of faces are integer submultiples of  (or zero). A complete presentation of an acute-angled polytope is given by a Gram matrix. Denote by
(or zero). A complete presentation of an acute-angled polytope is given by a Gram matrix. Denote by  the codimension one hyperplane containing the ith face of the polytope. A Gram matrix
the codimension one hyperplane containing the ith face of the polytope. A Gram matrix  is a symmetric matrix with entries:
is a symmetric matrix with entries:

where  is the minimum hyperbolic distance between the two hyperplanes which contain the two faces.
is the minimum hyperbolic distance between the two hyperplanes which contain the two faces.
A Coxeter diagram is an edge-labelled graph which represents almost all of the same information about the combinatorial structure of a Coxeter polytope. Each vertex of a Coxeter diagram corresponds to a face, and the labels for the edges are as presented in Table 1.
An edge corresponding to a dihedral angle of  is said to be of weight m. The number of vertices in a Coxeter diagram is called the order of the diagram. A connected Coxeter diagram is called elliptic (respectively parabolic) if the corresponding Gram matrix is positive definite (respectively semidefinite and degenerate). A Coxeter diagram that consists only of elliptic (respectively parabolic) connected components is called elliptic (respectively parabolic). The rank of a Coxeter diagram is equal to the rank of the Gram matrix. The Gram matrix of a disconnected Coxeter diagram can be transformed into a block diagonal matrix via permutations of the rows and the same permutations of the columns. Therefore the rank of a disconnected Coxeter diagram is the sum of the ranks of its connected components. The rank of a connected elliptic diagram is equal to its order, while the rank of a connected parabolic diagram is one less than its order. Complete lists of connected elliptic and parabolic Coxeter diagrams can be found in [10].
is said to be of weight m. The number of vertices in a Coxeter diagram is called the order of the diagram. A connected Coxeter diagram is called elliptic (respectively parabolic) if the corresponding Gram matrix is positive definite (respectively semidefinite and degenerate). A Coxeter diagram that consists only of elliptic (respectively parabolic) connected components is called elliptic (respectively parabolic). The rank of a Coxeter diagram is equal to the rank of the Gram matrix. The Gram matrix of a disconnected Coxeter diagram can be transformed into a block diagonal matrix via permutations of the rows and the same permutations of the columns. Therefore the rank of a disconnected Coxeter diagram is the sum of the ranks of its connected components. The rank of a connected elliptic diagram is equal to its order, while the rank of a connected parabolic diagram is one less than its order. Complete lists of connected elliptic and parabolic Coxeter diagrams can be found in [10].
The vertices of the Coxeter polytope P can be read from the Coxeter diagram. Let J denote the set of vertices of the Coxeter diagram, and 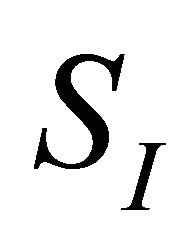 the subdiagram corresponding to a subset
the subdiagram corresponding to a subset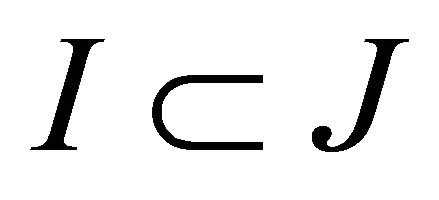 . We say that such a subset determines a face of the Coxeter polytope if the intersection of the faces in I is a face of P. We recall the following proposition (in this form) from [8], originally proven in [1] as Theorems 3.1 and 3.2.
. We say that such a subset determines a face of the Coxeter polytope if the intersection of the faces in I is a face of P. We recall the following proposition (in this form) from [8], originally proven in [1] as Theorems 3.1 and 3.2.
Proposition 2.1. ([8], Proposition 1)
1) A subset 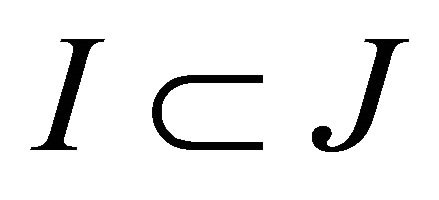 determines a face of the polytope P (apart from an infinitely distant vertex) if and only if the subdiagram
determines a face of the polytope P (apart from an infinitely distant vertex) if and only if the subdiagram  is elliptic. In this case the codimension of the corresponding face is the number of elements in I;
is elliptic. In this case the codimension of the corresponding face is the number of elements in I;
2) A subset 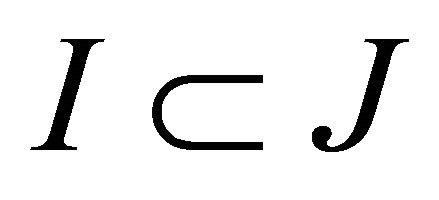 determines an infinitely distant vertex if and only if the subdiagram
determines an infinitely distant vertex if and only if the subdiagram  is not elliptic and there is a subset
is not elliptic and there is a subset 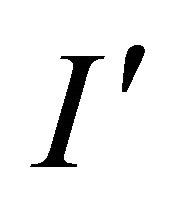 such that
such that  and
and  is parabolic of rank
is parabolic of rank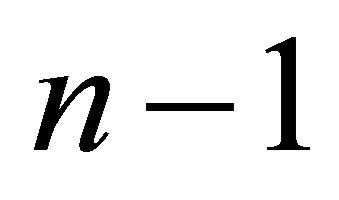 .
.
We can see from this proposition that if the order of a Coxeter diagram which determines a face of  is greater than
is greater than  it must correspond to an infinitely distant vertex, conversely if the order of a diagram which determines a face is less than
it must correspond to an infinitely distant vertex, conversely if the order of a diagram which determines a face is less than 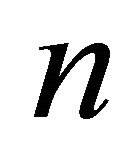 it must be elliptic.
it must be elliptic.
Table 1. The edges of a Coxeter diagram.
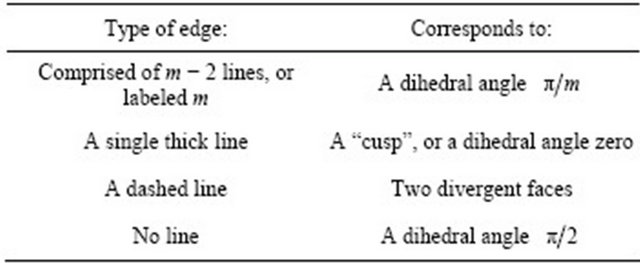
A connected Coxeter diagram all of whose proper subdiagrams are elliptic, and the whole diagram is not elliptic or parabolic, is called a Lannér diagram. These correspond to the bounded hyperbolic simplices. A connected Coxeter diagram all of whose proper subdiagrams are elliptic or connected parabolic, and the whole diagram is neither elliptic nor parabolic, is called a quasiLannér diagram. These correspond to the unbounded hyperbolic simplices of finite volume. Complete lists of Lannér and quasi-Lannér diagrams can be found in [10].
3. Pyramids
The following two lemmas are straightforward generalisations of Tumarkin’s results.
The first lemma was proven for p = 2 by Tumarkin [7]. This result was based on Vinberg’s general construction of unbounded Coxeter polytopes of finite volume which constructed hyperbolic Coxeter pyramids with n + 2 faces ([1], Chapter 2, §7). Tumarkin then proved the result again for p = 3. The following Lemma 3.2 is a generalization of Tumarkin’s Lemma 11 from [8].
Lemma 3.1. If a hyperbolic Coxeter 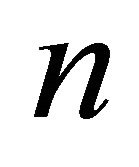 -polytope
-polytope 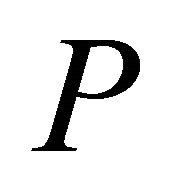 of finite volume is a pyramid with
of finite volume is a pyramid with 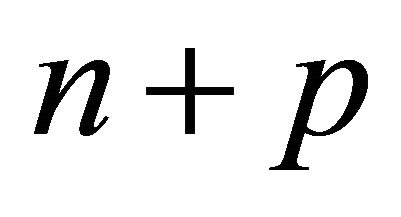 faces, then it is a pyramid over a product of
faces, then it is a pyramid over a product of 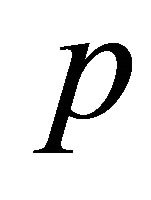 simplices.
simplices.
Proof. Suppose that P is a pyramid over some polytope . Then
. Then 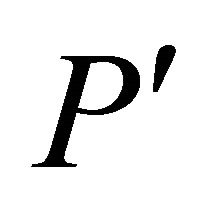 is the base of the pyramid above which is the apex A.
is the base of the pyramid above which is the apex A. 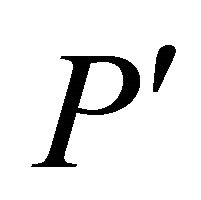 is bounded by
is bounded by  vertexes, each of which is connected to A by an edge of P. All of the faces of P excluding
vertexes, each of which is connected to A by an edge of P. All of the faces of P excluding 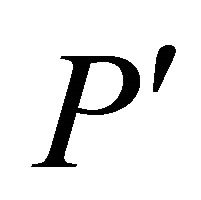 meet at A, and hence it is the confluence of
meet at A, and hence it is the confluence of 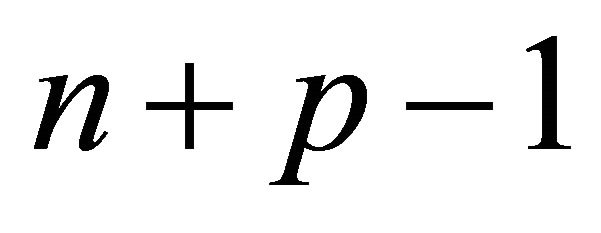 faces. When
faces. When 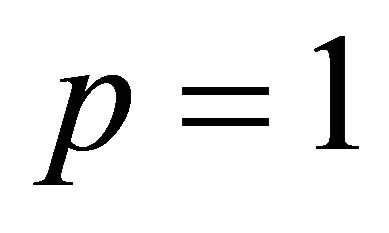 the polytope is a simplex, which is a pyramid over one simplex (of dimension n − 1). For
the polytope is a simplex, which is a pyramid over one simplex (of dimension n − 1). For  we see that
we see that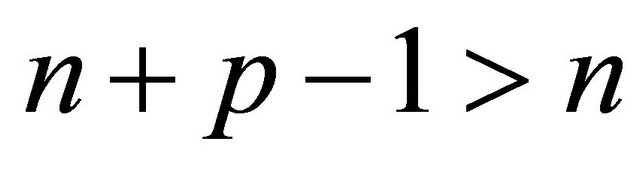 , and so the Coxeter diagram of a vertex is of order greater than
, and so the Coxeter diagram of a vertex is of order greater than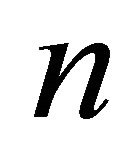 . We see from Proposition 2.1 that this forces A to be an infinitely distant vertex. For a sufficiently small horosphere h centred at A, the intersection
. We see from Proposition 2.1 that this forces A to be an infinitely distant vertex. For a sufficiently small horosphere h centred at A, the intersection  is covered by a reflection group. The fundamental domain of this reflection group is a Euclidean Coxeter polytope, which is of the same combinatorial type as P (c.f. [8]).
is covered by a reflection group. The fundamental domain of this reflection group is a Euclidean Coxeter polytope, which is of the same combinatorial type as P (c.f. [8]).
The geometry of a horosphere is equivalent to that of a Euclidean subspace of dimension 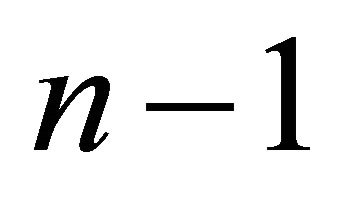 in Hyperbolic n-space. The hyperbolic Coxeter polytope P is the fundamental domain of a reflection group, which restricts to a Euclidean reflection group which covers the horosphere. Therefore,
in Hyperbolic n-space. The hyperbolic Coxeter polytope P is the fundamental domain of a reflection group, which restricts to a Euclidean reflection group which covers the horosphere. Therefore, 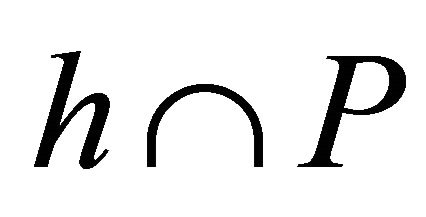 is a bounded Euclidean Coxeter n − 1- polytope with
is a bounded Euclidean Coxeter n − 1- polytope with 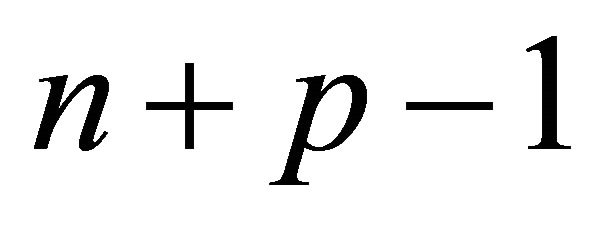 faces. The number of faces in the product of
faces. The number of faces in the product of 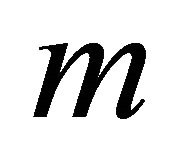 Euclidean simplices of dimension l is
Euclidean simplices of dimension l is , and we solve the following equation.
, and we solve the following equation.
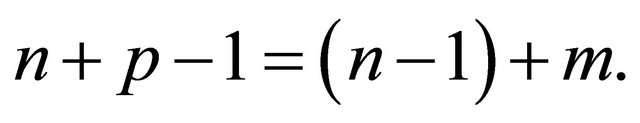
Therefore  is equivalent to the product of
is equivalent to the product of  simplices. ∎
simplices. ∎
The proof of this lemma is like that of Lemma 4 in [7].
Lemma 3.2. Let P be a hyperbolic Coxeter pyramid over a product of p simplices for  and
and 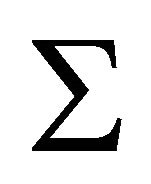 be a Coxeter diagram of P. Then
be a Coxeter diagram of P. Then 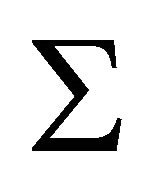 satisfies the following three conditions:
satisfies the following three conditions:
1) 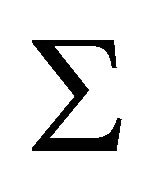 is a union of p quasi-Lannér diagrams
is a union of p quasi-Lannér diagrams . The intersection of the
. The intersection of the  is a unique node
is a unique node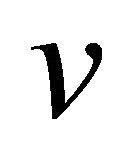 .
.  and
and 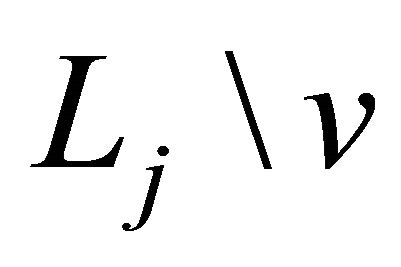 for
for  are not adjacent;
are not adjacent;
2) Each diagram  is parabolic. Any other subdiagram of
is parabolic. Any other subdiagram of  is elliptic;
is elliptic;
3) For any p vertices 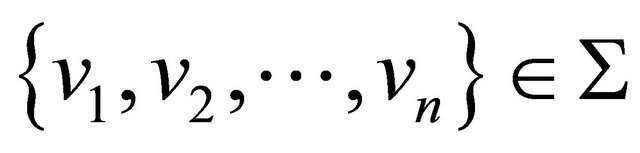 such that
such that 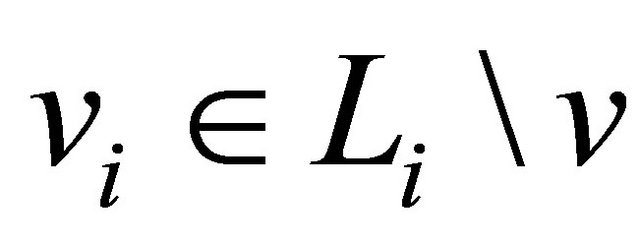 a diagram
a diagram 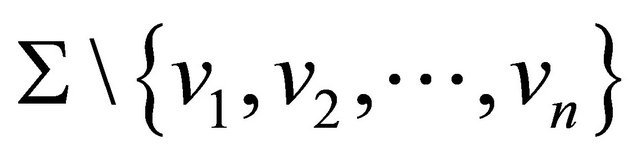 is either elliptic or connected parabolic.
is either elliptic or connected parabolic.
Any Coxeter diagram satisfying these conditions determines a hyperbolic Coxeter pyramid over a product of p simplices.
Proof. Let A be the apex of the pyramid P over a product of p simplices and 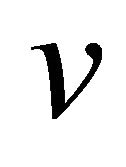 the node of
the node of 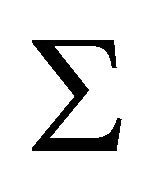 corresponding to the face opposite A. By Proposition 2.1 as A is an infinitely distant vertex the Coxeter diagram
corresponding to the face opposite A. By Proposition 2.1 as A is an infinitely distant vertex the Coxeter diagram 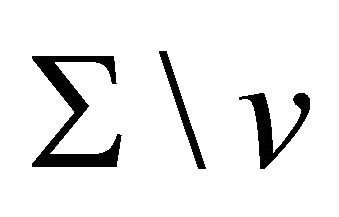 is parabolic of rank
is parabolic of rank . The number of faces in the product of
. The number of faces in the product of 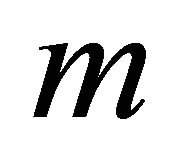 simplices of dimension
simplices of dimension  is
is , so the order of the Coxeter diagram is
, so the order of the Coxeter diagram is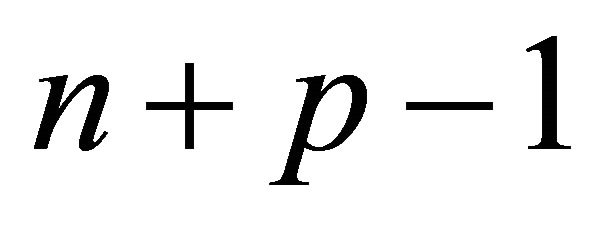 . For
. For 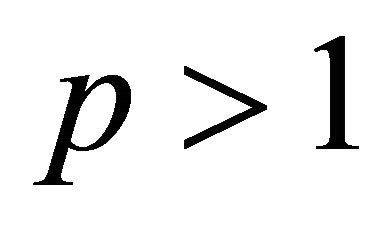 the Coxeter diagram is parabolic and has
the Coxeter diagram is parabolic and has  connected components which will be denoted
connected components which will be denoted ,
,  , all of which are by definition not adjacent. Note that all the subdiagrams of a connected parabolic Coxeter diagram are elliptic.
, all of which are by definition not adjacent. Note that all the subdiagrams of a connected parabolic Coxeter diagram are elliptic.
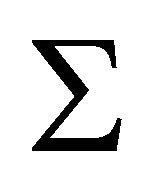 is the Coxeter diagram of a convex polytope of finite volume, and is therefore connected. Hence all of the connected components
is the Coxeter diagram of a convex polytope of finite volume, and is therefore connected. Hence all of the connected components 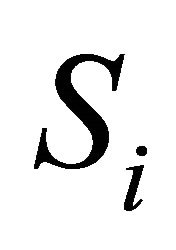 of
of  are connected to v by an edge, and
are connected to v by an edge, and  is the union of all of the
is the union of all of the , intersecting in the common node
, intersecting in the common node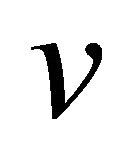 . All other proper subdiagrams of
. All other proper subdiagrams of 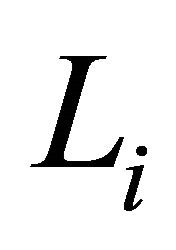 determine a face of P, and so are elliptic or parabolic. The smallest parabolic diagram is of order two, so the maximum order of a proper subdiagram of an
determine a face of P, and so are elliptic or parabolic. The smallest parabolic diagram is of order two, so the maximum order of a proper subdiagram of an 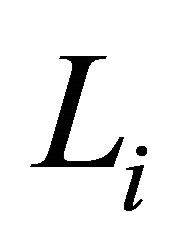 is
is 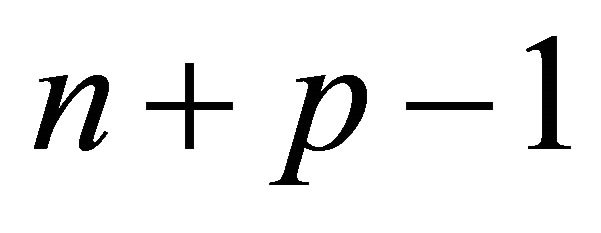 and hence for
and hence for  it must be elliptic. We see that, by definition, each of the
it must be elliptic. We see that, by definition, each of the 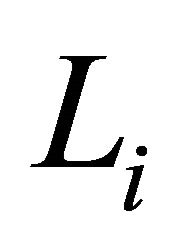 are quasiLannér.
are quasiLannér.
Any vertex of P except A corresponds to a subdiagram 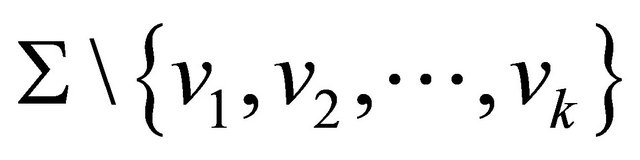 such that none of the vertices
such that none of the vertices 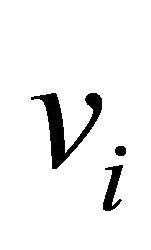 coincide with v. If
coincide with v. If  then the order of the resulting diagram is less than
then the order of the resulting diagram is less than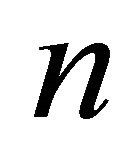 , and by Proposition 2.1 it determines a face of codimension
, and by Proposition 2.1 it determines a face of codimension , i.e. it does not determine a vertex. If
, i.e. it does not determine a vertex. If  then the order of the diagram is greater than n and the diagram must be parabolic, and at least one
then the order of the diagram is greater than n and the diagram must be parabolic, and at least one  remains without any vertices removed. This is a connected component of a parabolic diagram and is therefore parabolic, but it contains a parabolic diagram as a proper subdiagram. Hence
remains without any vertices removed. This is a connected component of a parabolic diagram and is therefore parabolic, but it contains a parabolic diagram as a proper subdiagram. Hence 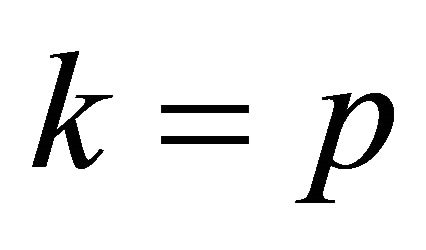 and at least one
and at least one 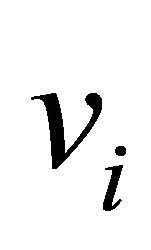 must be removed from each
must be removed from each .
.
Suppose that a Coxeter diagram  of order
of order 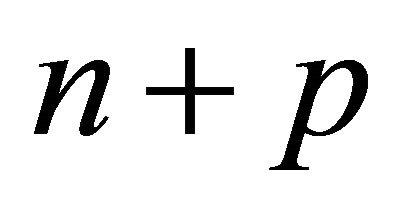 satisfies the three conditions of the lemma. Then
satisfies the three conditions of the lemma. Then  by Lemma 5.1 in [1]. By an argument identical to that in part 2 of the proof of Lemma 4 in [7] the Coxeter diagram
by Lemma 5.1 in [1]. By an argument identical to that in part 2 of the proof of Lemma 4 in [7] the Coxeter diagram  determines a Coxeter polytope P in
determines a Coxeter polytope P in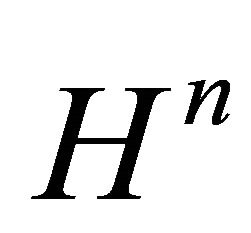 .
.
The polytope P is clearly a pyramid over the face v. Then by Lemma 3.1 it is a pyramid over a product of P simplices. ∎
These Lemmas provide a precise description of the combinatorial structure of the Coxeter diagram of a hyperbolic Coxeter pyramid. Recall that the hyperbolic pyramids with 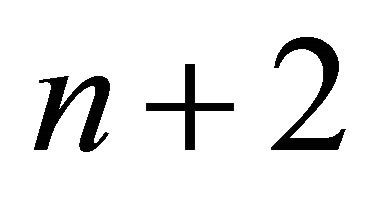 and
and  faces have been classified by Tumarkin ([7] and [8] respectively) and therefore we need only concern ourselves with
faces have been classified by Tumarkin ([7] and [8] respectively) and therefore we need only concern ourselves with . We now make use of the above results to find the remaining hyperbolic Coxeter pyramids.
. We now make use of the above results to find the remaining hyperbolic Coxeter pyramids.
Lemma 3.3. Let  be a hyperbolic pyramid with
be a hyperbolic pyramid with 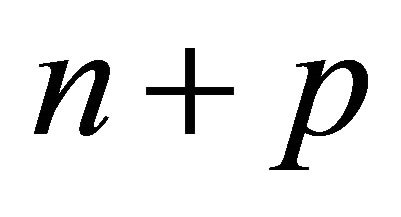 faces, then
faces, then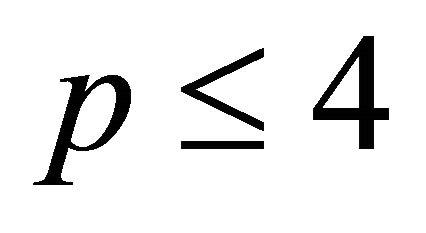 .
.
Proof. Let  be the Coxeter diagram of P. Choose
be the Coxeter diagram of P. Choose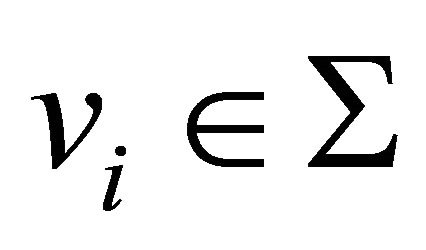 ,
, 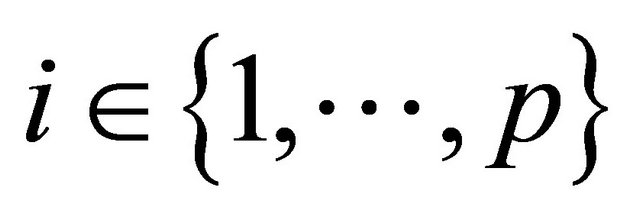 , which separates
, which separates  such that the connected component containing v consists of v and at least one vertex from each of the quasi-Lannér diagrams
such that the connected component containing v consists of v and at least one vertex from each of the quasi-Lannér diagrams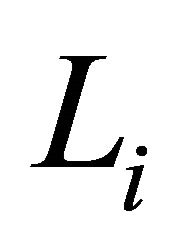 . The degree of v in the diagram
. The degree of v in the diagram  is not less than p, and by Lemma 3.2 part (3) the diagram is either elliptic or parabolic. By inspection of the elliptic and parabolic Coxeter diagrams the maximum degree of a vertex is equal to four, which is realised uniquely in the parabolic graph
is not less than p, and by Lemma 3.2 part (3) the diagram is either elliptic or parabolic. By inspection of the elliptic and parabolic Coxeter diagrams the maximum degree of a vertex is equal to four, which is realised uniquely in the parabolic graph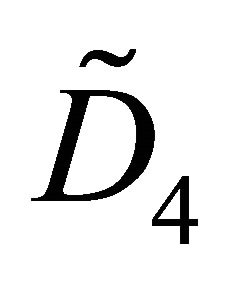 . ∎
. ∎
Note that the placement of the parabolic graph  constrains the labelling of the edges connecting the vertex v to the rest of the graph such that they must all be of weight 3.
constrains the labelling of the edges connecting the vertex v to the rest of the graph such that they must all be of weight 3.
Corollary 3.4. Let 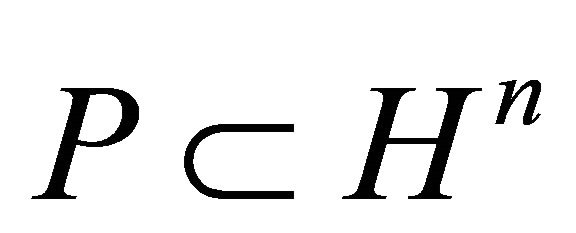 be a hyperbolic pyramid with
be a hyperbolic pyramid with  faces, then
faces, then .
.
Proof. Let  be the Coxeter diagram of P. Then
be the Coxeter diagram of P. Then 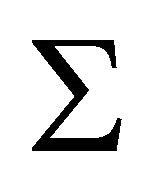 contains a particular
contains a particular 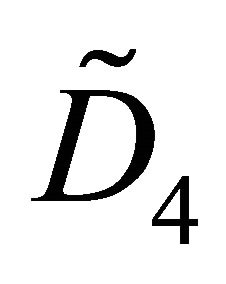 as a subgraph, and the vertex of degree four is the base of the pyramid. For P to have finite volume, it is necessary that any parabolic subgraph of
as a subgraph, and the vertex of degree four is the base of the pyramid. For P to have finite volume, it is necessary that any parabolic subgraph of  must be a component of a parabolic graph of rank
must be a component of a parabolic graph of rank 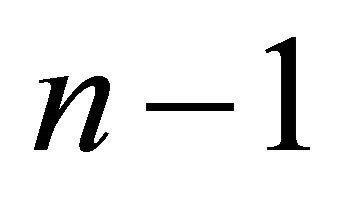 ([1], Proposition 4.2). Therefore
([1], Proposition 4.2). Therefore .
.
Assume that P has finite volume, and that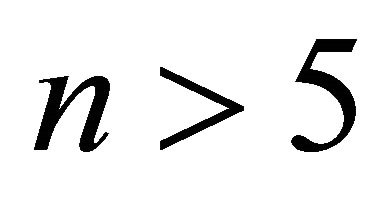 . Then
. Then 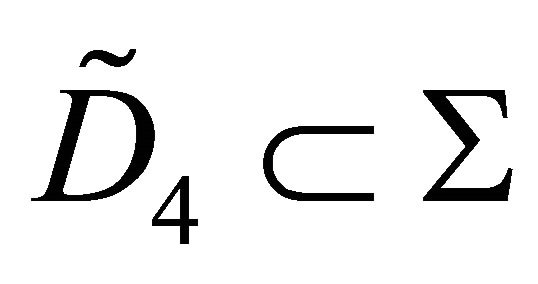 is a connected component of
is a connected component of , a parabolic graph of rank
, a parabolic graph of rank , and the graph
, and the graph  contains a parabolic graph of rank
contains a parabolic graph of rank . Therefore the connected components of
. Therefore the connected components of  are all parabolic subdiagrams of the quasi-Lannér diagrams
are all parabolic subdiagrams of the quasi-Lannér diagrams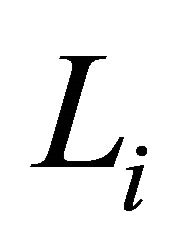 . However, by Lemma 3.2 part 2, each of the
. However, by Lemma 3.2 part 2, each of the 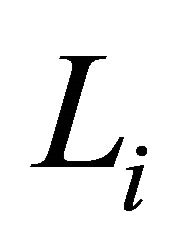 contain only one parabolic subdiagram, namely
contain only one parabolic subdiagram, namely , so
, so  is elliptic. Hence
is elliptic. Hence .
.
Proposition 3.5. A hyperbolic pyramid P with  faces has a Coxeter diagram which is among those given in Figure 2.
faces has a Coxeter diagram which is among those given in Figure 2.
Proof. By Corollary 3.4, hyperbolic pyramids with 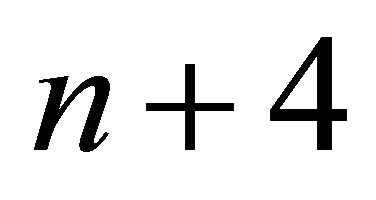 faces exist in
faces exist in  only. Therefore we have nine vertices, distributed between four quasi-Lannér diagrams which share a common vertex v. The smallest quasiLannér diagram is a family, each member of which is of rank 2 and has three vertices. Hence each of the four quasi-Lannér diagrams must be from this family, the members of which are shown in Figure 1.
only. Therefore we have nine vertices, distributed between four quasi-Lannér diagrams which share a common vertex v. The smallest quasiLannér diagram is a family, each member of which is of rank 2 and has three vertices. Hence each of the four quasi-Lannér diagrams must be from this family, the members of which are shown in Figure 1.
We know that every edge connecting 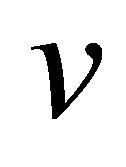 to another vertex has weight 3. Therefore the common vertex between all four quasi-Lannér diagrams must be the filled vertex in Figure 1 and the two labels
to another vertex has weight 3. Therefore the common vertex between all four quasi-Lannér diagrams must be the filled vertex in Figure 1 and the two labels  and
and  must be either 2 or 3. We can see that there are only two quasiLannér diagrams with this restriction.
must be either 2 or 3. We can see that there are only two quasiLannér diagrams with this restriction.
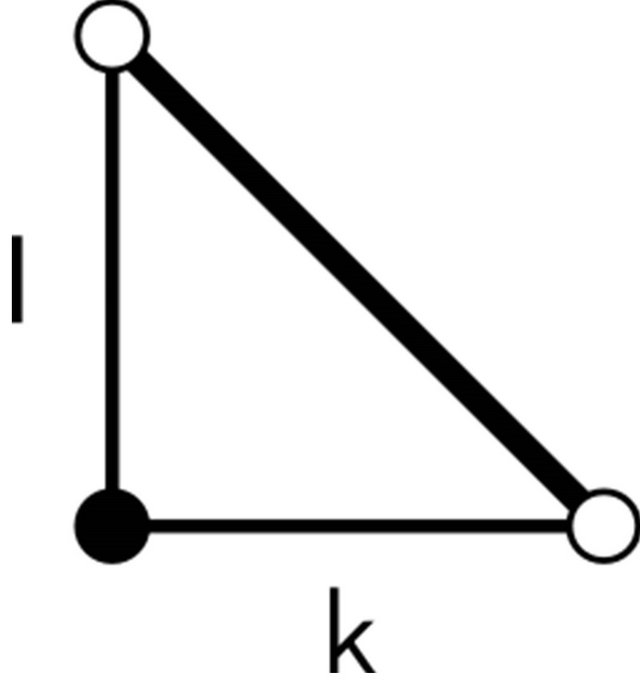
Figure 1. The Coxeter diagrams of the quasi-Lannér diagrams of rank 2 which have the following restrictions: ,
,  ,
, .
.
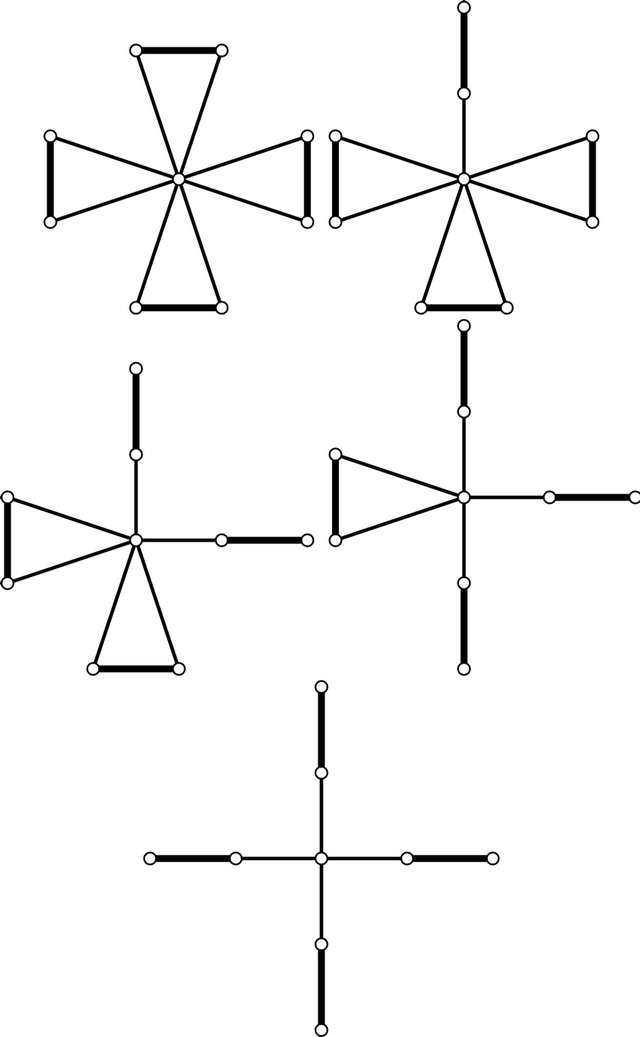
Figure 2. Coxeter diagrams of hyperbolic pyramids with 9 faces in H5.
There are five ways to assemble these into a complete Coxeter diagram of a hyperbolic pyramid, and those are presented in Figure 2. ∎
All together, we have proven the following.
Theorem 3.6. Let  be a Coxeter polytope in
be a Coxeter polytope in 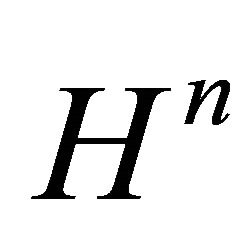 with Coxeter diagram
with Coxeter diagram  of order
of order 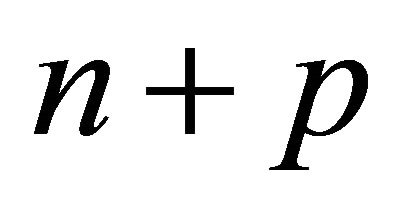 for
for . The combinatorial type of P is a hyperbolic pyramid over a product of p simplices if and only if it is one of the following:
. The combinatorial type of P is a hyperbolic pyramid over a product of p simplices if and only if it is one of the following:
1)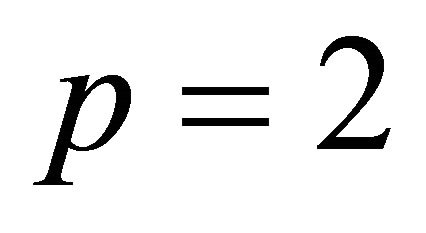 : among the list in Theorem 2 of [7];
: among the list in Theorem 2 of [7];
2)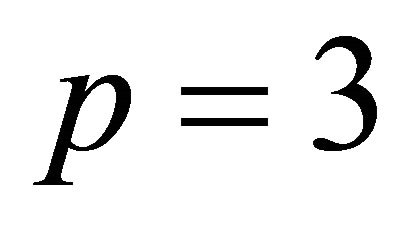 : among the list in §4 of [8];
: among the list in §4 of [8];
3)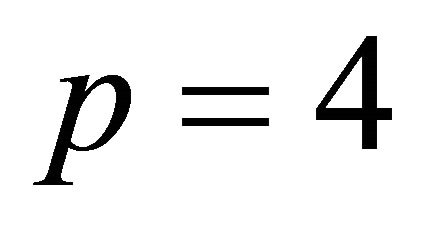 : when
: when  corresponds to a diagram in Figure 2, and this list is complete.
corresponds to a diagram in Figure 2, and this list is complete.
Remark 3.7. The two diagrams in Figure 2 with rotational symmetry of order four were among the root systems listed in Table 5.1 of [11].
4. Acknowledgements
The author would like to thank Pavel Tumarkin for his helpful comments on an earlier version of this article, and the anonymous reviewer for his comprehensive assessment of the manuscript.
REFERENCES
- È. B. Vinberg, “Hyperbolic Groups of Reflections,” Uspekhi Matematicheskikh Nauk, Vol. 40, 1985, pp. 29-66.
- F. Lannér, “On Complexes with Transitive Groups of Automorphisms,” Communications du Séminaire Mathématique de l'Université de Lund, Vol. 11, 1950, p. 71.
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe and S. T. Tschantz, “Commensurability Classes of Hyperbolic Coxeter Groups,” Linear Algebra and Its Applications, Vol. 345, No. 1, 2002, pp. 119-147. doi:10.1016/S0024-3795(01)00477-3
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe and S. T. Tschantz, “The Size of a Hyperbolic Coxeter Simplex,” Transformation Groups, Vol. 4, No. 4, 1999, pp. 329-353. doi:10.1007/BF01238563
- M. Chein, “Recherce des Graphes des Matrices de Coxeter Hyperboliques d’Ordre ≤10,” Revue Française Informatique Recherche Opérationnelle, Vol. 3, No. 2, 1969, pp. 3-16.
- A. A. Felikson, “Coxeter Decomposition of Hyperbolic Simplexes,” Sbornik: Mathematics, Vol. 193, No. 12, 2002, pp. 11-12. doi:10.1070/SM2002v193n12ABEH000702
- P. V. Tumarkin, “Hyperbolic Coxeter Polytopes in Hm with n + 2 Hyperfacets,” Mathematical Notes, Vol. 75, No. 5-6, 2004, pp. 848-854. doi:10.1023/B:MATN.0000030993.74338.dd
- P. V. Tumarkin, “Hyperbolic n-Dimensional Coxeter Polytopes with n + 3 Facets,” Transactions of the Moscow Mathematical Society, Vol. 58, No. 4, 2004, pp. 235-250.
- G. Ziegler, “Lectures on Polytopes,” Springer-Verlag, New York, 1995.
- È. B. Vinberg, “Geometry II,” Springer-Verlag, Berlin, 1993.
- A. A. Felikson and P. V. Tumarkin, “Hyperbolic Subalgebras of Hyperbolic Kac-Moody Algebras,” Transformation Groups, Vol. 17, No. 1, 2012, pp. 87-122. doi:10.1007/s00031-011-9169-y

