Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24501,6 pages DOI:10.4236/apm.2012.26062
A Characterization of Jacobson Radical in Γ-Banach Algebras
Department of Mathematics, Gauhati University, Guwahati, India
Email: nila_g2003@yahoo.co.in
Received August 7, 2012; revised September 25, 2012; accepted October 3, 2012
Keywords: Γ-Algebra; Right Quasi Regularity; Tensor Product; Operator Banach Algebra
ABSTRACT
Let 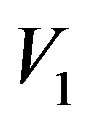 and
and 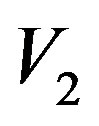 be two G-Banach algebras and
be two G-Banach algebras and 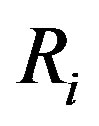 be the right operator Banach algebra and
be the right operator Banach algebra and 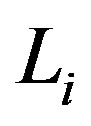 be the left operator Banach algebra of
be the left operator Banach algebra of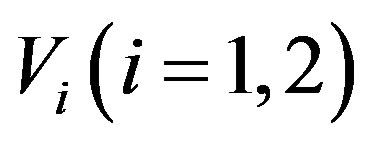 . We give a characterization of the Jacobson radical for the projective tensor product
. We give a characterization of the Jacobson radical for the projective tensor product 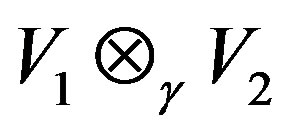 in terms of the Jacobson radical for
in terms of the Jacobson radical for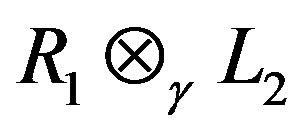 . If
. If 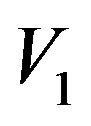 and
and 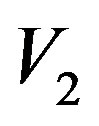 are isomorphic, then we show that this characterization can also be given in terms of the Jacobson radical for
are isomorphic, then we show that this characterization can also be given in terms of the Jacobson radical for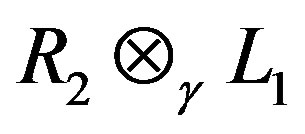 .
.
1. Introduction
In [1,2], using the right quasi regularity property, Kyuno and Coppage and Luh gave a characterization of Jacobson radical in G-rings. Many interesting results on the internal properties of Jacobson radical for G-rings were developed in [2-5] by different research workers. In [6], some of these results are extended to G-algebras. In this paper, we consider two G-Banach algebras V1 and V2 and consider their projective tensor product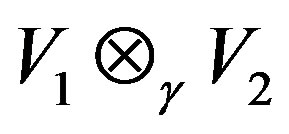 . Let Ri be the right operator Banach algebra and Li be the left operator Banach algebra of
. Let Ri be the right operator Banach algebra and Li be the left operator Banach algebra of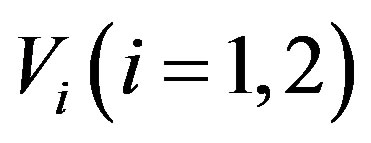 . We give a characterization of Jacobson radical
. We give a characterization of Jacobson radical 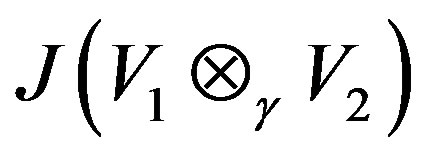 in terms of
in terms of 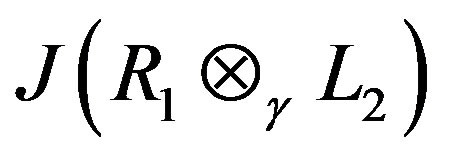
Before going to present our main results, we first give some basic terminologies (refer to [5-12]) which are needed in our discussion.
Definition 1.1
Let X be a ring having the unit element e. A new multiplication called the circle composition (refer to [5]) on X is defined by: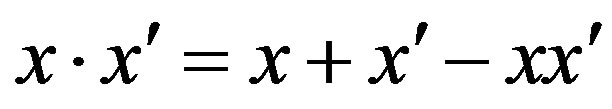 .This composition makes sense even when X does not have the unit element. An element x of X is said to be right quasi regular if it has a right quasi inverse w.r.t. this composition, i.e., there exists x¢ÎX such that
.This composition makes sense even when X does not have the unit element. An element x of X is said to be right quasi regular if it has a right quasi inverse w.r.t. this composition, i.e., there exists x¢ÎX such that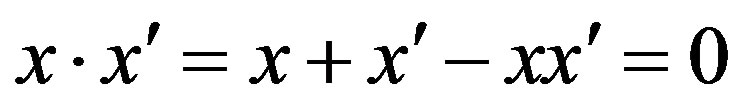 .
.
Definition 1.2
Let V and G be two linear spaces over a field F. V is said to be a G-algebra over F if, for x, y,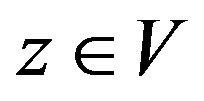 ;
;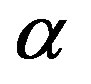 ,
,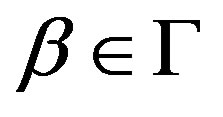 ;
;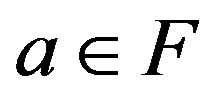 , the following conditions are satisfied:
, the following conditions are satisfied:
1)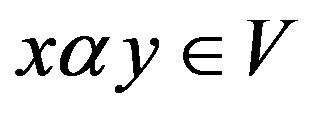 ;
;
2)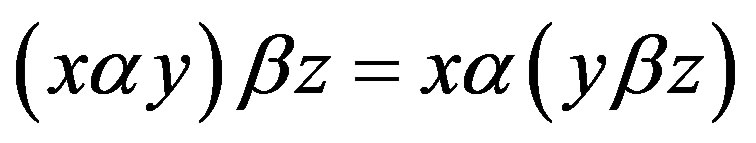 ;
;
3)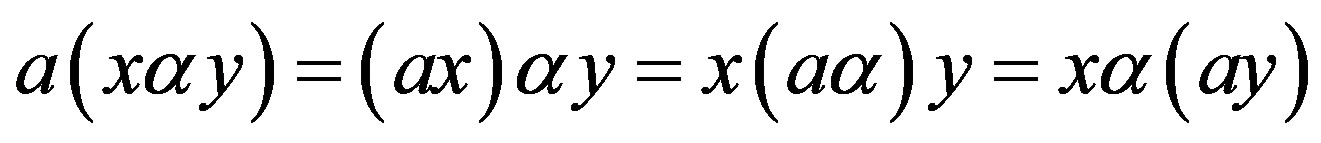 ;
;
4) 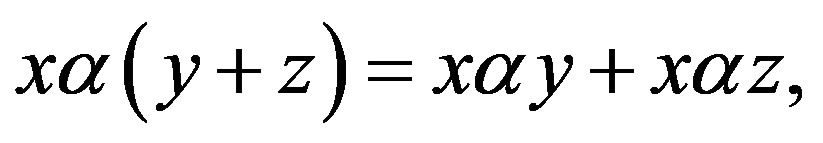
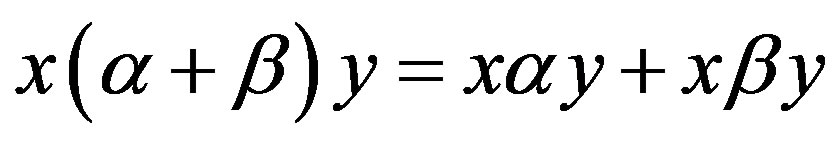 ,
,
 .
.
The G-algebra is denoted by . If V and G are normed linear spaces over F, then G-algebra
. If V and G are normed linear spaces over F, then G-algebra 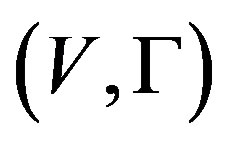 is called a G-normed algebra if conditions 1) to 4) hold and further 5)
is called a G-normed algebra if conditions 1) to 4) hold and further 5) 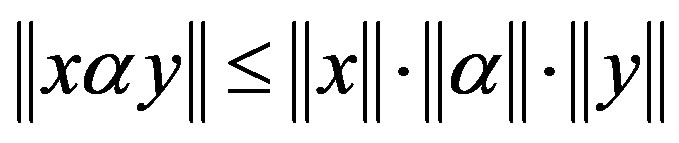 holds.
holds.
A G-normed algebra 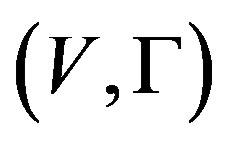 is called a G-Banach algebra if V is a Banach space. Any Banach algebra can be regarded as a G-Banach algebra by suitably choosing G.
is called a G-Banach algebra if V is a Banach space. Any Banach algebra can be regarded as a G-Banach algebra by suitably choosing G.
Definition 1.3
A subset I of a G-Banach algebra V is said to be a right (left) G-ideal of V if
1) I is a subspace of V (in the vector space sense);
2) 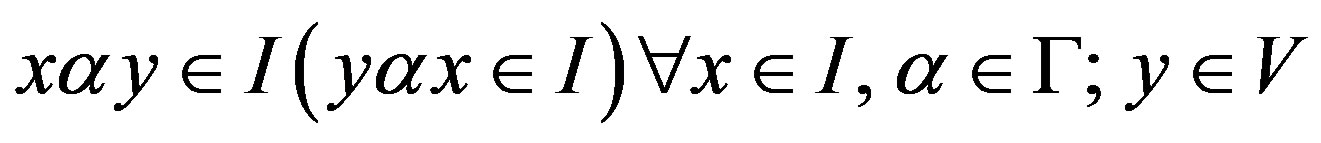
i.e.,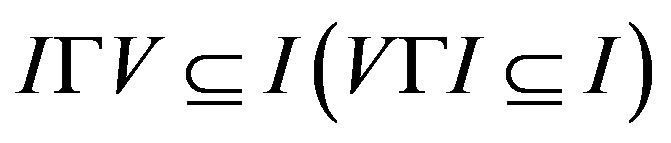 .
.
A right G-ideal, which is a left G-ideal as well, is called a two-sided G-ideal or simply a G-ideal.
Definition 1.4
Let V be a G-Banach algebra and let 
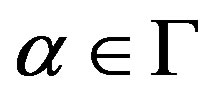 . Then the mapping
. Then the mapping 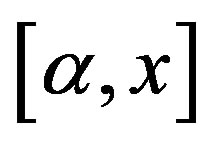 defined by
defined by 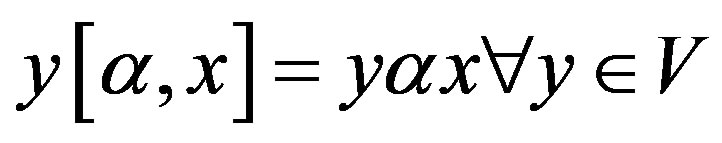 is a right Banach space endomorphism of V. The collection R of all endomorphisms generated by
is a right Banach space endomorphism of V. The collection R of all endomorphisms generated by ;
;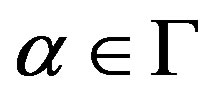 ,
, 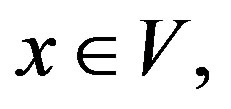 is a Banach algebra under the operations:
is a Banach algebra under the operations:
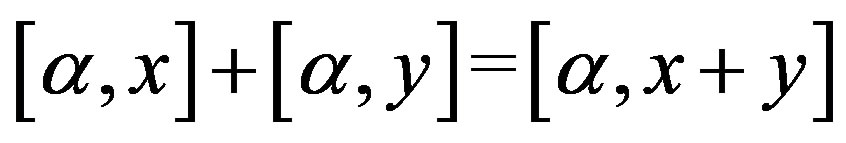 ,
,
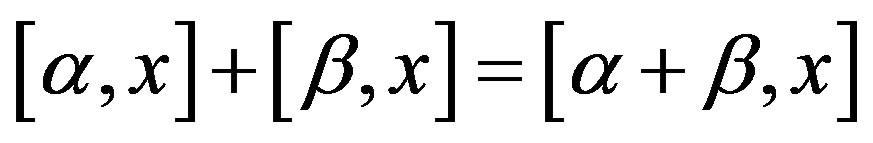
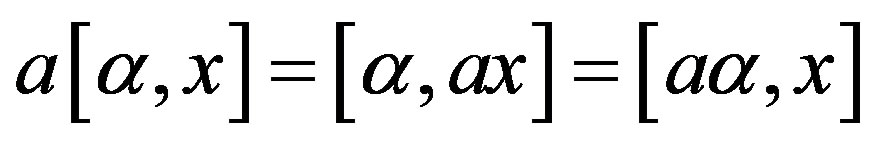
where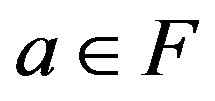 ,
,
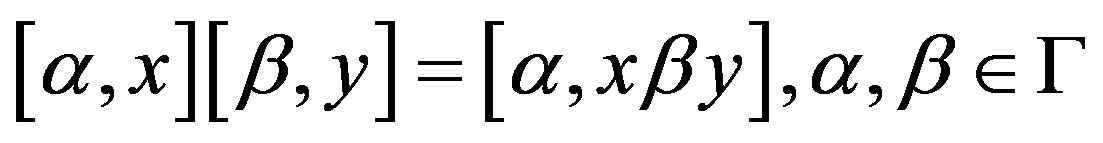 and the norm:
and the norm:
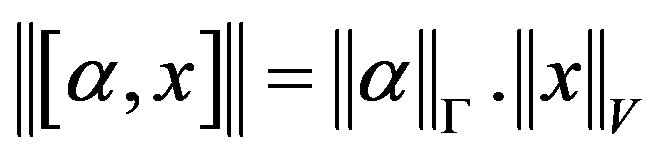 .
.
This Banach algebra is termed as the right operator Banach algebra of G-Banach algebra V. We can similarly define the left operator Banach algebra L of V as the Banach algebra generated by the set of all left endomorphisms of V in the form  where
where
 .
.
Definition 1.5
Let V and 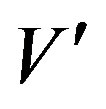 be G-Banach algebras over F and
be G-Banach algebras over F and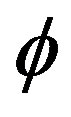 :
: 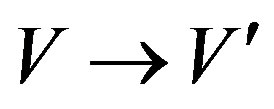 be a mapping. Then
be a mapping. Then 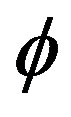 is called a G-Banach algebra homomorphism if 1)
is called a G-Banach algebra homomorphism if 1) 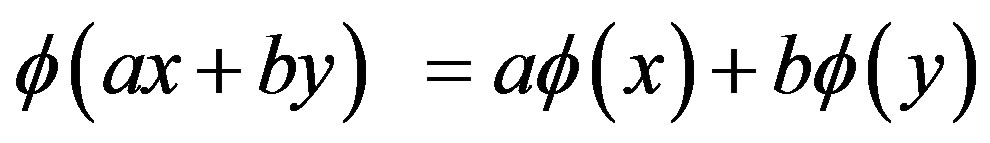 and 2)
and 2) 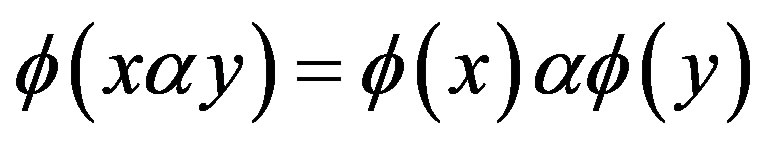 for all
for all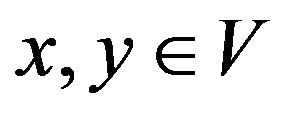 ;
;  and
and 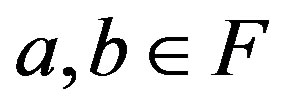
Definition 1.6
Let X and Y be two normed spaces. The projective tensor norm 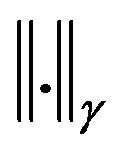 on
on  is defined as:
is defined as:
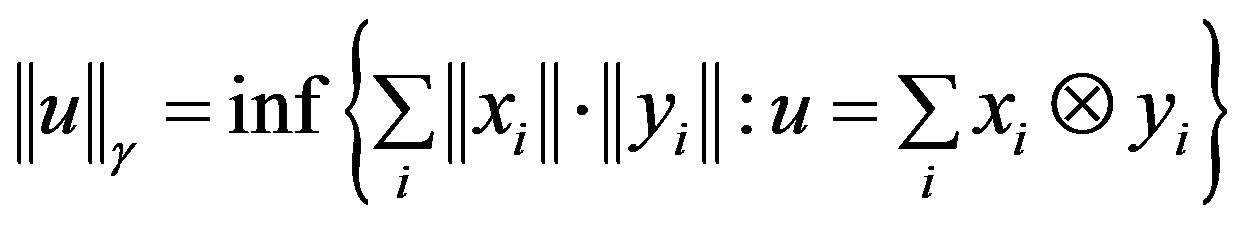
where the infimum is taken over all (finite) representations of u. The completion of 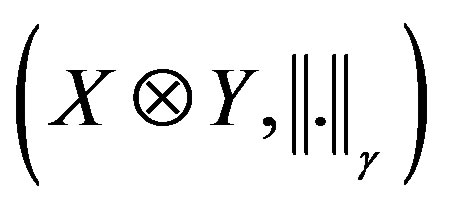 is called the projective tensor product of X and Y, and is denoted by
is called the projective tensor product of X and Y, and is denoted by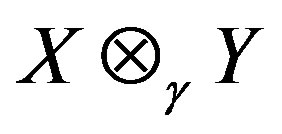 .
.
Let 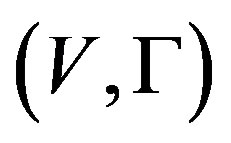 and
and 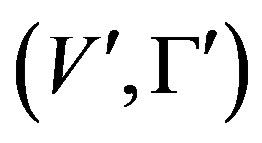 be G-Banach algebras over F1 and F2 isomorphic to F. The projective tensor product
be G-Banach algebras over F1 and F2 isomorphic to F. The projective tensor product  with the projective tensor norm is a
with the projective tensor norm is a 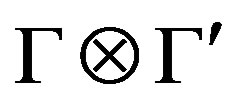 -Banach algebra over F, where a multiplication is defined by the formula:
-Banach algebra over F, where a multiplication is defined by the formula:

where x,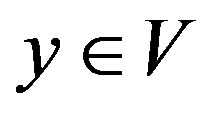 ;
;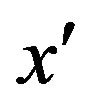 ,
, ;
;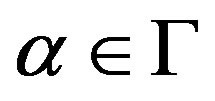 ,
,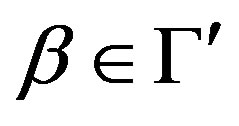 .
.
Definition 1.7
Let V be a G-Banach algebra. Let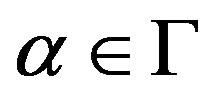 . An element x in V is said to be
. An element x in V is said to be 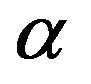 -right quasi regular with a-right quasi inverse y if
-right quasi regular with a-right quasi inverse y if . x is said to be a right quasi regular element of V if it is a-right quasi regular for each
. x is said to be a right quasi regular element of V if it is a-right quasi regular for each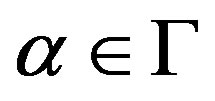 .
.
Equivalently, an element 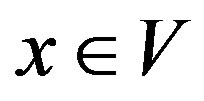 is called right quasi regular if for any
is called right quasi regular if for any , there exist
, there exist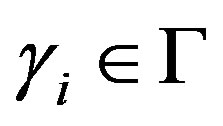 ,
, 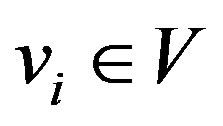 ,
, 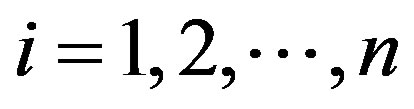 such that
such that
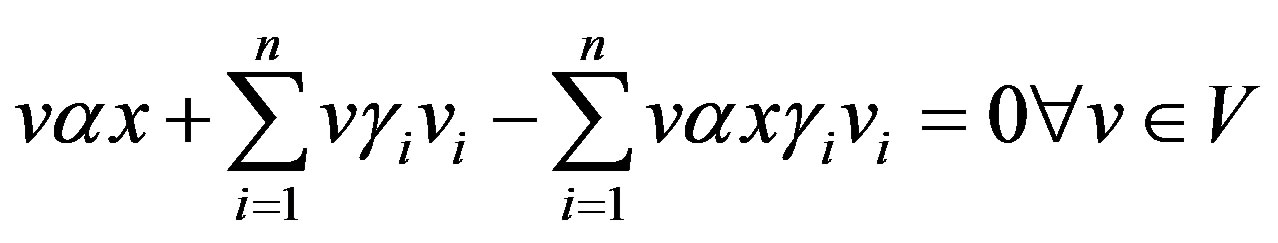
An ideal I of V is said to be right quasi regular if each of its elements is right quasi regular.
We have, right quasi regularity is a radical property in an algebra. The maximal right quasi regular ideal is called the Jacobson radical of V and it is denoted by J(V).
2. Main Results
In [6], we have the following Lemma regarding right quasi regularity of a G-Banach algebra and its operator algebra.
Lemma 2.1
An element x of a G-Banach algebra V is right quasi regular if and only if for all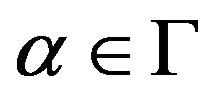 ,
, 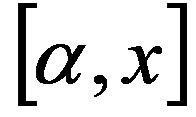 is right quasi regular in the right operator Banach algebra R of V.
is right quasi regular in the right operator Banach algebra R of V.
Extending this result to the projective tensor product of G-Banach algebras, we prove,
Lemma 2.2
Let V and  be two G and
be two G and 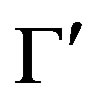 -Banach algebras respectively. Let R be the right operator Banach algebra of V and L be the left operator Banach algebra of
-Banach algebras respectively. Let R be the right operator Banach algebra of V and L be the left operator Banach algebra of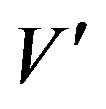 . If
. If
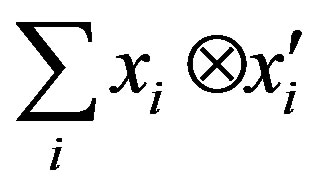 is right quasi regular in
is right quasi regular in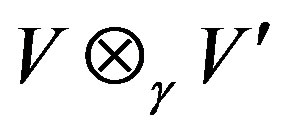 , then
, then
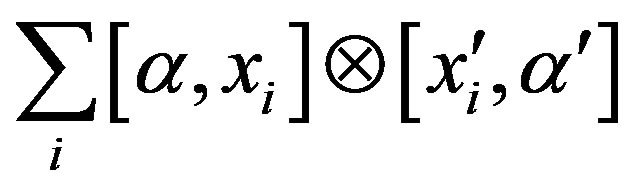 is right quasi regular in
is right quasi regular in 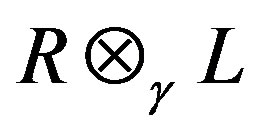 for
for
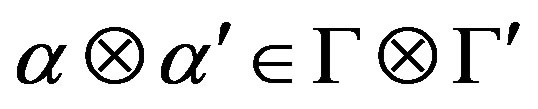 , and conversely.
, and conversely.
Proof. Since 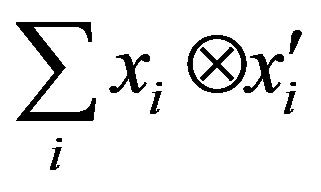 is right quasi regular in
is right quasi regular in  , so, for any
, so, for any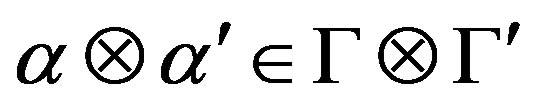 , there exist
, there exist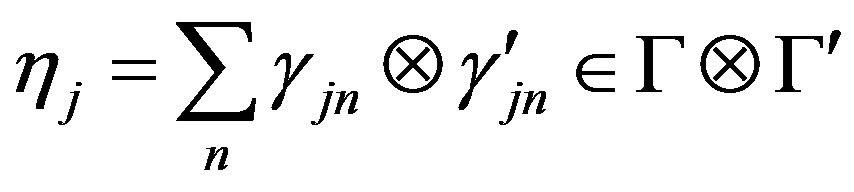 ,
, 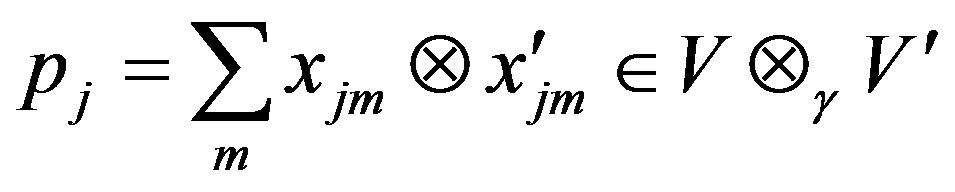 ,
,  such that for any
such that for any ,
,
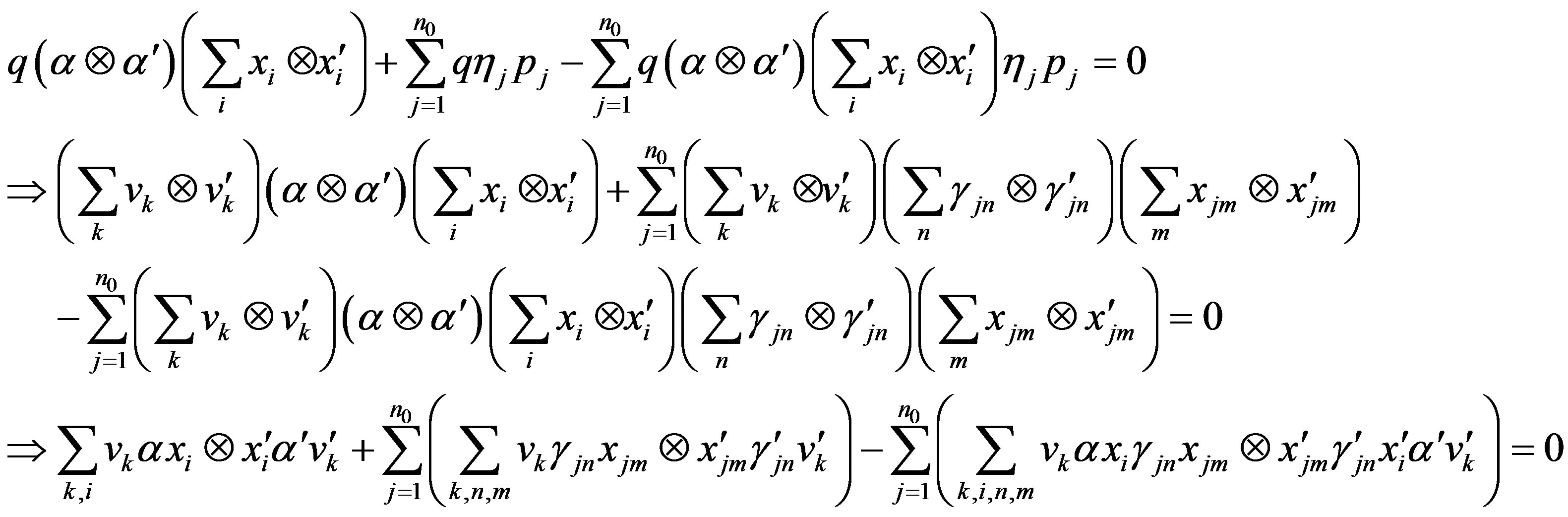 (2.1)
(2.1)
Let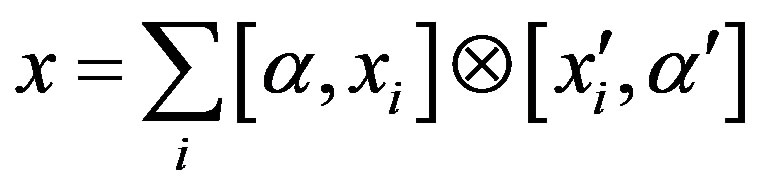 . We take
. We take 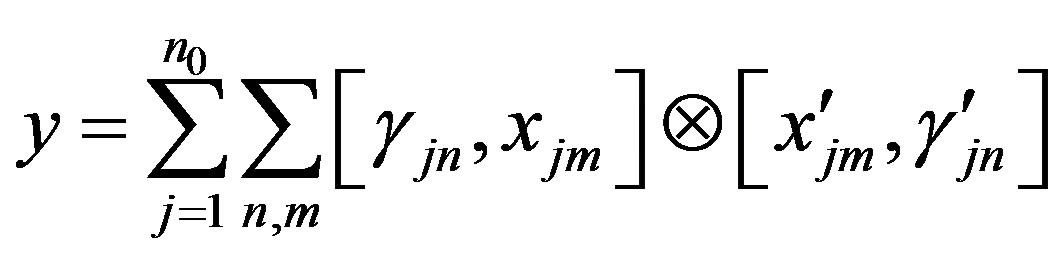
Now,
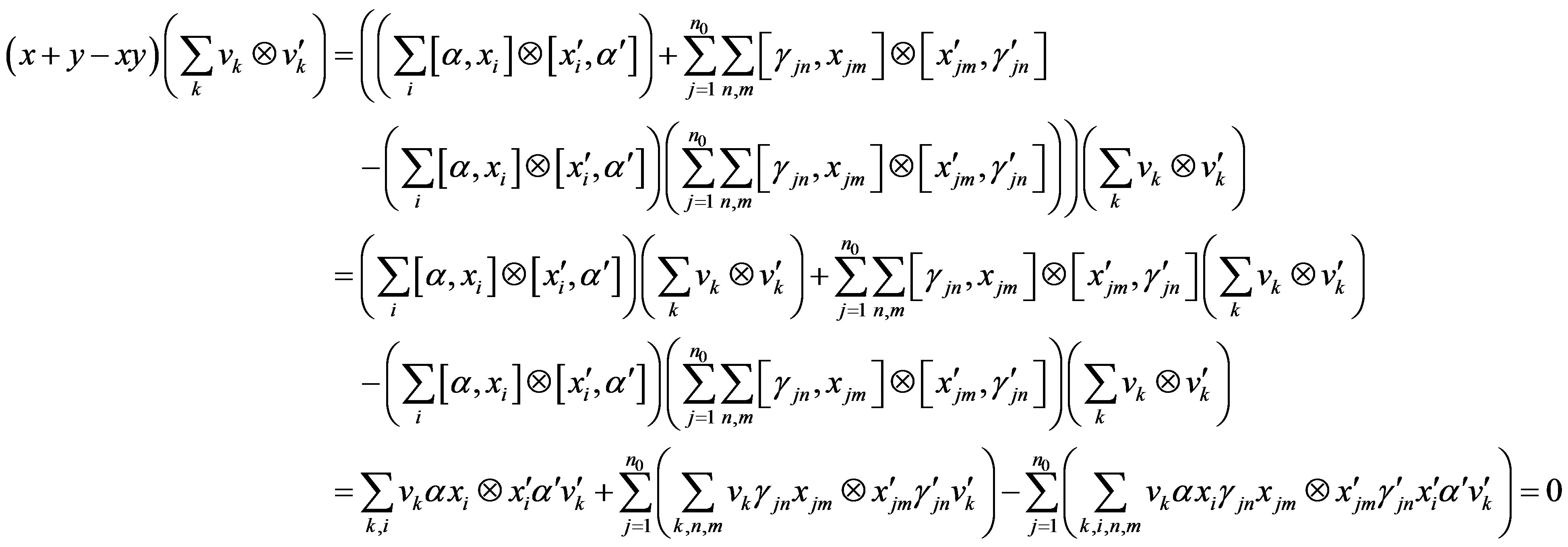
(by (2.1)).
But, 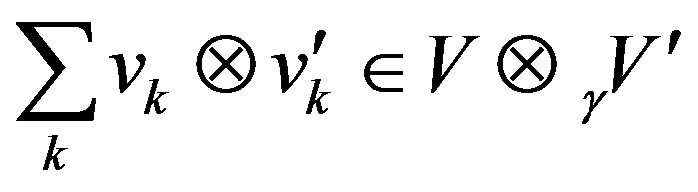 is arbitrary.
is arbitrary.
So, x + y - xy = 0. Thus, x, i.e., 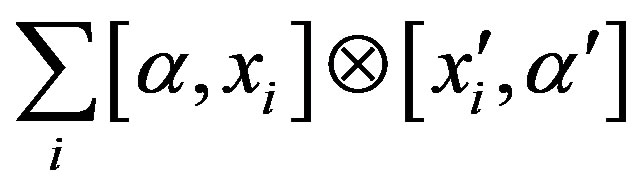 is right quasi regular in
is right quasi regular in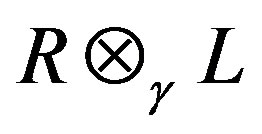 .
.
The converse follows in the same way. 
In [13], we have defined the following ideal for the projective tensor product of V and V¢.
Lemma 2.3
Let V and 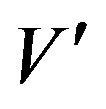 be two G and
be two G and  -Banach algebras respectively. Let R be the right operator Banach algebra of V and L be the left operator Banach algebra of
-Banach algebras respectively. Let R be the right operator Banach algebra of V and L be the left operator Banach algebra of . Let J be an ideal of
. Let J be an ideal of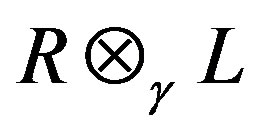 . We define:
. We define:
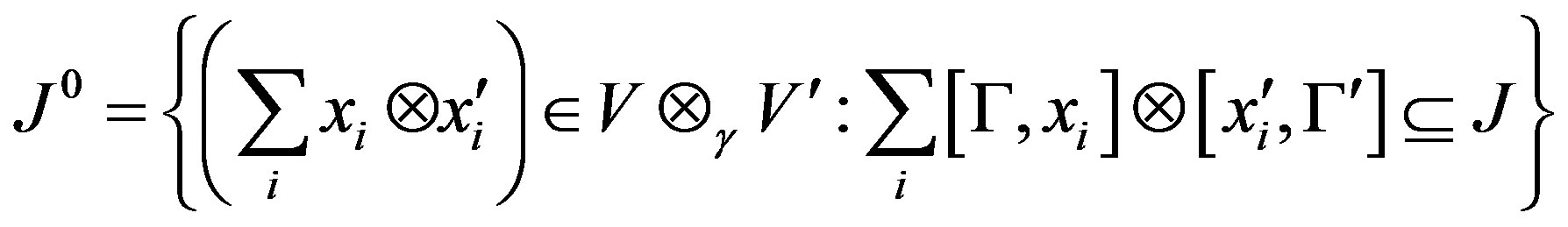
where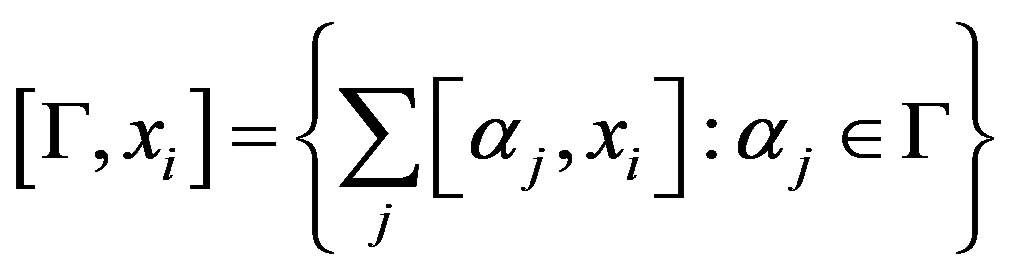 , and
, and 
Then 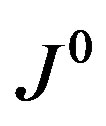 is an ideal of
is an ideal of .
.
Using the above defined ideal, now, we give the characterization of Jacobson radical for the projective tensor product of two G-Banach algebras 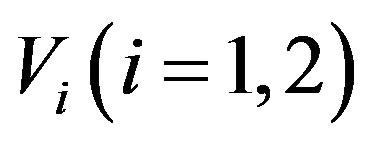 in terms of the Jacobson radical of the projective tensor product of corresponding right and left operator Banach algebras.
in terms of the Jacobson radical of the projective tensor product of corresponding right and left operator Banach algebras.
Theorem 2.4
Let Vi be a G-Banach algebra (over F) with right operator Banach algebra Ri and left operator Banach algebra 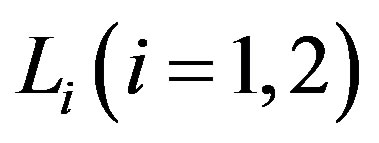 respectively. Then the Jacobson radical of
respectively. Then the Jacobson radical of  is given by:
is given by: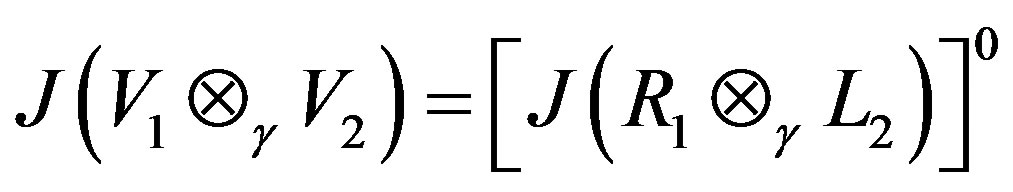 .
.
Proof. Let .
.
Then 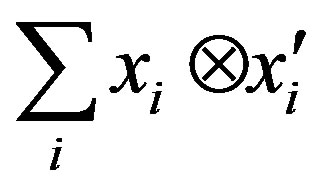 is a right quasi regular element of
is a right quasi regular element of
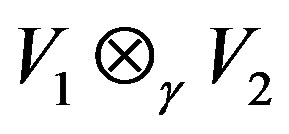 . By Lemma 2.2, for any a,
. By Lemma 2.2, for any a, 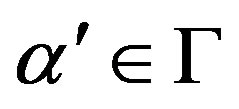 ,
,
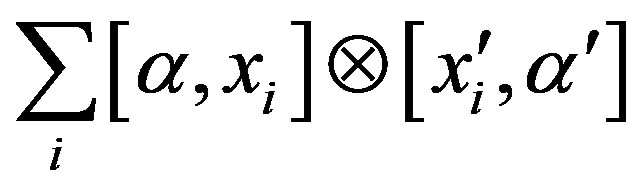 is a right quasi regular element of
is a right quasi regular element of
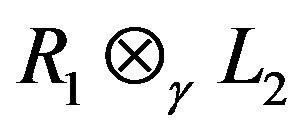 , i.e.,
, i.e.,
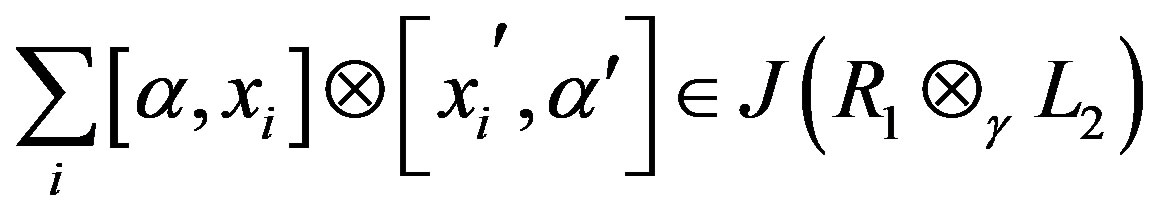 .
.
So,
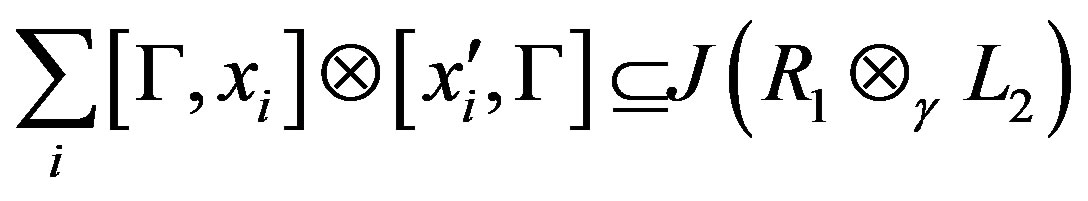 .
.
Hence,
 .
.
Thus,
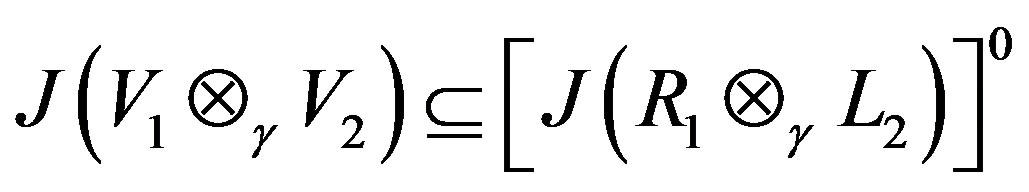 .
.
Conversely, let
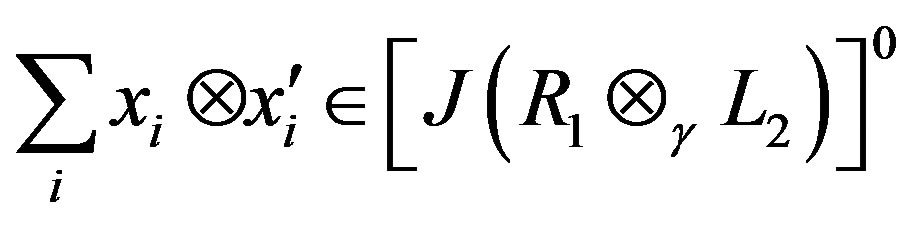 .
.
Then
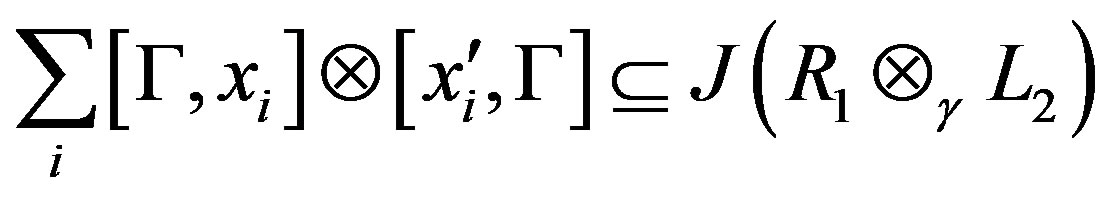 .
.
So, for any a, 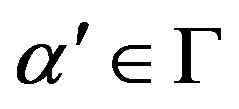 ,
, 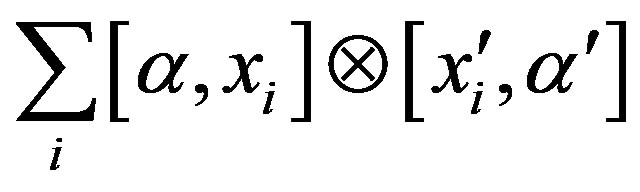 is a right quasi regular element of
is a right quasi regular element of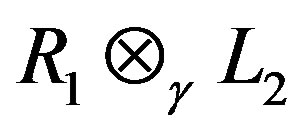 . By Lemma 2.2,
. By Lemma 2.2, 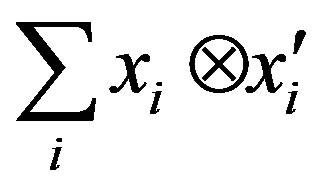 is a right quasi regular element of
is a right quasi regular element of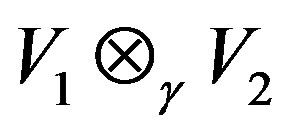 , i.e.
, i.e. 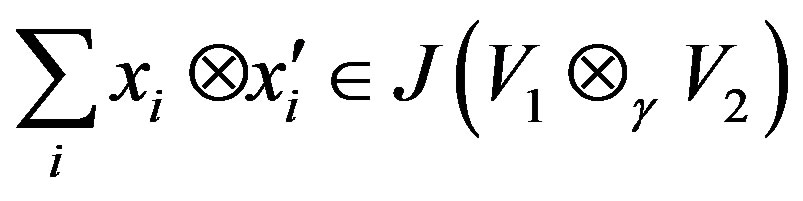 So,
So,  .
.
Thus,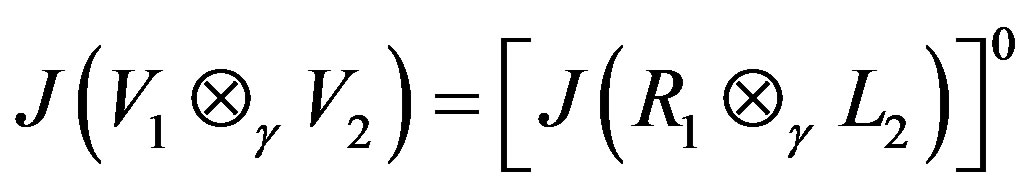 .
. 
Let the G-Banach algebras V1 and V2 are isomorphic. In that case, we have the following result.
Theorem 2.5
Let Vi be a G-Banach algebra (over F) with right operator Banach algebra Ri and left operator Banach algebra 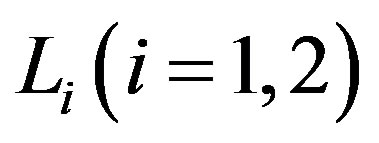 respectively. If there exists a G-Banach algebra isomorphism f from V1 onto V2, then
respectively. If there exists a G-Banach algebra isomorphism f from V1 onto V2, then 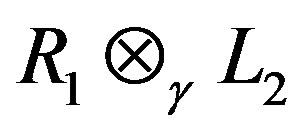 is a homomorphic image of
is a homomorphic image of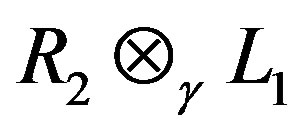 .
.
Proof. Let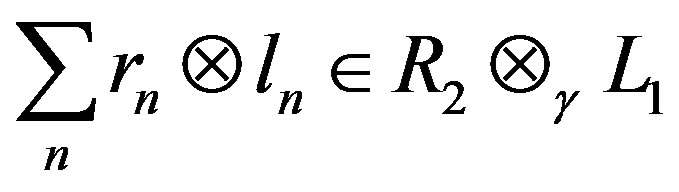 , where
, where ,
,
 . We define
. We define  by
by
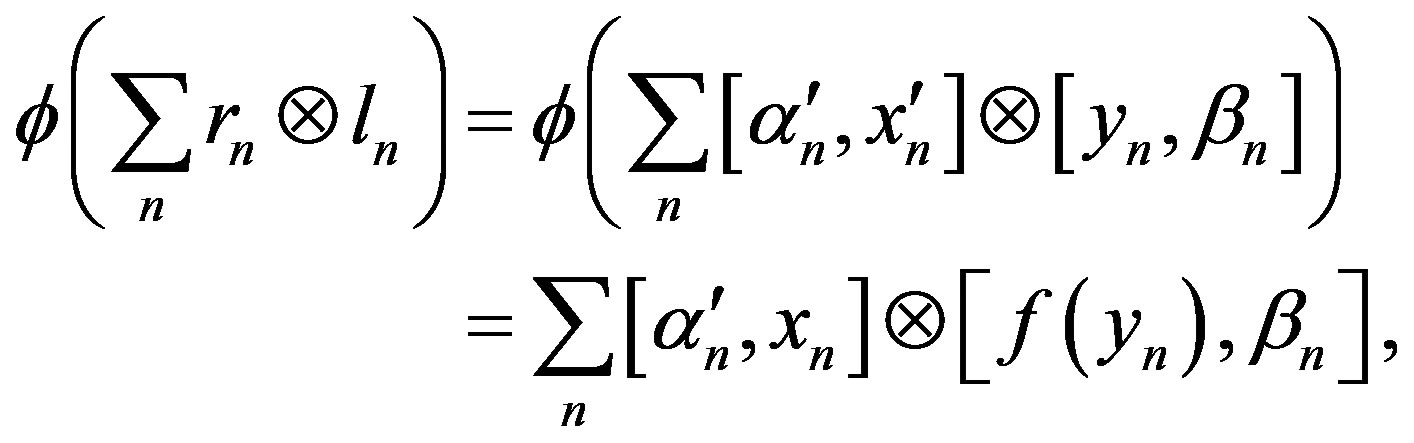
where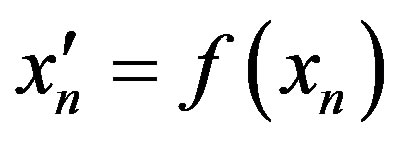 ,
,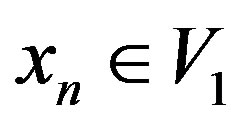 .
.
Let  (The dual space of R1).
(The dual space of R1).
We define 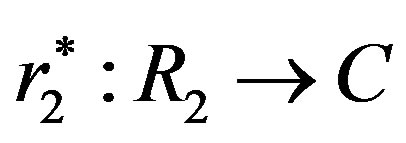 by
by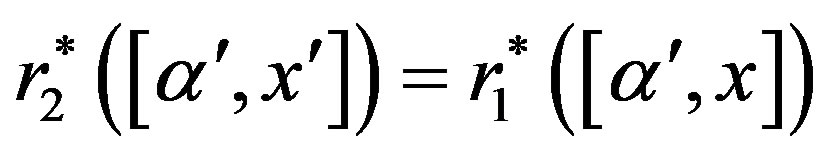 , where
, where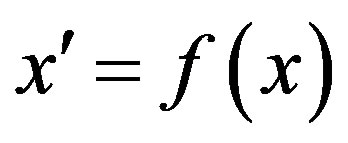 .
.
Then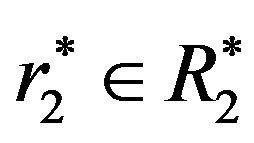 .
.
Similarly, for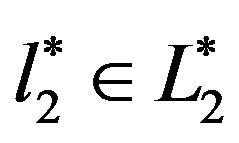 , we can define
, we can define 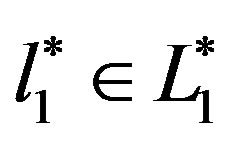 by
by
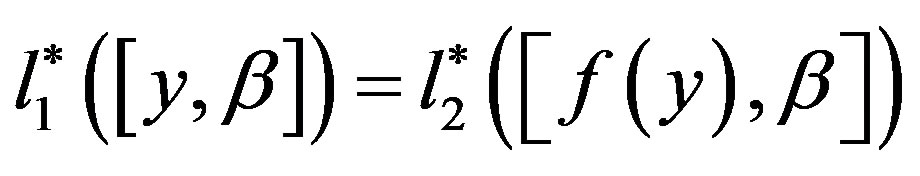 .
.
Now, let
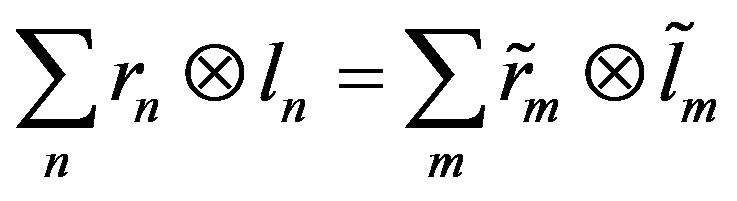 where
where
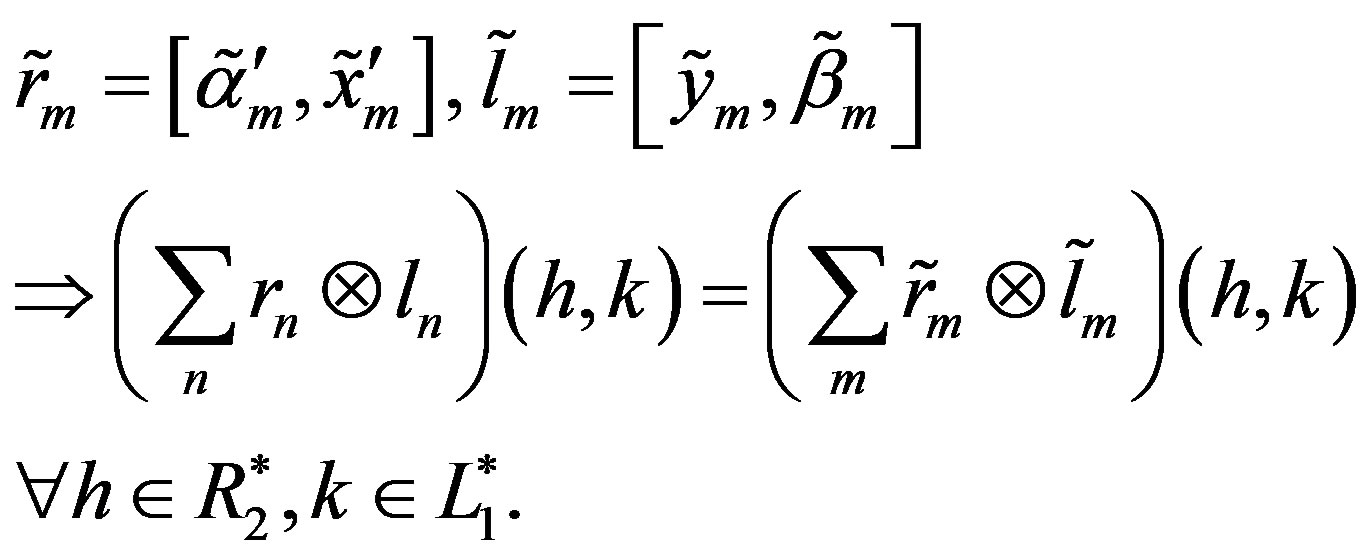
In particular, taking ,
,  , we get,
, we get,
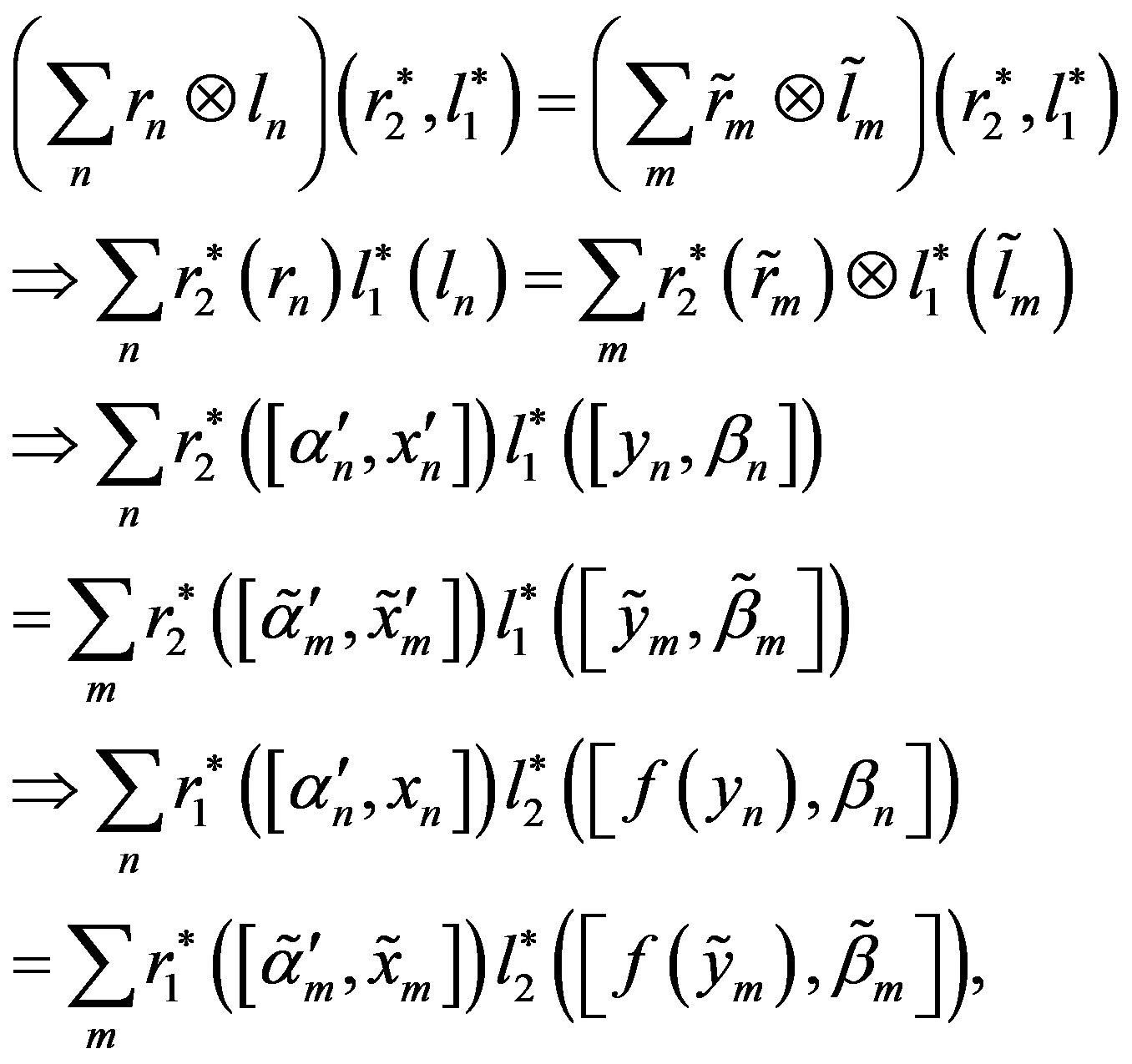
where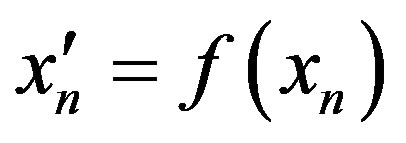 , and
, and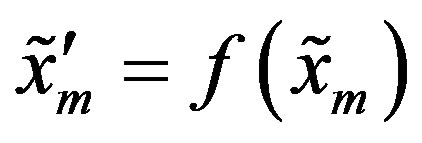 .
.

But  and
and 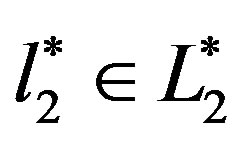 are arbitrary. So,
are arbitrary. So, 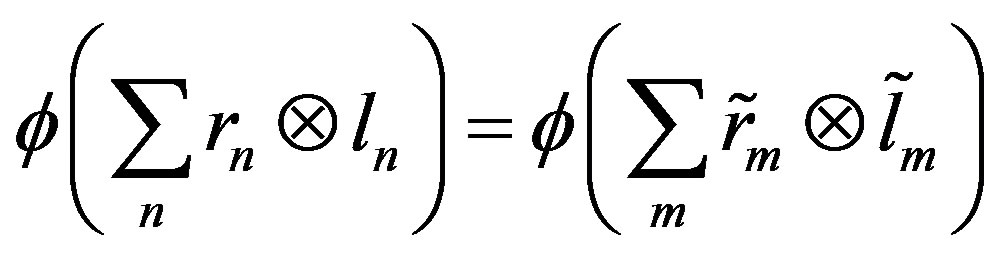 Thus
Thus 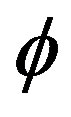 is well defined.
is well defined.
Now, Let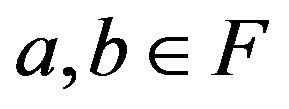 . Then
. Then
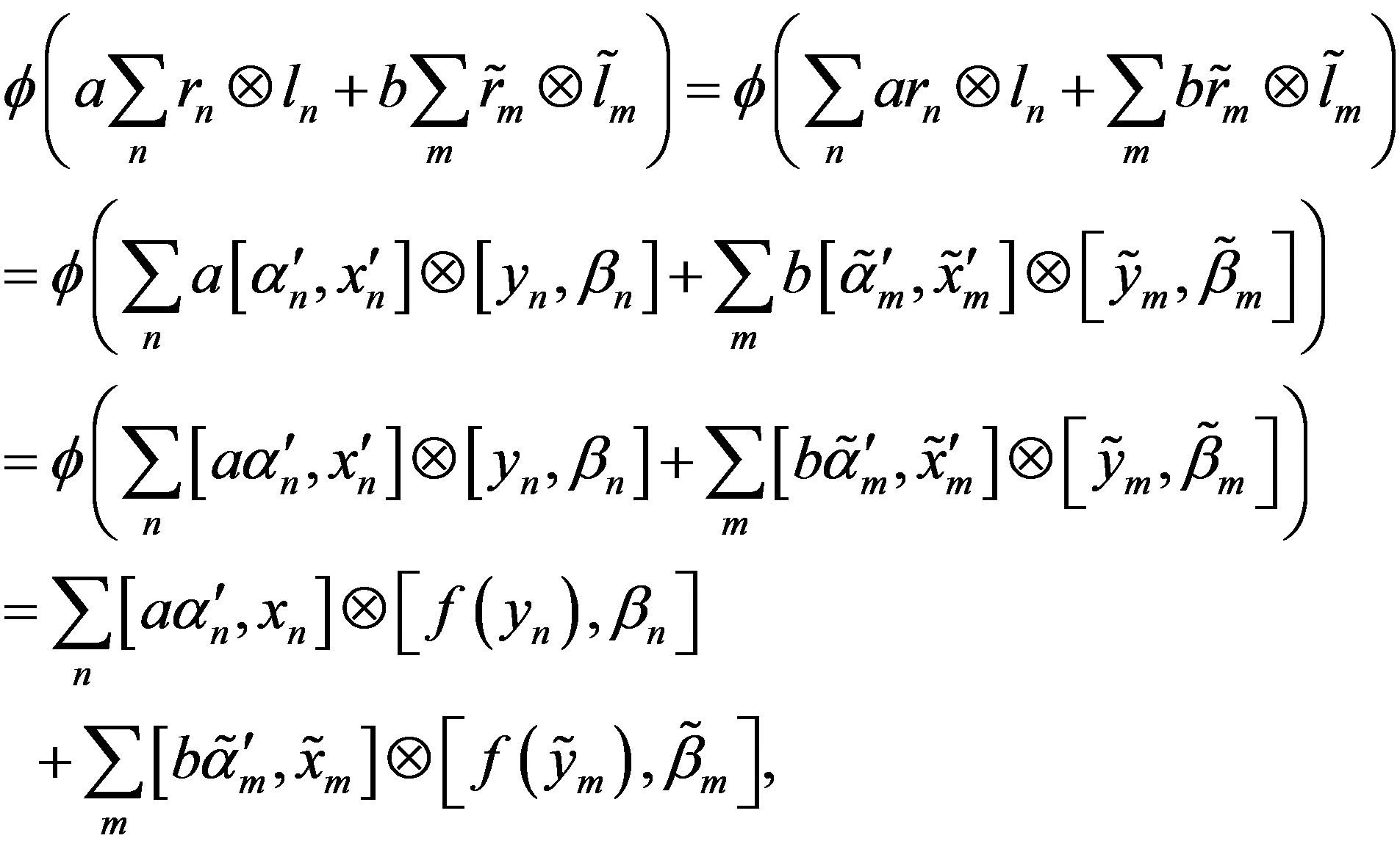
where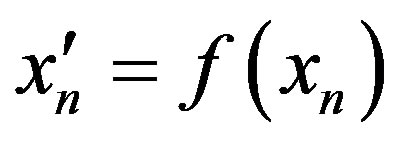 , and
, and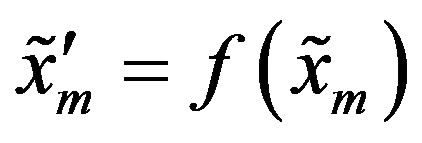 .
.
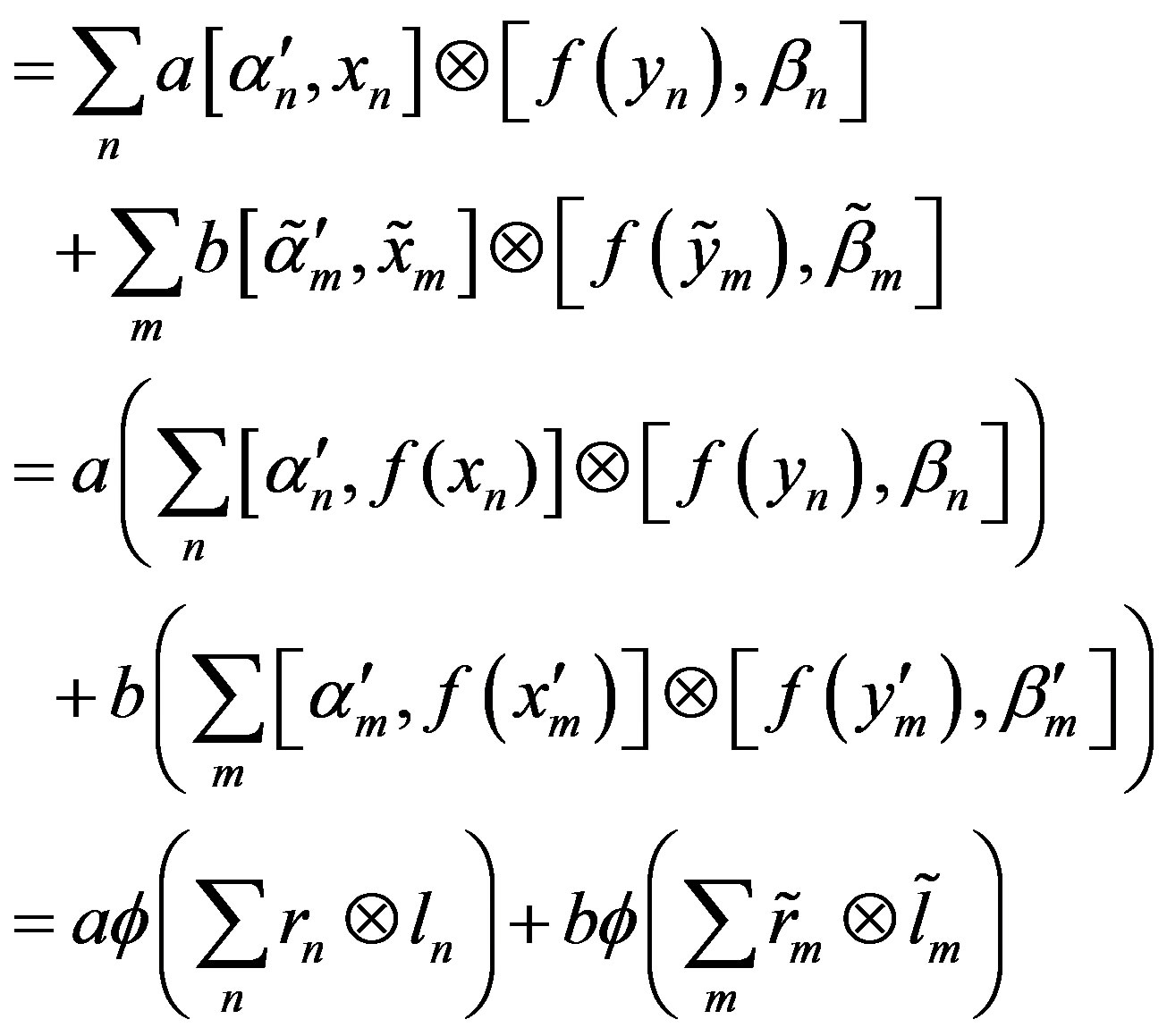
Again,
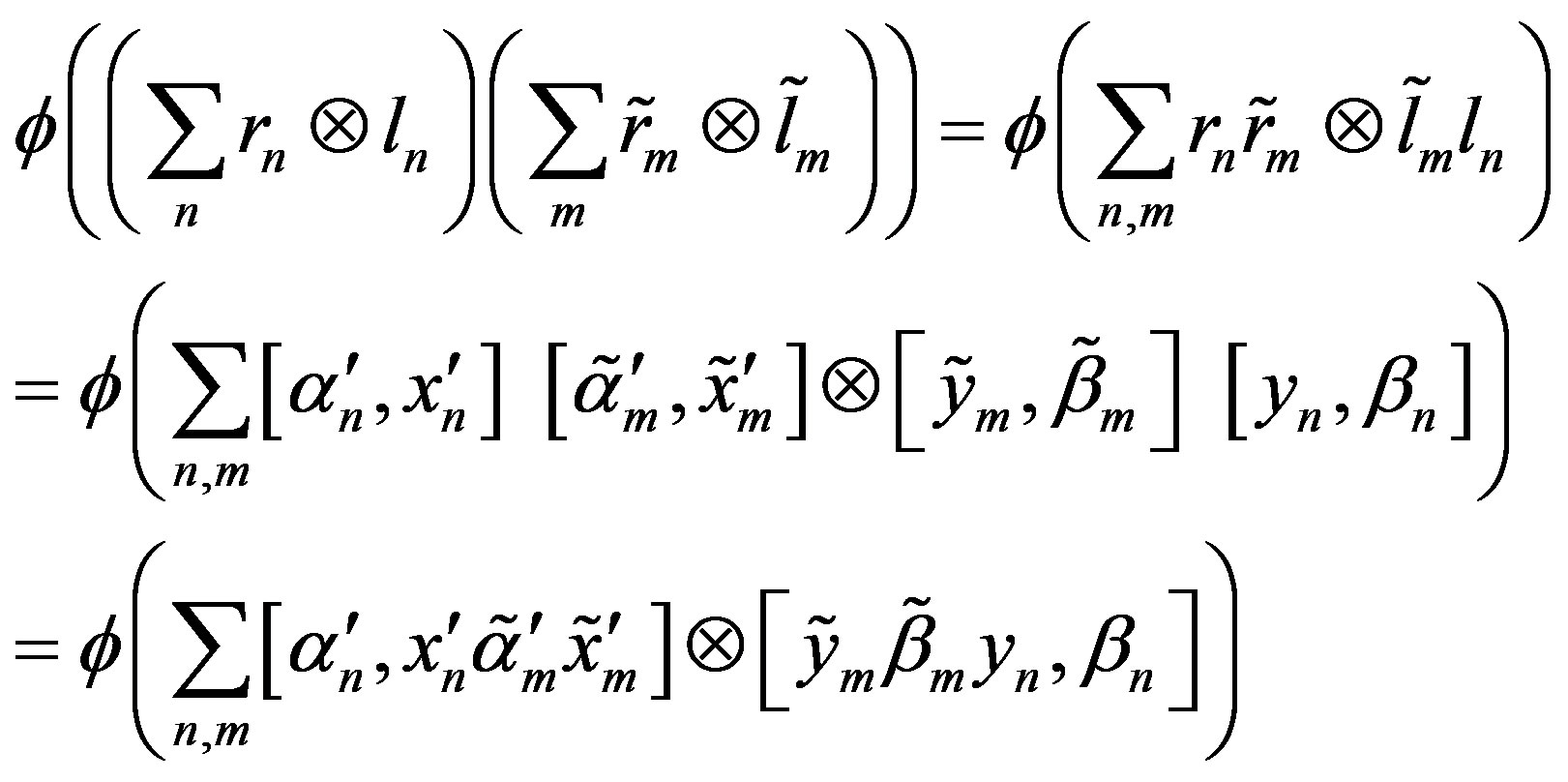 (2.2)
(2.2)
We have,  ,
, 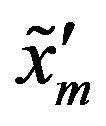 ÎV2. So, there exist
ÎV2. So, there exist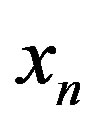 ,
, 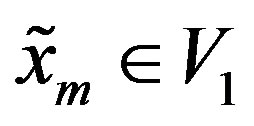 such that
such that ,
,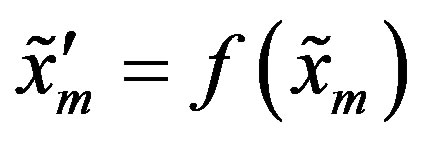 .
.
Now, 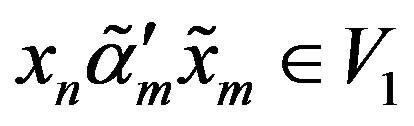 and
and
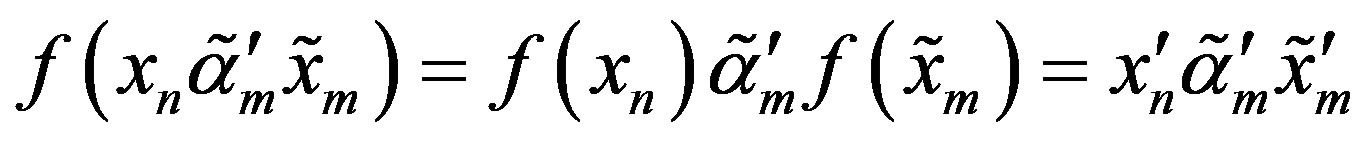
So, the expression (2.2) is equal to
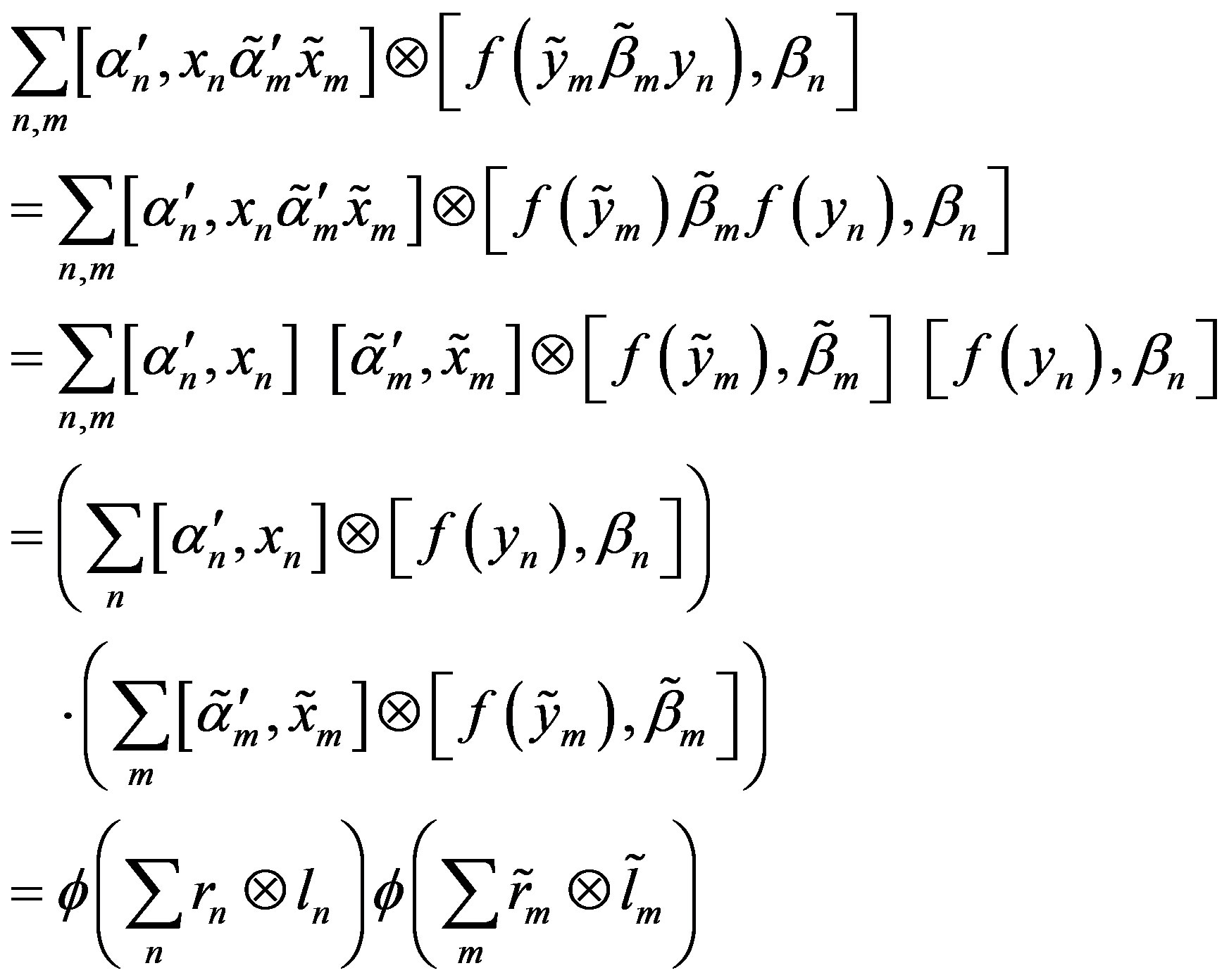
So,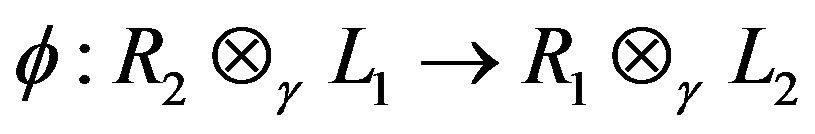 is a homomorphism.
is a homomorphism.
Since f is onto, so, 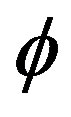 is also onto. Also, it can be shown that
is also onto. Also, it can be shown that 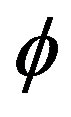 is one-one.
is one-one.
Thus,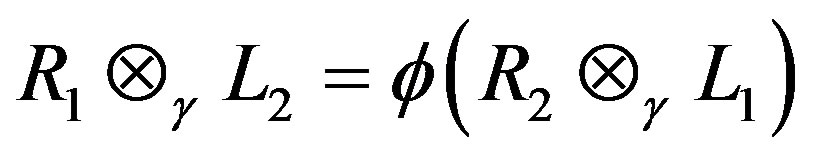 .
.
Corollary 2.6
Let the G-Banach algebras V1 and V2, as defined in Theorem 2.4 are isomorphic. Then we have,
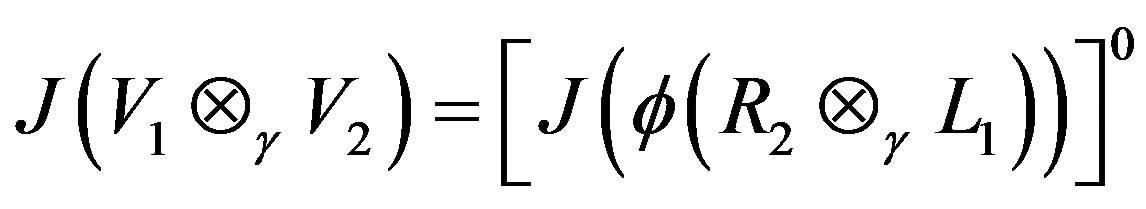 .
.
Remark 2.7
If the isomorphism f from V1 onto V2 is isometric, then we can show that 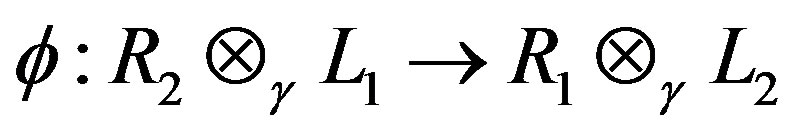 is also an isometry. So, in that case,
is also an isometry. So, in that case,
 .
.
The notion of direct summand for G-rings is discussed in [10] by Booth. For a G-Banach algebra V, an ideal P is called direct summand if there exists a G-ideal Q of V such that every element v of V is uniquely expressible in the form v = p + q, 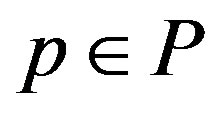 ,
,  , and V is written as
, and V is written as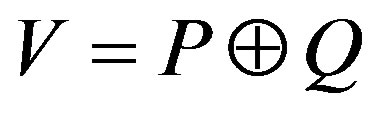 . Clearly, if
. Clearly, if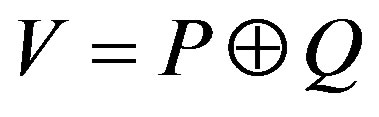 , then for
, then for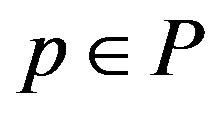 ,
, 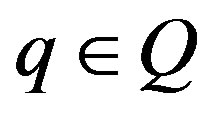 ,
, .
.
Now, we prove:
Deduction 2.8
If P is the direct summand for the G-Banach algebra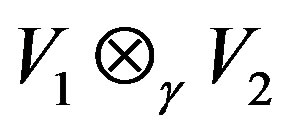 , then
, then 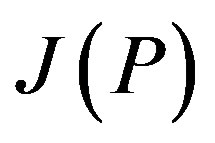 is the direct summand for
is the direct summand for
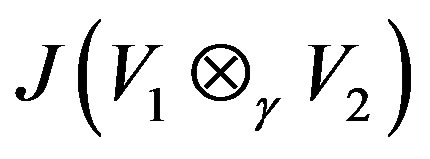 .
.
Proof. Let 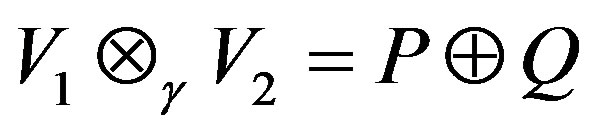 Clearly,
Clearly,
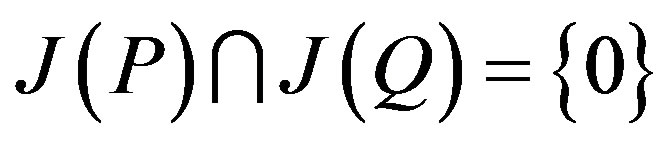 .
.
Let 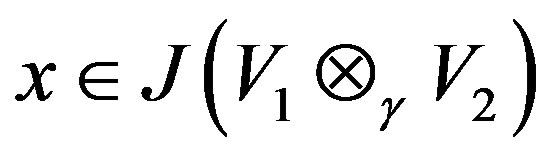 and x = p + q, where
and x = p + q, where ,
,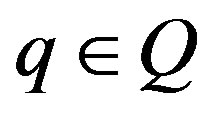 .
.
Since x is right quasi regular in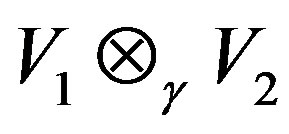 , so, for any
, so, for any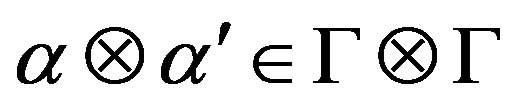 , we have, there exists
, we have, there exists 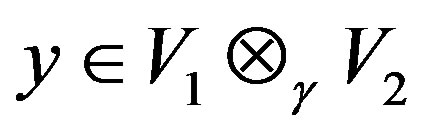 such that
such that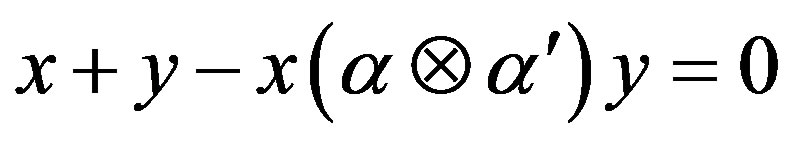 .
.
Let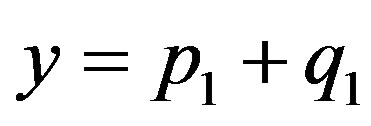 , where
, where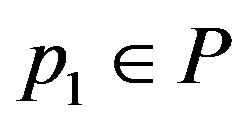 ,
,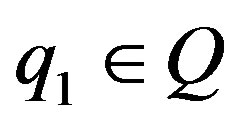 .
.
So,
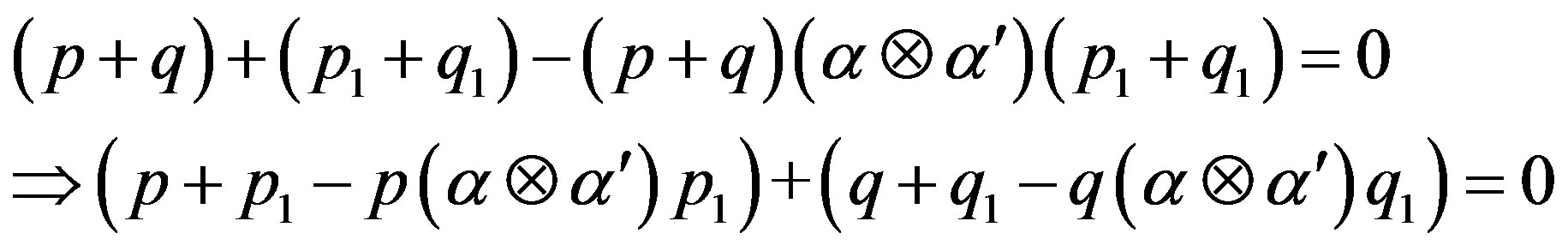
[since 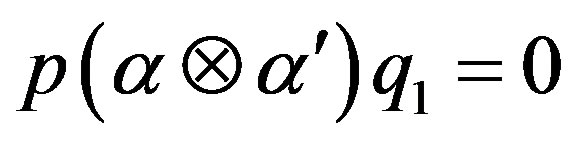 and
and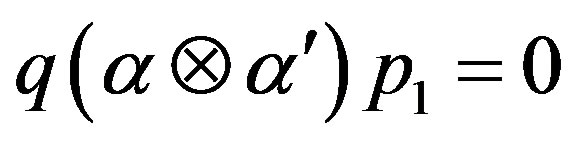 ]
]
But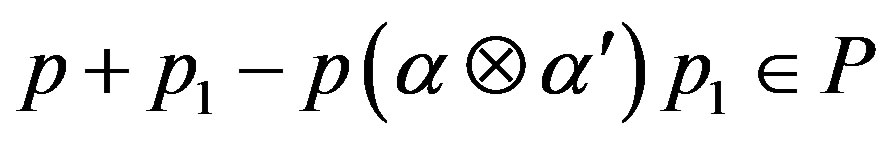 and
and
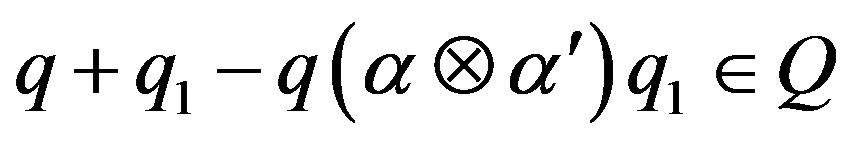 , and
, and .
.
So,  and
and 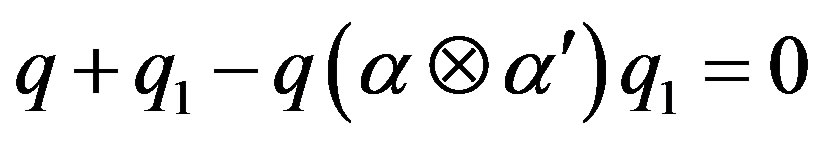 , for any
, for any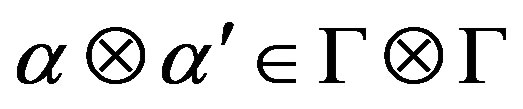 .
.
Thus p is right quasi regular in P and q is right quasi regular in Q, i.e., 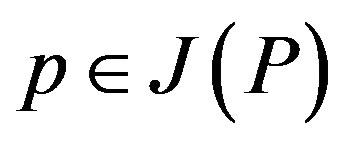 and
and .
.
Hence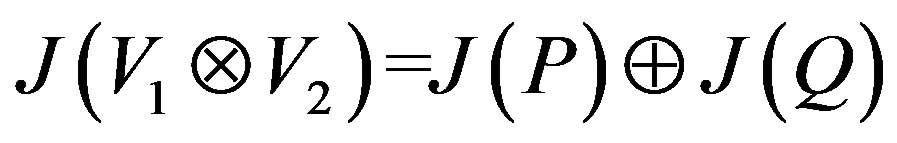 .
. 
In [4], there is a characterization of Jacobson radical for G-rings in terms of maximal regular left ideals.
Lemma 2.9
Let X be a G-ring. Then 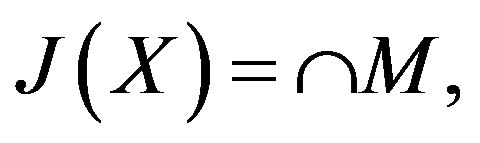 where the intersection is over all maximal regular left ideals M of X.
where the intersection is over all maximal regular left ideals M of X.
Considering this aspect, we can raise the following problem:
Let the structures of maximal regular left ideals of the operator Banach algebras R1 and L2 are given. Using this, can we obtain the structure of the Jacobson radical for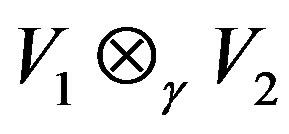 ?
?
In [6], Behrens radical for G-Banach algebras is introduced which contains the Jacobson radical. Let P denote the class of all subdirectly irreducible G-Banach algebras V such that the intersection of all non-zero ideals of V contains a non-zero idempotent element. The upper radical RB determined by the class P is called the Behrens radical for V.
Lemma 2.10
For a simple G-Banach algebra V,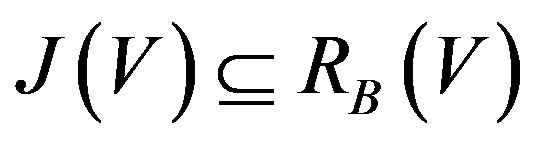 .
.
Now, another problem can be raised:
Can we derive analogous result as in Theorem 2.4 in case of the Behrens radical for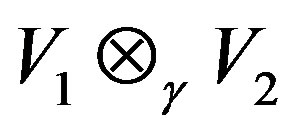 ?
?
REFERENCES
- S. Kyuno, “Notes on Jacobson Radicals of Gamma Rings,” Mathematica Japonica, Vol. 27, No. 1, 1982, pp. 107-111.
- W. E. Coppage and J. Luh, “Radicals of Gamma Rings,” Journal of the Mathematical Society of Japan, Vol. 23, No. 1, 1971, pp. 40-52. doi:10.2969/jmsj/02310040
- A. C. Paul and A. K. Azad, “Jacobson Radical for Gamma Rings,” Rajshahi University Studies Part-B. Journal of Science, Vol. 25, 1977, pp. 153-161.
- A. C. Paul and Md. S. Uddin, “On Jacobson Radical for Gamma Rings,” Ganit: Journal of Bangladesh Mathematical Society, Vol. 29, 2009, pp. 147-160.
- K. N. Raghavan, “The Jacobson Density Theorem and Applications,” 2005. http://www.imsc.res.in
- H. K. Nath, “A Study of Gamma-Banach Algebras,” Ph.D. Thesis, Gauhati University, Guwahati, 2001.
- W. E. Barnes, “On the G-Rings of Nobusawa,” Pacific Journal of Mathematics, Vol. 18, No. 3, 1966, pp. 411- 422.
- D. K. Bhattacharya and A. K. Maity, “Semilinear Tensor Product of G-Banach Algebras,” Ganita, Vol. 40, No. 2, 1989, pp. 75-80.
- F. F. Bonsall and J. Duncan, “Complete Normed Algebras,” Springer-Verlag, Berlin, 1973. doi:10.1007/978-3-642-65669-9
- G. L. Booth, “Operator Rings of a G-Ring,” Math Japonica, Vol. 31, No. 2, 1986, pp. 175-183.
- N. J. Divinsky, “Rings and Radicals,” George Allen and Unwin, London, 1965.
- N. Goswami, “Some Results on Operator Banach Algebras of a G-Banach Algebra,” Journal of Assam Academy of Mathematics, Vol. 1, 2010, pp. 40-48.
- N. Goswami, “On Levitzkinil Radical of Gamma Banach Algebras”, Global Journal of Applied Mathematics and Mathematical Sciences, 2012, in Press.

