World Journal of Condensed Matter Physics
Vol.06 No.02(2016), Article ID:67016,17 pages
10.4236/wjcmp.2016.62018
Increases in Lorentz Factor with Dielectric Thickness
J. W. McPherson
McPherson Reliability Consulting LLC, Plano, Texas, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 February 2016; accepted 28 May 2016; published 31 May 2016
ABSTRACT
For many years, a Lorentz factor of L = 1/3 has been used to describe the local electric field in thin amorphous dielectrics. However, the exact meaning of thin has been unclear. The local electric field Eloc modeling presented in this work indicates that L = 1/3 is indeed valid for very thin solid dielectrics (tdiel ≤ 20 monolayers) but significant deviations from L = 1/3 start to occur for thicker dielectrics. For example, L ≈ 2/3 for dielectric thicknesses of tdiel = 50 monolayers and increases to L ≈ 1 for dielectric thicknesses tdiel > 200 monolayers. The increase in L with tdiel means that the local electric fields are significantly higher in thicker dielectrics and explains why the breakdown strength Ebd of solid polar dielectrics generally reduces with dielectric thickness tdiel. For example, Ebd for SiO2 reduces from approximately Ebd ≈ 25 MV/cm at tdiel = 2 nm to Ebd ≈ 10 MV/cm at tdiel = 50 nm. However, while Ebd for SiO2 reduces with tdiel, all SiO2 thicknesses are found to breakdown at approximately the same local electric field (Eloc)bd ≈ 40 MV/cm. This corresponds to a coordi- nation bond strength of 2.7 eV for the silicon-ion to transition from four-fold to three-fold coordi- nation in the  tetrahedral structure.
tetrahedral structure.
Keywords:
Dielectrics, Dielectric Breakdown, Local Electric Field, Lorentz Factor, Time-Dependent Dielectric Breakdown, TDDB, Bond Breakage, Thermochemical E-Model

1. Introduction
Early on it was recognized by Mossotti and Clausius that the local electric field played a very important role in the polarization/distortion of molecules in the dielectric [1] [2] . Somewhat later, H. A. Lorentz [3] showed that the local electric field could be expressed (in rationalized mks units) as:
 , (1)
, (1)
where Ediel (=ΔVdiel/tdiel) is the average field in the dielectric, ΔVdiel is the voltage drop in the dielectric, P is the dielectric polarization (dipole moment per unit volume), ε0 is the permittivity in free space, and L is now commonly referred to as the Lorentz Factor. The local electric field arises from the superposition of fields produced by the conduction charges (on the conductive plates of capacitor) plus the field contribution from all the dipoles in the dielectric material. The local electric field plays a critically important role not only in polarization/distortion of molecules in the dielectric but it also plays a critically important role in the dielectric breakdown strength Ebd and in time-dependent dielectric breakdown (TDDB) [4] .
In linear, homogeneous and isotropic dielectrics, the polarization P can be written:
 , (2)
, (2)
where χ is the electric susceptibility and k is the dielectric constant. Using Equation (1) and Equation (2), the Lorentz equation is produced for the local electric field:
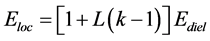 . (3)
. (3)
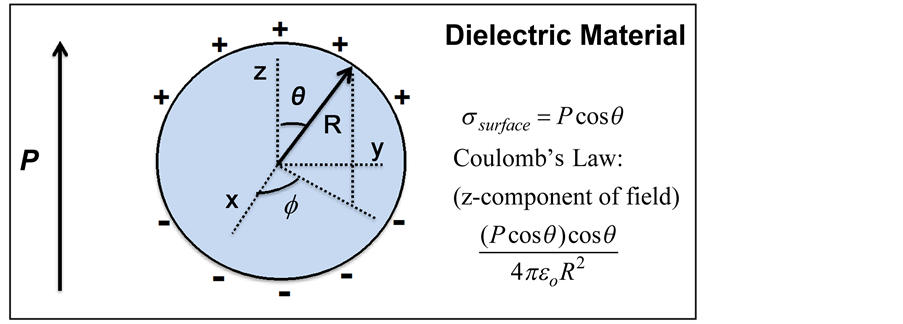
To determine L for a dielectric, Lorentz imagined a spherical cavity of dipoles (around an arbitrary lattice site in the dielectric) and treated their contribution to the local electric field discretely (by summation). The radius R of the sphere was chosen to be much larger than the lattice constant. Lorentz showed that, for such a spherical collection of dipoles (in a crystal with cubic symmetry), the dipolar contribution to the local electric field was zero. To find the local field contribution for dipoles outside of the sphere, Lorentz placed a surface polarization charge density σsurface = Pcosθ on the sphere, as illustrated in Figure 1.
Integrating the surface polarization charge density over the Lorentz sphere, as illustrated in Figure 1, gives a contribution to the local electric field at the origin that is commonly referred to as the Lorentz field:
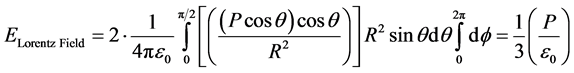 . (4)
. (4)
Comparing Equations (1) and (4), we see that the Lorentz factor is: L = 1/3. Thus, L = 1/3 has long been used and assumed to be valid for dielectrics having either cubic crystalline structure or having an amorphous structure [5] [6] .
For hyper-thin dielectrics, construction of a Lorentz sphere is difficult/impossible because the radius R of the sphere, as Lorentz suggested, should be chosen such that R is much larger than the lattice constant. For this reason, recently an alternative method to the standard Lorentz sphere approach is published for local electric field determination in hyper-thin dielectrics where the dielectric thickness may only be a few monolayers [7] . Fortunately, while this new method is used in local-field determination for hyper-thin dielectrics, the method is general enough that it can be easily extended to thicker dielectrics.
Figure 1. Lorentz sphere with a surface polarization charge density of σsurface = Pcosθ.
2. Approach for Local Electric Field Determination
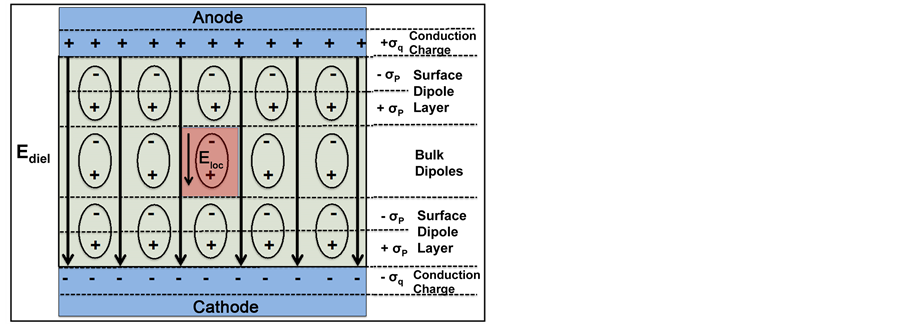
The Lorentz sphere approach is apparently impossible to apply for hyper-thin dielectrics where the dielectrics may only be a few monolayers thick. Thus, an alternative approach is needed to determine the local electric field. To properly determine the local electric field, care must be taken to account for all charges that are acting at an arbitrary site of interest. As illustrated in Figure 2, the local electric field is the cumulative field (at the site of interest) due to all the other charges acting. For a parallel plate capacitor (the greatest interest here) the charges include: external conduction charge density of σq on electrode surfaces, depolarization charge density of −σP on surface of dielectric, polarization charge density of σP near to the surface of dielectric, plus the impact of the all the other dipoles in the bulk of the dielectric referred to here as bulk dipoles.
First, we consider the average/macroscopic electric field in the dielectric Ediel due to the external charge density σq on electrode plates plus the dielectric surface depolarization charge density −σP. Using Gauss’ law for infinite parallel plate capacitors one obtains (in rationalized mks units):
 , (5)
, (5)
where χ is the electric susceptibility. Using the fact that the dielectric constant k is given by k = 1 + χ, and solving Equation (5) for Ediel, one obtains
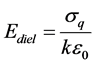 . (6)
. (6)
Ediel is the macroscopic/average-field in the dielectric. Integrating  from x = 0 to x = tdiel gives Ediel = ΔVdiel/tdiel, where ΔVdiel is the voltage drop in the dielectric. It is important to emphasize that Ediel is the macroscopic electric field that must be used in Maxwell’s equations for dielectric materials and is often referred to as the Maxwell field [Note that if electric displacement D is defined as
from x = 0 to x = tdiel gives Ediel = ΔVdiel/tdiel, where ΔVdiel is the voltage drop in the dielectric. It is important to emphasize that Ediel is the macroscopic electric field that must be used in Maxwell’s equations for dielectric materials and is often referred to as the Maxwell field [Note that if electric displacement D is defined as , then the lines of D start and terminate only on conduction charges]. Since the dielectric surface depolarization charge density −σP is already incorporated into Ediel, then next we must account for the sheet of near-surface polarization charge density σP as well as the field contribution from the bulk dipoles.
, then the lines of D start and terminate only on conduction charges]. Since the dielectric surface depolarization charge density −σP is already incorporated into Ediel, then next we must account for the sheet of near-surface polarization charge density σP as well as the field contribution from the bulk dipoles.
As illustrated in Figure 2, the total local electric field Eloc at an arbitrary site of interest in the hyper-thin dielectric becomes:
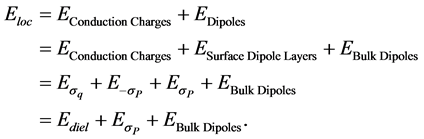 (7)
(7)
Figure 2. This figure shows various charges that contribute to the local electric field. The physical thickness (tdiel) of the hyper-thin dielectric illustrated is three monolayers.
The surface dipole layers (shown in Figure 2) have been treated in Equation (7) as closely spaced parallel sheets of uniform charge density σP, but with opposite polarity. The conduction charge layer σq plus the dielectric surface depolarization charge layer ?σP have been incorporated to produce Ediel. The remaining charge layer σP will be treated separately and will be referred to as the near surface polarization charge layer σP. For parallel- plate capacitors, the field due to the sheet of near-surface polarization charge σP can be written as:
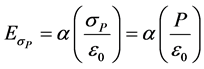 . (8)
. (8)
In Equation (8), α is a dimensionless parameter that is purely device-structure dependent (not a function of polarization or field). α can be determined from Coulomb’s Law by integrating/summing over the uniform sheet of near-surface polarization charge σP [7] . For an infinite parallel plate capacitor structures, α = 1.
Next we consider the bulk dipole contribution to the local electric field. As Lorentz orginially suggested, the dipolar contribution to the local electric field will be assumed to be proportional to the dielectric polarization P and can be written as,
 , (9)
, (9)
where β is a dimensionless structure-dependent parameter. Thus, using Equations (7)-(9), we obtain
 (10)
(10)
From Equation (10), we see that the Lorentz factor for dielectrics, in an infinite parallel plate capacitor arrangement, is given by: L = 1 + β.
3. Lorentz Factor L Determination
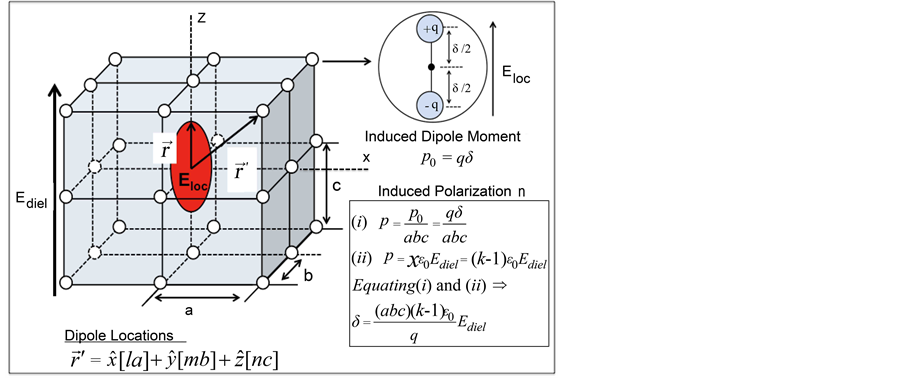
The dielectric polarization P is the number of dipoles per unit volume, and for cubic symmetry we have:
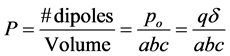
where po = qδ is molecular dipole moment (that is field induced) and the lattice parameters a = b = c for a crystal with cubic symmetry. Using Equations (9) and (11), we obtain for β:
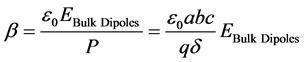
The method used for summing the bulk dipole contribution to the local electric field is illustrated in Figure 3.
Referring to Figure 3, the electrostatic potential at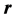

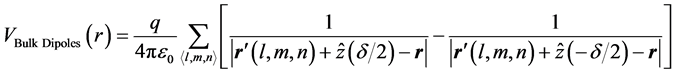
where:
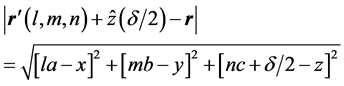
and
Figure 3. This figure shows the location of the bulk dipoles (in this cubic arrangement of dipoles). The dipole moment at each lattice site is p0 = qδ where the displacement δ is induced by the electric field Ediel.
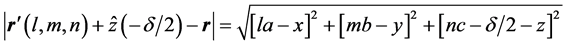
In the above dipole summation, the bracketed lattice sites 
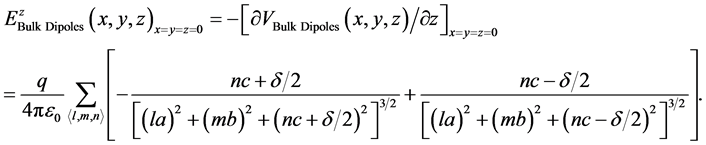
Using Equation (12) and Equation (16), we obtain the structural parameter β for the bulk dipoles:
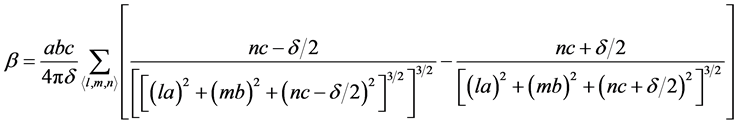
4. Layered Bulk-Dipole Summations
It is found to be most convenient (in order to gain relatively rapid convergence) to do bulk layered-dipole summations as originally suggested by Nijboer and De Wette [8] . By layered summation, it is meant that for each integer value of n [representing each monolayer of added bulk-dipole dielectric thickness] the field contribution to the local electric field Eloc (at the origin) is fully comprehended for all dipoles in the x-y plane. This is accomplished by allowing l and m to range as far as needed such that dipoles contributions outside this range make a negligible contribution to Eloc. Thus, in the layered dipole summation approach, β is given by:
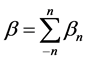
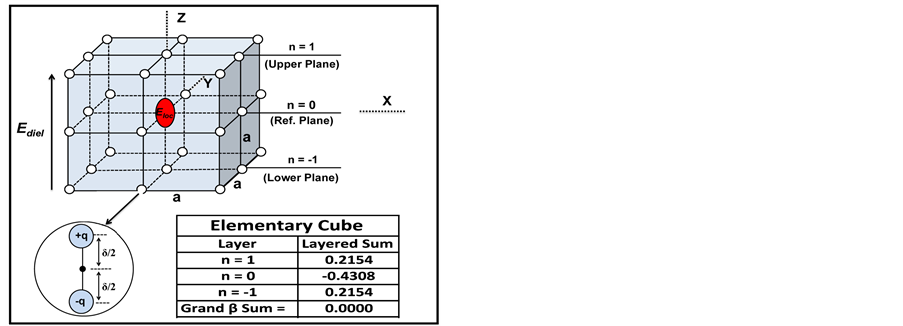
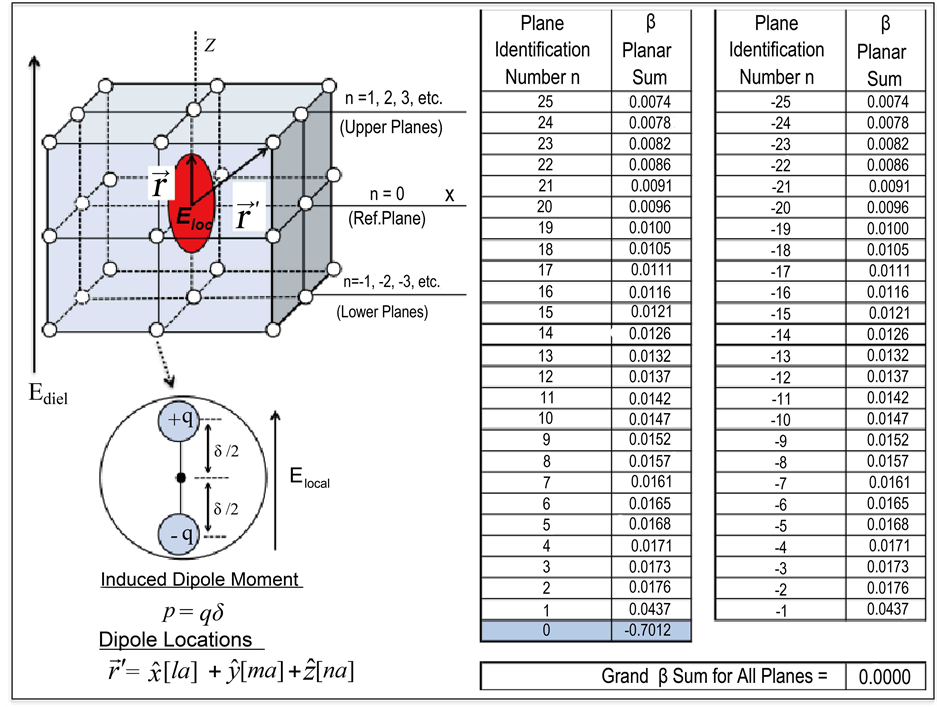
where βn is the full dipolar contribution from the nth layer of bulk dipoles. This layered-dipole summation approach for an elementary cube of dipoles is illustrated in Figure 4.
The dipole sum for the elementary cube shown in Figure 4 is β = 0. However, it is very important to emphasize that the net dipole sum is β = 0 for all cubes, independent of cube size. This is shown in Figure 5 where a
Figure 4. Layered bulk-dipole summation approach illustrated for an elementary cube. For the n = 0 reference plane, the contribution from dipoles in this plane β0 is opposite (negative) to the macroscopic field in the dielectric Ediel. The contribution from dipoles above n = 0 plane (β1) and below the reference plane (β−1) are positive such that net contribution to the local electric field is zero (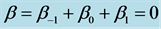
Figure 5. Monolayer-by-monolayer bulk-dipole contributions to β. For demonstration purposes, the planar bulk-dipole summations were conducted with l and m varying from −25 to +25. Each monolayer of dielectric thickness (assumed to be a = b = c = 2.5 Å) is indexed by n so that the thickness impact on β can be studied in detail. The reference plane (n = 0) produces the greatest single-layer bulk-dipole contribution to β. The negative sign means that the local field contribution of the β0 reference plane is actually opposite to Ediel. Note that each of the other monolayers of dielectric make a much smaller but positive contribution to β. Note also that when l, m, and n all range from −25 to +25, the macroscopic sample is in the shape of a perfect cube and the dipole sum, as expected, produces β = 0.
more extensive layered dipole summation is illustrated with l, m, and n all extending from −25 to +25 lattice sites. Note that, even for this much larger cube of dipoles, the net dipole summation β is still zero.
Figure 5 and the inserted summation table are very useful. For the n = 0 reference plane of bulk dipoles, that contains our origin, the reference-plane bulk-dipole summations (with l and m ranging from −25 to +25 lattice sites) produce β = β0 = −0.7012. The negative sign means that the contribution of the dipoles to the local electric field in the reference plane is opposite to Ediel. Let us now add a monolayer of bulk dipoles above and below the reference plane. The dipolar sum now becomes: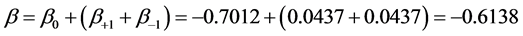
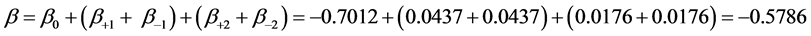
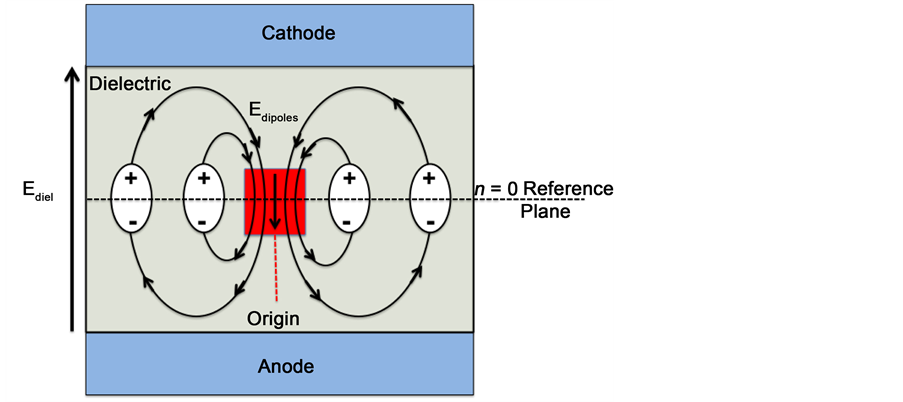
It is very important to emphasize that the n = 0 reference plane (that contains our origin) tends to dominate all the other individual dipole planes and its value is β0 ≈ −0.7. The reason for this is illustrated in Figure 6. All the dipoles in the n = 0 reference plane make a constructive contribution to the local electric field and the all these contributions are opposite to the macroscopic/Maxwell field Ediel in the dielectric.
The net contribution to the local electric field, from each of the other dipolar planes βn≠0 is in the same direction as Ediel but the individual-plane contributions are much smaller than β0. Thus, the value of the Lorentz factor L for hyper-thin dielectrics (a few monolayers of dielectric in an infinite parallel-plate capacitor structure) will be reasonably close to L ≈ 1 + β0 ≈ 1/3 and this is found to be in good agreement with the usual Lorentz factor assumption. However, for very thick dielectrics we expect β to asymptotically approach 0; thus, we expect L = 1 + β to asymptotically approach 1 for very thick dielectrics.
Before leaving this section, a question should be addressed: what must be the extent of the planar dipole summations (l and m) to insure that the contribution of the dipoles in each plane is fully comprehended? First, we note that, in the layered dipole sum approach, the dielectric thickness tdiel fixes the number of n monolayers (in the z-direction) that must be included in the β summation. However, the extent of the planar x-y dipole sum- mations is still an open question.
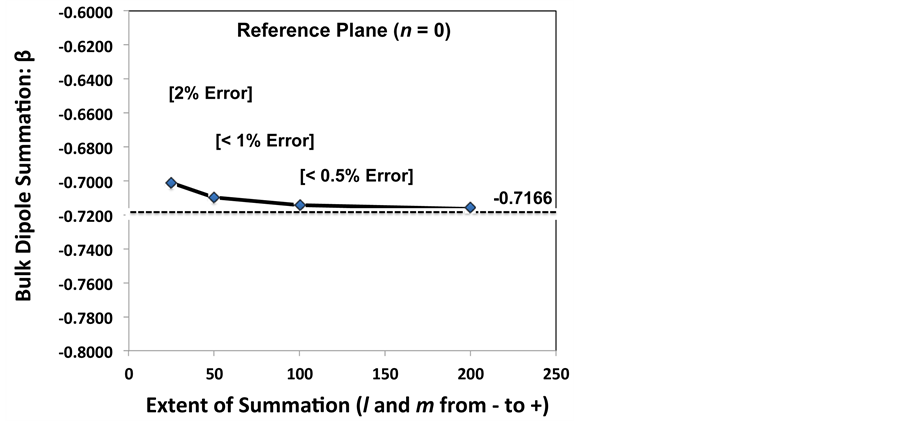
Since the n = 0 reference plane is the dominant plane, let us see how it is impacted as we extend the l, m summation range. The extended dipole summation results for the n = 0 reference plane are shown in Figure 7. It can be seen that planar dipole summation approach leads to a relatively rapid convergence for β0. This is because
Figure 6. All bulk dipoles in the n = 0 reference plane make a constructive contribution to the local electric field and the local electric field contribution from this plane is opposite to macroscopic/Maxwell field Ediel.
Figure 7. For the reference plane (n = 0), the x-y planar dipole summations were conducted over the indicated l and m ranges. Planar dipole summation convergence occurs relatively quickly with a summation error of only 2% when l and m extend from −25 to +25 lattice sites. A summation error of <1% results when l and m extend from −50 to +50 lattice sites. The asymptotic value for β0 is −0.7166.
dipole fields drop off relatively sharply as (1/r3). A summation error of <1% occurs in β0 determination if the planar dipole summations (l and m) are extended from −50 to +50 lattice sites. The infinite-plane asymptotic summation value for β0 (=−0.7166), shown in Figure 7, was obtained using a geometrical series approximation for the converging summation series [7] . This asymptotic value for β0 is consistent with values previously reported for the n = 0 reference plane: −0.7189 found in [9] and −0.72 found in [10] [So as to avoid confusion for reader, it should be noted that the actual value reported in [9] is −9.033622 but this value has to be divided by 4π to be consistent with the rationalized mks system of units used in this paper]. Therefore, planar dipole summations with l and m ranging from −50 to +50 lattice sites tend to produce an error of <1% in β0 determination. Thus, the range of l and m for planar summations will be from −50 to +50 lattice sites in the rest of this paper.
5. Bulk Layered-Dipole Summations for Thicker Dielectrics
A detailed example of planar dipole sums, for a moderately thick dielectric of 9 monolayers, will be now be conducted and then the method will be generalized to very thick dielectrics. Shown in Table 1 are the summation results for a dielectric that has a physical thickness of 9 monolayers thick (7 bulk dipole monolayers are summed). To minimize error (<1%) in the construction of Table 1, the x-y planar dipole summations were conducted with both l and m ranging from −50 to +50 lattice sites.
Since the local field contribution from the dielectric surface dipole-layers are already incorporated in the model, the bulk-dipole layer summations (shown in Table 1) are over 7 bulk monolayers of dipoles. As indicated in Table 1, the variation in L (with position within the dielectric thickness) was determined by shifting the reference plane from the bottom of the dielectric to the top. The results are illustrated in Figure 8.
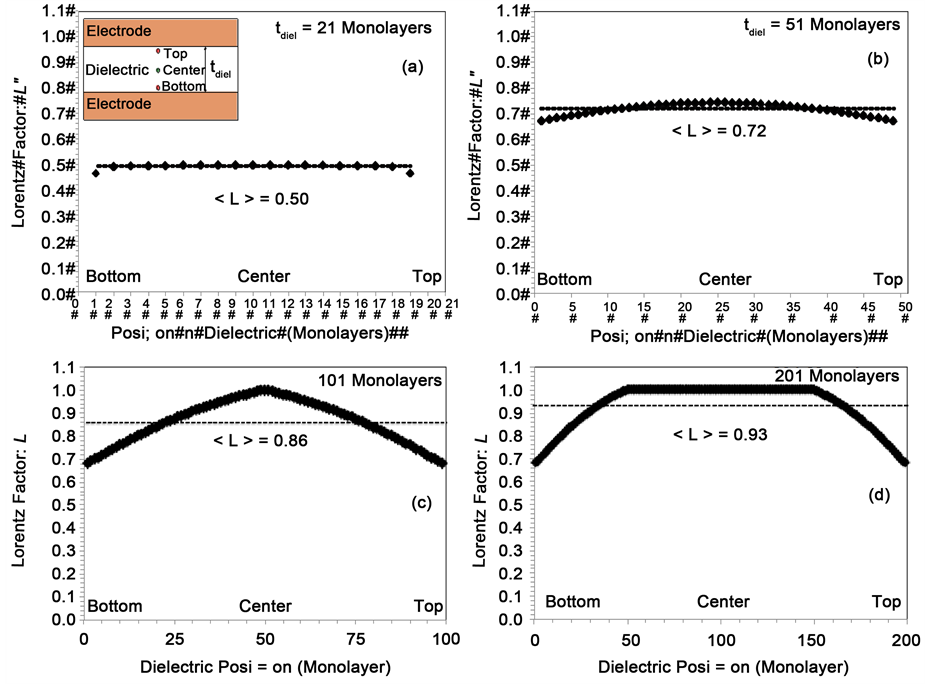
These planar dipole summation results indicate that some L variation does exist within thickness the dielectric, but generally the variations are small. Also, we note that the average value of the Lorentz factor does increase with thickness, but the average value
Using the summation approach [used for the construction of Table 1], we show the results for much thicker dielectrics. For each added monolayer of thickness [assumed to be 2.5 Å and indexed by n], all planar summations (l and m) were extended from −50 to +50 lattice sites. When n also extends over the range −50 to +50, the dipole sum becomes β = 0, thus L = 1 + β = 1.
Table 1. Lorentz factor across dielectric thickness.
Figure 8. Lorentz factor L determination for a dielectric of physical thickness of 9 monolayers. Only 7 monolayers are actually considered in the bulk dipole sum because the contribution of the surface dipole layers, to the local electric field, has already been included in model. The L variation within the thickness of hyper-thin dielectrics is found to be relatively small. Location points for the bulk dipole summations are indicated. The average value of L (
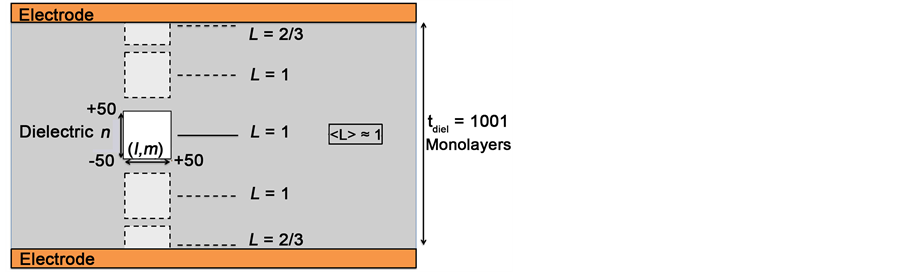
Figure 9 needs some discussion. The flat-top region in Figure 9(d) occurs because the full cube (with l, m, and n all ranging from −50 to 50 lattice sites) can fully fit within the dielectric thickness; in these locations β = 0, thus L = 1 + β = 1. A very thick dielectric (1001 monolayers) is illustrated in Figure 10. In most regions of the thick dielectric l, m, n can range unrestricted from −50 to +50 lattice sites so β = 0 and L = 1 + β = 1 over most
Figure 9. Shows Lorentz factor L as a function of position in dielectric thickness. The average value of the Lorentz factor
Figure 10. Note that if the dielectric is very thick, then bulk-dipole cubes (with l, m, and n all ranging from −50 to +50) can easily fit within the thickness of the dielectric and β = 0 for these cubes. Therefore, the average value of the Lorentz factor
of the very thick dielectric. However, as one approaches the top and bottom of the thick dielectric, the summation over n [Equation (18)] becomes truncated such that at the top and bottom surfaces of the thick dielectric layer: L = 1 − 0.36 ≈ 2/3. The dipole layer truncation, as one approaches the top and bottom dielectric surfaces, will cause more variation in L (from 2/3 to 1) within the thickness of thicker dielectrics.
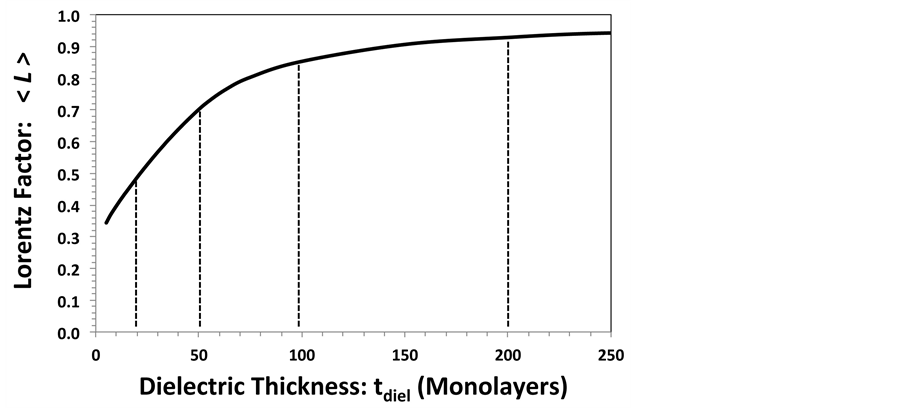
The above results are summarized into a single curve (see Figure 11) where the average Lorentz factor
6. Impact of Increases in L on Dielectric Breakdown Strength
One of the great mysteries in time-dependent dielectric breakdown (TDDB) physics has been: why does the dielectric breakdown strength Ebd reduce with increases in dielectric thickness tdiel? Until now, only extrinsic arguments have been given: thicker dielectrics are hypothesized to have greater pre-existing defect densities thus making it easier for percolation path development resulting in lower breakdown strength.
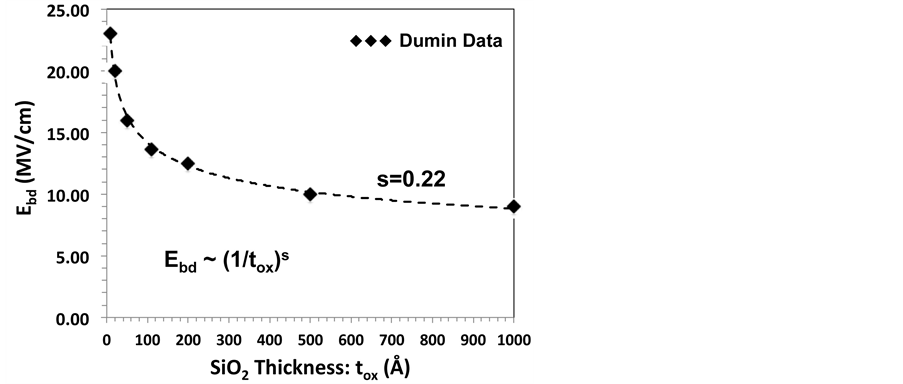
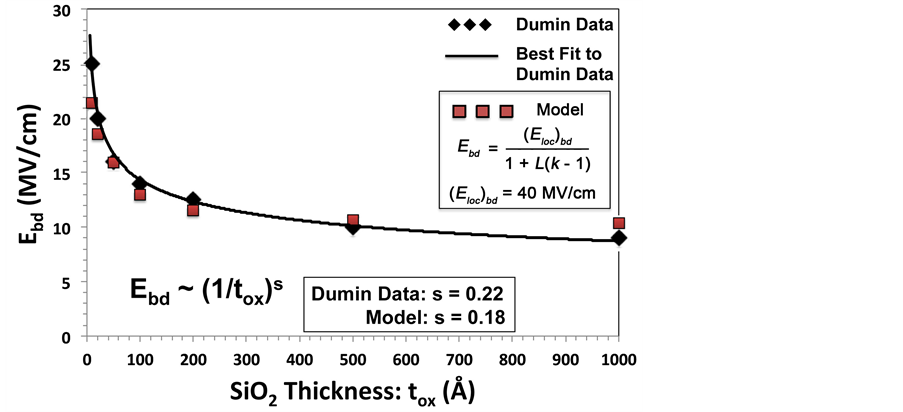
The fact that Ebd reduces with tdiel is well established. Early investigations by Klein and Gafni showed this to be true [11] . They found that, by testing silicon oxides deposited on glass, Ebd reduces with increases in tdiel. While the quality of these early-produced deposited-oxides can be certainly questioned, extensive work done much later by Dumin [12] showed clearly that, for thermally-grown semiconductor-quality SiO2 [see Figure 12], Ebd reduces with increases in tdiel. Figure 12 indicates that, for SiO2, Ebd~(1/tdiel)s with s = 0.22. The reduction in Ebd with increases in tdiel is not just a SiO2 characteristic but seems to be a general trend for all polar solid dielectrics [13] [14] .
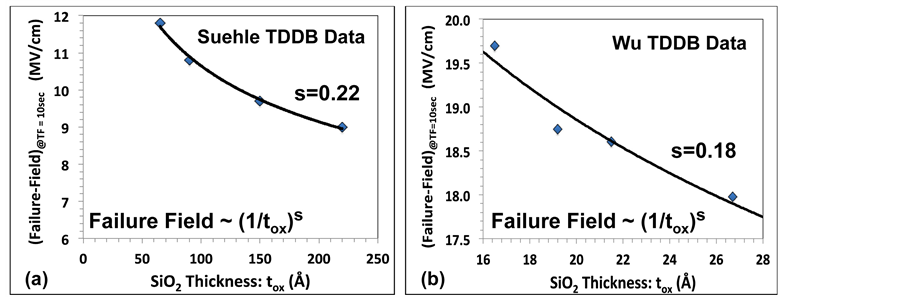
The reduction in Ebd with tdiel is also reflected in time-dependent dielectric breakdown (TDDB) data. For constant field, thicker dielectrics fail faster, or equivalently, for a constant time-to-failure TF (e.g., TF = 10 sec), the Failure Field reduces with tdiel. The Suehle TDDB data [15] , reproduced in Figure 13(a), are in good agreement with the Dumin breakdown data. The Wu TDDB data [16] for hyper-thin SiO2 [when stressing voltages are converted to fields (Eox = ΔV/tox)] are shown in Figure 13(b). While there is more dispersion in the Wu TDDB data, a power-law dependence (s = 0.18) is still evident.
The fact that thicker dielectrics breakdown at lower fields (and have lower TDDB performance) has been a great mystery and challenge for TDDB modeling. For current-based TDDB models, why would thinner SiO2
Figure 11. Average Lorentz factor as a function of dielectric thickness. For a very thin dielectrics (tdiel < 20 monolayers), < L > ≈ 1/3. For very thick dielectrics,
Figure 12. Dumin breakdown data [12] for SiO2. Shows Ebd versus dielectric thickness tox . The breakdown data shows an inverse-thickness power-law dependence with s = 0.22. The breakdown strength Ebd reduces sharply initially with dielectric thickness but then a more gradual reduction with dielectric thickness.
Figure 13. (a) Re-plotting of the Suehle TDDB data [15] , using Failure Field @ TF = 10 sec, reveals a power-law dependence (s = 0.22) reduction in failure-field with tox varying from 65 Å to 220 Å. (b) When converted to field (Eox = ΔV/tox), re-plotting of the Wu TDDB data [16] , using Failure Field @ TF = 10 sec, also indicates a power-law dependence (s = 0.18) with tox varying from 16.5 Å to 26.7 Å.
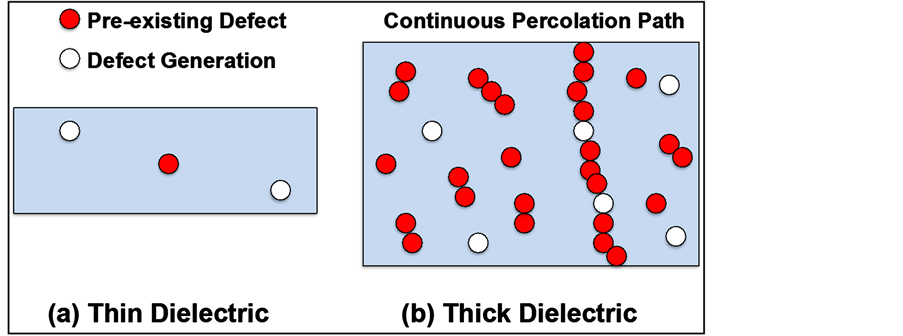
dielectrics have better breakdown strength and better TDDB performance when they tend to have higher leakages? As for field-based models, why isn’t the breakdown strength independent of thickness? To circumvent these fundamental reliability physics questions, TDDB models have tended to use the extrinsic hypothesis: thicker dielectrics must possess a greater pre-existing defect density. The extrinsic hypothesis is illustrated in Figure 14.
The extrinsic hypothesis (of a higher density of pre-existing defects in thicker dielectrics) has been widely embraced, without serious objections. The extrinsic hypothesis has gained wide acceptance because the thickness dependence can be easily incorporated into all commonly used TDDB models: E, 1/E, Root-E, or V−n [19] . All of these TDDB models have an adjustable pre-factor term into which the empirical thickness dependence (1/tdiel)s can be easily incorporated (as is commonly done for area scaling). Thus, all TDDB models tend to circumvent the thickness-dependence physics by simply hypothesizing that thicker dielectrics must have a much higher density of pre-existing defects.
After 50 years of intensive and extensive SiO2 dielectric research (by hundreds of investigators), if higher defect density was the fundamental reason for Ebd reduction with tdiel, then surely someone would have found (as is allowed by the Poisson distribution) a single thick-oxide capacitor having a breakdown strength of >20 MV/cm.
Figure 14. (a) Pre-existing defects can exist in dielectrics at time zero. Defects can be also generated during TDDB testing. (b) Percolation path develops and breakdown occurs when a combination of pre-existing defects and generated defects form a continuous conduction path. [17] [18] .
However, apparently, these thick-oxide/high-breakdown-field unicorns do not exist. Thus, the extrinsic hypothesis will be rejected and an effort is undertaken to find a more fundamental physics-based model for describing why thicker dielectrics have lower breakdown strength and lower TDDB performance. This has great relevance for low-k interconnect dielectrics [20] and high-voltage capacitors [21] where the dielectrics can be relatively thick.
The extrinsic hypothesis (of higher defect density) as for why Ebd reduces with tdiel has never been seriously challenged because, until now, there has never been an intrinsic/fundamental-physics reason presented for this. However, the increase in L with dielectric thickness (shown in Figure 11) is just the fundamental physics that is required to explain why the Ebd reduces with tdiel. Using Equation (3), we see that the Ebd can be written as:

It is clear from Equation (19) that the breakdown strength of the dielectric is predicted to reduce when the dielectric constant k increases [22] and also this work shows that Ebd reduces with increases in L (which increases with thickness).
Using Equation (19), with the thickness dependence of
A local electric field of 40 MV/cm corresponds to a bond strength of 2.7 eV [19] . This is in good agreement with the energy required to break bond-coordination [19] [23] , when the Si-ion goes from its normal 4-fold to 3-fold coordination in the 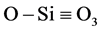
7. Impact of Local Electric Field on Bond Breakage
The local electric field Eloc, that distorts polar bonds (by stretching, compressing, bending, etc.) and brings about the polarization, also serves to weaken polar molecular bonds. The local electric field thus reduces the bond strength ΔH (activation energy required for bond breakage). Weakening of the molecular bonds is very important for any bond-breakage process, regardless of the actual breakage mechanism (standard Boltzmann processes and/or current driven processes). In previous work [23] , this author has shown that the reduction bond strength can be described by:
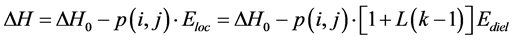
where ΔH0 is the energy required to break the bond in the absence of field and p(i,j) is the dipole moment associated
Figure 15. Comparison of model with Dumin breakdown data. The model shows clearly that Ebd reduces with dielectric thickness as (1/tox)s. The relatively good model fit to Dumin data suggests that the local electric field at breakdown is a constant (Eloc)bd ≈ 40 MV/cm for all SiO2 thicknesses.
with coordination bond breakage. The parameters i and j are the repulsive and attractive exponents, respectively, associated with the Mie-Gruneisen bonding potential. For strong polar/ionic bonding, the power-law molecular repulsive component “i” and the attractive ionic component “j” are typically given by i = 9 and j = 1, respectively. These polar molecular components produce a dipole moment for bond breakage of [23]
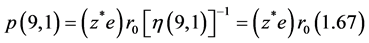
For SiO2, with tetrahedral bonding, the Si cat-ion has a charge state of 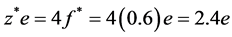
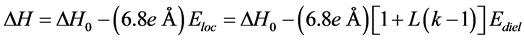
where k (=3.9) is the dielectric constant for SiO2. With a bond strength of ΔH0 = 2.7 eV, then the ultimate breakdown strength (ΔH®0) for very thin SiO2 (with L = 1/3) becomes: (Ediel)bd ≈ 20 MV/cm whereas the ultimate breakdown strength for very thick SiO2 (with L = 1) is (Ediel)bd ≈ 10 MV/cm .
8. Impact of Local Electric Field on TDDB
Time-dependent dielectric breakdown (TDDB) is a very important failure mechanism for metal oxide field effect transistors (MOSFETs) and capacitors [24] - [29] . As for the thermochemical TDDB model [4] for SiO2, bond strength ΔH reduction occurs because of the local electric field and bond breakage occurs due to Boltzmann/thermal processes:
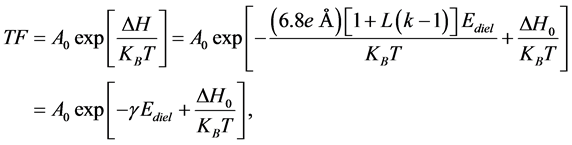
where the field acceleration parameter γ is given by :

For very thin SiO2 dielectric (with L ≈ 1/3) the effective dipole moment for bond breakage is peff = 13.4e Å and this value is widely observed in the TDDB data for thin SiO2 [23] . However, for very thick SiO2 (with L ≈ 1), Equation (24) predicts that peff should approximately double for very thick dielectrics. Therefore, while the breakdown strength Ebd is expected to decrease with thickness, the field acceleration parameter γ is expected to increase with dielectric thickness (because L increases with thickness)
9. Discussion
The local electric field Eloc (the field that polarizes, distorts, and weakens polar molecular bonds) is given by 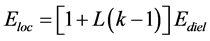
It has been determined that the n = 0 reference bulk-dipole plane dominates all the other individual planes above and below the reference plane. All the bulk dipoles in this n = 0 reference plane make a constructive contribution to the local electric field that is opposite to the macroscopic field Ediel in the dielectric. Therefore, the bulk-dipole sum for this n = 0 reference plane is negative and for an infinite reference plane of bulk dipoles: β0 = −0.72.
As for the layered bulk-dipole summations, it has been shown in this work that beyond 50 lattice constants the planar bulk-dipole contributions to the local electric field are very small/negligible. Thus, a planar bulk-dipole sum with (l,m) from −∞ to +∞ monolayers is approximately equal (an error of <1%) to the planar bulk-dipole sum with (l,m) varying from −50 to + 50 monolayers.
Since the other individual bulk-dipole planes (n ≠ 0) make a positive, but much smaller contribution to the local electric field, then for very thin dielectrics: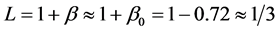
Even though two different thicknesses of a dielectric may have exactly the same macroscopic field Ediel in the dielectric, the local electric field is not the same. The thicker dielectric will have a larger L and thus a larger local field Eloc. Because of the higher local electric field Eloc in the thicker dielectric, the thicker dielectric will have lower breakdown strength. The definitions of thin and thick dielectrics have been established through planar bulk-dipole summations for L determination. L increases from L ≈ 1/3 for thin dielectrics (<20 monolayers) to nearly L ≈ 1 for very thick dielectric (>200 monolayers). The increase in Lorentz factor L with increase in dielectric thickness tdiel leads to higher local electric fields that produce more polar-bond distortion, thus a weakening of such bonds. Bond weakening leads to lower breakdown strength in thicker dielectrics and is independent of actual bond-breakage mechanism (field, current, or hydrogen release).
While the Ebd tends to reduce with dielectric thickness, all thicknesses tend to breakdown at approximately the same local electric field. As for SiO2, the local electric field at breakdown is (Eloc)bd ≈ 40 MV/cm and is independent of thickness. This local electric field (40 MV/cm) corresponds to a coordination bond energy of 2.7 eV. This is consistent with the reported energy required to transform the silicon-ion from four-fold coordination to three-fold coordination in the 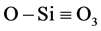
10. Conclusion
A Lorentz factor of L = 1/3 has long been assumed valid without consideration for dielectric thickness. While L = 1/3 is valid for thin dielectrics (having either cubic crystalline or amorphous structure), it is not valid for thick dielectrics. L increases from L ≈ 1/3 for thin dielectrics (<20 monolayers) to nearly L ≈ 1 for very thick dielectric (>200 monolayers). The increase in L with tdiel leads to higher local electric fields that produce more polar-bond distortion and thus a weakening of such bonds. Bond weakening leads to lower breakdown strength in thicker dielectrics and is independent of actual bond-breakage mechanism (field, current, or hydrogen release). While the Ebd tends to reduce with thickness, all thicknesses tend to breakdown at the same local electric field. As for SiO2, the local electric field at breakdown is (Eloc)bd ≈ 40 MV/cm and is independent of thickness. This local electric field of 40 MV/cm corresponds to an energy of 2.7 eV that is required to break bond-coordination in the 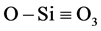
Cite this paper
J. W. McPherson, (2016) Increases in Lorentz Factor with Dielectric Thickness. World Journal of Condensed Matter Physics,06,152-168. doi: 10.4236/wjcmp.2016.62018
References
- 1. Mossotti, O. (1850) Mem. di mathem. e fisica in Modena. 24, 49.
- 2. Clausius, R. (1879) Die mechanische U’grmetheorie. 2, 62.
- 3. Lorentz, H. (1915) The Theory of Electrons and Its Application to the Phenomena of Light & Radiant Heat. 2nd Edition, Dover Publications, New York.
- 4. McPherson, J. and Mogul, H. (1998) Underlying Physics of the Thermochemical E Mode in Describing Low-Field Time-Dependent Dielectric Breakdown in SiO2 Thin Films. Journal of Applied Physics, 84, 1513.
http://dx.doi.org/10.1063/1.368217 - 5. Kittel, C. (1971) Introduction to Solid State Physics. 4th Edition, John Wiley Publishing, New York.
- 6. Ashcroft, N. and Mermin, N. (1976) Solid State Physics. Harcourt Brace College Publishers, New York.
- 7. McPherson, J. (2015) Lorentz Factor Determination for Local Electric Fields in Semiconductor Devices Utilizing Hyper-Thin Dielectrics. Journal of Applied Physics, 118, Article ID: 204106.
http://dx.doi.org/10.1063/1.4936271 - 8. Nijboer, R. and De Wette, F. (1958) The Internal Field in Dipole Lattices. Physica, 24, 422.
- 9. Vanzo, D., Topham, B. and Soos, Z. (2014) Dipole-Field Sums, Lorentz Factors, and Dielectric Properties of Organic Molecular Films Modeled as Crystalline Arrays of Polarizable Points. Advanced Functional Materials, 25, 2004-2012.
http://dx.doi.org/10.1002/adfm.201402405 - 10. Mueller, H. (1935) Theory of the Photo-Elastic Effect of Cubic Crystals. Physical Review, 47, 947.
http://dx.doi.org/10.1103/PhysRev.47.947 - 11. Klein, N. and Gafni, H. (1966) The Maximum Dielectric Strength of Thin Silicon Oxide. IEEE Transactions on Electron Devices, 13, 281-289.
http://dx.doi.org/10.1109/T-ED.1966.15681 - 12. Dumin, D., Ed. (2002) Oxide Reliability—A Summary of Silicon Oxide Wearout, Breakdown, and Reliability. World Scientific Publishing, Singapore, 173
- 13. Kim, H. and Shi, F. (2001) Thickness Dependent Dielectric Strength of a Low-Permittivity Dielectric Film. IEEE Transactions on Dielectrics and Electrical Insulation, 8, 248-252.
- 14. Chen, G. and Zhao, J. (2012) Space Charge and Thickness Dependent DC Electrical Breakdown of Solid Dielectrics. 2012 IEEE International Conference on High Voltage Engineering and Applications, Shanghai, 17-20 September 2012, 12-15.
- 15. Suehle, J. (2002) Ultrathin Gate Oxide Reliability: Physical Models, Statistics. IEEE Transactions on Electron Devices, 49, 958.
- 16. Wu, E., Vayshenker, A., Nowak, E., Sune, J., Vollertsen, R., Lai, W. and Harmon, D. (2002) Experimental Evidence of TBD Power-Law for Voltage Dependence of Oxide Breakdown in Ultrathin Gate Oxides. IEEE Transactions on Electron Devices, 49, 2244-2253.
- 17. Degraeve, R., Groseneken, G., Bellens, R., Ogier, J., Depas, M., Roussel, J. and Maes, H. (1998) New Insights in the Relation between Electron Trap Generation and the Statistical Properties Breakdown. IEEE Transactions on Electron Devices, 45, 904-911.
http://dx.doi.org/10.1109/16.662800 - 18. Sune, J., Jimenez, D. and Miranda, E. (2001) Breakdown Modes and Breakdown Statistics of Ultrathin SiO2 Gate Oxides. International Journal of High Speed Electronics and Systems, 11, 789.
http://dx.doi.org/10.1142/S0129156401001003 - 19. McPherson, J. (2012) Time Dependent Dielectric Breakdown Physics-Revisited. Microelectronics Reliability, 52, 1753-1760.
http://dx.doi.org/10.1016/j.microrel.2012.06.007 - 20. Lee, S.-C. and Oates, A. (2015) On the Voltage Dependence of Copper/Low-k Dielectric Breakdown. 2015 IEEE International Reliability Physics Symposium, Monterey, 19-23 April 2015, 3A.3.1.
- 21. Higgins, R. and McPherson, J. (2009) TDDB Evaluations and modeling of Very High-Voltage (10 kV) Capacitors. 2009 IEEE International Reliability Physics Symposium, Montreal, 26-30 April 2009, 432-436.
- 22. McPherson, J.W., Kim, J., Shanware, A., Mogul, H. and Rodriguez, J. (2003) Trends in the Ultimate Breakdown Strength of High Dielectric Constant Materials. IEEE Transactions on Electron Devices, 50, 1771.
- 23. McPherson, J. (2004) Determination of the Nature of Molecular Bonding in Silica from Time-Dependent Dielectric Breakdown Data. Journal of Applied Physics, 95, 8101.
http://dx.doi.org/10.1063/1.1728288 - 24. McPherson, J. and Baglee, D. (1985) Acceleration Factors for Thin Gate Oxide Stressing. International Reliability Physics Proceedings, Orlando, 25-29 March 1985, 1-5.
- 25. Chen, I., Holland, S. and Hu, C. (1985) A Quantitative Physical Model for TDDB in SiO2. International Reliability Physics Proceedings, Orlando, 25-29 March 1985, 24-31.
- 26. McPherson, J. and Mogul, H. (1998) Underlying Physics of the Thermochemical E Mode in Describing Low-Field Time-Dependent Dielectric Breakdown in SiO2 Thin Films. Journal of Applied Physics, 84, 1513.
http://dx.doi.org/10.1063/1.368217 - 27. McPherson, J., Kim, J., Shanware, A. and Mogul, H. (2003) Thermochemical Description of Dielectric Breakdown in High Dielectric Constant Materials. Applied Physics Letters, 82, 2121.
http://dx.doi.org/10.1063/1.1565180 - 28. Suehle, J. (2002) Ultrathin Gate Oxide Reliability: Physical Models, Statistics. IEEE Transactions on Electron Devices, 49, 958.
- 29. Wu, E., Vayshenker, A., Nowak, E., Sune, J., Vollertsen, R., Lai, W. and Harmon, D. (2002) Experimental Evidence of TBD Power-Law for Voltage Dependence of Oxide Breakdown in Ultrathin Oxides. IEEE Transactions on Electron Devices, 49, 2244-2253.
http://dx.doi.org/10.1109/TED.2002.805606