World Journal of Condensed Matter Physics
Vol.04 No.03(2014), Article ID:49398,26 pages
10.4236/wjcmp.2014.43023
The Pursuit of Fallacy in Density Functional Theory: The Quest for Exchange and Correlation, the Rigorous Treatment of Exchange in the Kohn-Sham Formalism and the Continuing Search for Correlation
A. Gonis
Physical and Life Sciences, Lawrence Livermore National Laboratory, Livermore, USA
Email: gonis1@llnl.gov
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 May 2014; revised 17 July 2014; accepted 30 July 2014
ABSTRACT
As pointed out in the paper preceding this one, in the case of functionals whose independent vari- able must obey conditions of integral normalization, conventional functional differentiation, de- fined in terms of an arbitrary test function, is generally inapplicable and functional derivatives with respect to the density must be evaluated through the alternative and widely used limiting procedure based on the Dirac delta function. This leads to the determination of the rate of change of the dependent variable with respect to its independent variable at each isolated pair, 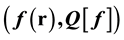 , that may not be part of a functional (a set of ordered pairs). This extends the con- cept of functional derivative to expectation values of operators with respect to wave functions leading to a density even if the wave functions (and expectation values) do not form functionals. This new formulation of functional differentiation forms the basis for the study of the mathemati- cal integrity of a number of concepts in density functional theory (DFT) such as the existence of a universal functional of the density, of orbital-free density functional theory, the derivative discon- tinuity of the exchange and correlation functional and the extension of DFT to open systems cha- racterized by densities with fractional normalization. It is shown that no universal functional ex- ists but, rather, a universal process based only on the density and independent of the possible ex- istence of a potential, leads to unique functionals of the density determined through the minimi- zation procedure of the constrained search. The mathematical integrity of two methodologies proposed for the treatment of the Coulomb interaction, the self-interaction free method and the optimized effective potential method is examined and the methodologies are compared in terms of numerical calculations. As emerges from this analysis, the optimized effective potential method is found to be numerically approximate but formally invalid, contrary to the rigorously exact re- sults of the self-interaction-free method.
, that may not be part of a functional (a set of ordered pairs). This extends the con- cept of functional derivative to expectation values of operators with respect to wave functions leading to a density even if the wave functions (and expectation values) do not form functionals. This new formulation of functional differentiation forms the basis for the study of the mathemati- cal integrity of a number of concepts in density functional theory (DFT) such as the existence of a universal functional of the density, of orbital-free density functional theory, the derivative discon- tinuity of the exchange and correlation functional and the extension of DFT to open systems cha- racterized by densities with fractional normalization. It is shown that no universal functional ex- ists but, rather, a universal process based only on the density and independent of the possible ex- istence of a potential, leads to unique functionals of the density determined through the minimi- zation procedure of the constrained search. The mathematical integrity of two methodologies proposed for the treatment of the Coulomb interaction, the self-interaction free method and the optimized effective potential method is examined and the methodologies are compared in terms of numerical calculations. As emerges from this analysis, the optimized effective potential method is found to be numerically approximate but formally invalid, contrary to the rigorously exact re- sults of the self-interaction-free method.
Keywords:
density functional theory, Variational Properties of density functional Theory, Self-interaction Error, Optimized effective Potential, Functional derivative, parametric Derivative, Functional Rate of change, Derivative Discontinuity, orbital-free Density functional theory,exchange and Correlation functional

1. Introduction
The paper preceding this one, referred to hereafter as I, established the formal result that conventional functional differentiation cannot be performed in the case of functionals in which the independent variable must obey conditions of integral normalization. In these cases, functional differentiation must be carried out in terms of the Dirac delta function, consistent with the interpretation that it describes the rate of change of a dependent variable (e.g., a functional) with respect to the change of the independent variable (a function) at some point in space. One of the central aims of the present paper is to apply this result to the analysis of a number of concepts that have evolved in connection with the formal aspects of density functional theory (DFT) [1] and the implemen- tation of the theory in terms of the Kohn-Sham formalism [2] . The paper also examines certain long-held beliefs prevalent in the field through analysis at the fundamental level.
In 1964, Hohenberg and Kohn published a paper [1] containing two incredible theorems, known as the theo-
rems of Hohnenberg and Kohn. The First Theorem demonstrated that if a density, 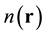 , represents the ground
, represents the ground
state of an interacting many-particle system under the action of an external potential, 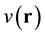 , then the potential is
, then the potential is
a uniquely defined (within a constant) functional of the density. In other words, given the density and only the density of the ground state of a system of 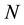 interacting particles (with a specified inter-particle potential, such as the Coulomb repulsion for electrons) one can determine the external potential uniquely, modulo a constant. The Second Theorem established the existence of an energy functional of the density associated with the po- tential in question whose minimum value materialized at the density of the system’s ground state where it equals the energy of that state. This energy functional has the form,
interacting particles (with a specified inter-particle potential, such as the Coulomb repulsion for electrons) one can determine the external potential uniquely, modulo a constant. The Second Theorem established the existence of an energy functional of the density associated with the po- tential in question whose minimum value materialized at the density of the system’s ground state where it equals the energy of that state. This energy functional has the form,
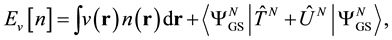 (0.1)
(0.1)
where 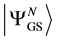 denotes the ground state of the N-particle interacting system under
denotes the ground state of the N-particle interacting system under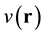 , and
, and 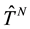 and
and 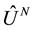 are,
are,
respectively, the operators representing the kinetic energy and inter-particle interaction potential of the system (Coulomb interaction for electrons). The expectation value in the definition of the energy functional is known as the Hohenberg and Kohn functional,
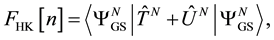 (0.2)
(0.2)
for densities that represent the ground state of a potential (referred to hereafter as 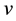 -representable densities). It is to be noted that the integral in (0.1) represents the expectation value of the (external) potential operator with
-representable densities). It is to be noted that the integral in (0.1) represents the expectation value of the (external) potential operator with
respect to the ground-state,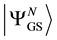 . It follows that the density,
. It follows that the density, 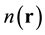 , is obtained from a wave function, (see
, is obtained from a wave function, (see
(0.7) and (0.10)), and is thus strictly normalized to an integer.
Most strikingly, the theorems imply that the wave function of the ground state of an interacting, N-particle system (say, electrons), admittedly an immensely complicated structure depending on the 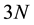 coordinates (and spins, for electrons) of an interacting system could be determined through knowledge of a function of three- dimensional coordinates, the particle density of the systems’s ground state. And this would be accomplished without the need to solve the many-particle Schrödinger equation for the interacting system!
coordinates (and spins, for electrons) of an interacting system could be determined through knowledge of a function of three- dimensional coordinates, the particle density of the systems’s ground state. And this would be accomplished without the need to solve the many-particle Schrödinger equation for the interacting system!
1.1. The Problem of v-Representability
At this point, however, a serious difficulty emerges: The set of v-representable densities is unknown, that is to say, there exists no rigorous mathematical procedure determining whether a given density is v-representable, so that the domain of definition of the Hohenberg and Kohn functional is also unknown, and correspondingly
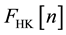 is ill-defined, e.g., [3] - [5] . This is the so-called and well-known v-representability problem.
is ill-defined, e.g., [3] - [5] . This is the so-called and well-known v-representability problem.
The implications of this feature can be understood by recalling the general definition of a functional, as a set of ordered pairs, 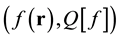 , in which the first entry, the independent variable, forming the domain of the functional, is a function of coordinates, and the second entry, the dependent variable or functional, referred to as the range of the functional, is given strictly and uniquely in terms of the independent variable [6] . Single- valuedness requires that no two independent variables coincide (corresponding to the definition of a function as a set of ordered pairs of real numbers,
, in which the first entry, the independent variable, forming the domain of the functional, is a function of coordinates, and the second entry, the dependent variable or functional, referred to as the range of the functional, is given strictly and uniquely in terms of the independent variable [6] . Single- valuedness requires that no two independent variables coincide (corresponding to the definition of a function as a set of ordered pairs of real numbers, 


Such a procedure would imply that the Hohenberg and Kohn functional is a mere function of the density or a functional of form, so that it is evaluated at the point (function) of a given density (as the function, 



The belief in the existence of a Hohenberg and Kohn functional that is a universal functional of the density in the sense that it is a function of the density is possibly the most enduring albeit mathematically unsupported belief in the development of DFT, if not in the whole of mathematical physics. The belief in such functions of the density is further expressed through the attempts to derive a function of the density that represents the so- called exchange and correlation functional [2] [3] in the Kohn-Sham [2] (KS) formulation for the practical implementation of DFT. The exchange and correlation functional [2] - [4] represents the difference,

In the KS formalism, 







It can be shown [7] that in the absence of degeneracy, 

Once again, the exchange and correlation functional, as well as the kinetic energy functional of non-inter- acting particles, 

Yet, in the presence of functionals that are mere functions of the density, expectation values, e.g., (0.2), would be determined without the explicit use of the wave function in direct contradiction of the premise that DFT determines the wave function from knowledge of the density.
1.2. Claims
It is generally accepted that DFT is characterized by the following features:
1) The wave function of the ground state of 

2) The external potential acting on an interacting system can be obtained uniquely (within a constant) through sole knowledge of the density of the system's ground state.
1.3. Consequences
There is a consequence of 1) above that in a deep sense is the most striking feature of DFT: The determination of a quantum state (an element of an abstract Hilbert space that defies observation) from sole knowledge of the density, an observable (an element of physical reality that is subject to observation and can be determined as the outcome of measurement). This utterly unexpected turn of events allows the fulfillment of the program of quantum mechanics, the determination of quantum states that yield measurement outcomes for interacting many- particle systems directly from knowledge of the outcome of measurement, notably bypassing, in principle, the conventional procedure of solving the Schrödinger equation for the systems.
This reveals the fundamental purpose behind the development of density functional theory as an alternative to the Schrödinger equation, at least with regard to the ground states of interacting many-particle systems.
The determination of the potential as a unique functional of the density carries its own brand of subtlety. One is to determine the potential based exclusively on knowledge of the density and nothing else. No room exists for considering values of functionals at different values of the density. Because the density may in fact describe a physical, interacting system, the condition of sole knowledge of the density corresponds to the condition that isolated systems under an external potential must be studied strictly in their own right independently of any other system, hence of any other density.
The mathematical implication of the last condition, dictated as it were by the make up of physical reality, is that no information about the states corresponding to a given density can be obtained from knowledge of only the states corresponding to another. In terms of derivatives, this implies that the functional derivatives with respect to a given density must be carried out strictly within the space of the density in question, namely the space defined by a single pair formed by the density and its dependent variable (irrespective of the possibility that this pair may belong to the domain of a functional).
Hohenberg and Kohn’s second theorem shows that the functional in (0.1) exhibits a minimum at the exact density of the ground state of the potential, 

in terms of the vanishing of the functional derivative of the energy functional with respect to the density eva- luated at the density of the ground state of the potential. This expression brings to the fore the need for close scrutiny of functional differentiation within DFT.
For example, as alluded in the previous paragraph, the derivative in the last expression must be evaluated at a
given density, 

of the functional, 
The section that follows reviews the concept of N-representability that allows the resolution of some of the difficulties connected to the v-representability problem, in particular regarding the definition of the Hohenberg and Kohn functional. It also sets up the framework for the explicit performance of derivatives with respect to the density.
2. N-representability and the Constrained Search
A function of coordinates, 



This represents the expectation value of the density operator,

where 




Unit normalization is a strict requirement because the modulus squared of the wave function represents the classical probability of finding a system of 


The notation, 

(0.7) [9] .
There are an infinite number of wave functions that lead to a given density, and a formal procedure for deter-
mining the complete set, 
lowski [10] - [12] . In the constrained search formulation introduced by Levy [8] and later Lieb [7] , one examines all such wave functions and determines the one (degeneracy excluded) that minimizes the expectation value of the sum of the kinetic and inter-particle potential operators,

Analogously, one defines the kinetic energy functional (see (0.4)),

in terms of a wave function that leads to the density and minimizes the expectation value of the kinetic energy of a system of 
Assuming the absence of degeneracy, the constrained search returns a single wave function,
wave function exists regardless of whether or not the density is v-representable. In the case in which the density happens to be 



under

In this case, the constrained search yields, 

Thus, the constrained search solves one aspect of the v-representability problem, i.e., provides a rigorous definition of a functional of the density that for v-representable densities defines
Furthermore, the present state of the formalism reveals a deep characteristic of the method: The Ho- henberg and Kohn functional, obtained through a procedure, that of the constrained search, is given as the expectation value of operators with respect to wave functions that generally are not mere functions of the density [13] .
2.1. Functionals of Form and of Process
Based on sole knowledge of a density, 




Functionals of form are mere functions of the independent variable, such as, for example, the functional defined by the integral,
On the other hand, the quantities 

procedure, here the constrained search. Such functionals are notorious for defying expression as functionals of form [14] . Yet, since the introduction of Kohn-Sham DFT, there has been an intense effort to develop func- tionals of form, (to say nothing about developing functionals by fitting to experiment [15] - [23] !)
With the exception of the so-called exact exchange treated within the optimized effective potential (OEP) method [24] (analyzed below) and the recently developed self-interaction free (SIF) method [25] , no functional proposed for the implementation of the Kohn-Sham is obtained as an expectation value of an operator with respect to a wave function, and hence none is formally valid. Furthermore, as discussed below, of the two me- thods that fulfill this condition, only the SIF methodology is obtained through rigorous derivation of the func- tional derivative of expectation values, based on the properties of Hilbert spaces and expansions in terms of orthonormal and complete bases in such spaces.
2.2. Are the Kohn-Sham Orbitals Functionals of the Density?
In the absence of degeneracy, the antisymmetric wave function that leads to a given density, 
and minimizes the expectation value of the kinetic energy of a system of 

takes the form of a Slater determinate [7] ,

where the 

density may induce the notion that the orbitals entering the definition of 
Even though the Slater determinant, 







does possess a derivative of the second entry (dependent variable, whether a wave function leading to the den- sity, or an expectation value with respect to such a wave function) with respect to the density, evaluated at the density in the pair.
This is an illustration of the general principle that even though a collection of objects may be a unique functional of the density, the individual elements of the collection do not necessarily have this property, but do possess derivatives with respect to the density. The absence of a functional also explains the absence of a Taylor- series-like expansion connecting two points in the range of the functional.
3. Derivatives with Respect to the Density
This section of the paper provides a summary of the notions underlying functional derivatives with emphasis on functionals whose independent variable is subject to normalization to an integral number. A more extensive discussion is given in I.
We recall the main result of that paper: A functional derivative is to be interpreted as the rate of change induced on the dependent variable through a change at a single point, 
3.1. Functional Derivatives of Density Functionals
Because of the fundamental importance of the density as the independent variable of density functional theory, we review some of the salient features of derivatives with respect to that quantity.
In analogy with derivatives of functions, conventional functional differentiation measures the rate of change in the functional with respect to the change in the independent variable [3] , where the difference is defined over all space (the domain of the independent variable). Consider, for example, the simple (linear) functional,

where 


where 

Comparing the last two integrals over the arbitrary function, 

Were the density function an ordinary function of coordinates, the last derivation of the functional derivative would be rigorous. In that case, 


The density must be non-negative, and must be normalized to an integer,









This also shows that conventional functional differentiation of the energy functional, 

The considerations above can be viewed as a proof by construction of the following theorem (see also discussion in I):
Theorem on functional derivatives in DFT: No conventional functional derivatives can be defined over the domain of densities with integral normalization.
As shown in I, conventional functional differentiation can also be interpreted as (indeed, be replaced by) the rate of change of the functional (dependent variable) with respect to change in the independent variably (say, the density) at a given coordinate point,

When this procedure is applied to the functional, 

3.2. Extensions to Ensembles and Non-Integral Normalization
Conventionally, attempts to bypass the difficulties associated with integral normalization in the performance of derivatives with respect to the density have been based on the concept of analytic continuation of the Hohenberg and Kohn functional or the constrained search functional to ensembles [28] [29] . An ensemble (mixed state) describes the statistics of measurement outcomes encoded in a density matrix,

If the 




Of interest to the present discussion is the case in which the individual states in the ensemble may correspond to systems with different numbers of particles.
Now, with

is no longer necessarily normalized to an integer. In this case, the constrained search functional takes the form [4] [7] ,

Note the appearance of an infimum rather than a minimum designating the lack of a rigorous procedure that allows a search over all possible density matrices leading to a given ensemble density (see also below).
3.3. Variational Treatment of Fractional Charges
The variational treatment of density functional theory rests on consideration of the expression,

where the Lagrange multiplier, 



with 
Under this assumption, functional derivatives are conventionally defined through the expression,

describing the change in the energy of the ensemble when the number of particles changes by
In the case of fractional charges, the energy functional is taken to have the form,

where the functional, 

where the minimum is defined with respect to a search over density matrices,


where

is normalized to a non-integral number.
The form of the integral in (0.27) is now consistent with the definition of conventional functional diffe- rentiation, evidently alleviating the drawbacks of integral normalization. This analysis has been used to study, for example, the properties of open systems [30] that, because of the possibility of exchanging particles with the environment are usually characterized by a fractionally normalized particle density.
Unfortunately, however, this formulation is fundamentally flawed.
First, the construction of the infimum in (0.24) requires a search over all possible superpositions over all possible densities with integral normalization that lead to a given ensemble density. Yet, it can readily be de- monstrated that even the construction of all possible densities with a given integral normalization is not possible (see Appendix). (Contrast this with the determination of all possible antisymmetric wave functions leading to a given density with integral normalization, as described by Cioslowski [10] - [12] ). Second, the formalism rests on the assumption that the constrained search functional is a functional of form that can be analytically continued to densities with fractional normalization. As shown above, however, this assumption is false. The constrained search functional is defined strictly with respect to quantum states with unit normalization leading to a density with integral normalization.
Finally, we recall the classical nature of a mixed state as representing the statistics of measurement outcomes.
The expression, 
of two densities. However, because of the classical character of an ensemble, the conventional functional derivative of the ensemble is by definition the ensemble of conventional functional derivatives, each of which, as already shown, fails to exist.
On the other hand, when the derivative of the functional in (0.31) with respect to the density is replaced with the derivative with respect to the occupation number, 

The change in the energy of the ensemble under a change, 

The last expression negates the notion of a chemical potential that is a continuous function of particle number. It also demonstrates that the derivative of the energy functional, 
3.4. Derivative Discontinuity
The analytic continuation of the constrained search functional (or the Hohenberg and Kohn functional) to fractionally normalized densities gives rise to the concept of a single function of the density representing the exchange and correlation functional associated with a mixed state. It seems to be one of the enduring fallacies in DFT that the exchange and correlation functional (and consequently
It is to be emphasized that 
3.5. Parametric Differentiation
As shown in I, conventional functional differentiation of density functionals is not possible. It is not the case that the minimum of the energy functions, 
tive, 
Direct evaluation of the functional at various densities will exhibit a minimum at the density of the ground state of the system of N-interacting particles under the potential,
in a continuous procedure through the vanishing of the conventional functional derivative,
At the same time, the rate of change of a functional obtained through parametric differentiation does vanish at extremal points, such as maxima, minima or inflection points. In this case, the rate of change of
constituent parts, namely,
The implications of this development are far reaching: Because parametric derivatives (and rates of change) are local depending only on the particular dependent and independent variables of a single ordered pair, de- rivatives with respect to the density are well defined with respect to any wave functions leading to a density, not only those that are functionals of the density. It follows that any expectation value of any operator with respect to any wave function leading to a given density can be differentiated with respect to the density to yield the corresponding rate of change with respect to that density. Because the set of all expectation values with respect to wave functions leading to a given density includes as a subset the expectation values that may be functionals of the density, such expectation values can also be differentiated uniquely with respect to the density (again yielding their corresponding rates of change).
It follows that all attributes of conventional functional derivatives carry over intact to the process of dif- ferentiation based on the Dirac delta function [31] through (0.21). In other words, as demonstrated in I, pa- rametric differentiation is identified with conventional functional differentiation in all cases, including those for which conventional differentiation procedures are blocked. Indeed, parametric differentiation is the procedure employed routinely for determining functional derivatives in all cases, especially in density functionally theory.
Using (0.21), the functional derivative of the functional, 

or

a result that agrees with (0.20). We conclude that for functionals of form subject to conventional functional differentiation, but also for those for which such procedures are blocked, the change described in terms of the Dirac delta function produces the rate of change (parametric derivative) with respect to the density known only at the density at which the derivative is performed.
3.6. Parametric Differentiation of Ensembles
The derivative of the energy, 
(0.21) to each element of the ensemble in (0.31). Parametric differentiation yields the expected result,

so that the parametric derivative (functional derivative) of the ensemble energy at its minimum vanishes modulo a constant (as is the case for pure states).
4. The Self-Interaction Error and Its Treatment
The self-interaction error (defined below) has been a veritable thorn on the side of DFT calculations essentially from the start. Indeed, its presence was spotted at the very inception of quantum mechanics as pointed by Fock [32] , when even Fermi suggested a correction [33] - [35] . Although easily realized that in applications of the Kohn-Sham formalism the self-interaction error can be rigorously removed through the explicit use of the ex- change term, such use is hampered by the inability to differentiate this term with respect to the density in order to determine the effective potential in the Kohn-Sham formalism. The difficulty is clear: The Kohn-Sham functionals are not written explicitly in terms of the density, and hence the concept of parametric differentiation finds no immediate application.
In the Kohn-Sham formulation of DFT, the Coulomb energy takes the form,

where 


real, and suppressing the spin variable), with 


They also define the two-particle density in the form,

where the exchange term is given by the expression,

With this definition, the Coulomb energy can be written as the sum of a so-called Hartree term and an exchange term,

In most (if indeed not all) conventional calculations based on the LDA [2] - [4] , the exchange term is subsumed into the so-called exchange and correlation functional, where it is treated approximately within some scheme, e.g., [36] . This procedure, however, reduces the description of the Coulomb energy to that of the Hartree term (first term on the right of the equals sign in the last expression). Given the form of the density in (0.39), this allows the interaction between two different electrons both in the same orbital, in violation of the Pauli ex- clusion principle and introducing the unphysical effect known as the self-interaction error.
The greatest defect in the treatment of the Coulomb energy, however, is at the fundamental level. There is no mathematical justification for splitting a single expectation value, (0.38), into two terms that are accorded disparate treatments. The classical expression for the interaction of a charge density with itself does not contain the quantum SI error (no violation of the exclusion principle), thus it is unjustified to consider the Hartree term in quantum mechanics as classical and relegate quantum effects to the exchange and correlation functional, the usual practice. Alternatively, there is as much quantum character in the Hartree terms as in the exchange terms; that’s why self-interaction cancels out exactly when the two are combined into the expression in (0.38). That all methodology so far developed provides an incorrect treatment of the Coulomb interaction now is clear.
We turn to a review of three formal methods suggested for the elimination of the SI effect.
4.1. The Self-Interaction Correction Method
Of the attempts used to attack the self-interaction problem, three can be singled out for special mention; the self-interaction correction (SIC) [37] method, the optimized effective potential (OEP) [24] [38] - [40] method, and the recently introduced self-interaction free (SIF) [25] method.
In the SIC method, a correction to the self-interaction error is attempted through a process of orbital pealing. Although this does reduce the error, it cannot be shown to do so rigorously. Equally troubling is the violation of the second theorem; applied to atomic systems [37] , for example, the method gives ground state energies that lie below experiment, the difference with experiment increasing with increasing atomic number.
From a formal standpoint, however, the most damaging aspect of the SIC method is its lack of analytic standing: The peeled expressions do not correspond to expectation values of operators. The method treats the first term on the right of the equals sign in (0.42), leaving the second, a large negative term that carries the full burden of self-interaction, being assigned to the exchange and correlation functional, undisturbed. Consequently, there can be no demonstration that the potential obtained through orbital pealing is identical to that given when the derivative of the exchange energy with respect to the density is added to the derivative of the Hartree term. The method proceeds along the widely held perception (underlying a number of concepts discussed here) that the functional expressions in DFT can be manipulated on the basis of classical expressions (specific forms presumed to describe expectation values). In retrospect, the violation of the bound demanded by the second theorem may not be all that surprising.
4.2. The Optimized Effective Potential (OEP) Method
The optimized effective potential method [24] [38] - [40] is explicitly concerned with the derivative of the Coulomb energy, in particular the contribution of the exchange term to the derivative with respect to the density. Denoting the exchange contribution to the Coulomb energy with

and the exchange contribution to the Coulomb potential,

It is clear that the derivative, 

In examining the merits of the OEP method, we focus on the approach taken in evaluating this derivative. We note that there is no explicit appearance of the density in the orbital, and hence parametric differentiation is not possible at this stage.
In the OEP method, one attempts to take advantage of the fact that the Kohn-Sham orbitals are the solutions of a single-particle Schrödinger equation characterized by the Kohn-Sham potential, and uses the chain rule of functional derivatives to arrive at the expression,

introducing derivatives of orbitals with respect to the potential, and that of the potential with respect to the density.
4.2.1. Derivatives with Respect to Potential
Although the orbitals do not exhibit explicitly the potential, they can be parametrically expressed in terms of the
potential (see also I). Because they satisfy the Schrödinger equation for a potential, say
obtained as the solutions of the Lippmann-Schwinger equation (LSE), the integral representation of the Schrödinger equation, at energy, 

where 




The functional derivative of the orbital with respect to the potential can now be obtained in parametric mode by elementary means,

In the coordinate representation, and in the limit, 

where the single-particle Green function of a system under an external potential, 


defined as a summation over all states of a single particle in 

The expression in (0.49) is definitive, providing a rigorous expression for the derivative,
an inherent property of the potential and the orbital, expressed strictly in terms of these quantities. Finally, assuming that the single-particle levels are not degenerate, the static density linear response function (static sus- ceptibility) of the Kohn-Sham system can be written in the form,

along with its inverse, 

This is a convenient point to compare with the results of the OEP method.
In the OEP method, the functional derivative, 
leading to the expression,

where the so-called Kohn-Sham Green function is defined by the expression,

Clearly, the Kohn-Sham Green function is mathematically a different quantity than its exact counterpart and, in fact, the absence of a pole disqualifies it as a Green function. Although numerically the exact expression in (0.49) and the approximate one in (0.53) may give similar results (and calculations often indicate this to be the case), formally the latter expression is invalid.
This is but the beginning of the difficulties underlying the OEP methodology. (For a rigorous analysis of perturbation theory used to evaluate functional derivatives, see Appendix)
4.2.2. Further Difficulties of the OEP Method
In spite of the absence of a pole in

that is calculated through the Green functions in (0.51) and (0.52), but see [41] , leading to the expressions,

corresponding to (0.49), and to

in the case of (0.53), where 
Taking advantage of the fact that 



This procedure is characterized by a number of formal difficulties:
1) Recall that every orbital has a derivative (rate of change) with respect to the density that depends only on the orbital and the density. Hence, the rate of change of every expectation value of any wave function that leads to any density can be uniquely obtained with respect to the density. Thus, it would be applicable to all ex- pectation values, regardless of their standing as a functional of the density or not. In particular, it would allow differentiation of the kinetic energy functional, or the expectation value of the kinetic energy operator with respect to any Slater determinant with respect to the density obtained from the determinant. Contrary to this rigorous analysis, the OEP method provides an expression for a derivative only if the orbital is v-representable, if the expectation value is a functional of the density and if the expectation value is associated with the minimum of a functional.
2) A functional that is known to exhibit a minimum has values above the minimum value and a method that claims to determine the minimum must be able to detect these values through the non-vanishing of the derivative. The OEP method is inapplicable to arbitrary points in a functional, however.
3) Most importantly, the OEP is inapplicable to an arbitrary expectation value of an operator with respect to a wave function leading to the density, if that expectation value and wave function are not functionals of the density.
Consider, for example, a density of the form,

where the 


Clearly, the density is that of an excited state of the non-interacting N-particle system under
Now, multiply the last equation from the left by (the complex conjugate of)

This expression cannot be differentiated with respect to the density within the formalism of the OEP method. There is no prescription for differentiating the kinetic energy, and 

4) The derivatives of wave functions (or individual orbitals) must be obtained strictly in the space of a given density. By searching over potentials, the OEP method violates that requirement and can no longer be shown formally to lead to the correct derivative of the exchange energy with respect to the density.
5) The OEP was developed in an attempt to treat what is referred to as orbital dependent functionals. Basing the formalism on the orbitals, or the wave function, is contrary to the premise of DFT in which the independent variable is the density. Contrary to the claims in the literature [24] (and as already pointed out above), the orbitals of OEP are not functionals of the density; the orbitals shift as the search is carried out for the optimized potential.
6) By expanding the search for a minimum to more than one density (and corresponding potentials) the OEP can be expected to lead to energies that are no higher than those obtained through a search pinned to a given density (as found by direct calculation [25] ).
7) The susceptibility-like function (density linear-response function) (0.51), represents the response of the density, 


These properties contrast with the general perception of the OEP method in which it is considered that the perturbation theory treatment is exact [24] . It can be said that the OEP method is of limited applicability, and even in the case of 
4.3. Potential Functional Theory
Potential functional theory [42] is an attempt to provide formal foundation for the procedure of OEP method. It is based on functionals of the potential and is proposed to be the dual space of that of DFT. However, dual spaces contain the same number of elements whereas the space of densities contains all N-representable den- sities not all of which are v-representable.
Furthermore, potential functional theory falls far short of the power of density functional theory, namely the determination of quantum states from the sole knowledge of physical observables.
4.4. Other Methods
Attempts to correct for self-interaction have also been introduced by Gidopoulos et al. [43] (and references therein). Unexceptionally, these methods fail to recognize the essential element causing the self-interaction error: The quantum nature of the Coulomb energy. This quantity is given through an expectation value of the Coulomb potential with respect to the determinantal state of the Kohn-Sham method, and must be treated as such. Its separation into a Hartree and exchange terms and the subsequent disparate treatment of the two terms is un- supported by analysis. Alternatively, the self-interaction error is eliminated exactly when the Coulomb energy is expressed in terms of the pair density obtained from the Kohn-Sham determinant and correctly differentiated with respect to the density.
None of the difficulties mentioned with respect to previous methods arise with respect to the formalism described in the following section.
5. The Self-Interaction Free (SIF) method
The self-interaction free (SIF) [25] method provides for the rigorous treatment of the Coulomb energy as a single expectation value and its functional derivative with respect to the density.
It is useful to keep in mind the constrained search formulation and Cioslowski’s procedure for generating all wave functions that lead to a density, and the demonstration [10] - [12] that every wave function has a derivative with respect to the density obtained within the space defined by the density.
Cioslowski’s procedure, however, is computationally exceedingly difficult if not altogether out of reach. In- stead, the derivative can be calculated through a general property of Hilbert spaces, the expansion of an element of the space in an orthonormal and complete basis that is written explicitly in terms of the density. Such an expansion is confined to the Hilbert space of a single density and is an identity that can be freely interchanged with the wave function (e.g., an orbital). In the present case, the explicit appearance of the density allows immediate implementation of parametric differentiation. The details of the method can be found in [24] .
Consistency
The SIF methodology provides a consistent treatment of the kinetic energy and the Coulomb interaction energy, both being determined as expectation values of operators with respect to the same Slater determinant. With the exception of the OEP method, all other computational schemes introduced for the implementation of the Kohn-Sham formalism fail to satisfy this consistency condition. And, as discussed above, the OEP method is mathematically flawed, failing to determine the functional derivative of the exchange term with respect to the density.
Lack of consistency and/or mathematical rigor can be blamed for the lack of uniqueness in treating the Coulomb interaction and the variety of results obtained in the many forms of implementation of the KS for- malism.
6. Numerical Comparison
figure 1, part of which is quoted in [25] , shows the exchange potential for atomic Argon determined by four different methods, two implementations of the OEP method [24] -[44] , SIF and a method based on classical electrostatics introduced by Harbola and Sahni [45] that is applicable to spherical charges. The differences between the two OEP methodologies can be found in the original papers and is analyzed in [44] .
Note that the two OEP methods, (that in the case of an exact theory should give identical results), deviate from one another and neither reproduces the exact results obtained by electrostatics that is, within numerical accuracy, indistinguishable from that of the SIF method.
These features can be understood based on the formal analysis of I and this paper. The OEP method gives results obtained to first order in perturbation theory that are by construction different (see Appendix) from the rate of change of the exchange potential with respect to the density. Note that the electrostatics result, like SIF, makes no reference to densities other than the one entering the construction of the exchange term, properly obtaining the inherent property of rate of change that depends strictly on a density and its dependent variable (here the exchange term).
The difference from the exact rate of change manifests itself in different ways in the two methods. In the conventional implementation of the OEP method [45] , it leads to oscillations in the potential that, in the OEP literature, are referred to inter-shell structure. Here, they are revealed to be spurious effects caused by the lack of formal validity of the OEP methodology. Harbola and Sahni correctly point out [44] that a negative slope in the exchange potential corresponds to the unphysical effect of a positive hole repelling a negative electron.
No inter-shell structure appears in the alternate scheme of Heaton-Burgess, et al., but unphysical effects per- sist. A spherical charge exerts no force at its center so that the exchange potential should approach the origin with zero slope. This condition is seemingly violated by the results of Heaton-Burgess [44] .
In contrast to the OEP results, the exact results obtained within classical electrostatics and SIF are free of unphysical behavior.
7. Correlation Energy
As follows form the discussion in the paper, the concept of exchange and correlation functional is both unnece- ssary as well as an impediment to formal developments. The correlation functional, on the other hand, is of fundamental importance to the theory.
With definitions given in the text, the correlation functional at given density has the form,

Figure 1. Comparison between the exchange potential of the Argon atom derived by the methods used in this paper (SIF, red, solid), the approach of Harbola and Sahni [45] (dashed, blue), and the results obtained by two different implementations of the OEP method: OEP designates the results obtained within first order perturbation theory (dashed, green), and Heaton-Burgess et al. [44] (dashed, orange).
To be acceptable as an approximation to the exact functional, 

guaranteeing the the minimum of the energy functional, 

The last inequality would be satisfied in the presence of approximate wave functions, 


where

The approximate wave functions are to be obtained in an implementation of the constrained search over a set of wave functions that lead to the density and chosen such that 


The use of the constrained search envisioned here is clearly a tedious task, and the use of the approximate wave functions should be based on verification of the inequalities in (0.63) on a case-by-case basis.
At the same time, in the limit 
8. The Fallacy of Universality and of Orbital-Free Density Functional Theory
To the date of this writing, it is generally held that the Hohenberg and Kohn functional exists as a universal (potential independent) functional of the density, but its exact form as a function of the density is unknown.
The inherent belief in the existence of such a form is realized by considering the more than two hundred forms [36] , including fits to experimental data, proposed during the last nearly fifty years in an attempt to fill it. It is also evidenced by attempts to derive, for example, an orbital-free (read wave-function free) form of density functional theory [47] - [52] . Yet, were such a functional available, it would represent a stunning negation of the very property, see 1) above, that makes DFT the remarkable formal scheme that it is claimed to be determining the wave function from the density.
Because the wave function is a solution of a many-particle Schrödinger equation, the search for an orbital-free DFT amounts to a search of a wave-function-free solution of the Schrödinger equation. Given the interpretation of the density (an observable) determining quantum states, it would also negate the use of quantum mechanics in the study of interacting systems since it would allow analysis of classical reality (experiment) in terms of experimental results (represented by expectation values) without the explicit need of determining wave functions (quantum states).
No confusion should arise from the existence of functionals of the density that may be expressed as functions of the density in special cases, such as, for example, the von Weizsäcker expression [3] for the kinetic energy of a single particle (or two particles of opposite spins on a single orbital), and the expressions for the kinetic energy and exchange energy (Dirac’s formula) [3] for the case of plane wave states that fill all space (jellium). Also, the
ground state of a single-particle system with density

exceptions that prove the rule: The expectation values of operators are to be evaluated with respect to wave functions describing N-particle systems on a case by case basis, and generally defy representation in terms of classical expressions, as mere functions of the density.
8.1. Hohenberg and Kohn Functional as Function of the Density
Equation (0.60) in I displays a form for the transformation defining the elements of a basis used to construct the N-particle, antisymmetric wave functions leading to a given density, 

It is also clear that all of the wave functions leading to a different density, 
This mitigates against the possibility of a Hohenberg and Kohn functional that is a mere function of the density. The same holds true for other functionals defined through the properties (minimization) of expectation values of operators.
More directly, in the preceding paper, a constructive argument was developed against the existence of a universal functional of the density. It was demonstrated that any wave function leading to a density, including those obtained through the constrained search, can be written exactly in the form of expansions in terms of the equidensity basis (see I). If the functional (i.e., the expectation value of operators with respect to such a wave function) were universal, requiring only a change in the density to proceed from one density to the next, then the coefficients of each such expansion in a functional of the density would be constant! A simple direct calculation easily demonstrates that this is not the case (see, for example [25] ).
8.2. The Fallacy of an Exchange and Correlation Functional
A previous paper [25] provides a derivation of the Kohn-Sham equations displaying a fundamental feature of the theory: The rigorous expression for the Kohn-Sham functional contains no exchange and correlation functional, but only a correlation energy functional (see [25] ). The conventional exchange and correlation functional [3] [4] is obtained when the exchange term from the Coulomb energy functional is lumped together with the correlation functional.
This conventional development is then coupled with the notion that the functionals of DFT are mere functions of the density giving rise to the large number of various forms produced for the description of exchange and correlation. It should be kept firmly in mind that elements of the Hilbert space, e.g., wave functions determining an expectation value, cannot be replaced with ordinary functions of an observable (the density) without raising the implication that quantum mechanics itself is unnecessary (see previous subsection). It follows that general expectation values cannot in principle be expressed in terms of mere functions of observables, e.g., the density. The effects of wave functions in determining expectation values of operators cannot be second-guessed from the classical side, invalidating (with minor exceptions, see previous section) the various expressions for the ex- change and correlation functional introduced in implementations of the Kohn-Sham formalism thus far.
Furthermore, given that the Hohenberg and Kohn functional is defined strictly in terms a pure state describing an integral number of particles, the notion that an exchange and correlation functional spans different particle numbers and that it displays a discontinuity at integral values of particle number is mathematically insensible.
9. Strongly Correlated Systems: Beyond Density Functional Theory?
It is customary to categorize systems in which the Coulomb energy exceeds (often by far) the kinetic energy

as being strongly correlated. It is also customary to view such systems as lying beyond the reach of density functional theory and to seek formal treatments that exceed the power of DFT, e.g., [53] (and references therein).
First, note that the determination of a system as strongly correlated cannot take place, at least at the formal level, until one has in hand an acceptable wave function that can only arise through a solution of the Schrödinger equation (through some means, such as DFT). This solution must be carried out in unbiased fashion―i.e., with no preconceptions as to the strength of correlation―or one runs the danger of tilting the solution towards the answer one has pre-determined would be appropriate for the problem. Biased results are generally not useful to analysis or to the understanding of nature through the methods of mathematical physics.
Second, given the mistreatment of the Coulomb interaction in all implementations (other than in the SIF me- thod) of the Kohn-Sham formalism to date, it is premature to discount DFT and call for more general metho- dology. It is indeed possible that the methodology is limited, ultimately requiring the development of more powerful methods for the treatment of interacting many-particle systems. Such methods, however, should be developed for application to all systems, regardless of how strongly or weakly correlated they may be judged to be. And before attempts in such a direction are initiated, the Kohn-Sham formalism should be implemented with an exact treatment of the exchange energy.
10. Discussion
The concept of functional plays a crucial role in the development of density functional theory. Therefore, it may come as somewhat of a surprise that the related concept, that of (conventional) functional derivative, it terms of an arbitrary test function, has no place in the theory. This is a consequence of the general result that every functional has a rate of change with respect to the independent variable, but not every functional has a conventional functional derivative. Indeed, functional derivatives with respect to the density have nothing in common with ordinary derivatives other than the interpretation, common to both, as rates of change (of the dependent variable with respect to the independent variable).
As shown in I, functional differentiation interpreted as a rate of change can proceed rigorously through the use of the Dirac delta function in place of the arbitrary test function. This leads to the determination of rates of change of expectation values (functionals of the density or not) confined strictly in the space of a given density. With reference to expansions in the equidensity basis, discussed above and in [25] , it is seen that the rates of change are evaluated at a given density with no reference made to the equidensity basis for another density. Rates of change are obtained by inducing the change, 
It bears emphasis that the study of the states of interacting many-particle systems is by nature quantum and it must be carried out in a well-defined Hilbert space. It is an unfortunate feature of computational developments in the realm of density functional theory that this requirement tends to be overlooked. Here, the tendency has been to introduce approximations for the various functionals representing expectation values of operators with respect to wave functions, in particular the Coulomb energy and the so-called exchange correlation functional based on arguments arrived at within the classical realm. An acceptable approximation to an expectation value can only be obtained through the replacement of the exact wave function by an approximate one. Forms re- presenting functionals in DFT that do not demonstrably correspond to expectation values of operators with res- pect to wave functions fail this fundamental requirement.
The formalism for treating the Coulomb energy in the SIF method is consistent with this requirement. It also provides a unique determination of the form of the Coulomb energy (in terms of the pair density of the Kohn- Sham determinant) and specifies its rigorous treatment. As discussed above, this is a consequence of the for- malism for determining the wave functions leading to a density and of differentiating these wave functions with respect to the density.
Bypassing the required connection to a wave function can lead to a number of formal developments that lack fundamental meaning, such as orbital-free density functional theory, the much sought derivative discontinuity of the exchange and correlation functional, and the treatment of ensembles.
Cioslowski’s procedure [10] - [12] provides a formal determination of the set 








The discussion in the paper also exposed a number of flaws with the OEP method. It demonstrated that the methodology is at best a numerical approximation to the rate of change (of a dependent variable with respect to a corresponding density), but is formally invalid as the functional derivative. On the other hand, the metho- dology developed in [25] is free of formal difficulties, providing a rigorous treatment of the Coulomb energy within KS-DFT.
Acknowledgements
Work supported by the US DOE under Contract DE-AC52-07NA27344 with LLNS, LLC.
Cite this paper
A.Gonis, (2014) The Pursuit of Fallacy in Density Functional Theory: The Quest for Exchange and Correlation, the Rigorous Treatment of Exchange in the Kohn-Sham Formalism and the Continuing Search for Correlation. World Journal of Condensed Matter Physics,04,200-225. doi: 10.4236/wjcmp.2014.43023
References
- 1. Hohenberg, P. and Kohn, W. (1964) Inhomogeneous Electron Gas. Physical Review, 136, B864-B871.
http://dx.doi.org/10.1103/PhysRev.136.B864 - 2. Kohn, W. and Sham, L.J. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review, 140, A1133-A1138.
http://dx.doi.org/10.1103/PhysRev.140.A1133 - 3. Parr, R.G. and Yang, C.Y. (1989) Density Functional Theory of Atoms and Molecules. Oxford University Press, Oxford.
- 4. Dreitzler, R.M. and Gross, E.K.U. (1990) Density Functional Theory. Springer Verlag, Berlin, New York.
- 5. Zumbach, G. and Maschke, K. (1983) New Approach to the Calculation of Density Functionals. Physical Review A, 28, 544-554.
http://dx.doi.org/10.1103/PhysRevA.28.544 - 6. The strict mathematical definition of a functional is that of a function of coordinates mapped onto a number, usually in terms of an integral. The definition used here includes the mapping of a function onto a function, or a set of functions.
- 7. Lieb, E.H. (1982) Density Functionals for Coulomb Systems. In: Shimony, A. and Feshbach, H., Eds., Physics as Natural Philosophy, Essays in Honor of Laszlo Tisza, MIT Press Cambridge, Massachusetts, 111-149.
See also, Lieb, E.H. (1985) Density Functional Methods in Physics. In: Dreizler, R.M., Ed., NATO ASI Series B 123, Plenum, New York, 31, and Lieb, E.H. (1983) in Int. J. Quantum Chem. 24, 243. - 8. Levy, M. (1979) Universal Variational Functionals of Electron Densities, First-Order Density Matrices, and Natural Spin-Orbitals and Solution of the v-Representability Problem. Proceedings of the National Academy of Sciences of the United States of America, 76, 6062-6065.
http://dx.doi.org/10.1073/pnas.76.12.6062 - 9. It is occasionally argued that the variational principle can be expressed in terms of the variational procedure, allowing, in principle, a fractionally normalized charge density. Here, the quantity, , is a Lagrange multiplier that guarantees the presence of a given normalization associated with wave functions not normalized to unity in terms of which the variational theorem takes the form. These considerations are both unnecessary as well as frought with formal danger. First, the wave functions considered with respect of the variational theorem can always be normalized to unity through division by the square root of its squared modulus. Second, a variational procedure based on a fractionally normalized density can easily misdirect developments along the treatment of ensembles of open systems in terms of formalism appropriate exclusively for pure states, as is discussed explicitly in the body of the paper. As a quick reminder, the wave functions used in the variational theorem must be of the form emerging as solutions to the Schr¨odinger equation, and those are normalized to unity.
- 10. Cioslowski, J. (1988) Density Functionals for the Energy of Electronic Systems: Explicit Variational Construction. Physical Review Letters, 60, 2141-2143.
http://dx.doi.org/10.1103/PhysRevLett.60.2141 - 11. Cioslowski, J. (1988) Density Driven Self-Consistent Field Method. I. Derivation and Basic Properties. The Journal of Chemical Physics, 89, 4871-4874.
http://dx.doi.org/10.1063/1.455655 - 12. Cioslowski, J. (1989) Density Driven Self-Consistent Field Method. II. Construction of All One-Particle Wave Functions that Are Orthonormal and Sum up to a Given Density. Quantum Chemistry Symposium. International Journal of Quantum Chemistry, 36, 255-262.
- 13. It is useful to use a function defined through a process to demonstrate the difficulties that can arise with respect to functionals defined by means of a procedure, rather than as functions of the independent variable. Consider the function, where is a real number, and is determined through the process of flipping a coin for any given, setting if the coin comes up heads, and if it comes up tales. Unlike a functional, however, this function of process has no parametric derivative (thus no derivative).
- 14. Some exceptions are known. The ground-state wave function of a single particle system is given in terms of the density, and the corresponding kinetic energy functional takes the von Weizsacker form. Also the kinetic energy and exchange energy of an infinite number of plane waves forming a density are given explicitly by means of the expression. These cases are the exceptions that prove the rule that functionals of the density defy representation as explicit functions of the density.
- 15. Becke, A.D. (1993) A New Mixing of Hartree-Fock and Local Density-Functional Theories. The Journal of Chemical Physics, 98, 1372.
http://dx.doi.org/10.1063/1.464304 - 16. Perdew, J.P., Ernzerhof, M. and Burke, K. (1996) Rationale for Mixing Exact Exchange with Density Functional Approximations. The Journal of Chemical Physics, 105, 9982.
http://dx.doi.org/10.1063/1.472933 - 17. Kim, K. and Jordan, K.D. (1994) Comparison of Density Functional and MP2 Calculations on the Water Monomer and dimer. The Journal of Physical Chemistry, 98, 10089-10094.
http://dx.doi.org/10.1021/j100091a024 - 18. Becke, A.D. (1988) Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Physical Review A, 38, 3098-3100.
http://dx.doi.org/10.1103/PhysRevA.38.3098 - 19. Lee, C., Yang, W.T. and Parr, R.G. (1988) Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Physical Review B, 37, 785-789.
http://dx.doi.org/10.1103/PhysRevB.37.785 - 20. Becke, A.D. (1993) Density-Functional Thermochemistry. III. The Role of Exact Exchange. The Journal of Chemical Physics, 98, 5648.
http://dx.doi.org/10.1063/1.464913 - 21. Heyd, J., Scuseria, G.E. and Ernzerhof, M. (2003) Hybrid Functionals Based on a Screened Coulomb Potential. The Journal of Chemical Physics, 118, 8207.
http://dx.doi.org/10.1063/1.1564060 - 22. Zhao, Y. and Truhlar, D.G. (2008) The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theoretical Chemistry Accounts, 120, 215241.
http://dx.doi.org/10.1007/s00214-007-0310-x - 23. Zhao, Y. and Truhlar, D.G. (2006) Density Functional for Spectroscopy: No Long-Range Self-Interaction Error, Good Performance for Rydberg and Chargetransfer States, and Better Performance on Average than B3LYP for Ground States. The Journal of Physical Chemistry A, 110, 13126-13130.
http://dx.doi.org/10.1021/jp066479k - 24. Kümmel, S. and Kronik, L. (2008) Orbital-Dependent Density Functionals: Theory and Applications. Reviews of Modern Physics, 80, 3-60.
http://dx.doi.org/10.1103/RevModPhys.80.3 - 25. Dane, M., Gonis, A., Nicholson, D.M. and Stocks, G.M. (2013) On the Solution of the Self-Interaction Problem in Kohn-Sham Density Functional Theory. Journal of Physics and Chemistry of Solids (Online Version), 75, 1160-1178.
- 26. This situation is not unlike that of the function defined over the set of natural numbers that exhibits a minimum but no derivative at the point of the minimum, e.g., defined over the integers and zero, has a minimum at 0, but no derivative there.
- 27. Trott, M. Functional Derivative. From MathWorld-A Wolfram Web Resource, Created by Eric W. Weisstein.
http://mathworld.wolfram.com/FunctionalDerivative.html - 28. English, H. and English, R. (1984) Exact Density Functional for Ground-State Energies I. General Results. Physica Status Solidi (b), 123, 373.
- 29. English, H. and English, R. (1984) Exact Density Functional for Ground-State Energies II. Details and Remarks. Physica Status Solidi (b), 124, 711.
- 30. Perdew, J.P., Parr, R.G., Levy, M. and Balduz, J.L. (1982) Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy. Physical Review Letters, 49, 1691-1694.
http://dx.doi.org/10.1103/PhysRevLett.49.1691 - 31. Indeed, one is hard put to find a case in quantum chemistry or condensed matter physics where functional differentiation is carried out in terms other that based on the Dirac delta function used as the arbitrary test function.
- 32. Fock, V. (1930) Naherungsmethode zur Losung des quantenmechanischen Mehrkorperproblems. Zeitschrift für Physik, 61, 126-148.
http://dx.doi.org/10.1007/BF01340294 - 33. Fermi, E. and Amaldi, E. (1934) Le orbite 8s degli elementi. Mem. Accad. d’Italia, 6, 119-149, number 82 in Refs. , .
- 34. Fermi, E. and Segre, E. (2011) Collected Papers, Note E Memorie, of Enrico Fermi V1: Italy, 1921-1938. Literary Licensing, LLC, Whitefish, MT.
- 35. Fermi, E. (1962) Enrico Fermi-Collected Papers (Note E Memorie), 1921-1938, Volume 1. The University of Chicago Press, Chicago and London; Accademia Nationale dei Lincei, Rome.
- 36. LibXC. www.tddft.org/programs/octopus/wiki/index.php/Libxc:manual
- 37. Perdew, J.P. and Zunger, A. (1981) Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Physical Review B, 23, 5048-5079.
http://dx.doi.org/10.1103/PhysRevB.23.5048 - 38. Kümmel, S. and Perdew, J.P. (2003) Simple Iterative Construction of the Optimized Effective Potential for Orbital Functionals, Including Exact Exchange. Physical Review Letters, 90, Article ID: 043004.
http://dx.doi.org/10.1103/PhysRevLett.90.043004 - 39. Grabo, T., Kreibich, T., Kurth, S. and Gross, E. (2000) Strong Coulomb Correlations in Electronic Structure Calculations: Beyond the Local Density Approximation. Gordon and Breach Science Publishers, Amsterdam, 203-311.
- 40. Yang, W.T. and Wu, Q. (2002) Direct Method for Optimized Effective Potentials in Density-Functional Theory. Physical Review Letters, 89, Article ID: 143002.
http://dx.doi.org/10.1103/PhysRevLett.89.143002 - 41. The reader unfamiliar with the mathematics of the OEP method may benefit by reading standard treatises, e.g., .
- 42. Yang, W.T., Ayers, P.W. and Wu, Q. (2004) Potential Functionals: Dual to Density Functionals and Solution to the v-Representability Problem. Physical Review Letters, 92, 146404.
http://dx.doi.org/10.1103/PhysRevLett.92.146404 - 43. Gidopoulos, N.I. and Lathiotakis, N.N. (2012) Constraining Density Functional Approximations to Yield Self-Interaction Free Potentials. The Journal of Chemical Physics, 136, Article ID: 224109. http://dx.doi.org/10.1063/1.4728156
- 44. Heaton-Burgess, T., Bulat, F.A. and Yang, W.T. (2007) Optimized Effective Potentials in Finite Basis Sets. Physical Review Letters, 98, Article ID: 256401.
http://dx.doi.org/10.1103/PhysRevLett.98.256401 - 45. Harbola, M.K. and Sahni, V. (1989) Quantum-Mechanical Interpretation of the Exchange-Correlation Potential of Kohn-Sham Density Functional Theory. Physical Review Letters, 62, 489-492.
http://dx.doi.org/10.1103/PhysRevLett.62.489 - 46. Ceperley, D.M. and Alder, B.J. (1980) Ground State of the Electron Gas by a Stochastic Method. Physical Review Letters, 45, 566-569.
http://dx.doi.org/10.1103/PhysRevLett.45.566 - 47. Gal, T. and Nagy, A. (2000) A Method to Get an Analytical Expression for the Non-Interacting Kinetic Energy Density Functional. Journal of Molecular Structure, 501-502, 167-171.
- 48. Wang, Y. and Nagy, A. (1993) Construction of Exact Kohn-Sham Orbitals from a Given Electron Density. Physical Review A, 47, R1591-R1593.
- 49. Parr, R.G., Kugler, A.A. and Nagy, A. (1995) Some Identities in Density-Functional Theory. Physical Review A, 52, 969-976.
- 50. Levy, M., Perdew, J.P. and Sahni, V. (1984) Exact Differential Equation for the Density and Ionization Energy of a Many-Particle System. Physical Review A, 30, 2745-2748.
- 51. Wang, A. and Carter, E.A. (2000) Chapter 5 of “Theoretical Methods in Condensed Phase Chemistry”. In: Schwartz, S.D., Ed., A New Book Series of “Progress in Theoretical Chemistry and Physics”, Kluwer, Dordrecht, 117-184.
- 52. Garcia-Gonzales, P., Alvarellos, J.E. and Chacon, E. Kinetic-Energy Density Functional: Atoms and Shell Structure. Physical Review A, 54, 1897.
- 53. Mirtschink, A., Seidl, M. and Gori-Giorgi, P. (2013) Derivative Discontinuity in the Strong-Interaction Limit of Density-Functional Theory. Physical Review Letters, 111, Article ID: 126402.
http://dx.doi.org/10.1103/PhysRevLett.111.126402 - 54. Landau, L.D. and Lifschitz, E.M. (1977) Quantum Mechanics: Non-Relativistic Theory. 3rd Edition, Elsevier Butterworth-Heinemann Linacre House, Jordan Hill, Oxford, Burlington.
Appendix
12. Search Over Densities
The extension of the concept of the constrained search to ensembles requires a search over all possible su- perpositions of all possible densities with integral normalization that lead to a given possibly fractionally normalized ensemble density. It is straightforward to show, however, that the set of all densities with a given normalization cannot be constructed.
For simplicity, the demonstration is carried out in terms of one-dimensional densities,
Assume that a set is proposed to contain all possible densities with a given normalization.
Consider the graphical representation of the densities in the set, and note that the set does not cover two- dimensional space continuously. Choose any point in the plane that does not lie on a curve representing one of the densities of the set, and draw two lines onto the horizontal axis such that the area of resulting triangle equals a preset normalization.
There are, in fact, an infinite number of densities that are not included in any proposed set assumed to includes all densities of a given normalization thus precluding the extension of the constrained search over ensemble densities.
13. Functional Derivatives through Perturbation Theory
As shown in I, the functional derivative, 
tion. The same result can also be obtained through perturbation theory.
The change in a solution of the single-particle Schrödinger equation due to a small change in potential, 


where the dots signify the presence of terms of third or higher order.
Summation of the perturbation expansion to all orders yields the exact solution of the Schrödinger equation at the perturbed potential,

where 

functional differentiation in terms of
That derivative, being exact, takes the form, (see (0.49))

where 



To these exact considerations, we can compare the formalism of the OEP method.
In the OEP method, the perturbation series is interpreted in terms of a Taylor series expansion of an orbital in terms of a perturbation, 

Now, if perturbation theory yields the functional Taylor series expansion, than the first-order term in the perturbation expansion of the first-order derivative, 


that clearly do not reproduce the terms in the curly brackets in (0.66).



