World Journal of Condensed Matter Physics
Vol.2 No.4(2012), Article ID:25010,4 pages DOI:10.4236/wjcmp.2012.24037
Two Dimensional Heisenberg Exchange Interaction in the Magnetization Studies of Multiferroic
![]()
Department of Physics, Addis Ababa University, Addis Ababa, Ethiopia.
Email: shegphd@gmail.com, psinghgbpup@yahoo.com
Received August 9th, 2012; revised September 10th, 2012; accepted September 18th, 2012
Keywords: Multiferroic; Multiple Ferroic Orders
ABSTRACT
Multiferroics are novel classes of materials that exhibit cross-coupling of mutually excluding phenomena, i.e. magnetism and ferroelectricity. In recent years, the coexistence of ferroelectricity and magnetic orderings has become a hot issue and drawn considerable attentions due to the promising applications to these days technology and the fundamental science involved in these classes of materials. The microscopic origins of magnetism and ferroelectricity differ fundamentally, while the real mechanism of ferroelectricity is still under debate. In the present work, we have started from a simple method Heisengerg hamiltonian and an interaction term resulting from electric field coupling with the magnetic spins with anisotropic limit, demonstrated that magnetization can be manipulated by electric field and anisotropic field in agreement with results experimentally observed. In the multiferroic thin film system the magnetic field tends to play a role in stabilizing the spins in preferred orientations and induces a coupling of magnetism and ferroelectricity that opens a route to switch magnetization with electric polarazation and vice-versa.
1. Introduction
Multiferroics are unique classes of materials whose fundamental state is both magnetic and ferroelectric [1]. In these materials magnetism and ferroelectric ordering coexist no matter how their course of existence varies [2]. The microscopic description of magnetism is based on the localized magnetic moments, mostly due to the partially filled d or f shell transition-metal or rare-earth elements electrons in which the exchange interactions between these localized moments exhibit magnetic orderings. Whereas the origin of ferroelectrics is wide range (can be due to: Charge ordering, lone pairs, etc.) and forbids the d shell electrons in contrast to magnetism [3,4]. Thus, multiferroics couples the two insurmountable phenomena. They remarkably show strong coupling between charges, spins, lattice and orbital degrees of freedom and the interplay between various competing orders gives rise to interesting features and varieties to these classes of materials. The overlap of strongly correlated magnetic and ferroelectric orders enables the spinnability of one domain over the other [5-7]. For instance, in ferromagnetic materials the magnetization M is easily switchable parameter on an application of external stimulating magnetic field, H and in ferroelectrics the polarization P is also a controllable parameter by an external electric field, E. However, on the other hand, in multiferroics these switchable order parameters, P and M are cross-linked, i.e. magnetization can be switched by external electric field and polarization can also be tunned by an applied magnetic field. The magnetoelectric spectra in GaFeO3 is found to be proportional to the photon energy which depends on the direction of magnetization [8-10].
2. Theoretical Model
We consider the spin Hamiltonian of the multiferroic thin film system that exhibits frustrated spin interactions [11,12]. The Hamiltonian of this anisotropic many body interaction system on the influence of external fields can be expressed by [13-15],
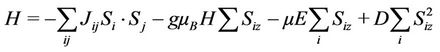 (1)
(1)
where Si(Sj) is spin operator at sites i(j). Jij is the exchange coupling that depends on the relative positions of neigbhoring spins and is defined by Jij = J(Ri − Rj). The constant g is the gyromagnetic ratio, and the second term of Equation (1) is the effective Zeeman field with an external deriving field while in this model chosen to be parallel to the +z axis to line up all the spins in the same direction. Whereas, the third term includes an electric field E that interacts with the spins in the system. The constant μ describes the coupling strength between the spins and the radiation field that is either intrinsic or extrinsic [16,17]. The terms μB and D are the Bohr magneton and magnetic anisotropic (or spin wave stiffness) constants, respectively [17,18]. The total spin operators in the Hamiltonian are:
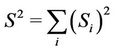

The ground state of N identical atoms of spin S is defined as


The total spin operator at any site i has components Siz, Six and Siz that should be treated independently with an identity Si. Si = S(S + 1). Transferring the spin operator problems into many body interaction systems upon replacing with bosonic creation and annihilation operators expressed as
 (2)
(2)
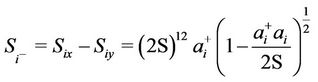 (3)
(3)
where ai† and ai are the creation and annihilation operators satisfying the commutation relation [ai, ai†] = δil It is also possible to transform this bosonic operators to magnon variable operators bk and bk† so that these operators can be related to the bosonic operators [19,20]

and
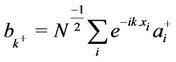
where the inverse transformation is

and
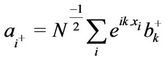
At low excitation i.e. where the interaction is predominated by bilinear spin variables, neglecting the interaction corresponding to higher order terms, the reduced Hamiltonian is of the form
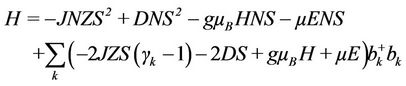 . (4)
. (4)
Here, z is defined to be the number of nearest neighbor spins. In this Hamiltonian we consider only the term bilinear to the magnon variables
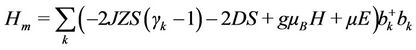 (5)
(5)
where, .
.
This simplified interaction term is equivalently expressed as , if we write
, if we write
 (6)
(6)
The dispersion equation on the approximation that 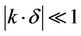 can be reduced to
can be reduced to
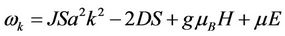 , (7)
, (7)
so that
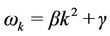 (8)
(8)
The above expression is a dispersion relation with some additional term 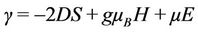 that tends to show how the dispersion term depends on the field components. Moreover, the constant
that tends to show how the dispersion term depends on the field components. Moreover, the constant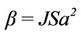 .
.
3. Results and Discussion
The spin-wave dispersion function of the multiferroic thin film system is obtained as a function of the wave vector and the field components.
A significant change in the dispersion relation is observed as depicted by Figure 1 above at different γ values [21]. This can be used to modify the behavior of the multiferroics up on appropriate selection of the magnetic

Figure 1. (color online) The figure indicated shows the variation of dispersion function for different gamma values.
and electric field values in some orientations. The inter-dependence of the magnetic and electric fields (their couplings) in multiferroic materials is also analyzed based on the spin-wave occupation number, .
.
The change in magnetization is obtained to be
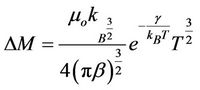
where  and
and 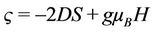 and the change in magnetization versus temperature at some specific γ is shown in Figure 2 below for low temperature limits.
and the change in magnetization versus temperature at some specific γ is shown in Figure 2 below for low temperature limits.
Consequently, the magnetization is a function of the γ values at low temperature as indicated by Figure 3 shown below [22,23]. Thus, the electric field dependence of
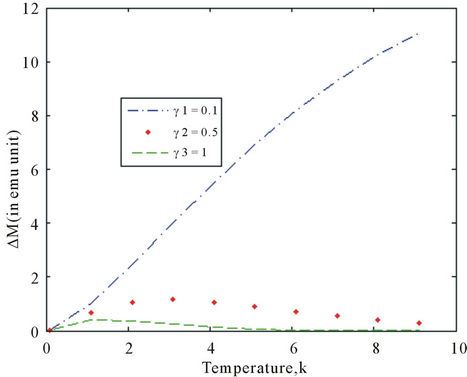
Figure 2. Change of magnetization versus temperature at different gamma values.
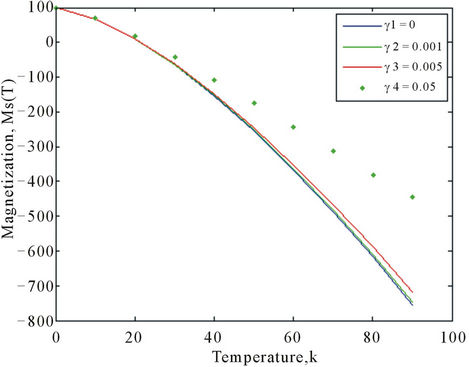
Figure 3. Dependence of magnetization on the parameter γ, which can be tuned by explicitly on the applied fields and the nature of magnetic anisotropy.
magnetization can be easily deduced from the expression γ = ζ + μE where ζ = −2DS + gμB H for some specific values of the parameters, D, S, and H at a particular temperature.
4. Acknowledgements
This work was supported by the research programm of Aaddis Ababa University, Ethiopia and Mizan-Tepi University, Ethiopia.
REFERENCES
- W. Kleemann, P. Borisov, S. Bedanta and V. V. Shvartsman, “Multiferroic and Magnetoelectric Materialsߞnovel Developments and Perspectives,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 57, No. 10, 2010, pp. 2228-2232. doi:10.1109/TUFFC.2010.1682
- G. A. Smolenskii and V. A. Bokov, “Coexistence of Magnetic and Electric Ordering in Crystals,” Journal of Applied Physics, Vol. 35, No. 3, 1964, pp. 915-918. doi:10.1063/1.1713535
- C. N. R. Rao and C. R. Serrao, Journal of Materials Chemistry, Vol. 17, 2007.
- D. Khomskii, “Trend: Classifying Multiferroics: Mechanisms and Effects,” Physics, Vol. 2, No. 20, 2009. doi:10.1103/Physics.2.20
- H. Schmid, “Some Symmetry Aspects of Ferroics and Single Phase Multiferroics,” Journal of Physics: Condensed Matter, Vol. 20, No. 43, 2008, Article ID: 434201. doi:10.1088/0953-8984/20/43/434201
- A. K. Singh, D. Jain, V. Ganesa, A. K. Nigam and S. Patnaik, “Field-Dependent Competing Magnetic Ordering in Multiferroic Ni3V2O8,” EPL, Vol. 86, No. 5, 2009, Article ID: 57001. doi:10.1209/0295-5075/86/57001
- N. Sharma, B. J. Kennedy, M. M. Elcombe, Y. Liu and C. D. Ling, “Coexistence of Ferroelectricity and Magnetism in Transition-Metal-Doped n = 3 Aurivillius Phases,” Journal of Physics: Condensed Matter, Vol. 20, No. 2, 2008, Article ID: 025215. doi:10.1088/0953-8984/20/02/025215
- J.-I. Igarashi and T. Nagao, “Analysis of Optical Magnetoelectric Effect in GaFeO3,” Physical Review B, Vol. 80, No. 5, 2009, Article ID: 054418. doi:10.1103/PhysRevB.80.054418
- J. H. Lee, et al., “A Strong Ferroelectric Ferromagnet Created by Means of Spin-Lattice Coupling,” Nature, Vol. 466, 2010, Article ID: 09331. doi:10.1038/nature09331
- A. Pimenov, A. M. Shuvaev, A. A. Mukhin and A. loidl, “Electromagnons in Multiferroic Manganites,” Journal of Physics: Condensed Matter, Vol. 20, No. 43, 2008, Article ID: 434209. doi:10.1088/0953-8984/20/43/434209
- A. B. Sushkov, M. Mostovoy, R. Valdes Aguilar, S.-W. Cheong and H. D. Drew, “Electromagnons in Multiferroic RMn2O5 Compounds and Their Microscopic Origin,” Journal of Physics: Condensed Matter, Vol. 20, No. 43, 2008, Article ID: 434210. doi:10.1088/0953-8984/20/43/434210
- D. Senff, N. Aliouane, D. N. Argyriou, A. Hiess, L. P. Regnault, P. Link, K. Hradil, Y. Sidis and M. Braden, “Magnetic Excitations in a Cycloidal Magnet: The Magnon Spectrum of Multiferroic TbMnO3,” Journal of Physics: Condensed Matter, Vol. 20, No. 43, 2008, Article ID: 434212. doi:10.1088/0953-8984/20/43/434212
- C. L. Jia and J. Berakdar, Physica Status Solidi B, Vol. 247, No. 3, 2010.
- H.-B. Chen, Y. Zhou and Y.-Q. Li, Journal of Physics: Condensed Matter, Vol. 23, 2011, Article ID: 066002.
- R. Valdes Aguilar, M. Mostovoy, A. B. Sushkov, C. L. Zhang, Y. J. Choi, S.-W. Cheong and H. D. Drew, Physical Review Letters, Vol. 102, 2009, Article ID: 047203.
- M. Mochizuki and N. Nagaosa, arxivi:1102.3762V1, 2011.
- J. C. Tung and G. Y. Guo, arxivi:1102.3737V1, 2011.
- L. You, C.-L. Lu, P. Yang, G. C. Han, T. Wu, U. Luders, W. Pnellier, K. Yao, L. Chen and J. L. Wang, Advanced Materials, Vol. 22, 2010.
- C. Kittel, “Quantum Theory of Solids,” 2nd Edition, Wiley, New York, 1987.
- P. L. Taylor and O. Heinonen, “A Quantum Approach to Condensed Matter Physics,” Cambridge University Press, Cambridge, 2002.
- I. Ortenburger and M. Sparks, Physical Review, Vol. 133, No. 3, 1964.
- C. Triguero, M. Porta and A. Planes, “Coupling between Lattice Vibrations and Magnetism in Ising-Like Systems,” Physical Review B, Vol. 73, No. 5, 2006, Article ID: 054401. doi:10.1103/PhysRevB.73.054401
- T. Kimura, S. Kawamoto, I. Yamada, M. Azuma, M. Takano and Y. Tokura, “Magnetocapacitance Effect in Multiferroic BiMnO3,” Physical Review B, Vol. 67, No. 18, 2003, Article ID: 180401. doi:10.1103/PhysRevB.67.180401

