Received 12 March 2016; accepted 15 April 2016; published 18 April 2016

ABSTRACT

The Ramsey rule is regarded as a convenient vehicle for estimating the social discount rate in general. Carbon pricing is treated as another theory of environmental economics. This study clarifies the theoretical relationship between the Ramsey rule and optimal carbon price, which has been overlooked in the existing research. It succeeds in deriving the optimal carbon price from the modified Ramsey rule in stationary state. Since the Ramsey rule decides the dynamics of an economy and a stationary state is its destination, by using the optimization condition of individual who are assumed to live infinitesimally short life, we can solve the optimal carbon price at stationary state.

Keywords:

Modified Ramsey Rule, Optimal Carbon Price, Social Discount Rate, Carbon Cycle

1. Introduction

Many studies utilize the Ramsey rule for estimating appropriate social discount rate (e.g., Cline [1] ; Stern [2] ; Nordhaus [3] ). However, as Kuninori and Otaki [4] point out, the causality presumed in existing studies is incorrect. A natural interpretation of optimal growth theory leads us to the following proper causality of the Ramsey rule. That is, consumption gradually increases when the rate of interest exceeds the rate of time preference because an individual is rewarded by higher utility from postponing consumption.

Since the Ramsey rule shows optimal consumption and/or investment path, if an original model is devised to include a negative intertemporal externality, it is evident that optimal carbon price can be calculated based on this formula. This study analyzes the relationship between the Ramsey rule and optimal carbon price and calculates such a price in reality.

It should be noted that the Ramsey rule evaluated in stationary state implies the tangency condition of optimality, that is, equalization of the marginal rate of substitution in consumption or production with the relative price of carbon. Unless such a condition is upheld in the long run, there is a room for improving utility. Accordingly, as far as the stationary state is optimal, the foregoing tangency condition can be induced from the Ramsey rule; thus, an integrated view is obtained on how the traditional estimation of the social discount rate based on the Ramsey rule is related to the optimal carbon pricing.

The rest of this paper is organized as follows. Section 2 reveals the relationship between the modified Ramsey rule and the optimal carbon price using Kuninori and Otaki [4] and Otaki [5] . One will find that the characteristic of the carbon cycle equation plays a crucial role in determining the carbon price. Section 3 provides brief concluding remarks.

2. Modified Ramsey Rule and Carbon Price

Based on Kuninori and Otaki [4] and Otaki [5] , this section derives the optimal carbon price from the modified Ramsey rule.

2.1. Intertemporal Negative Externality in Utility Function

Throughout this study, it is assumed that there is a negative intertemporal externality in the world economy originating from excess emissions of carbon dioxide (CO₂). In this subsection let us consider the case in which such a negative externality directly affects people’s utility. The concave instantaneous utility function, u, is assumed to be

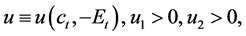(1)

c_t and E_t denote consumption and accumulated emissions (measured by CO₂ tonnage), respectively. u_i is the i-th partial derivative of the utility function.

The dynamics of the carbon cycle are assumed to be

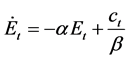, (2)

where denotes the absorption ratio of CO₂ by the Earth. denotes the efficiency of production measured by the amount of production (consumption) that can be produced by unit emissions¹.

The optimization problem is represented as follows:

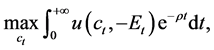subject to (2). (3)

The corresponding Hamiltonian, 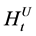, is

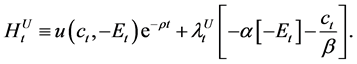(4)

The necessary and sufficient conditions for the maximization are Equation (2) and

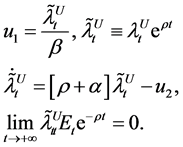(5)

Differentiating the top equation in (5) logarithmically, yields

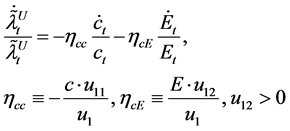(6)

Substituting Equation (6) into the middle equation in (5), it can be ascertained that the following relation holds:

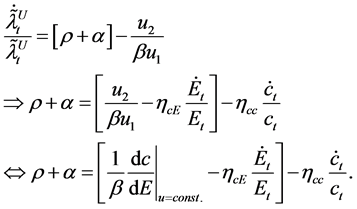(7)

The bottom equation in (7) is the modified Ramsey rule when a negative externality exists in the utility function. The economic implication is as follows: the left-hand side of the equation represents the effective social discount rate. The effectiveness implies that the absorption ratio, 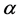, is added to the discount rate. This is because emitted CO₂ becomes harmless with the ratio, , at every moment and a social planner can be permitted to discount future damages originating from global warming at a higher rate than the rate of time preference, ρ.

The first bracket of the right-hand side of the modified Ramsey rule (the bottom equation in (7)) corresponds

to the net marginal benefit in terms of utility. 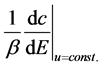denotes the marginal substitution rate of consump-

tion to emissions, which represents the utility obtained from unit emissions. When β is large, people can enjoy high consumption with less emissions. Accordingly, ceteris paribus, the obtained marginal utility decreases due

to the saturation of consumption. 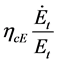is the marginal disutility from emissions; summing them, the net mar-

ginal utility originating from emissions is obtained.

The second term of the right-hand side of the modified Ramsey rule (the bottom equation in (7)) indicates the optimal path of consumption. The optimal consumption decreases proportionately to the difference between the effective social discount rate and the net marginal utility obtained by emissions. In other words, as people become more impatient or marginal utility from emissions more attractive, the optimal consumption stream is concentrated in the near future; and thus, decreases as time goes by. The dynamics of the economy are fully described by the differential Equations (2) and (7).

Thus, we have established the modified Ramsey rule wherein a negative intertemporal externality originating from CO₂ emissions directly affects people’s utility function. Using Equation (7), let the optimal carbon price be calculated in the stationary state as follows:

By the definition of stationary state, 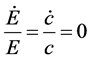holds, which yields

. (8)

Because the left-hand side of Equation (8) is the marginal substitution rate of consumption to emissions reduction (i.e., the tangency of an indifference curve in the plane), the right-hand side of Equation (8) in-

dicates the inverse of the optimal carbon price in terms of unit emissions. That is, people should pay

times of money for consumption in exchange for the social cost incurred by unit emissions. This result coincides with that of Otaki [5] .

2.2. Intertemporal Negative Externality in Production Function

In this subsection, we derive the modified Ramsey rule wherein a negative intertemporal externality affects the production function. Let the strictly concave production function, F, be denoted as

, (9)

where y_t is total output of goods, and k_t denotes input of goods for production. It is assumed that anthropogenic combustion of fossil fuels concentrates CO₂ emissions and lowers productivity. Accordingly, the partial derivative of the production function is positive. In such a case, the differential equation that describes the carbon cycle becomes

. (10)

The optimization problem to be solved is

, subject to Equations (8) and (9), (11)

where v is a strictly concave instantaneous utility function. The corresponding Hamiltonian, , is

. (12)

The necessary-sufficient conditions are Equation (10) and

(13)

Combining the middle equation in (13) with the top equation, yields

(14)

Combining the two equations in (14), we obtain

(15)

where is defined as

. (16)

Equation (15) corresponds to the modified Ramsey rule. The left-hand side of this equation represents the effective social discount rate as in Equation (8). The first term on the right-hand side of Equation (15) is the marginal substitution rate of emissions to intermediate goods, which means the marginal benefit of emissions in conjunction with economizing intermediate goods. The second term on the right-hand side of Equation (15) denotes the increase rate of marginal propensity to consume. If this rate is heightened, this saves more artificial production resources; and thereby improves the efficiency of production. The third term on the right-hand side of Equation (14) implies the decrease in marginal utility in proportion to the increase rate of consumption. Future consump-

tion increases monotonously if the marginal benefit of emissions, , exceeds the rate of tolerance

to current consumption,. Hence, it can be ascertained that Equation (15) is the modified Ramsey rule wherein an intertemporal negative externality exists within the production process.

The carbon price relative to the unit emission reducing cost at the stationary state can be solved by letting

. This yields

. (17)

The profit-maximization condition implies

, (18)

where p is the carbon price (i.e. goods price) in terms of unit emissions reducing cost. Accordingly, by combining Equations (17) and (18), the optimal carbon price, p, is solved as

. (19)

It is evident from the discussion in Subsection 2.1, that the optimal carbon price is invariant with where the negative externality exists.

2.3. Kuninori-Otaki’s [4] Case

Kuninori and Otaki [4] is the first study that finds some modification is necessary for the Ramsey rule to be tenable for analyzing the global warming problem. Their model differs from the foregoing two models in this paper on the point that it includes a capital accumulation process and that a negative externality emerges from capital accumulation. This is because the authors assume that the overall production capacity is determined by capital stock and excess emissions stem from the production process. Although the model is transformed in order to include capital accumulation, one can ascertain the similar formula concerning the optimal carbon price derived as follows.

Kuninori and Otaki [4] assume the following negative externality in the concave production function:

(20)

The maximization problem is

, subject to. (21)

The corresponding Hamiltonian H^K is defined as

. (22)

The necessary-sufficient conditions for optimality are

(23)

Combining the top and middle equations in (23), the following modified Ramsey rule is obtained. That is,

(24)

where Ψ^* is the optimal carbon tax rate, and π denotes the average productivity of capital. This corresponds to the modified Ramsey rule in Kuninori and Otaki [4] .

From the static profit maximization condition, as far as one wishes to achieve the first-best allocation by a market economy,

(25)

holds. The optimal carbon price of a consumption goods measured by unit social emissions cost incurred by capital accumulation in the stationary state satisfies

, (26)

where p^* is the optimal relative carbon price (or goods price). Comparing Equation (26) with Equation (19), it is found that Kuninori and Otaki [4] correspond to the case in which,. This is evident from the structure of the model that Kuninori and Otaki [4] regards the absorption rate by the earth, , as zero and set the parameter of the carbon efficiency, β, to unity. Accordingly, Equation (26) is a special case of Equation (19); thus, in this case too, we succeed in driving the optimal carbon price from the corresponding modified Ramsey rule.

To summarize our assertion, since each modified Ramsey rule represents the optimal consumption/emissions path, it is clear that it is possible to calculate the optimal carbon price in the stationary state which is the destination of the optimal path.

3. Concluding Remarks

This study analyzed the relationship between the modified Ramsey rule and the optimal carbon price levied on consumption goods. Regardless of the origin of an intertemporal negative externality, the modified Ramsey rule solves the optimal carbon price in the stationary state, p, as

. (27)

When the rate of time preference, ρ, is high and people are impatient, the carbon price becomes lower because such an economy deeply discounts future damages. If the earth’s absorption capacity of emission is higher and takes a larger value, the carbon price is lowered. This is because emitted CO₂ does not stay within the atmosphere for a long time and is less harmful. Finally, the larger emissions efficiency, which corresponds to a high value of β, the less emissions are necessary for producing goods. Accordingly, it is acceptable to reduce the carbon price in such a case.

Acknowledgements

This paper owes much to the discussions with Professor Morio Kuninori. I am thankful for the warm-heartedness of him and staffs of DBJ Research Center on Global Warming. In addition, the research is funded by MEXT/ JSPS KAKENHI Grant Number 60183761.

Cite this paper

Masayuki Otaki, (2016) Modified Ramsey Rule and Optimal Carbon Tax. Atmospheric and Climate Sciences,06,267-272. doi: 10.4236/acs.2016.62022

References

NOTES

¹Another type of equation of the carbon cycle is examined in Subsection 2.3.