International Journal of Astronomy and Astrophysics
Vol.05 No.03(2015), Article ID:60070,19 pages
10.4236/ijaa.2015.53026
Mass Transfer in Binary Stellar Evolution and Its Stability
Seblu Humne Negu, Solomon Belay Tessema
Astronomy and Astrophysics Research Division, Entoto Observatory and Research Center (EORC), Addis Ababa, Ethiopia
Email: seblu1557@gmail.com, tessemabelay@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 May 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
The evolution of a binary star system by various analytical and numerical approximations of mass transfer rate normalized to the equilibrium rate and its stability conditions are investigated. We present results from investigations of mass transfer and stability in close binary star systems using the different orbital parameters. The stability and instability of mass transfer in binary star evolution depends on the exchange of material which the response of the binary to the initial Roche lobe overflow causes the donor to loose even more material. Our work is mainly focused on basic mathematical derivations, analytical and numerical solutions in order to explain the mass transfer system in different orbital parameters as well as the results are compared with previous studies in both cases. Mass transfer is usually stable, as long as the winds specific angular momentum does not exceed the angular momentum per reduced mass of the system. This holds for both dynamical and thermal time scales. Those systems which are not stable will usually transfer mass on the thermal time scale. The variation of Roche lobe radius with mass ratio in the binary, for various orbital parameters in the conservative and non-conservative mass transfer, as well as the evolution equations, orbital angular momentum of the binary system and the corresponding analytical and numerical solutions for different cases, under certain restrictive approximations is derived, simulated and discussed.
Keywords:
Mass Transfer, Binary Star, Stellar Evolution, Stability, Instability

1. Introduction
The dominant feature in the evolution of stars is in closed binaries, and the one which distinguishes it from the evolution of single stars is the presence of various forms of mass transfer between the two stars. Mass transfer occurs in many different types of systems, to widely varying effects [1] . Contamination of the envelope of a less evolved star with chemically processed elements, as in Barium stars [2] , and catastrophic mass transfer, by common envelope phase, as in W UMa systems; or a slow, steady mass transfer by Roche lobe overflow [2] .
Close binary stars consisting of two compact stellar remnants (white dwarfs (WDs), neutron stars (NSs), or black holes (BHs)) are considered as primary targets of the forthcoming field of gravitational wave (GW) astronomy [3] since their orbital evolution has entirely controlled by the emission of gravitational waves and leads to ultimate coalescence (merger) of the components. GW emission is the sole factor responsible for the change of orbital parameters of a pair of compact (degenerate) stars. However, at the early stages of binary evolution, it is the mass transfer between the components and the loss of matter and its orbital angular momentum that play a dominant dynamical role.
Mass transfer is particularly interesting if one considers the evolution of a system with at least one degenerate star. In these cases, mass transfer produces spectacular effects, resulting in part from the intense magnetic and gravitational fields of the compact objects, pulsed X-ray emission, nuclear burning, novae outbursts, and so on. Also, since the mass transfer rates can be high and orbital period measurements accurate, one may see the dynamical effects of mass transfer on the binary orbit, as in Cygnus X-3 [4] .
In the case of cataclysmic variables (CVs) and low mass X-ray binary system (LMXBs), one has a highly evolved, compact star (CVs and LMXBs contain white dwarfs and neutron stars, respectively) and a less evolved main sequence or red giant star. Mass transfer usually proceeds by accretion onto the compact object, and is secularly stable. Most of these objects involve one component filling its Roche lobe (the donor or secondary), trans- ferring mass to a compact star (the accretor or primary) and the mass leaking out of the inner Lagrangian point forms an accretion disk around the accretor. A binary system starts out as detached [4] [5] , with both stars in hydrostatic equilibrium and filling an equipotential surface inside their Roche lobes. In a binary, both stars (e1 and e2 can fill their Roche lobes at subsequent evolutionary stages). We use the convention which e1 denotes the primary star, and e2 denotes the secondary star of the binary. In this convention, the mass ratio is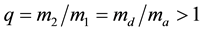 . During phases of mass transfer, we denote the mass-losing star, the “donor”, with subscript “d” and the companion star, the “accretor”, with subscript “a”. The transfer will be accompanied by a stellar wind from the mass-losing star, or ejection of matter from the accretor, as in novae and galactic jet sources.
. During phases of mass transfer, we denote the mass-losing star, the “donor”, with subscript “d” and the companion star, the “accretor”, with subscript “a”. The transfer will be accompanied by a stellar wind from the mass-losing star, or ejection of matter from the accretor, as in novae and galactic jet sources.
There are various unanswered questions in the evolution of LMXBs into low mass binary pulsars (LMBPs, in which a millisecond radio pulsar is in a binary with a low mass white dwarf companion) and of CVs. Among these are the problem of the disparate birthrates of the LMXBs and the LMBPs (Kulkarni and Narayan1988), estimation of the strength of X-ray heating induced winds from the donor star.
Now, if a star is a member of a binary star system, then it is possible that as the components evolving, one of them (or both) can fill up its Roche lobe. Thomas (1977) classified mass transferring binaries on the basis of what state of evolution the donor is in as follows:
Case A: If the orbital separation is small enough (usually a few days), the star can fill its Roche lobe during its slow expansion through the main-sequence phase while still burning hydrogen in its core.
Case B: If the orbital period is less than about 100 days, but longer than a few days, the star will fill its Roche lobe during the rapid expansion to a red giant with a helium core. If the helium core ignites during this phase and the transfer is interrupted, the mass transfer is Case B.
Case C: If the orbital period is above 100 days, the star can evolve to the red supergiant phase before it fills its Roche lobe. In this case, the star may have a CO or ONe core.
Case A mass transfer occurs during the slow growth, Case B during the first rapid expansion, and Case C du- ring the final expansion phase. The nature of the remnant depends upon the state of the primary during the onset of RLOF and the orbital properties of the resultant binary depend upon the details of the mass transfer.
The problem of mass transfer in binaries by Roche lobe overflow has received a good deal of attention in the literature over the past few decades, typically in investigations of one aspect or another of orbital evolution or stability. [6] examined mass transfer by isotropic winds and accretion, in investigating the evolution of short period binary X-ray sources with extreme mass ratios, and developed models with accretion and (typically) isotropic re-emission of transferred matter, in the context of the period gap in cataclysmic variables.
Stability has become an important in many area of astrophysical research. Many authors has been studied the stability in different models (for example, [7] [8] ). Both authers didn’t address stability and mass transfer in binary stellar evolution. [1] [2] [4] were tried to study stability criteria for mass transfer in binary stellar evolution using limits of pure models of mass transfer and extreme mass ratio. The present study will address the mass transfer in binary stellar evolution using analytical and numerical methods which will give brief relations about stability and mass transfer.
The aim of this paper is to study mass transfer in binary stellar evolution behavior using mass transfer and different orbital parameters. This will be used to study stability properties of binary stars using analytical and numerical solutions. We calculate the rate of change of orbital angular momentum, orbital periods, angular speed and stability analysis of mass transfer rates, with relevant evolution in general form.
The paper is organized as follows:
In Section (2), we derive basic equations of mass transfer, mass transfer and evolution of orbital parameters, conservative and non-conservative mass transfer and evolution equations; in Section (3), stability analysis of mass transfer and its rate will be determined; in Section (4), analytical and numerical solutions will be presented. Finally our main conclusions are summarized in Section (5).
2. Basic Equations of Mass Transfer
2.1. Mass Transfer and the Evolution of Orbital Parameters
In this section, expressions for the variation of orbital parameters with loss of mass from one of the stars are derived. In what follows, the two stars will be referred to as 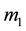 and
and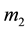 , with the latter the mass losing star.
, with the latter the mass losing star.
The angular momentum (AM) of binary component i in a circular orbit is expressed as:
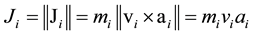 (1)
(1)
where 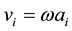 is the velocity of accretor and donor star; “i” stands for the accretor “a” and donor “d” stars respectively,
is the velocity of accretor and donor star; “i” stands for the accretor “a” and donor “d” stars respectively,  is the position of the accretor and donor star, and
is the position of the accretor and donor star, and  is the orbital angular spin frequency.
is the orbital angular spin frequency.
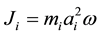
Roche geometry changes are governed by the total orbital angular momentum J of the system which is given by
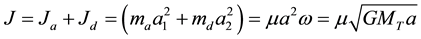 (2)
(2)
where 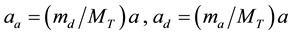 are the distance of the two stars from the center of mass (semi major-axis),
are the distance of the two stars from the center of mass (semi major-axis), 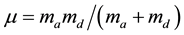 is the reduced mass,
is the reduced mass, 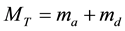 is the total mass, and the mass ratio is
is the total mass, and the mass ratio is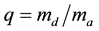 . Throughout this paper, we consider an eccentricity e will be zero.
. Throughout this paper, we consider an eccentricity e will be zero.
The period “P”, the semi major axis “a” and the total mass transfer related through Kepler’s law as:
 (3)
(3)
which implies that the orbital angular momentum J can be written as:
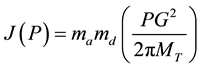 (4)
(4)
The angular momentum for binary component “i” is given by
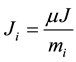 (5)
(5)
and the specific angular momentum for binary component “i” can be written as:

where 

From Kepler’s 

Hence from Equation (4) the orbital angular momentum J of a binary star is given by

In many cases the angular momentum stored in the rotation of the two stars is negligible compared to the orbital angular momentum, so that Equation (8) also represents the orbital angular momentum of the binary, to good approximation. By differentiating this expression we obtain a general equation for the evolution of orbital parameters:

and

In Equation (10), e is a parameter that determines the amount by which its orbit around another body deviates from a perfect circle. From Equation (7) and Equation (10) the rate of change of orbital period, semi major axis, and total mass transfer can be written as:
or

which depends on time “t”.
By integrating Equation (11) we obtain:

where 
In the case of Roche lobe overflow in an already circularized binary, the last term is zero. The 
2.2. Conservative Mass Transfer
When no ejected matter leaves a binary system, the mass transfer is said to be conservative. During conservative mass transfer, the orbital elements of the binary can change due to transfer of angular momentum from one star to the companion. Consider a system with a total mass

will also be conserved, where G, is universal gravitational constant.
We first consider conservative mass transfer, in which the total mass and orbital angular momentum of the binary are conserved. In that case we can set as:
In circular, 



where

Using the Kepler’s third law in Equation (15), the period variation with time 

and integrating Equation (16) which leads us

An explicit relation between the separation and the masses can be found by integrating Equation (15) with

Applying Kepler’s law we obtain similar relation between the rate of change of the orbital period 


The importance of Equation (15) and Equation (18) is that it allows to determine the mass transfer rate of observed semi-detached binaries, if the masses and the period derivative can be measured. This is complicated by the fact that many binaries show short-term period fluctuations, while for the long-term average of the period derivative, the trend has been determined with reasonable conditions as follows:
If

If

2.3. Non-Conservative Mass Transfer
In case of non-conservative mass transfer both mass and angular momentum can be removed from the system. Following [9] Orbital Angular Momentum (OAM) of a two body system is given by

where 

Assuming isotropic mass loss from the surface of the components, then, we have the rate of angular momentum:

Since the dynamics of a two body system obey Kepler’s third law therefore one expects transfer of mass would change the, a, P and M accordingly

Assume q as a constant, differentiating Equation (19) with respect to time gives:

Substituting Equation (21) into Equation (22) we get the following two equations:

and

Therefore, the two equations tell us how the loss of OAM and mass are caused the orbital period, P, and orbital radius, a, to change. The isotropic mass loss implies:

This equation implies that the only source of OAM loss is mass loss, which were assumed to be isotropic. Substituting 

In Equation (26), since the 

Now if we use the following equations taken from Stepien (1995) to calculate relative angular momentum lost from a system as:


and hence the relative OAM lost only by magnetized star wind:

where

This equation (Equation (30)) tells us the total rate of change of the orbital angular frequency of the binary related to the mass lost from the system.
2.4. Evolution Equations
Now we have to enumerate some of the physical mechanisms that can influence the evolution of a binary, we can proceed to derive mathematical expressions in order to quantify these effects. To reiterate, we work under the following assumptions:
i) Roche potential describes the gravitational field;
ii) Kepler’s laws are valid, and that the stars orbit around their common center of mass in circular orbits;
iii) the spin and orbit axes are all parallel to one another and;
iv) tidal effects are included even though we ignore the effects of the distortion of the stars, i.e. we assume spherically symmetric stars.
Now, the total angular momentum of the system is given by

where 



The rate of change of the spin momenta can be given as the sum of a consequential angular momentum term and a tidal term as:

where, 

The second term in the Equation (33) represents the tidal term, which is a function of the degree of 


Substituting Equation (33) and Equation (34) into Equation (31).

where

Accordingly, from Equation (35) the rate of change of the orbital separation is given by

which we re-write for the convenience as:


The sign of the terms on the right hand side of Equation (37) determines if the orbit is shrinking or expanding. 
If 

The tidal terms have a more complicated behavior because the sign of the tidal torque 

We now determine how the depth of contact evolves to complete the set of equations we need to specify the evolution of the binary system. We can write equation of the Roche lobe size as:

where





Symbolically, generalizing the meaning of the symbols introduced by [5]



where the symbol 



where 



where 





The secular evolution of the binary takes place on the mass transfer time scale

Thus,

Finally, setting 


This expression shows that if the evolution is much slower than the thermal relaxation (
3. Stability Analysis of Mass Transfer
Mass Transfer Rate
Mass transfer will proceed on a time-scale which depends critically on the changes in the radius of the donor star and that of its Roche lobe in response to the mass loss; if the star expands faster than its Roche lobe or shrinks less rapidly than its Roche lobe for a prolonged time, mass transfer will be unstable and the donor star may disintegrate. If the donor star expands less rapidly or shrinks faster than its Roche lobe, mass transfer will generally be stable and may continue for a long time.
We now introduce the concept of the equilibrium mass transfer rate, which is the mass transfer rate that a stable, semi-detached binary undergoes for a given rate of driving. The equilibrium mass transfer rate is a function of the driving rate, the consequential angular momentum loss mechanisms and the value of the mass ratio q. The mass transfer rate can be written generally as:

Under the assumption that 


For equilibrium mass transfer, we let

where,

is the critical mass ratio for stability of mass transfer. For example, for a polytropic donor with 



In general one can write from Equation (51).

when



One of the components of the binary gets into contact with its Roche lobe either due to the expansion of the star (the donor) and/or due to shrinking of the Roche lobe as a result of angular momentum loss by GWR. In order to determine exactly when a binary with given total mass and mass ratio q becomes semi-detached, one needs to specify the radii of the component stars and their corresponding Roche lobes. The condition for stability can be expressed as:

which simply states that the donors radius must shrink at least as fast as its Roche lobe or that the donor can expand no faster than its Roche lobe expands.
The first factor we will consider is the change in the orbital separation resulting from a mass transfer event. The orbital angular momentum, 

to eliminate the angular frequency from Equation (2) to obtain:

If we logarithmically differentiate Equation (57) with respect to time and from Equation (10) with

From Equation (15), Equation (58) becomes

We can then see that if the donor is the more massive star (q > 1), the orbital separation will shrink upon mass transfer. Conversely, if q < 1, a will increase.
From Roche lobe geometry and following [10] , the Roche lobe radius 

A more accurate approximation for the Roche lobe radius was determined by Eggleton (1983) and is given by

for 

Combining Equation (62) with Equation (58) we arrive at

which implies

For conservative mass transfer Equation (64) becomes

which parametrized as:

In the conservative case Equation (65) indicates that if 
upon mass loss as 
Finally, we consider the response of the donors radius to change in its mass. For stars like the sun it is well known that the mass and radius are approximately proportional to one another. Using the expression of (66), the mass radius relation for solar type stars implies

If we substitute Equation (65) and Equation (67) into Equation (55) we obtain a limiting stable mass ratio for the binary star.

If the mass ratio exceed this values the Roche lobe will be shrink faster than the star can contract and mass
transfer will proceed on a dynamical time scale. If 
rate detach from is Roche lobe. From Equation (64) any mechanism Schutz (1990) that removes orbital angular momentum from the binary will cause the Roche lobe of the donor to contract.
4. Analytical and Numerical Solutions
4.1. Analytical Solutions
Before we proceed upon studying the complete numerical solutions for the evolution of orbital parameters and the evolution equations we derived in Section (2) for different astrophysical scenarios, we obtain analytic solutions for the time evolution of the geometry of mass transfer rate. We can do this only on the assumption that most of the parameters characterizing the binary remain constant or evolve slowly as compared to the evolution of the mass transfer rate. [5] was among the first to attempt such analysis and following them, we generalize their results to an arbitrary polytropic index and to isothermal atmospheres. Analytic solutions are useful in providing physical insights into the expected behaviour of the binary system in the limit where the assumptions imposed to obtain the analytic solutions are valid approximately. To make Equations ((60), (61) and (68)), the two figures are plotted for different values of the mass ratio 
The simple form of Equation (60) is a reasonable approximation to the more accurate Eggleton [11] formula for mass ratios

Figure 1. Comparison of [10] (Eq. (60), blue curve) and [11] (Eq. (61)) formulae for the Roche radius, normalized to the binary separation vs. mass ratio
Figure 2. Change in the orbital angular momentum of the binary system with time.
Thus if 

orbit will be shirk. This means the radius of a Roche lobe filling star depends only on the binary separation and the mass ratio. The blue curve shows that the stable conservative mass transfer while the green one is the unstable mass transfer.
In Figure 2, we have plotted the equilibrium angular momentum values for a range of binary system with a time and for a mass ratio q = 1, taking the mass of the black hole


The change in mass for both the accretion and donor as well as the changing of the orbital angular frequency with time are derived in Equation (21) within the pre-assigned time scale of mass exchange as 
Considering an interacting double degenerate system with initial masses of donor and accretor 


From Equation (18), the change of orbital period is proportional to the change in
4.2. The Binary Parameters
It is worthwhile to describe the binary parameters used by [4] [5] in their pioneering analysis in some detail, since we are using it as a comparison to our numerical solutions in Section (4.4). We shall thus obtain analytic as well as numerical solutions for a general polytropic index n to compare our results with those obtained from a full numerical evolution. The mass transfer rate for a polytropic donor is given by Jedrzejec (1969) assuming laminar flow, quoted by Paczynski & Sienkiewicz (1972) and from Equations. ((51)-(54)) we obtain:

Figure 3. Orbital period (

Figure 4. The total rate of change of the orbital angular frequency of the binary (Eq. (30)) related to the mass lost from the system of two point masses which will coalesce due to gravitational wave emission in a time interval shorter than 1010 yr, as a function of the donor mass in solar unit





Raising both sides of the Equation (69) to the power 

where we have set the factor 

Defining a positive dimensionless mass transfer


The solution can be easily inverted to yield

where 
Returning now to Equation (70), with the same definitions as Equation (72) for X and τ, we obtain for the general case in which driving is present

where 




Considering Equation (70) again we define

The differential equation for the evolution of mass transfer now becomes

Thus, for the stable case (



Though it is not possible to invert this general solution to obtain the mass transfer rate X as a function of time, particular solutions for specific values of n can be inverted to obtain simple solutions. For example, n = 3/2 yields the [5] solution:

where, 

Likewise, n = 1/2 yields



4.3. Isothermal Atmospheres
In case of isothermal atmospheres, the mass transfer rate [13] [14] is given by

where, α is the scale height. This form of the mass transfer equation is much simpler to integrate than the one for the polytropes considered above. With the same approximations and notation as in the steps leading to Equation (73), and defining

This is easily integrable and invertible to get the following:

where 







The result is again simple and instructive.

In the stable case, for any initial mass transfer, the system will detach and mass transfer will tend to zero. In the unstable case, any non-zero initial mass transfer will grow and diverge in a finite time.
We specify the parameters of the binary at its initial state;




and 

dius of the star increases at a rate faster than the Roche lobe radius, and the resulting mass transfer is unstable.
The analytic solutions, both the stable and the unstable, are shown in Figure 5.
Note that initially, the stable and the unstable solutions in Figure 5 almost exactly overlap. This is true as long as the system is either detached or the depth of contact is relatively small. As soon as the binary evolves to deeper contact, the unstable solution diverges rapidly and blows up in a finite time. This outcome is predicted by the unstable analytic solution which has been obtained by assuming that the basic primary parameters: the mass ratio q, driving rate 
4.4. Numerical Solutions
In Section (4.2 and 4.3), we have derived the basic evolution equations; Equations ((72), (73), (75), and (76)) from Equations ((51)-(54)) in Section (3.1) that for the numerical results and the corresponding analytic solutions for different cases, under certain restrictive approximations. These analytic solutions are a useful reference to compare our numerical results to, since in the limit that the assumptions used to derive the analytic solution are met, the numerical solutions should approach the analytic ones. However, in general, the analytic solutions cannot explain the behavior of a given system accurately and especially when the system evolves rapidly, solving the evolution equations numerically leads to a different outcome than what one would expect analytically.
Limitations of the Analytic Solutions
The analytic solutions of equations in Section (4.2 and 4.3) from Section (2.4) and through Section (3.1) are obtained under the following assumptions:
1) The driving rate given by 
2) The separation “a” of the binary is effectively constant even though the mass transfer rate changes, which is not true for “a” “real system” (see Equation (36)).
Figure 5. The solutions for the stable (dotted line) and unstable cases.
3) The tidal effects are effectively ignored.
4) A system that is initially unstable (
In order to overcome some of these shortcomings one has to numerically integrate the evolution equations in a self consistent way. In particular, in what follows, we allow for the changes in the masses of the components assuming conservative mass transfer (and hence the mass ratio q), allow the binary separation to change as a result of any driving present, and compute the values of 



Figure 6. Numerical and Analytic Solutions for Polytropes. Comparison of numerical integrations with the analytic solution in Section (4.2). The mass transfer rate in solar mass normalized to the initial equilibrium rate as a function of time in units of the initial τ: analytic (red curve) and numerical- green (q = 0.985), blue (q = 0.875), magenta (q = 0.816), cyan (q = 0.656 same as [5] ), Darkred (q = 0.625) and orange (q = 0.416).
Figure 7. Comparison of numerical integrations with the analytic solutions for isothermal atmospheres. The natural logarithm of the mass transfer rate normalized to the initial equilibrium rate for the case with q = 0.663, is shown as a function of time in units of
Figure 8. Loss of orbital angular momentum and decrease in the mass of the secondary with time (in year).
We simulate exactly the same initial conditions as the ones assumed to derive the analytic solution, a constant driving rate and the same mass-radius relationship. We then relax the constraints and let the system evolve in a self-consistent manner for different values of the mass ratio q. We observe that initially all the curves overlap, but as the depth of contact increases, the mass transfer rate increases. As the system evolves, the orbital separation, which is decreasing initially, begins to increase as per Equation (36) which in turn decreases the driving rate. At some point during the evolution q becomes less than 

In Figure 7, we plot the analytic and numerical solutions for an isothermal donor for different values of the mass ratio. Unlike the polytropic donor case, which has a fixed reference point where the donor fills its Roche lobe (


Thus we here produce a numerical analysis for the rate of change of orbital angular momentum(green line), the rate of change of mass of the secondary star (blue line), and Increase in the mass of the primary with time (in year) in a close binary system taking the initial masses of the primary as 





5. Conclusions
We have presented a simple, analytical and numerical approach to describe the mass transfer in the evolution of binary star systems in which we track the mass of each component, the total mass of the system, the orbital angular momentum and the spin angular momenta of each component. We have included the effects of mass and angular momentum loss from the system and also the exchange of mass and angular momentum between the components of the binary.
The main reason why many binary systems transfer matter at some stage of their evolutionary lifetimes is during the system evolution. One of the stars in a binary system may increase in radius filling its Roche lobe, or the binary separation may shrink because orbital angular momentum is being lost from the system as a consequence of stellar wind mass loss, or gravitational radiation.
There are two general mechanisms for the transferring angular momentum out of the system: First, binary systems emit gravitational radiation, which carries away angular momentum. The rate of angular momentum loss increases as the orbital separation decreases, but it decreases as the total mass of the system decreases. Because both the secondary mass and the orbital separation decrease as CV systems evolving, the net effect is a loss mechanism that does not depend strongly on the orbital period.
Our investigation indicates that the stability of the mass transfer processes depends on: how the radius of the donor star responds to the mass loss, how the orbit responds to mass transfer, and how the mass-gainer responds to the matter that is being dumped on it.
The Roche lobe of the mass donor shrinks as a consequence of its mass loss, increasing the rate at which it loses mass is referred to unstable mass transfer and the Roche lobe of the mass donor grows as a consequence of its mass loss, stopping the mass transfer is referred to stable mass transfer.
In this paper we have made an effort to find a numerical and analytical solutions for conservative and non-conservative mass transfer in close binary systems which can address the gradually reducing rate of the mass accretion by the accretor from the donor with respect to time as well as with respect to the increase in mass of the accretor [15] . In view of this we have presented the time dependent profiles of the masses of both the component stars in a close binary as well as the orbital angular momentum of the system. Our analytical solutions shows for the non-conservative mass transfer in close binary system taking the initial masses of the primary and secondary as 







In conservative mass transfer and from Equation (15); if 

We have also presented a new finding (analytic and numeric solutions) for the evolution of binary systems, generalizing the results of [4] to binaries with any polytropic index and to binaries with isothermal atmospheres. The analytic solutions always predict that if a binary attains contact when the mass ratio q is such that the ensuing mass transfer is unstable, the binary merges in a finite time. On the other hand, the numerical solutions predict that a binary that undergoes unstable mass transfer at initial contact can evolve to a state of stable mass transfer, survive and evolve into an AM CVn type system. Moreover, the analytic solutions also discussed here assume that the driving rates 


asymptotically to zero over a characteristic time
time equal to
Finally, the most useful thing, is that if one assumes only accretion and wind-like mass transfer, then most every binary in which mass is transferred from the less massive star is stable on both dynamical and thermal time scales. If the mass donor has a radiative envelope (not treated here), it will shrink in response to mass loss, and lose mass stable. If the donor has a convective envelope, a modestly sized core will stabilize it sufficiently to prevent mass loss on the dynamical time scale.
Acknowledgements
We thank Entoto Observatory and Research Center for supporting this research. Negu, thanks Jigjiga University for giving study leave. This research has made use of NASA’s Astrophysical Data System.
Cite this paper
Seblu HumneNegu,Solomon BelayTessema, (2015) Mass Transfer in Binary Stellar Evolution and Its Stability. International Journal of Astronomy and Astrophysics,05,222-241. doi: 10.4236/ijaa.2015.53026
References
- 1. Shore, S.N. (1994) Observations and Physical Processes in Interacting Binaries. Springer, Berlin Heidelberg, 1-133.
http://dx.doi.org/10.1007/3-540-31626-4_1 - 2. Soberman, G.E., Phinney, E.S. and van den Heuvel, E.P.J. (1997) Stability Criteria for Mass Transfer in Binary Stellar Evolution. Astronomy and Astrophysics, 327, 620-635.
- 3. Konstantin, A.P. (2014) The Evolution of Compact Binary Star Systems. Living Reviews in Relativity, 17, 3.
- 4. Pennington, R.(1985) Interacting Binary Stars. Pringle, J.E. and Wade, R.A., Eds., Cambridge Astrophysics Series, Cambridge University Press, Cambridge, 197-199.
- 5. Hjellming, M.S. and Webbink, R.F. (1987) Thresholds for rapid mass transfer in binary systems. I—Polytropic Models. The Astrophysical Journal, 318, 794-808.
http://dx.doi.org/10.1086/165412 - 6. Ruderman, M., Shaham, J. and Tavani, M. (1989) Accretion Powered by Compact Binaries. The Astrophysical Journal, 3, 507.
- 7. Tessema, S.B. (2014) Stability of Accretion Discs around Magnetized Stars. International Journal of Astronomy and Astrophysics, 4, 319-331.
http://dx.doi.org/10.4236/ijaa.2014.42026 - 8. Lightman, A.P. and Eardley, D.M. (1974) Black Holes in Binary Systems: Instability of Disc Accretion. The Astrophysical Journal, 187, L1.
- 9. Gharami, P., Ghosh, K. and Rahaman, F. (2014) A Theoretical Model of Non-Conservative Mass Transfer with Non-Uniform Mass Accretion Rate in Close Binary Stars. General Relativity and Quantum Cosmology, 366, 1511.
- 10. Plavec, A. and Paczynski, B. (1971) Numerical Simulations of Dynamical Mass Transfer in Binaries. Annual Review of Astronomy and Astrophysics, 9, 183.
- 11. Lajoie, C.-P. and Sills, A. (2010) Mass Transfer in Binary Stars Using Smoothed Particle hydrodynamics. II. Eccentric Binaries. The Astrophysical Journal, 726, 13 p.
- 12. Tsugawa, M. and Osaki, Y. (1997) Disk Instability Model for the AM Canum Venaticorum Stars. PASJ: Publ. Astron. Soc. Japan, Vol. 49, 75-84.
- 13. Paczynski, B. and Sienkiewicz, R. (1972) Mass Transfer Effects in Binary Star Evolution. Acta Astronautica, 22, 73.
- 14. Vayujeet, G. (2007) Mass Transfer and Evolution of Compact Binary Stars. Astronomy & Astrophysics, 202, 93.
- 15. Izzard, R.G., de Mink, S.E., Onno, RP., Langer, N., Sana, H. and de Koter, A. (2013) Massive Binary Stars and Self-Enrichment of Globular Clusters. Memorie della Società Astronomica Italiana, 1, 1-4.











