International Journal of Astronomy and Astrophysics
Vol.4 No.2(2014), Article
ID:46776,5
pages
DOI:10.4236/ijaa.2014.42035
Another Way of the Continuous Linkup of Neutron-Star-Body and Surrounding Empty-Space Metrics
Luboš Neslušan
Astronomical Institute, Slovak Academy of Sciences, Tatranská Lomnica, Slovakia
Email: ne@ta3.sk
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 March 2014; revised 10 May 2014; accepted 17 May 2014
ABSTRACT
The metrics of the compact objects should be the continuous function of coordinates. The metrics inside every object is set by its internal structure. The metrics in the adjacent empty space is described by the outer Schwarzschild or Kerr solution of the Einstein field equations. It appears that the linkup of both object-interior and empty-space metrics is not continuous at the physical surfaces of the objects for the common, generally (by convention) accepted set of assumptions. We suggest the new way of how to achieve the success in the linkup, which does not assume the higher value of the relativistic speed limit in the empty space governed by the object, in contrast to our previous suggestion. We also give a more detailed explanation of the existence of inner physical surface of compact objects and suggest the way of the linkup of metrics in this surface. To achieve the continuous linkup, we assume a lower value of the speed limit in the object’s interior as well as a new gauging of the outer Schwarzschild solution for the inner empty space of the object. Newly established gauging constants are calculated and the success of the linkup is shown in several examples. The new gauging implies a lower gravitational attraction (lower gravitational constant) in the inner empty space in comparison with that in the outer space, which is measured in the common, observed, gravitational interactions of material objects.
Keywords:Gravitation, Classical General Relativity, Neutron Star, Tolman-Oppenheimer-Volkoff Problem

1. Introduction
The first description of the internal structure of dead stars, which spent all storage of their nuclear fuel, was published by Oppenheimer and Volkoff [1] about three quarters of century ago. These authors derived the equations for the numerical integration to calculate the behavior of state quantities in the object’s interior. They assumed the non-rotating object consisting exclusively of neutrons. Later, their concept was improved considering a more complex composition and several effects in stiff matter discovered meanwhile. And, the advanced models have been worked out for the rotating objects. Nevertheless, the original Oppenheimer-Volkoff concept was again considered, recently, to demonstrate two new essential features of neutron stars (NSs, hereinafter).
In 2011, Chinese researcher Ni [2] published the solution of the equations in the original Oppenheimer-Volkoff problem, which implies an inner physical surface of the object. The solution could be obtained after abandoning a relativistic postulate (more specified in Section 2). Ni concluded that his solution has no upper mass limit1. In our earlier paper [5] (Paper I, hereinafter), we corrected this conclusion related to the pure neutron objects. Since the neutron is an unstable particle in the neutron gas with a density lower than a certain critical value, the mass of stable neutron objects cannot exceed several ten thousand to few hundred thousand solar masses (however, this correction does not exclude an existence of more massive stable objects, but consisting of the gas of other kind).
In Paper I, we pointed out the second feature that every realistic concept of NS must possess: the spacetime metrics must be the continuous function of radial distance from the object’s interior up to the adjacent outer space. It appears, the continuity is not obvious at the outer physical surface of the object. The metrics inside the object's body can be calculated from the model of the object’s internal structure. In the case of non-rotating object, the metrics of the outer space is described by the outer Schwarzschild (OSCH, hereinafter) solution [6] of the Einstein field equations [7] [8] . We showed that the continuous linkup is impossible, if the OSCH solution is gauged in the common, generally well-known way (until now).
To solve the problem of the linkup, we suggested the alternative way of gauging of one integration constant in the OSCH solution. Namely, there should be a specific relativistic speed limit, ![]() , in the outer spacetime governed by the given compact object. We empirically found that
, in the outer spacetime governed by the given compact object. We empirically found that![]() , where
, where ![]() is the common speed limit or the velocity of light in vacuum (measured in our laboratories).
is the common speed limit or the velocity of light in vacuum (measured in our laboratories).
The fact that there is assumed the speed limit larger than ![]() implies some difficulties in physics. For example, the space around the compact object should behave as a concave lens deflecting the light rays away from the object. We have no observational indication of such an effect.
implies some difficulties in physics. For example, the space around the compact object should behave as a concave lens deflecting the light rays away from the object. We have no observational indication of such an effect.
Meanwhile we found that the assumption of the limit ![]() is not any sole possibility to solve the linkup problem. The gauging can be done in another alternative way, which is presented in this paper. In the new gauging, the maximum speed limit remains c, but the velocity of light figuring in the equations determining the internal structure of the compact object is assumed lower than c, on contrary.
is not any sole possibility to solve the linkup problem. The gauging can be done in another alternative way, which is presented in this paper. In the new gauging, the maximum speed limit remains c, but the velocity of light figuring in the equations determining the internal structure of the compact object is assumed lower than c, on contrary.
We note, we create a “global” model, which describes the overall internal structure of compact neutron object, here. It means, we do not give any description of local phenomena or fields (e.g., magnetic field), which can occur at the surface of the object or in its close vicinity. The ignorance of these phenomena or fields does not represent, however, any principal problem, since the outer physical surface in all presented models is situated above the corresponding event horizon. Thus, the modeling is analogous to that of the internal structure of common stars. The local phenomena at the stars often used to be described in addition to the stellar model as a whole.
Concerning the structure of our paper, it is following. In the second section of our paper, we explain, once more, the mechanism of the formation of inner physical surface of compact object. In Section 3, we recall the basic equations determining the internal structure of non-rotating neutron object and also explain how the alternative gauging of the OSCH solution can be done. In the beginning of Section 4, the first way of the alternative gauging of integration constant in the OSCH solution is reminded. Then, the new assumption is presented in detail and the appropriate modified constants are given. In Section 5, we present a series of solutions for the internal structure of neutron objects with the description of whole metrics as well as some interesting dependencies concerning the relationship between the mass and outer radius or that between both outer radius and Schwarzschild gravitational radius, etc. In this paper, we also deal with the linkup in the inner physical surface, in Section 6. Some conclusion remarks are written in Section 7.
2. Inner Physical Surface
In the Newtonian physics with the flat, Euclidean space, the area of a spherical surface delineated by a spherical angle is proportional to the quadrate of the distance from the area. The Newtonian gravitational force and, hence, the corresponding acceleration is proportional to the reciprocal quadrate of the distance.
In general relativity, the metrics of the vacuum in a vicinity of spherically symmetric distribution of matter is OSCH, according to the Birkhoff theorem. It means that the time component, 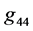 , of the metric tensor is equal to
, of the metric tensor is equal to , where
, where ![]() is an integration constant. Because of the singularity in
is an integration constant. Because of the singularity in![]() , it is however postulated that
, it is however postulated that 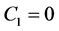 and the metrics is, therefore, flat inside a spherical shell. Thus there is no difference between the Newtonian physics and general relativity concerning the metrics in the vacuum inside the spherical shell.
and the metrics is, therefore, flat inside a spherical shell. Thus there is no difference between the Newtonian physics and general relativity concerning the metrics in the vacuum inside the spherical shell.
In the following, let us nevertheless to discuss the case when we abandon the postulate and consider the nondegenerated OSCH metrics also inside the shell (or, the postulate 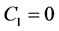 is reduced to be valid only in
is reduced to be valid only in ![]() to avoid the singularity).
to avoid the singularity).
Taking into account this assumption, let us consider a spherically symmetric, thin material shell (Figure 1). There is vacuum as outside the shell as well as in its interior. The gravitational acceleration of a test particle situated outside the shell is non-zero and oriented toward its center. We denote it by 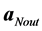 in the Newtonian case (Figure 1, upper scheme). Inside the shell, the net Newtonian force and corresponding acceleration (
in the Newtonian case (Figure 1, upper scheme). Inside the shell, the net Newtonian force and corresponding acceleration ( in the upper scheme in Figure 1) of a particle are zero. Let us further do a thinking experiment that the shell consists of a gas with the internal pressure. The gradient of the pressure pushes the gas as outward as inward the shell. The outward acting gradient can be balanced by the gravity and this is the mechanism of how the outer physical surfaces of, e.g., stars or gaseous planets form. Since the net gravity inside the shell is zero, there is nothing to balance the inward acting gradient of pressure. No stable configuration with an inner physical surface can occur in the case of Newtonian gravity. The whole interior of shell must be, earlier or later, filled in with a gas. This is, likely, the physical justification of our psychological belief that every gaseous object is a full sphere.
in the upper scheme in Figure 1) of a particle are zero. Let us further do a thinking experiment that the shell consists of a gas with the internal pressure. The gradient of the pressure pushes the gas as outward as inward the shell. The outward acting gradient can be balanced by the gravity and this is the mechanism of how the outer physical surfaces of, e.g., stars or gaseous planets form. Since the net gravity inside the shell is zero, there is nothing to balance the inward acting gradient of pressure. No stable configuration with an inner physical surface can occur in the case of Newtonian gravity. The whole interior of shell must be, earlier or later, filled in with a gas. This is, likely, the physical justification of our psychological belief that every gaseous object is a full sphere.
Let us further consider the analogous shell, but so compact that its gravity significantly curves the spacetime, therefore the relativistic description of gravity is relevant. Inside the shell, there is a point-like test particle in the position characterized with a radius vector. The plane containing the particle and perpendicular to the particle’s radius vector (indicated with the violet dashed straight-line in the bottom schemes in Figure 1) divides the shell to the outer (red in Figure 1) and inner (blue in Figure 1) parts with respect to the shell’s center. The relativistic gravitational acceleration from the matter in the outer (inner) part of the shell is 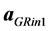
 . Notice that the vector
. Notice that the vector 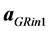 is naturally oriented in the outward direction, toward the acting material part of the shell (we emphasize that the gravity is always regarded as the attractive force).
is naturally oriented in the outward direction, toward the acting material part of the shell (we emphasize that the gravity is always regarded as the attractive force).
The solution of the Einstein field equations found by Ni implies that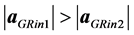 , when no postulate is applied. It means that the resultant acceleration vector in the general-relativistic case,
, when no postulate is applied. It means that the resultant acceleration vector in the general-relativistic case, 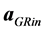 , is oriented outward (as shown in the bottom-right scheme in Figure 1). If we now repeat the thinking experiment, we find that there is an agent, the outward oriented gravity, which can balance the inward acting gradient of pressure. The mechanism of formation of the inner physical surface is essentially the same as that leading to the formation of outer surface.
, is oriented outward (as shown in the bottom-right scheme in Figure 1). If we now repeat the thinking experiment, we find that there is an agent, the outward oriented gravity, which can balance the inward acting gradient of pressure. The mechanism of formation of the inner physical surface is essentially the same as that leading to the formation of outer surface.
The object with the inner surface is further referred to as the “hollow sphere”. Inside such the object, there is always a distance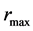 , in which pressure and energy density acquire the maximum values. This distance is, of course, larger than the radius of the inner surface
, in which pressure and energy density acquire the maximum values. This distance is, of course, larger than the radius of the inner surface 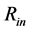 and smaller than the radius of outer surface
and smaller than the radius of outer surface . We note that it is possible to construct the models with arbitrarily small values of
. We note that it is possible to construct the models with arbitrarily small values of 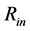 and
and . If the step of the numerical integration, used to gain the behavior of state quantities, is
. If the step of the numerical integration, used to gain the behavior of state quantities, is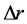 , we can find such input values entering the numerical integration, which imply the values of
, we can find such input values entering the numerical integration, which imply the values of 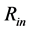 and
and 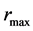 satisfying inequalities
satisfying inequalities 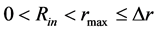 , but
, but 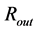 is as large as expected for a typical outer radius of NS. Four examples of the numerical integration with the extremely small values of
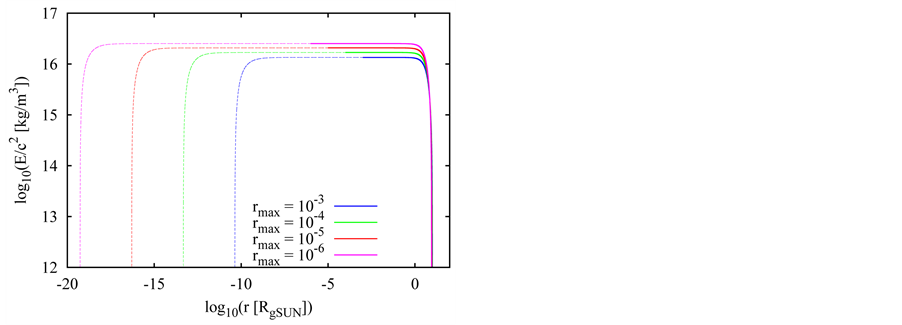
is as large as expected for a typical outer radius of NS. Four examples of the numerical integration with the extremely small values of 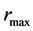 are shown in Figure 2. Specifically,
are shown in Figure 2. Specifically,  ,
, 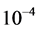 ,
, 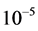 , and
, and 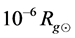 (i.e. about 300, 30, 3, and
(i.e. about 300, 30, 3, and  cm, respectively). We use the gravitational radius of the Sun,
cm, respectively). We use the gravitational radius of the Sun,  , as the unit of length.
, as the unit of length.
Distance 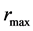 is, in fact, the critical distance in which the orientation of the vector of gravitational attraction changes from inward to outward direction. Its existence can also be deduced if we realize that the vector of gravitational attraction is oriented outward inside the spherically symmetric material shell introduced above. When we consider a test particle near the outer physical surface of compact object, there are much more material layers
is, in fact, the critical distance in which the orientation of the vector of gravitational attraction changes from inward to outward direction. Its existence can also be deduced if we realize that the vector of gravitational attraction is oriented outward inside the spherically symmetric material shell introduced above. When we consider a test particle near the outer physical surface of compact object, there are much more material layers
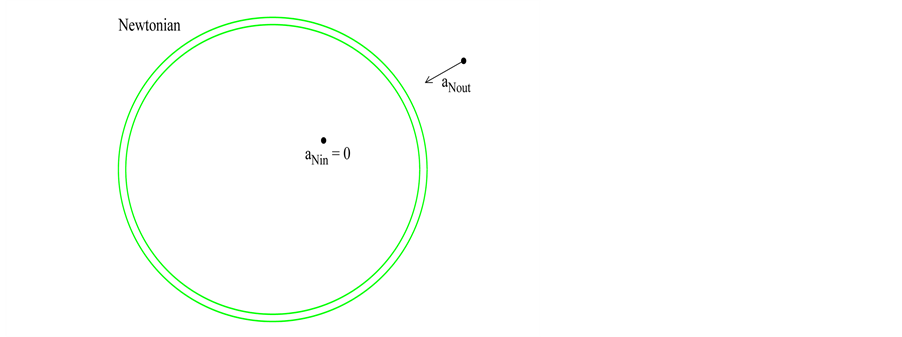

Figure 1. The schemes helping to explain the formation of the inner physical surface of compact object. The green (upper scheme) and blue-red (bottom schemes) circles represent a thin, spherically symmetric material shell in the case of Newtonian (upper scheme) and general-relativistic (bottom schemes) description of gravity. The violet dashed straight-line indicates the plane passing through a test particle, situated inside the shell, and perpendicular to the particle’s radius vector. The acceleration of a particle being outside of shell due to its gravity is denoted by aNout or aGRout. The acceleration of test particle being inside the shell due to its outer (inner) part is denoted by aGRin1(aGRin2) and the acceleration of this particle due to the net force is aNin or aGRin.
 (a)
(a) (b)
(b)
Figure 2. The behavior of density inside four compact objects with the extremely small distance rmax and inner radius Rin. The density is given in the logarithmic scale and the radial distance in both linear (a) and logarithmic (b) scales. The thick, solid curves illustrate the behavior in the distances from rmax to the outer radius Rout and thin, dashed curves that from rmax down to the inner radius Rin.
below this particle and it is obviously more attracted by these layers than by few layers above it. If we consider the particle in a shorter and shorter object-centric distances, there are less and less layers below and more and more layers above it. Therefore, the particle is in a lesser and lesser degree attracted by the lower layers and more and more attracted by the upper layers. Considering the solution by Ni, we get to the distance, where the attraction of the lower layers (toward the center) is balanced by the attraction of the upper layers (outward the center).
The gradient of pressure, balancing the gravity, also changes its orientation in distance . The formula giving the gradient can be written in the following form. We know that the general relativity has to converge to the Newtonian physics in the limit of weak field and this requirement yields the gauging in the relations for the metric-tensor components
. The formula giving the gradient can be written in the following form. We know that the general relativity has to converge to the Newtonian physics in the limit of weak field and this requirement yields the gauging in the relations for the metric-tensor components 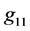 and
and  in the OSCH solution in the form
in the OSCH solution in the form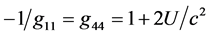 , where
, where ![]() is the gravitational potential. The auxiliary function
is the gravitational potential. The auxiliary function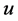 , which was established by Oppenheimer and Volkoff [1] as
, which was established by Oppenheimer and Volkoff [1] as
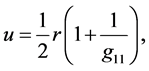 (1.1)
(1.1)
can be given with the help of ![]() as
as 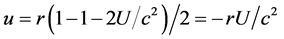 or
or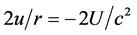 . Although this is derived for the OSCH solution, it would be strange to represent function u as directly related to the potential in the OSCH solution, but as related to some else quantity in the NS body. Therefore, the well-known formula for the gradient of pressure,
. Although this is derived for the OSCH solution, it would be strange to represent function u as directly related to the potential in the OSCH solution, but as related to some else quantity in the NS body. Therefore, the well-known formula for the gradient of pressure, 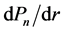 , figuring in the Oppenheimer-Volkoff problem, can be given as
, figuring in the Oppenheimer-Volkoff problem, can be given as
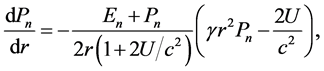 (1.2)
(1.2)
where 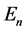 and
and ![]() are the energy density and pressure, and constant
are the energy density and pressure, and constant 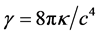 in the used SI units (
in the used SI units (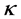 is the gravitational constant).
is the gravitational constant).
The pressure reaches its maximum value when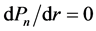 , i.e.
, i.e. . It appears, if
. It appears, if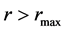 , then
, then  and
and 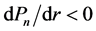 (we empirically found that there is always valid
(we empirically found that there is always valid  in the denominator of Equation (1.2)). On contrary, if
in the denominator of Equation (1.2)). On contrary, if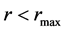 , then
, then  and
and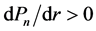 .
.
We note that, according to some solutions of the Einstein field equations, the matter can still be distributed from the true center of NS in such a way that the vector of the gravitational attraction is oriented inward from this center to infinity and gradient of pressure always acts against this attraction inside the NS body.
3. Structure of Compact Neutron Object
The equations to describe the non-rotating object, without any internal source of energy, consisting of a cold, degenerated, Fermi-Dirac gas, has been presented many times, starting with the famous paper by Oppenheimer and Volkoff [1] . Therefore, we only remind that the final set of the equations for numerical integration, written with the help of denotation used in Paper I, is
 (1.3)
(1.3)
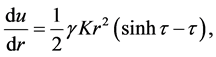 (1.4)
(1.4)
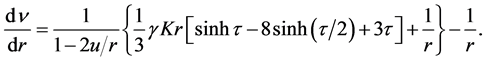 (1.5)
(1.5)
Components  and
and  of the metric tensor were also written with the help of auxiliary functions
of the metric tensor were also written with the help of auxiliary functions 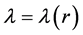 and
and  in the form
in the form  and
and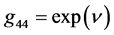 . The energy density,
. The energy density, 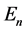 , and pressure,
, and pressure, ![]() , of the considered neutron gas can be given as the functions of the auxiliary quantity
, of the considered neutron gas can be given as the functions of the auxiliary quantity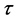 :
: 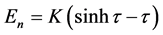 and
and  [9] . Quantity
[9] . Quantity  is related to the Fermi impulse,
is related to the Fermi impulse, 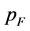 , as
, as
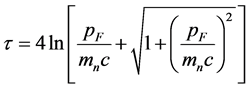 (1.6)
(1.6)
( is the rest mass of neutron) and constant
is the rest mass of neutron) and constant ![]() can be expressed as
can be expressed as
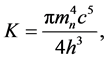 (1.7)
(1.7)
therefore the product  figuring in Equations (1.3)-(1.5) equals
figuring in Equations (1.3)-(1.5) equals
 (1.8)
(1.8)
where  is the Planck constant.
is the Planck constant.
A model of internal structure of a neutron object as the hollow sphere can be calculated assuming a set of input values 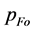 (or
(or ),
), ![]() , and
, and ![]() in a distance
in a distance  inside the object, i.e. satisfying inequalities
inside the object, i.e. satisfying inequalities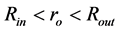 . Because of practical reason, it is worth to eliminate at least one input parameter. As already mentioned in Section 2, in the object occupying the hollow sphere, there is always such the distance
. Because of practical reason, it is worth to eliminate at least one input parameter. As already mentioned in Section 2, in the object occupying the hollow sphere, there is always such the distance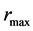 , in which
, in which 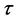 and, consequently,
and, consequently, ![]() and
and  acquire the maximum values. We can start the integration just in
acquire the maximum values. We can start the integration just in  and utilize that
and utilize that
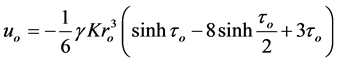 (1.9)
(1.9)
in this distance. The latter is derived from the condition for the local maximum of function , i.e. from
, i.e. from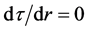 . After we put
. After we put , we have to choose only the input values
, we have to choose only the input values  (or
(or ), and
), and ![]() in
in .
.
The sum of the rest masses of all neutrons constituting the object, i.e. the object’s rest mass, can be calculated as
 (1.10)
(1.10)
and the object’s total or gravitational mass as
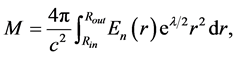 (1.11)
(1.11)
where 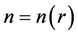 is the number density of neutrons given by relation
is the number density of neutrons given by relation
 (1.12)
(1.12)
In the case of the spherical symmetry, only the components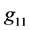 ,
,  ,
, 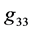 , and
, and  of metric tensor are non-zero. Further, the components
of metric tensor are non-zero. Further, the components 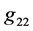 and
and  are identical for both object’s interior and outer empty space. In a search for a continuous metrics, we therefore need to deal only with the components
are identical for both object’s interior and outer empty space. In a search for a continuous metrics, we therefore need to deal only with the components 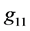 and
and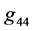 .
.
In the process of the derivation of OSCH solution, we obtain the differential equation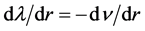 . Integrating the latter, we obtain
. Integrating the latter, we obtain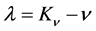 , where
, where  is the integration constant. If it is converted to constant
is the integration constant. If it is converted to constant  as
as , the line element of the metrics for vacuum, described by the OSCH solution, is
, the line element of the metrics for vacuum, described by the OSCH solution, is
 (1.13)
(1.13)
in the spherical coordinate frame![]() ,
, ![]() , and
, and![]() . In the classical gauging of the OSCH solution, only the universal speed limit,
. In the classical gauging of the OSCH solution, only the universal speed limit, ![]() , is considered, therefore only zero
, is considered, therefore only zero  (i.e.
(i.e.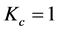 ) is relevant.
) is relevant.
Although the line element (1.13) with constant  is derived for the vacuum, we generalize it also for a material environment in our further considerations. Specifically, we will use constants
is derived for the vacuum, we generalize it also for a material environment in our further considerations. Specifically, we will use constants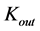 ,
,  , and
, and 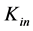 for the outer empty space, material interior of the NS body, and inner empty space, respectively (Term “body” is used to specify the part of object between its inner and outer physical surfaces, without the internal void).
for the outer empty space, material interior of the NS body, and inner empty space, respectively (Term “body” is used to specify the part of object between its inner and outer physical surfaces, without the internal void).
4. Gauging of Internal-Structure Speed Limit
Using  and according to relation (1.1),
and according to relation (1.1),
 (1.14)
(1.14)
inside the NS. Let us denote function 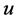 in the distance
in the distance 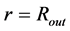 by
by . The first requirement for the continuous metrics is equality of the function
. The first requirement for the continuous metrics is equality of the function 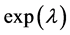 given by (1.14) in
given by (1.14) in  and its OSCH-metrics counterpart in this distance, i.e.
and its OSCH-metrics counterpart in this distance, i.e. . From the latter, we gain the requirement
. From the latter, we gain the requirement
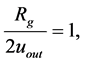 (1.15)
(1.15)
where  is the Schwarzschild gravitational radius. It can be determined considering the object’s mass,
is the Schwarzschild gravitational radius. It can be determined considering the object’s mass,  , given by relation (1.11). So, it is unique for the given object. The value of
, given by relation (1.11). So, it is unique for the given object. The value of  is also unique, implied by the model of internal structure of the given object.
is also unique, implied by the model of internal structure of the given object.
In Paper I, we constructed the dependencies of the ratio 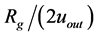 on the input value
on the input value  for a series of maximum distances
for a series of maximum distances  and found that there is always valid
and found that there is always valid 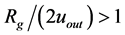 for every
for every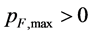 . It means, component
. It means, component 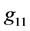 determined for the object does not equal to that for the OSCH metrics in
determined for the object does not equal to that for the OSCH metrics in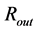 . There is a principal displacement of
. There is a principal displacement of 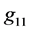 in this distance when the traditional values of all concerning constants are considered.
in this distance when the traditional values of all concerning constants are considered.
The second requirement of acceptable linkup of metrics is equality of 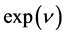 calculated for the object and its OSCH-solution counterpart in
calculated for the object and its OSCH-solution counterpart in . Denoting function
. Denoting function 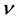 in
in  with the symbol
with the symbol 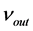 and realizing that
and realizing that  in the OSCH solution in
in the OSCH solution in , we obtain the mathematical form of the second requirement
, we obtain the mathematical form of the second requirement
 (1.16)
(1.16)
When the input values of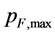 ,
, ![]() , and
, and  are chosen ad hoc, condition (1.16) is not satisfied. However, it is always possible, via an iteration, to find such the input
are chosen ad hoc, condition (1.16) is not satisfied. However, it is always possible, via an iteration, to find such the input![]() , at given combination of
, at given combination of 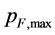 and
and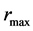 , that the condition is satisfied. By the way, this circumstance implies that not all input parameters to the numerical integration of Equations (1.3)-(1.5) are free.
, that the condition is satisfied. By the way, this circumstance implies that not all input parameters to the numerical integration of Equations (1.3)-(1.5) are free.
The continuous linkup however requires that also the derivatives of 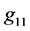 and
and 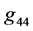 with respect to
with respect to ![]() for both object and empty space have to equal each other, respectively, in the neutron-object’s surface. It means,
for both object and empty space have to equal each other, respectively, in the neutron-object’s surface. It means,
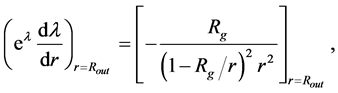 (1.17)
(1.17)
 (1.18)
(1.18)
Because of the above-mentioned displacement of  in
in , it is meaningless to investigate if condition (1.17) is satisfied. Condition (1.18) was not found to be satisfied for any of several hundred solutions calculated in Paper I in the case of
, it is meaningless to investigate if condition (1.17) is satisfied. Condition (1.18) was not found to be satisfied for any of several hundred solutions calculated in Paper I in the case of  (and, we implicitly assumed,
(and, we implicitly assumed, ).
).
In Paper I, we assumed that the active agent that shapes the local spacetime and also determines its intrinsic properties is the mass accumulation in the object. The metrics of the adjacent empty space should thus be adapted to become a smooth continuation of that, which was found for the object alone. Consequently, we suggested the alternative gauging of the OSCH solution postulating that the requirement (1.15) must be satisfied and replacing the value of speed limit, ![]() , with the product
, with the product , whereby whatever real value of constant
, whereby whatever real value of constant 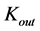 was allowed.
was allowed.
Product 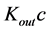 was denoted by symbol
was denoted by symbol ![]() and represented, in Paper I, as the new relativistic speed limit. After replacing
and represented, in Paper I, as the new relativistic speed limit. After replacing ![]() with
with![]() , the “modified” gravitational radius is
, the “modified” gravitational radius is . Or,
. Or, . With the new postulate and assumptions, requirement (1.15) can be re-written as
. With the new postulate and assumptions, requirement (1.15) can be re-written as 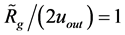 or
or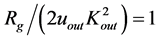 . From the latter,
. From the latter,
 (1.19)
(1.19)
After the new, alternative gauging, components  and
and  of metric tensor are
of metric tensor are
 (1.20)
(1.20)
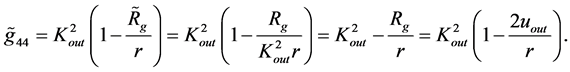 (1.21)
(1.21)
When this OSCH solution is considered, the displacement in  in the linked
in the linked  disappears. And, the conditions (1.17) and (1.18), in which
disappears. And, the conditions (1.17) and (1.18), in which  is replaced with
is replaced with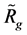 , appear to be satisfied, i.e. the functions
, appear to be satisfied, i.e. the functions  as well as
as well as 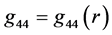 appear to be continuous in
appear to be continuous in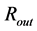 . It is remarkable that making a single assumption (that
. It is remarkable that making a single assumption (that ![]() should be replaced with
should be replaced with![]() ) results in the satisfaction of three requirements at the same time.
) results in the satisfaction of three requirements at the same time.
The dependence of 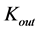 and, therefore, the new speed limit
and, therefore, the new speed limit ![]() on
on  and
and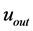 , according to relation (1.19), means that the object changes the intrinsic properties of the spacetime, where its gravity dominates, and this action results in the specific speed limit for each material object.
, according to relation (1.19), means that the object changes the intrinsic properties of the spacetime, where its gravity dominates, and this action results in the specific speed limit for each material object.
We empirically found, in Paper I, that  and, therefore,
and, therefore,![]() . This conclusion has, however, several problematic consequences. For example, the space around the object (with the velocity of light equal to
. This conclusion has, however, several problematic consequences. For example, the space around the object (with the velocity of light equal to![]() ) would behave as a concave lens, which deflects the light rays away from the object. As far as we know, such a type of lensing has not been spotted in any observation.
) would behave as a concave lens, which deflects the light rays away from the object. As far as we know, such a type of lensing has not been spotted in any observation.
Meanwhile, we noticed another possibility of the successful linkup of the metrics under our study, with velocity ![]() retained to be the maximum. Our assumption that the active agents determining the properties of spacetime are the material objects was based on the fact that the energy density and pressure of vacuum in a vicinity of an object are assumed to be zero in general relativity. This could however be only an approximation valid for a local spacetime. In the elementary-particle physics, vacuum is assumed, on contrary, to possess an energy. It is possible that this energy summed through the entire universe is the dominant agent that determines the properties of free space. These properties are not, then, dependent on the local material objects.
retained to be the maximum. Our assumption that the active agents determining the properties of spacetime are the material objects was based on the fact that the energy density and pressure of vacuum in a vicinity of an object are assumed to be zero in general relativity. This could however be only an approximation valid for a local spacetime. In the elementary-particle physics, vacuum is assumed, on contrary, to possess an energy. It is possible that this energy summed through the entire universe is the dominant agent that determines the properties of free space. These properties are not, then, dependent on the local material objects.
Considering the new assumption, we retain the original, historical gauging of the integration constants in the OSCH solution and change constant ![]() in the relations describing the internal structure and properties of spacetime corresponding to the object. In other words, we keep constant
in the relations describing the internal structure and properties of spacetime corresponding to the object. In other words, we keep constant ![]() in the
in the 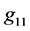 and
and  components of the OSCH metrics putting
components of the OSCH metrics putting  and replace velocity
and replace velocity ![]() with
with  (whereby
(whereby ) in relations (1.6)-(1.8), (1.11), and (1.12) finding the appropriate value of
) in relations (1.6)-(1.8), (1.11), and (1.12) finding the appropriate value of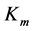 , which is lower than unity. This procedure is enabled by the fact that the success in the linkup should not depend on the specific numerical values of
, which is lower than unity. This procedure is enabled by the fact that the success in the linkup should not depend on the specific numerical values of ![]() and
and![]() . So, it should appear, in our previous alternative gauging, also for the formal replacements
. So, it should appear, in our previous alternative gauging, also for the formal replacements ![]() and
and .
.
We remind, constant 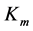 relates the newly established velocity
relates the newly established velocity 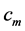 and
and![]() , whereby
, whereby
 (1.22)
(1.22)
Ratio  in the new gauging can obviously be expected different from ratio
in the new gauging can obviously be expected different from ratio 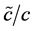 in the old gauging, therefore the new constant
in the old gauging, therefore the new constant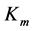 , for the metrics in the material environment, has to be found in an iteration. In more detail, we have to find such a value of
, for the metrics in the material environment, has to be found in an iteration. In more detail, we have to find such a value of  at the given combination of input parameters
at the given combination of input parameters 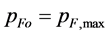 and
and  that the model is characterized with
that the model is characterized with  (implying
(implying ) and
) and  satisfying condition (1.15).
satisfying condition (1.15).
The decrease of the velocity of light in a material environment is the effect well described in optics. It is known that the relative permittivity in an optically thick environment is larger than that in vacuum (unity) and, thus, the velocity of light in this environment is smaller than the velocity of light in vacuum. Our new gauging of the speed limit is, however, related to the properties of spacetime resulting in the effects that discriminate between the relativistic physics and its Newtonian approximation. It is disputable if the optical effects can be identified with the latter. There are also further questions like, e.g., what is the mass of a particle if the value of speed limit decreases from ![]() to
to  and we require the validity of the energy-conservation law, according to which there should be valid
and we require the validity of the energy-conservation law, according to which there should be valid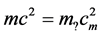 ? Or, is the inertial mass (identical to
? Or, is the inertial mass (identical to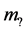 ) increased to
) increased to 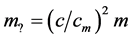 inside the NS matter? We postpone a hard, complicated discussion about these and another fundamental problems, yielding from the necessary alternative gauging of the speed limit, to future.
inside the NS matter? We postpone a hard, complicated discussion about these and another fundamental problems, yielding from the necessary alternative gauging of the speed limit, to future.
In gases, the relative permittivity depends on their density. Analogously, a similar dependence can be expected for the value of gauged speed limit, 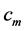 , in the neutron gas. Unfortunately, we have no idea, at the moment, how to determine the behavior of
, in the neutron gas. Unfortunately, we have no idea, at the moment, how to determine the behavior of 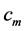 with the radial distance. In the following, we do a farther study considering a toy model with the constant velocity
with the radial distance. In the following, we do a farther study considering a toy model with the constant velocity 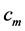 inside the whole body of neutron object.
inside the whole body of neutron object.
5. Some Examples and Relations
Let us now to describe two examples of the metrics, when the new gauging of the velocity of light in the equations of internal structure is done. The examples are for the hollow spheres, but the same principles are also valid for the full-sphere solutions. The behaviors of gas density, component of metric tensor , and component
, and component  in the two examples are given in plots (a, b), (c, d), and (e, f), respectively, in Figure 3. In this figure, while the blue, thick, dashed curves illustrate the behavior of given quantity, when the gauging with
in the two examples are given in plots (a, b), (c, d), and (e, f), respectively, in Figure 3. In this figure, while the blue, thick, dashed curves illustrate the behavior of given quantity, when the gauging with , introduced in Paper I, is done, the red, thick, solid curves illustrate the corresponding behavior, when the gauging with
, introduced in Paper I, is done, the red, thick, solid curves illustrate the corresponding behavior, when the gauging with , introduced in this paper, is done. The thin, dotted curves of corresponding color in plots (c)-(f), which touch the thick curves in their right end-points, illustrate the corresponding behavior of
, introduced in this paper, is done. The thin, dotted curves of corresponding color in plots (c)-(f), which touch the thick curves in their right end-points, illustrate the corresponding behavior of 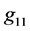 and
and  in the OSCH solution.
in the OSCH solution.
In both discussed types of gauging, the numerical integration in the first example is started in 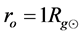 and in the second example in
and in the second example in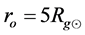 . In the earlier type of gauging
. In the earlier type of gauging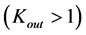 , there is put
, there is put 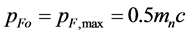 and in the current type
and in the current type 
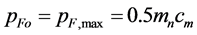 , in both examples. In all models, initial
, in both examples. In all models, initial ![]() is calculated from the condition (1.9) for the local maximum and
is calculated from the condition (1.9) for the local maximum and ![]() is found in the iteration to link
is found in the iteration to link  for the object with that for the OSCH solution.
for the object with that for the OSCH solution.
In the first example in Figure 3 (plots a, c, e), the classical Schwarzschild gravitational radius,  , is smaller than the object’s outer physical radius,
, is smaller than the object’s outer physical radius, 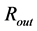 , when the internal structure is calculated with the original, nonreduced speed limit,
, when the internal structure is calculated with the original, nonreduced speed limit, ![]() (the blue, thick, dashed curves). In the second example in Figure 3 (plots b, d, f), there is valid opposite relation
(the blue, thick, dashed curves). In the second example in Figure 3 (plots b, d, f), there is valid opposite relation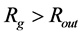 . However, if the speed limit is replaced with
. However, if the speed limit is replaced with  (the red, thick, solid curves), then the outer radius always exceeds
(the red, thick, solid curves), then the outer radius always exceeds . The mass of the object in
. The mass of the object in 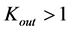
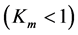 gauging is
gauging is 
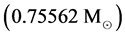 , in the first example. In the second example, the mass is
, in the first example. In the second example, the mass is 
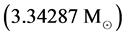 , respectively. We note that the numerical value of
, respectively. We note that the numerical value of  given in
given in  (as radii
(as radii 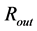 are given) is the same as the numerical value of
are given) is the same as the numerical value of 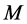 given in
given in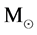 .
.
In Figure 4, we show the dependence of mass, 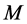 , on the input impulse
, on the input impulse  for a series of models with
for a series of models with 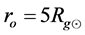 in both variants of gauging. In the case of gauging
in both variants of gauging. In the case of gauging , the masses are systematically lower, not only in the shown example (The excess is caused, in part, by the fact that the input
, the masses are systematically lower, not only in the shown example (The excess is caused, in part, by the fact that the input  in this gauging is smaller than the corresponding input
in this gauging is smaller than the corresponding input 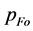 in gauging
in gauging , which occurs because of inequality of
, which occurs because of inequality of 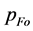 units related as
units related as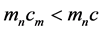 ).
).
To gain a more complex information of how some quantities are mutually related, we construct a set of models for all combinations of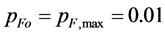 , 0.1, 0.3, 0.5,···,
, 0.1, 0.3, 0.5,···,  and
and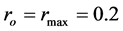 , 1, 5, 25, and
, 1, 5, 25, and  considering the gauging
considering the gauging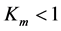 . All input values
. All input values ![]() are calculated according to the condition (1.9) for maximum
are calculated according to the condition (1.9) for maximum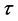 . Since the neutron is the stable particle only in the environment with density exceeding a certain critical limit,
. Since the neutron is the stable particle only in the environment with density exceeding a certain critical limit,  (
( according to Shapiro and Teukolsky [10] ), we use the auxiliary parameter
according to Shapiro and Teukolsky [10] ), we use the auxiliary parameter  to evaluate of how the equation of state for the pure neutron gas is appropriate in the given model. Quantity
to evaluate of how the equation of state for the pure neutron gas is appropriate in the given model. Quantity  is the mass inside the volume with the density,
is the mass inside the volume with the density, 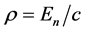 , larger than
, larger than . We arbitrarily regard the usage of equation of state for neutron gas as appropriate and the given model as acceptable, if its
. We arbitrarily regard the usage of equation of state for neutron gas as appropriate and the given model as acceptable, if its![]() .
.
In Figure 5, we illustrate the mass of neutron objects,  , as the function of
, as the function of 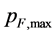 for various
for various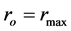 . The points corresponding to models with
. The points corresponding to models with ![]() are large and connected with solid lines. The points corresponding to the formally constructed models with
are large and connected with solid lines. The points corresponding to the formally constructed models with ![]() are small and connected with the models in a neighboring phase space of
are small and connected with the models in a neighboring phase space of  with dashed lines. This discrimination is also applied in Figure 6. As seen in Figure 5, the increase of
with dashed lines. This discrimination is also applied in Figure 6. As seen in Figure 5, the increase of 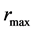 results in the increase of
results in the increase of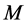 . Requiring
. Requiring![]() , we found that the maximum mass can be a little larger than about
, we found that the maximum mass can be a little larger than about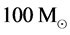 . The maximum rest mass can also exceed the limit of
. The maximum rest mass can also exceed the limit of .
.
The relative excess of mass 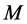 over rest mass
over rest mass , i.e. the quantity
, i.e. the quantity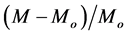 , as the function of
, as the function of 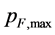 is shown in Figure 6 for the considered variety of
is shown in Figure 6 for the considered variety of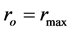 . We can see, the excess systematically
. We can see, the excess systematically



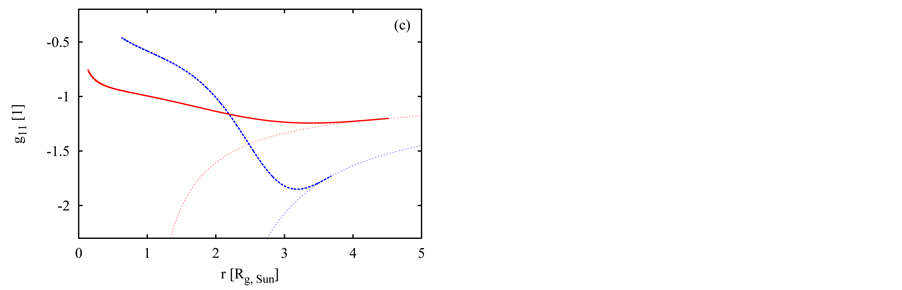


Figure 3. Two examples of behaviors of the density (a), (b) and components g11 (c), (d) and g44 (e), (f) of metric tensor inside a compact object described by the concept of hollow sphere (thick curves) and corresponding OSCH solutions (thin, dotted curves). The blue, dashed, thick curves, labeled by “1” (red, solid, thick curves labeled by “2”), give the behaviors if the OSCH solution is gauged alternatively as in Paper I (if the constants of the internal structure are gauged as suggested in this paper). While the outer physical radius of the object in the first example (left-hand plots (a), (c), (e)) is larger than the gravitational radius, it is smaller than Rg in the second example (right-hand plots (b), (d), (f)), when no alternative gauging is done.
increases for the low values of 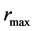 and converges to practically the same behavior for relatively large
and converges to practically the same behavior for relatively large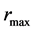 . The curves for
. The curves for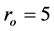 , 25, and
, 25, and 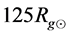 are almost identical.
are almost identical.
The occupied radial extent, from the inner radius, 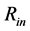 , up to the outer radius,
, up to the outer radius, 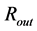 , for the neutron objects of various masses is shown in Figure 7. Interestingly, the objects with the same
, for the neutron objects of various masses is shown in Figure 7. Interestingly, the objects with the same 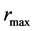 of both relatively small and relatively large masses occupy the larger volume (with a larger difference of
of both relatively small and relatively large masses occupy the larger volume (with a larger difference of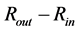 ) than the objects of the intermediate masses (with a relatively small
) than the objects of the intermediate masses (with a relatively small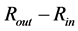 ). The black, thin, dotted straight line shows the behavior of the gravitational radius,
). The black, thin, dotted straight line shows the behavior of the gravitational radius, 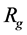 , corresponding to mass
, corresponding to mass . We can see that there is valid
. We can see that there is valid 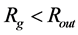 for all presented models. The second gauging assuming
for all presented models. The second gauging assuming 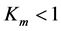 obviously also causes that a stable neutron object cannot be collapsed below its event horizon regardless to its mass.
obviously also causes that a stable neutron object cannot be collapsed below its event horizon regardless to its mass.
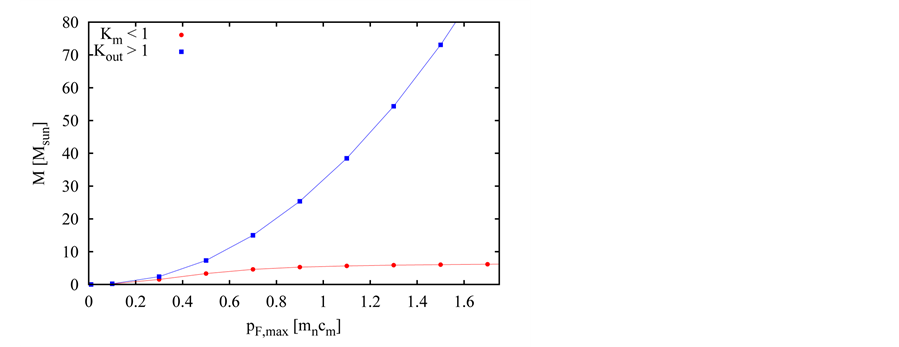
Figure 4. The comparison of the dependence of the object’s mass, M, on the maximum Fermi impulse,  , in the case
, in the case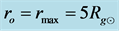 . The dependence is shown for both kinds of gauging,
. The dependence is shown for both kinds of gauging,  (blue, full squares) as well as
(blue, full squares) as well as  (red, full circles). Impulse
(red, full circles). Impulse 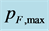 is given in the unit of
is given in the unit of 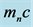
 for the first (second) kind of the gauging.
for the first (second) kind of the gauging.

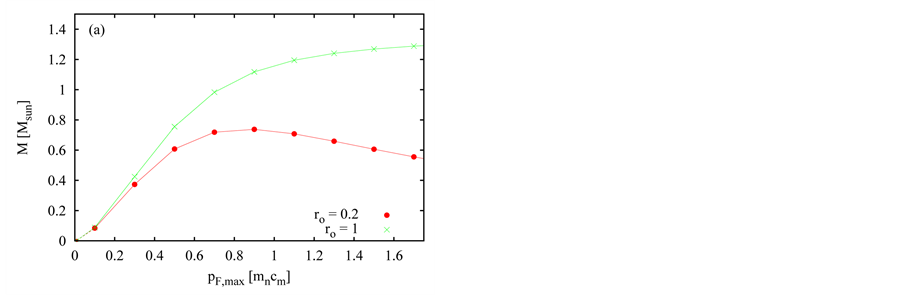
Figure 5. The dependence of neutron-object mass, M, on the maximum Fermi impulse,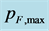 . The given curve corresponds to the specific distance
. The given curve corresponds to the specific distance . Its value, in
. Its value, in , is indicated in the legend.
, is indicated in the legend.

Figure 6. The relative excess of the total mass of object, M, over its rest mass, Mo, for various  and
and .
.
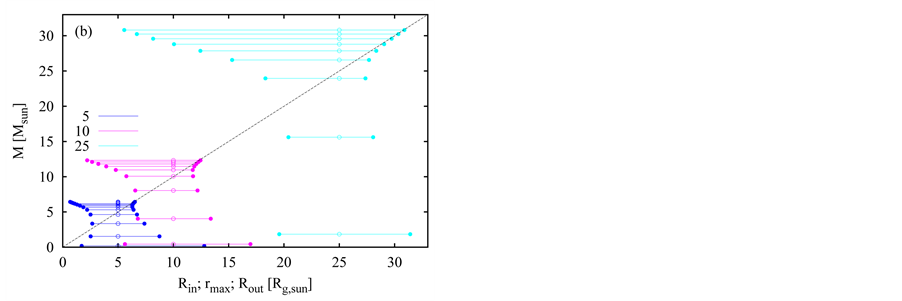
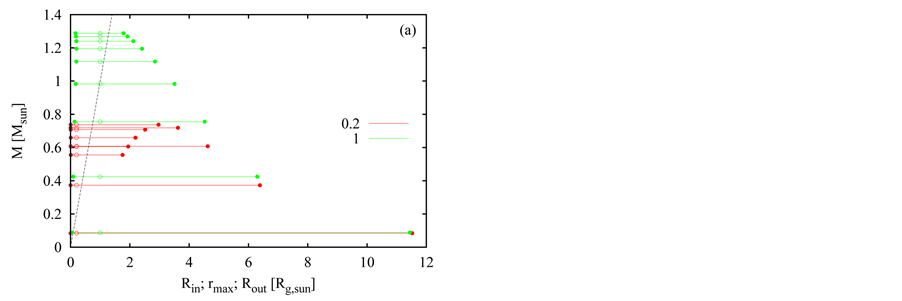
Figure 7. The relation between mass of object, M, and its inner 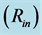 and outer
and outer  physical radius. The positions of the radii in the graphs are shown with solid circles and the extent from
physical radius. The positions of the radii in the graphs are shown with solid circles and the extent from 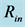 to
to  with the lines linking the corresponding pair of the solid circles. The empty circles show the position of the distance
with the lines linking the corresponding pair of the solid circles. The empty circles show the position of the distance 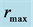 (given in legend in
(given in legend in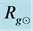 ). The black, dashed, straight line shows the behavior of the gravitational radius.
). The black, dashed, straight line shows the behavior of the gravitational radius.
6. Linkup at Inner Surface
It appears that the OSCH solution can be linked also to the NS-body metrics at the non-rotating-NS inner surface, when the hollow-sphere model of NS is considered (Our attempt with a linking up the inner Schwarzschild solution did not result in any continuous metrics, with the equal derivatives in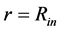 ). This fact is in the agreement with the Birkhoff theorem. Of course, we must remember the form of components
). This fact is in the agreement with the Birkhoff theorem. Of course, we must remember the form of components 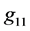 and
and  written with the gravitational potential,
written with the gravitational potential, ![]() , in purpose of gauging of the integration constants, which was mentioned in Section 2. Specifically,
, in purpose of gauging of the integration constants, which was mentioned in Section 2. Specifically, . Outside the NS, the vector of the gravitational acceleration is oriented inward, therefore
. Outside the NS, the vector of the gravitational acceleration is oriented inward, therefore ![]() and hence we re-wrote
and hence we re-wrote . In the region
. In the region , we demonstrated, in Section 2, that the vector is oriented outward from the center of considered coordinate frame, therefore
, we demonstrated, in Section 2, that the vector is oriented outward from the center of considered coordinate frame, therefore ![]() and we have to put
and we have to put  in the inner empty space bordered by
in the inner empty space bordered by .
.
We found that constant  has to be decomposed to the sum of two constants,
has to be decomposed to the sum of two constants,  and
and , i.e.
, i.e. . We again establish the alternative denotation of the constants:
. We again establish the alternative denotation of the constants:  and
and . With the help of latter, the radial and time components of metric tensor can be written as
. With the help of latter, the radial and time components of metric tensor can be written as
 (1.23)
(1.23)
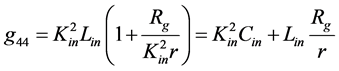 (1.24)
(1.24)
for .
.
Let us denote the speed limit in the internal empty space by symbol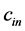 . Constant
. Constant 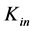 is the transformation constant between
is the transformation constant between  and
and![]() , whereby
, whereby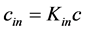 . And constant
. And constant 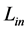 characterizes the change of the magnitude of gravity. It is apparent from relation (1.24) when we calculate the gravitational acceleration given, in the static case, as
characterizes the change of the magnitude of gravity. It is apparent from relation (1.24) when we calculate the gravitational acceleration given, in the static case, as  (e.g., [11] ). The derivative of the first term in (1.24), i.e.
(e.g., [11] ). The derivative of the first term in (1.24), i.e.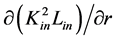 , is zero, therefore the value of constant
, is zero, therefore the value of constant  does not influence the acceleration (Analogous constant
does not influence the acceleration (Analogous constant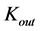 , considered in the first alternative gauging with
, considered in the first alternative gauging with  described in Paper I, also does not influence the gravitational acceleration in region
described in Paper I, also does not influence the gravitational acceleration in region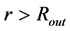 ). However, constant
). However, constant  also figures in the second term of (1.24), therefore
also figures in the second term of (1.24), therefore  is the product of the classical gravitational acceleration and constant
is the product of the classical gravitational acceleration and constant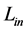 , which is empirically found
, which is empirically found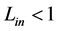 . The product of
. The product of  can, likely, be regarded as the modified gravitational constant for the region
can, likely, be regarded as the modified gravitational constant for the region 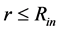 (since there is no analogous constant
(since there is no analogous constant , or we could put
, or we could put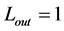 , in the region
, in the region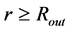 , the gravity is the same in this region regardless we make or not make an alternative gauging of the speed limit).
, the gravity is the same in this region regardless we make or not make an alternative gauging of the speed limit).
Constant  can be again found from the requirement of the identity of
can be again found from the requirement of the identity of  determining both NS-body metrics and its OSCH-solution counterpart in
determining both NS-body metrics and its OSCH-solution counterpart in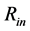 , i.e. from the equation
, i.e. from the equation  (we denoted
(we denoted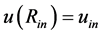 ). Hence,
). Hence,
 (1.25)
(1.25)
Since it always appears that , form
, form  and constant
and constant 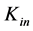 remains the real-valued constant.
remains the real-valued constant.
Let us denote 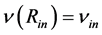 and
and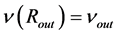 . Component
. Component 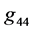 is linked up in
is linked up in  if
if  is equal to the function given by relation (1.24) for this distance. From the equality, the constant
is equal to the function given by relation (1.24) for this distance. From the equality, the constant 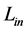 can be calculated as
can be calculated as
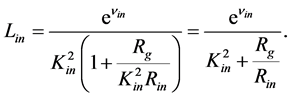 (1.26)
(1.26)
Or, the equality can be divided by analogous equality which is set by the requirement of the linkup in , i.e. we divide
, i.e. we divide  with
with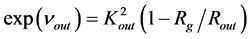 . From the equation occurring as the result of the division, we can derive
. From the equation occurring as the result of the division, we can derive
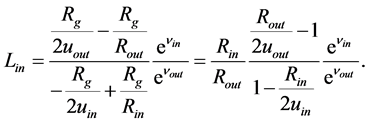 (1.27)
(1.27)
We empirically found that there is valid, at least in our toy model with the constant  considered, that
considered, that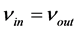 . It enables to omit the fraction
. It enables to omit the fraction  in relation (1.27). So, we can calculate
in relation (1.27). So, we can calculate 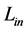 without knowing
without knowing . (In practice, we need not to perform the iteration to find the appropriate input value
. (In practice, we need not to perform the iteration to find the appropriate input value ![]() before the calculation of
before the calculation of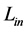 .)
.)
An example of the successful linkup of metrics in both physical surfaces of a hollow-sphere NS is shown in Figure 8.
In Figure 9, we show the dependence of velocity 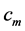 (plot a) and
(plot a) and  (plot b) on
(plot b) on  for various
for various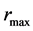 . Velocity
. Velocity 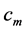 anti correlates with
anti correlates with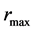 . While always
. While always  as expected, the velocity
as expected, the velocity 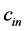 can be as smaller as larger than
can be as smaller as larger than ![]() in our models with the constant
in our models with the constant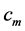 . For some values of
. For some values of , it is possible to find that
, it is possible to find that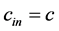 . If we consider the reasonable interval of
. If we consider the reasonable interval of  ranging from zero to
ranging from zero to  (which corresponds to the energy per particle equal to twice the rest energy) and accept only the objects satisfying our arbitrary criterion
(which corresponds to the energy per particle equal to twice the rest energy) and accept only the objects satisfying our arbitrary criterion![]() , equality
, equality 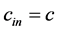 can be found for
can be found for  ranging from about 0.7 to about
ranging from about 0.7 to about . It corresponds to the neutron object’s masses from about 1.05 to about
. It corresponds to the neutron object’s masses from about 1.05 to about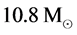 .
.
7. Conclusion Remarks
When we consider a particle inside the compact, relativistic object, the material layers situated above the particle attract it outward from the center if the flat metrics is not postulated in the interior of a spherically symmetric distribution of matter. Such the attraction is a qualitative difference from the Newtonian physics with the zero net gravity of the upper layers. In the compact object, there can, consequently, be such an object-centric distance, 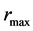 , in which the net gravity of lower layers is balanced by the net gravity of upper layers and, further, the vector of gravitational acceleration is oriented outward in distances
, in which the net gravity of lower layers is balanced by the net gravity of upper layers and, further, the vector of gravitational acceleration is oriented outward in distances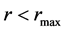 .
.
If the numerical integration of the equations to describe the internal structure of compact pure-neutron object starts in an object-centric distance larger than zero, then we can demonstrate that it never provides any model in the form of exact full sphere. At the present, all models of the NSs are constrained to be the full spheres by a postulate. In the general relativity deliberated from such the postulate, there are also possible the NS models as the hollow spheres. In the model of this kind, the energy density and pressure reach the maximum values at the non-zero object-centric radial distance . And the object is bordered not only by the outer physical surface, but by the inner physical surface as well.
. And the object is bordered not only by the outer physical surface, but by the inner physical surface as well.

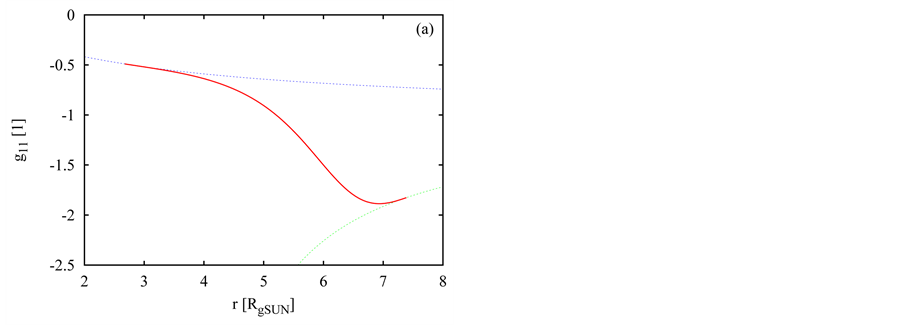
Figure 8. The example of behaviors of the components g11 (a) and g44 (b) of metric tensor inside the hollow-sphere compact object (thick red curves) and corresponding OSCH solutions (thin, dotted curves) in both inner and outer empty space (blue and green thin dotted curves).

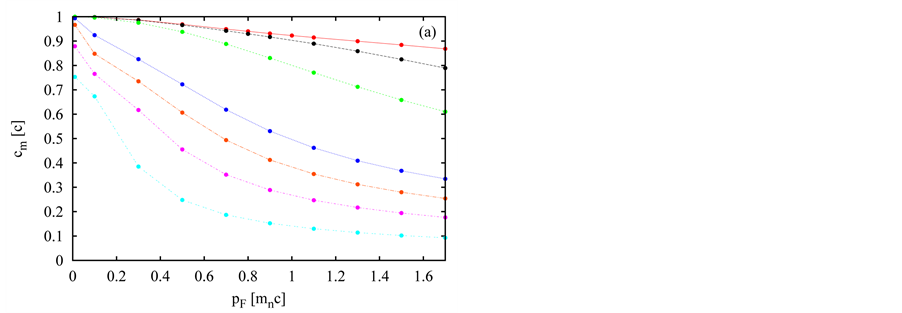
Figure 9. The relation between the velocity of light, cm, inside the neutron object (a) as well as the velocity of light, cin, in the vacuum in region  (b) and the maximum Fermi impulse,
(b) and the maximum Fermi impulse, 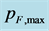 , for a series of values of the distance
, for a series of values of the distance , in which this impulse occurs. Each curve is for a single value of rmax which is indicated in the legend in plot (b).
, in which this impulse occurs. Each curve is for a single value of rmax which is indicated in the legend in plot (b).
Distance  and the radius of the inner surface,
and the radius of the inner surface,  , can be arbitrarily small, therefore an approximation of the corresponding pure-neutron hollow sphere with a full sphere is possible. However, we do not know any reason in physics why
, can be arbitrarily small, therefore an approximation of the corresponding pure-neutron hollow sphere with a full sphere is possible. However, we do not know any reason in physics why 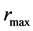 (and
(and  if exists) should be limited only to small, zero-approaching values.
if exists) should be limited only to small, zero-approaching values.
In this paper, we demonstrated that the physically acceptable, continuous linkup of metrics is possible also in the concept of unique relativistic speed limit in the vacuum outside the material objects, in the interstellar and intergalactic space. If this value of the speed limit is the maximum limit of velocity of any entity motion, then the velocity of light inside the compact neutron objects has to be reduced to achieve the continuous linkup. The reduction has, however, an impact on the total mass of the objects, which subsequently appears to be relatively lower.
If we consider the neutron object as the hollow sphere and allow the distances 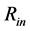 and
and 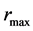 to acquire whatever real value, the mass of the pure neutron object is constrained only by the fact that neutron is unstable particle in a relatively low-density environment. Considering our simple models with constant light velocity
to acquire whatever real value, the mass of the pure neutron object is constrained only by the fact that neutron is unstable particle in a relatively low-density environment. Considering our simple models with constant light velocity , we estimated the maximum mass of the neutron object to be a little higher than
, we estimated the maximum mass of the neutron object to be a little higher than . (So, it is a much smaller value than that in the case of the first gauging described in Paper I, where this limit was estimated to be from several ten thousand to few hundred thousand solar masses.) If the compact object consists of other kind of gas or plasma, the maximum mass can obviously acquire a much higher value. A preliminary modeling of hollow-sphere compact objects with masses of several million solar masses occurs to be viable when we consider an iron plasma, the state of which is described by the polytropic equation of state. At these objects, we can furthermore expect an atmosphere containing many chemical elements. Consequently, a wide variety of spectral lines can be observed (one can deduce the state properties of the internal matter that imply a runaway thermonuclear burning during a certain period after the formation of the objects of this kind. Hence, a lot of heavy chemical elements have to occur inside).
. (So, it is a much smaller value than that in the case of the first gauging described in Paper I, where this limit was estimated to be from several ten thousand to few hundred thousand solar masses.) If the compact object consists of other kind of gas or plasma, the maximum mass can obviously acquire a much higher value. A preliminary modeling of hollow-sphere compact objects with masses of several million solar masses occurs to be viable when we consider an iron plasma, the state of which is described by the polytropic equation of state. At these objects, we can furthermore expect an atmosphere containing many chemical elements. Consequently, a wide variety of spectral lines can be observed (one can deduce the state properties of the internal matter that imply a runaway thermonuclear burning during a certain period after the formation of the objects of this kind. Hence, a lot of heavy chemical elements have to occur inside).
If the spacetime of vacuum below the inner surface of compact hollow sphere is again described with the OSCH solution of the Einstein field equations, as demanded due to the Birkhoff theorem, then this metrics can be successfully linked up to the NS-body metrics also in the inner physical surface of radius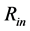 . The metrics within the sphere of radius
. The metrics within the sphere of radius  has to be gauged in a little different way than in the region outside the NS. Namely, the size of the relative scale between the spatial components (
has to be gauged in a little different way than in the region outside the NS. Namely, the size of the relative scale between the spatial components ( ,
, , and
, and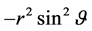 ) and the time component
) and the time component  of the metric tensor has to be changed by the factor of
of the metric tensor has to be changed by the factor of . Consequently, the gravitational constant is changed by this factor. The specific value of
. Consequently, the gravitational constant is changed by this factor. The specific value of  is implied by the structural properties of the object wrapping the region
is implied by the structural properties of the object wrapping the region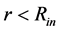 . In the models with the constant
. In the models with the constant , we empirically found that inequality
, we empirically found that inequality 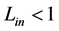 is always valid.
is always valid.
We believe that the concept of hollow sphere, with the perfectly continuous behavior of spacetime metrics, will be further developed and used to construct the models of real compact objects. Because the outer surfaces of the compact objects with the continuous behavior of metrics are always situated above the event horizon (regardless the objects are hollow or full spheres), the advanced realistic models will have to deal with an atmosphere, magnetic field, and a variety of local phenomena, which can be potentially observed at the outer surface. So, there is a lot of work for a number of another researchers who will, let us hope, also join this interesting, new stream in the astrophysics of relativistic compact objects.
Acknowledgements
The work was supported, in part, by the VEGA―the Slovak Grant Agency for Science, grant No. 2/0031/14, and by the Slovak Research and Development Agency under the contract No. APVV-0158-11.
References
- Oppenheimer, J.R. and Volkoff, G.M. (1939) On Massive Neutron Cores. Physical Review, 55, 374-381. http://dx.doi.org/10.1103/PhysRev.55.374
- Ni, J. (2011) Solutions without a Maximum Mass Limit of the General Relativistic Field Equations for Neutron Stars. Science China, Physics, Mechanics, and Astronomy, 54, 1304-1308. http://dx.doi.org/10.1007/s11433-011-4350-9
- Fiziev, P.P. (2004) Novel Geometrical Models of Relativistic Stars. I. The General Scheme. arXiv:astro-ph/0409456.
- Fiziev, P.P. (2004) Novel Geometrical Models of Relativistic Stars. II. Incompressible Stars and Heavy Black Dwarfs. arXiv:astro-ph/0409458.
- Neslu?an, L. (2014) Non-Trivial Linkup of Both Compact-Neutron-Object and Outer-Empty-Space Metrics. International Journal of Astronomy and Astrophysics, 4, 1-10.�
- Schwarzschild, K. (1916) über das Gravitationsfeld eines Massenpunktes nach der Einstein’schen Theorie. Sitzungsberichte der K?niglich Preussischen Akademie der Wissenschaften zu Berlin, Phys.-Math. Klasse, 1, 189-196.�
- Einstein, A. (1915) Die Feldgleichungun der Gravitation. Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin, 1915, 844-847.
- Einstein, A. (1916) Die Grundlage der allgemeinen Relativit?tstheorie. Annalen der Physik, 354, 769-822. http://dx.doi.org/10.1002/andp.19163540702�
- Chandrasekhar, S. (1935) The Highly Collapsed Configurations of a Stellar Mass (Second Paper). Monthly Notices of the Royal Astronomical Society, 95, 207-225.
- Shapiro, S.L. and Teukolsky, S.A. (1983) Black Holes, White Dwarfs, and Neutron Stars. The Physics of Compact Objects. John Wiley and Sons, New York. http://dx.doi.org/10.1002/9783527617661
- Tolman, R.C. (1969) Relativity, Thermodynamics, and Cosmology. Clarendon Press, Oxford.
NOTES

1The solution without the upper mass limit was also found by Fiziev several years earlier . This author assumed an alternative gauging of field equations. Besides the common radial coordinate, he established another variable, which started to have the physical meaning from a certain critical value.

