International Journal of Astronomy and Astrophysics
Vol.3 No.3(2013), Article ID:36515,7 pages DOI:10.4236/ijaa.2013.33033
The Effect of Radiogenic Heating on the Amino Acid Content of an Early Cometary Body
Dipartimento di Chimica, Università di Torino, Torino, Italy
Email: carlo.canepa@unito.it
Copyright © 2013 Carlo Canepa. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 14, 2013; revised July 15, 2013; accepted July 23, 2013
Keywords: Amino Acids; Radiogenic Heating; Comet; Prebiotic Chemistry
ABSTRACT
This study compares the rates for the formation and destruction of amino acids in the liquid cometary core subjected to radiogenic heating by the β+ decay of the cosmogenic nuclide 26Al. The evolution of the temperature and mass of the comet were computed along with the dynamics of relatively complex organic species such as amino acids. Given the experimentally determined rate coefficient for the radiolysis of amino acids in water solution, the destruction of amino acids is virtually completed after an absorbed radiation dose of ~1 kGy. The calculations suggest that the liquid water core in comets with an initial radionuclide abundance that is sufficient to crystallize and melt the original amorphous ice is subjected to a dose of 100 - 1500 kGy. Any amino acid concentration formed in water either by radiolysis of simpler compounds or by thermal processes such as the synthesis of Strecker could not survive the irradiation delivered by the decay of 26Al.
1. Introduction
It was suggested that radiogenic heating with the consequent possible formation of liquid water in comet cores in the early solar system may have promoted chemical processes otherwise it is impossible in the frozen matrices of water and carbon monoxide ices [1]. The radionuclide 26Al, that decays 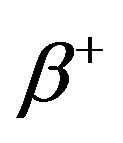 to the stable
to the stable 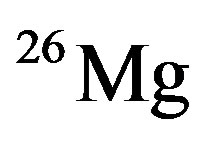 with a decay constant
with a decay constant 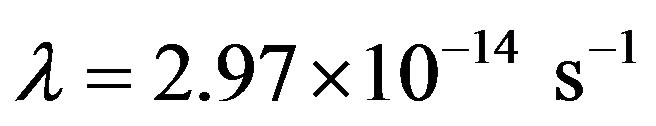 [2], is responsible for the delivery of the major portion of the energy to the newly formed cometary body. Other contributions, which are more important for large bodies and neglected in this study, come from the long lived 40K, 232Th, 235U, and 238U. In an early study, Prialnik et al. [3], concluded that the present-day observation of amorphous ice comets suggests that the initial mass fraction of 26Al could not exceed
[2], is responsible for the delivery of the major portion of the energy to the newly formed cometary body. Other contributions, which are more important for large bodies and neglected in this study, come from the long lived 40K, 232Th, 235U, and 238U. In an early study, Prialnik et al. [3], concluded that the present-day observation of amorphous ice comets suggests that the initial mass fraction of 26Al could not exceed , since any value above this threshold would result in complete crystallization. A subsequent study [4] also considered the porosity of cometary bodies with the consequent added transport of heat given by the sublimation of gases through the pores enhancing the effective thermal conductivity and ruling out melting of the cores unless the porosity was very low [5].
, since any value above this threshold would result in complete crystallization. A subsequent study [4] also considered the porosity of cometary bodies with the consequent added transport of heat given by the sublimation of gases through the pores enhancing the effective thermal conductivity and ruling out melting of the cores unless the porosity was very low [5].
Since comets constitute a major source of interplanetary dust [6], which has been proposed as a source of organic molecules in the early times of the Earth’s chemical evolution, we aim to determine if the amount of radiation delivered to a non-porous comet by the decay of a radionuclide which is compatible with the existence of complex organic molecules. Organic compounds dispersed in a condensed phase exposed to a radiation field decay with a rate law proportional to the dose rate  (in
(in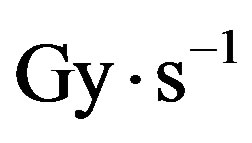 ) according to the law
) according to the law
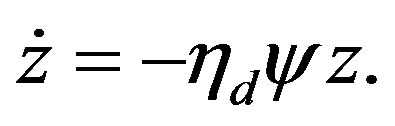 (1)
(1)
The proportionality is constant between the dose rate and the rate of depletion of the organic species is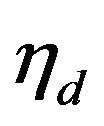 , in
, in . Since we are interested in processes occurring in liquid water, it is appropriate to use the value obtained from the data given in the kinetic study of Mita et al. [7] on the possible formation of amino acids upon UV irradiation of simple organic compounds in water solution. The results indicate that the concentration of amino acids approached zero after about
. Since we are interested in processes occurring in liquid water, it is appropriate to use the value obtained from the data given in the kinetic study of Mita et al. [7] on the possible formation of amino acids upon UV irradiation of simple organic compounds in water solution. The results indicate that the concentration of amino acids approached zero after about 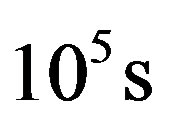 of irradiation, corresponding to
of irradiation, corresponding to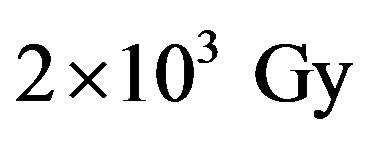 . Assuming an absorption coefficient of
. Assuming an absorption coefficient of 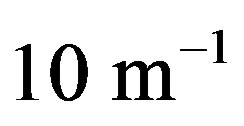 for water at
for water at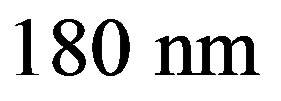 , we obtain for the glycine solution the values
, we obtain for the glycine solution the values  and
and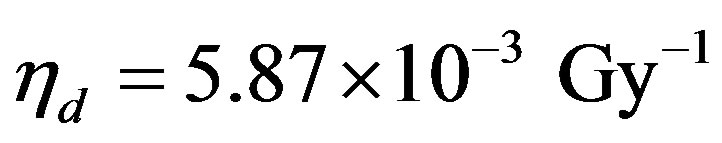 . The study ruled out the stability of amino acids under irradiation; in fact the rate coefficient for decomposition is about one order of magnitude greater than the corresponding rate coefficient for amino acid formation. We also note that an absorbed dose of a few
. The study ruled out the stability of amino acids under irradiation; in fact the rate coefficient for decomposition is about one order of magnitude greater than the corresponding rate coefficient for amino acid formation. We also note that an absorbed dose of a few 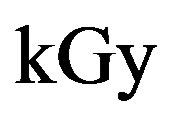 is able to decompose most organic compounds [8].
is able to decompose most organic compounds [8].
Amino acids and nucleotides are the basic building blocks of informational polymers, and the detection of amino acids in polar meteorites [9] supported the view that micrometeorites could seed the early Earth with the monomers of catalytic polypeptides. However, in space, a particle is subjected to a flux of 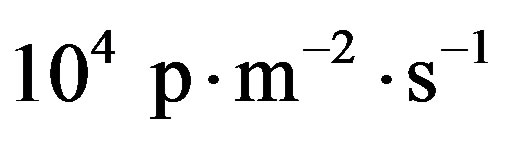 of galactic cosmic rays with energy
of galactic cosmic rays with energy 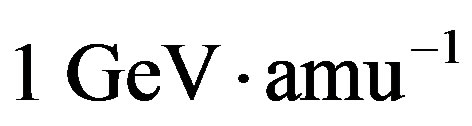 and
and 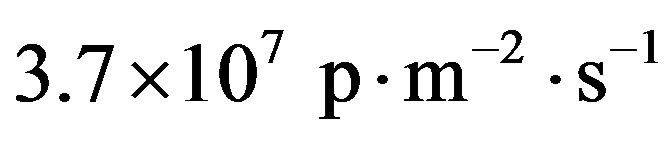 of solar cosmic rays with energy
of solar cosmic rays with energy 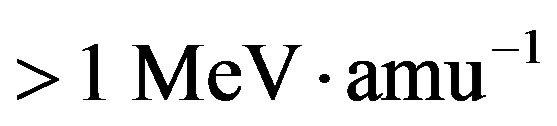 [10]. The resulting energy flux on a body exposed to cosmic rays is
[10]. The resulting energy flux on a body exposed to cosmic rays is 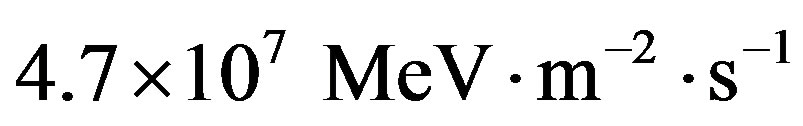 and the dose rate absorbed by simple compounds with average number density
and the dose rate absorbed by simple compounds with average number density 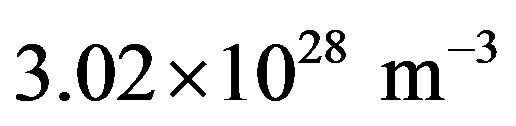 on the surface of comets given by Yeghikyan [11] is
on the surface of comets given by Yeghikyan [11] is 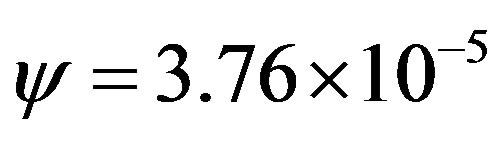
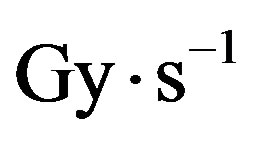 . In the solid phase, the experimental determination of Cataldo et al. [12] with a total delivered dose of 3.2 MGy of 60Co gamma rays (corresponding to
. In the solid phase, the experimental determination of Cataldo et al. [12] with a total delivered dose of 3.2 MGy of 60Co gamma rays (corresponding to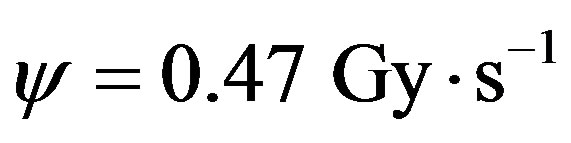 ) gives
) gives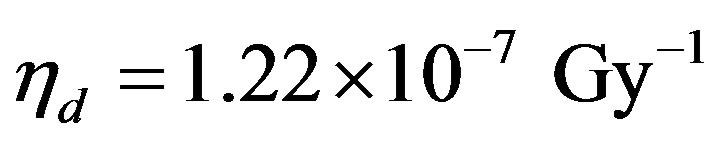 , a considerably lower value with respect to the water solution. Through Equation (1) we obtain for the solid phase the half-life
, a considerably lower value with respect to the water solution. Through Equation (1) we obtain for the solid phase the half-life , corresponding to a total delivered dose of
, corresponding to a total delivered dose of 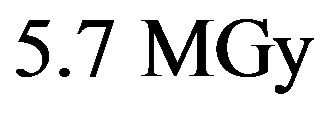 for each half-life. In their estimate of amino acid lifetimes under proton irradiation in various environments, Gerakines et al. [13] made use of the much lower dose equivalent of
for each half-life. In their estimate of amino acid lifetimes under proton irradiation in various environments, Gerakines et al. [13] made use of the much lower dose equivalent of 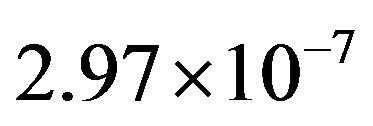
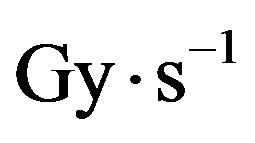 (or 1 eV per 16-amu molecule every 106 yr) for the Oort-cloud region. On the surface of a comet or a small interstellar dust particle the corresponding half-life would thus be ~1 Myr. Considering that amino acid polymerization requires a liquid solvent to allow diffusion of reactants, the suggestion of a key role of an extraterrestrial source of amino acids prompts the evaluation of amino acid lifetimes under irradiation both in the solid and liquid phase; the solid phase pertaining to micrometeorites and the liquid phase to the hypothetical liquid cores of comets.
(or 1 eV per 16-amu molecule every 106 yr) for the Oort-cloud region. On the surface of a comet or a small interstellar dust particle the corresponding half-life would thus be ~1 Myr. Considering that amino acid polymerization requires a liquid solvent to allow diffusion of reactants, the suggestion of a key role of an extraterrestrial source of amino acids prompts the evaluation of amino acid lifetimes under irradiation both in the solid and liquid phase; the solid phase pertaining to micrometeorites and the liquid phase to the hypothetical liquid cores of comets.
This work aims to determine if amino acids could be produced and stored in large bodies shielded from cosmic rays and survive long enough to be a source for the early Earth after fragmentation to micrometeorites and atmospheric re-entry.
2. Results and Discussion
In order to compute the dose of radiation delivered to the liquid water stage of a comet by the decay of 26Al, we must know the duration of every preceding stage and estimate the amount of radionuclide left at the beginning of the liquid stage, when chemical processes forming complex organic species may take place. To obtain the time evolution of the cometary body we follow the approach of Prialnik and Podolak [5], that makes use of the equation for energy balance (in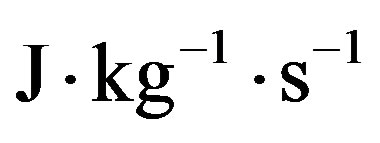 ) for a homogeneous spherical body of radius
) for a homogeneous spherical body of radius 
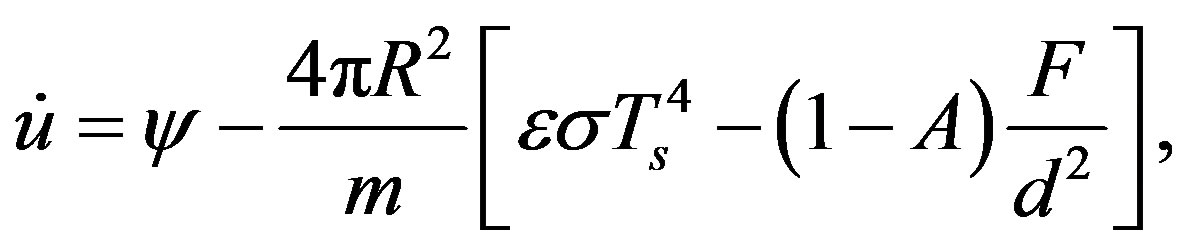 (2)
(2)
with 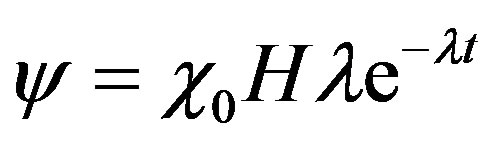 being the dose rate delivered to the cometary body from the decay of an initial mass fraction
being the dose rate delivered to the cometary body from the decay of an initial mass fraction 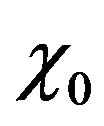 of 26Al. In Equation (2) the term in brackets is the difference between the black-body emission from the surface at temperature
of 26Al. In Equation (2) the term in brackets is the difference between the black-body emission from the surface at temperature 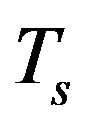 and the absorption of solar radiation by the surface of albedo
and the absorption of solar radiation by the surface of albedo  at a distance of
at a distance of 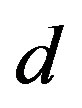 astronomical units from the Sun (
astronomical units from the Sun (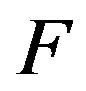 is the solar constant at 1 AU). The difference between the radiative heat fluxes is due to heat conduction in the body with thermal conductivity
is the solar constant at 1 AU). The difference between the radiative heat fluxes is due to heat conduction in the body with thermal conductivity , and may be approximated as
, and may be approximated as
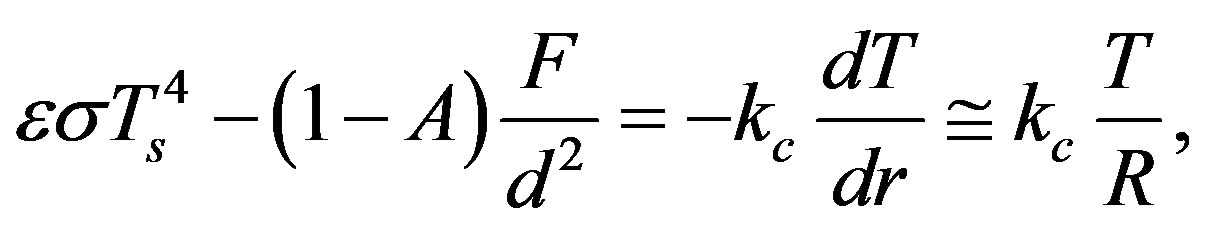 (3)
(3)
that in turn gives for the time derivative of the energy per unit mass the equation
 (4)
(4)
where we have used 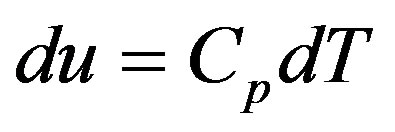 [14]. It is convenient to change the time variable to the non-dimensional
[14]. It is convenient to change the time variable to the non-dimensional  and define
and define  as the total increase in temperature due to radiogenic heating without radiative loss of energy
as the total increase in temperature due to radiogenic heating without radiative loss of energy
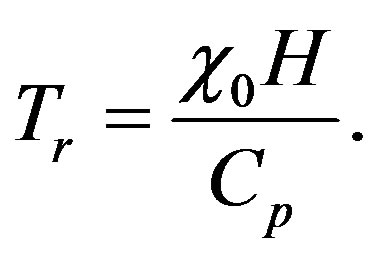 (5)
(5)
For ,
, ,
, 
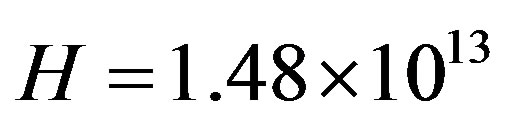 [5], and
[5], and 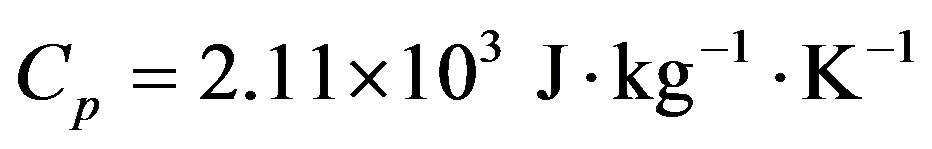 for ice [14],
for ice [14],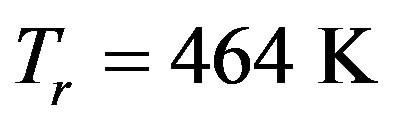 .We also define the non-dimensional quantity
.We also define the non-dimensional quantity
 (6)
(6)
as the relative temperature change of the body in time  in the absence of radiogenic heating. With the value of the thermal conductivity for ice
in the absence of radiogenic heating. With the value of the thermal conductivity for ice 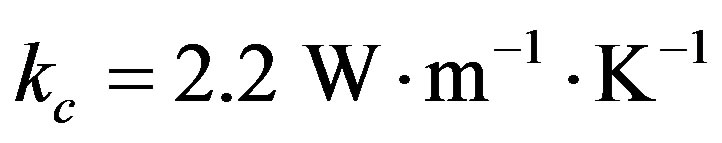 [14], density
[14], density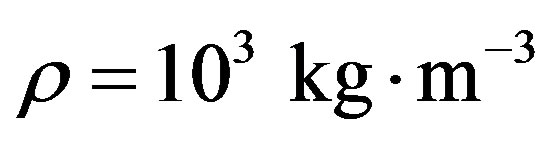 , and radius
, and radius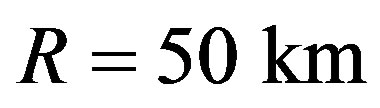 , gives
, gives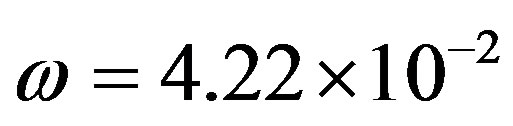 . This low value is an indication that the cooling rate is low compared to the mean lifetime of the radionuclide. The condition of fast cooling
. This low value is an indication that the cooling rate is low compared to the mean lifetime of the radionuclide. The condition of fast cooling 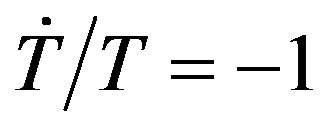 is met for values of the radius
is met for values of the radius
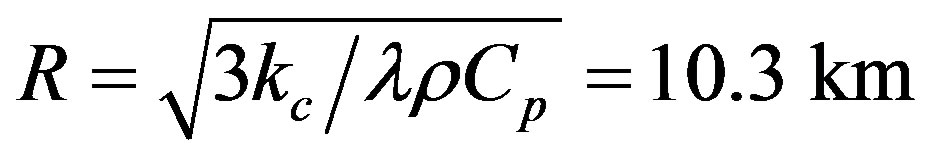 .
.
With the definitions given by Equations (5) and (6), Equation (4) becomes
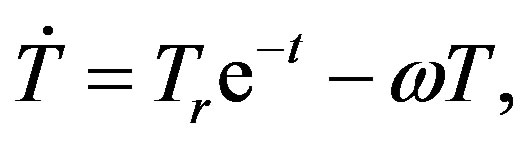 (7)
(7)
where the parameters 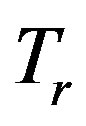 and
and  are functions of temperature through the terms
are functions of temperature through the terms 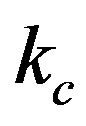 and
and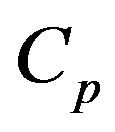 . If we use constant averages for
. If we use constant averages for 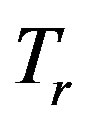 and
and  in a body with homogeneous composition, Equation (7) becomes analytically integrable with the solution
in a body with homogeneous composition, Equation (7) becomes analytically integrable with the solution
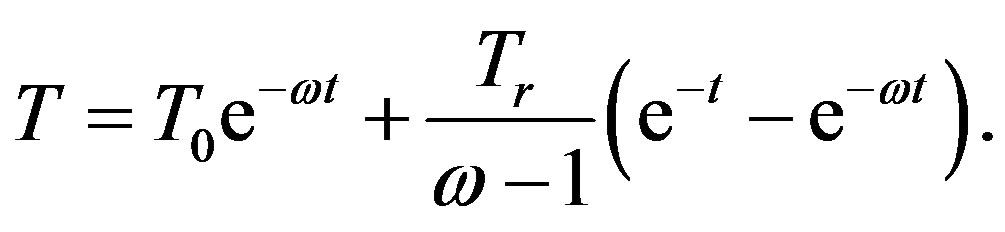
Throughout this work, we assume , corresponding to the equilibrium temperature
, corresponding to the equilibrium temperature
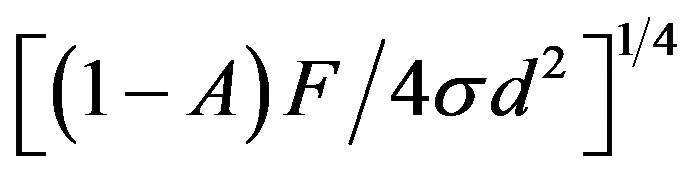 of a body at 777 AU from the Sun.
of a body at 777 AU from the Sun.
Besides the heating of the cometary body, we must also take into account the various phase transitions occurring at constant temperature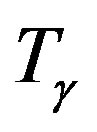 . We thus envisage the various stages of evolution of a comet composed of amorphous ice and CO as: (a) heating of amorphous ice from
. We thus envisage the various stages of evolution of a comet composed of amorphous ice and CO as: (a) heating of amorphous ice from 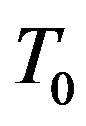 to 67.9 K; (b) sublimation of CO at 67.9 K with the consequent change of mass; (c) heating of the amorphous ice from 67.9 K to 136.8 K; (d) transition of amorphous ice to crystalline ice at 136.8 K with change of density; (e) heating of crystalline ice from 136.8 K to 273 K; (f) melting of the ice; (g) liquid water (at the assumed pressure of 6 mb); and (h) subsequent cooling, with all the relevant phase transitions taking place at constant temperature.
to 67.9 K; (b) sublimation of CO at 67.9 K with the consequent change of mass; (c) heating of the amorphous ice from 67.9 K to 136.8 K; (d) transition of amorphous ice to crystalline ice at 136.8 K with change of density; (e) heating of crystalline ice from 136.8 K to 273 K; (f) melting of the ice; (g) liquid water (at the assumed pressure of 6 mb); and (h) subsequent cooling, with all the relevant phase transitions taking place at constant temperature.
Considering a body with total mass 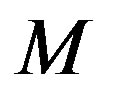 and a carbon monoxide content
and a carbon monoxide content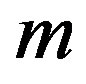 , the time derivative of the specific energy during the phase transition with heat of transition
, the time derivative of the specific energy during the phase transition with heat of transition  is
is
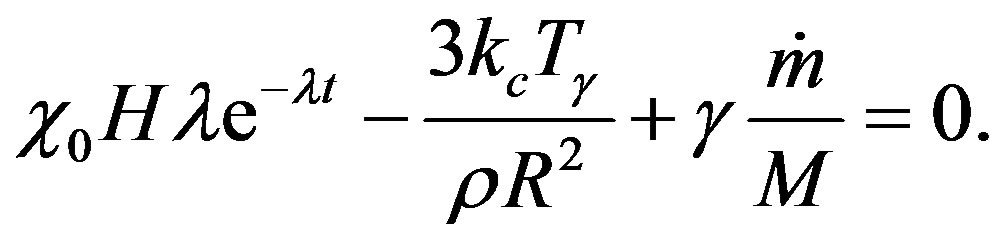 (9)
(9)
With the definitions given by Equations (5) and (6), Equation (9) becomes
 (10)
(10)
which can be used to calculate the mass as a function of time during the phase transition. It should be noted that in Equation (10) both  and
and  are now functions of
are now functions of 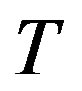 and
and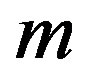 . The ratio of the total energy per unit mass released by the decay of 26Al and the heat of sublimation of carbon monoxide (5 kJ/kg) [5] is
. The ratio of the total energy per unit mass released by the decay of 26Al and the heat of sublimation of carbon monoxide (5 kJ/kg) [5] is  for each 10−8 unit of
for each 10−8 unit of , an indication that the radiogenic heat exceeds the energy required to sublimate the whole CO content of the comet. More demanding is the energy requirement to heat the cometary body to the melting temperature of ice; in fact the ratio
, an indication that the radiogenic heat exceeds the energy required to sublimate the whole CO content of the comet. More demanding is the energy requirement to heat the cometary body to the melting temperature of ice; in fact the ratio 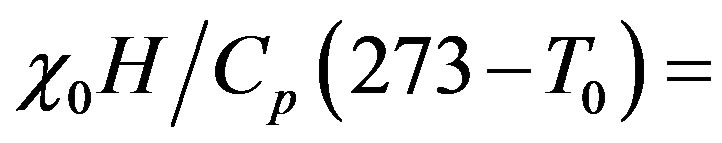
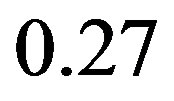 for each 10−8 unit of
for each 10−8 unit of  suggests that at least an initial mass fraction
suggests that at least an initial mass fraction 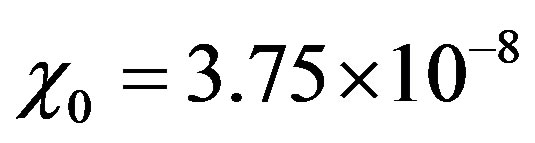 of radionuclide is required to reach the melting temperature of ice, even in the absence of cooling. For large radii and small t, we may neglect the term
of radionuclide is required to reach the melting temperature of ice, even in the absence of cooling. For large radii and small t, we may neglect the term 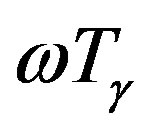 in Equation (10) and obtain, for a body with an initial mass fraction
in Equation (10) and obtain, for a body with an initial mass fraction 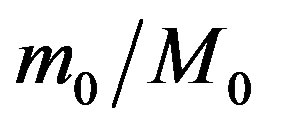 of sublimable material,
of sublimable material,
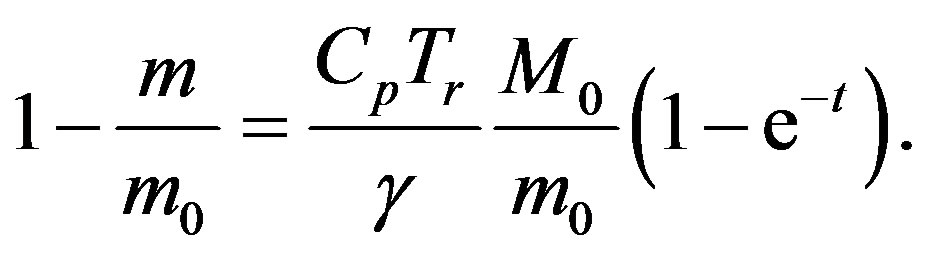 (11)
(11)
Equation (11) affords  to complete CO sublimation for
to complete CO sublimation for  and
and .
.
During the phase transition at constant mass (crystallization), the mass 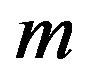 represents amorphous ice and the total mass
represents amorphous ice and the total mass  is a constant. Since the heat of transition
is a constant. Since the heat of transition  is now being released by the crystallization, the r.h.s. of Equation (10) changes its sign. With the value
is now being released by the crystallization, the r.h.s. of Equation (10) changes its sign. With the value  [5] and
[5] and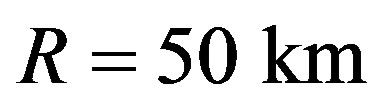 , Equation (11) affords
, Equation (11) affords 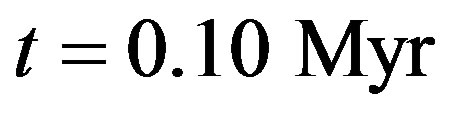 for ice crystallization.
for ice crystallization.
The duration of the various stages are listed in Table 1 for comets of various radii and initial mass fraction of the radionuclide. The values of  are selected to allow the formation of liquid water for the particular value of the initial radius. Lower values would not be sufficient to
are selected to allow the formation of liquid water for the particular value of the initial radius. Lower values would not be sufficient to
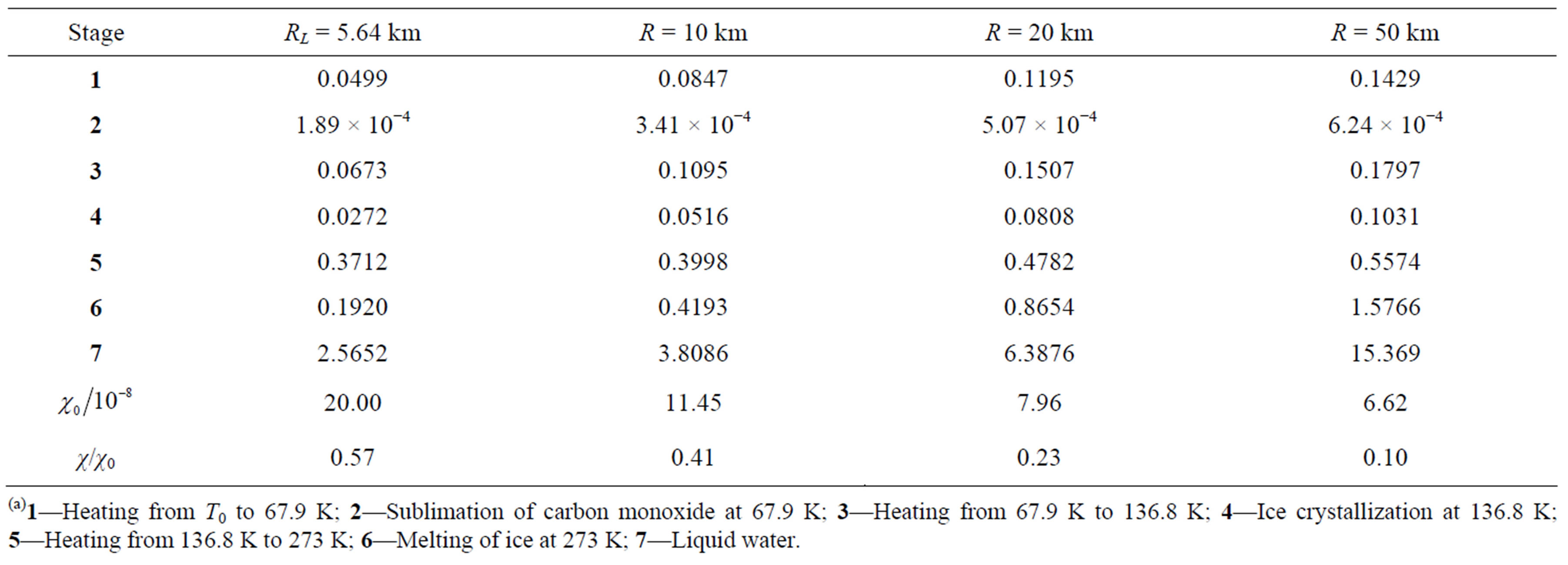
Table 1. Elapsed time (Myr) for the stages of thermal evolution(a) of a comet for various values of the initial radius. The initial mass fraction of the  is reported in units of 10−8 and was selected to allow for the formation of liquid water. The surviving fraction of radionuclide at the beginning of the liquid stage is reported as
is reported in units of 10−8 and was selected to allow for the formation of liquid water. The surviving fraction of radionuclide at the beginning of the liquid stage is reported as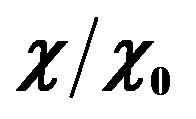 .
.
(a)1—Heating from T0 to 67.9 K; 2—Sublimation of carbon monoxide at 67.9 K; 3—Heating from 67.9 K to 136.8 K; 4—Ice crystallization at 136.8 K; 5—Heating from 136.8 K to 273 K; 6—Melting of ice at 273 K; 7—Liquid water.
supply enough heating and the comet would remain solid, higher values would exceed the boiling point of water at low pressure and disintegrate the comet. In Figure 1 an estimate of the range of the key parameter 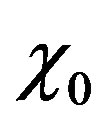 necessary to attain a liquid water core in comets of various radii is given, and the actual value of
necessary to attain a liquid water core in comets of various radii is given, and the actual value of  used in each calculation is the average of the maximum and minimum fraction of radionuclide at a given radius. The limit temperature representing the boiling point of water is of course dependent on the pressure allowed to build inside the body by the tensile strength of the outer layer of kerogen. For simplicity we used the value of one bar and the boiling point 273 K. Below the limit value
used in each calculation is the average of the maximum and minimum fraction of radionuclide at a given radius. The limit temperature representing the boiling point of water is of course dependent on the pressure allowed to build inside the body by the tensile strength of the outer layer of kerogen. For simplicity we used the value of one bar and the boiling point 273 K. Below the limit value 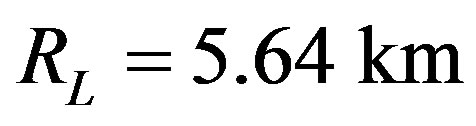 the amount of 26Al that heats the crystalline ice to 273 K is also sufficient to provide the latent heat of fusion and raise the water temperature to the boiling point, disintergrating the comet. The temperature of the body during the liquid stage is shown in Figure 2 for
the amount of 26Al that heats the crystalline ice to 273 K is also sufficient to provide the latent heat of fusion and raise the water temperature to the boiling point, disintergrating the comet. The temperature of the body during the liquid stage is shown in Figure 2 for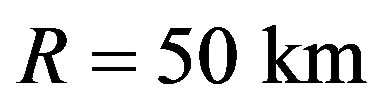 .
.
We now turn our attention to the dynamics of the concentration of amino acids z in the radiation field. In the case where the production of amino acids from a species of concentration a and the destruction of the product are both caused by the energy delivered to the medium by the radioactive decay, the concentration of the organic species follows the equation
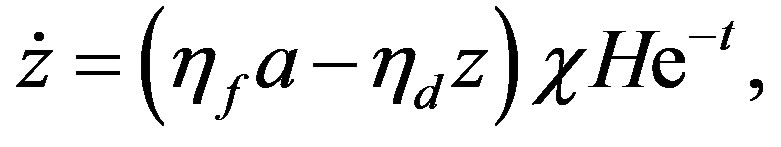 (12)
(12)
and we can only have an increase in the concentration of the product if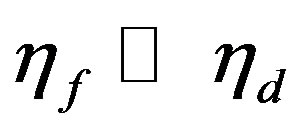 . The experimental study of Mita et al. [7] determined that
. The experimental study of Mita et al. [7] determined that 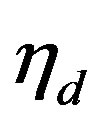 exceeds
exceeds 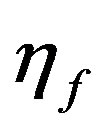 by one order of magnitude and the accumulation of amino acids does not occur. On the other hand, we may also envision the production of amino acids by a thermal reaction, for example the synthesis of Strecker from aldehydes, ammonia and HCN. In this case, the production of amino acids from simple precursors would start as soon as the liquid phase was attained and would be completed in less time compared to the thermal evolution of the cometary body. In fact, using the abundance of formaldehyde (0.37 M) and ammonia (0.41 M) in comets [6] and the rate coefficient for the alkaline hydrolysis of acetonitrile
by one order of magnitude and the accumulation of amino acids does not occur. On the other hand, we may also envision the production of amino acids by a thermal reaction, for example the synthesis of Strecker from aldehydes, ammonia and HCN. In this case, the production of amino acids from simple precursors would start as soon as the liquid phase was attained and would be completed in less time compared to the thermal evolution of the cometary body. In fact, using the abundance of formaldehyde (0.37 M) and ammonia (0.41 M) in comets [6] and the rate coefficient for the alkaline hydrolysis of acetonitrile 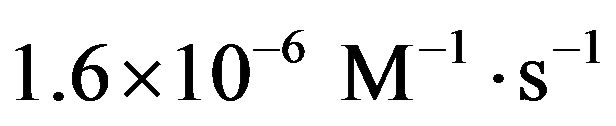 [15], we obtain
[15], we obtain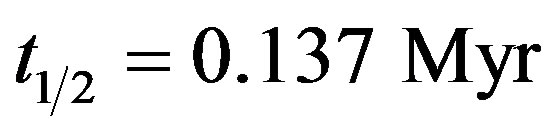 , which makes the formation of the amino acid one order of magnitude faster than the time scale of the liquid stage
, which makes the formation of the amino acid one order of magnitude faster than the time scale of the liquid stage
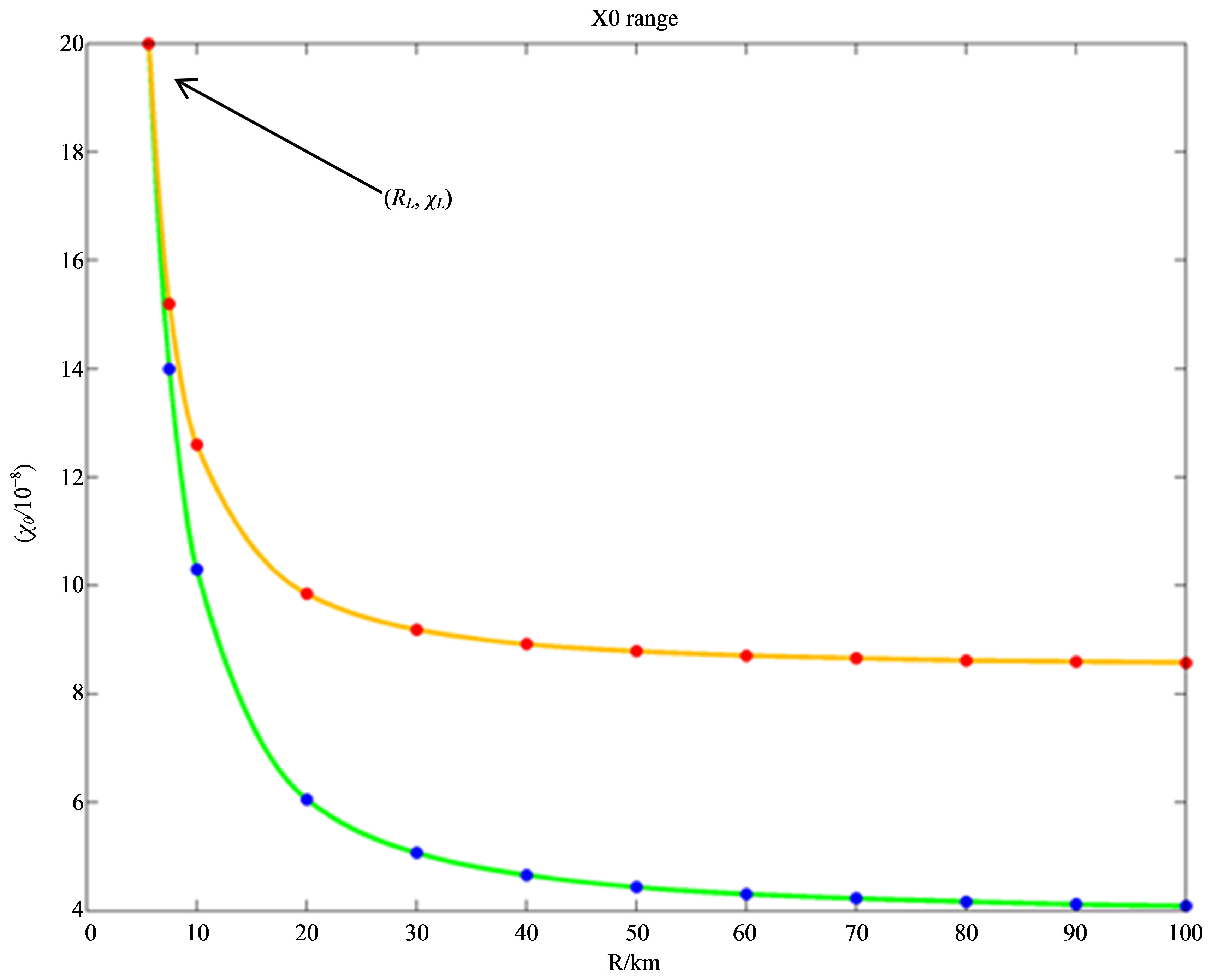
Figure 1. Range of initial mass fraction χ0 of the radionuclide 26Al necessary to attain liquid water in a comet of radius R. Below the green curve the heat delivered by the radioactive decay is not sufficient to melt the crystalline ice, above the orange curve the temperature of water would exceed the boiling point.
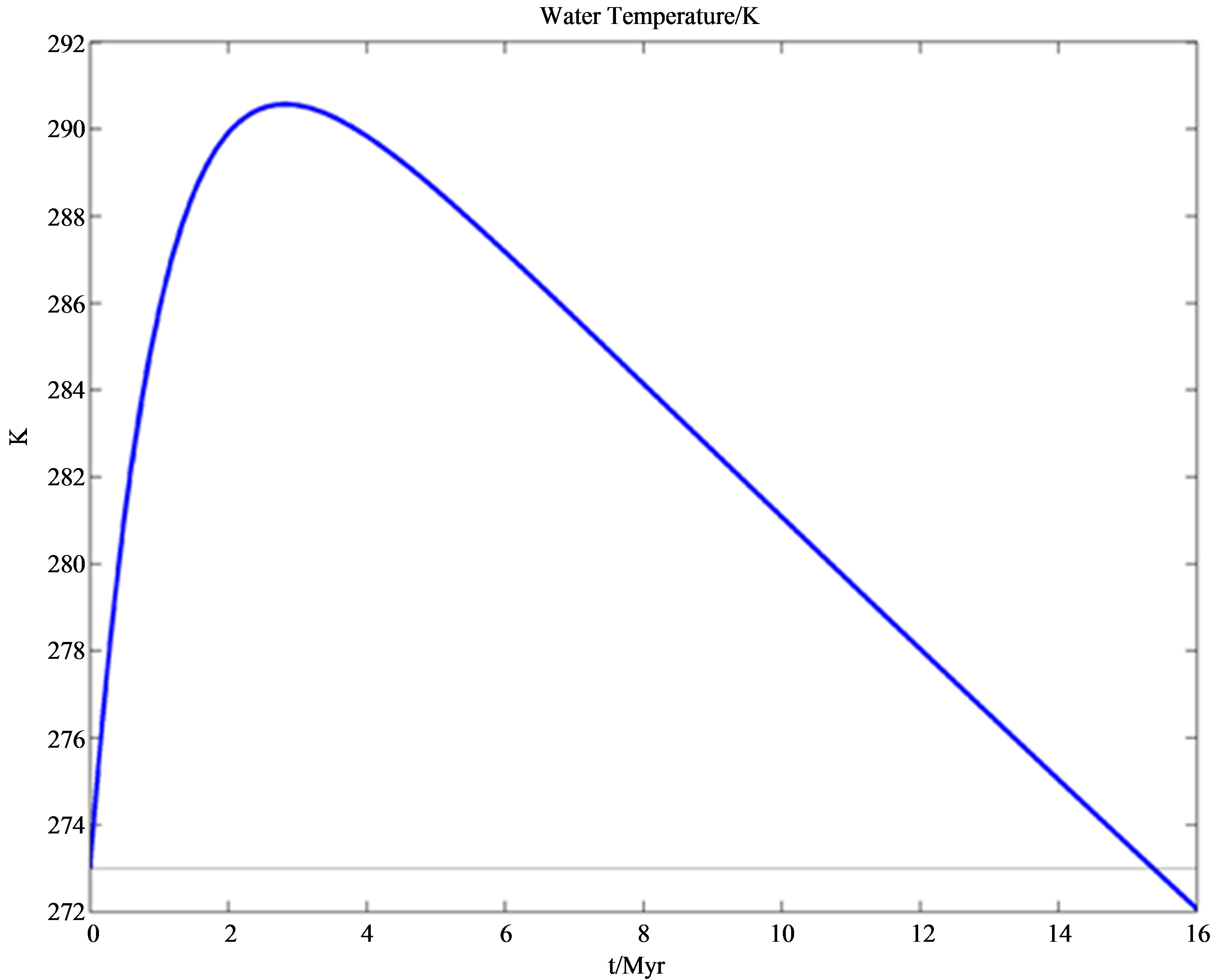
Figure 2. Temperature (K) during the liquid stage of a comet of initial radius 50 km and initial mass fraction of 26Al 6.62 × 10−8.
of comet evolution. The survivability of the organic species in a radiation field mainly constituted by the 1.809 MeV gamma rays given by the decay of 26Al [14] and the 0.511 MeV gamma rays from the positron annihilation following the decay would be governed by the equation
 (13)
(13)
The dose rate  in Equation (13) is delivered by the remaining mass fraction
in Equation (13) is delivered by the remaining mass fraction 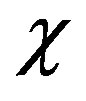 of the radionuclide at the end of the previous stages of comet evolution. From the solution of Equation (13)
of the radionuclide at the end of the previous stages of comet evolution. From the solution of Equation (13)
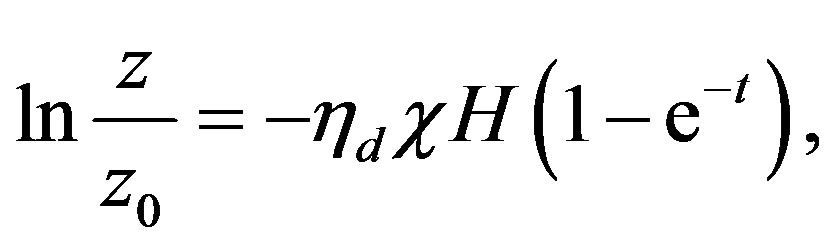 (14)
(14)
we are able to calculate the fraction of the organic compounds surviving irradiation during the time  during which the core of the comet remains liquid, given by solving Equation (8) for
during which the core of the comet remains liquid, given by solving Equation (8) for  with
with . The factor
. The factor 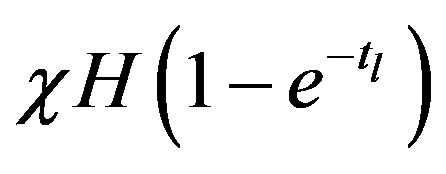 in Equation (14) thus represents the integrated specific dose that the body absorbed in time
in Equation (14) thus represents the integrated specific dose that the body absorbed in time  reported in Figure 3 for the liquid stage of a comet of radius
reported in Figure 3 for the liquid stage of a comet of radius 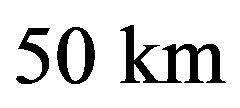 and in Table 2 for all the stages of comet evolution. For example, a cometary body with radius
and in Table 2 for all the stages of comet evolution. For example, a cometary body with radius 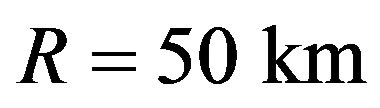 exhibits
exhibits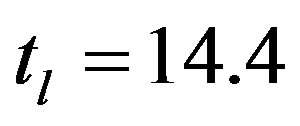 , corresponding to 15.4 Myr. This figure is two orders of magnitude greater than the half-life of the synthesis of glycine from formaldehyde and ammonium cyanide according to Strecker. With the computed time elapsed for the preceding phase transitions
, corresponding to 15.4 Myr. This figure is two orders of magnitude greater than the half-life of the synthesis of glycine from formaldehyde and ammonium cyanide according to Strecker. With the computed time elapsed for the preceding phase transitions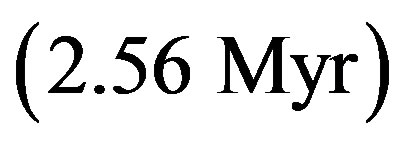 , the residual radionuclide mass fraction is
, the residual radionuclide mass fraction is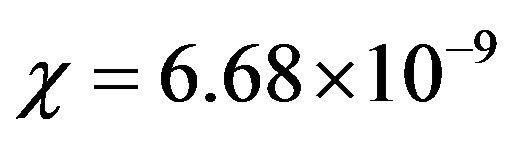 , and
, and  corresponding to
corresponding to 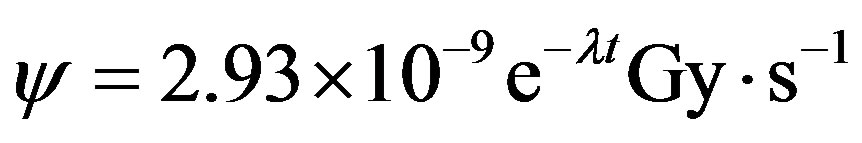 and implying that, as in a thermal process generating the amino acids, the fraction
and implying that, as in a thermal process generating the amino acids, the fraction  of organics surviving the liquid phase is negligible.
of organics surviving the liquid phase is negligible.
Since it was suggested that micrometeorites could have acted as chemical reactors forming amino acids from organic precursors upon contact with water and warm temperatures following re-entry [16] (Maurette et al., 2000), the considerations offered in this study for amino acids should also be extended to amino acid precursors to determine if the precursors themselves are stable with respect to the radiation field. Rimola et al. [17] proposed NH2CH2CN as the possible intermediate of the Strecker synthesis of glycine that could have been delivered to the early Earth.
3. Conclusions
1) The solution of the equation for the time derivative
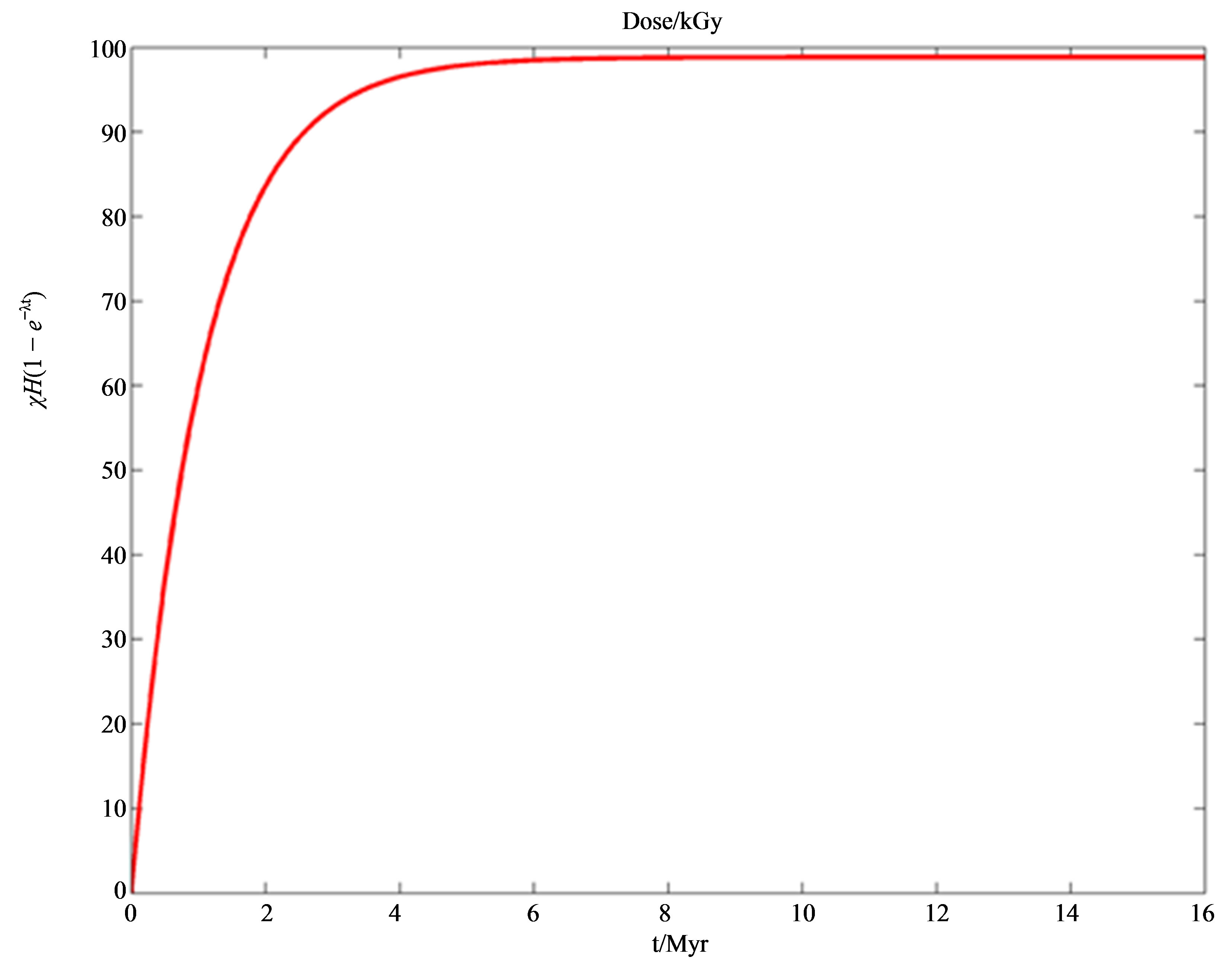
Figure 3. Absorbed dose (kGy) during the liquid stage (15.4 Myr) of a comet of initial radius 50 km and χ0 = 6.62 × 10−8.
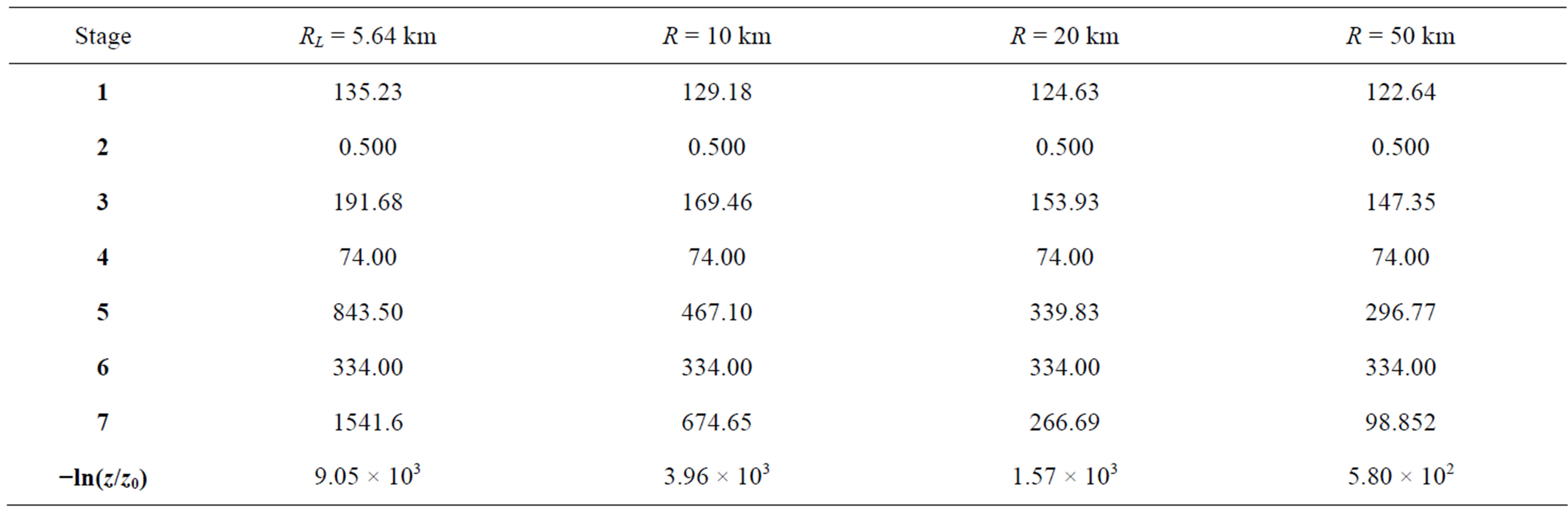
Table 2. Integrated dose (kGy) delivered to a comet by the decay of 26Al during the stages of thermal evolution for various values of the initial radius and mass fraction of the radionuclide 26Al. The last line reports 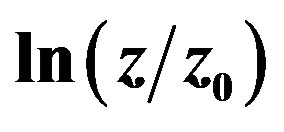 from Equation (14).
from Equation (14).
of the specific energy for a cometary body with a significant initial mass fraction of the radionuclide 26Al allows the calculation of the duration of the various stages of evolution of a non-porous comet, involving heating at constant composition and phase transitions at constant temperature;
2) Radiogenic heating delivered by the decay of 26Al allows for the formation of liquid water only for specific values of the radius and the initial content of radionuclide, under the assumption that an outer layer of kerogen is able to keep the internal pressure above 6 mb;
3) The experimentally determined values of the rate coefficient for the decomposition of amino acids in water solution under irradiation indicate that the amino acid concentration is lowered to virtually zero at a dose of ~1 ;
;
4) The formation of amino acids either by radiolysis of simple organic compounds or by thermal processes exhibits half-lives at least one order of magnitude shorter than the liquid stage of comet thermal evolution;
5) During the stage corresponding to a liquid core of a comet, the absorbed dose range is 100 - 1500 kGy, precluding the survival of previously formed amino acids.
REFERENCES
- J. T. Wickramasinghe, N. C. Wickramasinghe and M. K. Wallis, “Liquid Water and Organics in Comets: Implications for Exobiology,” International Journal of Astrobiology, Vol. 8, No. 4, 2009, pp. 281-290. 0Hdoi:10.1017/S1473550409990127
- T. P. Kohman, “Aluminum-26: A Nuclide for All Seasons,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 219, 1997, pp. 165-176. 1Hdoi:10.1007/BF02038496
- D. Prialnik, A. Bar-Nun and M. Podolak, “Radiogenic Heating of Comets by 26Al and Implications for Their Time of Formation,” Astrophysical Journal, Vol. 319, 1987, pp. 993-1002. 2Hdoi:10.1086/165516
- D. Prialnik and M. Podolak, “Radioactive Heating of Porous Comet Nuclei,” Icarus, Vol. 117, No. 2, 1995, pp. 420-430. 3Hdoi:10.1006/icar.1995.1166
- D. Prialnik and M. Podolak, “Changes in the Structure of Comet Nuclei Due to Radioactive Heating,” Space Science Reviews, Vol. 90, No. 1-2, 1999, pp. 169-178. 4Hdoi:10.1023/A:1005202215579
- J. Llorca, “Organic Matter in Comets and Cometary Dust,” International Microbiology, Vol. 8, No. 1, 2005, pp. 5-12.
- H. Mita, N. Shirakura, H. Yokoyama, S. Nomoto and A. Shimoyama, “Kinetic Study of Abiotic Amino Acid Formation by UV-Irradiation,” Advances in Space Research, Vol. 33, No. 8, 2004, pp. 1282-1288. 5Hdoi:10.1016/j.asr.2003.08.035
- M. Trojanowicz, A. Bojanowska-Czajka, G. Kciuk, K. Bobrowski, M. Gumiela, A. Koc, G. Nałęcz-Jawecki, M. Torun and D. S. Ozbay, “Application of Ionizing Radiation in Decomposition of Selected Organic Pollutants in Waters,” European Water, Vol. 39, 2012, pp. 15-26.
- G. Matrajt, S. Pizzarello, S. Taylor and D. Brownlee, “Concentration and Variability of the AIB Amino Acid in Polar Micrometeorites: Implications for the Exogenous Delivery of Amino Acids to the Primitive Earth,” Meteoritics & Planetary Science, Vol. 39, No. 11, 2004, pp. 1849- 1858. 6Hdoi:10.1111/j.1945-5100.2004.tb00080.x
- M. Maurette, “Micrometeorites and the Mysteries of Our Origin,” Springer, Berlin Heidelberg, Berlin, 2006, p. 126. 7Hdoi:10.1007/3-540-34335-0
- A. G. Yeghikyan, “Theoretical Investigation of Cosmic Ray Processing of Solar System Ices,” Astrophysics and Space Sciences Transactions, Vol. 4, No. 2, 2008, pp. 47- 50. 8Hdoi:10.5194/astra-4-47-2008
- F. Cataldo, G. Angelini, S. Iglesias-Groth and A. Manchado, “Solid State Radiolysis of Amino Acids in an Astrochemical Perspective,” Radiation Physics and Chemistry, Vol. 80, No. 1, 2011, pp. 57-65. 9Hdoi:10.1016/j.radphyschem.2010.08.012
- P. A. Gerakines, R. L. Hudson, M. H. Moore and J.-L. Bell, “In Situ Measurements of the Radiation Stability of Amino Acids at 15 - 140 K,” Icarus, Vol. 220, No. 2, 2012, pp. 647-659. 10Hdoi:10.1016/j.icarus.2012.06.001
- R. Merk and D. Prialnik, “Early Thermal and Structural Evolution of Small Bodies in the Transneptunian Zone,” Earth, Moon Planets, Vol. 92, No. 1, 2003, pp. 359-374. 11Hdoi:10.1023/B:MOON.0000031952.89891.a4
- T. Ghaffar and A. W. Parkins, “The Catalytic Hydration of Nitriles to Amides Using a Homogeneous Platinum Phosphinito Catalyst,” Journal of Molecular Catalysis A: Chemical, Vol. 160, No. 2, 2000, pp. 249-261. 12Hdoi:10.1016/S1381-1169(00)00253-3
- M. Maurette, J. Duprat, C. Engranda, M. Gounellea, G. Kuratc, G. Matrajta and A. Toppanid, “Accretion of Neon, Organics, CO2, Nitrogen and Water from Large Interplanetary Dust Particles on the Early Earth,” Planetaryand Space Science, Vol. 48, No. 11, 2000, pp. 1117-1137. 13Hdoi:10.1016/S0032-0633(00)00086-6
- A. Rimola, M. Sodupe and P. Ugliengo, “Deep-Space Glycine Formation via Strecker-Type Reactions Activated by Ice Water Dust Mantles. A Computational Approach,” Physical Chemistry Chemical Physics, Vol. 12, No. 20, 2010, pp. 5285-5294. 14Hdoi:10.1039/b923439j

