Advances in Chemical Engineering and Science
Vol.3 No.4(2013), Article ID:38605,8 pages DOI:10.4236/aces.2013.34036
Process Optimization of Effective Partition Constant in Progressive Freeze Concentration of Wastewater
Chemical Engineering Department, Faculty of Chemical Engineering, Universiti Teknologi Malaysia, Skudai, Malaysia
Email: *mazura@cheme.utm.my
Copyright © 2013 Mazura Jusoh et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 29, 2013; revised September 30, 2013; accepted October 8, 2013
Keywords: Effective Partition Constant; Wastewater Treatment; Progressive Freeze Concentration
ABSTRACT
Response surface methodology (RSM) was employed to optimize the process parameters for effective partition constant (K) in progressive freeze concentration (PFC) of wastewater. The effects of coolant temperature, circulation flowrate, initial solution concentration and circulation time on the effective partition constant were observed. Results show that the data were adequately fitted into a second-order polynomial model. The linear and quadratic of independent variables, coolant temperature, circulation flowrate, initial solution concentration and circulation time as well as their interactions have significant effects on the effective partition constant. It was predicted that the optimum process parameters within the experimental ranges for the best K would be with coolant temperature of −8.8˚C, circulation flowrate of 1051.1 ml/min, initial solution concentration of 6.59 mg/ml and circulation time of 13.9 minutes. Under these conditions, the effective partition constant is predicted to be 0.17.
1. Introduction
Water is often ranked by its quality. However, there are many different quantifications of water quality, and the quality of water often depends upon its use. Wastewater is any water that has been adversely affected in quality by anthropogenic influence. It comprises liquid waste discharged by domestic residences, commercial properties, industry, and/or agriculture and can encompass a wide range of potential contaminants and concentrations. Meanwhile, water treatment can be defined as the manipulation of the water from various sources to achieve a water quality that meets specified goals or standards set by the community through its regulatory agencies.
Most wastewater is treated in industrial-scale wastewater treatment plants which may include physical, chemical and biological treatment processes. There are numerous processes that can be used to clean up waste waters depending on the type and amount of contamination. Evaporation is a process commonly used to treat and concentrate wastewater, where the vapour from a boiling liquid solution is removed and a more concentrated solution remains [1]. However one of the major drawbacks of evaporation in wastewater treatment is when the wastewater contains volatile organic compounds (VOCs), therefore evaporation is absolutely not an operation that should be appointed in treating it. Another dewatering method is reverse osmosis which can produce almost pure water and use the least amount of energy because it involves no phase change [2]. The membrane however can by far be clogged by the content of the wastewater resulting in high osmotic pressure difference across the membrane interface [3], which affects the cost highly when the membrane has to be changed [4].
Hazardous industrial waste disposed by incineration and other high temperature waste treatment systems, are described as the thermal treatment process. In order to avoid the usage of huge power to destroy the hazardous compound, freeze concentration was introduced to lessen energy requirement. Freeze concentration is the process where the water component in a solution is frozen and crystallized as ice so that a more concentrated solution will be left behind in a smaller volume. Advantages of freeze wastewater treatment are 1) less energy is needed to incinerate the resulted concentrated wastewater 2) wastewater including toxic compounds [5] or heavy metals [6] can be treated which is difficult to treat biologically, and 3) a smaller facility is required compared to biological wastewater treatment [7]. There are two methods available for freeze concentration, conventional suspension freeze concentration (SFC) and progressive freeze concentration (PFC). SFC involves production of small ice crystal in suspension of the mother liquor, while PFC forms ice crystals as a block on the cooled surface. The ice seeds are usually produced by a scraped surface heat exchanger (SSHE), and then transferred to a recrystallizer to start ice crystal ripening [8]. The resulting ice slurry requires a filtration and washing process in order to obtain highly pure water in the end, and this adds to the capital and operation cost of the system. PFC on the other hand only requires draining out the concentrate from the crystallizer in order to separate the liquid and solid phase, thus giving lower financial implication.
The efficiency of PFC system can be affected by many factors including coolant temperature, circulation flowrate, initial solution concentration and circulation time. In most of the previous studies, the process conditions have been merely optimized by conducting one factor-at-atime experiments. The results of one-factor-at-a-time experiments do not reflect actual changes in the environment as they ignore interactions between factors that are present simultaneously. Therefore, these factors may be collectively studied to validate the optimal extraction conditions. The response surface methodology (RSM) has been demonstrated to be a powerful tool for determining the effects of the factors and their interactions, which allow process optimization to be conducted effectively [9]. This method is the preferred experimental design for fitting polynomial model to analyze the response surface of multi-factor combinations. RSM is a faster and more economical method ingathering research results than the classic one-variable-at-a-time or full-factors experimentation.
In this work, the optimization of process parameters was carried out by conducting experiments according to statistical design of experiments (DOE) and RSM. In DOE, all factors are varied simultaneously within the experimental runs, which is a structured and systematic method in determining the relationship between factors that affect the responses [10]. RSM was applied to optimize coolant temperature, circulation flowrate, initial solution concentration and circulation time to give the best effective partition constant in a PFC system.
2. Materials and Method
2.1. Materials
Glucose particles with purity of 99% were used in this study, mixed with distilled water to represent real wastewater. Analytical grade of ethylene glycol solution of 50% (v/v) with water was used as coolant in the refrigerated waterbath.
2.2. Experimental Method
A schematic diagram of the experimental apparatus is given in Figure 1 and the apparatus is called coil crystallizer. Glucose solution was first prepared which depends on concentration to be studied. The glucose solution was prepared in two parts, one to be pre-cooled close to the freezing point of water, where the temperature was set to be 2˚C. Another part was frozen to its solid form. The waterbath requires an amount of 25 liters of coolant to fill to the top of the coolant space. Ethylene glycol for the refrigerated waterbath coolant was mixed with water to achieve 50% v/v. The refrigerated waterbath takes less than 2 hours to achieve the desired temperature between −4˚C to −10˚C. Both glucose solutions (cooled liquid and solid form) were mixed in the feed tank, which is immersed in ice cubes. The glucose solution was then pumped by a peristaltic pump.
When the crystalliser and the whole piping were filled with glucose solution, the feed tank was removed and the solution was circulated for a designated period of time. After the designated time has been achieved, the circulation was discontinued and the coil crystallizer was drained to take the glucose concentrate out. The flanges were unconnected and the whole volume of the concentrated solution was collected. The ice layer thickness at each flange point was quantified and a sample of the ice layer produced was collected. The volume of the thawed ice and the concentrates is measured to assist calculation of K.
2.3. Experimental Design
For experimental design of the PFC, coolant temperature, circulation flowrate, initial concentration and circulation time were chosen as the parameters that will most likely influence the efficiency of the system. The low, middle and high levels for all the independent variables were from the limitations of the apparatus used and also based
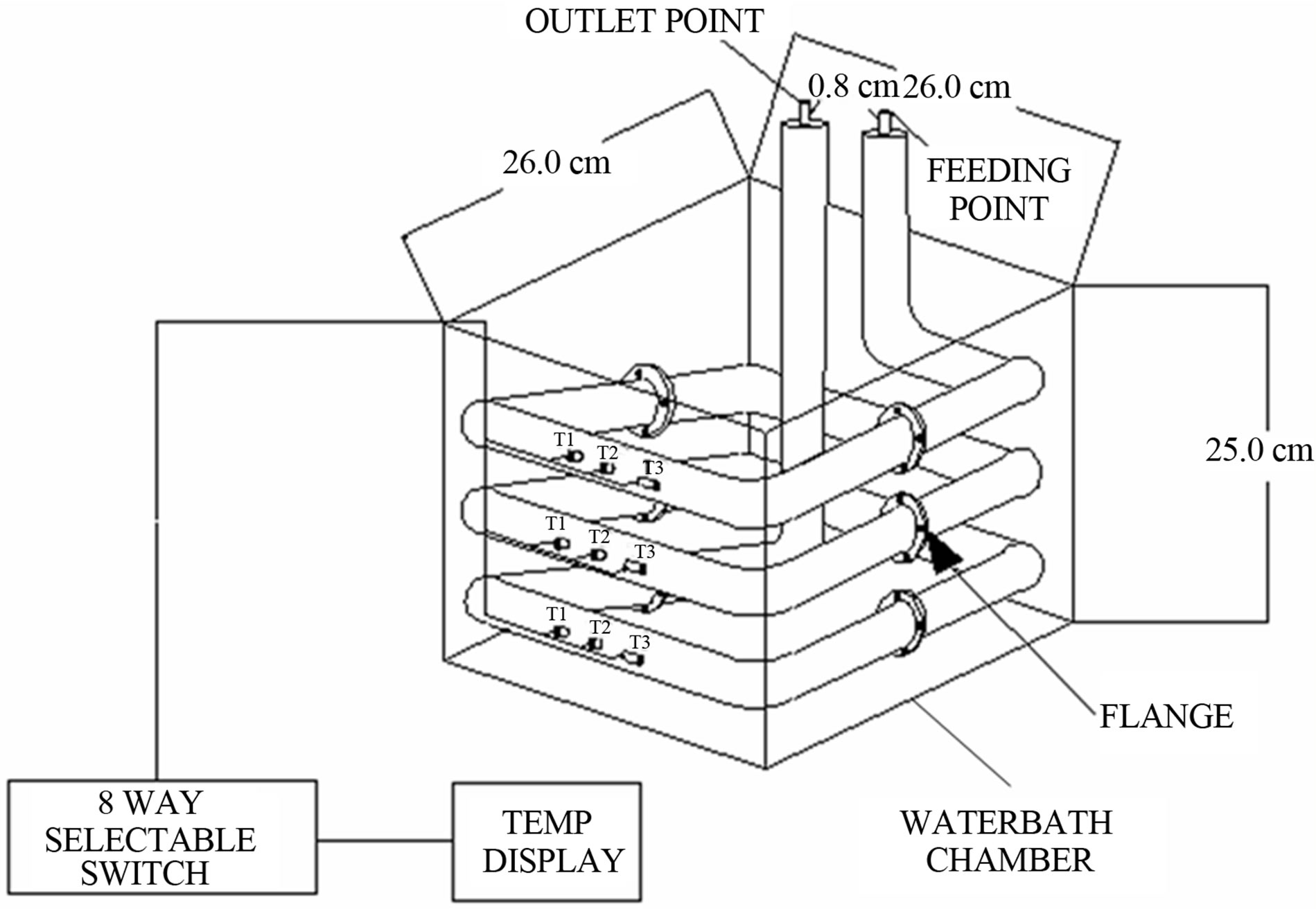
Figure 1. The structure of the helical coil crystallizer.
on prior screening of the literatures, as listed in Table 1. It was found that a total of 27 runs are necessary to optimize the PFC system designed. The runs were performed in duplicate.
The substitution of the chosen parameters into the resulting model enabled a calculation of a predicted response as shown in Equation (1).
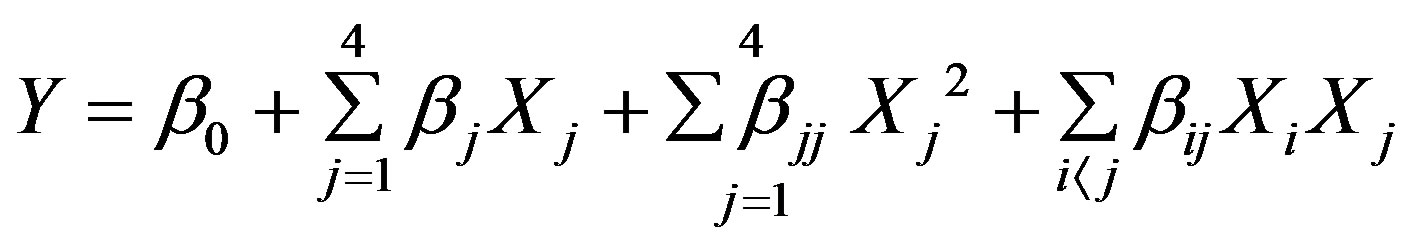 (1)
(1)
where Y is the predicted response value, β is the regression coefficient, a weighting factor which is a number calculated by the statistical program to fit the experimental data, X is an experimental factor influencing the process.
3. Results and Discussions
3.1. Model Adequacy
Figure 2 illustrates an example of the ice formed from the PFC process. The results of response K for each run are tabulated in Table 2. The response, K, was correlated with the four variables studied by using multiple regression analysis, employing a second order polynomial as presented by Equation (1). Regression analysis was carried out using STATISTICA software, which was later also utilized to determine the significance of each factor
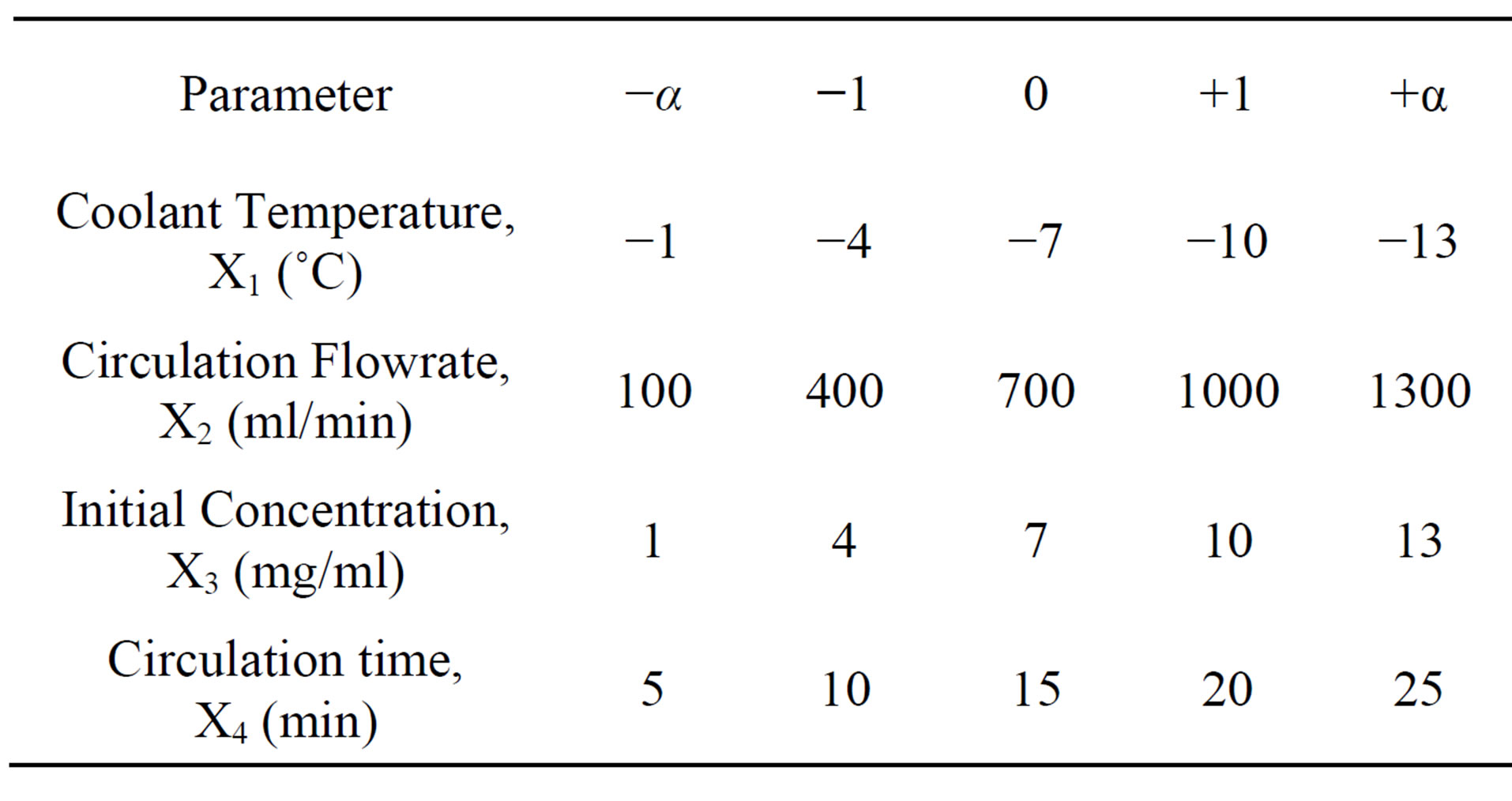
Table 1. Range of process parameters for the PFC process.

Figure 2. Example of ice crystal formed in coil crystallizer.
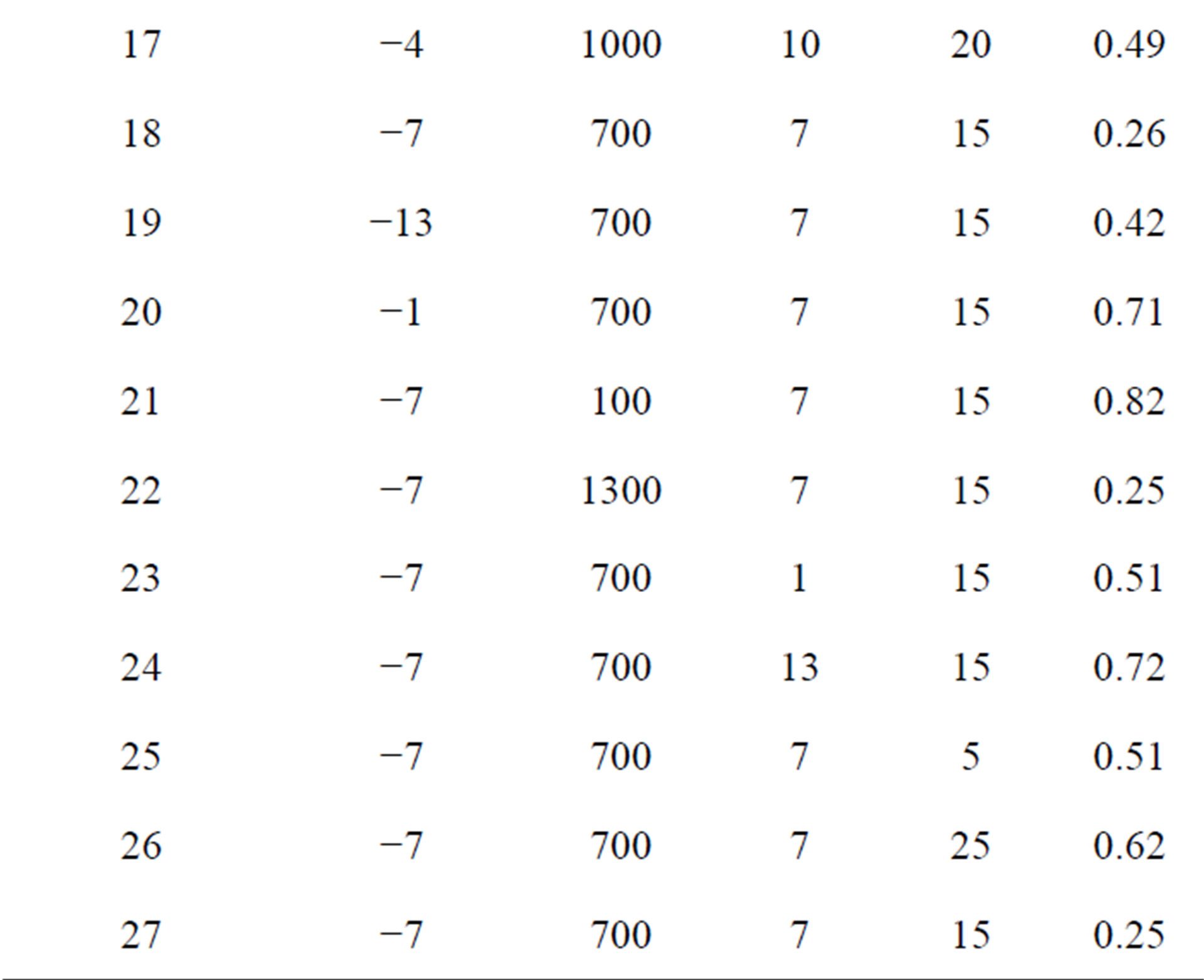
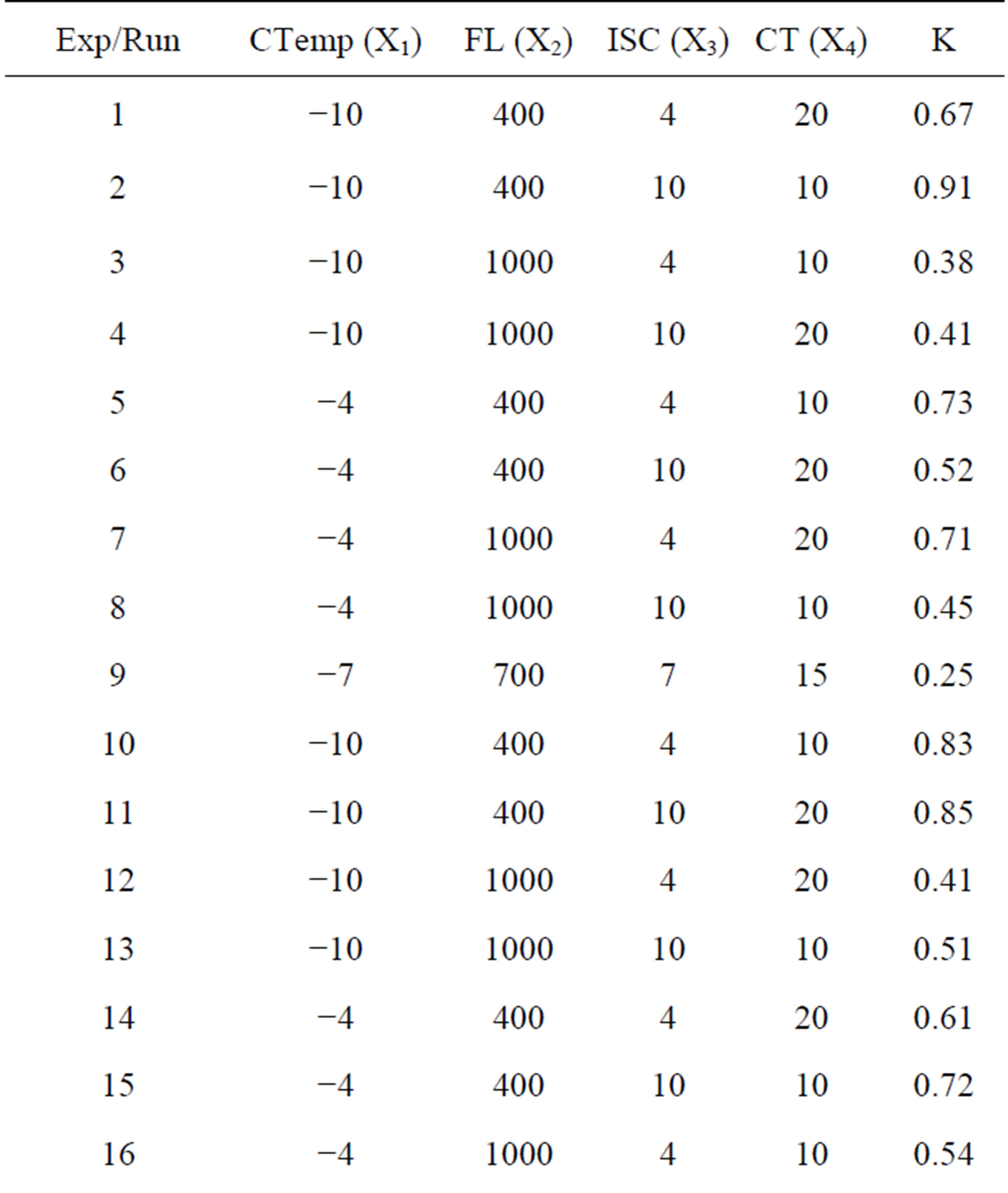
Table 2. DOE and the response.
investigated. A regression equation for K as a function of CTemp (X1), FL (X2), ISC (X3) and CT (X4) and their interaction using linear and quadratic regression coefficient of main factors and linear-by-linear regression coefficients of interaction was derived, as presented in Equation (2):

(2)
where Y1 is the predicted effective partition constant, K. The coefficients with one factor represent the effect of the particular factor, while the coefficients with two factors signify interaction between the two terms. Coefficients with second order terms denote the quadratic effect of the factor. The positive and negative signs in front of each coded variables indicate parallel and adverse effect of the factors to the responses respectively. The models were selected based on the highest order of polynomials where the models were significant and not aliased [11].
Having generated the regression model equation to represent the effect of each variable including their interactions with each other on the value of K, an analysis to evaluate the adequacy of the model should and has been carried out using the same software. The first criteria evaluated to see the model adequacy is by judging the appropriateness of the model from the determination coefficient, the R-squared value, which reveals the total variation of the observed values of activity about its mean [12-16].
R-squared for the regression model relating all four effects to K is 0.901, which is considered as very good in describing the validity of the model generated. According to the R-squared value, 90.1% of the sample variation could be attributed to the variable and only 9.9% of the total variance could not be explained by the model. Using the regression model generated, a predicted value for the response in each run of the experimental design was obtained, as listed in Table 3, demonstrated by graphs shown in Figures 3(a) and (b).
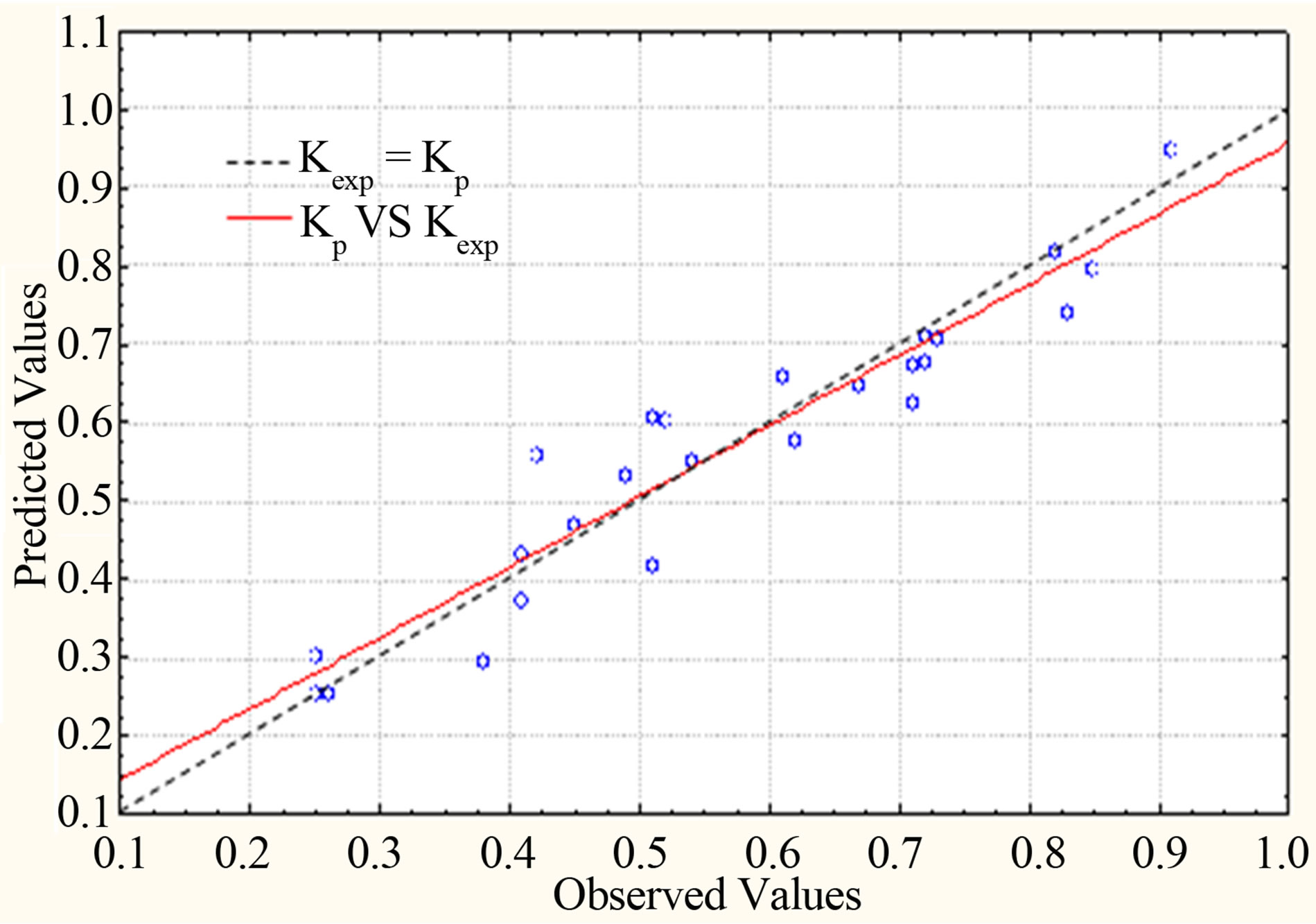
Figure 3(a) shows the variation of the experimental data against the predicted value and Figure 3(b) relates the predicted values to the residuals. The residuals indicate the difference between the predicted to the observed/experimental value. From Figure 3(a), it could clearly be observed that the linear line plotted out of points calculated according to the regression model deviates very slightly from the line of Kexp = Kp, where Kexp and Kp are K from experimental data and predicted K, respectively, showing appropriateness of the model generated. The predicted values calculated from the regression model also in majority falls very near to the line plotted as expected from the reasonably good value of R-squared. Figure 3(b) relating the residuals and the predicted value shows a random plot, which means homogenous error variances across the observed values [17]. The plot also shows no patterns or trend between the positive and negative values, indicating a good distribution of errors. The residual values fall between −0.15 and 0.15, with 17 out of 27 values between −0.05 and 0.05, which is approximately 63% of the total points, showing closeness of predicted and observed values [18].
The adequacy of the generated regression model was
 (a)
(a)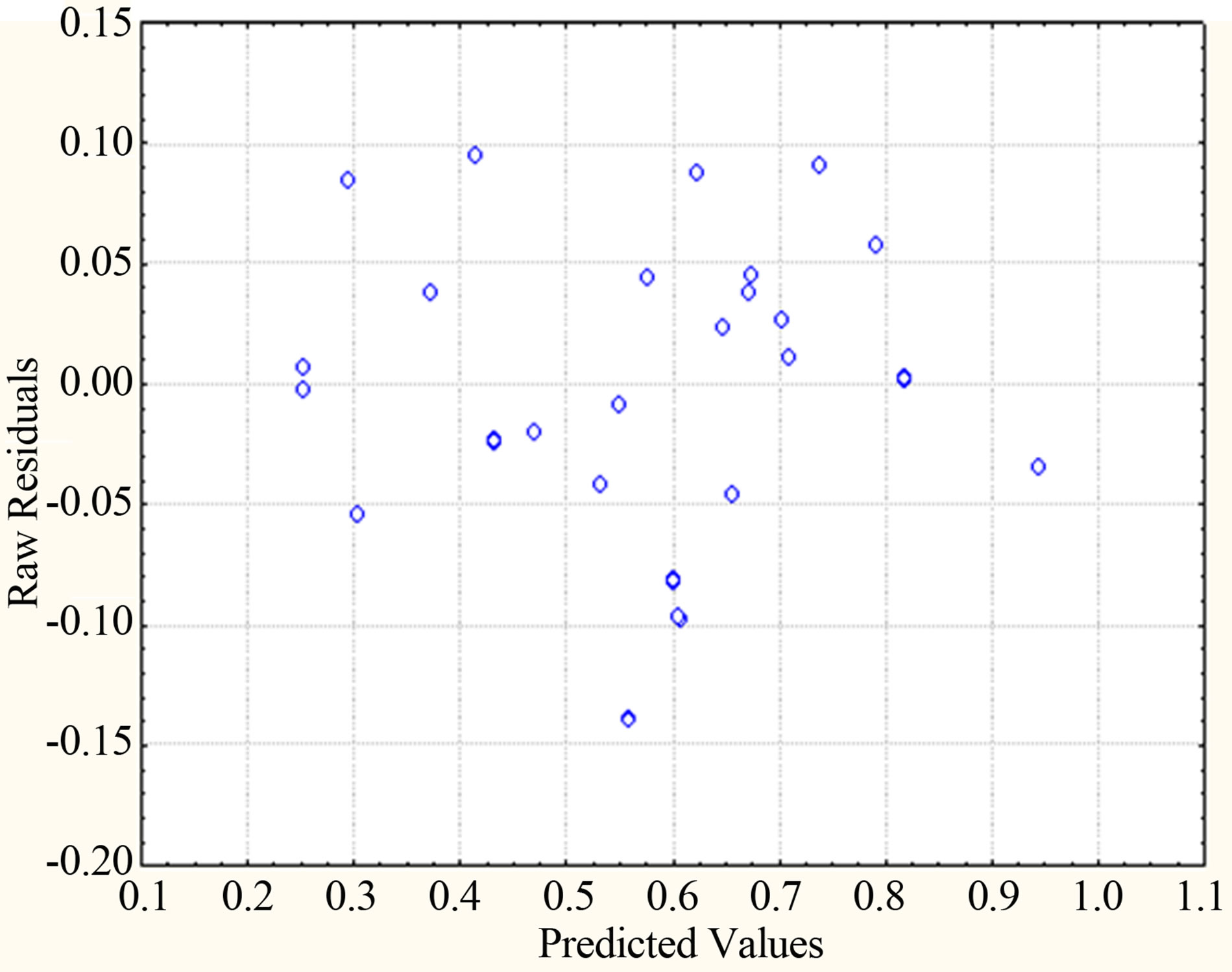 (b)
(b)
Figure 3. (a) Predicted versus observed (experimental) of the response; (b) Residual plot of the quadratic model for the response.
also evaluated using ANOVA method, which is very useful to determine significant effects of process variables to the response and to fit the second order polynomial models to the experimental data [19]. Table 4 shows the outcome of such an analysis. In order to evaluate the adequacy or accuracy of the model using ANOVA, the important value to be observed is the Fvalue, which is the ratio of mean square due to regression to the mean square due to residual error. In general the F-value calculated from ANOVA should be several times greater to the tabulated value for the model to be considered appropriate. F-value calculated for the K model is 10.59, which has already exceeded the tabulated F-value for 95% confidence (F0.05,14,12) (2.64) at more than 4 times.
Once the validity and adequacy of the regression model has been assessed, it is very useful to identify the variables that would affect the process significantly. The results presented in Table 5 show the sorted multiple
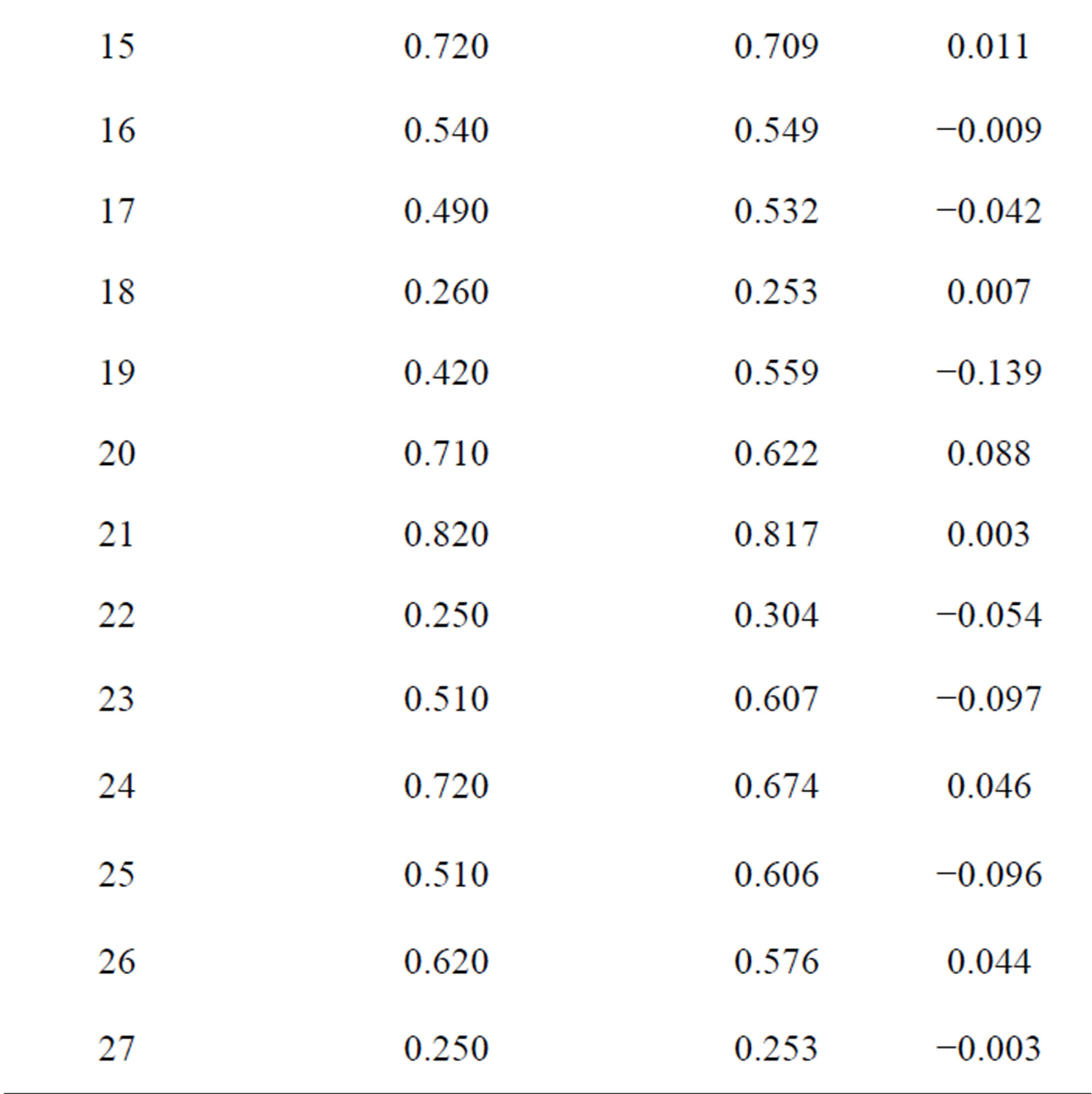
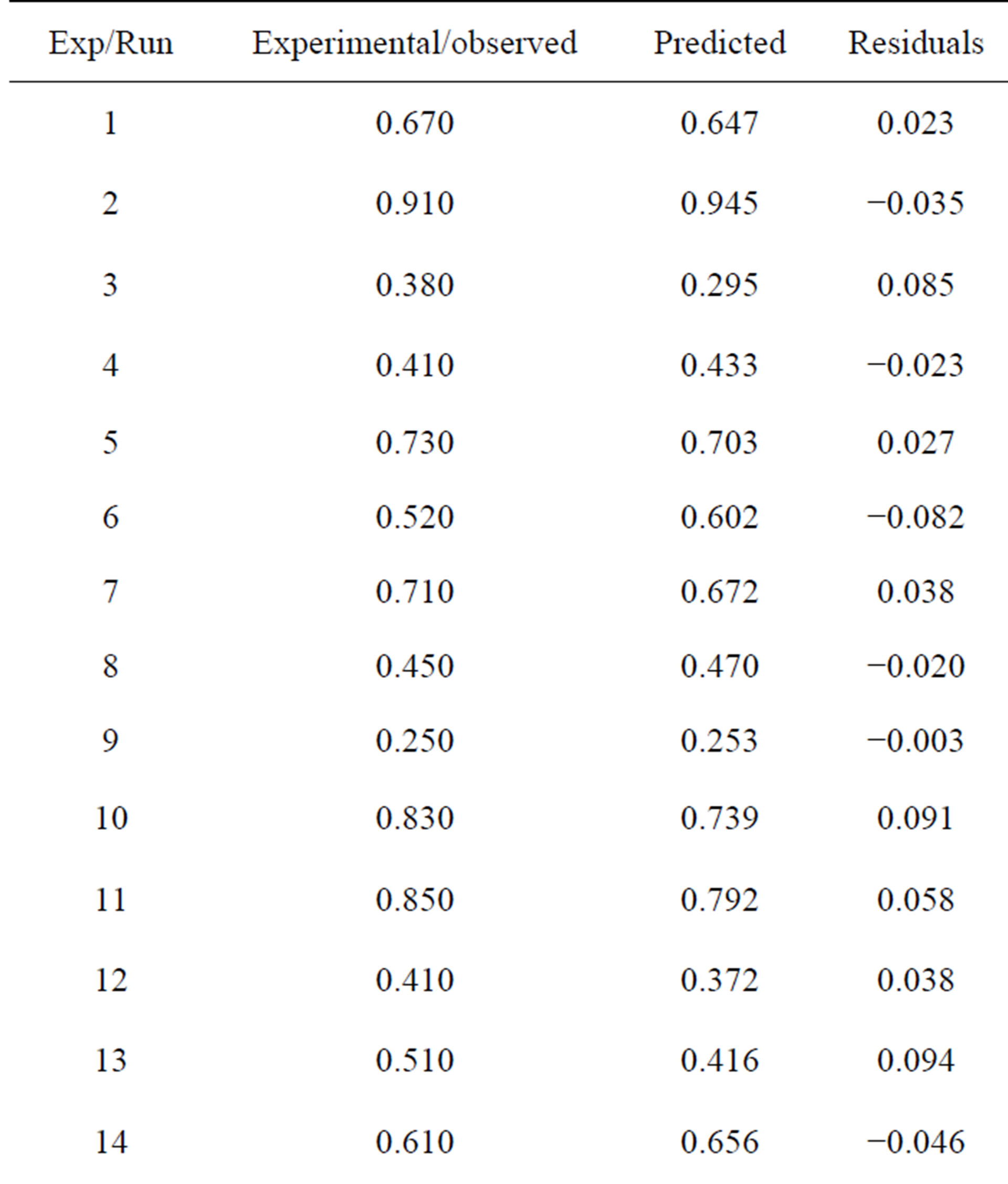
Table 3. Experimental and predicted K for each run.
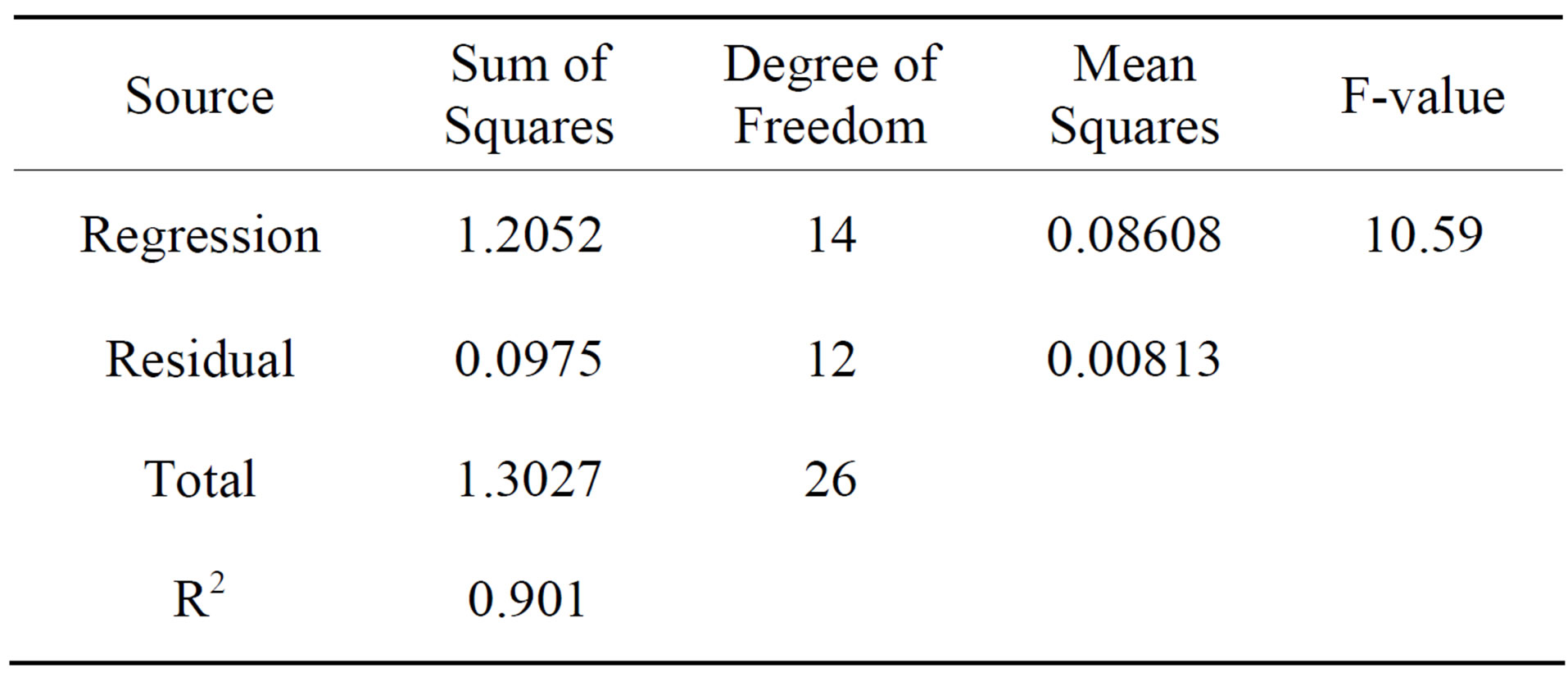
Table 4. ANOVA results for the model relating K to the operating parameters.
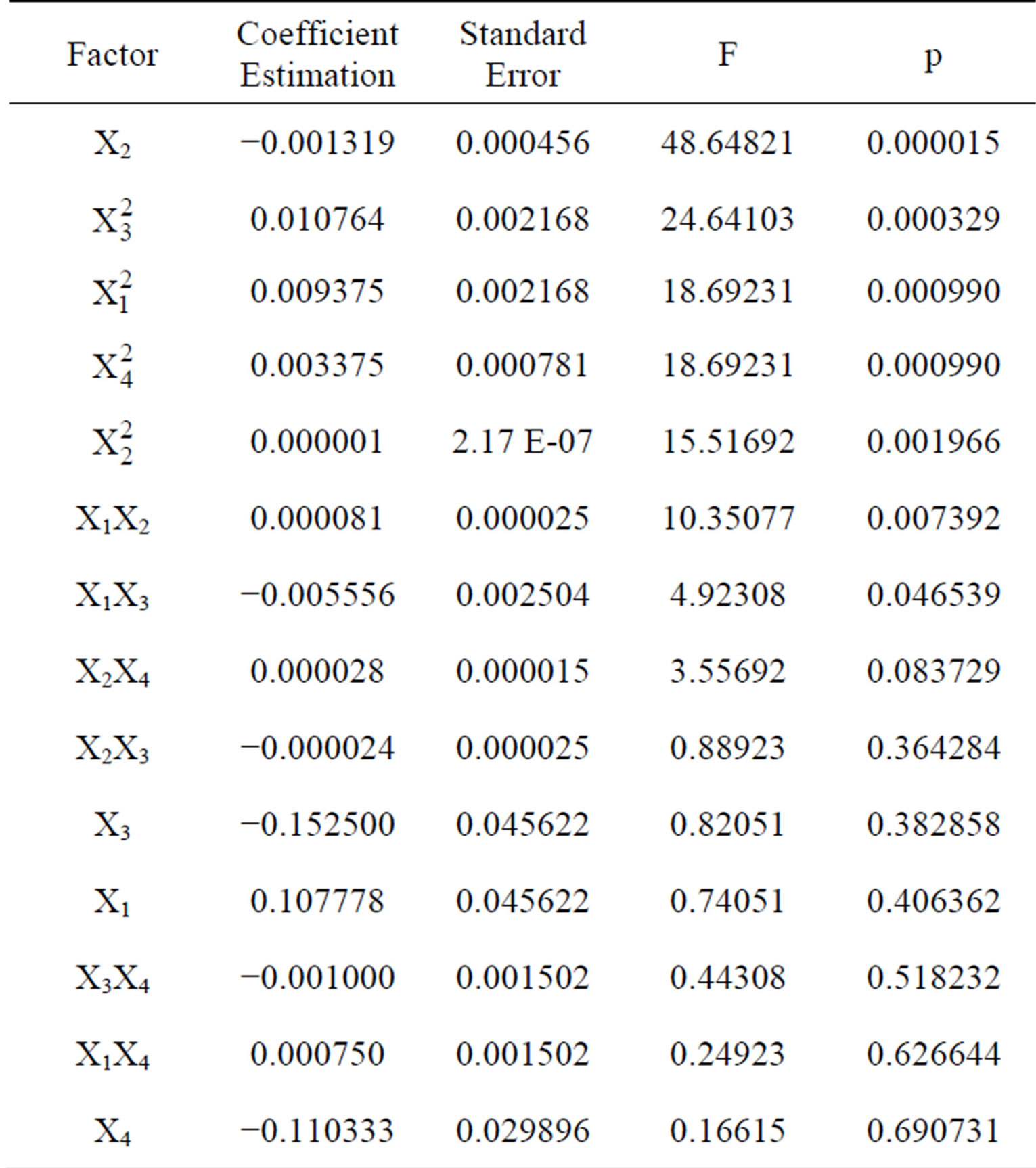
Table 5. Regression analysis for K.
regression results, which later would be used to evaluate the significance of each factor in the model. Factor with the lowest p-value and the highest F-value is considered the most significant, with all other factors listed in descending order of significance. It is evident that the linear term of X2 (FL) has the most effect on K with p-value of 0.00015 at F-value 48.65. Other factors rated as signifycant are quadratic of ISC, quadratic of CTemp, quadratic of CT and quadratic of FL. This is followed by two other factors in descending order of significance, which are the interaction effect of CTemp and FL, followed by interaction term of CTemp and ISC. The limiting value for p is 0.05, which is based on the confidence level fixed for the ANOVA analysis carried out; hence all factors with pvalue lower than 5% are judged significant. Other factors not mentioned are all rated as insignificant to affect the value of K in the process.
In Figure 4, the bars exceeded to the right of the line p = 0.05 indicates significant factors with the linear term of FL and interaction between CTemp and ISC rated as the most and least significant respectively. All other factors, as previously determined, rated as insignificant.
3.2. Response Surface Contour Plots Analysis
Contour plots of the response towards variation of two factors at a time could be obtained to see their effect and interaction on the response at the middle point of the other two variables. The effects of any two independent variables on the response could be observed by plotting a 3D surface plot of the response against the two independent variables, as the third and fourth variables are kept at the centre of their range as demonstrated in Figures 5(a)-(f).
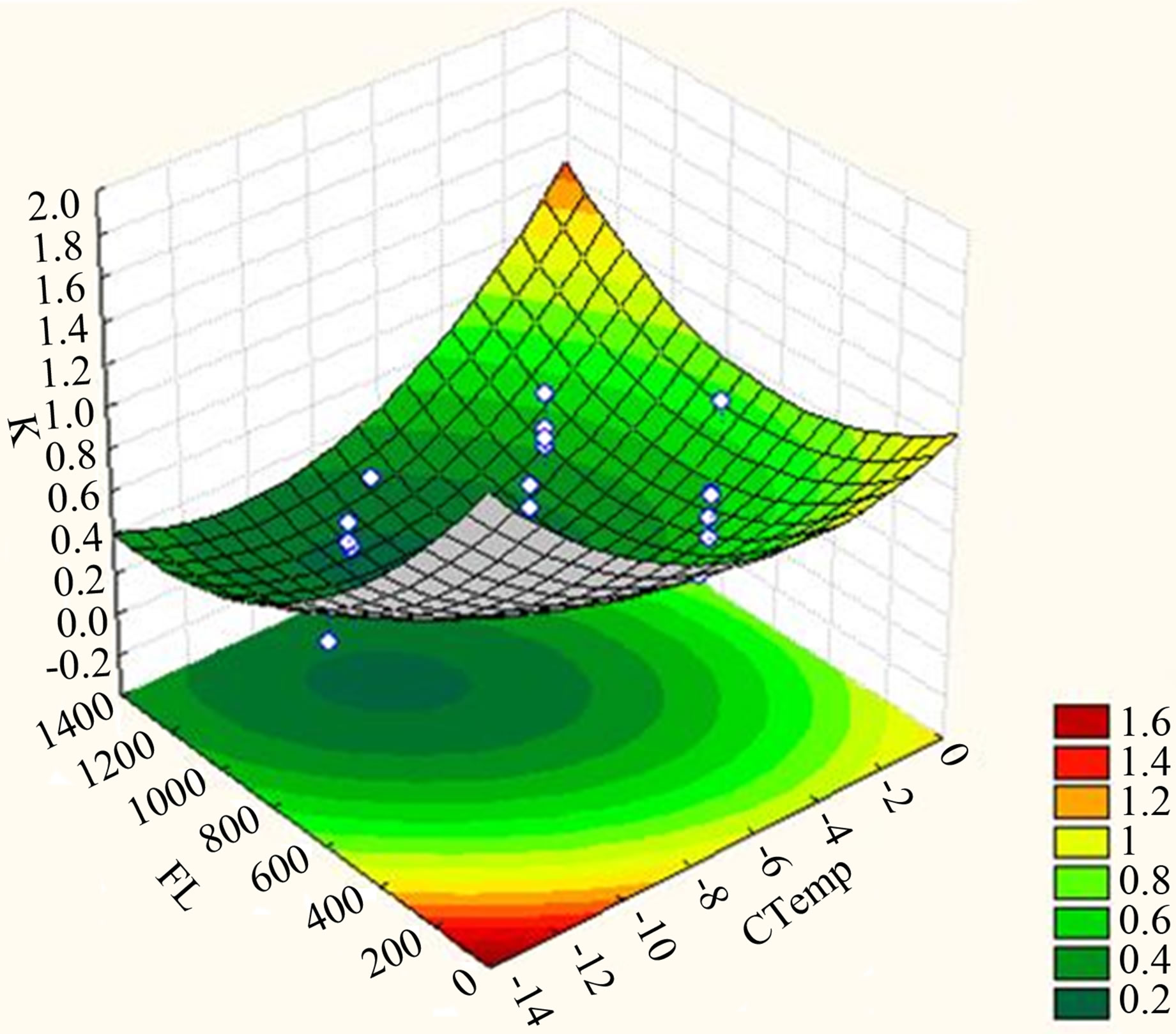
The contour plots presented in Figure 5(a) for value of K as a function of CTemp and FL with ISC and CT kept at 7 mg/ml and 15 min respectively, indicates that K decreases as the CTemp is brought down and FL increases. The elliptical contour obtained portrays a perfect interaction between the independent variables [20].
The decreasing trend of K is observed to change when CTemp achieved a certain value, too low that would cause ice growth rate to be too high, causing higher solute inclusion into the ice, consequently causing K to be higher. The CTemp for this phenomenon could clearly be observed in a 2D contour plot. In order to observe the interaction of CTemp and ISC and their effects on the response, a surface plot of K against CTemp and ISC was plotted while FL (X2) and CT (X3) was kept at 700 ml/min and 15 minutes respectively, as presented in Figure 5(b). It could be seen that K also decreases when ISC is increased, up to a concentration where the solute inclusion in the solid phase is influenced by the increaseing solute concentration, where K started to increase. The range of CTemp giving the lowest K possible is −5.0 to −9.8˚C while for ISC, the range is found to be 4.5 to 8.8 mg/ml as observed in 2D contour plot for the effect of
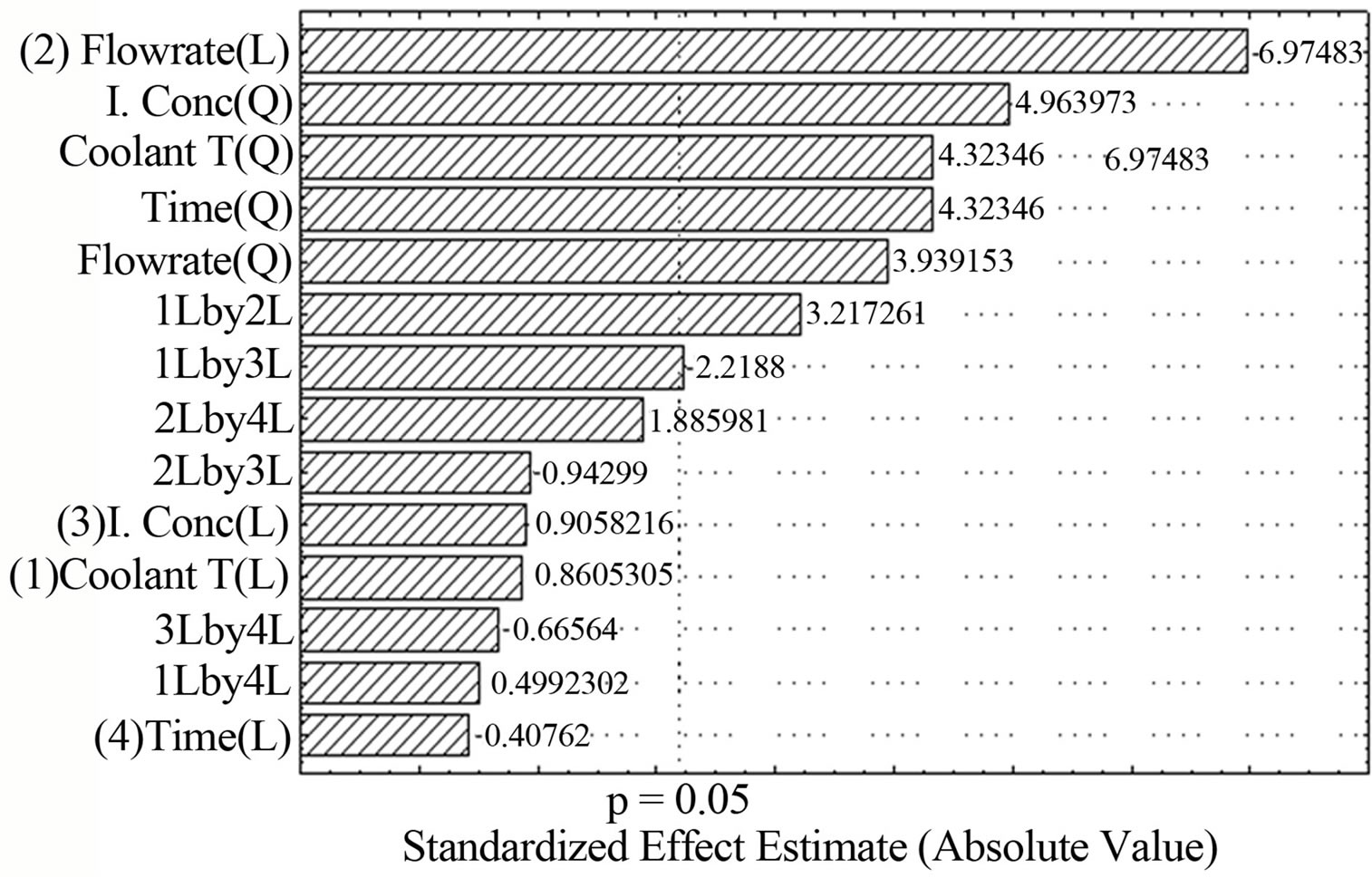
Figure 4. Pareto chart of effects of variable on K.
these two operating conditions on K. The effects and interactions of CTemp and CT were also investigated via a surface plot, presented in Figure 5(c). As CT was increased, K decreases illustrating freeze concentration progresses satisfactorily. However, after a certain time, the solution is believed to be saturated with solutes, thus causing some inclusions of the solute into the ice formed. A 2D contour plot reveals that the range of CT producing the lowest K possible is between 11.8 to 18.8 minutes at CTemp between −5.2˚C to −9.6˚C. Evident from Figure 5(d), FL and ISC consistently shows similar trend of effects towards K parallel to what was revealed previously. However, compared to the other previous combinations of factors, the range of each investigated variable at this designated value of CTemp and CT is slightly different. As observed from the 2D contour plot, the range of FL giving the highest K possible is 600 to 1290 ml/min and 4 to 10 mg/ml for ISC. The effects and interactions of FL (X2) and CT (X4) on K are illustrated in Figure 5(e), while Figure 5(f) shows the effect and interaction of ISC (X3) and CT (X4) on the investigated response.
3.3. Optimum Condition
The statistical method used is fully capable of generating a regression model to predict an appropriate value of the response, and also investigating the effect of each operating condition as well as their interaction with each other. The ultimate goal however, is to achieve or obtain a specific value for each variable involved in this investigation to finally result in the most efficient freeze concentration, by looking at the value of K. It is evident from the findings of investigations of effects and interactions of all possible combination of variables towards the response that the yielded range to produce the best response possible to be different in each one. The summary of the range of the investigated parameter on the response is tabulated in Table 6. The optimum value for each operating parameter is in fact in the yielded range from the surface and contour plot analysis as given in the table.

Table 6. Optimum range for operating conditions.
 (a)
(a)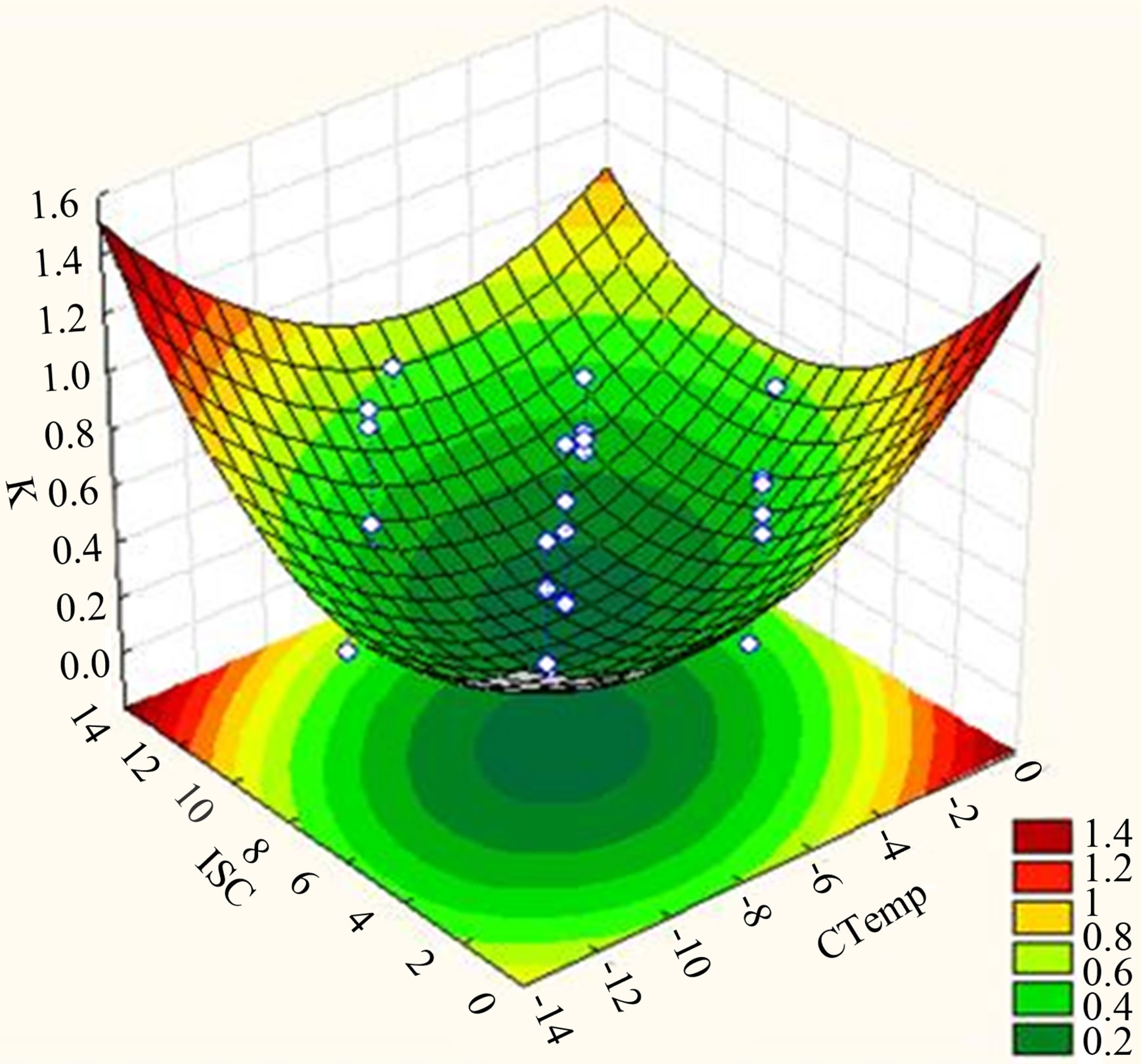 (b)
(b)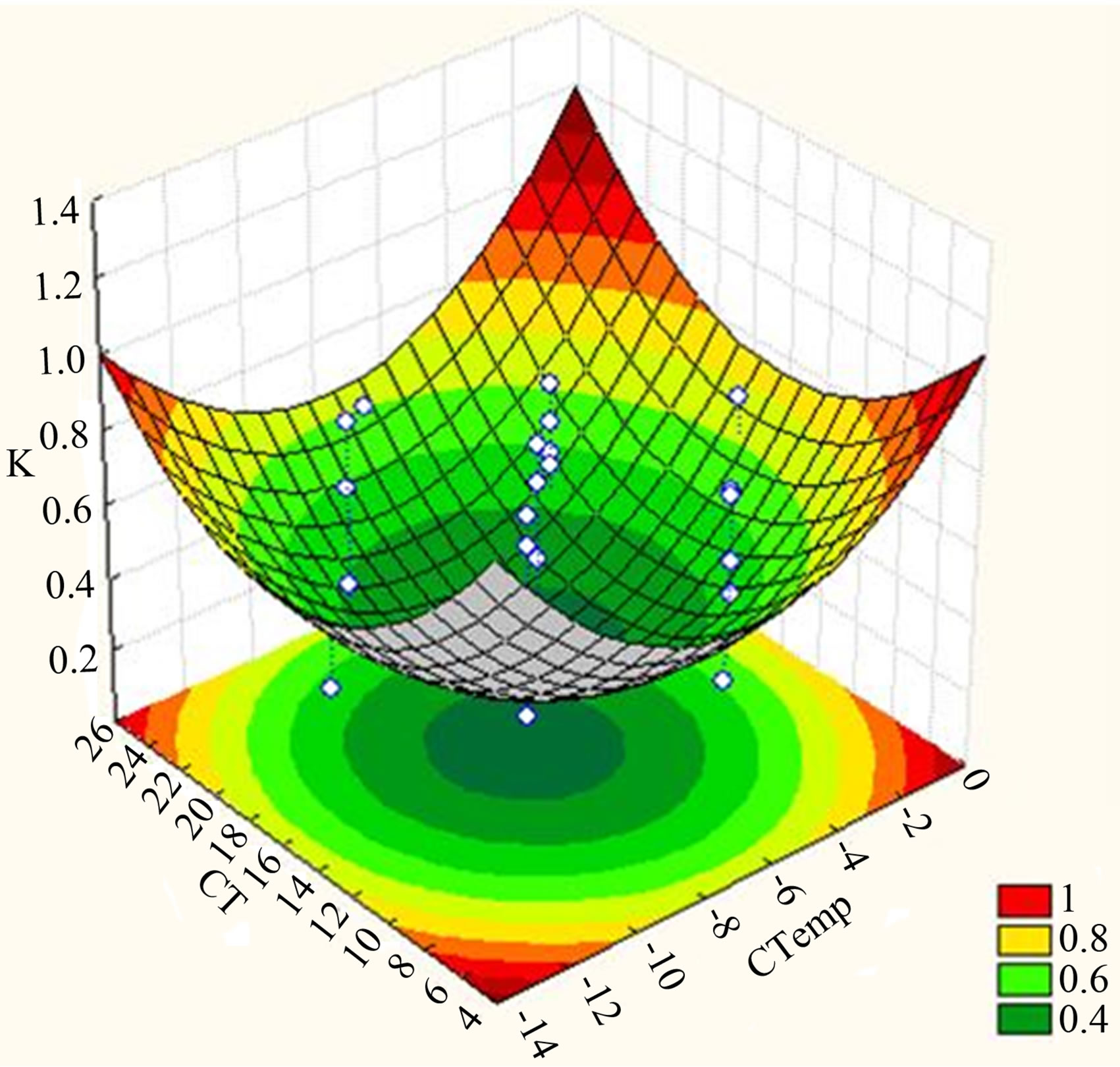 (c)
(c)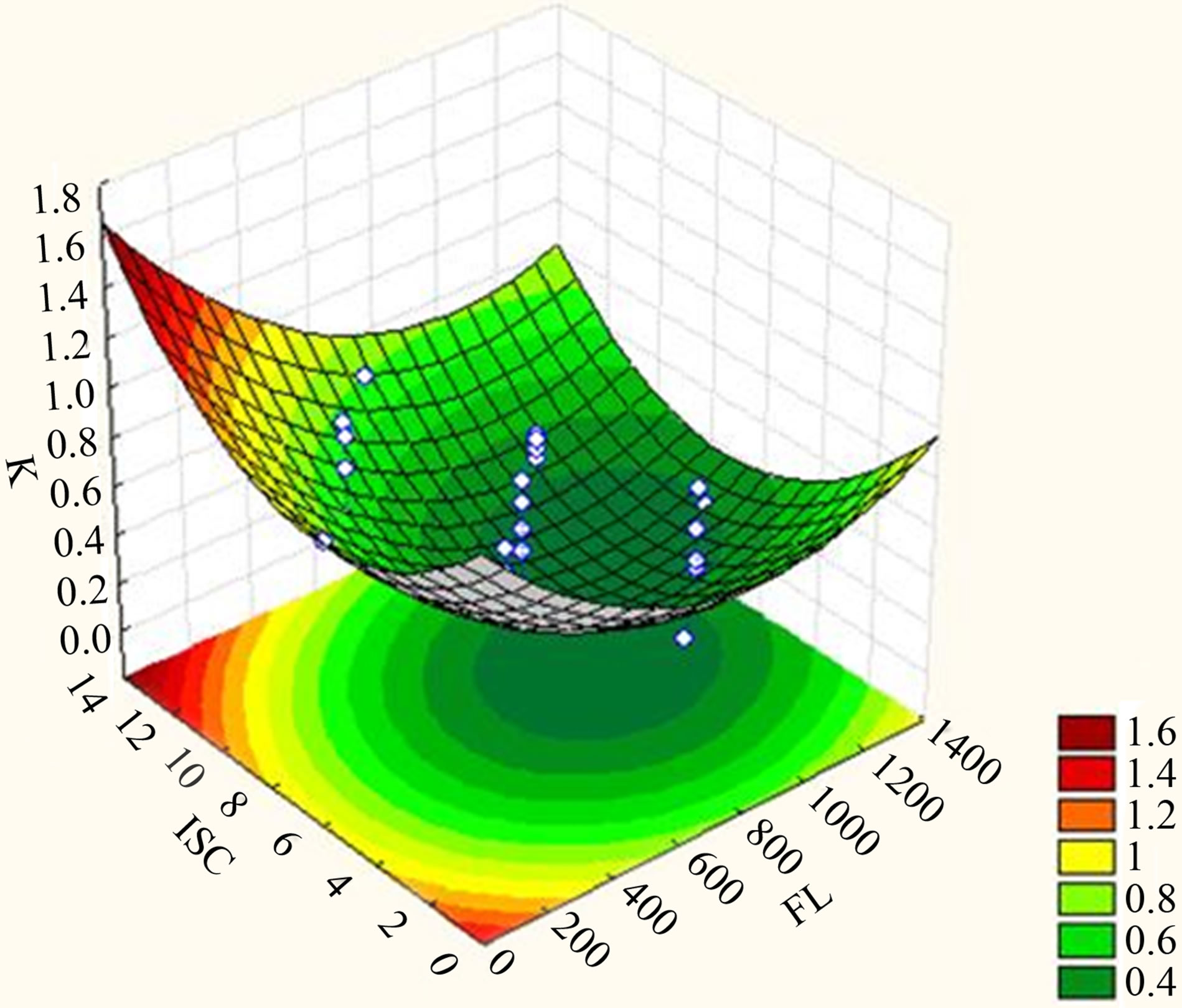 (d)
(d)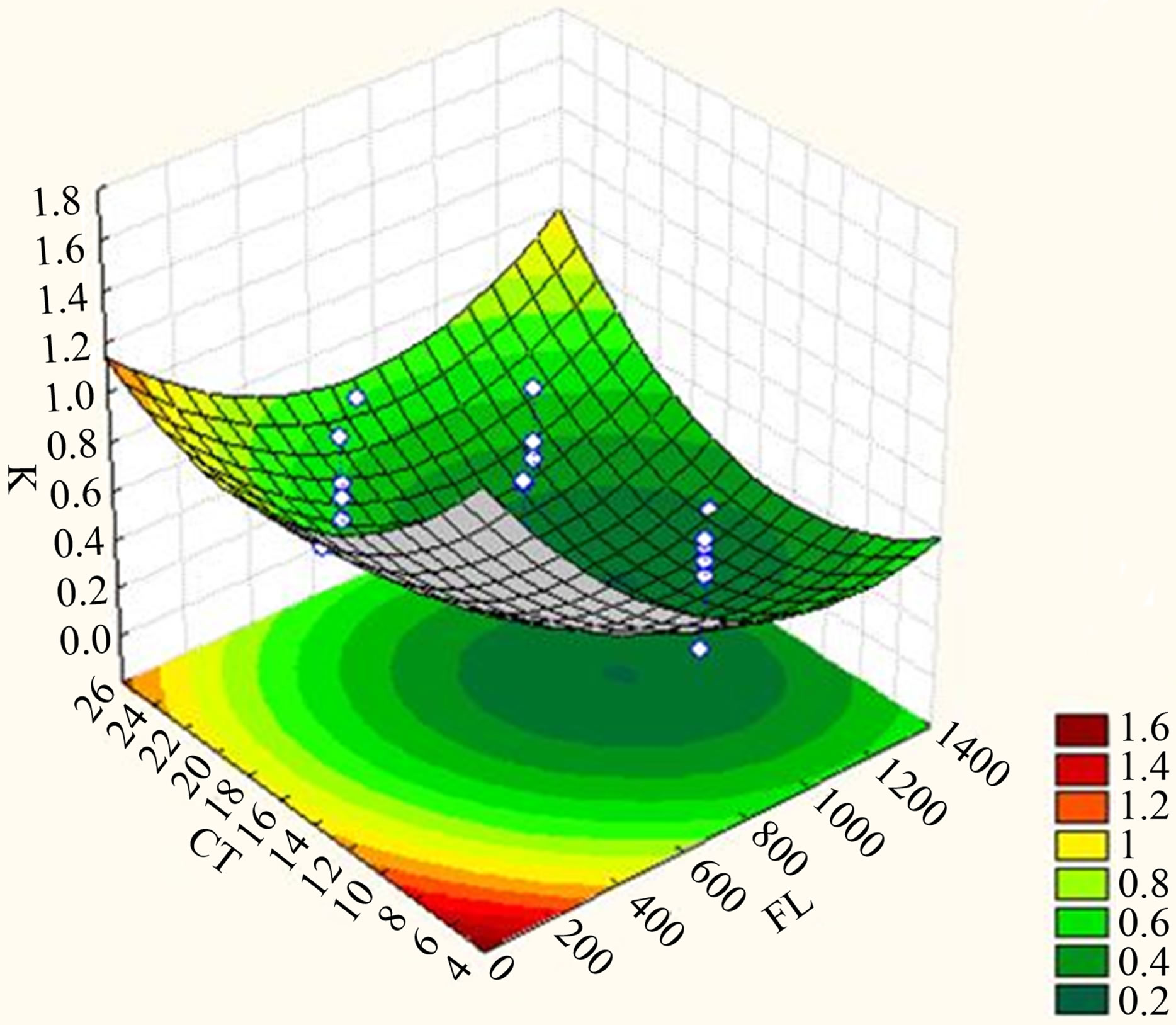 (e)
(e)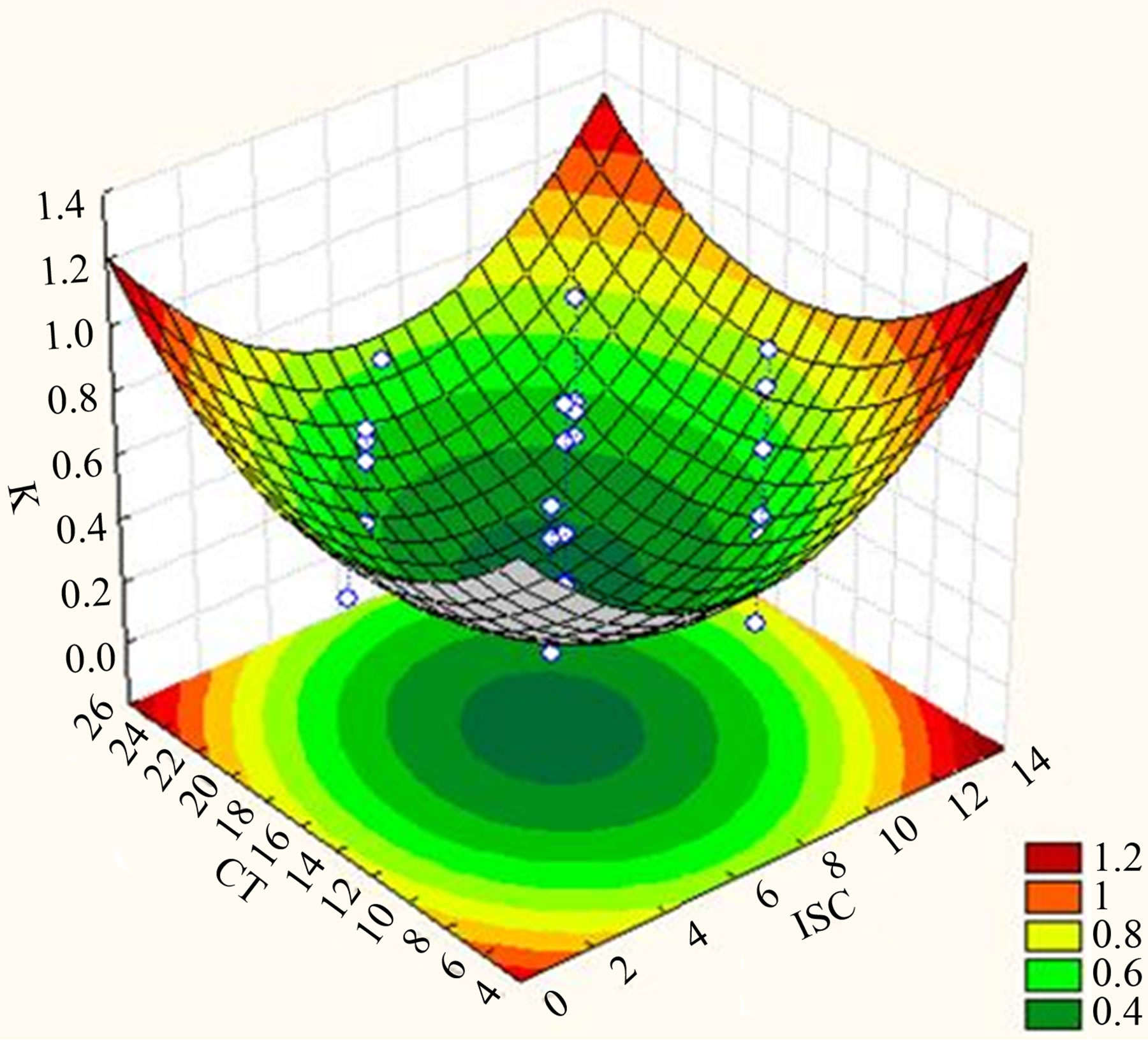 (f)
(f)
Figure 5. Contour plots manifesting interactions between factors affecting K.
4. Conclusion
PFC using the constructed multi-layer crystallizer was proven reliable to result in an effective partition constant (K) of wastewater. RSM is the best tool in determining suitable or optimum value for each operating condition to assist the maximum K. According to the statistical software, it found that the best K system could achieve is 0.17 when CTemp = −8.8˚C, FL = 1051.1 ml/min, ISC = 6.59 mg/ml and CT =13.9 minutes.
5. Acknowledgements
The financial supports of Government Malaysia and Universiti Teknologi Malaysia are gratefully acknowledged.
REFERENCES
- C. J. Geankoplis, “Transport Processes and Unit Operations,” 3rd Edition, Prentice Hall, New Jersey, 1993.
- M. Rodriguez, S. Luque, J. R. Alvarez and J. Coca, “A Comparative Study of Reverse Osmosis and Freeze Concentration for the Removal of Valeric Acid from Wastewater,” Desalination Journal, Vol. 127, No. 1, 2000, pp. 1-11. http://dx.doi.org/10.1016/S0011-9164(99)00187-3
- J. N. Shena, D. D. Li, F. Y. Jianga, J. H. Qiua and C. J. Gaob, “Purification and Concentration Of Collagen By Charged Ultrafiltration Membrane Of Hydrophilic Polyacrylonitrile Blend,” Separation and Purification Technology, Vol. 66, No. 2, 2009, pp. 257-262. http://dx.doi.org/10.1016/j.seppur.2009.01.002
- O. Miyawaki, L. Liu, Y. Shirai, S. Sakashita and, K. Kagitani, “Tubular Ice System for Scale-Up of Progressive Freeze-concentration,” Journal of Food Engineering, Vol. 69, No. 1, 2005, pp. 107-113. http://dx.doi.org/10.1016/j.jfoodeng.2004.07.016
- R. Ruemerkof, “Freeze Concentration: Its Application in Hazardous Wastewater Treatment,” Journal of Environmental Sciences and Pollution Control Series, Vol. 7, 1994, pp. 513-524.
- V. Partyka, “Freeze for Wastewater Recovery,” Metal Finishing, Vol. 84, No. 11, 1986, pp. 55-57.
- Y. Shirai, T. Sugimoto, M. Hashimoto, K. Nakanishi and R. Matsuno, “Mechanism of Ice Growth in a Batch Crystallization with an External Cooler for Freeze Concentration,” Agricultural and Biological Chemistry, Vol. 51, No. 9, 1987, pp. 2359-2366. http://dx.doi.org/10.1271/bbb1961.51.2359
- F. G. F. Qin, X. Yang and M. Yang, “An Adhesion Model of the Axial Dispersion in Wash Columns of Packed Ice Beds,” Separation and Purification Technology, Vol. 79, No. 3, 2011, pp. 321-328. http://dx.doi.org/10.1016/j.seppur.2011.03.016
- J. A. Cornell, “How to Apply Response Surface Methodology,” American Society for Quality Control Statistics Division (ASQC), 1990.
- C. Cojocaru and M. Khayet, “Sweeping Gas Membrane Distillation of Sucrose Aqueous Solutions: Response Surface Modeling and Optimization,” Separation and Purification Technology, Vol. 81, No. 1, 2011, pp. 12-24. http://dx.doi.org/10.1016/j.seppur.2011.06.031
- I. A. W. Tan, A. L. Ahmad and B. H. Hameed, “Preparation of Activated Carbon from Coconut Husk: Optimisation Study on Removal of 2,4,6-Trichlorophenol Using Response Surface Methodology,” Journal of Hazardous Material, Vol. 153, No. 1-2, 2008, pp. 709-717. http://dx.doi.org/10.1016/j.jhazmat.2007.09.014
- K. M. Carley, N. Y. Kamneva and J. Reminga, “Response Surface Methodology,” CASOS Technical Report, Carnegie Mellon University, 2004.
- L. D. Montgomery, R. W. Montgomery and R. Guisado, “Rheoencephalographic and Electroencephalographic Measures of Cognitive Workload: Analytical Procedures,” Biological Psychology, Vol. 40, No. 1-2, 1995, pp. 143-159. http://dx.doi.org/10.1016/0301-0511(95)05117-1
- G. M. Clarke and R. E. Kempson, “Introduction to the Design and Analysis Experiments,” Arnold, London, 1997.
- J. A. Cornell, “How to Apply Response Surface Methodology,” Vol. 8. American Society for Quality Control Statistics Division, Winconsin, 1990.
- G. E. P. Box, W. G. Hunter and J. S. Hunter, “Statistics for Experimenters: An introduction to Design, Data Analysis and Model Building,” John Wiley and Sons, New York, 1978.
- H. Lee, M. Song and S. Hwang, “Optimising Bioconversion of Deproteinated Cheese Whey to Mycelia of Ganoderma Lucidum,” Process Biochemistry, Vol. 38, No. 12, 2003, pp. 1685-1693. http://dx.doi.org/10.1016/S0032-9592(02)00259-5
- N. M. Sachindra and N. S. Mahendrakar, “Process Optimization for Extraction of Carotenoids from Shrimp Waste with Vegetable Oils,” Bioresource Technology, Vol. 96, No. 10, 2005, pp. 1195-1200. http://dx.doi.org/10.1016/j.biortech.2004.09.018
- Z. Erbay and F. Icier, “Optimisation of Hot Drying of Olive Leaves Using Response Surface Methodology,” Journal of Food Engineering, Vol. 91, No. 4, 2009, pp. 533-541. http://dx.doi.org/10.1016/j.jfoodeng.2008.10.004
- R. V. Muralidhar, R. R. Chirumamila, R. Marchant and P. Nigam, “A response Surface Approach for the Comparison of Lipase Production by Candida Cylindriea Using Two Different Carbon Sources,” Biochemical Engineering Journal, Vol. 9, No. 1, 2001, pp. 41-45. http://dx.doi.org/10.1016/S1369-703X(01)00117-6
NOTES
*Corresponding author.

