Journal of Signal and Information Processing
Vol.3 No.3(2012), Article ID:22129,4 pages DOI:10.4236/jsip.2012.33046
A New Image Denoising Scheme Using Soft-Thresholding
![]()
Department of Computer Science and Engineering, Indian School of Mines, Dhanbad, India.
Email: mantoshb@gmail.com, hariom4india@gmail.com
Received April 16th, 2012; revised May 20th, 2012; accepted May 31st, 2012
Keywords: Wavelet Thresholding; Image Denoising; Peak Signal-to-Noise Ratio
ABSTRACT
The VisuShrink is one of the important image denoising methods. It however does not provide good quality of image due to removing too many coefficients especially using soft-thresholding technique. This paper proposes a new image denoising scheme using wavelet transformation. In this paper, we modify the coefficients using soft-thresholding method to enhance the visual quality of noisy image. The experimental results show that our proposed scheme has better performance than the VisuShrink in terms of peak signal-to-noise ratio (PSNR) i.e., visual quality of the image.
1. Introduction
One of the main tasks of image processing is to distinguish between noise and actual contents so that the unwanted noise from the image signal can be removed. The distortion of an image by noise is very common that gets introduced during its acquisition, processing, compression, transmission, and reproduction. The noise is generally assumed to be additive white Gaussian noise. Several techniques using wavelet-based thresholding have been discussed in literature to reduce the noise from an image [1-4]. Donoho has proposed VisuShrink using hard and soft thresholding methods for image denoising [5-7]. This scheme exterminates many wavelet coefficients that might contain useful image information. However, the major problem with both these methods is the selection of a suitable threshold value [8]. In this paper, we discuss a new image denoising scheme that performs better than the VisuShrink. The rest of the paper is organized as follows. The soft-thresholding method is discussed in Section 2. Section 3 discusses the proposed work and Section 4 discusses the results. In our experiments, we take three commonly used images in literature to establish the efficacy of our proposed method. Finally, the paper is concluded in Section 5.
2. Soft-Thresholding Denoising Method
Consider an image signal fij of size M × M. Assume that it is corrupted by independent and identically distributed (i.i.d) zero mean, white Gaussian noise zij with standard deviation σ. The corrupted image, denoted by yij, is given as follows.
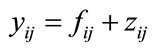 (1)
(1)
From this noisy image signal yij, we want to find an approximation 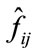 of the original image fij. Let W and W−1 be the two-dimensional orthogonal discrete wavelet transform (DWT) and its inverse (IDWT) matrices, respectively [9,10]. After applying the wavelet transform W to (1), we have
of the original image fij. Let W and W−1 be the two-dimensional orthogonal discrete wavelet transform (DWT) and its inverse (IDWT) matrices, respectively [9,10]. After applying the wavelet transform W to (1), we have
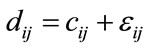 (2)
(2)
where dij = W yij, cij = W fij, and εij = W zij, i, j = 1, 2, ···, M.
Since W is orthogonal transform, εij is also an i.i.d Gaussian random variable, i.e., εij ~ M (0, σ2). Let T (·) be the wavelet thresholding function. The estimate 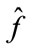 of the original image f after applying wavelet thresholding is obtained as follows
of the original image f after applying wavelet thresholding is obtained as follows
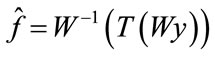 (3)
(3)
Here the estimate 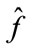 is derived from the noisy image y by first applying wavelet transform on it, followed by thresholding, and then taking inverse wavelet transform of the resultant. We will use soft thresholding in this paper that is defined as follows.
is derived from the noisy image y by first applying wavelet transform on it, followed by thresholding, and then taking inverse wavelet transform of the resultant. We will use soft thresholding in this paper that is defined as follows.
In soft thresholding method, the thresholding function is defined as follows [5]:
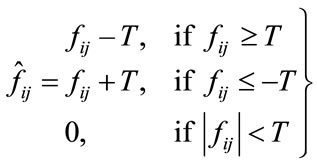 (4)
(4)
Using soft thresholding we will try to remove the noise from the image. The proposed algorithm is discussed in next section.
3. Proposed Denoising Algorithm
In our proposed scheme first we determine the threshold value and then apply it on the wavelet coefficients of the image. First we discuss the thresholding function that will be used in our method followed by denoising method.
3.1. Thresholding Function
1) We calculate new threshold function T1 using the following formula [11,12]:
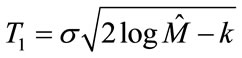
where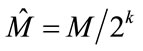 , here k = 1, 2, ···, J; where J represents the number of decomposition levels which is prespecified and M represents the size of original image and σ2 is noise variance.
, here k = 1, 2, ···, J; where J represents the number of decomposition levels which is prespecified and M represents the size of original image and σ2 is noise variance.
2) Now, we fix the new threshold value, TNew, using the following steps [13]:
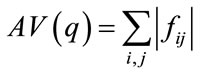
for q = 0, 1, 2, 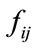 represents horizontal, vertical, and diagonal wavelet coefficients, respectively. Define
represents horizontal, vertical, and diagonal wavelet coefficients, respectively. Define
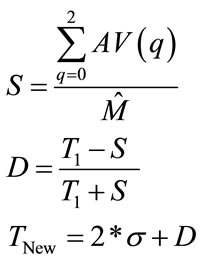 (5)
(5)
The VisuShrink uses a Universal threshold, T, which is proportional to the standard deviation of the noise, and is defined as [5]:
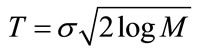
where M represents signal size and σ2 is noise variance, which is given by
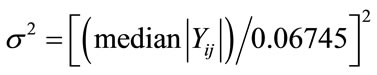 where,
where, 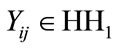 subband thresholding.
subband thresholding.
3.2. Denoising Algorithm
The proposed procedure is given as follows:
1) Perform multiscale decomposition on the image corrupted by Gaussian noise. The 2-D orthogonal wavelet transform W on a noisy image y is performed up to Jth level to generate several subbands. For each level, compute TNew as a threshold using (5).
2) For each subband (except the low pass residual), apply TNew and then use the Soft-thresholding method to the noisy coefficients to get the noiseless wavelet coefficients.
3) Finally take inverse wavelet transform of the resultant image obtained in step 2) in order to obtain the denoised image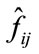 .
.
4. Results
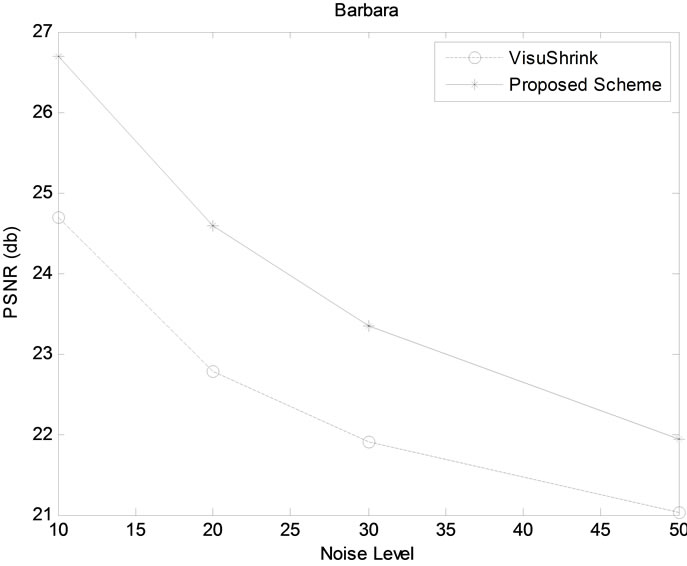
In our experiments, we have taken three gray scale images each of size 512 × 512. These images are Lena, Barbara and Cameraman (refer Figure 1) and the noise levels are taken as 10, 20, 30 and 50. The wavelet transform that we have employed is Daubechies least asymmetric compactly-supported wavelet with two vanishing moments with four scales of orthogonal decomposition [14, 15]. To evaluate the performance of the proposed method, we have computed visual quality in terms of Peak Signalto-Noise Ratio (PSNR) using the proposed and VisuShrink thresholding functions for all three images. The results are given in Table 1. It is evident from Table 1 that our scheme outperforms the VisuShrink for all three images and for all values of noise levels considered in experiments. In other words, our scheme removes noise significantly. Figure 2 show the original image, noisy image, denoised image using VisuShrink and proposed method of Barbara image using noise level 10. As it is evident from Figures 2(c)-(d), our scheme provides the image with better visual quality. Similar results were obtained for other noise levels. Because of repetitive
 (a)
(a) (b)
(b) (c)
(c)
Figure 1. Original test images of size 512 × 512 pixels: (a) Barbara; (b) Lena; (c) Cameraman.

Table 1. Denoising numerical results (PSNR in db) for Barbra, Lena and cameraman images.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 2. Barbara image with (a) Original; (b) Noisy image with noise level 10; (c) Denoising using visushrink; (d) Denoising using proposed scheme.
nature of results, we have shown the images for noise level 10 only.
We have also shown the results (i.e., PSNR gain) in graphical form for our proposed scheme and VisuShrink scheme in Figures 3(a)-(c) for all noise level of all three
 (a)
(a)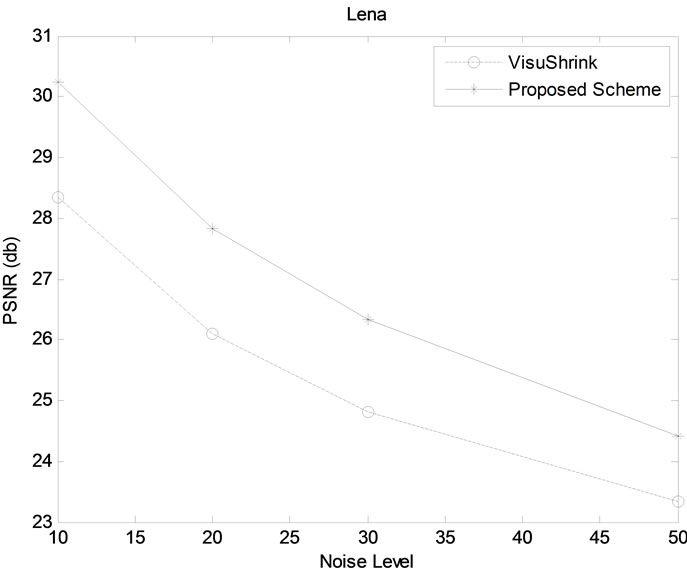 (b)
(b)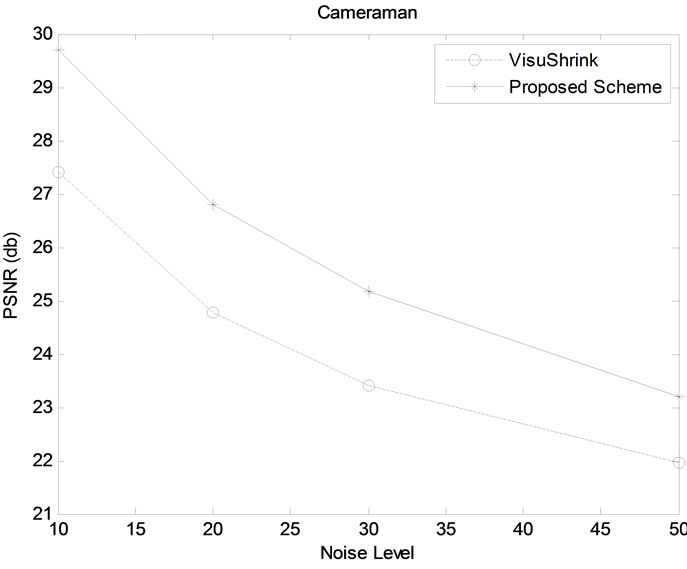 (c)
(c)
Figure 3. PSNR gain vs. noise level of Proposed and VisuShrink methods: (a) Barbara; (b) Lena; (c) Cameraman.
images. It is evident from these figures that our scheme performs much better than the VisuShrink scheme for all three images.
As mentioned above, we have shown images for noise level 10 only; but our scheme performs much better for other noise values. Thus, we have shown that our scheme performs much better than the VisuShrink scheme, i.e., it removes the noise from the image significantly. We have not shown the images for other two images, i.e., Barbara and Goldhill because of repetitive nature of results.
5. Conclusion
In this paper, we have proposed a new soft-thresholding scheme that removes the noise significantly and performs the VisuShrink in terms of PSNR for all value all values of noise level.
6. Acknowledgements
The authors express their sincere thanks to Prof. S. Chand for his invaluable comments and suggestions.
REFERENCES
- M. Jansen, “Noise Reduction by Wavelet Thresholding,” Springer Verlag Inc., New York, 2001.
- J. Gao, H. Sultan, J. Hu and W. W. Tung, “Denoising Nonlinear Time Series by Adaptive Filtering and Wavelet Shrinkage: A Comparison,” IEEE Signal Processing Letters, Vol. 17, No. 3, 2010, pp. 237-240. HUdoi:10.1109/LSP.2009.2037773U
- A. Khademi, A. A. Venetsanopoulos and A. R. Moody “Image Enhancement and Noise Suppression for FLAIR MRIs with White Matter Lesions,” IEEE Signal Processing Letters, Vol. 17, No. 12, 2010, pp. 989-992. HUdoi:10.1109/LSP.2010.2082527U
- D. B. H. Tay “Daubechies Wavelets as Approximate Hilbert-Pairs?” IEEE Signal Processing Letters, Vol. 15, 2008, pp. 57-60. HUdoi:10.1109/LSP.2007.910318U
- D. L. Donoho, “De-Noising by Soft Thresholding,” IEEE Transactions on Information Theory, Vol. 41, No. 3, 1995, pp. 613-627. HUdoi:10.1109/18.382009U
- D. L. Donoho and I. M. Johnstone, “Adapting to Unknown Smoothness via Wavelet Shrinkage,” Journal of American Statistical Association, Vol. 90, No. 432, 1995, pp. 1200-1224. HUdoi:10.1080/01621459.1995.10476626U
- D. L. Donoho and I. M. Johnstone, “Ideal Spatial Adaptation via Wavelet Shrinkage,” Biometrika, Vol. 81, No. 3, 1994, pp. 425-455. HUdoi:10.1093/biomet/81.3.425U
- D. L. Donoho and I. M. Johnstone, “Wavelet Shrinkage: Asymptotic?” Journal of the Royal Statistical Society, Series B (Methodological), Vol. 57, No. 2, 1995, pp. 301- 369.
- C. S. Burrus, R. A. Gopinath and H. Guo, “Introduction to Wavelet and Wavelet Transforms: A Primer,” Prentice Hall, Upper Saddle River, 1998.
- M. Vattereli and J. Kovacevic, “Wavelets and Subband Coding,” Prentice Hall, Englewood Cliffs, 1995.
- H. Om and M. Biswas, “An Improved Image Denoising Method Based on Wavelet Thresholding,” Journal of Signal and Information Processing (USA), Vol. 3, No. 1, 2012, pp. 109-116. HUdoi:10.4236/jsip.2012.31014U
- H. Om and M. Biswas, “An Enhanced Image Denoising Scheme,” International Journal of Advanced Computer Engineering, Review, 2012.
- H. Q. Li and S. Q. Wang, “A New Image Denoising Method Using Wavelet Transform,” International Forum on Information Technology and Applications, Chengdu, 15-17 May 2009, pp. 111-114.
- S. Gupta and L. Kaur, “Wavelet Based Image Compression using Daubechies Filters,” Proceeding of 8th National Conference on Communications, I.I.T., Bombay NCC, 2002.
- I. Daubechies, “Ten Lectures on Wavelets,” Proceeding of CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, Philadelphia, 1992.

