Applied Mathematics
Vol.4 No.6(2013), Article ID:33036,5 pages DOI:10.4236/am.2013.46127
Existence and Uniqueness of Solution to Two-Point Boundary Value for Two-Sided Fractional Differential Equations
School of Science, Beijing University of Civil Engineering and Architecture, Beijing, China
Email: shiailing@bucea.edu.cn
Copyright © 2013 Ailing Shi, Yu Bai. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 28, 2012; revised March 1, 2013; accepted March 9, 2013
Keywords: Existence; Uniqueness; Two-Sided Fractional Differential Equations
ABSTRACT
In this paper, existence and uniqueness of solution to two-point boundary value for two-sided fractional differential equations involving Caputo fractional derivative is discussed, by means of the Min-Max Theorem.
1. Introduction
In this paper, using the Min-Max Theorem, we will devote to considering the existence and uniqueness result of solution to the following two-sided fractional differential equations boundary value problems (BVP for short)
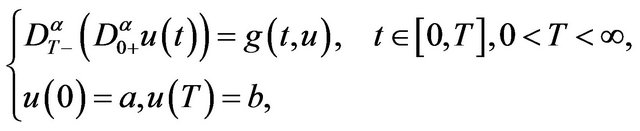 (1.1)
(1.1)
where 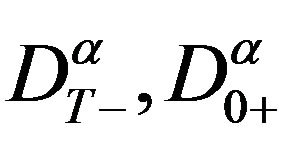 denote the right-side and left-side Caputo fractional derivative of order
denote the right-side and left-side Caputo fractional derivative of order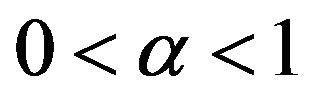 , respectively,
, respectively, 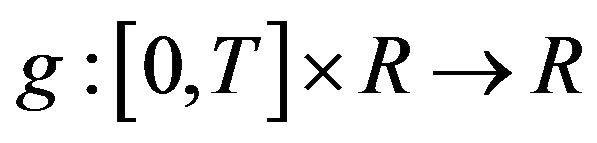 is a continuous differential function with respect to all variables, and
is a continuous differential function with respect to all variables, and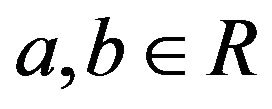 .
.
In particular, if , BVP (1.1) reduces to the standard second order boundary value problem of the following form
, BVP (1.1) reduces to the standard second order boundary value problem of the following form
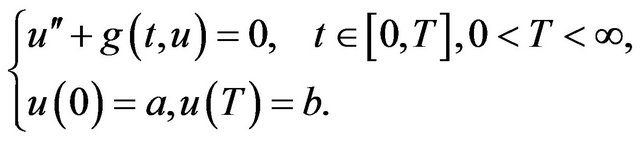
Recently, fractional differential equations have been verified to be valuable tools in the modeling of many phenomena in various fields of science and engineering. There have many papers which are concerning with the existence of solutions for fractional differential equations boundary value problems, by means of some classic fixed point theorems and monotone iterative methods, such as [1-11], etc. But, as far as we known, there are few papers which considered the existence of solutions for fractional differential equations boundary value problems using the variable method, such as the direct method, the critical point theory. Recently, there appeared some interesting works [12,13] considering existence of solution to fractional differential problems, by means of the variable way, In [13], by the critical point theory, author considered the existence of solutions of the following a twopoint boundary value problem for some class of fractional differential equation containing the left and right Riemann-Liouville fractional derivative operators
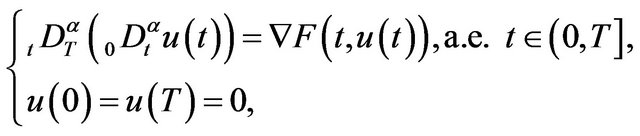 (1.2)
(1.2)
where 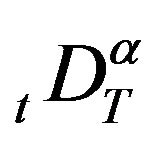 and
and ![]() are the right and left RiemannLiouville fractional derivatives of order
are the right and left RiemannLiouville fractional derivatives of order  respectively,
respectively, 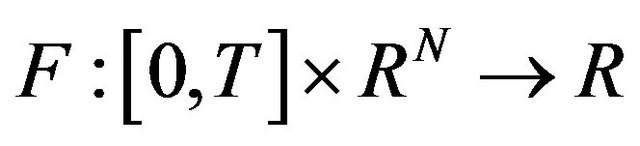 is a given function satisfying some assumptions and
is a given function satisfying some assumptions and  is the gradient of
is the gradient of 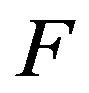 at
at![]() . This is a very interesting and meaning works, this is the first time that the existence of solutions for fractional differential equation two-point boundary value problem via the critical point theory.
. This is a very interesting and meaning works, this is the first time that the existence of solutions for fractional differential equation two-point boundary value problem via the critical point theory.
The following are definitions and some properties of Riemann-Liouville fractional integral and derivative, the Caputo fractional derivative, for the details, please see [1].
The left Riemann-Liouville fractional integrals (LFLI) of order 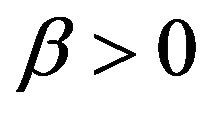 of function
of function 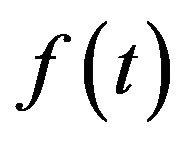 which is defined as follows,
which is defined as follows,
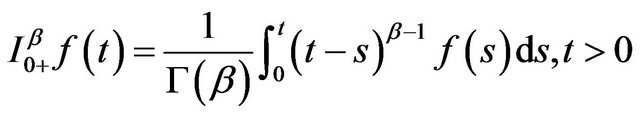 (1.3)
(1.3)
The right Riemann-Liouville fractional integrals (RFLI) of order 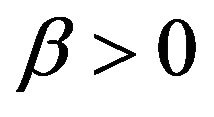 of function
of function 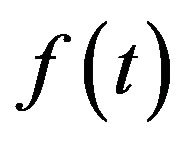 which is defined as follows,
which is defined as follows,
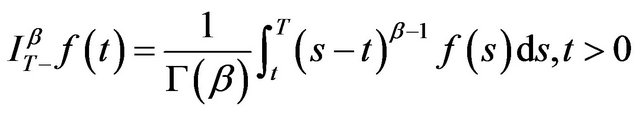 (1.4)
(1.4)
The left Riemann-Liouville fractional derivative (LFLD) of order 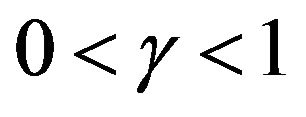 of function
of function 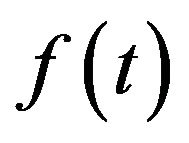 which is defined as follows,
which is defined as follows,
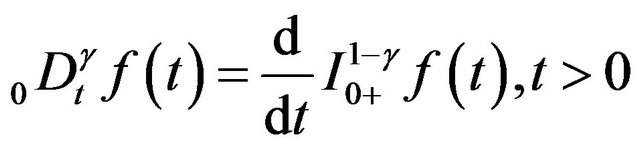 (1.5)
(1.5)
The right Riemann-Liouville fractional derivative (RFLD) of order 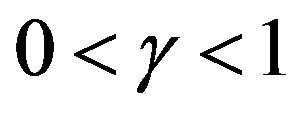 of function
of function 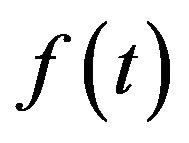 which is defined as follows,
which is defined as follows,
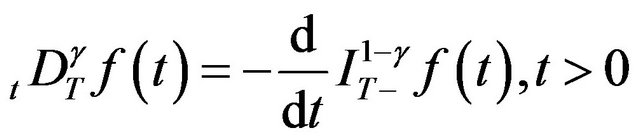 (1.6)
(1.6)
The left Caputo fractional derivative (LCFD) of order 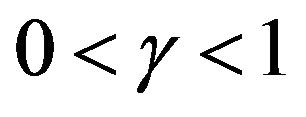 of function
of function 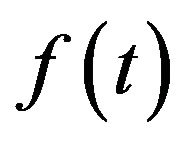 which is defined as follows,
which is defined as follows,
 (1.7)
(1.7)
The right Caputo fractional derivative (RCFD) of order 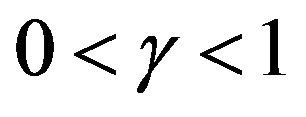 of function
of function  which is defined as follows,
which is defined as follows,
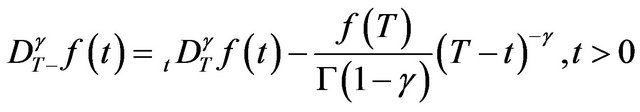 (1.8)
(1.8)
Remark 1.1. Obviously, if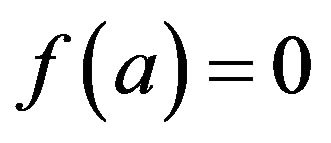 , then
, then
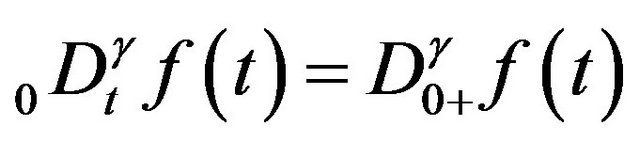 ; it
; it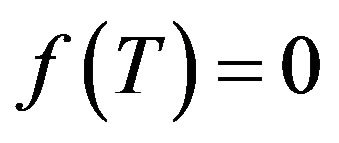 , then
, then
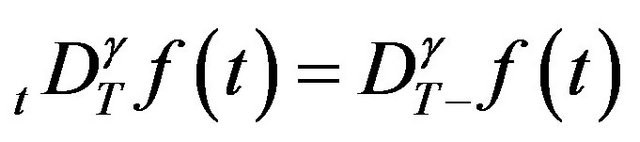 .
.
It is well known that there are several kinds of fractional derivatives, such as, Riemann-liouville fractional derivative, Marchaud fractional derivative, Caputo derivative, Griinwald-Letnikov fractional derivative, etc. Since as cited in [2] there have appeared a number of works, especially in the theory of viscous elasticity and in hereditary solid mechanics, where fractional derivatives are used for a better description of material properties. Mathematical modeling based on enhanced rheological models naturally leads to differential equations of fractional order and to the necessity of the formulation of initial conditions to such equations. Applied problems require definitions of fractional derivatives allowing the utilization of physically in interpretable initial conditions, which contain , etc". In fact, the same requirements apply for boundary conditions. Therefore, we cannot impose initial and boundary conditions, such as
, etc". In fact, the same requirements apply for boundary conditions. Therefore, we cannot impose initial and boundary conditions, such as 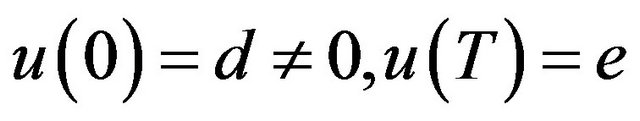 on problems involving the Riemann-Liouville fractional derivative
on problems involving the Riemann-Liouville fractional derivative ![]() or
or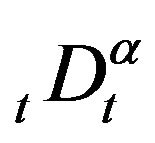 . We find that Caputo fractional derivative exactly satisfies these demands. Therefore in this article, we deal with boundary value problem for fractional differential equation involving Caputo derivative.
. We find that Caputo fractional derivative exactly satisfies these demands. Therefore in this article, we deal with boundary value problem for fractional differential equation involving Caputo derivative.
The following is the rule of fractional integration by parts for LFLI and RFLI.
Let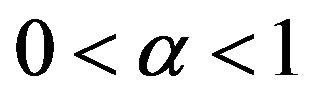 ,
, 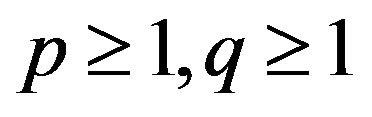 , and
, and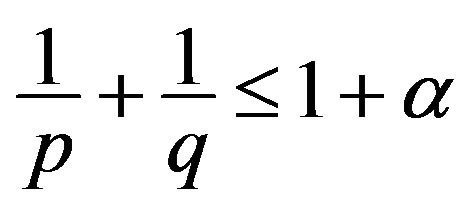 . If
. If
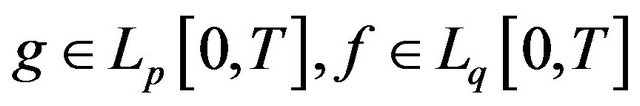 , then
, then
 (1.9)
(1.9)
We let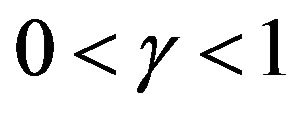 ,
, 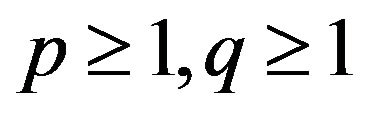 , and
, and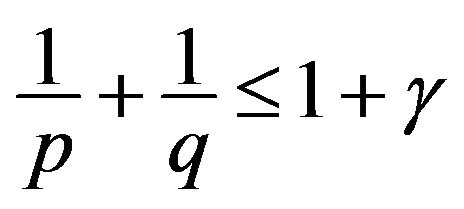 , if
, if
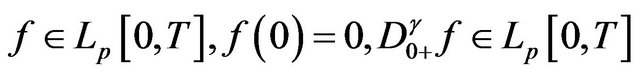 ,
,
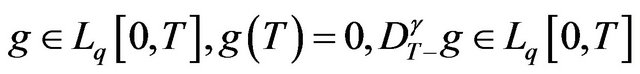 , then, by (1.9) and Remark 1.1, we have that
, then, by (1.9) and Remark 1.1, we have that
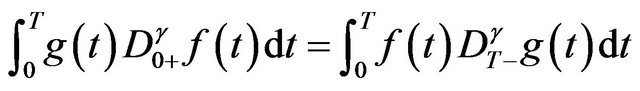 (1.10)
(1.10)
Inspired by [12,13], in this paper, we will consider the unique existence of solution to problem (1.1), by means of the following Min-Max Theorem.
Min-Max Theorem (Manasevich). [14] Let H be a real Hilbert space and let 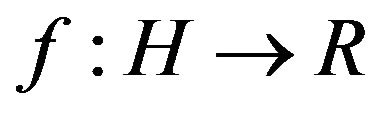 be of class
be of class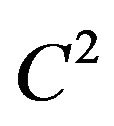 . Suppose that there exist two closed subspaces X and Y such that
. Suppose that there exist two closed subspaces X and Y such that 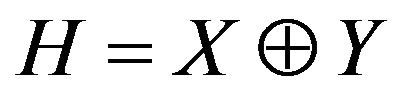 and two continuous non-increasing functions
and two continuous non-increasing functions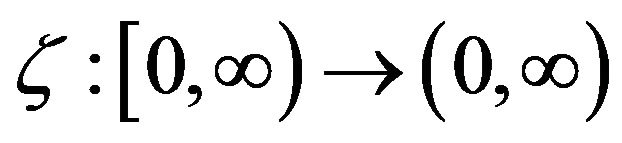 ,
, 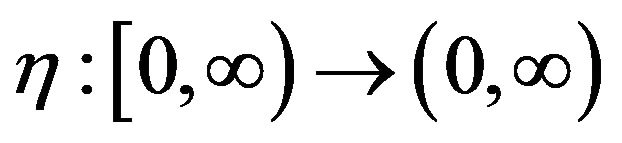 such that
such that

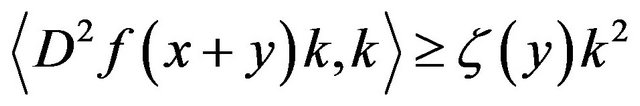
for all 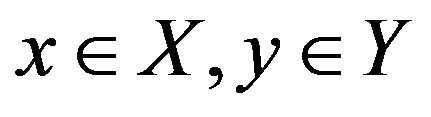 and
and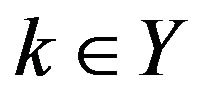 , and
, and

for all 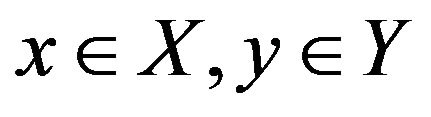 and
and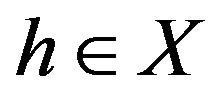 . Then 1) there exists a unique
. Then 1) there exists a unique 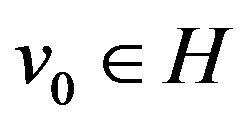 such that
such that
 ;
;
2) 
Here,  and
and 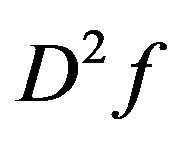 denote the gradient and the Hessian of
denote the gradient and the Hessian of 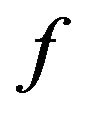 at
at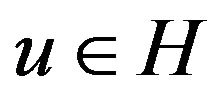 , respectively. In this case,
, respectively. In this case,
 is a
is a 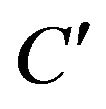 mapping and
mapping and 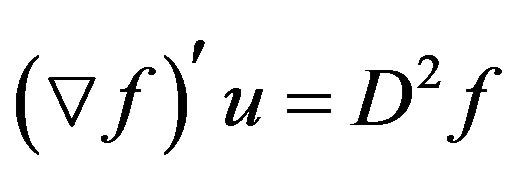 is a bounded self-adjoins linear operator on
is a bounded self-adjoins linear operator on .
.
2. Basic Facts
In [13], authors gave the definition of solution to (1.2) as following Definition 2.1. [13] A function  is called a solution of BVP (1.2) if
is called a solution of BVP (1.2) if
(i) ![]() and
and 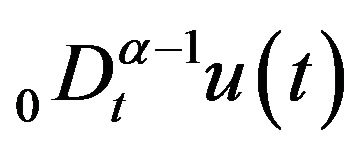 are derivative for almost every
are derivative for almost every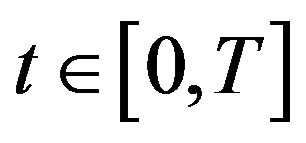 , and (ii)
, and (ii) ![]() satisfies (1.2).
satisfies (1.2).
In [13], in order to establish a variational structure which enables ones to reduce the existence of solutions of BVP (1.2) to the one of critical points of corresponding functional, authors constructed an appropriate function spaces , which depend on
, which depend on 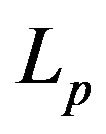 -integrability of the Riemann-Liouville fractional derivative of a function.
-integrability of the Riemann-Liouville fractional derivative of a function.
Definition 2.2. [13] Let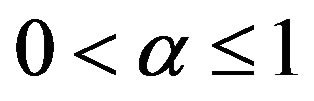 ,
,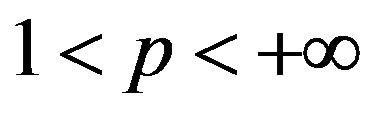 . The fractional derivative space
. The fractional derivative space 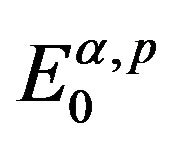 is defined by the closure of
is defined by the closure of ![]() with respect to the norm
with respect to the norm
 (2.1)
(2.1)
It is obvious that space 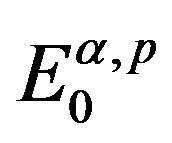 is the space of functions
is the space of functions ![]() having an
having an ![]() -order fractional derivative
-order fractional derivative ![]() and
and
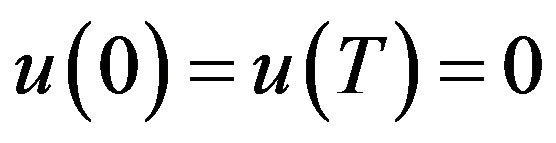 . Furthermore, it is easy to verify that
. Furthermore, it is easy to verify that 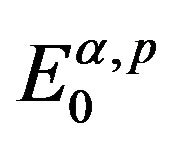 is a reflexive and separable Banach space.
is a reflexive and separable Banach space.
Theorem 2.3. [13] Let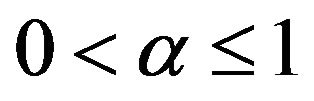 ,
,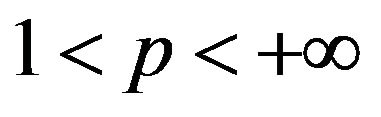 . The space
. The space 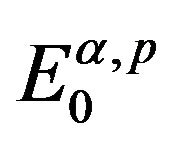 is a reflexive and separable Banach space.
is a reflexive and separable Banach space.
Proposition 2.4. [13] Let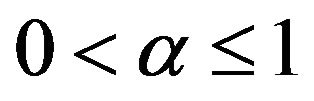 ,
,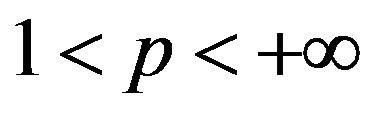 . For all
. For all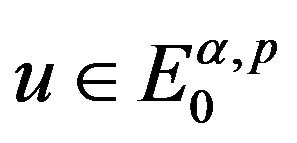 , if
, if  or
or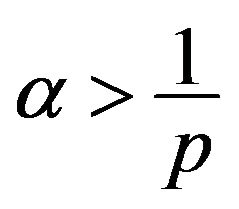 , we have
, we have
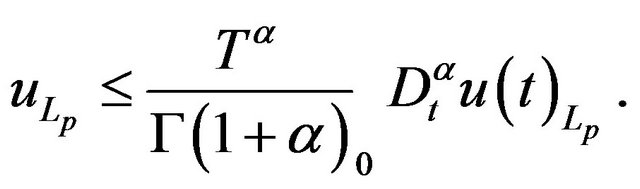
with this property, one can consider 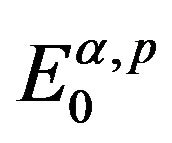 with respect to the norm
with respect to the norm
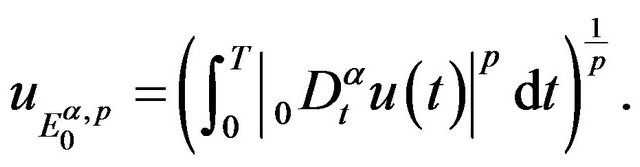
If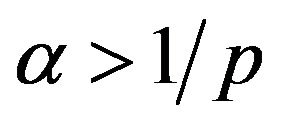 , the following theorem is useful for us to establish the variational structure on the space
, the following theorem is useful for us to establish the variational structure on the space 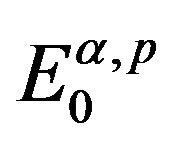 for BVP (1.2).
for BVP (1.2).
Theorem 2.5. [13] Let ,
, 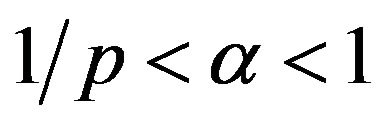 and
and
 ,
, 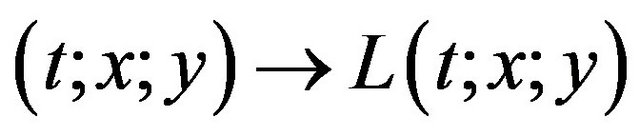 be measurable in t for each
be measurable in t for each 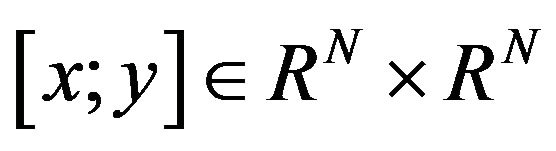 and continuously differentiable in
and continuously differentiable in 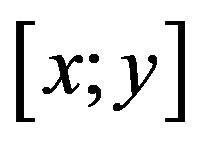 for almost every
for almost every . If there exists
. If there exists![]() ;
; ![]() and
and
![]() ;
; , such that, for a.e.
, such that, for a.e.
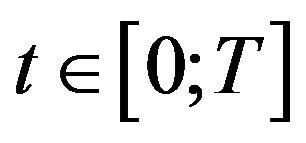 and every
and every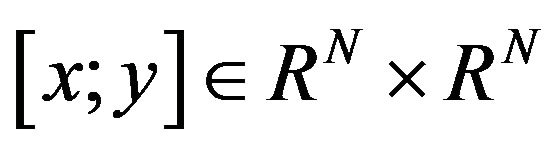 , one has
, one has
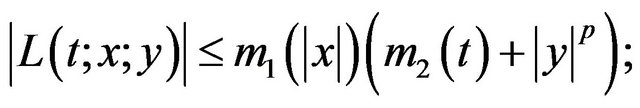
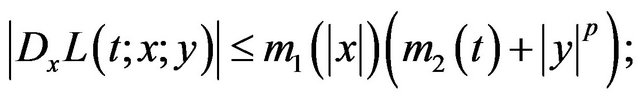
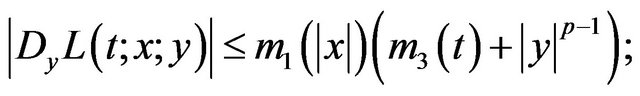
where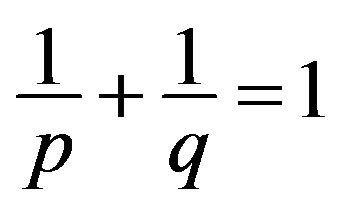 , then the functional defined by
, then the functional defined by
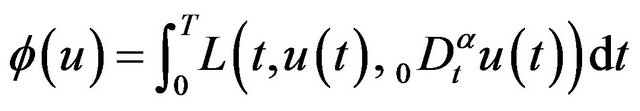
is continuously differentiable on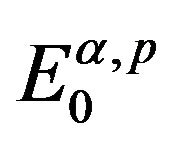 , and
, and
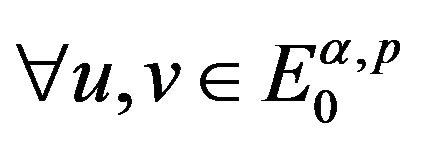 , we have
, we have
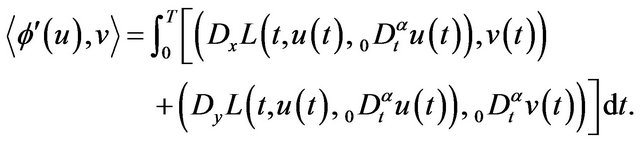
From, we known that, for a solution 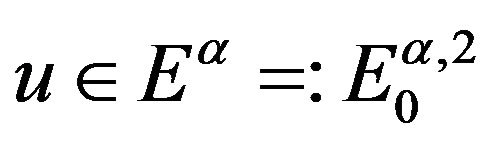
of BVP (1.2) such that![]() , multiplying (1.2) by
, multiplying (1.2) by ![]() yields
yields
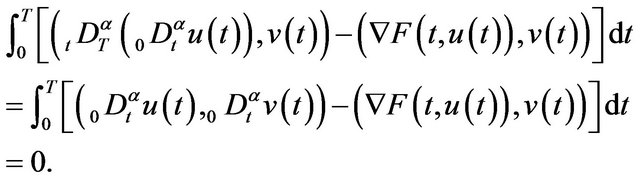
According these facts, authors [13] gave the definition of weak solution for BVP (1.2) as follows.
Definition 2.6. [13] By the weak solution of BVP (1.2), we mean that the function 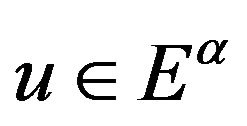 such that
such that
![]() and satisfies the above equality for all
and satisfies the above equality for all![]() .
.
Using the direct method and the Mountain pass theorem, authors obtain two existence results of weak solution to (1.2), please see [13].
Basing on some deductions, authors verified that a weak of (1.2) is also its solution.
3. Main Result
From the Remark 1.1 and Definition 2.2, we will use function space 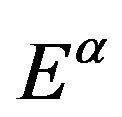 in the following arguments.
in the following arguments.
Theorem 3.1. Assume that 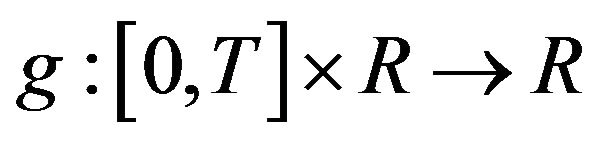 is continuous differentiable with respect to its two variablesthere is a constant
is continuous differentiable with respect to its two variablesthere is a constant  such that
such that
 for all
for all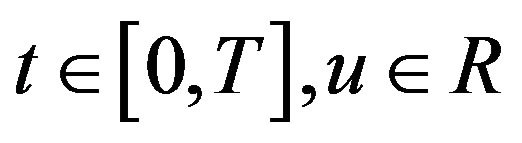 . Then problem (1.1) exists unique solution
. Then problem (1.1) exists unique solution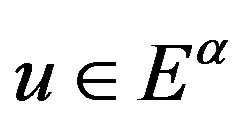 .
.
Proof. We can decompose (1.1) into the following two problems
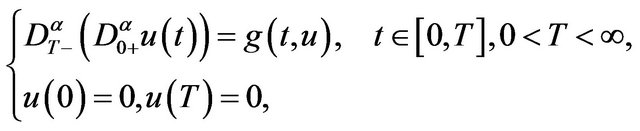 (3.1)
(3.1)
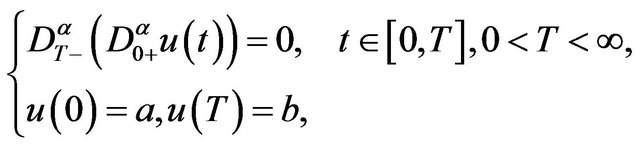 (3.2)
(3.2)
according to the linearity of 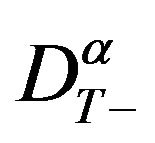 and
and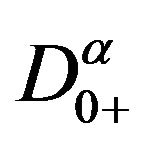 , we can easily know that if
, we can easily know that if 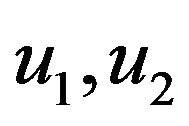 are solution of (3.1), (3.2), respectively, then
are solution of (3.1), (3.2), respectively, then 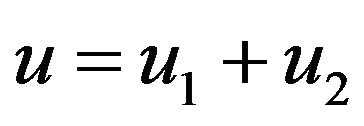 is a solution of (1.1). Obviously,
is a solution of (1.1). Obviously,  is unique solution of (3.2). Next, we will verify that (3.1) exists unique solution
is unique solution of (3.2). Next, we will verify that (3.1) exists unique solution , by means of the Min-Max Theorem (Manasevich).
, by means of the Min-Max Theorem (Manasevich).
From [13], we know that 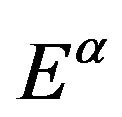 is a real Hilbert space with the inner product by
is a real Hilbert space with the inner product by
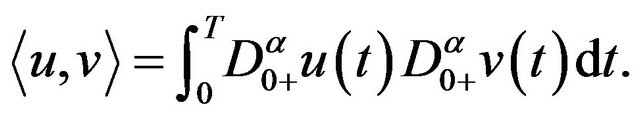 (3.3)
(3.3)
It follows from assumptions on function ![]() that we can easily know that g satisfies assumption of Theorem 2.5.
that we can easily know that g satisfies assumption of Theorem 2.5.
We let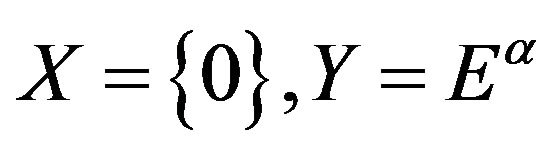 , clearly, we have
, clearly, we have  . From the Algebra knowledge, it is well know that
. From the Algebra knowledge, it is well know that 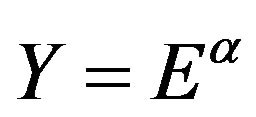 and
and  are closed subsets of
are closed subsets of 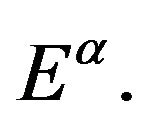 From the previous arguments, we can complete this proof through two steps.
From the previous arguments, we can complete this proof through two steps.
The first step, we will consider the existence of critical point of functional defined as following
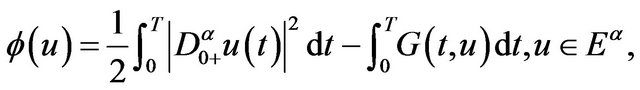 (3.4)
(3.4)
where . From the arguments in [13], we know that
. From the arguments in [13], we know that
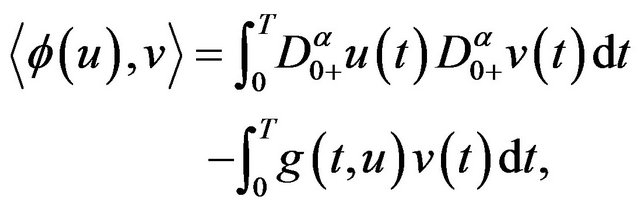 (3.5)
(3.5)
for . By the assumptions and the analogy arguments with, we have that
. By the assumptions and the analogy arguments with, we have that
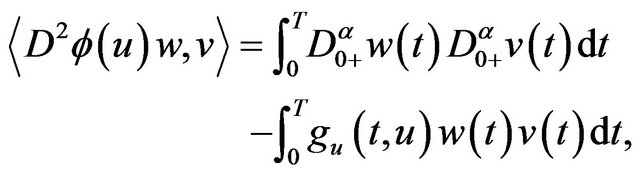 (3.6)
(3.6)
for .
.
For all 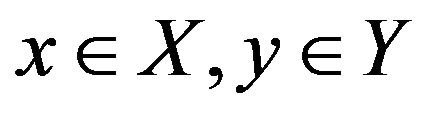 and
and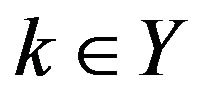 , by Proposition 2.4, we have that
, by Proposition 2.4, we have that
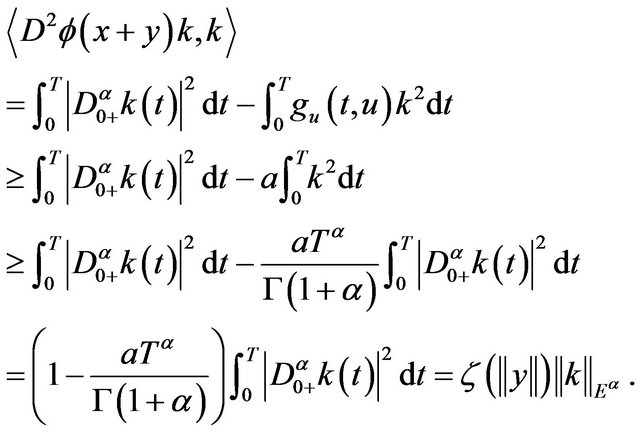
For all 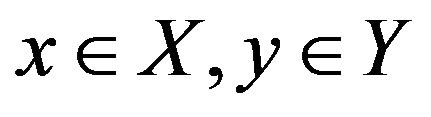 and
and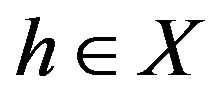 , we have that
, we have that
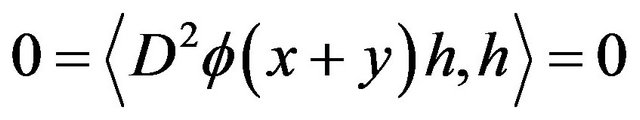
which implies that
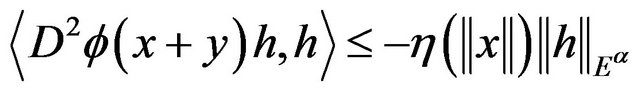
holds for all 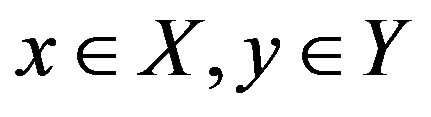 and
and . Obviously, functions
. Obviously, functions 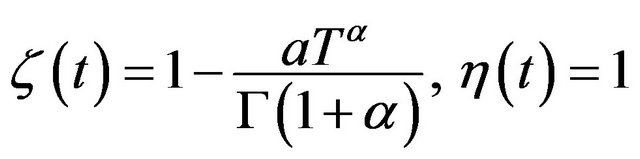 satisfy assumption conditions of the Min-Max Theorem. Hence, the MinMax Theorem assures that there exists unique
satisfy assumption conditions of the Min-Max Theorem. Hence, the MinMax Theorem assures that there exists unique 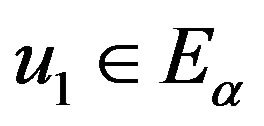 such that
such that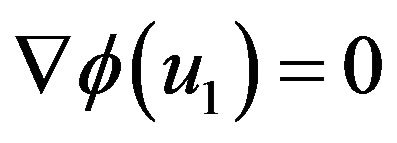 , which means that
, which means that 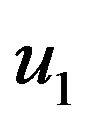 is a unique weak solution of (3.1).
is a unique weak solution of (3.1).
It follows from 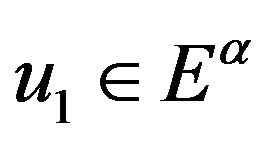 that
that , hence the left Caputo fractional equal to the left Riemann-Liouville fractional derivative. Hence, by the similar proofs of lemma theorem, we know that this weak solution
, hence the left Caputo fractional equal to the left Riemann-Liouville fractional derivative. Hence, by the similar proofs of lemma theorem, we know that this weak solution 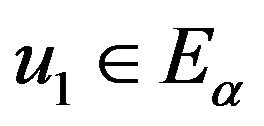 is also a solution of (3.1). Thus, we obtain that
is also a solution of (3.1). Thus, we obtain that  is unique solution of (1.1).
is unique solution of (1.1).
4. Conclusion
In this paper, using a Min-Max Theorem (Manasevich), we considered the existence and uniqueness of solution to some class of two-sided fractional differential equations with two-point boundary value problems.
5. Acknowledgements
The authors would like to thank those listed references for their helpful suggestions, which helped to improve the quality of the paper. This research supported by 2013 Science and Technology Research Project of Beijing Municipal Education Commission (KM201310016001) and 2011 Science and Technology Research Project of Beijing Municipal Education Commission (KM2011100160 12).
REFERENCES
- A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, “Theory and Applications of Fractional Differential Equations,” Elsevier, Amsterdam, 2006.
- I. Podlubny, “Fractional Differential Equations,” In: Mathematics in Science and Engineering, Academic Press, San Diego, 1999.
- D. Delbosco and L. Rodino, “Existence and Uniqueness for a Nonlinear Fractional Differential Equation,” Journal of Mathematical Analysis and Applications, Vol. 204, No. 2, 1996, pp. 609-625. doi:10.1006/jmaa.1996.0456
- V. Lakshmikantham and A. S. Vatsala, “Theory of Fractional Differential Inequalities and Applications,” Communications on Pure and Applied Analysis, Vol. 11, No. 3-4, 2007, pp. 395-402.
- V. Lakshmikantham and A. S. Vatsala, “General Uniqueness and Monotone Iterative Technique for Fractional Differential Equations,” Applied Mathematics Letters, Vol. 21, No. 8, 2008, pp. 828-834. doi:10.1016/j.aml.2007.09.006
- V. Lakshmikantham and A. S. Vatsala, “Basic Theory of Fractional Differential Equations,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 69, No. 8, 2008, pp. 2677-2682. doi:10.1016/j.na.2007.08.042
- H. Liang and J. H. Zhang, “Positive Solutions for Boundary Value Problems of Nonlinear Fractional Differential Equation,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 71, No. 11, 2009, pp. 5545-5550. doi:10.1016/j.na.2009.04.045
- S. Q. Zhang, “Positive Solutions to Singular Boundary Value Problem for Nonlinear Fractional Differential Equation,” Computers & Mathematics with Applications, Vol. 59, No. 3, 2010, pp. 1300-1309. doi:10.1016/j.camwa.2009.06.034
- Z. Bai and H. Lu, “Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation,” Journal of Mathematical Analysis and Applications, Vol. 311, No. 2, 2005, pp. 495-505. doi:10.1016/j.jmaa.2005.02.052
- R. P. Agarwal, Y. Zhou, J. R. Wang and X. N. Luo, “Fractional Functional Differential Equations with Causal Operators in Banach Spaces,” Mathematical and Computer Modelling, Vol. 54, No. 5-6, 2011, pp. 1440-1452. doi:10.1016/j.mcm.2011.04.016
- F. L. Chen, J. J. Nieto and Y. Zhou, “Global Attractivity for Nonlinear Fractional Differential Equations,” Nonlinear Analysis: Real World Applications, Vol. 13, No. 1, 2012, pp. 287-298. doi:10.1016/j.nonrwa.2011.07.034
- F. Jiao and Y. Zhou, “Existence of Solutions for a Class of Fractional Boundary Value Problems via Critical Point theory,” Computers & Mathematics with Applications, Vol. 62, No. 3, 2011, pp. 1181-1199. doi:10.1016/j.camwa.2011.03.086
- F. Jiao and Y. Zhou, “Existence of Solutions for a Class of Fractional Boundary Value Problems via Critical Point Theory,” International Journal of Bifurcation and Chaos, Special Issue, to Appear.
- R. F. Manasevich, “A Min-Max Theorem,” Journal of Mathematical Analysis and Applications, Vol. 90, No. 1, 1982, pp. 64-71. doi:10.1016/0022-247X(82)90044-0

