Agricultural Sciences
Vol. 3 No. 7 (2012) , Article ID: 24661 , 13 pages DOI:10.4236/as.2012.37116
Global sensitivity analysis for choosing the main soil parameters of a crop model to be determined
![]()
1Syngenta Crop Protection Münchwilen AG, Stein/AG, Switzerland; *Corresponding Author: hubert_vincent.varella@syngenta.com
2INRA, UMR 1114 INRA-UAPV EMMAH, Avignon, France
3INRA, Unite Agroclim, Avignon, France
Received 10 August 2012; revised 12 September 2012; accepted 8 October 2012
Keywords: Global Sensitivity Analysis; Uncertainty Analysis; Soil Parameters; Crop Model STICS; Management Decision Support; Agro-Environmental Variables
ABSTRACT
The use of a crop model like STICS for appropriate management decision support requires a good knowledge of all the parameters of the model. Among them, the soil parameters are difficult to know at each point of interest and costly techniques may be used to measure them. It is therefore important to know which soil parameters need to be determined. It can be stated that those which affect significantly the output variable deserve an accurate determination while those which slightly affect the model output variable do not. This paper demonstrates how a global sensitivity analysis method based on variance decomposition can be applied on soil parameters in order to divide them in the two categories. The Extended FAST method applied to the crop model STICS and a set of 13 soil parameters first allows to calculate the part of variance explained by each soil parameter (giving global sensitivity indices of the soil parameters) and the coefficient of variation of the output variables (measuring the effect of the parameter uncertainty on each variable). These metrics are therefore used for deciding on the importance of the parameter value measurement. Different output variables (Leaf Area Index and chlorophyll content) are evaluated at different stages of interest while others (crop yield, grain protein content, soil mineral nitrogen) are evaluated at harvest. The analysis is applied on two different annual crops (wheat and sugar beet), two contrasted weather and two types of soil depth. When the uncertainty of the output generated by the soil parameters is large (coefficient of variation > 1/3), only the parameters having a significant global sensitivity indices (higher than 10%) are retained. The results show that the number of soil parameters which deserve an accurate determination can be significantly reduced by the use of this relevant method for appropriate management decision support.
1. INTRODUCTION
Dynamic crop models are very useful to predict the behavior of crops in their environment and are widely used in a lot of agro-environmental work such as crop monitoring, yield prediction or decision making for cultural practices [1-3]. These models usually have many parameters and their spatial application for agro-environmental predictions is difficult without a good knowledge of these parameters [4-6].
The crop model parameters can be divided in three groups: those related to the agricultural techniques, those related to the genotype of the crop and those related to the soil properties. Generally, agricultural techniques are quite easy to know as they are those used by the farmer. Crop parameters can be determined from literature, or estimated from experimental work or calibrated on a large database [7-9]. The knowledge of the soil parameters is an important issue because the spatial variability of the crop model simulations depends for a large part on the soil parameter values [10] and predictions obtained with the model are not reliable when inaccurate parameter values are used. This knowledge may be especially difficult to acquire because parameter values can greatly vary in space [11,12]. The use of existing soil maps and associated pedotransfer functions can be considered where accurate soil map are available [13]; but in many cases, the spatial accuracy of the map is too limited for accurate applications such as for example precision agriculture [14]. In those cases, these parameters should be determined in another way. Measurements can be made directly with soil sampling analysis at different locations of the study area or indirectly by using electrical geophysical measurements [15,16]. Whatever the technique of measurement used, it is submitted to practical limitations and to time and financial constraints. Another way of gathering quite accurate values on soil parameters consists in estimating them through an inverse modeling approach using a crop model and observations on the crop state variables [11,17,18]. However, the soil parameters may not have the same contribution to the performance of the crop model and do not require the same precision of determination for a given objective: some of them deserve an accurate determination while the others can be fixed at nominal values [19,20]. Considering this aspect, the practical limitations of soil parameter measurements, as well as time and financial constraints should be reduced by considering only a subset of the crop model soil parameters depending on the objective and configuration of the study.
The combination of uncertainty analysis and sensitivity analysis techniques should help in identifying these key parameters. The objective of sensitivity analysis is to study how the variation of selected outputs of a model can be apportioned to different sources of variation [21]. In particular, sensitivity analysis methods can be used to rank uncertain input factors with respect to their effects on the model output variables by calculating quantitative or qualitative indices. Nevertheless, the fact that some factors are detected as important for a given output variable on the basis of sensitivity analysis results is not sufficient to decide that the uncertainties on these factors should be reduced. Indeed, if the variation of the considered output variable induced by the uncertainties on the factors is low, the results of sensitivity analysis on this output variable should not be taken into account. The description and quantification of these variations is the objective of uncertainty analysis.
Some authors [19,22-26] used uncertainty analysis techniques to quantify the uncertainties of a selection of crop models output variables generated by uncertainties on some selections of input parameters. Others authors [27-32] used global sensitivity analysis to evaluate the contribution of the parameters to the variance of the model output variables. In this study we propose a helpful combination of these techniques to identify soil parameters that need particular accuracy for simulating a set of given output variables of interest in spite of the financial and practical interests of such a study.
A variance-based sensitivity analysis method is used in order to rank the soil parameters relatively to their importance on some selected outputs of the crop model STICS (Simulateur multidisciplinaire pour les Cultures Standard) [33] and to select those which deserve an accurate determination by considering also the coefficient of variation of the outputs, that is the variation of the outputs compared to their magnitude. We considered 13 soil parameters and their effects on 5 dynamic output variables of the STICS crop model, at different phenological stages, which are involved in decision making for crop management. Two different crops (winter wheat and sugar beet) growing on different seasons are considered in order to illustrate the impact of soil properties on crop growth. Each crop considered is simulated under different pedological conditions and weather.
2. METHODS
2.1. The STICS Model
The STICS model [33,34] is a nonlinear dynamic crop model simulating various crops. For a given crop, STICS takes into account the weather, the type of soil and the cropping techniques used, and simulates the carbon, water and nitrogen balances of the crop-soil system on a daily time-scale. In this study, winter wheat and sugar beet crops are simulated. The crop is essentially characterized by its above-ground biomass carbon and nitrogen, and leaf area index. The soil is considered as a series of layers where the transfer of water and nitrate is described by a reservoir-type analogy. The main outputs are agronomic variables (yield, grain protein content for wheat) as well as environmental variables (water and nitrate leaching).
The STICS model includes more than 200 parameters. The global sensitivity analysis described in this study only concerns the soil parameters. The values of the parameters related to the crop have been determined either from literature, from experimental works conducted on specific processes included in the model (e.g. mineralization rate, critical nitrogen dilution curve etc.) or from a calibration based on a large experimental database [35]. Cropping techniques and soil parameters ranges are described in Section 2.5.
2.2. The Soil Parameters
Among the available options for simulating the soil system, the simplest was chosen in this study, by considering only the transfers in the microporosity and ignoring those in the macroporosity, the cracks, pebbles, and processes like capillary rise and nitrification. We then considered the soil as a succession of two horizontal layers, the top layer having a thickness fixed at 30 cm.
These different hypotheses made on the soil description lead to consider a set of 13 soil parameters, defined in Table 1. They refer to permanent characteristics and initial conditions. Among the permanent characteristics, clay and organic nitrogen content of the top layer are

Table 1. Definition of the 13 soil parameters and their ranges of variation.
involved mainly in organic matter decomposition processes. Water content at field capacity of both layers affects the water (and nitrogen) movements and storage in the soil reservoir and the thickness of the second layer defines the volume of the reservoir. The initial conditions correspond to the water and nitrogen content, Hinit and NO3init, at the beginning of the simulation, in this case the sowing date.
2.3. Model Output
In this study, the STICS output variables of interest are:
1) The amount of nitrogen absorbed by the plant (QN) and the leaf area index (LAI) at two (for sugar beet) or three (for wheat) different key stages during the season, which are important variables for making a diagnosis on crop growth2) The yield, and the mineral nitrogen content in the soil at harvest (for both crops) plus the grain protein content (for wheat), which are of particular interest for decision making, especially for monitoring nitrogen fertilization.
The different stages of interest and the corresponding variables are displayed for each crop on Table 2. For the wheat, the three key stages concern the maximum leaf growth rate-beginning of stream elongation-(AMF), the maximum leaf areaor booting-(LAX) and the flowering (FLO). For the sugar beet, the two key stages concern the maximum leaf growth rate (AMF) and the maximum leaf area (Summer).
2.4. Sensitivity and Uncertainty Analysis
Among the available methods of sensitivity analysis, variance-based methods are well adapted for non-linear models that need less than 1 minute for a simulation [36]. These methods are widely used in different contexts [27,28,30-32]. Their principle is to evaluate the contribution of the given uncertain factors to the variance of the model output variables selected. We will describe in this section the sensitivity indices that can be computed with these methods and the EFAST variance-based method we have used in this study to compute these indices. Uncertainty analysis is performed here by computing the coefficient of variation of the output variables considered from the simulations realized for the sensitivity analysis.
2.4.1. Sensitivity Indices and Coefficient of Variation
We note further Y an output variable of STICS. Y will represent in turn LAI and QN computed at the different phenological stages and the variables computed at harvest. The total variance of Y, V(Y), is partitioned as follows [37]:
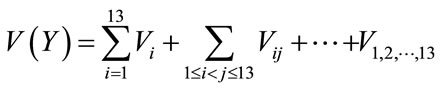 (1)
(1)
where V(Y) is the total variance of the output variable Y induced by the 13 soil parameters q, 

Table 2. Definition of the variables and the stages of interest.
measures the main effect of the parameter qi, i = 1, ···, 13, and the other terms measure the interaction effects. Decomposition (1) is used to derive two types of sensitivity indices defined by:
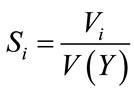 (2)
(2)
 (3)
(3)
where V−i is the sum of all the variance terms that do not include the index i.
Si is the first-order sensitivity index of the ith parameter. It computes the fraction of Y variance explained by the uncertainty of parameter qi and represents the main effect of this parameter on the output variable Y. STi is the total sensitivity index of the ith parameter and is the sum of all effects (first and higher order) involving the parameter qi. Si and STi are both in the range (0, 1), low values indicating negligible effects, and values close to 1 huge effects. STi takes into account both Si and the interactions between the ith parameter and the 12 other parameters, interactions which can therefore be assessed by the difference between STi and Si. The interaction terms of a set of parameters represent the fraction of V(Y) induced by these parameters but that is not explained by the sum of their main effects. The two sensitivity indices Si and STi are equal if the effect of the ith parameter on the model output is independent of the values of the other parameters: in this case, there is no interaction between this parameter and the others and the model is said to be additive with respect to qi. Selecting the parameters that have a negligible effect and that can thus be fixed to nominal values is called factor fixing in the literature [38]. Total effects must be considered in this case. Indeed, a factor that has a small main effect but a medium to high total effect cannot be considered as negligible: its effect depends on the value of other uncertain factors and can be important in some cases.
The coefficient of variation of the output variable Y can be calculated by:
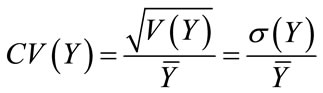 (4)
(4)
where, s(Y) is the standard deviation of the output variable Y and  is the mean of Y induced by the 13 soil parameters q.
is the mean of Y induced by the 13 soil parameters q.
2.4.2. Extended FAST
Sobol’s method and Fourier Amplitude Sensitivity Test (FAST) are two of the most widely used methods to compute Si and STi [11]. We have chosen here to use the extended FAST (EFAST) method, which has been proved, in several studies [30,39,40], to be more efficient in terms of number of model evaluations than Sobol’s method. The main difficulty in evaluating the first-order and total sensitivity indices is that they require the computation of high dimensional integrals. The EFAST algorithm performs a judicious deterministic sampling to explore the parameter space which makes it possible to reduce these integrals to one-dimensional ones using Fourier decompositions. The reader interested in a detailed description of EFAST can refer to [40].
We have implemented the EFAST method in the Matlab® software, as well as a specific tool for computing and easily handling numerous STICS simulations. The uncertainties considered for the soil parameters are described in the next section. A preliminary study of the convergence of the sensitivity indices allowed us to set the number of simulations per parameter to 5000, leading to a total number of model runs of 13 × 5000 = 65,000 to compute the main and total effects for all output variables and parameters considered here. One run of the STICS model takes about 1s with a Pentium 4, 2.9 GHz processor.
2.5. Data
In this study, we have considered two crops: winter wheat and sugar beet. This allows to illustrate the difference of sensitivities of different crops to the soil properties. For the same reason, each crop is simulated for two different weathers and two different types of soil depth. The weather data were obtained from the meteorological station of Roupy (49.48˚N, 3.11˚E). The first set of data is chosen to characterize a dry weather (1975-1976) and the second set is chosen to characterize a wet weather (1990-1991). Table 3 shows the amount of rainfall calculated for each season and weather data set. The wheat crop simulated in this study is sown on October 30th while the sugar beet crop is sown on March 30th. The amount of fertilizer provided on wheat varies between 200 kg (shallow soil) and 240 kg (deep soil), while the amount provided on sugar beet varies between 150 kg (shallow soil) and 200 kg (deep soil).
The range of parameter values considered in this study correspond to the soil description of the precision agriculture experimental site in northern France near Laon, Picardie (Chambry 49.35˚N, 3.37˚E) [41]. In this study, the uncertainties of these 13 soil parameters are observed in the literature (for parameters related to albedo, evapotranspiration or drip rainfall) or measured in the experimental site (for the other parameters), and their ranges of variation are displayed on Table 1. Concerning the parameter NO3init two ranges of variation are considered, depending on the crop cultivated just before the one considered: in this study, the wheat is cultivated after sugar beet and the sugar beet is cultivated after a bare soil. The different previous crops used determine the quantity of nitrogen NO3init at the beginning of the corresponding crop season. The two different types of soil depth are defined by their ranges of variation (Table 1) and correspond to a shallow soil and a deep soil. The uncertainties considered in the global sensitivity analysis for the soil parameters are assumed independent and follow uniform distributions. The ranges of variation of the distributions are given in Table 1.
3. RESULTS AND DISCUSSION
Only the main results of the study are presented here for the sake of clarity. These results concern: 1) wheat crop simulated with dry, then wet weather and a shallow soil and 2) sugar beet crop simulated with dry, then wet weather and a deep soil.
3.1. Global Sensitivity Analysis
Figure 1 shows the sensitivity indices calculated for the 13 soil parameters and for each output variable of the wheat crop simulated with a dry weather and a shallow soil. For the early stage the initial water content is dominant because in the considered weather, the rainfall is light in autumn when the wheat is sown (see Table 3): at the stage AMF (Figure 1(a)), Hinit is the only parameter
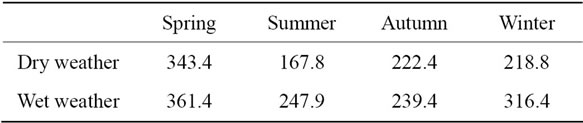
Table 3. Amount of rainfall (in mm) calculated for each season and weather.
contributing (for more than 90%) to the output variance for both variables LAI and QN. In the later stages, the effects of parameters evolve with the soil volume explored by the roots (first layer, then second one), up to the flowering stage where the root development is maximum: at the stage LAX (Figure 1(b)) and FLO (Figure 1(c)), the effect of Hinit disappears and that of HCC(1) and epc(2) increase, with a dominant position of epc(2). At Harvest (Figure 1(d)), the variables are much sensitive to epc(2) followed by HCC(1), HCC(2) and Hinit for the three variables and albedo for the variable protein of the grain. In those conditions of dry weather and shallow soil, the parameters related to water availability (epc(2), HCC(1), HCC(2) and Hinit) are the main parameters contributing to the variance of the outputs. Those concerned by the turnover of organic nitrogen in the soil are not concerned, because the water stress is the dominant limiting factor and also because the mineralization processes are reduced by dry conditions.
When considering wet conditions (Figure 2), the water stress is not so much a limiting factor: maximum LAI is equal to 3.61 in average, whereas it is equal to 2.57 in dry conditions (see Table 4). The roots grow more rapidly at the beginning of the season and the size of the soil reservoir (via the parameter epc(2)) is important since the AMF stage: the depth of roots is equal to 55.84 in average (3 months after the sowing), whereas it is equal to 45.62 in dry conditions (see Table 4). Moreover, in these conditions, the mineralization of the soil organic matter is increased and the effects of the concerned parameters argi and Norg do so: the cumulative mineral nitrogen arising from humus is equal to 23.95 in average (at stage LAX), whereas it is equal to 18.09 in dry conditions (see Table 4). This does not seem to influence the effects of the different parameters on LAI at stage AMF since they are very similar to these obtained with the dry weather. On the contrary, the sensitivities of the variable QN to the different parameters are very different from the ones obtained with a dry weather: there is no contribution of Hinit but epc(2), HCC(1) and parameters involved in the mineralization process (argi, Norg and NO3init) contribute to the output variance.
This is also the case for both LAI and QN on later stages, with an increasing dominancy of epc(2). At Harvest (Figure 2(d)), the variables are sensitive to the parameters epc(2), HCC(1) and HCC(2) with still a slight sensitivity to argi and Norg for the soil mineral nitrogen
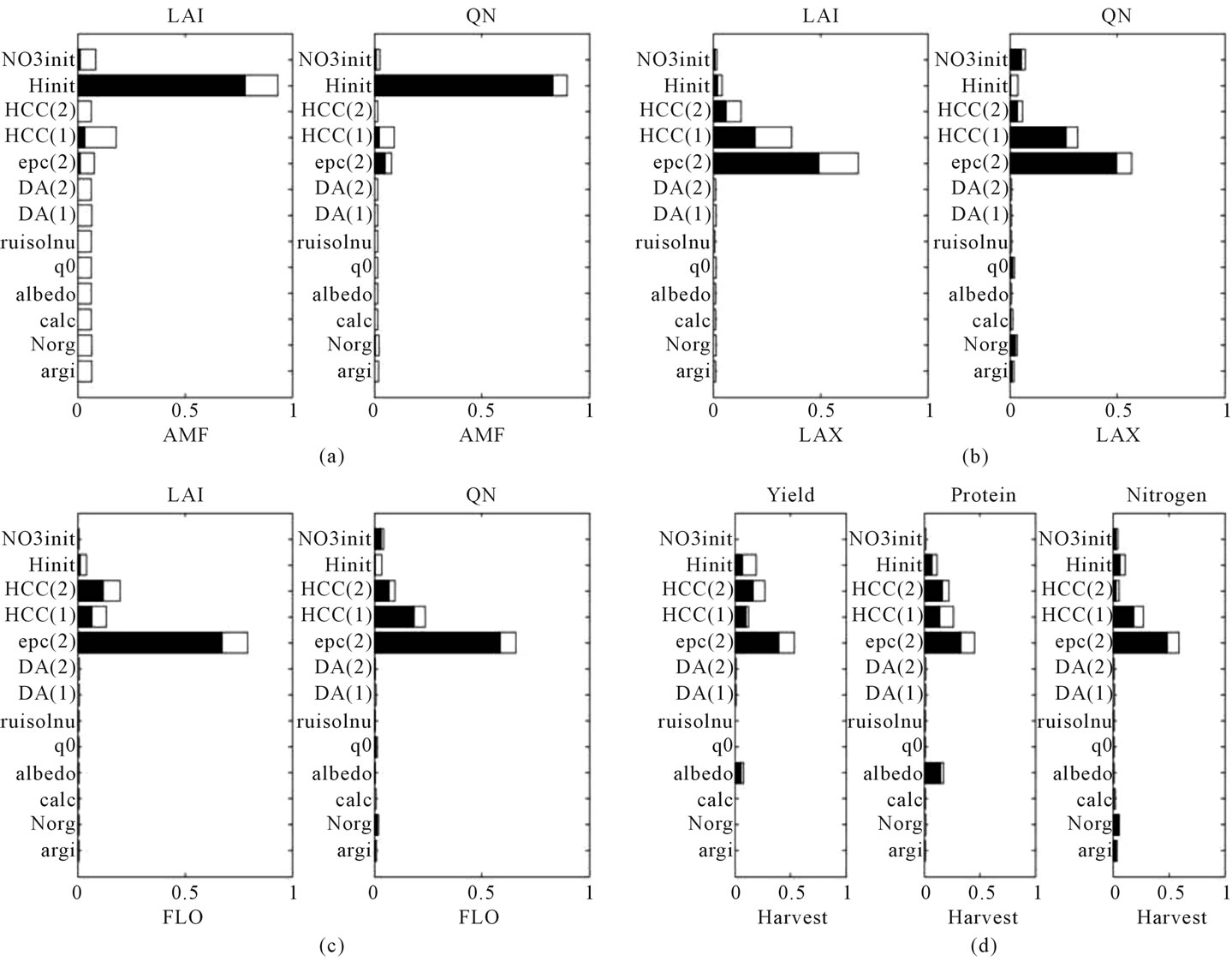
Figure 1. Sensitivity indices of the 13 soil parameters for each model output of the wheat crop simulated with a dry weather and a shallow soil. The outputs (a) correspond to LAI and QN at stage AMF; (b) correspond to LAI and QN at stage LAX; (c) correspond to LAI and QN at stage FLO and (d) correspond to Yld, Prot and Nit at Harvest. First-order indices are in black and interactions in white.
content. The main difference between these results and those presented in Figure 1 lies in the sensitivity to parameters involved in the mineralization process (especially argi and Norg).
When considering wet conditions (Figure 2), the water stress is not so much a limiting factor: maximum LAI is equal to 3.61 in average, whereas it is equal to 2.57 in dry conditions (see Table 4). The roots grow more rapidly at the beginning of the season and the size of the soil reservoir (via the parameter epc(2)) is important since the AMF stage: the depth of roots is equal to 55.84 in average (3 months after the sowing), whereas it is equal to 45.62 in dry conditions (see Table 4). Moreover, in these conditions, the mineralization of the soil organic matter is increased and the effects of the concerned parameters argi and Norg do so: the cumulative mineral nitrogen arising from humus is equal to 23.95 in average (at stage LAX), whereas it is equal to 18.09 in dry conditions (see Table 4). This does not seem to influence the effects of the different parameters on LAI at stage AMF since they are very similar to these obtained with the dry weather. On the contrary, the sensitivities of the variable QN to the different parameters are very different from the ones obtained with a dry weather: there is no contribution of Hinit but epc(2), HCC(1) and parameters involved in the mineralization process (argi, Norg and NO3init) significantly contributes to the variance of this variable. This is also the case for both LAI and QN on later stages, with an increasing dominancy of epc(2). At Harvest (Figure 2(d)), the variables are sensitive to the parameters epc(2), HCC(1) and HCC(2) with still a slight sensitivity to argi and Norg for the soil mineral nitrogen content. The main difference between these results and those presented in Figure 1 lies in the sensitivity to parameters involved in the mineralization process (especially argi and Norg).

Figure 2. Sensitivity indices of the 13 soil parameters for each model output of the wheat crop simulated with a wet weather and a shallow soil. The outputs (a) correspond to LAI and QN at stage AMF; (b) correspond to LAI and QN at stage LAX; (c) correspond to LAI and QN at stage FLO and (d) correspond to Yld, Prot and Nit at Harvest. First-order indices are in black and interactions in white.
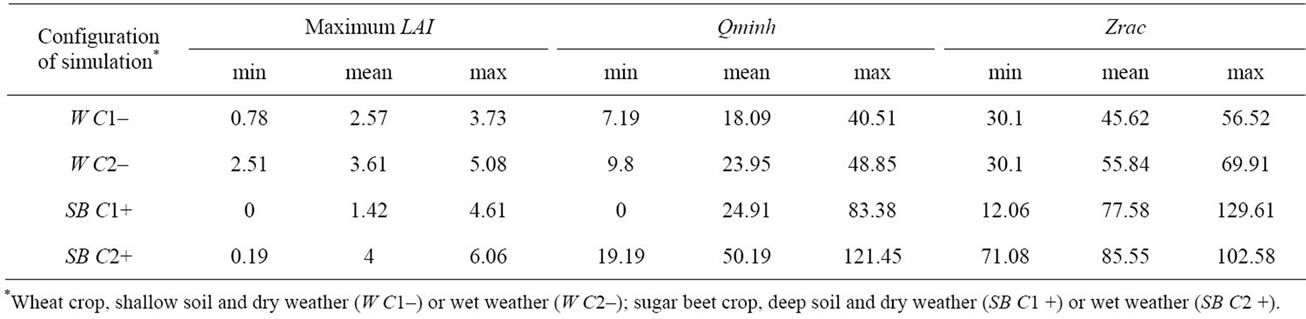
Table 4. Ranges of some output variables uncertainties generated by the uncertainties on the soil parameters. The output concerns the value of maximum LAI, the cumulative mineral nitrogen arising from humus Qminh (calculated at the stage LAX or Summer) and the depth of roots Zrac (calculated 3 months after the sowing date).
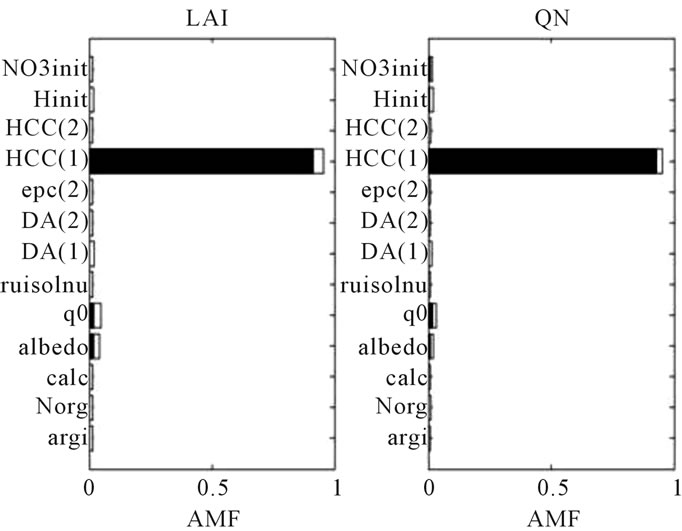
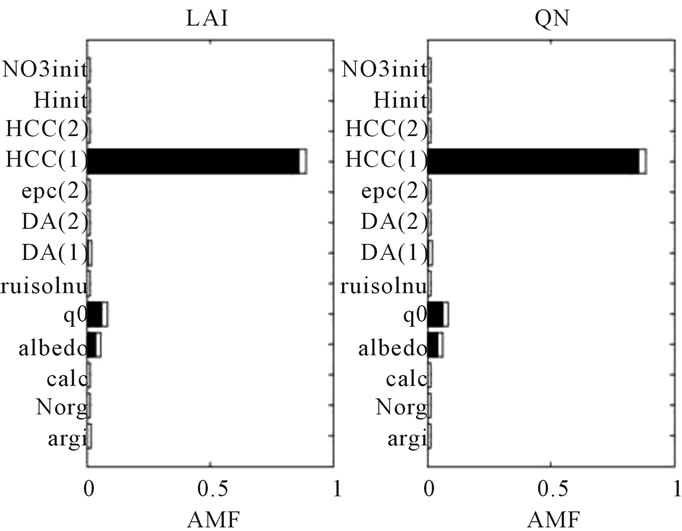
Figure 3 shows the sensitivity indices calculated for the 13 soil parameters and for each output variable of the sugar beet crop simulated with a deep soil and a dry weather. In this case, the crop grows mainly in summer where it experiences a severe water stress, leading to a value of maximum LAI equal to 1.42 in average (see Table 4). The depth of the second layer (parameter epc(2)) does not have any importance here. This is also the case for wheat crop with a deep soil (results not shown here). Indeed, as the root growth is no longer limited by the
 (a)
(a)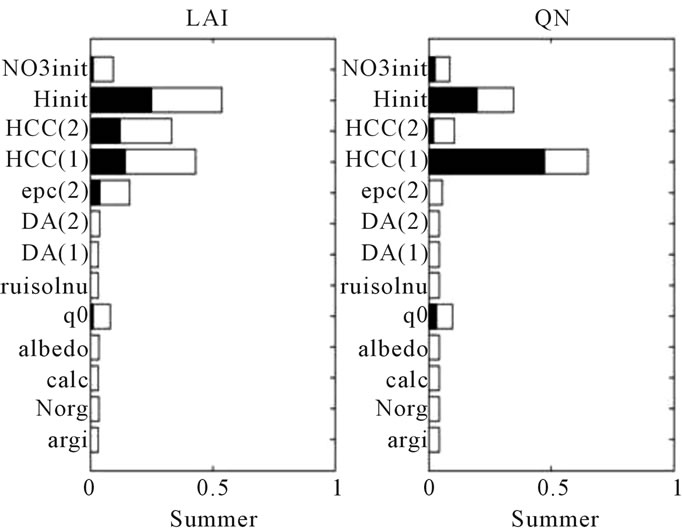 (b)
(b)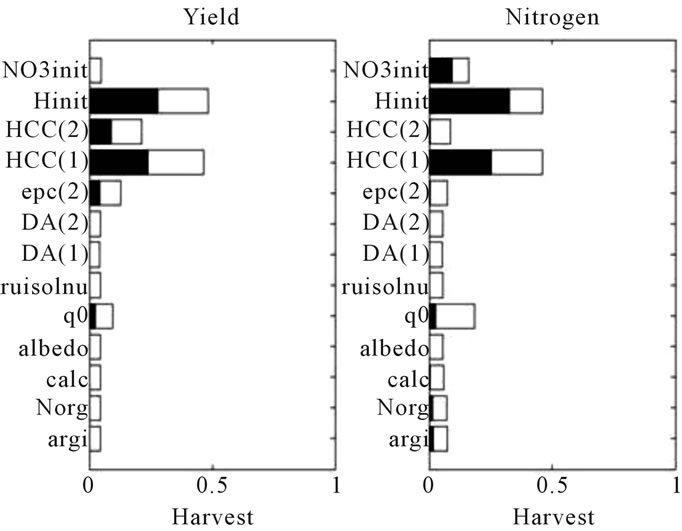 (c)
(c)
Figure 3. Sensitivity indices of the 13 soil parameters for each model output of the sugar beet crop simulated with a dry weather and a deep soil. The outputs (a) correspond to LAI and QN at stage AMF; (b) correspond to LAI and QN at Summer and (c) correspond to Yld and Nit at Harvest. First-order indices are in black and interactions in white.
thickness of soil (the depth of roots is equal to 77.58 in average), the output variables are no longer sensitive to the parameter epc(2) when the soil is deep. Moreover, the outputs are not at all sensitive to the initial water content Hinit because the amount of rainfall is quite important in spring, when the sugar beet is sown (see Table 3). The soil water reserve is therefore the main limiting factor and it depends only on HCC(1) for the early stage AMF: it contributes for 95% of the total output variance of LAI and QN. For the Summer stage (Figure 3(b)), which correspond to the maximum of water stress index, LAI is mainly sensitive to parameters linked to water availability of both soil layers (HCC(1) and HCC(2)) with an increase of the sensitivity to Hinit. QN is more sensitive to characteristics of the top layer (HCC(1) and Hinit) where is concentrated the organic nitrogen, as it influences the fate of available nitrogen coming from mineralization. The same tendencies are noticed for the output variables at Harvest, the yield being more linked to LAI and soil mineral nitrogen to QN. Many interactions are visible between all these parameters. It is also noticeable that, as in the case of wheat, the output variables have very low sensitivity to the parameters concerned with nitrogen turnover in the soil, due to the dry weather and limited mineralization. The main differences of these results with respect to those presented for the wheat crop (Figures 1 and 2) is: 1) that HCC(1) contributes a lot to the variance of the output variables during all the crop season; 2) that Hinit has no contribution to the variance of the output variables at the beginning of the sugar beet season and 3) that epc(2) does not affect the output variables when the soil is deep.
When considering wet conditions (Figure 4), the sugar beet crop growth is less affected by the water stress: maximum LAI is equal to 4 in average, whereas is equal to 1.42 in dry conditions (see Table 4). The soil water reserve of the second layer is not a limiting factor in deep soil and wet conditions for both stages AMF and Summer because the soil reservoir has a large size and the water stress is low. Thus, LAI and QN are only sensitive to the soil water reserve of the first layer which only depends on HCC(1) (it does not depend on Hinit because of the high amount of rainfall in spring). Nevertheless, the soil water reserve of the second layer becomes a limiting factor at the end of the sugar beet crop season, when the roots are deep, involving a significant sensitivity of the output Yld to the parameters HCC(1), HCC(2) and epc(2). Moreover, the mineralization of the soil organic matter slightly increases in wet conditions and so do the effects of the concerned parameters on QN at Summer and Nit at yield: the cumulative mineral nitrogen arising from humus is equal to 50.19 in average, whereas is equal to 24.91 in dry conditions (see Table 4). The main difference between these results and those presented in Figure 3, lies
 (a)
(a)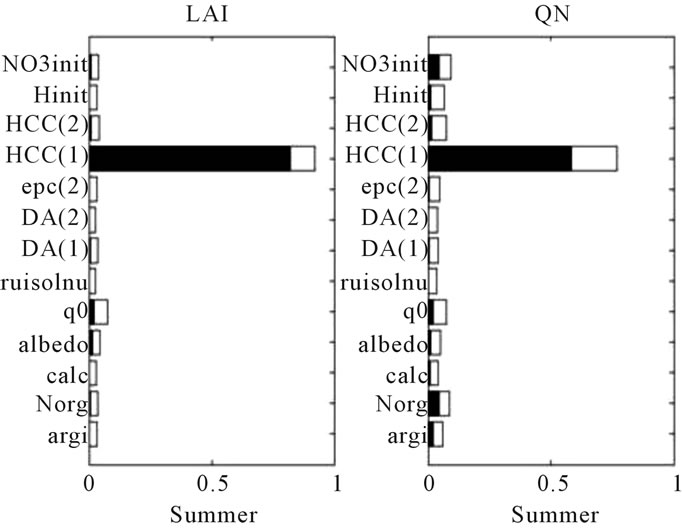 (b)
(b)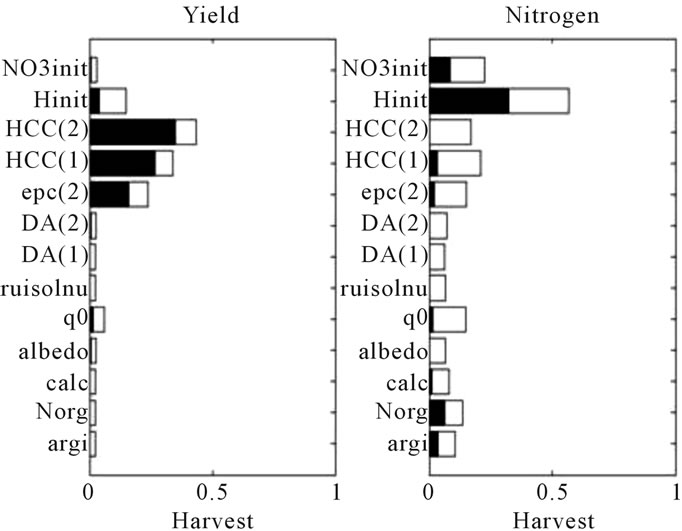 (c)
(c)
Figure 4. Sensitivity indices of the 13 soil parameters for each model output of the sugar beet crop simulated with a wet weather and a deep soil. The outputs (a) correspond to LAI and QN at stage AMF; (b) correspond to LAI and QN at Summer and (c) correspond to Yld and Nit at Harvest. First-order indices are in black and interactions in white.
in the lower sensitivity of the soil water reserve parameters of the second layer at the two first stages of interest.
3.2. Total Effect and Coefficient of Variation
For each configuration of simulation presented above, Figure 5 shows the coefficient of variation CV of each output variable and the corresponding total effect ST of each parameter. The horizontal dashed line is situated at an arbitrary minimum value ST = 10% and the vertical dashed line is situated at another arbitrary minimum value CV = 1/3. The threshold of 10% for ST has been proposed by [30] for screening the significant sensitivity values. When wheat crop is simulated with a dry weather and a shallow soil (see Figure 5(a)), three output variables have a coefficient of variation higher than 1/3: Prot (CV = 0.37), Yld (CV = 0.54) and LAI at the stage FLO (CV = 0.62). For these outputs, only 5 soil parameters have a ST higher than 10%: epc(2), HCC(1), HCC(2), Hinit and albedo. This means that for simulating correctly these output variables of the wheat crop when the weather is dry and the soil depth is shallow, only epc(2), HCC(1), HCC(2), Hinit and albedo have to be determined accurately and the other parameters can be fixed at a nominal value (assuming the arbitrary thresholds ST = 10% and CV = 1/3). When wheat crop is simulated with a wet weather and a shallow soil (Figure 5(b)), only the variable Nit has a coefficient of variation slightly higher than 1/3 (CV = 0.38). The corresponding parameters having a ST higher than 10% are epc(2), HCC(1), HCC(2) and Norg, meaning that these parameters are important to be determined accurately for simulating correctly the wheat crop in this case. The first main difference between the results presented in Figures 5(a) and (b) is that only one output variable has a CV higher than 1/3 when the weather is wet, instead of three when the weather is dry. The second main difference is that the parameters albedo and Hinit, which contribute for a significant part of the output variance when the weather is dry, are replaced by the parameter Norg, which is involved in the mineralization process and contribute for a significant part of the variance of the outputs when the weather is wet.
Considering the results presented in Figures 5(a) and (b), the parameter Hinit, which contributes for a large part to the variance of the output variables LAI and QN at the stage AMF of the wheat crop (see Section 3.1), does not need in fact an accurate determination for simulating correctly these output variables. Its ST values are higher than 0.8 for these outputs but the CV values of these outputs are lower than 0.1. If only the results provided by sensitivity analysis are used, Hinit would have been considered as an important parameter to be determined, but considering also the coefficient of variation allows stating that this parameter is not as important as previously
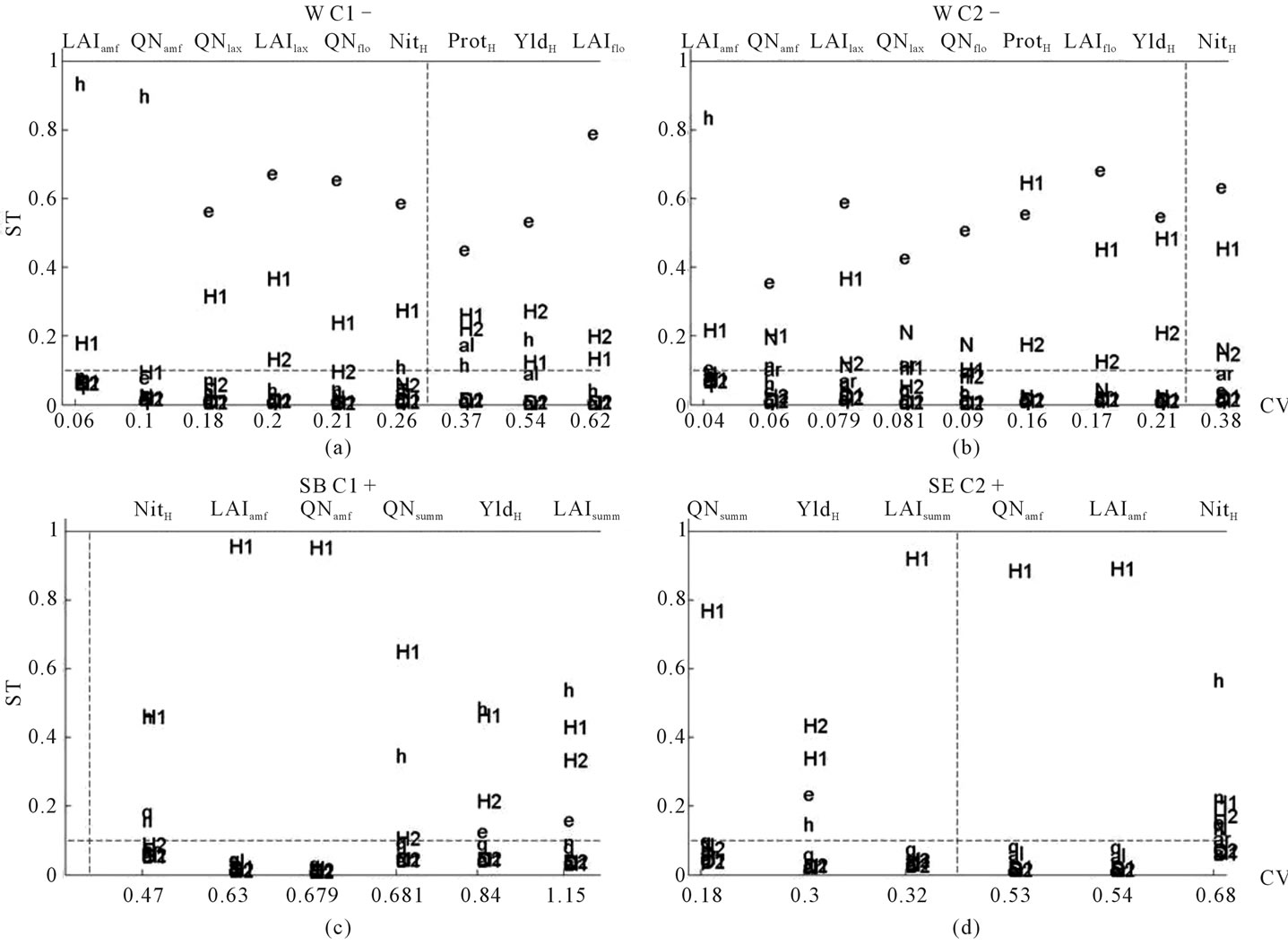
Figure 5. Coefficient of variation CV of each output variables and the corresponding total effects ST of the 13 soil parameters. The horizontal dashed line is situated at ST = 10% and the vertical dashed line is situated at CV = 1/3. The outputs are simulated for (a) wheat crop, dry weather and shallow soil, (b) wheat crop, wet weather and shallow soil, (c) sugar beet crop, dry weather and deep soil and (d) sugar beet crop, wet weather and deep soil. Label C1 correspond to the dry weather and C2 to the wet one, W correspond to the wheat crop and SB to sugar beet, − correspond to a shallow soil and + to a deep one. Parameter labels are presented in Table 1.
thought. The parameter epc(2), which contributes for a large part to the variance of all the output variables during all the wheat crop season (see Section 3.1), proves to be the most important parameter to be determined accurately for simulating the wheat crop when the type of soil depth is shallow.
The Figure 5(c) shows the results when the sugar beet crop is simulated with a dry weather and a deep soil. It reveals that all the output variables have a coefficient of variation higher than 1/3 meaning that the uncertainties on the soil parameters generate a large uncertainty on the considered variables. Among those parameters, five need to be measured accurately: epc(2), HCC(1), HCC(2), Hinit and q0. The main difference between the results presented in Figures 5(a) and (c) is that all the output variables are strongly affected by the measurement of the soil parameters when the sugar beet is simulated. When sugar beet is simulated with a deep soil and a wet weather (Figure 5(d)), only the output variables LAI and QN at the stage AMF and Nit have a CV higher than 1/3 (resp. CV = 0.54, 0.53 and 0.68). For LAI and QN at the stage AMF, the only parameter having a ST higher than 10% is HCC(1). For Nit, a lot of parameters exceeds this threshold: argi, Norg, q0, epc(2), HCC(1), HCC(2), Hinit and NO3init. It is thus necessary to determine accurately a lot of parameters for simulating correctly the output Nit, while it is necessary to determine only one parameter for simulating correctly LAI and QN at AMF.
When sugar beet is simulated with a deep soil and a wet weather (Figure 5(d)), only the output variables LAI and QN at the stage AMF and Nit have a CV higher than 1/3 (resp. CV = 0.54, 0.53 and 0.68). For LAI and QN at the stage AMF, the only parameter having a ST higher than 10% is HCC(1). For Nit, a lot of parameters exceeds this threshold: argi, Norg, q0, epc(2), HCC(1), HCC(2), Hinit and NO3init. It is thus necessary to determine accurately a lot of parameters for simulating correctly the output Nit, while it is necessary to determine only one parameter for simulating correctly LAI and QN at AMF. The main difference between these results and those presented in Figure 5(c) is that, excepted for the output Nit, at most one parameter has to be accurately known for simulating correctly the sugar beet crop in deep soil and wet conditions. The parameter HCC(1), which contributes for a large part to the variance of all the output variables during all the sugar beet crop season (see Section 3.1), proves to be the most important parameter to be measured accurately for simulating the sugar beet crop when the soil is deep.
4. CONCLUSIONS
Global sensitivity analysis is an interesting tool for ranking parameters with respect to their contribution to the variance of the output variables of a model. However, the only use of sensitivity indices proves to be unsatisfactory for deciding which parameters should be accurately measured in a given configuration. Only the combination of uncertainty and sensitivity analysis is relevant to reach this goal. We propose in this study a simple and easy to use method that combines these two analysis in order to select the parameters that needs particular accuracy for simulating a set of variables of interest with an acceptable precision. This method, which can be easily applied to any crop model and group of parameters, has three steps: 1) compute the global sensitivity indices for each uncertain parameter; 2) compute the coefficient of variation of the outputs of interest from the set of simulations performed at step 1); and 3) select the parameters to be accurately measured for simulating correctly these outputs by setting thresholds on sensitivity indices and coefficients of variation. Of course the results of this method are strongly linked to the uncertainties hypothesized for the parameters and special attention must be paid to this aspect. Coefficients of variation and sensitivity indices thresholds should be adapted to each case depending on the level of measurements constraints and of the accuracy wishes for model output simulations.
We apply this method to the crop model STICS for selecting soil parameters that need to be measured at a field scale. Practically this needs the knowledge of the conditions under which the crop grows (weather, type of soil depth, agricultural techniques…) and it has been shown here that the results depend on these conditions. Moreover, the field scale variability of soil parameters, assumed in this application, gives a larger importance to parameters related to water availability than those related to mineralization. Concerning non-permanent soil parameters such as initial conditions, the application of the method needs thus to be based on future scenarios. This application shows that the number of STICS soil parameters to be measured accurately for simulating correctly the output variables considered here for wheat and sugar beet crops (given the parameters uncertainties used and in the configurations studied) can be significantly reduced by the use of this method. This is of particular interest given the time and financial cost of soil measurements.
![]()
![]()
REFERENCES
- Batchelor, W.D., Basso, B. and Paz, J.O. (2002) Examples of strategies to analyze spatial and temporal yield variability using crop models. European Journal of Agronomy, 18, 141-158. doi:10.1016/S1161-0301(02)00101-6
- Gabrielle, B., Roche, R., Angas, P., Cantero-Martinez, C., Cosentino, L., Mantineo, M., Langensiepen, M., Henault, C., Laville, P., Nicoullaud, B. and Gosse, G. (2002) A priori parameterisation of the CERES soil-crop models and tests against several European data sets. Agronomie, 22, 119-132. doi:10.1051/agro:2002003
- Houlès, V., Mary, B., Guérif, M., Makowski, D. and Juste, E. (2004) Evaluation of the crop model STICS to recommend nitrogen fertilization rates according to agro-environmental criteria. Agronomie, 24, 1-9. doi:10.1051/agro:2004036
- Launay, M. and Guérif, M. (2003) Ability for a model to predict crop production variability at the regional scale: An evaluation for sugar beet. Agronomie, 23, 135-146. doi:10.1051/agro:2002078
- Tremblay, M. and Wallach, D. (2004) Comparison of parameter estimation methods for crop models. Agronomie, 24, 351-365. doi:10.1051/agro:2004033
- Varella, H., Guérif, M., Buis, S. and Beaudoin, N. (2010) Soil properties estimation by inversion of a crop model and observations on crop improves the prediction of agroenvironmental variables. European Journal of Agronomy, 33, 139-147. doi:10.1016/j.eja.2010.04.005
- Flenet, F., Villon, P. and Ruget, F.O. (2003) Methodology of adaptation of the STICS model to a new crop: Spring linseed (Linum usitatissimum, L.). STICS Workshop, Camargue, FRANCE, 367-381.
- Hadria, R., Khabba, S., Lahrouni, A., Duchemin, B., Chehbouni, A., Carriou, J. and Ouzine, L. (2007) Calibration and validation of the STICS crop model for managing wheat irrigation in the semi-arid Marrakech/Al Haouzi plain. Arabian Journal for Science and Engineering, 32, 87-101.
- Singh, A.K., Tripathy, R. and Chopra, U.K. (2008) Evaluation of CERES-Wheat and CropSyst models for waternitrogen interactions in wheat crop. Agricultural Water Management, 95, 776-786. doi:10.1016/j.agwat.2008.02.006
- Guérif, M. and Duke, C. (1998) Calibration of the SUCROS emergence and early growth module for sugar beet using optical remote sensing data assimilation. European Journal of Agronomy, 9, 127-136. doi:10.1016/S1161-0301(98)00031-8
- Ferreyra, R.A., Jones, J.W. and Graham, W.D. (2006) Parameterizing spatial crop models with inverse modeling: Sources of error and unexpected results. Transactions of the Asabe, 49, 1547-1561.
- Irmak, A., Jones, J.W., Batchelor, W.D. and Paz, J.O. (2001) Estimating spatially variable soil properties for application of crop models in precision farming. Transactions of the ASAE, 44, 1343-1353.
- Nemes, A., Timlin, D.J., Pachepsky, Y.A. and Rawls, W.J. (2009) Evaluation of the Rawls et al. (1982) Pedotransfer Functions for their Applicability at the US National Scale. Soil Science Society of America Journal, 73, 1638-1645.
- King, D., Daroussin, J. and Tavernier, R. (1994) Development of a soil geographic database from the soil map of the European communities. Catena, 21, 37-56. doi:10.1016/0341-8162(94)90030-2
- Bourennane, H., King, D., Couturier, A., Nicoullaud, B., Mary, B. and Richard, G. (2007) Uncertainty assessment of soil water content spatial patterns using geostatistical simulations: An empirical comparison of a simulation accounting for single attribute and a simulation accounting for secondary information. Ecological Modelling, 205, 323-335. doi:10.1016/j.ecolmodel.2007.02.034
- Samouelian, A., Cousin, I., Tabbagh, A., Bruand, A. and Richard, G. (2005) Electrical resistivity survey in soil science: A review. Soil & Tillage Research, 83, 173-193. doi:10.1016/j.still.2004.10.004
- Braga, R.P. and Jones, J.W. (2004) Using optimization to estimate soil inputs of crop models for use in site-specific management. Transactions of the ASAE, 47, 1821-1831.
- Varella, H., Guérif, M. and Buis, S. (2010) Global sensitivity analysis measures the quality of parameter estimation: The case of soil parameters and a crop model. Environmental Modelling & Software, 25, 310-319. doi:10.1016/j.envsoft.2009.09.012
- Bouman, B.A.M. (1994) A framework to deal with uncertainty in soil and management parameters in crop yield simulation: A case-study for rice. Agricultural Systems, 46, 1-17. doi:10.1016/0308-521X(94)90166-D
- St'astna, M. and Zalud, Z. (1999) Sensitivity analysis of soil hydrologic parameters for two crop growth simulation models. Soil & Tillage Research, 50, 305-318. doi:10.1016/S0167-1987(99)00021-5
- Saltelli, A., Chan, K. and Scott, E.M. (2000) Sensitivity analysis. John Wiley and Sons, New York.
- Aggarwal, P.K. (1995) Uncertainties in crop, soil and weather inputs used in growth-models: Implications for simulated outputs and their applications. Agricultural Systems, 48, 361-384. doi:10.1016/0308-521X(94)00018-M
- Blasone, R.S., Madsen, H. and Rosbjerg, D. (2008) Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling. Journal of Hydrology, 353, 18-32. doi:10.1016/j.jhydrol.2007.12.026
- Lawless, C., Semenov, M.A. and Jamieson, P.D. (2008) Quantifying the effect of uncertainty in soil moisture characteristics on plant growth using a crop simulation model. Field Crops Research, 106, 138-147. doi:10.1016/j.fcr.2007.11.004
- Tolson, B.A. and Shoemaker, C.A. (2008) Efficient prediction uncertainty approximation in the calibration of environmental simulation models. Water Resources Research, 44, W04411. doi:10.1029/2007WR005869
- Van der Keur, P., Hansen, J.R., Hansen, S. and Refsgaard, J.C. (2008) Uncertainty in simulation of nitrate leaching at field and catchment scale within the odense river basin. Vadose Zone Journal, 7, 10-21. doi:10.2136/vzj2006.0186
- Campolongo, F. and Saltelli, A. (1997) Sensitivity analysis of an environmental model an application of different analysis methods. Reliability Engineering & System Safety, 57, 49-69. doi:10.1016/S0951-8320(97)00021-5
- Gomez-Delgado, M. and Tarantola, S. (2006) GLOBAL sensitivity analysis, GIS and multi-criteria evaluation for a sustainable planning of a hazardous waste disposal site in Spain. International Journal of Geographical Information Science, 20, 449-466. doi:10.1080/13658810600607709
- Lamboni, M., Makowski, D., Lehuger, S., Gabrielle, B. and Monod, H. (2009) Multivariate global sensitivity analysis for dynamic crop models. Field Crops Research, 113, 312-320. doi:10.1016/j.fcr.2009.06.007
- Makowski, D., Naud, C., Jeuffroy, M.H., Barbottin, A. and Monod, H. (2006) Global sensitivity analysis for calculating the contribution of genetic parameters to the variance of crop model prediction. Reliability Engineering & System Safety, 91, 1142-1147. doi:10.1016/j.ress.2005.11.015
- Pathak, T.B., Fraisse, C.W., Jones, J.W., Messina, C.D. and Hoogenboom, G. (2007) Use of global sensitivity analysis for CROPGRO cotton model development. Transactions of the ASABE, 50, 2295-2302.
- Saltelli, A., Tarantola, S. and Campolongo, F. (2000) Sensitivity analysis as an ingredient of modeling. Statistical Science, 15, 377-395. doi:10.1214/ss/1009213004
- Brisson, N., Launay, M., Mary, B. and Beaudoin, N. (2008) Conceptual basis, formalisations and parameterization of the STICS crop model. Quae, Versailles.
- Brisson, N., Ruget, F., Gate, P., Lorgeou, J., Nicoullaud, B., Tayot, X., Plenet, D., Jeuffroy, M.H., Bouthier, A., Ripoche, D., Mary, B. and Juste, E. (2002) STICS: A generic model for simulating crops and their water and nitrogen balances. II. Model validation for wheat and maize. Agronomie, 22, 69-92. doi:10.1051/agro:2001005
- Launay, M., Graux, A.-I., Brisson, N. and Guérif, M. (2009) Carbohydrate remobilization from storage root to leaves after a stress release in sugar beet (Beta vulgaris L.): Experimental and modelling approaches. The Journal of Agricultural Science, 147, 669-682. doi:10.1017/S0021859609990116
- Cariboni, J., Gatelli, D., Liska, R. and Saltelli, A. (2004) The role of sensitivity analysis in ecological modelling. 4th Conference of the International Society for Ecological Informatics, Busan, 24-28 October 2004, 167-182.
- Chan, K., Tarantola, S., Saltelli, A. and Sobol, I.M. (2001) Variance-based methods. In: Saltelli, A., Chan, K. and Scott, E.M., Eds., Sensitivity Analysis, Wiley, New York, 167-197.
- Ratto, M., Young, P.C., Romanowicz, R., Pappenberger, F., Saltelli, A. and Pagano, A. (2007) Uncertainty, sensitivity analysis and the role of data based mechanistic modeling in hydrology. Hydrology and Earth System Sciences, 11, 1249-1266. doi:10.5194/hess-11-1249-2007
- Saltelli, A. and Bolado, R. (1998) An alternative way to compute Fourier amplitude sensitivity test (FAST). Computational Statistics & Data Analysis, 26, 445-460. doi:10.1016/S0167-9473(97)00043-1
- Saltelli, A., Tarantola, S. and Chan, K.P.S. (1999) A quantitative model-independent method for global sensitivity analysis of model output. Technometrics, 41, 39-56. doi:10.1080/00401706.1999.10485594
- Guérif, M., Beaudoin, N., Durr, C., Machet, J.M., Mary, B., Michot, D., Moulin, D., Nicoullaud, B. and Richard, G. (2001) Designing a field experiment for assessing soil and crop spatial variability and defining site specific management strategies. Proceedings 3rd European Conference on Precision Agriculture, Montpellier, 677-682.

