Received 29 June 2015; accepted 23 July 2015; accepted 29 July 2015

ABSTRACT

At present there is no theory of sea and oceanic currents due to the lack of understanding of the driving forces. The currents have a vortex character, so only moments of force can set them in motion. In the article, it is shown that the gravitation field of the Moon affecting the rotating Earth produces two moments of force: associated and tidal. Although the gravitation field is potential, the rotating Earth is a nonenertial system, in which the moment can occur due to the external potential force. Estimates show that the associated force can be sufficient to produce the observed flow rates. The associated force field tends to increase the natural rotation of the Earth and slow down the speed of the revolution of the Moon around the Earth, i.e. bring the Moon nearer the Earth, its action is opposite to the action of the tidal force. The action of the associated force is examined by the example of the circumpolar and local currents. The associated force produces vortices counterclockwise in the Northern hemisphere and clockwise in the Southern one. The associated force affects the atmosphere resulting in the observed predominance of western winds. It is necessary to take into account the above force when considering such atmospheric phenomena as cyclones and anticyclones, tradewinds, monsoons, etc. In the lithosphere, the associated force makes tectonic plates turn.

Keywords:

Sea and Oceanic Currents, Driving Forces of Sea Currents, Atmospheric Vortices, Tectonic Plate Movement, Tides in the Lithosphere

1. Introduction

Today there is no physical theory of sea currents, and even their driving forces have not been established yet. The currents are not permanent, with the speeds changing in time and space. Some hypotheses have been suggested linking the existence of oceanic currents with temperature, salinity differences, fresh water ingress, evaporation, winds, tides and long-period waves [1] [2] . Their main drawback is that the above physical pro- cesses are completely determined by thermodynamic potentials, so the forces they cause are potential. It is known from mathematics that the work of potential forces in translation along a closed contour is zero [3] . A potential field cannot produce a vortex movement in principle. Heating water does not result in producing a vortex with a vertical rotation axis. Only a convective movement can occur which is not a vortex. Addition of fresh water into brine does not lead to vortices. It follows from the potentiality of thermodynamic forces that a vortex current cannot be caused by chemical processes, differences in temperatures, pressures, concentrations, as well as by explosions, volcano eruptions, earthquakes, rising or lowering of the sea bottom, the movement of the continents, etc. Due to viscosity, there appear vortices near streamline surfaces. Viscosity is a nonpotential value. For vortices to appear there must be the main current exceeding the size of viscous vortices [4] . Besides, viscosity is a dissipative value suppressing a current rather than producing it.

2. Associated Power

The gravitation potential is written as

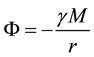
Here 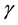is the gravitation constant, M is the body mass denoted as A producing the gravitation field, r is the distance to its mass center (Figure 1). The gravitation force acting on point B of the mass m is

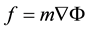
Here, 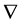is gradient symbol. Suppose point A with the coordinate 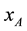in the laboratory coordinate system is the source of gravitation. It moves at a constant speed 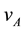and point B at a constant speed v. The coordinate B is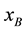. Point B moves under the action of two forces: the gravitation f and the external force F. The work of point B at the distance 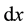is

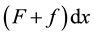
If, then point moves under the action of only the gravitation, and the work of the gravitation force 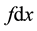is completely spent on the change of the kinetic energy of point B.

If B moves at a constant speed v, it means that the resultant of the forces acting on B is zero, that is

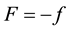
When B moves to A, it passes the section 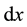during the time

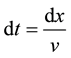(1)

When B moves towards A, consider that. If it moves from point A, then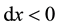. If B moves towards A over the time, point B will approach A at a distance

and if it moves from point A over the time, it withdraws from it at a distance

The gravitation work is as follows

The total work at straightforward and backward movement is

(2)

The above expression (2) can be written as

The value has the force dimensional representation, let us call it associated force. Since, then, which means that the associated force tends to withdraw points A and B. Dividing (2) by (1) we derive the power produced by the associated force

(3)

Let us call it the associated power. If the speed of point B is constant, then the external force work, and the total work of the gravitation force and the external force F is zero. If its speed changes, then the force F does not make up for the gravitation action, and the total work.

3. The Associated Power of the Moon

Let us consider the effect of the associated force on the Earth-Moon system. Figure 2 shows two points and on the Earth located at the same distance from the Moon center (point A) and at the same angular distance from the line AO connecting the Earth and Moon centers.

The linear speeds of points and produced by the Earth’s rotation are and, with the equality taking place. Point moves away from the Moon at the speed, and approaches it at the

speed. The vectors and are the projections of the speeds and on the line connecting the above points with the center of the Moon. The vectors and are equal in modulus, i.e.. The work performed by the two points is determined by the relations (2)-(3). The Moon moves counterclockwise, and so does the Earth if watched on the side of the Polar star. To simplify the calculation, let us consider that the Moon’s orbit is a circle with the radius R lying in the equator plane. We use the spherical coordinate system with the origin in the center of the Earth. The azimuthal angle is counted off from the point of vernal equinox, the zenith angle (or the polar distance) from the northern part of the axis of the rotation of the Earth. The latitude is expressed through the zenith angle. The Cartesian and spherical coordinates are linked by the relations

The Moon’s position is set by the vector and that of point by the vertor, the initial azimuth of the Moon is. The sidereal angular speed of the Moon’s revolution around the Earth is, the sidereal speed of the rotation of the Earth is. The azimuth of the Moon’s center at the arbitrary moment of time t is. The Cartesian coordinates of and the Moon are as follows

(4)

Here is the initial azimuth of point. The vector, which starts in the center of the Moon’s mass and finishes at point, has the following coordinates

(5)

The distance between the Moon center and point is

(6)

Here. Differentiating with respect to time (5) we find the vector of the speed of point:

(7)

The dependence of the coordinates on the time (4) was needed for calculation of the speed. The obtained formulas hold for the arbitrary moment of time. Further on the time dependence is of no interest and we shall consider the moment of time. Turning in (7) to spherical coordinates one derives the azimuthal speed in the form

(8)

The idea of the formula (8) is simple: the linear speed of point relative to the center of the Moon, is the linear speed of point caused by the rotation of the Earth minus the addition resulting from the revolution of the Moon around the Earth. The addition plays the part of the speed in the formula of the associated power (3), that is

The gravitation potential of Moon at a point with the coordinates r is

Here M is the mass of the Moon. The azimuthal component of the gravitation force acting on unit of volume in the direction of the rotation of the Earth (is the Earth’s density) is

According to (3) the associated power is written as

(9)

Here expansion into the Tailor series in is performed. The average power acting on unit of volume is written as

(10)

Integration between the limits from 0 to is performed because the contribution of the symmetric points is taken into account in the power (9). The plot of the values of for, , , , , is shown in Figure 3.

The average specific power of the associated force changes depending on the latitude from 0 at the pole to 8 mW/m³ at the equator. The associated power (9) at an arbitrary point changes in. However, sea currents do not appear within one day or one rotation of the Earth but take much longer time. Therefore, it is the average power (10) that determines the current parameters. The associated force is directed to the east and tends to accelerate the rotation of the Earth and, at the same time, decrease the linear speed of the revolution of the Moon around the Earth and draw it nearer the Earth. Its action is opposite to that of the tidal force, which, as is known, slows down the rotation of the Earth and increases the linear speed of the Moon’s revolution increasing the distance between the Earth and the Moon.

The solar associated power is an order of magnitude less than that of the Moon, so it can be neglected in the first approximation.

4. Circumpolar Current

The circumpolar current is directed to the east as the associated force. It crosses all the meridians, therefore, it is called the global current. The current speed on the surface is. For evaluation take an average depth of the current. As is known [4] , the decay time of a viscous current is

(11)

The kinematic coefficient of the laminar viscosity for water, therefore, the decay time of the circumpolar current is 300 years. Dividing the kinetic energy per cubic meter of the volume by the dissipation time (11) one derives the dissipation power of the kinetic energy of the order of. At present the parameters describing sea currents are determined with low accuracy. Therefore, it is possible to

compare the theory and the measurement data only by the order of magnitude. The power of laminar dissipation turns out to be three orders of magnitude less than that of the associated power. Hence, the value of the associ- ated force is enough to overcome viscous dissipation. There are several reasons for the discrepancy between the associated and dissipation powers. The main of them are as follows:

・ The dissipation power is undervalued, since the turbulent viscosity coefficient can be several orders of magnitude higher than that of the laminar viscosity in (11) [4] .

・ The associated force is counteracted by the tidal force, the latter is not taken into account here. Now there are no reliable theoretical estimations of this force.

5. Local Vortices

The circumpolar current is the only global vortex, all other currents are local ones. Let us consider a closed contour on the Earth’s surface in the northern hemisphere (Figure 4) in the form of a quadrangle with the apices at points, , , , their coordinates are indicated to the left of the points.

Two sides AB and CD go parallel, with the side CD being nearer the northern pole and the side AB nearer the equator, and the other sides AD and BC are directed along meridians. Let us calculate the average work value along the contour ABCD in the counterclockwise direction as shown in Figure 4. Along the meridian sides BC and AD movement occurs perpendicular to the lunar orbit plane, that is perpendicular to the direction of the Moon’s movement, therefore, their associated force is zero. On section AB the associated force is directed to the east at point B. In this case, positive work is performed and using (10) it is written as

Similarly,

Here minus is used because on section CD integration is performed from the east to the west, that is in the direction opposite to the action of the associated force. Adding together (4) and (5) we derive the associated force work along the ABCD contour counterclockwise in the form

The total work along the contour counterclockwise turns out positive, which means that there exists a moment of force turning water counterclockwise in the northern hemisphere. For the contour located in the

southern hemisphere positive work is performed clockwise and water spins up in the same direction.

6. Taking into Account the Inclination of the Lunar Orbit

Inclination of the lunar orbit with respect to the equator is 5˚ [5] . The speed component in the associated power (9) should be multiplied by. The real inclination of the lunar orbit allows the correction of the order of several tenths of a percent, therefore it can be neglected.

7. Atmosphere

The action of the associated force is well observed on the atmosphere. Western winds were long ago noted to dominate in the atmosphere [6] [7] . There is even a hypothesis on the formation of the circumpolar current due to the above winds [1] . In general, the atmosphere rotates faster than the Earth, which cannot be explained by the Coriolis force. The atmosphere should be characterized by the equality of two powers: associated and dissipation ones. The viscosity coefficient of the air is. In the atmosphere the turbulence is considerably higher than in water due to the powerful vertical currents caused by the strong dependence of the air density on the temperature. The air is heated due to solar radiation in the lowest part of the atmosphere near the Earth’s surface, which contributes greatly to the appearance of convective currents in the atmosphere. The speeds of the air currents are higher than those of the sea currents, which results in increasing the dissipation energy. When calculating the atmospheric currents such as cyclones, anticyclones, tradewinds, monsoons, etc., it is necessary to take into account the associated power because it can contribute greatly to the process of their formation and further development. As a matter of fact, in the northern hemisphere cyclones twist counter- clockwise, while in the southern hemisphere-clockwise according to the direction of the moment of associated force.

8. Lithosphere

At present whirling currents of the Earth’s crust have been reliably established [8] . The movement of the continents as well as that of the Earth’s crust is accounted for by the mantle movement and the viscous engagement of the mantle with the crust. Since the mantle is solid, it is not clear what viscous currents and engagements are meant. Why are the above viscous currents absent in the solid crust? There remains a question - what forces produce vortices in the mantle? Geophysicists shifted the problem from the surface into the depth of the Earth, where, in their opinion, nothing can be tested at the moment, which seems to eliminate the problem. However, as a matter of fact, the problem remains and new serious questions arise, e.g., “viscous” interaction between the mantle and the crust and the accompanying heating. A current in the lithosphere or in the core must be necessarily whirling just as the movement in closed space. Only nonpotential forces can produce the above movement whose nature should be determined. It is suggested to search for the cause of turning of the plates in the mantle convection. However, the rotation even if it occurs at convection, takes place around the horizontal axis, whereas the plates turn around the vertical axis. To change the rotation axis from the horizontal position to the vertical, it is necessary to apply an external moment of force [9] . Here again one faces the problem of the moment. Besides, the idea of convective movements in a solid looks strange and should be supported with reliable experimental data that are absent, which suggests that convection can hardly be the cause of the plate movement. In order to explain the rotations in the lithosphere, the mantle is imparted with the properties of the Newton viscous liquid with a very high viscosity coefficient that is twenty orders higher than that of water and other real viscous substances. The plastic deformation rate for the Newton viscous liquid depending on the shear stress is assigned by the Newton law

(12)

At low shear stresses the plastic deformation of solids occurs according to the thermoactivation law of Arrenius [10]

(13)

The viscosity coefficient is not related to the above law. The Arrenius liquids are described by other parameters, e.g., the activation energy, the pre-exponential multiplier. For the above reason, appli- cation of the Newton law of the viscous liquid flow to lithosphere is not justified. Since the real parameters of the flow are described with the inequality, the dependence of the plastic flow rate (13) on stress and temperature is very high compared with (12). Slight changes of stress and (or) temperature in (13) result in increasing the rate of the plastic flow by orders of magnitude. Heating by

Increases in (13), approximately, e times. From the measurement data the activation energy value is per one atom. The Boltzmann constant is per one atom. As a result, for room temperature 300 K the value, i.e., an increase in temperature by 8 degrees leads to an increase in the plastic deformation rate e times, whereas an increase by 160 K results in increasing the plastic defor- mation rate 10⁹ times. The strong dependence of the plastic deformation rate on the temperature leads to its high localization. There appear zones with an increased temperature, where the plastic flow is concentrated. Outside the above zones the plastic flow rate is small and the plates turn as integral with the plastic deformation concentrated on their boundaries.

9. Tidal Stresses

In astronomy the revolution of the Moon around the Earth is considered as simultaneous revolution of two bodies around one mass center, the so-called barycenter [11] . The barycenter (point B in Figure 6) is located on the line connecting the mass centers of the Earth and the Moon at a distance

from the Earth’s center. The Earth rotates round its axis passing through the Earth’s center at the sidereal angular speed and simultaneously revolves around the barycenter at an angular speed. Its rotation leads to the formation of the axisymmetric field of the centrifugal force and, as a result, the Earth has an axisymmetric shape with the equatorial radius larger than the polar one. The revolution around the barycentre has no axis symmetry, as a result, an elastic field of displacements and stresses is formed which has no axis symmetry either. Figure 5 shows schematically the values and directions of the action of the centrifugal bary- centric, the lunar gravitation of the forces and their resulting for three points. The forces and differ both in value and direction and they cannot counterbalance each other. The force of the lunar gravitation is directed toward the Moon’s center and the barycentric centrifugal force is directed from the barycenter. The resulting force is counterbalanced by the elasticity force, which leads to the formation of the field of the elastic displacemets U in the lithosphere. If, then the rotation speed of the Earth would equal the angular speed of the Moon’s revolution around the Earth and the barycenter could be located on the straight line OA passing through the mass centers of the Earth and the Moon. The elastic field would be symmetric with respect to it as shown in the example of two symmetric points D and in Figure 5. The symmetric stress field does not produce moments of forces and, therefore, cannot change the angular speeds both of the Earth’s rotation and the revolution of the Moon around the Earth. In fact, the rotation speed of the Earth nearly 30 times as many as the angular speed of the revolution of the Moon around the Earth. There- fore, the elastic field rotates with respect to the material points of the Earth at an angular speed producing tides in the lithosphere of the elastic nature. Due to the Earth’s rotation the barycenter is withdrawn from the line OA toward the rotation direction as shown in Figure 6. In this case, the symmetry of the elastic shear field disappears.

The elastic field will be asymmetric both with respect to the line OA and the line passing through the Earth’s center and the barycenter. Due to the asymmetry of the elastic field there appear two moments of force, one of them tending to slow down the Earth’s rotation around its axis and the other accelerating the Moon, which tends to move to a higher orbit, that is moves away from the Earth. Given the lunar gravitation and the centrifugal barycentric force, the dynamic elasticity equation [12] is written as

(14)

Here U is the vector of the elastic displaycement, G is the shear modulus, is the density,

is the longitudinal speed of sound

is the transverse speed of sound, is the Poisson coefficient. The centrifugal barycentric acceleration is a potential value and it is written as

Here r is the radius-vector counted off from the barycentric rotation axis. The acceleration of the lunar gravitation is as follows

Here (6) is used. At an established process the displaycement vector must be the periodic function of time with a period equal to

Equation (14) has not been solved yet, therefore, it is not possible to estimate the effect of the Earth’s revolution around the barycenter on the deceleration of the Earth’s rotation and the acceleration of the Moon. The tidal effect is opposite to the associated effect, therefore, to correctly study the effect of the gravitation and rotation on the Earth, it is necessary to take into account their combined action.

10. Discussion

At present the following hypotheses have been put forward to explain how oceanic currents appear:

1) Temperature difference.

2) Salinity difference.

3) Evaporation, precipitation.

4) Atmospheric wind.

5) The Coriolis force.

6) Isolated waves.

The first three variants are potential values, which means that they cannot produce vortices in principle.

An increase in temperature by one degree results in increasing the water enthalpy by the value h~4000 J/m³. The kinetic energy density at a current speed of 1 m/s is 500 J/m³. One can imagine that the energy is more than sufficient for an oceanic current to appear. However, this is not the case. According to the thermodynamics laws, enthalpy is the function of two variables, namely, the pressure and entropy. At a constant entropy (for example, when thermal conductivity can be neglected), the work performed at the distance is written as

If the vector lies in the horizontal plane, then, which means that, i.e., no change of the water internal energy into the kinetic one takes place. Temperature difference cannot result in horizontal move- ment. If the above vector is vertical, then. Then there appears a convective movement at which volumes of warm water rise and those of cold water descend resulting in horizontal translation. The speed field will look like a turbulent whirl one, with the rotation axis having an accidental horizontal orientation. The expected value of the orientation (the mean value of the direction of the axis rotation) is zero. The horizontal stochasticity of the direction of the rotation axis for various volumes of water rules out the formation of a large vortex with the vertical rotation axis. Besides, the size of convective vortices is incomparably small as compared to that of sea currents. In order to change a vortex with the horizontal rotation axis into that with the vertical rotation axis, it is necessary to apply the external moment of force [11] . The above moments have not been suggested yet. Heating due to solar radiation in water occurs in the upper part of a free surface, which rules out the appearance of convective currents. Convection occurs when water is heated from the bottom, which holds true for the atmosphere. The convective hypothesis does not explain the interaction between the stream direction and the Earth’s rotation. Thus, temperature nonuniformity cannot give rise to sea currents.

The same is true for salinity difference, although in this case, a different thermodynamic potential should be used instead of enthalpy [13] . Vortical movement can be caused by the forces of friction (viscosity). In mechanics it is shown that the effect of viscosity at a flow around a solid surface is significant only in the boundary layer [4] . The boundary layer size is much smaller than that in the flow core, where viscosity is not significant. In the sea the current core is the current itself. At the interaction with the flow surface there can appear local whirls. However, their size is much smaller than the current depth and especially the size of the current itself. Sea currents are characterized by a small value of the Reynolds number, which means that viscosity makes an insignificant contribution to the current turbulization and vortex formation. Thus, the hypothesis of the existence of oceanic currents due to viscosity is rejected.

The Coriolis force: even by the name it is clear that the Coriolis force is a force rather than a moment. It takes place in the presence of the meridianal speed component. Theoretically, it can be only responsible for the formation of the global vortex, which crosses all the meridians. In accordance with the law of conservation of mass, if somewhere there is a flow along a meridian in one direction, then there must be a counterflow with the same mass transfer, with the Coriolis force in the counterflow in the opposite direction. Thus, if the circumpolar current is caused by the Coriolis force, there must exist somewhere, for instance, in the depth the same current in the opposite direction. However, there is no such current. Therefore, the Coriolis force as a cause of oceanic currents should be excluded from consideration.

Another idea as a cause of the appearance of vortices is the presence of wave objects of different nature. The reasoning is simple and can be summarized like this. If there is a wave, then there appears a vortex. However, a wave itself is not a vortex, so its formation remains outside the scope of explanation. Currents in large water reservoirs (seas, oceans, lakes), the so-called cyclonic currents, are related the Earth’s rotation [2] . However, there exist fewer anticyclonic vortices. I do not consider that currents occur under the action of the associated force only. Other forces may take part, for instance, the tidal forces described in Section 5. Estimation of their influence requires further investigation.

Potential forces themselves do not produce moments of force [11] . However, if the movement in the gravita- tion field is affected by additional conditions, e.g. the Earth’s rotation, i.e., noninertial behaviour, they can really appear.

Cite this paper

AlexanderIvanchin, (2015) Gravitation of the Moon Gives Rise to Oceanic Currents. International Journal of Geosciences,06,750-760. doi: 10.4236/ijg.2015.67061

References