Food and Nutrition Sciences
Vol.06 No.16(2015), Article ID:62100,11 pages
10.4236/fns.2015.616162
Bicomponent Solutions of Food Polysaccharide and Edible Films on Their Basis
Huo Po1, T. Savitskaya2, L. Gotina2, S. Makarevich3, I. Reznikov3, D. Grinshpan3
1School of Biology and Environmental Engineering, Zhejiang Shuren University, Hangzhou, China
2Faculty of Chemistry, Belarusian State University, Minsk, Belarus
3Research Institute for Physical and Chemical Problems, Minsk, Belarus

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 October 2015; accepted 19 December 2015; published 22 December 2015
ABSTRACT
The study of the rheological properties of aqueous solutions of corn starch (CS) blends with sodium alginate (SA) and agar-agar (AA) as well as the physical and mechanical properties of bicomponent films on their basis has been carried out. The data show that adding of both polymers to starch solution causes an increase in viscosity which is higher in the case of SA. Activation energy for viscosity flow of solutions of CS blended with SA has minimum value at CS:SA ratio = 98:2. The above mentioned dependence is not typical for AA, as flow activation energy in this case raises steadily with the growth of AA content in the solution, like viscosity of the CS:AA. The extreme behavior of polymer blends with low content of one of the polymers is described in terms of mutual solubility or thermodynamic compatibility. There is a tendency that mechanical properties and water solubility increase with the increasing of SA and AA polymers in corn starch matrix. Obtained data evidence the benefits of bicomponent films production instead of starch-based films.
Keywords:
Corn Starch, Sodium Alginate, Agar-Agar, Solutions, Rheological Properties, Edible Films, Physical and Mechanical Properties

1. Introduction
Among a number of means to help preserving the health of the environment, one can find photo-, bio- and water degradable packaging made from certain polymer materials. Starch was the first natural polymers for the production of biodegradable packaging materials because of its good biodegradability and low cost.
Edible films and coatings are becoming the next new thing in the field of biodegradable packaging, attracting attention of scientists, manufactures and consumers. Starch once again remains at the forefront of edible film making. However, the application area of starch is limited as it is an example of hydrophilic, hygroscopic substance with retrogradation properties (change of structure during storing) [1] . Starch is blended with other natural polymers to modify its properties [2] [3] .
Sodium alginate (SA) widely used for food purposes is of special interest for such a strategy line. Sodium alginate is a water soluble salt of alginic acid, a naturally occurring non-toxic polysaccharide found in all species of brown algae [4] . It contains two uronic acids, (1-4)-linked β-D-mannuronic acid (M) and (1 - 4)-linked α-L- guluronic acid (G). It is composed of homopolymeric blocks M-M or G-G, and blocks with an alternative sequence of M-G blocks. Agar-agar (AA) or simply agar consists of a mixture of agarose and agaropectin. Agarose, the predominant component of agar, is a linear polymer, made up of the repeating monomeric unit of agarobiose. Agarobiose is a disaccharide made up of D-galactose and 3,6-anhydro-L-galactopyranose. Agaropectin is a heterogeneous mixture of smaller molecules that occur in lesser amounts, and is made up of alternating units of D-galactose and L-galactose heavily modified with acidic side-groups, such as sulfate and pyruvate [5] .
Many recent studies have focused on rheology of the above mentioned food polymers solutions. Their main focus was the influence of amylose content [6] , plant source [7] , second polymer [8] [9] and some other additives on the rheological properties [10] [11] of starch solutions. Numerous studies have examined thermal, mechanical properties, and water vapor permeability of films based on these solutions [12] [13] . None of the investigators, however, have looked at the starch blends with other polymers paying particular attention to the area of low additive concentration.
The present study was aimed at investigating the rheological properties of aqueous solutions of corn starch (CS) blended with sodium alginate (SA) and agar-agar (AA) in a wide range of concentration as well as the physico-mechanical qualities of bicomponent films on their basis.
2. Materials and Methods
2.1. Solutions Preparation
The CS solutions were prepared by dispersing starch powder in distilled water under mechanical stirring during 15 min at room temperature, followed by heating of the dispersion at 90˚C for 30 minutes under stirring. IKA Werke equipment was used for stirring. The concentration of CS in the solutions was 5%, 6%, 8% and 10% (mass). Pure CS produced in China that contains 25% of amylose with water content ≤14% was used. The SA solutions were prepared by dissolving sodium alginate powder in distilled water under stirring during 45 min at room temperature. The concentrations of SA solutions under study were 2%, 3% and 4% (mass). We used pure sodium alginate (SA) extracted from sea plant Kelp (sea tangle), produced in China with water content ≤14%. The following ratio of polymers in CS:SA blends were investigated: CS:SA = 100:0; 99:1; 98:2; 95:5; 90:10; 80:20; 70:30; 60:40; 50:50; 0:100. The total concentration of polymers in the solution was taken 8% (mass) as the most suitable concentration for film casting and production by drying. Polymer blend solutions were prepared by simultaneous dispersion of CS and SA in distilled water at stirring during 15 min, followed by heating of dispersion at 90˚C for 30 minutes under stirring. The overall polymer concentration was 8% (mass) at different blending ratio of CS:SA. The solutions of CS and AA were prepared by the same way.
2.2. Rheological Measurements
Rheological measurements were carried out using a CC25 coaxial cylinder measuring unit of the R/S Brookfield rotational rheometer with a constant shear rate regime. The shear stress was measured as a function of shear rate that varied from 0.5 to 1000 s−1. The shear rate measurement sequence was programmed in a step-by-step increase rather than a gradual increase in order to improve the accuracy of the measurement. Seventeen milliliters of prepared solution were loaded into the cylindrical cup and cooled in a water bath to specific temperature. All analyses were performed at least three times between 20% - 80% full torque scales. Data were analyzed using MS-Excel and Mathematica software. Measurements were made starting at 343 К followed by consistent cooling to 333 К, 323 К, 313 К and 303 К at which the measurements were ended. Measurements for gels were made at 303, 323 and 343 К. The formed gels were carefully placed into the measuring cell of rheometer to fully preserve the gel structure. Since the gel structure was destroyed when measured, the measurements at each given temperature were carried out consecutively as long as viscosities did not stop to change. Measurement procedure was performed at least twice at each temperature.
2.3. Activation Energy of Viscous Flow Calculation
The value of measured viscosity is a measure of a fluid’s resistance to flow. In order for the solution to flow, certain amount of energy is required to overcome the resistance and allow molecular motion to occur. This energy is known as the “activation energy of viscous flow” Ea and can be calculated using Eyring’s Equation (1) [14] . The equation explains the physical meaning of the activation energy of viscous flow, as the energy required for the molecule to pass through the energy barrier that surrounds motionless molecules. The number of molecules possessing this energy correlates with the Boltzmann factor, therefore the viscosity of the liquid can be expressed by Equation (1):
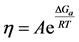 . (1)
. (1)
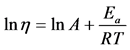 . (2)
. (2)
We used the dependence of viscosity versus reverse value of temperature to calculate the activation energy of viscous flow at constant shear rate. In the case of linear plot simple mathematical operations were performed, suggesting that A is constant within a narrow range of temperatures Equation (2).
2.4. Films Preparation
Films were prepared from CS 8% water solutions (mass) and SA combinations at the following ratios: CS:SA = 99.5:0.5; 99:1; 98:2; 95:5; 90:10; 80:20; 70:30; 60:40; 50:50 (mass), consisting glycerin as a plasticizer, by pouring the solution on a glass surface with a subsequent spreading of a solution layer on the glass surface with the use of special scraper. During the formation process the temperature of solution, drying duration and conditions of film storage were varied.
2.5. Mechanical Characteristics Measurement
Tensile strength and relative elongation as the mechanical properties of the films were measured with the use of the tensile-testing machine Zwick/RoellZ 0.5 at the ambient temperature and 35% relative humidity value. The testing was held with the following machine settings: distance between captures―20 mm; preload of a sample―1 N; preloading speed―10 mm/min; testing speed―40 mm/min. All samples were conditioned in the desiccator with 65% relative humidity before measurement.
2.6. Moisture Permeability Measurement
Moisture permeability of films samples was measured according to ASTME standard 96 - 95. Measurements were made by the method of water evaporation through the films which was gravimetrically controlled each 12 hours during 10 days.
3. Results and Discussion
3.1. Rheological Properties of Corn Starch Blends with Sodium Alginate and Agar-Agar
The dependence of viscosity on polymer ratio for bicomponent solutions derived from starch with addition of SA and AA in the temperature range from 303 to 343 К is illustrated by Figure 1. The data show that adding both polymers to starch solution causes an increase in viscosity that is higher in case of SA. AA has a lower thickening impact on the starch solution, whereas the introduction of SA gives such a gelling effect (viscosity increase) that it has been impossible to measure the viscosity of the solutions with SA of 30 or more percent, in the temperatures lower than 333 К given the allowable shear stress range of the instrument.
This graph pinpoints several sections for all the temperatures studied. The first section shows viscosity increase for additive content of less than 2%. The second depicts almost no change, 2% - 5%, and the third represents

Figure 1. Dependence of bicomponent solutions viscosity on SA (a) and AA (b) content at different temperatures (shear stress rate 1000 с−1): а: 1―343 К, 2―333 К, 3―323 К, 4―313 К, 5―303 К; b: 1―353 К, 2―343 К, 3―333 К, 4―323 К, 5―313 К.
monotonous viscosity increase.
Small amounts of the second polymer have slightly influence on the starch solution viscosity. Then, for example, with AA content of more than 10% the number of agarose molecules is just enough to form double spirals that later create small soluble domains of 8 - 12 spirals. The AA ability to produce such sophisticated structures in a solution makes it a major contributor to the total viscosity.
3.2. The Influence of Blends Content on Activation Energy of Viscous Flow
Activation energy of viscous flow is defined as the minimum energy needed to cross the energy barrier and set macromolecule segments responsible for the flow in motion. Macromolecules cannot move as an entity in the solution as they are rather big in size. Kinetic macromolecule segments are the units of viscous flow. Solutions viscous flow is a sequence of events such as segments shifts toward force direction and changing of the equilibrium state. Activation energy is involved in breaking bonds and destroying temporary knots in fluctuation grid present in concentrated solutions, therefore can be used as a measurement of the system structuredness.
The level of activation energy is mainly associated with shear rate, molecular mass and thermodynamic properties of the solvent. It should be noted that the value estimated using Eyring’s equation can qualify as activation energy only when all the particles in the system have identical shape, size etc. Macromolecules in polymer solutions are polydispersed, hence the given temperature coefficient cannot be attributed to activation energy in its strict physical meaning, it can be referred to as apparent activation energy of viscosity flow.
Curve 1 of Figure 2 shows that activation energy for viscosity flow of solution blends of CS and SA has minimum value at CS:SA ratio = 98:2 [3] . Data represented at Figure 2 correspond to average value of activation energy for the interval of shear rate of 4 - 140 с−1. Flow activation energy versus polymer blend composition curves determined at 310,660 and 1000 s−1 follow the similar trend.
Monotonous activation energy growth with SA blend content of more than 10% is explained by the increased concentration of the component with higher activation energy. It means that for the SA macromolecules to cause the flow they should overcome a higher energy barrier than CS ones. As a result flow activation energy level should go up with the growing number of these molecules. The numerical values of flow activation energy for 8% starch solution and 2% SA solution are 10.6 and 15.8 kJ/mol correspondingly.
The extreme behavior of polymer blends with low content of one of the polymers is described in terms of mutual solubility or thermodynamic compatibility [15] . It is possible to form one polymer solution in another, however the process is restricted by narrow concentration (up to bimodal phase diagram) and temperature ranges. The separation of polymer at the starting point (in the region of binodal and spinodal) results in extracting one of the polymers as a fine phase of colloid size, that is accompanied by a drastic enlargement of interphase surface in the system. Large interphase surface leads to the boost of free volume, which is a vital to rheological behavior of any fluid. During the separation phase of the polymer blend the intramolecular bonds weaken and the flow decreases, lowering the flow activation energy.
Figure 2. Dependence of flow activation energy with the constant shear rate (650 s−1) on second polymer content in 8% blends CS:SA (1) and CS:AA (2).
The abovementioned is not typical for AA, as flow activation energy in this case raises steadily (Figure 2, curve 2) with the growth of AA content in the solution, like viscosity of the CS:AA. Flow activation energy growth is solely dependent on the formation agarose double spirals domains. The absence of extremum can arise from the compatibility of starch and agar which was mentioned in [12] .
3.3. Rheological Models for Experimental Rheological Curves
The correspondence of experimental rheological curves for the solutions after study to rheological models was checked with the equations:
Ostwald?de Waele (power law) 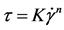
Herschel-Bulkley 
Bingham 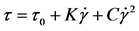
Casson 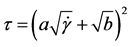
In power equations, e.g. Herschel-Bulkley equation, it is difficult to interpret some of the τ0 values (critical shear stress). Its negative values lack physical sense, as this parameter is used to determine stress levels, beyond which the substance acts as an elastic body, above―behaves as a fluid with plastic consistency.
It can be taken that the solutions with more than 10% of SA are not likely to perform as elastic bodies. Although negative value of shear stress dismisses physical sense, it shows that for these solutions to attribute elastic bodies’ characteristics the fluids should be additionally structured. In other words as these solutions demonstrate the qualities of elastic bodies when liquid transforms into gel, the critical shear stress value in Herschel-Bulkley equation derives that adding SA to CS solutions hinders the gel formation.
A more detailed analysis of critical shear stress dependence on temperature and amount of SA added revealed a similar dependency described for flow activation energy: extremum at 2% SA that becomes more defined with a temperature drop (Figure 3).
The dependences of К value versus second polymer content have maximum at SA content = 10% for T ≤ 323 К and SA = 20% for T > 323 К. Considering n as a flow behavior index, that describes deviation from Newtonian fluids about flow behavior, it was found, that the value with increasing SA contents changes its behavior from a curve with strongly marked maximums, through a curve with feebly marked minimum to monotonous decreasing curves. Similar to К parameter, spoken above, for isothermal conditions the dependences with a maximum n value are widely presented
We should give considerable attention to the Ostwald-de Waele equation coefficients. It should be noted that as n determines the flow behavior, n < 1 parameter shows that all solutions are pseudoplastic. When increasing SA content the rheological behavior of the solutions approaches to the Newtonian fluid flow, however does not get close to its n parameter of 1.
Temperature dependence of К and n coefficients deserves special attention, as it is different for the region of
Figure 3. Dependence of shear stress in Herschel-Bulkley equation on SA content: 1―303 К, 2―313 К, 3―323 К, 4―333 К, 5―343 К.
minor (less than 5%) and major (more than 5%) concentration (content) levels.
The К parameter tends to decrease with increasing temperature at low SA concentrations, showing extremely high values at 303 K. However with higher SA concentration and temperature increase the К parameter progressively rises. The same is applicable for n index: lower concentrations and higher temperatures result in n factor going up, and higher concentrations and higher temperatures make n go down.
This effect becomes more prominent when SA content enhances, i.e. that equation variables incline to be more temperature dependent. AA poor thickening abilities, compared to SA, affect n coefficient in Ostwald-de Waele equation. These systems also demonstrate pseudoplastic qualities, but n approaches 1.
Figure 4 exhibits that n more likely affected by solution content change than temperature index. Parameter n increasingly grows with the growth rate of system viscosity, that is articulate for higher temperatures where gel formation plays little role.
The shear stress parameter in Herschel-Bulkley and Bingham is affected by the appearance of cross-linked aggregates in CS:AA solutions (Figure 5). As AA content grows, and the temperature goes down, the critical shear stress number rises. It can be attested that CS:AA systems manifest qualities of AA solutions: solid gel formation.
3.4. Gel Rheological Properties
Gelation consequently changes the rheological properties of the studied solutions for CS:SA systems, namely: when primary deformed gels and jellies show the properties of thixotropic fluids, that under “shear stress rate increase-decrease” conditions demonstrate hysteretic loop on the flow curve (Figure 6, curve 1). The spatial network grid, responsible for gel formation, is destroyed because of the shear pull. Subsequently it does not restore its structure. The follow-up measurements of the same gel sample did not show any hysteretic loop (Figure 6, curve 2). The flow curve of the destroyed gel approaches values true to the solution (Figure 6, curve 3).
CS solutions have been used to test gel’s elastic memory after mechanical destruction. It turns out that gel does not recover inside the measurement cylinder even 7 hours later after the primary measurement at the temperature of 303 К that is a priori lower than gelation temperature.
Hysteretic loop area indicates the level of gel structuredness and maturity. Figure 7 illustrates that SA increase contributes to monotonous decrease of hysteretic loop area in a whole that may suggest the reduction in
Figure 4. Dependence of n parameter in Ostwald-de Waele equation for CS:AA ration on temperature and AA content.

Figure 5. Dependence of τ0 parameter in Herschel-Bulkley equation (а) and Bingham equation (b) for CS:AA system on temperature and AA content.
Figure 6. Curves for gel flow and freshly made solution CS:SA = 80:20 at 303 К, 1―first gel mea- surement, 2―second gel measurement, 3―solution measurement.
number of knots in fluctuation network (hydrogen bonds and physical engagements) formed by starch macromolecules in the solution and responsible for gelation. System behavior with lower concentrations appears to be exceptional: dependence of loop area on composition component ratio has the minimum for gel containing 2%
Figure 7. Dependence of hysteresis loop on SA content for CS:SA system 1―at 303 К, 2―at 343 К.
of SA. This fact is explained by the peculiarities of phase separation in polymer blends in the region of low concentrations of one of them.
The possibility of thermal melting has also been put to test together with mechanical gel destruction. Table 1 shows that the solution with 40% SA is not capable of gelation even at 4˚C; gel with 30% SA is easily destroyed at room-like temperature. It is also noted that gel destruction temperature steadily enhances. Gels formed from pure CS solutions are not thermo reversible: the water in the gel starts to boil earlier than gel commences to destroy.
Comparative analysis of gels destruction temperatures and hysteretic loop calculated areas shows that gels thermo reversibility affects drastic area decrease. Specifically that with temperatures above gel melting point, the value of hysteretic loop area sharply drops below 6000 Па∙с−1. This number characterizes polymer solution
that is why it is more of a marker for solution’s degree of structuredness than of the original gel.
3.5. Physical and Mechanical Properties of the Films
Blending CS and SA in water, as a common solvent, resulted in bicomponent films, characterized by extreme dependency of physico-mechanical properties on the content with low SA concentrations. For example, 2% SA concentration enhances CS film tensile strength by 36% and grows elongation. Figure 8 demonstrates that the following SA content increase indicates gradual tenacity improvement. This is true since SA film is almost 3 times stronger than CS film. Relative elongation of bicomponent films diminishes, but does not become lower than CS film parameters.
By contrast, blending of AA with CS doesn’t result in extremal dependency between mechanical properties and AA content. Introduction of AA increases the mechanical properties of bicomponent films monotonously.
SA introduction into the blends augments the consistency of the forming solution due to the reduction of temperature for gelation of CS solutions, which serve as polymer matrix. This attributes to formation of bicomponent films at lower temperatures without affecting their strength, as compared to CS based films with small or no SA quantity. Figure 9 demonstrates the dependence of films tensile strength on the temperature of their preparation.
Water permeability dependency on SA concentration has also extreme parameters (Figure 10). Maximum water permeability is reached at SA of 5% and 10%, minimum―at 20% and 30%. Weakening of water permeability can be attributed to the rise of SA concentration in the blend. The intensification of this high crystalline polymer content leads to the formation of a more tightly-structured film with less free volume for water molecules migration. The water solubility of films grows with the second polymer content at the same time.
The extremums presented on the dependencies of physico-mechanical properties of bicomponent films on concentration correlated with non-monotonous dependency of viscous flow features of casting solutions.
Table 1. Gel melting temperature at different SA content.
Figure 8. Dependence of tensile strength and elongation for bicomponent CS:SA films on SA content.
Figure 9. Dependence of tensile strength of bicomponent films on formation temperature, where 1―10%, 2―20%, 3―30% is SA concentration.
Figure 10. Dependence of water permeability for bicomponent films on SA content.
4. Conclusion
Blending of CS with SA and AA in water as a common solvent resulted in bicomponent edible films preparation. The increase of SA or AA in the starch solutions was shown to improve the physical-mechanical properties of the films produced on their basis. The extreme dependency of tensile strength, elongation and water permeability that appears at low SA content correlates with the rheological properties of the casting solutions.
Acknowledgements
Authors acknowledge Zhejiang Science and Technology Department (key project “Starch-protein edible and degradable packaging materials”) and State Administration of Foreign Affairs (“High-end Foreign expert project”) for financial support.
Cite this paper
HuoPo,T.Savitskaya,L.Gotina,S.Makarevich,I.Reznikov,D.Grinshpan, (2015) Bicomponent Solutions of Food Polysaccharide and Edible Films on Their Basis. Food and Nutrition Sciences,06,1571-1581. doi: 10.4236/fns.2015.616162
References
- 1. Lu, D.R., Xiao, C.M. and Xu, S.J. (2009) Starch-Based Completely Biodegradable Polymer Materials. Express Polymer Letters, 3, 366-375.
http://dx.doi.org/10.3144/expresspolymlett.2009.46 - 2. Jimknez, A., Fabra, M., Taw, P. and Chiralt, A. (2012) Edible and Biodegradable Starch Films. Food and Bioprocess Technology, 5, 2058-2076.
http://dx.doi.org/10.1007/s11947-012-0835-4 - 3. Huo, P., Savitskaya, T., Gotina, L., Reznikov, I. and Grinshpan, D. (2015) Rheological Properties of Casting Solutions for Starch Edible Films Production. Open Journal of Fluid Dynamics, 5, 58-67.
http://dx.doi.org/10.4236/ojfd.2015.51008 - 4. Harnsilawat, T., Pongsawatmanit, R. and McClements, D.J. (2006) Characterization of β-Lactoglobulin–Sodium Alginate Interactions in Aqueous Solutions: A Calorimetry, Light Scattering, Electrophoretic Mobility and Solubility Study. Food Hydrocolloids, 20, 577-585.
http://dx.doi.org/10.1016/j.foodhyd.2005.05.005 - 5. Lahrech, K., Safouane, A. and Peytellasse, J. (2005) Sol State Formation and Melting of Agar Gels Rheological Study. Physica A: Statistical Mechanics and Its Application, 358, 205-211.
http://dx.doi.org/10.1016/j.physa.2005.06.022 - 6. Lii, C.-Y., Tsai, M.-L. and Tseng, K.-H. (1996) Effect of Amylose Content on the Rheological Property of Rice Starch. Cereal Chemistry, 73, 415-420.
- 7. Singh, N., Singh, J., Kaur, L., Sodhi, N.-S. and Gill, B.-S. (2003) Morphological, Thermal, and Rheological Properties of Starches from Different Botanical Sources. Food Chemistry, 81, 219-231.
http://dx.doi.org/10.1016/S0308-8146(02)00416-8 - 8. Odeniyi, M.A. and Ayorinde, J.O. (2012) Material and Rheological Properties of Yam Starch/Polymer Blend Hydrogel. International Journal of Pharmacology and Pharmaceutical Technology, 1, 23-28.
- 9. Bertolini, A.C., Creamer, L.K., Eppink, M. and Boland, M.J. (2003) Some Rheological Properties of Sodium Caseinate—Starch Gels. Journal of Agricultural and Food Chemistry, 81, 219-231.
- 10. Ma, N.S., Png, j., Xu, N., Li, M.G. and Lin, Q. (2008) Rheological Properties of Sodium Alginate-Agar-Montmorillonite. Journal of Applied Polymer Science, 109, 4075-4081.
- 11. Drozdz, W. and Tomaszewska-Ciosk, E. (2007) Rheological Properties of Potato Starch Pastes with the Addition of Kaolin. Polish Journal of Food and Nutrition Sciences, 57, 113-117.
- 12. Wu, Y., Geng, F., Chang, P.R., Yu, J. and Ma, X. (2009) Effect of Agar on the Microstructure and Performance of Potato Starch Films. Carbohydrate Polymers, 76, 299-304.
http://dx.doi.org/10.1016/j.carbpol.2008.10.031 - 13. The, D.P., Debeaufort, F., Voilley, A. and Luu, D. (2009 Biopolymers Interactions Affect the Functional Properties of Edible Films Based on Agar, Cassava Starch and Arabinoxylan Blends. Journal of Food Engineering, 90, 548-558.
http://dx.doi.org/10.1016/j.jfoodeng.2008.07.023 - 14. Gedde, U.W. (1999) Polymer Physics. Springer, 298 p.
- 15. Lipatov, I.S. (1988) Colloid Chemistry of Polymers. Elsevier.












