Advances in Remote Sensing
Vol. 2 No. 2 (2013) , Article ID: 32873 , 9 pages DOI:10.4236/ars.2013.22015
A Simplified Approach for Interpreting Principal Component Images
1Department of Earth Sciences, Indian Institute of Technology Roorkee, Roorkee, India
2PLANEX, Physical Research Laboratory, Ahmedabad, India
Email: *rpgupta.iitr@gmail.com, reetkamal@gmail.com, varinder126@gmail.com, sneerajprl@gmail.com
Copyright © 2013 Ravi P. Gupta et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 22, 2013; revised May 20, 2013; accepted May 28, 2013
Keywords: Principal Component Images; Remote Sensing; Eigenvectors; Spectral Behavior
ABSTRACT
Principal component transformation is a standard technique for multi-dimensional data analysis. The purpose of the present article is to elucidate the procedure for interpreting PC images. The discussion focuses on logically explaining how the negative/positive PC eigenvectors (loadings) in combination with strong reflection/absorption spectral behavior at different pixels affect the DN values in the output PC images. It is an explanatory article so that fuller potential of the PCT applications can be realized.
1. Introduction
Principal component transform (PCT), also known as eigenvector transformation, Hotelling transformation, Karhunen-Loève (K-L) transformation, eigenvalue-eigenvector decomposition, is a standard and highly powerful technique for processing multidimensional data. This statistical technique aims at reducing variance and dimensionality of the data set by projecting the data along new non-correlated axes. The mathematical principles of the technique are well established [1,2]. The PC transform technique has found extensive applications in almost all disciplines of physical sciences and engineering.
In the field of remote sensing data processing, PCA has been extensively used. Like all other techniques, it also has its set of advantages and disadvantages. The foremost advantage is that it identifies patterns in data. It transforms the data in such a way so as to accentuate its similarities and differences. Also, a PC transform does not lead to any loss of information contained in a dataset; instead it segregates those data bands which are most informative thus saving computational time. Moreover, if all of the axes are kept, then no data is lost as the original data can be recovered from the principal components.
The disadvantages include scene dependence, i.e. if several remote sensing image data sets of a region are acquired at different times or seasons, and even though the character of a certain object may remain unchanged in different scenes, its manifestation in PC images varies depending upon the temporal behavior of other pixels in the scene. Thus, the manifestation of the same object is not related to only intrinsic properties but also varies depending on temporal scene conditions or data in other pixels. Additionally, it is observed that the PC image display is software dependent, i.e. if different software is used for generating PC images from the same input data set, the computed PC image displays may appear different depending upon the way the computations are made in different software (see below). Further, the interpretation procedure for PC images needs more elaboration and clarification especially in terms of effects of different combinations of negative/positive eigenvectors with high/ low input image DN values.
The purpose of the present article is to elucidate the procedure for interpreting PC images. In the field of remote sensing data processing, numerous examples of principal component analysis (PCA) have been described; however, examples of its logical interpretations and applications have been rather limited. In this article, the salient points we intend to elaborate are: what governs the gray tones (DN values) in a PC image, how important are the negative/ positive eigenvectors (i.e. loadings) and how in combination with strong reflection/absorption spectral properties do they affect the DN values in the PC images.
Most commonly PCT is performed on remote sensing data sets using various software packages, and the resulting PC images invariably appear quite different to the input spectral band images. We attempt to logically describe the procedure for interpreting PC images in a simplified manner. This paper is an explanatory material so that fuller potential of the PCT applications can be realized. It draws examples from satellite remote sensing data, and is written mainly for remote sensing data user community; however, it can be conveniently adapted and extended also to various other scientific disciplines.
The paper has been organized into several sections. Firstly, basic concepts and terminology of PCA are described. After this a brief review of earlier studies on applications of PCA in remote sensing is given. This is followed by scope of the present work and illustration of the dependence of PC image displays on software. Finally, an assessment and evaluation of effect of combinations of eigenvectors with DN values of spectral bands (with the help of examples), followed by brief conclusions are presented.
2. Principal Component Analysis—Basic Concepts
In the simplest terms, PCA is a method of identifying patterns in data. It transforms the data in such a way so as to accentuate its similarities and differences. PCA is defined as an orthogonal linear transformation that re-expresses multivariate data. It extracts and displays the greatest variance in a data on the first axis (called the first principal component), the second greatest variance on the second axis (which is orthogonal to the first) and so on. It is also used to reduce the dimensionality of a data set consisting of a large number of interrelated variables [3]. Dimension reduction leads to visualization of the data clearly and subsequent data analysis more manageable [2]. If the purpose is to compress the data, then the higher order principal components are dropped but if the purpose is to orthogonalize the data for further processing, then all the components are retained [4].
PCA does not lead to any loss of information; instead it helps in picking up those data sets or bands which are most informative. Also, additional clarity is provided as signal to noise ratio is improved and inter-band correlations are removed.
Satellite remote sensing digital images are numeric; therefore, their dimensionality can be reduced using PCA [5]. After PC transformation, new pixel values are computed and stored but the coordinates of the pixel remains the same.
The various terms used in conjunction with PCA are described below.
Standardized and unstandardized PCA: PCA can be performed in two ways. If the principal components are calculated using the covariance matrix then it is called unstandardized PCA, but if it is calculated using the correlation matrix then it is called standardized PCA.
In multispectral remote sensing, the standardized PCA is reported to have improved signal to noise ratio (SNR) as compared to the unstandardized PCA for the same data set [6,7].
Data space: A multispectral data has a vector space with the number of axes corresponding to the number of spectral components associated with each pixel. For example, Landsat Thematic Mapper (TM) data will have seven dimensions while Terra-ASTER data will have fourteen dimensions. A pixel is plotted as a point in this vector space and its coordinates correspond to the brightness values of that pixel in the appropriate spectral components.
Eigenvectors and Eigenvalues: Let C be an n × n matrix with I as its identity matrix. The eigenvalues of C are defined as the roots of the equation:
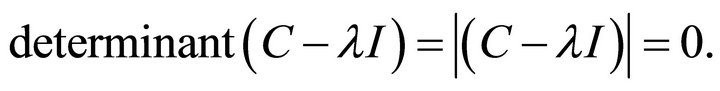 (1)
(1)
Equation (1) is called the characteristic polynomial equation of C and has n roots.
Associated with each eigenvalue is a set of coordinates defining the direction of the associated principal axis [4]. It is called as eigenvector (x) and is computed as:
 (2)
(2)
Thus, the magnitudes of the eigenvalues describe the length and eigenvectors describe the direction of the principal axes.
Pixel value in an image: Pixel value at a point in a particular PC axis image is calculated by multiplying the eigenvector with the corresponding DN value in the original image, and adding all these to get the final pixel value. For example, in an m-band data set, the pixel value at 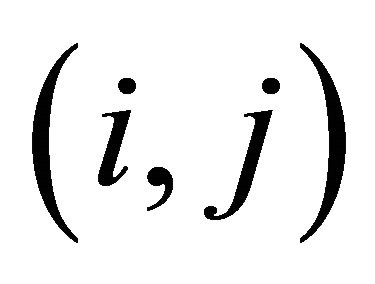 point for the first component (PC-1) is calculated by the following equation:
point for the first component (PC-1) is calculated by the following equation:
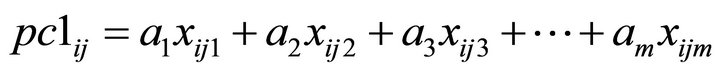 (3)
(3)
where  is the value of the pixel at row i, column j in the first principal component image, the values
is the value of the pixel at row i, column j in the first principal component image, the values 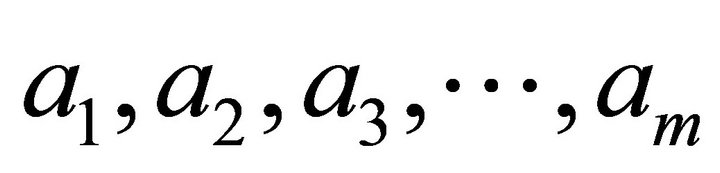 are the elements of the first eigenvector for different bands, and
are the elements of the first eigenvector for different bands, and  is the observed pixel value at
is the observed pixel value at  location in different bands
location in different bands 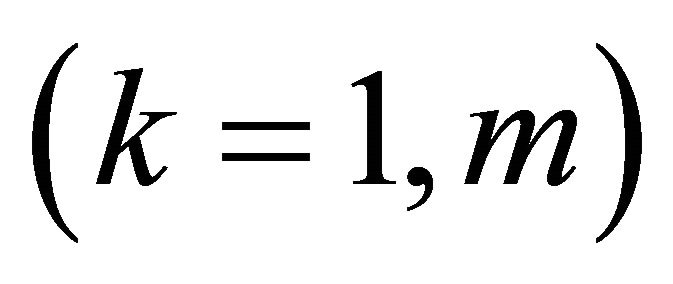 [4]. Thus, a PC image is generated as the sum of the products of eigenvectors and corresponding DN values for spectral bands at each pixel.
[4]. Thus, a PC image is generated as the sum of the products of eigenvectors and corresponding DN values for spectral bands at each pixel.
Loadings: They are simple correlations between the pixel values in PC image and the DN values in original image. The correlation estimates the information they share [8]. They are also treated as “weights”. They give an estimate of the importance of each input parameter (viz. spectral band) to the particular PC axis. These are determined by simple scaling of the underlying eigenvectors and are calculated by multiplying the eigenvector with the square root of the corresponding eigenvalue [2].
Contribution: Contribution is a fractional measure of importance of a particular spectral band for a PC axis. It is computed as square of the eigenvector component for the particular band divided by the sum of squares of all the components of the eigenvector.
 (4)
(4)
Some of the software (e.g. ERDAS, ENVI) normalize the eigenvectors to unit length, such that the sum of squares of every eigenvector of a particular PC axis is always one. Thus, the denominator in the above equation gets normalized to 1 in Equation (4). Then, the percent contribution of a particular band in a PC axis is obtained by multiplying the square of fractional contribution of the band (from Equation (4)) with 100 [9].
3. Applications of PCA in Remote Sensing— A Brief Review
In the field of remote sensing, PCA has been used in various applications like pattern recognition, change detection, data reduction, image data transformation, image classification, image extraction and fusion. It was in 1985 that the concept of standardized and unstandardized PCA in remote sensing was introduced [10]. The comparative analysis of these two methods showed that there was considerable improvement in signal-to-noise ratio using the standardized PCA method as compared to the unstandardized method [7].
In the Kitchener-Waterloo-Guelph area in Canada, PCA was used to calculate the land-cover changes based on both standardized and unstandardized methods. It was reported that standardized PCs provide more accurate information for change detection than unstandardized PCs [6]. PCA is applicable to data set of any number of bands, and any three of the resulting principal components may be displayed as a colour composite.
Reference [11] gave a method called “feature oriented principal components selection” (FPCS). In this they selectively used only those spectral bands for PC analysis which would have relevance for particular mineral discrimination and identification. They tested its effectiveness in detecting spectral anomalies due to ferric iron oxide minerals.
The “Crosta technique” was used for mapping alteration minerals using TM and airborne TM imagery of the Great Basin region of western United States. He conducted PC analysis on selectively taken set of spectral bands suited for detecting iron oxide and then on another set of spectral bands for detecting hydroxyl-bearing minerals [12]. This technique has been applied by many workers for mapping alteration minerals using PCA [13-15].
PCA can also be used for characterizing land cover at global scales using long time-series satellite data from the NOAA-AVHRR [16]. A new technique was developed, called vegetation vector, derived from the first two PCs, to visualize variations in vegetation cover and the phenological characteristics of diverse land covers.
Healthy and bleached coral can also be differentiated using PCA on remote sensing data. The results of PCA were reported to be consistent with those of cluster analysis and spectral derivative analysis in remotely detecting and delineating areas of submerged healthy and bleached corals [17].
PCA has been used for component separation [18]. They performed PCA on albedo time series and reported that different principal components represent different features in the data. These components were then segregated to temporal factors and stable factors based on visual interpretation and quantitative analysis.
PCA was used as a method of change detection for the Kafue Flats, Zambia, using four scenes of Landsat’s multispectral (MSS) and TM data [5]. Three bands from each image were combined to form a 12-band image for change detection and PCA was performed. The colour composite of first three eigen images from the merged data set indicated changed as well as unchanged areas. PCA was reported to be better than classification comparison approach for change detection.
Many authors have used PCA in the past for various applications. A few of those applications are: spatial principal component analysis (SPCA) for analyzing ecoenvironmental vulnerability in upper reaches of Minjiang river in China [19]; to detect geomorphologic features and sediment textural classes along El Tineh coastal plain in Egypt [20]; to examine the environmental impact of the East Port Said harbour project on the surrounding landscape during 1972-1991 [21]; as one of the index in Decision tree classifier for land use classification of delta oasis of the Weigan and Kuqa rivers in China from ETM+ data [22]; to distinguish between geologic features in west Qatar [23].
PCA was used as an image enhancement technique to improve the spectral signal of burnt surfaces [24]. They proposed a new method based on forward/backward PCA and image differencing, which creates a new spectral space that preserves the original spectral patterns while enhancing particular structures of the original satellite data.
4. Scope of the Work
As mentioned earlier, the PCA is a standard technique for multidimensional data analysis. In this presentation, the attempt is to briefly describe the methodology of PC image generation, with the intention of elaborating what governs the gray tone (DN value) at pixels in a PC image. The idea is to particularly discuss how the negative/ positive eigenvectors in combination with spectral behaviour (high/ low DN values) in the input bands affect the final DN-values in the computed PC image. The purpose of this article is to clarify such issues logically, so that the potential of the powerful PCA technique can be fully realized.
5. Dependence of PC Image Displays on Software
These days, frequently software are used for computing PC images. Out of the lot, two very extensively used software in remote sensing data processing are the ERDAS and ENVI and a basic software is MATLAB. For the sake of example, a subscene of ASTER multispectral image data (VNIR—0.52 - 0.86 µm and SWIR—1.60 - 2.43 µm) of Cuprite Mining District (Nevada, USA), was selected for analysis by different software and subsequent comparative analysis.
In ERDAS IMAGINE, PC analysis is done only by covariance matrix, whereas in ENVI, both the options, i.e. employing covariance and correlation matrices exist. In view of the present aim of a comparative analysis, we have used covariance matrix option in both the software. Table 1(a) shows the eigenvectors calculated using ERDAS IMAGINE and Figures 1(a) and 2(a) show the corresponding PC-2 and PC-3 images. Further, Table 1(b) shows the eigenvectors calculated using ENVI and Figures 1(b) and 2(b) show the examples of corresponding PC-2 and PC-3.
It is observed that the eigenvectors calculated from ERDAS IMAGINE and ENVI sometimes have mutually inverted relationship, i.e., though the numeric values from the two methods are the same, they differ in sign (positive or negative), e.g. in the case of PC-1, PC-2 and PC-3 (see Tables 1(a) and 1(b)). This results in inversion of the images (bright pixels in ERDAS IMAGINE PC-2 and PC-3 images becoming dark in ENVI PC-2 and PC-3 images, and vice-versa, see Figures 1 and 2). However, in higher order PCs, i.e. PC-4, PC-5 or PC-6, the eigenvector values generated by the two softwares (ERDAS IMAGINE, ENVI) are exactly similar in both the numeric value and sign.
In order to have a better comparative assessment, PC transforms have also been calculated by using MATLAB. It is observed that eigenvectors generated from MATLAB (Table 1(c)) are similar to that from ERDAS IMAGINE except for the case of PC-5 where there occurs a sign reversal.
(a)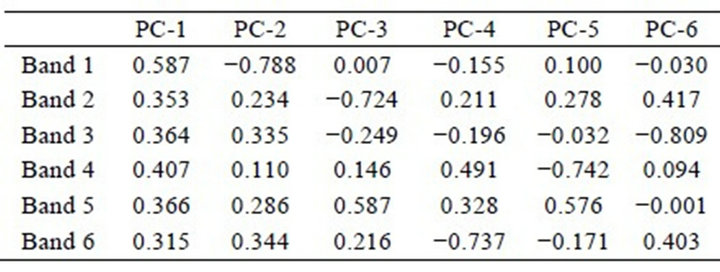 (b)
(b)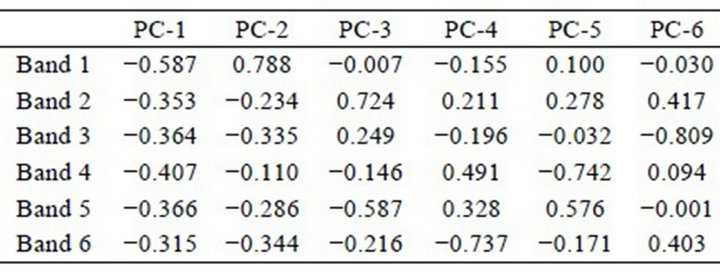 (c)
(c)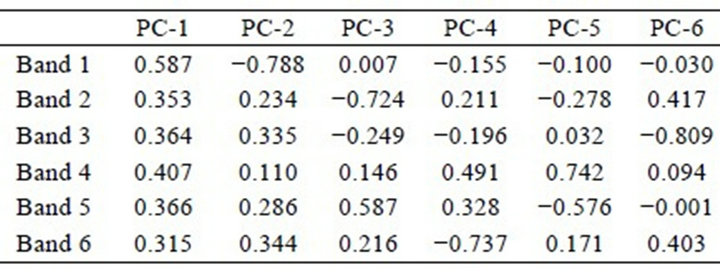
Tables 1. (a) Eigenvector matrix as calculated by ERDAS IMAGINE; (b) Eigenvector matrix as calculated by ENVI; (c) Eigenvector matrix as calculated by MATLAB.
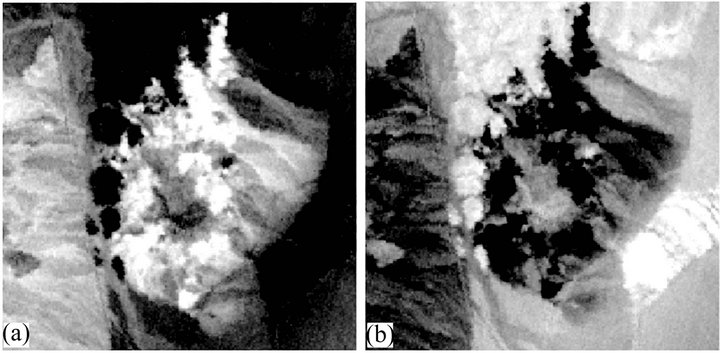
Figure 1. Comparison of PC-2 images produced from two different software packages: (a) ERDAS IMAGINE and (b) ENVI.

Figure 2. Comparison of PC-3 images produced from two different software packages: (a) ERDAS IMAGINE and (b) ENVI.
Therefore, it is important to realize that the eigenvector sign is dependent on how the multi-dimensional space or mathematical space is conceived. As far as PC image displays are concerned, it is observed that relative change in the sign of eigenvector leads to inversion of gray tone in the PC image. For example, in PC-2 the pixels which are dark in ERDAS IMAGINE are bright in ENVI, and vice-versa, as mentioned earlier. Therefore, the image display is primarily dependent on the way how PC’s eigenvectors are calculated.
6. Effect of Combinations of Eigenvectors with DN Values of Spectral Bands on PC Images
It has been discussed above that the PC image is generated as the sum of the products of eigenvectors and DN values for respective spectral bands at each pixel, i.e.
 (5)
(5)
Obviously a larger numeric value of eigenvector (positive or negative) has a higher influence on the PC image. A low numeric value of eigenvector implies that the particular band has relatively low significance for that PC axis. Here we will consider the effects of large (positive or negative) eigenvectors as combined with high or low DN value of the image (which in turn imply strong reflection or strong absorption, respectively). Cases of low values of the eigenvectors are not considered specifically as these would have minimal influence on the resulting PC image.
These examples have been generated using the ASTER image data of Cuprite Mining District (Nevada, USA) and of Indo-Gangetic plains (Uttrakhand, India). Different image data subsets have been used to serve as suitable illustrations.
6.1. Example 1 (Figure 3)
For an image data subset (Figure 3(a)) of Cuprite Mining District comprising of VNIRSWIR bands, Figure 3(b) shows the eigenvector of PC-3 image. The spectral band B4 has a very high positive eigenvector and all other bands have small negative eigenvectors. The spectral curve for the pixel under consideration is shown in Figure 3(c). The pixel is characterized by a very strong reflection (high DN) in B4 and weaker reflection (low DN values) in all other bands. On the resulting PC image, due to the combination of large positive eigenvector in B4 and very high DN value in B4 image, the pixel appears very bright (Figure 3(a)).

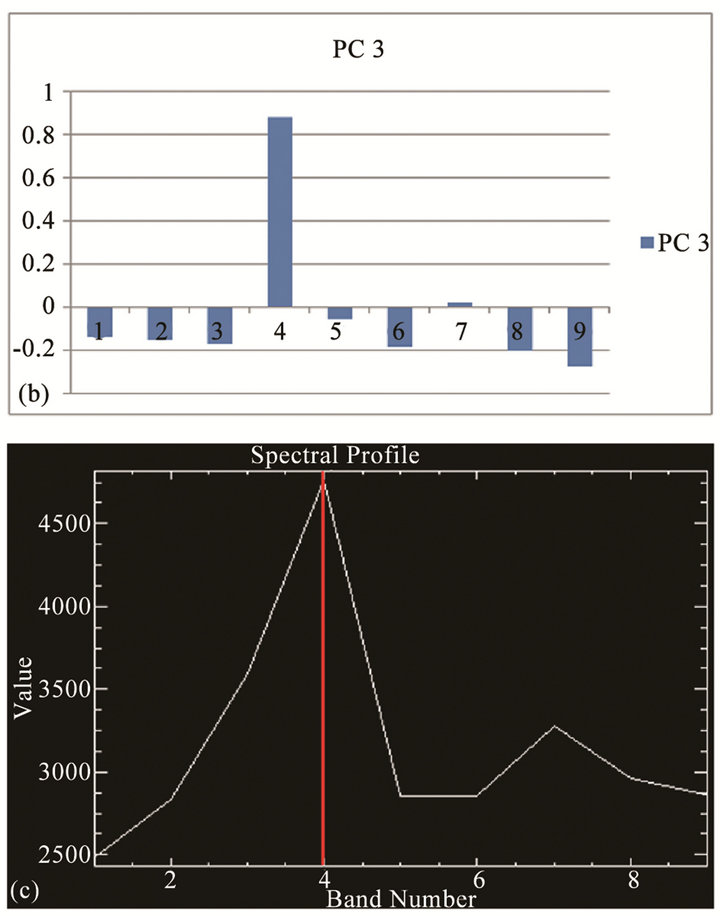
Figure 3. (a) A sub-scene of PC-3 image (Cuprite Mining District, USA); (b) Eigenvectors of PC-3 image in (a) above; (c) Representative spectral plot (VNIR-SWIR) of pixels inside the marked box in (a) above. For further explanation, see text.
6.2. Example 2 (Figure 4)
Figure 4(a) shows a SWIR image data subset of Cuprite Mining District, for which eigenvectors for PC-2 are depicted in Figure 4(b). The spectral band B1 has very large negative eigenvector and all other bands have small positive eigenvectors. The spectral profile of the pixel under consideration is (Figure 4(c)) showing high DN value (strong reflection) in B1. Product of large negative eigenvector and high DN value in B1 image results in
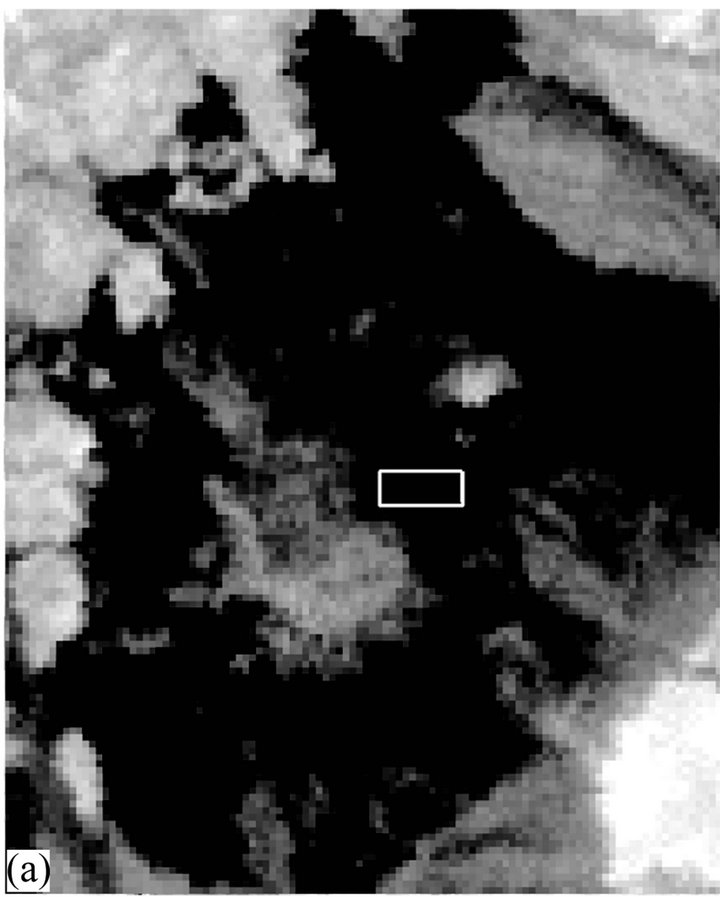

Figure 4. (a) A sub-scene of PC-2 image (Cuprite Mining District, USA); (b) Eigenvectors of PC-2 image in (a) above; (c) Representative spectral plot (SWIR) of pixels inside the marked box in (a) above. For further explanation, see text.
making the pixel very dark in the PC-2 image (Figure 4(a)).
6.3. Example 3 (Figure 5)
Figure 5(a) is an ASTER image data subset of IndoGangetic plains. The PC-2 eigenvectors for the VNIRSWIR bands of the subscene are shown in Figure 5(b). The spectral band B3 has a very large negative eigenvector. The spectral profile for the selected pixel is

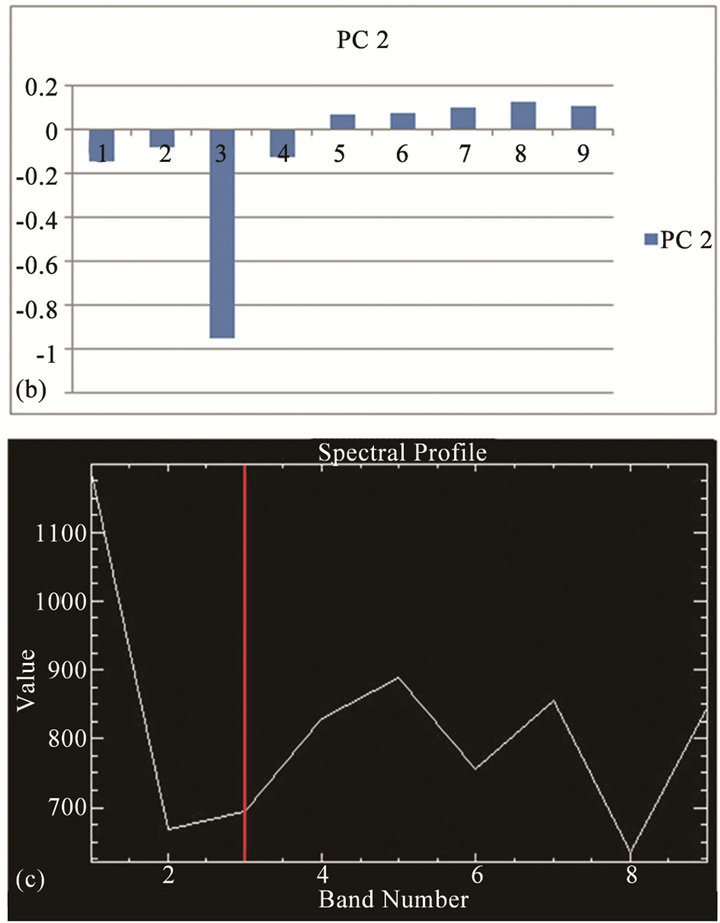
Figure 5. (a) A sub-scene of PC-2 image (Indo-Gangetic plains, India); (b) Eigenvectors of PC-2 image in (a) above; (c) Representative spectral plot (VNIR-SWIR) of pixels inside the marked box in (a) above. For further explanation, see text.
shown in Figure 5(c). The pixel is characterized by strong absorption (very low DN value) in B3. All other bands show either small positive or negative eigenvectors; therefore they are relatively not important. On the resulting PC-2 image, the combination of very large negative eigenvector and strong absorption leads to the pixel becoming bright (Figure 5(a)).
A bit of explanation seems necessary here. In such a case when large negative eigenvector value is multiplied with various pixel DN values in the input image, the lowest DN value (dark) pixels in the input image get to have relatively smallest negative computed values in the PC image; on the other hand, other pixels which have relatively higher DN values in the input band acquire corresponding higher negative computed values. On rescaling for image display, the pixels with smallest (lowest) negative computed values become bright.
6.4. Example 4 (Figure 6)
Figure 6(a) is a PC-2 subscene derived from ASTER VNIR-SWIR image data of Indo-Gangetic plains. The corresponding PC-2 eigenvectors are shown in Figure 6(b). The spectral profile of the selected pixel is shown in Figure 6(c). Eigenvectors for all the spectral bands except B3 are small negative or positive. Spectral bands B3 and B4 are marked by strong reflection. The combination of B3 high DN values and large negative eigenvector results in large negative computed values on the PC image making the pixel dark (Figure 6(a)).
6.5. Example 5 (Figure 7)
Figure 7(a) shows a PC-3 subscene resulting from ASTER image data of Cuprite Mining District, for which PCA on SWIR bands was carried out. The corresponding PC-3 eigenvectors are shown in Figure 7(b). Spectral curve for a selected pixel is provided in Figure 7(c). Although there is high DN value in spectral band B1, the corresponding eigenvector is very small; therefore, this band becomes relatively insignificant for this PC image. Spectral band B2 has moderate DN value and the largest negative eigenvector. B5 has highest positive eigenvector and lowest DN value (strong spectral absorption). The combination of these factors results in the pixel becoming dark in this PC image (Figure 7(a)).
6.6. Example 6 (Figure 8)
Figure 8(a) shows a PC-4 image subscene derived from ASTER VNIR-SWIR image data of Cuprite Mining District, and Figure 8(b) shows the corresponding eigenvectors. The spectral profile for the selected pixel is shown in Figure 8(c). In spectral band B1, the eigenvector value is high positive but there is low DN value (strong absorption); B3 is marked by largest negative eigenvector and very high DN value (strong reflection). B4 is insignificant as the eigenvector is very small. B5 has large positive eigenvector but very low DN value (strong absorption). All other bands have low eigenvectors (positive or negative) and low DN values; therefore they are non-significant. The combination of all the above factors, i.e. eigenvectors of B1, B3 and B5 with corresponding DN values leads to the pixel becoming dark (Figure 8(a)).

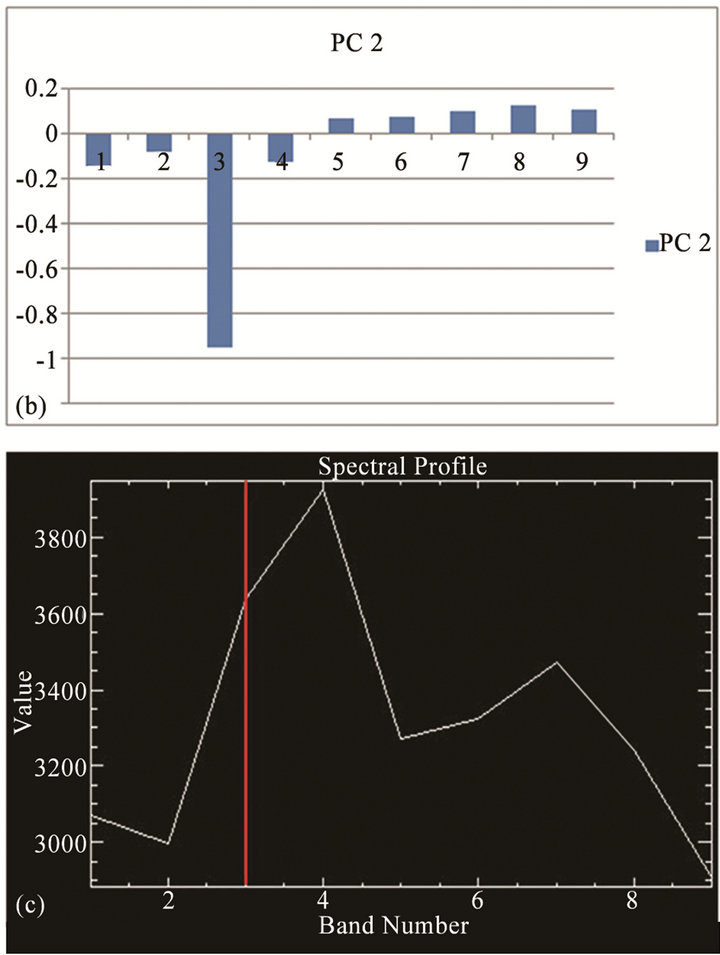
Figure 6. (a) A sub-scene of PC-2 image (Indo-Gangetic plains, India); (b) Eigenvectors of PC-2 image in (a) above; (c) Representative spectral plot (VNIR-SWIR) of pixels inside the marked box in (a) above. For further explanation, see text.
7. Concluding Remarks
Though PCA is a standard technique for multidimensional data analysis, there has been no well outlined procedure for interpreting PC images. The present article attempts to fill this gap and provides a straight forward logical approach for PC image interpretation.
A PC image is generated as the sum of products of eigenvectors and corresponding DN values for various


Figure 7. (a) A sub-scene of PC-3 image (Cuprite Mining District, USA); (b) Eigenvectors of PC-3 image in (a) above; (c) Representative spectral plot (SWIR) of pixels inside the marked box in (a) above. For further explanation, see text.
input spectral bands at each pixel.
The DN value in the spectral band depends upon the spectral characteristics of the object—being high DN value for strong reflection and low DN value for strong absorption.
The magnitude of the band eigenvector relates the significance of the spectral band to the PC axis, a large numeric value implying greater significance of the particular band for the PC image.
The following cases of combination of large eigen-
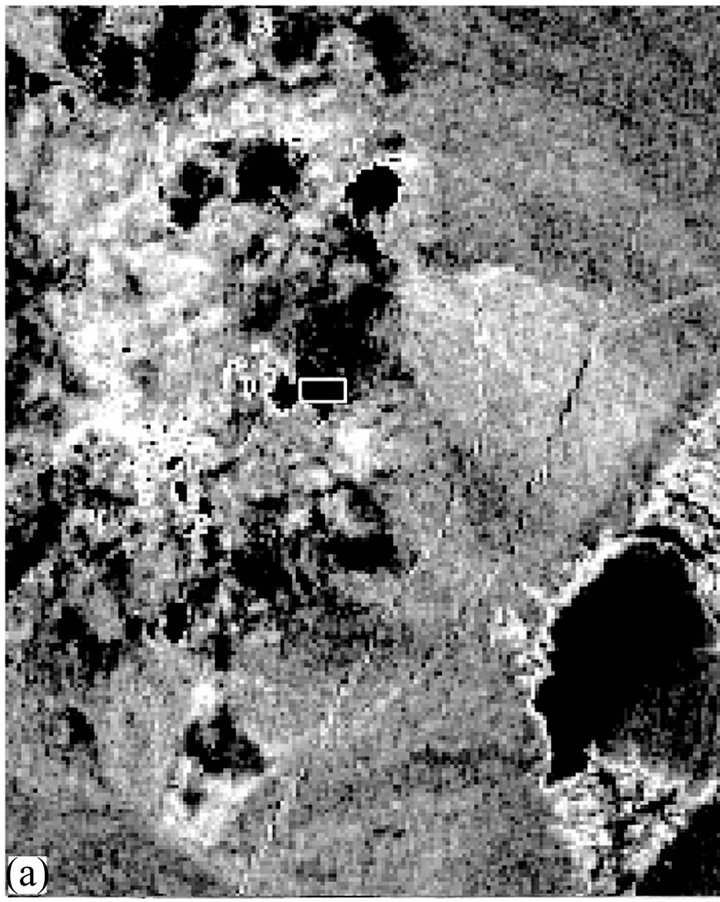
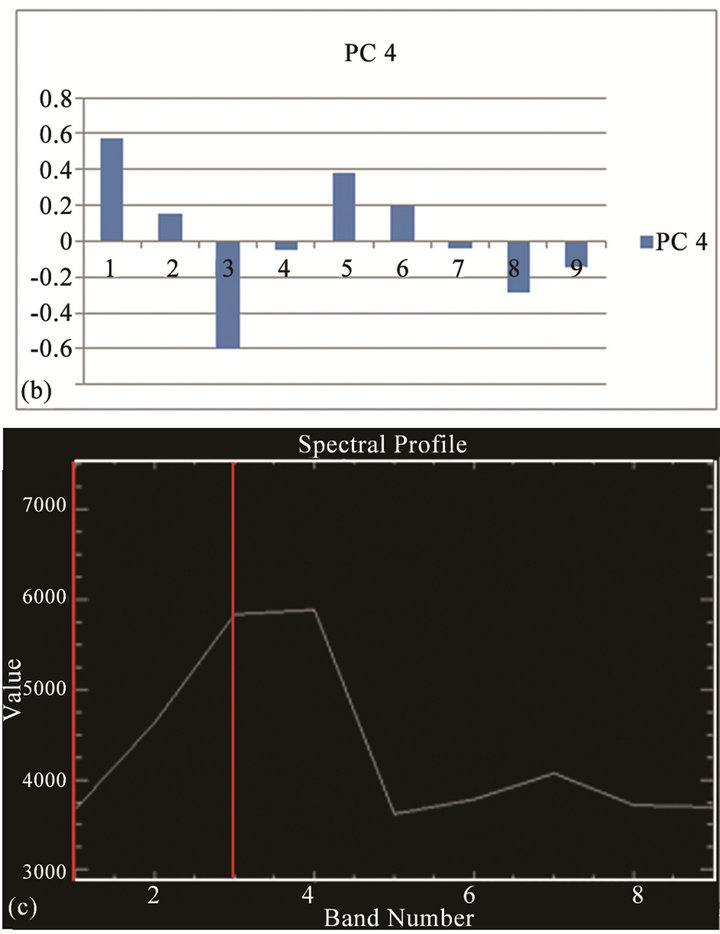
Figure 8. (a) A sub-scene of PC-4 image (Cuprite Mining District, USA); (b) Eigenvectors of PC-4 image in (a) above; (c) Representative spectral plot (VNIR-SWIR) of pixels inside the marked box in (a) above. For further explanation, see text.
vector with DN values at pixels are specifically important to consider:
1) Large positive eigenvector in combination with high DN value of the input image (implying strong reflection at the pixel) results in a bright pixel in the PC image.
2) Large positive eigenvector combined with low DN values in the input image (implying strong absorption) results in dark pixels in the PC image.
3) Large negative eigenvector combined with high DN value of the input image (implying strong reflection) results in dark pixels.
4) Large negative eigenvector combined with low DN value (implying strong absorption) results in bright pixels in the PC image.
Thus, the final DN value in the PC image depends upon magnitude and sign of the eigenvectors along with DN values in the input image.
REFERENCES
- R. A. Johnson and D. W. Wichern, “Applied Multivariate Statistical Analysis,” Prentice Hall, New Jersey, 2001.
- J. M. Lattin, J. D. Caroll and P. E. Green, “Analyzing Multivariate Data,” Brooks/Cole, Thomson Asia Pte. Ltd., Singapore, 2004.
- I. T. Jolliffe, “Principal Component Analysis,” SpringerVerlag, New York, 2002.
- P. M. Mather, “Computer Processing of Remotely-Sensed images,” John Wiley & Sons Ltd, West Sussex, 2004.
- C. Munyati, “Use of Principal Component Analysis (PCA) of Remote Sensing Images in Wetland Change Detection on Kafue Flats, Zambia,” Geocarto International, Vol. 19, No. 3, 2002, pp. 11-22. doi:10.1080/10106040408542313
- T. Fung and E. LeDrew, “Application of Principal Components Analysis to Change Detection,” ISPRS Journal of Photogrammetry and Remote Sensing, Vol. 53, No. 12, 1987, pp. 1649-1658.
- L. Eklundh and A. Singh, “A Comparative Analysis of Standardised and Unstandardised Principal Components Analysis in Remote Sensing,” International Journal of Remote Sensing, Vol. 14, No. 7, 1993, pp. 1359-1370. doi:10.1080/01431169308953962
- G. P. Quinn and M. J. Keough, “Experimental Design and Data Analysis for Biologists,” Cambridge University Press, Cambridge, 2002. doi:10.1017/CBO9780511806384
- EXELIS, “How to Figure out Principal Component Analysis Band Weightings,” 2000. http://www.exelisvis.com/Support/HelpArticlesDetail/TabId/219/ArtMID/900/ArticleID/2807/2807.aspx
- A. Singh and A. Harrison, “Standardised Principal Components,” International Journal of Remote Sensing, Vol. 6, No. 6, 1985, pp. 883-896. doi:10.1080/01431168508948511
- A. P. Crosta and J. M. Moore, “Enhancement of Landsat Themetic Mapper Imagery for Residual Soil Mapping in SW Minas Gerais State, Brazil: A Prospecting Case History in Greenstone Belt Terrain,” Proceedings of the Seventh Thematic Conference on Remote Sensing for Exploration Geology, Calgary, 2-6 October 1989, pp. 1173- 1187.
- W. P. Loughlin, “Principal Component Analysis for Alteration Mapping,” Photogrammetric Enggineering and Remote Sensing, Vol. 57, No. 9, 1991, pp. 1163-1169.
- J. R. Ruiz-Armenta and R. M. Prol-Ledesma, “Techniques for Enhancing the Spectral Response of Hydrothermal Alteration Minerals in Thematic Mapper Images of Central Mexico,” International Journal of Remote Sensing, Vol. 19, No. 10, 1998, pp. 1981-2000. doi:10.1080/014311698215108
- M. H. Tangestani and F. Moore, “Porphyry Copper Alteration Mapping at the Meiduk Area, Iran,” International Journal of Remote Sensing, Vol. 23, No. 22, 2002, pp. 4815-4825. doi:10.1080/01431160110115564
- A. B. Pour and M. Hashim, “Spectral Transformation of ASTER Data and the Discrimination of Hydrothermal Alteration Minerals in a Semi-Arid Region, SE Iran,” International Journal of Physical Sciences, Vol. 6, No. 8, 2011, pp. 2037-2059.
- Y. Hirosawa, S. E. Marsh and D. H. Kliman, “Application of Standardized Principal Component Analysis to LandCover Characterization Using Multitemporal AVHRR Data,” Remote Sensing of Environment, Vol. 58, No. 3, pp. 267-281. doi:10.1016/S0034-4257(96)00068-5
- H. Holden and E. LeDrew, “Spectral Discrimination of Healthy and Non-Healthy Corals Based on Cluster Analysis, Principal Components Analysis, and Derivative Spectroscopy,” Remote Sensing of Environment, Vol. 65, No. 2, 1998, pp. 217-224. doi:10.1016/S0034-4257(98)00029-7
- D. Yuan, J. R. Lucas and D. E. Holland, “A Landsat MSS Time Series Model and Its Application in Geological Mapping,” ISPRS Journal of Photogrammetry and Remote Sensing, Vol. 53, No. 1, 1998, pp. 39-53. doi:10.1016/S0924-2716(97)00027-0
- A. Li, A. Wang, S. Liang and W. Zhou, “Eco-Environmental Vulnerability Evaluation in Mountainous Region Using Remote Sensing and GIS—A Case Study in the Upper Reaches of Minjiang River, China,” Ecological Modelling, Vol. 192, No. 1-2, 2006, pp. 175-187. doi:10.1016/j.ecolmodel.2005.07.005
- K. H. M. Dewidar and O. E. Frihy, “Thematic Mapper Analysis to Identify Geomorphologic and Sediment Texture of El Tineh Plain, North-Western Coast of Sinai, Egypt,” International Journal of Remote Sensing, Vol. 24, No. 11, 2003, pp. 2377-2385. doi:10.1080/01431160110115807
- M. F. Kaiser, “Environmental Changes, Remote Sensing, and Infrastructure Development: The Case of Egypt’s East Port Said Harbor,” Applied Geology, Vol. 29, No. 2, 2009, pp. 280-288.
- J.-L. Ding, M.-C. Wu and T. Tiyip, “Study on Soil Salinization Information in Arid Region Using Remote Sensing Technique,” Agricultural Sciences in China, Vol. 10, No. 3, 2011, pp. 401-411.
- A. Sadiq and F. Howari, “Remote Sensing and Spectral Characteristics of Desert Sand from Qatar Peninsula, Arabian/Persian Gulf,” Remote Sensing, Vol. 1, No. 4, 2009, pp. 915-933. doi:10.3390/rs1040915
- N. Koutsias, G. Mallinis and M. Karteris, “A Forward/ Backward Principal Component Analysis of Landsat-7 ETMC Data to Enhance the Spectral Signal of Burnt Surfaces,” ISPRS Journal of Photogrammetry and Remote Sensing, Vol. 64, No. 1, 2009, pp. 37-46. doi:10.1016/j.isprsjprs.2008.06.004
NOTES
*Corresponding author.

