Advances in Nanoparticles
Vol.2 No.4(2013), Article ID:39013,8 pages DOI:10.4236/anp.2013.24048
Study of Nanomaterials under High Pressure
Department of Physics and Electronics, National University of Lesotho, Roma, Lesotho
Email: m.singh@nul.ls
Copyright © 2013 Madan Singh, Moruti Kao. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 11, 2013; revised October 13, 2013; accepted October 25, 2013
Keywords: Equation of State; Nanomaterials; Murnaghan EOS
ABSTRACT
A simple theory is proposed to predict the effect of pressure for study of volume expansion of nanomaterials. Different possible forms of equation of state are discussed with their correlations. Only two input parameters, namely, the bulk modulus and its first pressure derivative, are required for calculations. We have considered a wide variety of nanomaterials, such as, CdSe (4.2 nm), Fe-Cu (14 nm), ƴ-Al2O3 (67 nm), ƴ-Al2O3 (37 nm), Ni (20 nm), Fe (10 nm), CeO2 (cubic Fluorite phase) (15 nm), CeO2 (Orthorhombic Phase) (15 nm), CuO (24 nm) and TiO2 (rutile phase) (10 nm) to analyze the effect of pressure on them. The theoretical predictions for the given nanomaterials agree with the experimental results and the other theoretical models.
1. Introduction
The study of nanocrystalline materials with dimension less than 100 nm is the active area of research in physics, chemistry and engineering [1]. Nanomaterial is a field that takes a material science based on the approach to nanotechnology. Nanomaterials differ significantly from the bulk materials by virtue of their small size. Often, the behavior of nanomaterials may depend more on its surface area than particle’s composition itself. Electrical, optical and chemical properties of nanomaterials are very different at large scale. More than half of the material atoms are on the surface, increasing relative surface area and quantum effects. These factors can change or enhance the properties such as reactivity, strength, electrical and optical characteristics. Various physical properties such as hardness, melting temperature, sintering ability and electronic structure depend upon particle size [2- 7]. Nanomaterials, nanoparticles, nanowires and nanotubes have been reported to show physical, chemical and mechanical properties that are noticeably different from their corresponding bulk counterparts.
For example, phonon frequency blue shift in nanosemiconductors and nanometals, increase of elastic modulus in thin films and nanoparticles, decrease of melting temperature and thermal conductivity in nanocrystals are associated with the particle size of the material under consideration [8,9]. There are four classes of materials that are used to make nano-sized products including metal, carbon, composites and dentrimers. These products have a variety of application and are used in the automotive industry, biomedical industry, in films and much more. Metal-based nanomaterials are those such as nanogold, quantum dots and nanosilver. Quantum dots come in several sizes with a maximum size of several hundred nanometers. The dot contains semiconductor crystals that are packed together so thousands of atoms are all in a very small area. Other metal-based chemicals used at this small scale include types of metal oxides. Carbon-based nanomaterials are those that are mostly made of carbon. The carbon is shaped into hollow tubes, ellipsoids or spheres. Ellipsoidal and spherical carbon nanomaterials are called fullerenes. Nanomaterials are expected to be the turning point of the next technological revolution in solid-state electronics, to emerge as new structural materials, to serve as systems for controlling drug delivery and to have a considerable impact in practically all domains of science. These materials, remarkable for their extremely small size, have the potential for wide ranging industrial, biomedical, and electronic applications. Miguel [10] has critically reviewed the expected effects and benefits of the effect of pressure on nanomaterials. Pressure and temperature dependence of volume V/V0, bulk modulus B, and coefficient of volume thermal expansion was investigated by varying the temperature from room temperature to 2000 K, and pressure from room pressure to 200 kbar. Due to high pressure on nanomaterials, many effects happen such as pressure ionization, modification in electronic properties etc. Therefore, pressure volume relation of condensed matter known as equation of state (EOS) is an important idea. As many EOS exist in literature, there is still a need to explain the effect of pressure at constant temperature for nanomaterials. Lithium-alumino-silicate ceramics have gained considerable commercial attention because of very low thermal expansion, transparency, high chemical durability and strength.
They are very sensitive to the external parameters like pressure and temperature. The physical properties of these materials depend strongly on structure and interatomic distances. Pressure can vary these distances, which implies that we can study relationships between structure and properties of the materials [11]. Therefore, it is not just a matter of great interest, but also a necessity, to study the thermodynamic properties of nanocrystalline (NC) materials.
Investigation of the behavior of NC materials under high pressure can provide valuable information about their intrinsic microstructural characteristics. The study of nanomaterials with varying pressure can help us to study a wide range of solid state materials. High temperature-pressure applications have the potential to constitute a unique way for the elaboration of new materials in a controlled manner. Pressure application, as for bulk materials, allows the continuous modification of the interatomic interactions of the nano-object and constitutes an invaluable tool to explore physico-chemical interactions at the nanoscale and their link with physical properties of interest.
The physical properties of materials depend strongly on the structure and interatomic distances. High pressure can vary these distances, which implies that we can study relationships between structure and properties of the materials. Due to the high pressure on nanomaterial, many effects occur, such as 1) transformation of nano-constitutive elements, 2) transformations of the interaction between nano-objects, and 3) modification of interactions between the nano-object and pressure transmitting medium. Due to such applications, the effects of pressure on nanomaterials have attracted the attention of the researchers. In many applications, the understanding of material properties that are influenced by pressure becomes crucial. Therefore, investigation of the behavior of nano-sized materials under high pressure is indispensable, especially due to the immense potential of applications associated with these materials. Several experiments have been performed to study and explain the behavior of nonmaterial [7-10,12-18]. It is then not surprising that high-pressure investigations of nanomaterials develop in parallel to the growth of nanoscience either for better understanding of the properties of nanomaterials or providing alternative methods for nanostructuration. Experimental data [7-10,12-18] used by different techniques such as X-Ray diffraction under hydrostatic pressure in a diamond anvil cell (DAC) method are obtained, using high energy Synchrotron radiation and Raman spectroscopic technique, High pressure X-Ray diffraction and X-Ray absorption, Neutron diffraction studies of compressibility method, Synchrotron X-Ray diffraction method and Laser induced vapour phase reaction.
An equation of state (EOS) recently proposed for nanomaterials is discussed critically. Different possible forms of the EOS are discussed with their correlations. We have considered 20 nanomaterials for this purpose, viz. CdSe (4.2 nm), Fe-Cu (14 nm), ƴ-Fe2O3 (10 nm), ƴ-Al2O3 (67 nm), ƴ-Al2O3 (37 nm), Ni (20 nm), Fe (10), CeO2 (cubic Fluorite phase) (15 nm), CeO2 (Orthorhombic Phase) (15 nm), CuO (24 nm), TiO2 (rutile phase) (10 nm), TiO2 (anatase) (40 nm), 3C-SiC (30 nm), AIN (Hexagonal wurtzite Phase) (10 nm), ƴ-Si3N4 (10 nm), AIN (Cubic rocksalt Phase) (10 nm), ZnO (wurtzite Phase) (10), ZnO (Rocksalt Phase) (10), SnO2 (14 nm) and SnO2 (8 nm). The results have been found to present a good agreement with the available experimental data.
2. Method of Analysis
The dependence of volume on pressure can be written as,
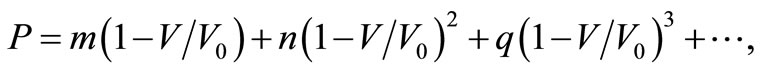 (1)
(1)
where, V/V0 is the relative change in volume, and m, n and q are size dependent parameters, which may be determined from the definition of bulk modulus, and its first and second order pressure derivatives, respectively. In Equation (1), the higher order terms may be ignored because of the smaller contributions. This is advantageous also because higher order pressure derivatives of bulk modulus, which are not available for nanomaterials, are involved in these higher terms.
The Bulk modulus is defined as,

Using this definition of bulk modulus, Equation (1) may be written as,
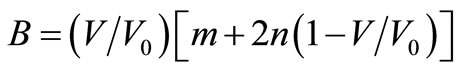 (2)
(2)
First order pressure derivative of bulk modulus is defined as,
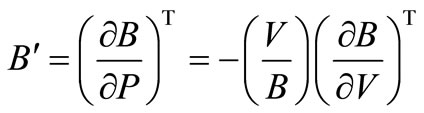 or,
or, 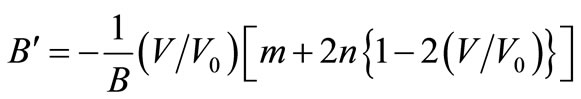
Using all the above equations and applying the boundary conditions, B = B0, when V = V0, we obtain, m = B0 and
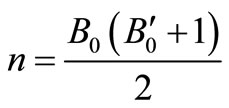 .
.
Substituting these values of m and n in Equation (1), we get the EoS as,
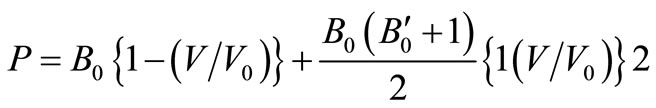 (3)
(3)
Interestingly, Equation (3) can also be derived using the theory of Mie-Gruneisen EoS, which defines pressure as,
 where, PTh is the thermal pressure and U, the lattice potential energy. This Equation gives the relation for thermal expansion as:
where, PTh is the thermal pressure and U, the lattice potential energy. This Equation gives the relation for thermal expansion as:
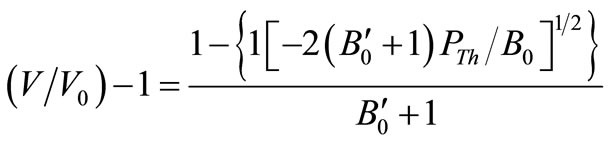 (4)
(4)
It has been claimed that Equation (4) may be written as when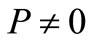 ,
,
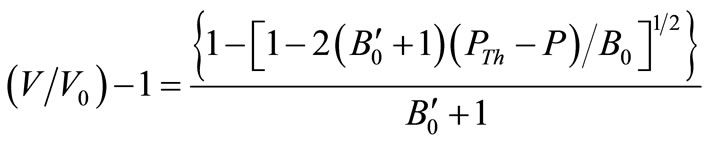 (5)
(5)
When thermal pressure is zero (PTh = 0), Equation (5) may be written as,
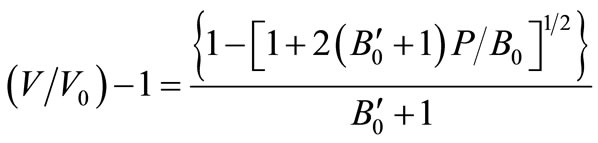 (6)On rearranging we get,
(6)On rearranging we get,
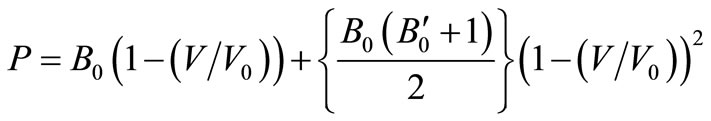 (7)
(7)
It is the same as Equation (3), which supports the legitimacy of Equation (3). We are including some other equation of state (EOS) for comparison purpose such as Murnaghan EOS and Vinet EOS.
On assuming Anderson parameter, 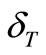 , independent of V/V0, Murnaghan EOS [19] looks as
, independent of V/V0, Murnaghan EOS [19] looks as
 (8)
(8)
Also one can recited Vinet EOS [20] as
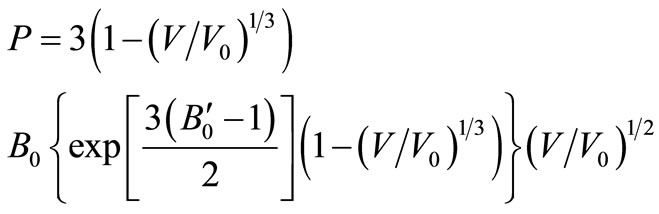 (9)
(9)
3. Result and Discussion
In Equation (1), the next higher order terms have not been considered, we have considered only up to the second term of the series. Because inclusion of higher terms requires second and higher order pressure derivatives of the bulk modulus, which are still not available for most of the nanomaterials. Moreover, it is legitimate and may be useful to discuss the effect of higher order terms in Equation (1). The values of volume expansion (V/V0) have been calculated as a function of pressure, using Equations (7), (8) and (9), respectively for CdSe (4.2 nm), Fe-Cu (14 nm), ƴ-Fe2O3 (10 nm), ƴ-Al2O3 (67 nm), ƴ-Al2O3 (37 nm), Ni (20 nm), Fe (10), CeO2 (cubic Fluorite phase) (15 nm), CeO2 (Orthorhombic Phase) (15 nm), CuO (24 nm), TiO2 (rutile phase) (10 nm), TiO2 (anatase) (40 nm), 3C-SiC (30 nm), AIN (Hexagonal wurtzite Phase) (10 nm)ƴSi3N4 (10 nm), AIN (Cubic rocksalt Phase) (10 nm), ZnO (wurtzite Phase) (10), ZnO (Rocksalt Phase) (10), SnO2 (14 nm), SnO2 (8 nm) nanomaterials. We have used Equation (1) to predict the compression behavior of these nanomaterials. To make the analysis more rigorous, we also included some more EOSs, i.e. Murnagham EOS, Vinet EOS. The results obtained are shown in figures and compared with experimental data. The deviation occur from experimental values at high pressure, it may be because of that we are ignoring higher order terms in Equation (1).
We have selected these materials because of the fact that the experimental data are available. The input data required are given in Table 1. The results obtained are reported in Figures 1-20 along with the available experimental data [14-18] for the sake of comparison. It is found that the results obtained from Equation (7) are in good agreement with the experimental data. It may be concluded that Equation (1) is quite satisfactory for these materials in the pressure range considered in the present

Figure 1. Volume expansion (V/V0) as a function of pressure (GPa) for Fe (10 nm).

Figure 2. Volume expansion (V/V0) as a function of pressure (GPa) for ƴ-Al2O3 (37 nm).
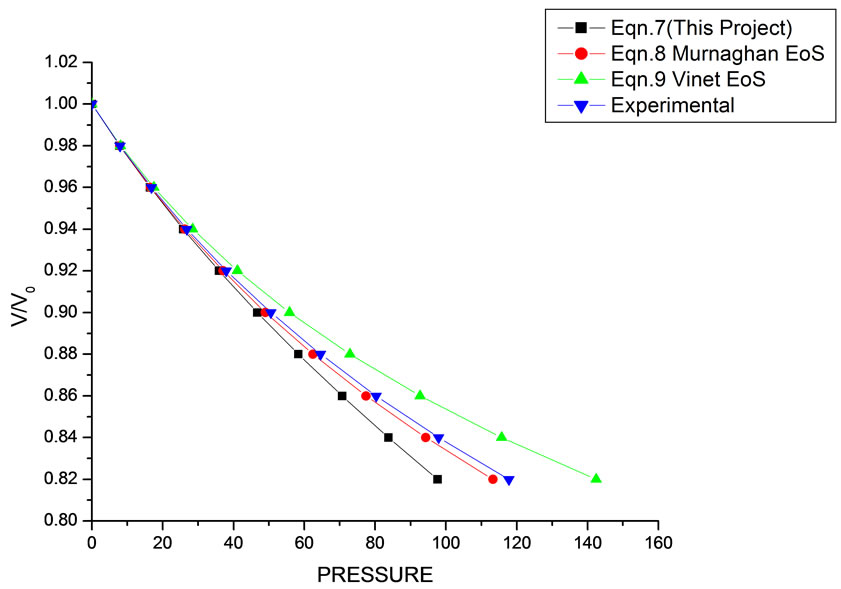
Figure 3. Volume expansion (V/V0) as a function of pressure (GPa) for ƴ-Fe2O3 (10 nm).
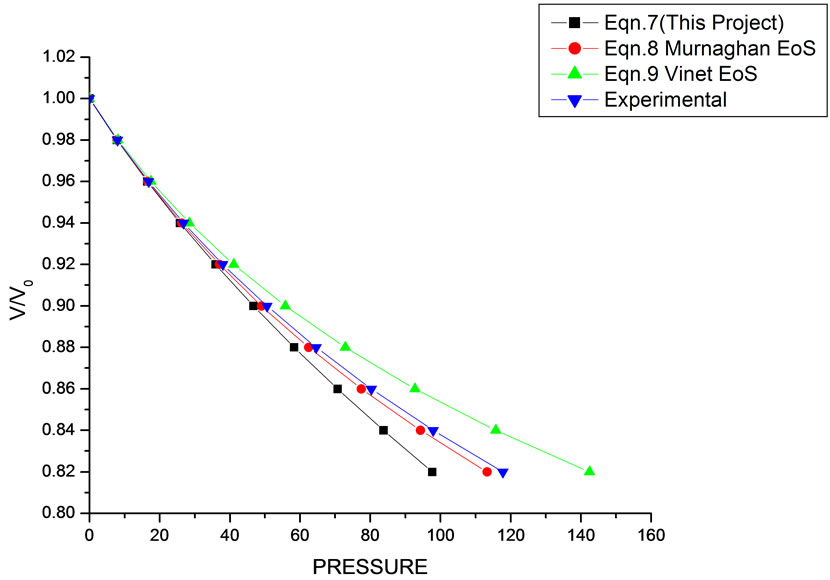
Figure 4. Volume expansion (V/V0) as a function of pressure (GPa) for CdSe (4.2 nm).
paper. This clearly demonstrates that the approximation used in Equation (1) is justified. It should also be understood that all equations of state discussed in this work (Murnaghan and Vinet) have matched with the experimental data. There was a good agreement between the

Figure 5. Volume expansion (V/V0) as a function of pressure (GPa) for Fe-Cu (14 nm).

Figure 6. Volume expansion (V/V0) as a function of pressure (GPa) for Ni (20 nm).

Table 1. Input parameters [7-9,12-18] used in theoretical calculations.
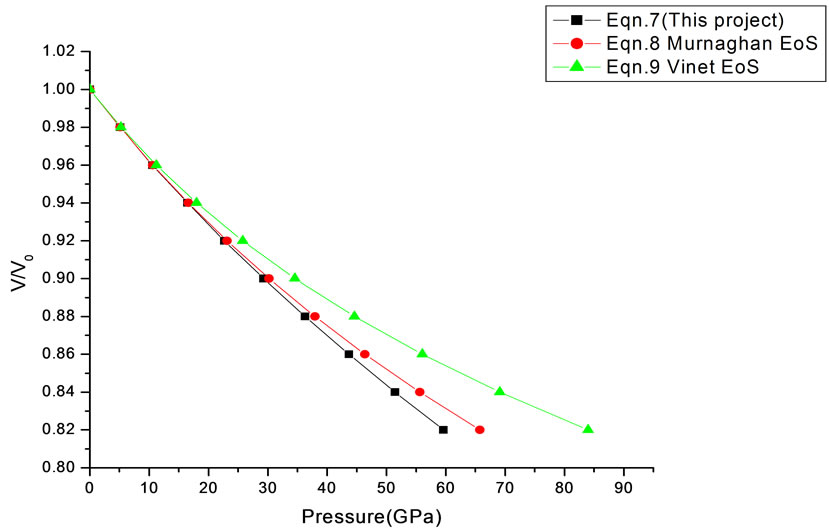
Figure 7. Volume expansion (V/V0) as a function of pressure (GPa) for 3C-SiC (3O nm).
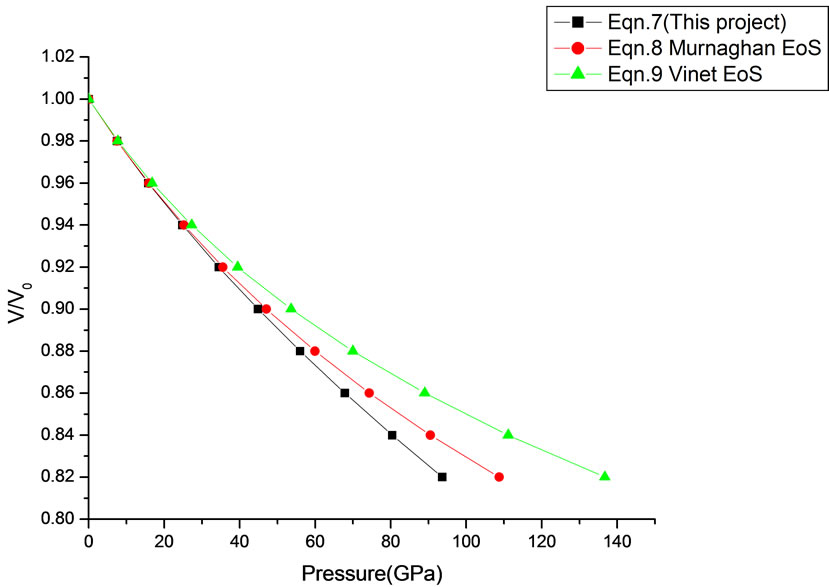
Figure 8. Volume expansion (V/V0) as a function of pressure (GPa) for AIN (Cubic rocksalt Phase) (10 nm).

Figure 9. Volume expansion (V/V0) as a function of pressure (GPa) for AIN (Hexagonal wurtzite Phase) (10 nm).
theoretical values of V/V0 as a function of P, obtained from Equation (7) as has been found with the corresponding experimental data for CdSe (4.2 nm), Fe-Cu (14 nm), Ni (20 nm), ƴ-Fe2O3 (10 nm), Fe (10 nm), and ƴ-Al2O3 (37 nm) nanomaterials [14-18]. It may be concluded from the above discussion that the EoS obtained
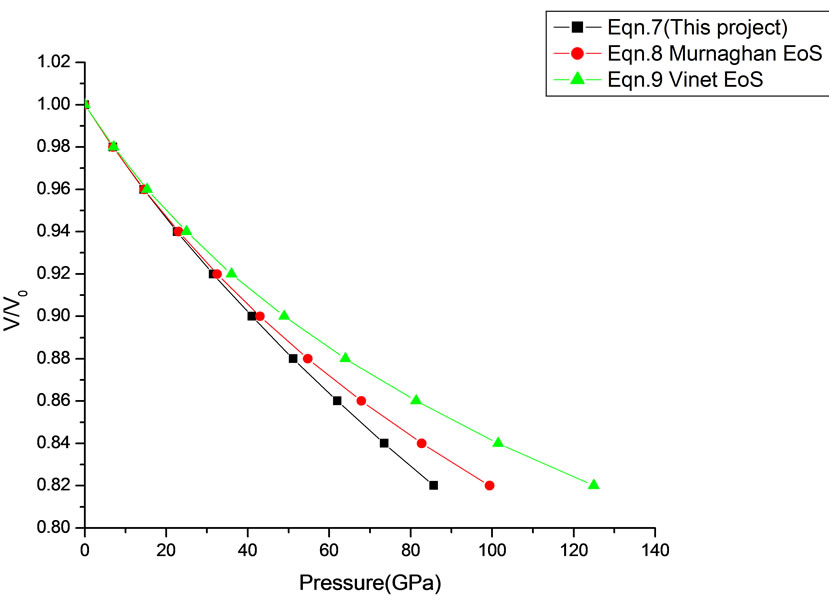
Figure 10. Volume expansion (V/V0) as a function of pressure (GPa) for CeO2 (cubic Fluorite) (15 nm).

Figure 11. Volume expansion (V/V0) as a function of pressure (GPa) for CeO2 (Orthorhombic Phase) (15 nm).
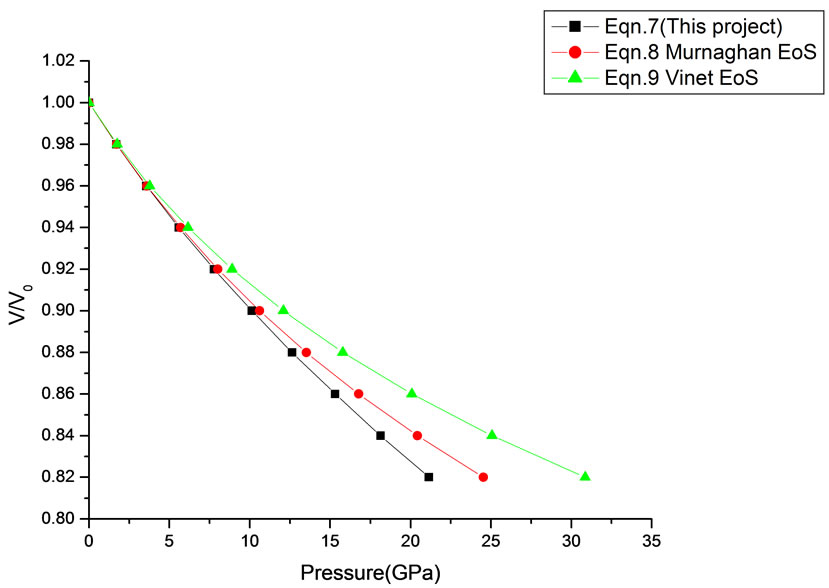
Figure 12. Volume expansion (V/V0) as a function of pressure (GPa) for CuO (24 nm).
in this work [Equation (7)], in general, can produce much better pressure dependent volume expansion data, as compared to other equations of state, for a wide range of nanomaterials.

Figure 13. Volume expansion (V/V0) as a function of pressure (GPa) for SnO2 (14 nm).
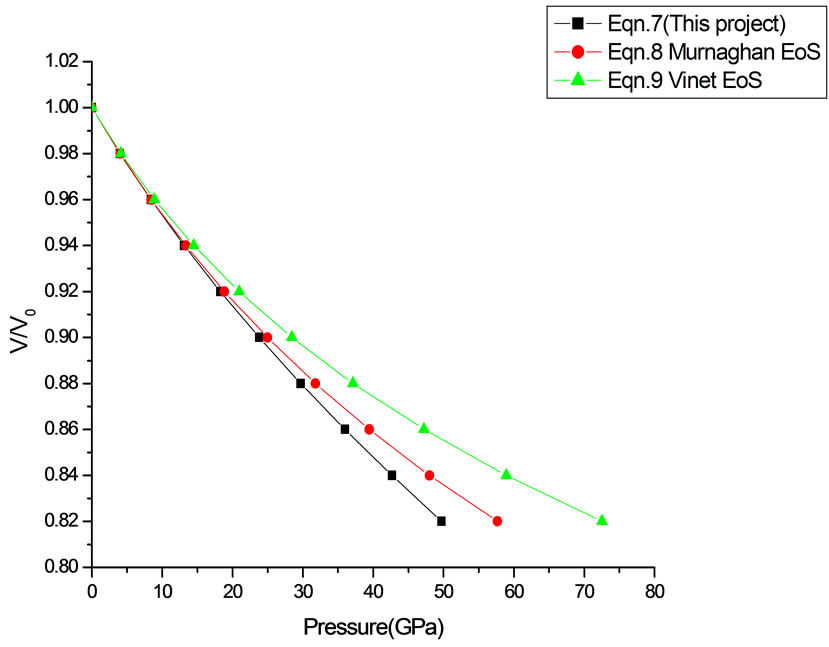
Figure 14. Volume expansion (V/V0) as a function of pressure(GPa) for TiO2 (anatase) (40 nm).

Figure 15. Volume expansion (V/V0) as a function of pressure (GPa) for TiO2 (rutile phase) (10 nm).
4. Conclusion
The behavior of volume expansion as a function of pressure for some nanomaterials is studied. The results ob-

Figure 16. Volume expansion (V/V0) as a function of pressure (GPa) for ZnO (Rocksalt Phase) (10 nm).

Figure 17. Volume expansion (V/V0) as a function of pressure (GPa) for ZnO (Wurtzite Phase) (10 nm).
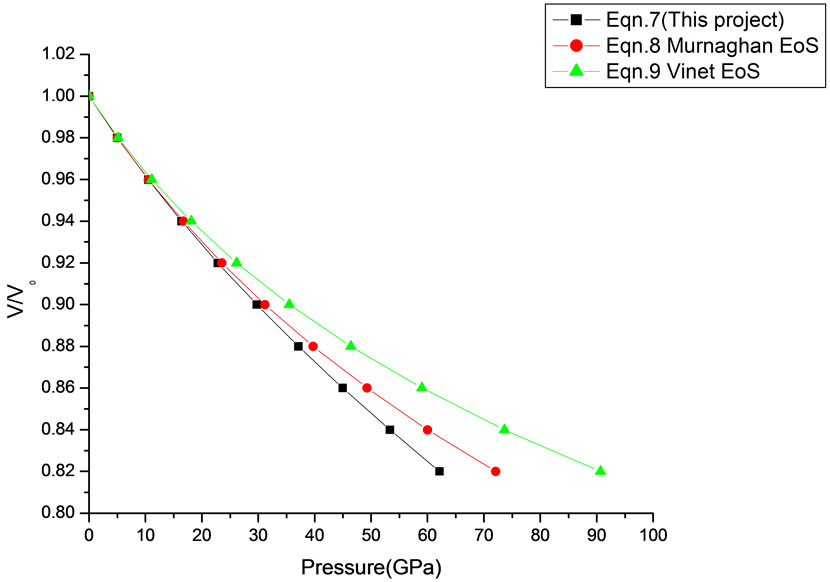
Figure 18. Volume expansion (V/V0) as a function of pressure (GPa) for ƴ-Al2O3 (67 nm).
tained are in good agreement with the available experimental data [14-18] as compared with the other EOSs such as Vinet’s [20]. Very significant agreement has been observed in the low pressure values. Our theory agrees with the experiments throughout the pressure

Figure 19. Volume expansion (V/V0) as a function of pressure (GPa) for ƴ-Si3N4 (10 nm).

Figure 20. Volume expansion (V/V0) as a function of pressure (GPa) for SnO2 (8 nm).
range investigated for a given nanomaterial, whereas there is some deviation, in general, towards low V/V0 values, especially at high pressure. We have extended the formulation for a number of nanomaterials and found good agreement with the experimental data, which demonstrate the validity of the formulation developed. Thus, the present work is a simple method to study and analyze the effect of pressure on nanomaterials.
REFERENCES
- H. Gleiter, “Nanostructured Materials, Basic Concept and Microstructure,” Acta Materialia, Vol. 48, No. 1, 2000, pp. 6243-6248.
- Q. Jiang, L. H. Liang and D. S. Zhao, “Lattice Contraction and Surface Stress of Fcc Nanocrystals,” Journal of Physical Chemistry B, Vol. 105, No. 27, 2001, pp. 6275- 6277. http://dx.doi.org/10.1021/jp010995n
- F. H. Streitz, K. Sieradzki and R. C. Cammarata, “Elastic Properties of Thin Fcc Films,” Physical Review B, Vol. 41, No. 17, 1990, pp. 12285-12287. http://dx.doi.org/10.1103/PhysRevB.41.12285
- L. H. Liang, J. C. Li and Q. Jiang, “Size-Dependent Elastic Modulus of Cu and Au Thin Films,” Solid State Communications, Vol. 121, No. 8, 2002, pp. 453-455. http://dx.doi.org/10.1016/S0038-1098(02)00026-1
- J. H. Zhang, Q. A. Huang, H. Yu and J. Wang, “The Influence of Surface Effects on Size-Dependent Mechanical Properties of Silicon Nanobeams at Finite Temperature,” Journal of Physics D, Vol. 42, No. 4, 2009, Article ID: 045409.
- M. Fujii, T. Nagareda, S. Hayashi and K. Yamamoto, “Low Frequency Raman Scattering from Small Silver Particles Embedded in SiO2 Film,” Physical Review B, Vol. 44, No. 12, 1991, pp. 6243-6248. http://dx.doi.org/10.1103/PhysRevB.44.6243
- W. F. Zhang, Y. He, M. S. Zhang, Z. Yin and Q. Chen, “Raman Scattering Study on Anatase TiO2 Nanocrystals,” Journal of Physics D, Vol. 33, No. 8, 2000, pp. 912. http://dx.doi.org/10.1088/0022-3727/33/8/305
- H. Liang and B. Li, “Size-Dependent Thermal Conductivity of Nanoscale Semiconducting Systems,” Physical Review B, Vol. 73, No. 15, 2006, Article ID: 153303.
- H. W. Kroto, J. R. Heath, S. C. O. Brien, R. F. Curl and R. E. Smalley, “C60: Buckminsterfullerene,” Nature, Vol. 318, No. 6042, 1985, pp. 162-163. http://dx.doi.org/10.1038/318162a0
- A. S. Miguel, “Nanomaterials under High Pressure,” Chemical Society Reviews, Vol. 35, No. 10, 2006, pp. 876-889. http://dx.doi.org/10.1039/b517779k
- M. Singh, P. Singh, B. Gupta and M. Kumar, “Temperature and Pressure Dependence of Elastic Constants,” High Temperature-High Pressures, Vol. 33, No. 2, 2001, pp. 199-206. http://dx.doi.org/10.1068/htjr012
- S. Karmakar, S. M. Sharma, P. V. Teredesai and A. K. Sood, “Pressure-Induced Phase Transitions in Iron-Filled Carbon Nanotubes: X-Ray Diffraction Studies,” Physical Review B, Vol. 69, No. 16, 2004, Article ID: 165414.
- B. Kiefer, S. R. Shieh and T. S. Duffy, “Strength, Elasticity, and Equation of State of the Nanocrystalline Cubic Silicon Nitride γ-Si3N4 to 68 GPa,” Physical Review B, Vol. 72, No. 1, 2005, Article ID: 014102. http://dx.doi.org/10.1103/PhysRevB.72.014102
- S. H. Tolbert and A. P. Alivisatos, “The Wurtzite to Rock Salt Structural Transformation in CdSe Nanocrystals under High Pressure,” The Journal of Chemical Physics, Vol. 102, No. 11, 1995, pp. 4642-4656. http://dx.doi.org/10.1063/1.469512
- J. Z. Jiang, J. S. Olsen, L. Gerward and S. Mørup, “Compressibility of Nanostructured Fe-Cu Materials Prepared by Mechanical Milling,” Nanostructured Materials, Vol. 12, No. 5-8, 1999, pp. 847-850. http://dx.doi.org/10.1016/S0965-9773(99)00249-4
- B. Chen, D. Penwell and M. B. Kruger, “The Compressibility of Nanocrystalline Nickel,” Solid State Communications, Vol. 115, No. 4, 2000, pp. 191-194. http://dx.doi.org/10.1016/S0038-1098(00)00160-5
- J. Zhao, L. Guo, J. Liu, Y. Yang, et al., “High Bulk Modulus of Nanocrystal γ-Fe2O3 with Chemical Dodecyl Benzene Sulfonic Decoration under High Pressure,” Chinese Physics Letters, Vol. 17, No. 2, 2000, p. 126. http://dx.doi.org/10.1088/0256-307X/17/2/018
- B. Chen, D. Penwell, M. B. Kruger, A. F. Yue and B. Fultz, “Nanocrystalline Iron at High Pressure,” Journal of Applied Physics, Vol. 89, No. 9, 2001, p. 4794. http://dx.doi.org/10.1063/1.1357780
- O. L. Anderson, “Equation of State for Geophysics and Ceramic Sciences,” Oxford University Press, Oxford, 1995.
- P. Vinet, J. Ferrente, J. R. Smith and J. H. Rose, “A Universal Equation of State for Solids,” Journal of Physics C: Solid State Physics, Vol. 19, No. 20, 1986, p. L467.

