ABSTRACT

The local gas-flow behavior is almost unknown for low pressure plasma systems, except parallel plate reactors for semiconductor purposes. To overcome this lack of knowledge, this study starts with the influence investigation of the gas feed-in systems technical layout on the homogeneity of the gas supply for large volume plasma enhanced chemical vapor deposition (PECVD) chambers. Computational fluid dynamics (CFD) simulations are used as a tool to determine velocity and pressure distribution inside the gas feed-in pipe as well as in the PECVD-chamber itself. The parameters varied were: flow rate, pipe length, number of holes, hole diameter and aspect ratio of the pipe section. The calculated pressure values are compared with the experimentally measured ones to validate the simulation results. An excellent conformity of the calculated and measured pressures is observed. With the aim to evaluate the homogeneity of gas distribution through the pipe holes the nonuniformity coefficient (Φ) was created. The results show the influence of each layout parameter in the homogeneity of the gas distribution. Hence in future correct technical layouts of gas feed-in systems can easily be applied. With these results construction guidelines has been formulated.

Keywords:

Gas Feed-in Systems, Gas Flow Distribution, CFD, PECVD, Coating

1. Introduction

Plasma enhanced chemical vapor deposition (PECVD) processes are applied at a large range of industrial fields such as aircraft, automotive and medical devices for the application of functional coatings e.g. anti-bacterial, anti-scratch, anti-reflection and enhance wear resistance [1] [2] [3] [4] . Within the PECVD process the substrate allocated in a vacuum chamber is exposed to the influence of the plasma. To create the functional coatings precursor gases are feed into the process zone where they are fragmented by the plasma. Those fragments are able to react and form a thin film on a substrate positioned in or near to the plasma. Hence, the plasma polymerization and the resulting coating strongly depend on the PECVD process parameters such as the chemistry of the precursor gases as well as the chamber operational characteristics. According to the operational conditions one precursor gas can lead to a variety of films, and thus a precursor with a particular chemical structure will not necessarily result in a desired plasma polymer [5] . Nevertheless, the PECVD process parameters can be successfully tailored to achieve the aimed coating properties. Noborisaka and coauthors [3] reported for example on the importance of the selection of the right precursor gas mixture for the coating formation. The appropriate mixture ratio of the precursor gases trimethylsilane and oxygen (TMS and O₂) was investigated to obtain polycarbonate films as alternative to conventional windows glasses. The results revealed that hardness and tran- sparency properties could be tailored by changing the gas mixture ratio.

To improve the cost effectiveness of industrial PECVD coating processes there is a demand for large volume coaters. Nonetheless, the scaling-up of the PECVD processes face, among other points, challenges regarding the control of the local deposition rate to satisfy one necessary requirement for coating homogeneity inside the whole chamber. In this context, the design of the PECVD chamber plays a crucial role on the quality of the resulting thin film. Thus, the electrodes design, the gas exhausts and gas feed-in systems are parameters inherent of the PECVD chamber that influence the homogeneity of deposition rate as well as the coating properties. Regarding the present state of the art of the controlling of gas deposition rates most of the relevant achievements are documented in patents especially when considering small PECVD chambers. For instance, there are few issued patents in the field of semiconductor fabrication focused on the installation of a perforated electrode plate (showerhead) to distribute the gas evenly on the surface of the silicon wafer [6] [7] [8] [9] . Concerning large volume chambers, which in most cases are installed in other industries, there is scarce information due to confidential issues or due to lack of knowledge.

Therefore, the homogeneity of the deposition rate is directly related to the plasma formation through the electrical field, as well as to the associated local precursor gas flow rate. The fragmentation and the corresponding chemical reactions occur in a certain time frame and then the coating is formed. On the one hand, when the gas velocity is too high there is not enough time for the chemical reactions to occur and the resulting deposition rate is compromised. On the other hand, when the gas velocity is too low the renewal of the precursor gas within the chamber will take too long. The plasma fragmented precursor gas species will not be able to react during the total time interval and the deposition rate is compromised as well. Consequently, the local gas flow behavior is one key factor to ensure an equal gas distribution inside the chamber. The management of the gas feed-in and the gas exhaust systems can be used to control the local gas flow behavior [7] .

In this work, the gas flow behavior within the chamber is investigated in correlation with the gas feed-in system features. The study identifies and evaluates relevant parameters which influence determining the homogeneity of gas distribution. The results are used to formulate designing construction guidelines for PECVD chambers as a solution to homogeneously perform coating on large structures or on several substrates simultaneously. The investigation of the gas flow behavior inside gas feed-in system was performed via computational fluid dynamics (CFD) simulations. The simulation results are compared to experimentally obtained data for validation purposes.

1.1. PECVD Chamber Model

The gas feed-in distributor under analysis consists of a rectangular pipe closed at both ends. At the bottom of the gas feed-in distributor the gas inlet is centrally placed. The rectangular pipe contains equally spaced perforations to provide the gas flow into the PECVD chamber. The sketch of the gas feed-in distributor model is shown in Figure 1(a) and the PECVD chamber model is presented in Figure 1(b).

The present work is focused on determining and evaluating conditions that influence the gas flow homogeneity inside the PECVD chambers and therefore also inside the gas feed-in distributor. Hence, a condition to achieve a homogenous gas flow at every feed-in hole is related to a constant gas pressure along the whole length of the gas feed-in distributor. However, the pressure distribution can mainly influenced by one of the following two scenarios: 1) due to the gas friction with the internal surface of the pipe the pressure decreases in the direction of the flow, or 2) the velocity of the gas is reduced caused by the loss of the gas which is flowing via the holes into the PECVD

chamber, i.e. the momentum of the gas is reduced and the pressure rises in the direction of the flow [10] [11] .

Consequently, a proper balance between these two influence conditions on the pressure is crucial to obtain an equal gas feed-in along the length of the distributor. Further aspects influence the gas flow within this simple construction model as the geometry parameters. The cross section of the pipe and the number and diameter of the holes, the length of the pipe, and the flow rate are among the parameters which can strongly cause changes in the gas flow [12] [13] . For this reason, predicting the precursor gas flow inside the gas feed-in system is very useful for the construction design and consequently to improve the process performance.

1.2. Knudsen Number

On fluid dynamics the Knudsen (Kn) number is an important parameter to evaluate and classify the gas flow behavior. The Kn is defined as the ratio between the molecular mean free path and the characteristic dimension of the flow geometry (Equation (1)) [14] [15] [16] . Based on the Kn the degree of rarefaction of the gas and the validity of the continuum flow assumption can be determined.

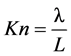(1)

where λ is the mean free path and L is the characteristic dimension or characteristic length of the flow system.

According to the Knudsen number the gas flow can be divided in 4 regimes [14] [15] [16] as illustrated in Figure 2. For Kn ≤ 0.001, called continuum flow regime, the continuum hypothesis is suitable and the flow can be analyzed using the Navier-Stokes equations with conventional no-slip boundary conditions. For 0.001 ≤ Kn ≤ 0.1, named slip-flow regime, rarefaction effects start to influence the flow. In order to use the Navier-Stokes equations tangential slip-velocity boundary conditions must be provided along the walls of the flow domain. As the gas becomes more rarefied, 0.1 ≤ Kn ≤ 10, the flow is characterized as transient. For this regime, as the continuum assumption of the Navier-Stokes equations begins to break down, alternative simulation techniques such as particle based direct simulation Monte Carlo (DSMC) approaches must be adopted. For the Kn ≥ 10, the continuum assumption is completely broken and the regime can then be described as being a free molecular flow.

The pressure range values in vacuum technology are presented in Table 1. According to the model configuration different Kn values can occur for different regions of the PECVD chamber depending on the variations of the pressure and of the characteristic length values. For instance, different Kn values can occur when the pressure inside the gas feed-in distributor is much higher than the pressure inside the chamber. A further reason for different Kn values is when the characteristic length of the gas feed-in distributor is much smaller than the characteristic length of the chamber.

Most of all PECVD applications work within the medium vacuum range [5] . For all the PECVD chamber conditions investigated in this work the Kn values are in the range of the slip-flow regime (0.001 ≤ Kn ≥ 0.1). In the results section the Kn values are presented for the conditions and parameters evaluated in this work.

2. Methods

2.1. CFD Simulation

Computational fluid dynamics (CFD) simulations is a valuable tool to determine the gas flow behavior inside gas feed-in system in low pressure environment considering that experimentally the local gas flow behavior inside a PECVD system cannot be directly measured. The CFD was employed to predict the gas flow behavior inside the gas feed-in system aiming at achieving a homogeneous gas supply through the investigated pipe holes.

The CFD simulations were performed applying the software package Ansys Fluent 16.0®. The starting point was the gas flow simulation for five distinct pipe section areas (Figure 3), keeping constant other reference parameters as presented in Table 2, the resulting curve was named as reference curve. Afterwards, the CFD simulations were performed varying the values of some parameters as shown in Table 2 under the changed parameters column. For each simulation one parameter was varied while the others were kept constant. The pipe was placed on the bottom of the PECVD chamber as illustrated in Figure 1, the chamber volume considered is 1 m³.

Experimentally the local gas flow could not be accessed and in order to validate the simulations with available experimental data the pressure values were calculated via the CFD simulations to obtain a pressure curve. Considering those cases where experimental and simulation data could be compared, further simulations were performed varying some of the parameter values to acquire the pressure curve. Hence, for the pipe section cases of 10 mm × 10 mm and 30 mm × 30 mm the simulations were carried out varying

*Refers to the pipe section aspect ratio keeping constant the equivalent section area.

the gas flow rate from 100 to 600 sccm in intervals of 100 sccm, and different number of pipe holes were considered. These parameters and all the respective values are presented in Table 3.

The 3D models were created using one symmetry plane (Figure 4) to minimize the simulation time keeping a proper mesh resolution. For all CFD simulations carried out the boundary conditions were defined in order to reproduce the conditions of the experiment (Table 4). The number of elements in each model was approximately 2,500,000. Grid independence tests were performed to determine the greatest mesh refinement. The mesh was refined inside the pipe, inner holes, gas inlet and gas outlet. The solutions were considered to be converged when all the residuals were smaller than 10⁻⁵ for the continuity and momentum equations and smaller than 10⁻⁶ for the energy equation.

2.2. Experiment

Experiments were conducted inside a 1 m³ PECVD chamber for two different pipe section area values and for pipes containing 7 and 14 holes (Table 3), leading a total of four configurations of pipe i.e. four pressure measurement trials were performed. For all cases 2 mm holes were drilled manually using a drilling machine. For each trial the nitrogen gas was used as working gas. The gas flow rate varied from 100 to 600 sccm and the pressure value on the gas outlet was kept equal to 0.03 hPa.

The pressure was measured in one of the closed sides of the pipe using a handheld

*Different flow rates were applied according with the objective desired. The unit [sccm] was converted to [kg/s].

vacuum gauge (Pfeiffer TPG202) and compared to the previous simulations predictions. The experiment setup is shown in Figure 5.

3. Results and Discussion

3.1. Simulation

The CFD simulations were first performed to understand the effect of the pipe sectional area (Figure 3) on the gas flow distribution through the pipe holes.

In order to compute the homogeneity of gas flow distribution through the holes, one

dimensionless coefficient Φ was used [18] . Its definition is given as follows:

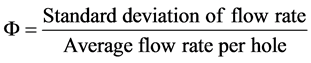(2)

The homogeneity of the gas flow distribution is inversely proportional to the value of Φ, i.e. smaller the value of Φ more homogeneous is the gas flow distribution.

Figure 6(a) presents the flow rate in each hole for different pipe section areas. The pipe image on the top left side highlights the gas inlet from the middle of the pipe. Part b of Figure 6 shows the nonuniformity coefficient for different pipe section areas and emphasizes through the dash dot line the construction border we recommend.

The flow rate tends to decrease from the gas inlet to the sides of the pipe, i.e. the holes closer to the gas inlet discharge more gas as depicted in Figure 6(a). It indicates that the friction effects may predominate. Further evidence from these effects are displayed in Figure 7(a) and Figure 7(b) where the pipe with smaller section area, and thus more pressure drop, presented more pressure gradient then the pipe with larger section area.

Typical acceptable values of the dimensionless coefficient Φ when taking plasma polymerization process into account are in the range Φ < 5%, therefore this value is applied in this work as construction border value (Figure 6(b)).

From Figure 6(a) it can also be observed that there is a crosspoint between hole 10 and hole 11. Additionally is noteworthy that as only the cross section area was changed, all plots display the same behavior. As the difference of flow rate between the holes is a consequence of the pressure drop, the crosspoint suggests that the mean pressure inside

the pipe is achieved always in the same distance from the inlet for all the configurations under analysis.

The results of the pressure contour and velocity contour for two different pipe section areas and gas flow rate of 200 sccm are depicted in Figure 7. Figure 7(a) refers to the pipe with 10 mm × 10 mm section area. The left image from Figure 7(a) shows the pressure contour inside the chamber (blue) and inside the pipe (color gradient). The right image from Figure 7(a) shows the velocity contour inside the chamber (blue gradient) and inside the pipe (color gradient). Likewise, Figure 7(b) shows the pressure contour (left) and velocity contour (right) for the pipe with 30 mm × 30 mm section area. For instance, looking into pressure both Figure 7(a) (left) and Figure 7(b) (left) presents a homogeneous blue color inside the chamber. Nevertheless Figure 7(a) (left) shows a color gradient inside the pipe (10 mm × 10 mm). The same pattern is not observed inside the 30 mm × 30 mm pipe in Figure 7(b) (left). Concerning velocity contour, Figure 7(a) (right) and Figure 7(b) (right) show a blue gradient inside the chamber. This is a hint of how much of the chamber gas volume is influenced by the gas feed-in system and by the gas outlet (gas exhaust system). Similarly, Figure 7(a) (right) presents a color gradient inside the 10 mm × 10 mm pipe. Figure 7(b) (right) shows also a color gradient inside the 30 mm × 30 mm pipe but slight in comparison with Figure 7(a) (right). These plots contour are a visual representation from the nonuniformity coefficient of Figure 6(b), i.e. for the smaller section area pipe (10 mm × 10 mm) higher pressure and velocity gradient are found inside the pipe resulting in a higher nonuniformity coefficient in comparison with the bigger one (30 mm × 30 mm).

Aiming at evaluating the influence of further parameters in the homogeneity of the gas flow distribution, additional simulations were done using the parameters as presented in Table 2. In Figure 8 is plotted the nonuniformity coefficient in a logarithmic

scale for five different pipe section areas: 6 mm × 6 mm, 10 mm × 10 mm, 15 mm × 15 mm, 20 mm × 20 mm and 30 mm × 30 mm in diverse parameters arrangement. In each circumstance one parameter was changed keeping the others constant. The parameters varied were: flow rate, pipe length, number of holes, hole diameter and aspect ratio of the pipe section. It is observed with an increase of the gas flow the increase of the homogeneity of the gas distribution. The pipe section aspect ratio does not lead to a significant impact in the homogeneity. Thus, the influence of the section area on the homogeneity of the gas distribution is more relevant. Increasing on the values of the length of the pipe, diameter and number of holes decrease the homogeneity of the gas flow distribution. The pipe section dimensions of 30 mm × 30 mm and 20 mm × 20 mm are in a safe area regarding to homogeneous flow distribution, i.e. under the Φ based construction border.

The gas flow regime of the current work was classified in terms of calculated Kn values. Based on the CFD calculations of pressure, the gas and PECVD chamber parameters the Kn values were obtained for the pipe section area of 6 mm × 6 mm and 30 mm × 30 mm. For the CFD calculation the low pressure boundary slip condition was applied in order to consider the slip-velocity conditions [14] [16] . From the analysis the current work showed to be in the range of the slip-flow regime (0.001 ≤ Kn ≥ 0.1) as depicted in Table 5.

3.2. Experiment

Considering that experimentally the local gas flow behavior inside a PECVD chamber cannot be measured directly, the measurement of pressure values are employed to validate the simulations. The pressure inside the pipe (measured in one side of the pipe) and the pressure calculated with the CFD software in both cases changing the gas flow rate is plotted (Figure 9). In detail Figure 9(a) shows the measured and calculated pressure values for the pipe with 10 mm × 10 mm section area and 7 holes. Figure 9(b), right beside shows the results for a pipe with 14 holes. Likewise, Figure 9(c) and Figure 9(d) display the measured and calculated pressure values for the pipe with 30 mm × 30 mm section area.

The simulations are in agreement with experimental findings leading to a maximum error of 10%. For instance, concerning the 10 mm × 10 mm pipe section area with 7 holes and flow rate of 200 sccm the internal measured pressure in one side of the pipe

*Pressure (mbar) calculated with the CFD software.

was 1.4 hPa and the calculated one was 1.3 hPa. This variance could be attributed to the fact that the drilled holes were not perfectly with 2 mm diameter due to the manual preparation process, especially for the pipe with larger section area, and thus more holes would mean a statistical average that is closer to the model.

4. Conclusions

To get access to the local gas flow behavior inside large volume PECVD chambers in this work, gas feed-in systems are studied. Thereby relevant construction parameters are identified as well as their influence toward the homogeneity of the gas distribution.

In detail the gas pressure and velocity are calculated using CFD simulations. Experiments were run in a PECVD chamber varying the following parameters: pipe section area, number of holes, diameter of holes, pipe length, aspect ratio of the pipe section and the amount of gas. The boundary conditions applied to the CFD model were based on the experiments conditions. The main conclusions extracted from the results are:

1) From the analyzed parameters the pipe section area was the most relevant one influencing the homogeneity of gas distribution.

2) By decreasing the pipe section area, the pressure gradient increases resulting in a nonhomogeneous gas distribution through the holes. For instance, the nonuniformity coefficient for the 30 mm × 30 mm pipe section area is 0.1% and for the 6 mm × 6 mm one 45%.

3) Taking the construction border (Φ < 5%) into consideration the results showed that the pipe section area above 20 mm × 20 mm are in a safety area regarding the homogeneity of gas distribution.

4) The pressure values from the CFD simulations are in good agreement with the obtained experimental data.

Taking all the results into account this work shows that CFD simulations are an efficient approach to support the construction of gas feed-in systems for PECVD chambers.

The obtained knowledge of the dependence of the analyzed parameters on the gas feed-in system is intended to be used for construction guidelines of gas exhaust systems. Afterwards, the gained knowledge in synergy will be useful for the scaling-up PECVD processes either for the coating deposition onto large area substrates or on several substrates simultaneously. Therefore, the present study represents a valuable step in order to produce homogeneous coatings in an industry environment.

Acknowledgements

The authors are grateful to the Science without Borders programme (Ciênciasem Fronteiras, Gustavo Simiema de Freitas Barbosa 201387/2014-0) and the Brazilian National Council of Technological and Scientific Development (CNPq) for the financial support. The authors wish also to thank Dr. Welchy Leite Cavalcanti for a critical reading of the manuscript.

Cite this paper

de Freitas Barbosa, G.S., Vissing, K. and Mayer, B. (2016) Creation and Evaluation of Construction Guidelines Using CFD for Low Pressure Plasma Gas Feed-in Systems to Homogenize the Precursor Gas Flow. Open Journal of Fluid Dynamics, 6, 391-405. http://dx.doi.org/10.4236/ojfd.2016.64029

References