Open Journal of Fluid Dynamics
Vol.05 No.01(2015), Article ID:54559,15 pages
10.4236/ojfd.2015.51010
Kinetic Foundation for the Multimoment Hydrodynamics Equations
Igor V. Lebed
Zhukovsky Central Institute of Aerohydrodynamics, Moscow, Russia
Email: lebed-i@newmail.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 February 2015; accepted 4 March 2015; published 11 March 2015
ABSTRACT
The equations for the pair distribution functions are derived directly from the second equation of the Bogolyubov-Born-Green-Kirkwood-Yvon (BBGKY) hierarchy. The derivation is fulfilled within the frameworks of the multiscale method. The equations for the pair distribution functions are the kinetic foundation for the multimoment hydrodynamics equations. Solutions to the equations for the pair distribution functions predetermine the possibility of constructing the hydrodynamics equations with an arbitrary number of principle hydrodynamic values specified beforehand. The tendency to increase the number of principal hydrodynamic values is caused by the necessity of interpreting the behavior of the system after the loss of stability. Solutions to the classic hydrodynamics equations constructed for only three principle hydrodynamic values are unable to predict the direction of instability evolution. Solutions to the multimoment hydrodynamics equations are capable of reproducing correctly the phenomenon of emergence and development of instability.
Keywords:
Multimoment Hydrodynamics, Pair Functions, Instability

1. Introduction
Possibility to study the unstable phenomena by means of the direct numerical integration of the Navier-Stokes equations became feasible comparatively recently. The direct numerical integration of the Navier-Stokes equations in the problem of a flow around a solid sphere was performed by various numerical methods. Nevertheless, the results of all these numerical experiments were absolutely identical (see, review [1] ). After some critical Reynolds number value  is reached; the ground axisymmetric stationary solution
is reached; the ground axisymmetric stationary solution  loses its stability. Nonstationary solution
loses its stability. Nonstationary solution 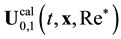 ensures the transition from the
ensures the transition from the 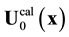 solution that loses its stability to the stable stationary nonaxisymmetric solution
solution that loses its stability to the stable stationary nonaxisymmetric solution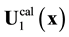 . The attainment of the second critical Reynolds number value
. The attainment of the second critical Reynolds number value 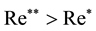 is accompanied by the loss of stability of the
is accompanied by the loss of stability of the 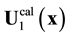 solution. Nonstationary solution
solution. Nonstationary solution 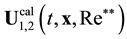 ensures the transition from the
ensures the transition from the 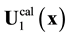 solution that loses its stability to the stable nonstationary limiting cycle
solution that loses its stability to the stable nonstationary limiting cycle . After attainment of the third critical Reynolds number value
. After attainment of the third critical Reynolds number value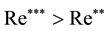 , the
, the  solution loses its stability. Nonstationary solution
solution loses its stability. Nonstationary solution 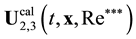 ensures the transition from the
ensures the transition from the 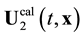 limiting cycle that loses its stability to the new stable position about which multiperiodic, that is, almost chaotic,
limiting cycle that loses its stability to the new stable position about which multiperiodic, that is, almost chaotic, 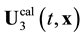 motion occurs.
motion occurs.
Experiment records two stable medium states presented by the  and
and![]() , velocity distributions, and a stable state of a central type with the
, velocity distributions, and a stable state of a central type with the ![]() velocity distribution. The
velocity distribution. The![]() ,
, ![]() , and
, and ![]() stable flows are satisfactorily reproduced by stable solutions
stable flows are satisfactorily reproduced by stable solutions![]() ,
, ![]() , and
, and![]() . Besides three stable medium states, experiment records six different nonstationary one-periodic and two-periodic vortex shedding modes and one pulsating mode.
. Besides three stable medium states, experiment records six different nonstationary one-periodic and two-periodic vortex shedding modes and one pulsating mode.
Non-stationary solutions![]() ,
, ![]() , and
, and ![]() are aperiodic, and are limited in time. Non-stationary solutions exist only at a critical value of the Reynolds number. These solutions cannot be put in correspondence to observed periodic vortex shedding modes exceedingly prolonged along the Re scale. Correlation of multiperiodic, that is, chaotic in essence, solution
are aperiodic, and are limited in time. Non-stationary solutions exist only at a critical value of the Reynolds number. These solutions cannot be put in correspondence to observed periodic vortex shedding modes exceedingly prolonged along the Re scale. Correlation of multiperiodic, that is, chaotic in essence, solution ![]() with the observed strictly periodic vortex shedding modes is hardly possible. So, the
with the observed strictly periodic vortex shedding modes is hardly possible. So, the ![]() limiting cycle is likely the only possibility of establishing correlation between the observed vortex shedding and experiment.
limiting cycle is likely the only possibility of establishing correlation between the observed vortex shedding and experiment.
The idea of bringing the ![]() stable solution to interpret the six observed vortex shedding modes and the pulsation mode in the range
stable solution to interpret the six observed vortex shedding modes and the pulsation mode in the range ![]() initially seems to have no prospects. Moreover, this idea is not able to resolve the encountered discrepancies when evaluating the results of the direct numerical integration of the Navier-Stokes equations against experiment. Namely, three of six observed vortex shedding regimes are the two-periodic modes. The
initially seems to have no prospects. Moreover, this idea is not able to resolve the encountered discrepancies when evaluating the results of the direct numerical integration of the Navier-Stokes equations against experiment. Namely, three of six observed vortex shedding regimes are the two-periodic modes. The ![]() one-periodic solution seems to have no prospects to be set in accordance with two-periodic regimes. At some values of
one-periodic solution seems to have no prospects to be set in accordance with two-periodic regimes. At some values of![]() , the various experiments register qualitatively different vortex shedding regimes. The
, the various experiments register qualitatively different vortex shedding regimes. The ![]() solution is incapable of reproducing several different vortex shedding modes simultaneously.
solution is incapable of reproducing several different vortex shedding modes simultaneously.
As expected, the idea of bringing the ![]() solution to interpret the phenomenon of vortex shedding did not give the desired result. None of numerical experiments detected the slightest indications of vortex shedding on flow pictures presented both by the streamlines and by the streaklines, (see reviews [1] [2] ). So, the calculated
solution to interpret the phenomenon of vortex shedding did not give the desired result. None of numerical experiments detected the slightest indications of vortex shedding on flow pictures presented both by the streamlines and by the streaklines, (see reviews [1] [2] ). So, the calculated ![]() limiting cycle satisfactorily reproduces the
limiting cycle satisfactorily reproduces the ![]() stable central-type state but proves a complete failure when attempts are made to reproduce the vortex shedding modes. In accordance with interpretation of [1] - [3] , the responsibility for the failure of the calculations is laid on the Navier-Stokes equations themselves.
stable central-type state but proves a complete failure when attempts are made to reproduce the vortex shedding modes. In accordance with interpretation of [1] - [3] , the responsibility for the failure of the calculations is laid on the Navier-Stokes equations themselves.
The problems encountered by classic hydrodynamics when interpreting the unstable phenomena were not unexpected. They were predicted in [6] . The possibility of improvement of classic hydrodynamics equations is sought on the way toward an increase in the number of principle hydrodynamic values [1] - [3] . The formalism of [5] allows hydrodynamics equations to be derived with an arbitrary number of principle hydrodynamic values specified beforehand. The multimoment hydrodynamics equations were used in [6] - [9] to study the phenomenon of instability appearance and development in the problem of a flow around a solid sphere at a wide range of Reynolds number values. The multimoment hydrodynamics equations follow directly from the equations for pair distributions functions. The equations for pair distribution functions were previously derived heuristically in [10] . These equations were derived immediately from the Liouville equation in [11] . The derivation [11] was fulfilled in terms of conditional possibilities. In the present work the equations for pair distribution functions are derived directly from the second equation of the BBGKY hierarchy within the frameworks of the multiscale method. The common ideology of the multiscale method is given in [12] . The common ideology [12] is used to derive the kinetic equation for one-particle distribution function in Section 2. The equations for pair distribution functions are derived in Section 3.
2. Equations for One-Particle Distribution Functions on the Kinetic Stage
The s-particle distribution function ![]() is specified in [4] . The
is specified in [4] . The ![]() function has a meaning of the probability that at some time
function has a meaning of the probability that at some time ![]() one particle, say particle 1, finds itself within an unit element of phase space near point
one particle, say particle 1, finds itself within an unit element of phase space near point![]() , another particle, say particle 2, within an unit element near point
, another particle, say particle 2, within an unit element near point ![]() and particle
and particle ![]() -near point
-near point![]() , regardless of the position in phase space of the remaining
, regardless of the position in phase space of the remaining ![]() particles. The
particles. The ![]() function obeys the
function obeys the ![]() -equa- tion of the BBGKY hierarchy
-equa- tion of the BBGKY hierarchy
![]() (2.1)
(2.1)
The BBGKY hierarchy is closed by the Liouville equation for![]() . In the thermodynamic limit,
. In the thermodynamic limit, ![]() ,
, ![]() , yet
, yet ![]() is a finite,
is a finite, ![]() is the volume of the system.
is the volume of the system.
Following common ideology of the multiscale method [12] , let us begin to study the evolution of ![]() and
and ![]() functions. Let us consider only the case of rarefied gas, where the characteristic free path substantially exceeds the characteristic size of particles
functions. Let us consider only the case of rarefied gas, where the characteristic free path substantially exceeds the characteristic size of particles![]() . Presuming that a particle may be present at all phase space locations with equal probabilities, recast the first of Equations (2.1) in terms of dimensionless variables. On the initial
. Presuming that a particle may be present at all phase space locations with equal probabilities, recast the first of Equations (2.1) in terms of dimensionless variables. On the initial ![]() -scale, the first equation can be specified in terms of dimensionless time and coordinates as
-scale, the first equation can be specified in terms of dimensionless time and coordinates as
![]() (2.2a)
(2.2a)
![]() (2.2b)
(2.2b)
here,
![]()
![]()
![]() is the characteristic velocity of a particle, and the hat appears above the dimensionless quantities. At the derivation of Equations (2.2), N was estimated as ratio of the system volume V to the characteristic volume
is the characteristic velocity of a particle, and the hat appears above the dimensionless quantities. At the derivation of Equations (2.2), N was estimated as ratio of the system volume V to the characteristic volume ![]() occupied by a single particle, i.e., the dimensionality
occupied by a single particle, i.e., the dimensionality![]() .
.
According to Equation (2.2а), the one-particle distribution function ![]() remains unchanged with time along a rectilinear particle trajectory to within
remains unchanged with time along a rectilinear particle trajectory to within ![]() in the 6-dimensional phase space at the times, proportional to
in the 6-dimensional phase space at the times, proportional to![]() . So, the variation of the distribution function in the order of own magnitude along the particle trajectory occurs only at longer times, proportional to
. So, the variation of the distribution function in the order of own magnitude along the particle trajectory occurs only at longer times, proportional to![]() . Similarly, in accordance with Equation (2.2b), the
. Similarly, in accordance with Equation (2.2b), the ![]() distribution function with the error
distribution function with the error ![]() does not change along the trajectory of two particles in the 12-dimensional phase space at the times, proportional to
does not change along the trajectory of two particles in the 12-dimensional phase space at the times, proportional to![]() .
.
Let us switch from phase coordinates ![]() of two particles first to phase coordinates
of two particles first to phase coordinates![]() ,
, ![]() ,
, ![]() ,
, ![]() , and then to phase coordinates
, and then to phase coordinates![]() ,
,![]() ,
, ![]() ,
, ![]() . Then,
. Then,
![]() (2.3)
(2.3)
Let us recast the second equation of the BBGKY hierarchy (2.1) in terms of two-particle distribution functions![]() , written in
, written in![]() ,
, ![]() ,
, ![]() ,
, ![]() variables. Let us integrate the second equation with respect to
variables. Let us integrate the second equation with respect to ![]() and
and![]() . The integration with respect to
. The integration with respect to ![]() is limited by the
is limited by the ![]() interaction domain of two particles:
interaction domain of two particles:
![]() (2.4)
(2.4)
In Equation (2.4), the vectors ![]() and
and ![]() have the cylindrical coordinates
have the cylindrical coordinates ![]() and
and ![]() respectively in the reference frame with the
respectively in the reference frame with the ![]() axis parallel to the
axis parallel to the ![]() vector,
vector, ![]() is the impact parameter, and
is the impact parameter, and ![]() is the azimuthal angle. The
is the azimuthal angle. The ![]() function in the second term on the right hand side of Equation (2.4) corresponds to a pair of particles 1 and 2, which leave the interaction domain
function in the second term on the right hand side of Equation (2.4) corresponds to a pair of particles 1 and 2, which leave the interaction domain ![]()
![]() at velocities
at velocities ![]() and
and![]() , Figure 1. The
, Figure 1. The ![]() function in the second term on the left hand side of Equation (2.4) corresponds to a pair of particles 1 and 2, which enter the interaction domain
function in the second term on the left hand side of Equation (2.4) corresponds to a pair of particles 1 and 2, which enter the interaction domain ![]()
![]() at velocities
at velocities ![]() and
and![]() .
.
Express the ![]() function in terms of the two-particle distribution function at the entrance to the domain
function in terms of the two-particle distribution function at the entrance to the domain![]() . To do this, it is expedient to pass from function
. To do this, it is expedient to pass from function ![]() to function
to function ![]() written in
written in![]() ,
, ![]() ,
, ![]() ,
, ![]() variables. In accordance with Equation (2.2b),
variables. In accordance with Equation (2.2b), ![]() experiences changes of about
experiences changes of about ![]() due to triple collisions of particles, as particles 1 and 2 travel in the domain
due to triple collisions of particles, as particles 1 and 2 travel in the domain ![]() along the 12-dimensional phase trajectory:
along the 12-dimensional phase trajectory:
![]() (2.5)
(2.5)
here, ![]() is the time within which the particles traverse the interaction domain
is the time within which the particles traverse the interaction domain![]() , The cylindrical coordinates of the
, The cylindrical coordinates of the ![]() vector are
vector are ![]() in the reference frame with the
in the reference frame with the ![]() axis parallel to
axis parallel to![]() . If particles 1 and 2 enter the
. If particles 1 and 2 enter the ![]() at velocities
at velocities ![]() and
and![]() ,
, ![]() , then they have velocities
, then they have velocities ![]() and
and ![]() respectively at the exit of the
respectively at the exit of the![]() , Figure 1.
, Figure 1.
Further transformation of relations (2.5) gives:
![]() (2.6)
(2.6)
The ![]() function corresponds to a pair of particles 1 and 2, which enter the interaction domain
function corresponds to a pair of particles 1 and 2, which enter the interaction domain ![]()
![]() . Function
. Function ![]() remains inva-
remains inva-
![]()
Figure 1. The interaction domain of a pair of particles C0.
riant along the trajectory of the center of mass of a pair of particles to within ![]() at the times, proportional to
at the times, proportional to![]() . Weak dependence of the
. Weak dependence of the ![]() function on
function on ![]() -scale at the boundary of interaction domain
-scale at the boundary of interaction domain ![]() is specified by weak dependence of the
is specified by weak dependence of the ![]() function on
function on ![]() -scale, see Equations (3.10) and (3.11). Boundary condition (3.6) connects functions
-scale, see Equations (3.10) and (3.11). Boundary condition (3.6) connects functions ![]() and
and![]() .
.
Apply Equation (2.2b) to penetrate the domain![]() . Let vector
. Let vector ![]() specifies any respective location of particles in pair within the
specifies any respective location of particles in pair within the ![]() domain, Figure 1. The
domain, Figure 1. The ![]() vector has the cylindrical coordinates
vector has the cylindrical coordinates![]() ,
, ![]() in the frame of reference with the
in the frame of reference with the ![]() axis parallel to the
axis parallel to the ![]() vector. Then,
vector. Then,
![]() (2.7)
(2.7)
The pair of particles with the parameters ![]() and
and ![]() enters the domain
enters the domain ![]() at time
at time ![]()
![]() at velocity
at velocity ![]() and reaches the location
and reaches the location ![]() by the time
by the time![]() , Figure 1.
, Figure 1.
Let us apply the operator ![]() upon Equation (2.7). Function
upon Equation (2.7). Function ![]() corresponds to a pair of particles, which enter the interaction domain
corresponds to a pair of particles, which enter the interaction domain ![]()
![]() . In accordance with the aforesaid, function
. In accordance with the aforesaid, function ![]() remains invariant along the trajectory of the center of mass of
remains invariant along the trajectory of the center of mass of
a pair of particles to within ![]() at the times, proportional to
at the times, proportional to![]() . After action of the operator
. After action of the operator![]() , the left side of Equation (2.7) assumes the form:
, the left side of Equation (2.7) assumes the form:
![]() (2.8)
(2.8)
Equation (2.8) is specified in terms of dimensionless time and coordinates on the initial scale. Recast Equation (2.8) in terms of distribution function![]() , written in
, written in![]() ,
, ![]() ,
, ![]() ,
, ![]() variables, then
variables, then
![]() (2.9)
(2.9)
Upon substituting the third term on the left hand side of Equation (2.4) into the force term of the first equation of hierarchy (2.1), this equation assumes the form:
![]() (2.10)
(2.10)
Let us bring Equation (2.10) into the dimensionless form and assess the order of magnitudes of its constituent terms. In accordance with Equation (2.2а), ![]() varies only slightly with time along the
varies only slightly with time along the ![]() -particle trajectory on the initial scale. Then, the
-particle trajectory on the initial scale. Then, the ![]() function varies in the order of own magnitude along this trajectory exclusively at the times, proportional to
function varies in the order of own magnitude along this trajectory exclusively at the times, proportional to![]() , i.e., the first term on the left hand side of Equation (2.10) is of order
, i.e., the first term on the left hand side of Equation (2.10) is of order![]() . So is the second term on the left hand side of Equation (2.10).
. So is the second term on the left hand side of Equation (2.10).
To assess the order of magnitude of the first term on the right hand side of Equation (2.10) we use the Equation (2.9). Generally, there are no reasons to believe that the ![]() function varies slightly with
function varies slightly with ![]() on the scale of particle size
on the scale of particle size![]() , therefore, let us save for the first term on the right side of Equation (2.10) the order of
, therefore, let us save for the first term on the right side of Equation (2.10) the order of![]() . The order of the second term on the right hand side of Equation (2.10), allowing for triple collisions, is
. The order of the second term on the right hand side of Equation (2.10), allowing for triple collisions, is![]() .
.
Expand the dimensionless one-particle distribution function in a perturbation theory series in terms of the virial parameter![]() :
:
![]() (2.11)
(2.11)
Following Equation (2.11), expand functions ![]() and
and ![]() in a perturbation theory series. Substitute received series into the dimensionless Equation (2.10). Take into account the aforesaid estimates of the terms. Equating the multipliers at equal degrees of
in a perturbation theory series. Substitute received series into the dimensionless Equation (2.10). Take into account the aforesaid estimates of the terms. Equating the multipliers at equal degrees of![]() , let us specify the equation for
, let us specify the equation for![]() . Omitting the superscript of distribution functions and going back to the dimensional quantities, one obtain:
. Omitting the superscript of distribution functions and going back to the dimensional quantities, one obtain:
![]() (2.12)
(2.12)
![]()
The transition (Equations (2.5) and (2.6)) from the ![]() function at the outlet of the
function at the outlet of the ![]() interaction domain to that at the inlet of this domain in the first term on the right hand side of Equation (2.12) enables one to recast Equation (2.12) differently:
interaction domain to that at the inlet of this domain in the first term on the right hand side of Equation (2.12) enables one to recast Equation (2.12) differently:
![]() (2.13)
(2.13)
![]()
In accordance with Equation (2.2а), ![]() varies slightly along the
varies slightly along the ![]() -particle trajectory at the times, proportional to
-particle trajectory at the times, proportional to![]() . However, there are no reasons to believe that the
. However, there are no reasons to believe that the ![]() function varies slightly on the initial
function varies slightly on the initial ![]() -scale in space and with time separately. Assume that
-scale in space and with time separately. Assume that
![]() (2.14)
(2.14)
The spatial integration in Equation (2.14) is performed within the ![]() region having the characteristic linear size
region having the characteristic linear size![]() ,
,![]() . Averaging (2.14) removes the term
. Averaging (2.14) removes the term ![]() on the right side of Equations (2.12) and (2.13) from the main order of magnitude. The averaged
on the right side of Equations (2.12) and (2.13) from the main order of magnitude. The averaged ![]() and
and ![]() functions weakly change on the scale of particle size
functions weakly change on the scale of particle size![]() . Because
. Because ![]() and hence,
and hence, ![]() change only slightly with time along the particle trajectory on the initial
change only slightly with time along the particle trajectory on the initial ![]() -scale,
-scale, ![]() varies slightly with time also on the initial scale. Analogously, the
varies slightly with time also on the initial scale. Analogously, the ![]() function varies slightly in space on the initial
function varies slightly in space on the initial ![]() -scale. The particles described by the
-scale. The particles described by the ![]() function don’t enter the domain of their interaction
function don’t enter the domain of their interaction ![]()
![]() . Thus, in accordance with Equation (2.2b), the
. Thus, in accordance with Equation (2.2b), the ![]() function varies slightly with time also on the initial scale.
function varies slightly with time also on the initial scale.
The ![]() argument of the
argument of the ![]() distribution function is the coordinate of particle 1. The
distribution function is the coordinate of particle 1. The ![]() argument of the
argument of the ![]() distribution function isn’t the coordinate of individual particle. The
distribution function isn’t the coordinate of individual particle. The ![]() argument of the
argument of the ![]() distribution function marks the place in space in the vicinity of which a set of particles is concentrated within an unit volume. Multiply the
distribution function marks the place in space in the vicinity of which a set of particles is concentrated within an unit volume. Multiply the ![]() function by the number of ways in which a pair of particles can be selected from an ensemble of
function by the number of ways in which a pair of particles can be selected from an ensemble of ![]() particles:
particles:
![]() (2.15)
(2.15)
The one-particle distribution function ![]() has the meaning of the probable number of particles situated at time
has the meaning of the probable number of particles situated at time ![]() in an unit volume element near point
in an unit volume element near point ![]() and having velocities in an unit interval near the
and having velocities in an unit interval near the ![]() point. Multiply Equations (2.12) and (2.13) by
point. Multiply Equations (2.12) and (2.13) by![]() , and average these equations over
, and average these equations over ![]() within region
within region![]() :
:
![]() (2.16)
(2.16)
![]()
In Equation (2.16) collision integral assumes the form:
![]() (2.17a)
(2.17a)
![]() (2.17b)
(2.17b)
Recast collision integral ![]() (2.17b) in terms of two-particle distribution functions
(2.17b) in terms of two-particle distribution functions![]() , written in
, written in![]() ,
, ![]() ,
, ![]() ,
, ![]() variables:
variables:
![]() (2.18)
(2.18)
![]()
The velocity ![]() of the center of mass of pair particles and the modulus
of the center of mass of pair particles and the modulus ![]() of the relative velocity of particles,
of the relative velocity of particles, ![]() , are invariants of a binary particle collision. The enumeration of all the admissible target parameter values
, are invariants of a binary particle collision. The enumeration of all the admissible target parameter values ![]() and
and ![]() and the directions of relative motion velocity
and the directions of relative motion velocity ![]() at a fixed
at a fixed ![]() and
and ![]() values then gives all the possible velocity directions
values then gives all the possible velocity directions![]() . It follows that a collision-caused decrease in the number of pairs of particles from an unit phase volume interval near the
. It follows that a collision-caused decrease in the number of pairs of particles from an unit phase volume interval near the ![]() point characterized by all the admissible
point characterized by all the admissible ![]() and
and ![]() parameter values and relative motion
parameter values and relative motion ![]() orientations is strictly balanced by a collision induced increase in the number of pairs of particles in this interval with these parameters,
orientations is strictly balanced by a collision induced increase in the number of pairs of particles in this interval with these parameters,
![]() (2.19)
(2.19)
here![]() , and
, and ![]() and
and ![]() are the spherical coordinates of the
are the spherical coordinates of the ![]() vector.
vector.
Suppose that![]() ,
, ![]() , is an arbitrary weight function of velocities
, is an arbitrary weight function of velocities ![]() and
and![]() . The pair properties of the
. The pair properties of the![]() ,
, ![]() , are invariants of a particle binary collision. Let us multiply the
, are invariants of a particle binary collision. Let us multiply the ![]() collision integral determined by Equation (2.18) by
collision integral determined by Equation (2.18) by![]() ,
, ![]() , and integrate the result with respect to velocities. By virtue of Equation (2.19), we then have,
, and integrate the result with respect to velocities. By virtue of Equation (2.19), we then have,
![]() (2.20)
(2.20)
This means that particle collisions cannot influence the formation of hydrodynamic values constructed on the properties of the![]() ,
, ![]() , pair. In other words, particle collisions cannot tune the distributions of all these hydrodynamic values to distributions of some other hydrodynamic values. That is, the set of hydrodynamic values constructed on the property of
, pair. In other words, particle collisions cannot tune the distributions of all these hydrodynamic values to distributions of some other hydrodynamic values. That is, the set of hydrodynamic values constructed on the property of![]() ,
, ![]() ,
,
![]() (2.21)
(2.21)
is a set of the principal hydrodynamic values. The ![]() proportionality coefficient allows discovering the correspondence between the
proportionality coefficient allows discovering the correspondence between the ![]() moments and the moments of the one-particle distribution function. Set (2.21) contains not only the lower function
moments and the moments of the one-particle distribution function. Set (2.21) contains not only the lower function ![]() moments but also all the higher moments without exception. To summarize, the analysis of the properties of the
moments but also all the higher moments without exception. To summarize, the analysis of the properties of the ![]() collision integral reveals the existence of an infinite number of principal hydrodynamic values.
collision integral reveals the existence of an infinite number of principal hydrodynamic values.
The equation for the ![]() one-particle distribution function (2.16) is written in a six-dimensional phase space of one particle (
one-particle distribution function (2.16) is written in a six-dimensional phase space of one particle (![]() space). The dimension of the
space). The dimension of the ![]() space allows only the properties of a particle
space allows only the properties of a particle![]() ,
, ![]() , to be accommodated in it; binary particle collision invariants, that is,
, to be accommodated in it; binary particle collision invariants, that is, ![]() ,
, ![]() , do not fit into the
, do not fit into the ![]() space. Let us sequentially accommodate the properties of a particle
space. Let us sequentially accommodate the properties of a particle![]() ,
, ![]() , in the
, in the ![]() space. We then have:
space. We then have:
![]() (2.22)
(2.22)
It follows [3] that the integrals in the right hand side of (2.22) that contain the lower particle properties 1, ![]() and
and ![]() as weight functions are strictly reduced to the integrals with the 1,
as weight functions are strictly reduced to the integrals with the 1, ![]() ,
, ![]() weight functions belonging to
weight functions belonging to![]()
![]() , invariants. It follows that, according to Equation (2.20), these integrals are strictly zero. The integrals of all the other higher properties of a particle
, invariants. It follows that, according to Equation (2.20), these integrals are strictly zero. The integrals of all the other higher properties of a particle ![]() different from 1,
different from 1, ![]() and
and ![]() are not zero [3] .
are not zero [3] .
It follows that, when we pass to the hydrodynamic stage from the phase space of one particle, such hydrodynamics equations cannot be constructed using more than three lower principal hydrodynamic values corresponding to the ![]() particle properties. The transition to the hydrodynamic stage from the phase space of one particle excludes higher principal hydrodynamic values (2.21) from participation in the construction of hydrodynamics equations. However, there is no rigorous passage to hydrodynamics from the
particle properties. The transition to the hydrodynamic stage from the phase space of one particle excludes higher principal hydrodynamic values (2.21) from participation in the construction of hydrodynamics equations. However, there is no rigorous passage to hydrodynamics from the ![]() space. This passage is closed because Equation (2.16) is not closed.
space. This passage is closed because Equation (2.16) is not closed.
The use of the Boltzmann hypothesis (“Stosszahlansatz”) opens up the possibility of approximate passage to hydrodynamics. Following Boltzmann, let us factorize two-particle distribution functions in the ![]() collision integral (2.17b):
collision integral (2.17b):
![]() (2.23)
(2.23)
Boltzmann hypothesis (2.23) closes Equation (2.16). The obtained classic kinetic equation for the ![]() one-particle distribution function is called the Boltzmann equation [4] :
one-particle distribution function is called the Boltzmann equation [4] :
![]() (2.24)
(2.24)
So, the physical meaning of the error introduced by the Boltzmann hypothesis (2.23) into hydrodynamics is as follows. It follows that just Boltzmann hypothesis allows us to construct hydrodynamics on only three lower principal hydrodynamic values. It follows that the use of the Boltzmann hypothesis excludes higher principal hydrodynamic values (2.21) from the participation in the formation of classic hydrodynamics equations. To include the higher principal hydrodynamic values, we must find passage to hydrodynamics from the phase space capable of accommodating the whole set of binary particle collision![]() ,
, ![]() , invariants.
, invariants.
3. Equations for Pair Distribution Functions
The second equation of the BBGKY hierarchy (2.1), like the first one, is not closed. The integral term of the second hierarchy equation contains a three-particle distribution function responsible for interaction of particles 1 and 2 with some third particle 3. The absence of closeness of the second hierarchy equation prevents us from the direct transition to the hydrodynamic stage from the phase space of two particles.
![]() (3.1)
(3.1)
In accordance with Equation (3.1), under absence of collisions with particle 3, particles 1 and 2, which at the time ![]() was located with a probability
was located with a probability ![]() within an unit element of the phase space near the point
within an unit element of the phase space near the point ![]() , will be at time
, will be at time ![]() within an unit element of the phase space near the point
within an unit element of the phase space near the point![]() . The second and the third terms on the right-hand side of Equation (3.1) are responsible for the interaction of particles 1 and 2 with particle 3 respectively. The second term on the right hand side of Equation (3.1) has the meaning of probability that particle 1 experiences a collision with particle 3 during the time interval
. The second and the third terms on the right-hand side of Equation (3.1) are responsible for the interaction of particles 1 and 2 with particle 3 respectively. The second term on the right hand side of Equation (3.1) has the meaning of probability that particle 1 experiences a collision with particle 3 during the time interval ![]()
![]() . The third term on the right hand side of Equation (3.1) has the meaning of probability that particle 2 experiences a collision with particle 3 during the time interval
. The third term on the right hand side of Equation (3.1) has the meaning of probability that particle 2 experiences a collision with particle 3 during the time interval ![]()
![]() . Based on the generally accepted assumption that a particle may be present at all phase space locations with equal probabilities, evaluate the contribution of the second and the third terms on the right side of Equation (3.1):
. Based on the generally accepted assumption that a particle may be present at all phase space locations with equal probabilities, evaluate the contribution of the second and the third terms on the right side of Equation (3.1):
![]() (3.2)
(3.2)
In accordance with Equation (3.2), the distribution function ![]() varies slightly along the trajectory of the two particles in
varies slightly along the trajectory of the two particles in ![]() -space on the scale of particle size
-space on the scale of particle size![]() . As the time interval
. As the time interval ![]() grows, the error
grows, the error ![]() monotonically increases. On the scale of free path
monotonically increases. On the scale of free path![]() , the error reaches the order of magnitude of the
, the error reaches the order of magnitude of the ![]() function itself. The arbitrariness in the location of particle 3 with respect to particles 1 and 2 in the second and the third terms on the right-hand side of Equation (3.1) is the cause of monotonic increase of the error (3.2). When evaluating the order of magnitude of the terms in Equation (3.1), the assumption that a particle may be present at all phase space locations with equal probabilities was used for any position in space of particles 1 and 2. However, there exist such mutual arrangements of particles 1 and 2, for which the assumption on equality of probabilities gives a wrong estimation of the order of the second and the third terms on the right side of Equation (3.1).
function itself. The arbitrariness in the location of particle 3 with respect to particles 1 and 2 in the second and the third terms on the right-hand side of Equation (3.1) is the cause of monotonic increase of the error (3.2). When evaluating the order of magnitude of the terms in Equation (3.1), the assumption that a particle may be present at all phase space locations with equal probabilities was used for any position in space of particles 1 and 2. However, there exist such mutual arrangements of particles 1 and 2, for which the assumption on equality of probabilities gives a wrong estimation of the order of the second and the third terms on the right side of Equation (3.1).
Let us evaluate the typical number of particles![]() , which experience a binary collision within an unit space volume at any time moment
, which experience a binary collision within an unit space volume at any time moment![]() :
:
![]()
In accordance with this estimation, the order of magnitude of ![]() is
is![]() . Two particles take part in a collision, so the typical number of collisions
. Two particles take part in a collision, so the typical number of collisions ![]() within an unit space volume at any time
within an unit space volume at any time ![]() is
is![]() . If the duration of the collision is
. If the duration of the collision is ![]()
![]() , then the typical number of particles, which experience a binary collision within an unit space volume during the time of free path
, then the typical number of particles, which experience a binary collision within an unit space volume during the time of free path ![]() equals
equals![]() . The order of magnitude of
. The order of magnitude of ![]() is
is![]() , i.e.,
, i.e.,![]() . Therefore, the typical number of collisions
. Therefore, the typical number of collisions ![]() within an unit space volume during the time of free path is
within an unit space volume during the time of free path is![]() . Let us multiply the second term on the right hand side of Equation (3.1) by
. Let us multiply the second term on the right hand side of Equation (3.1) by ![]() and integrate it with respect to
and integrate it with respect to ![]() and
and![]() . The
. The ![]() value should be used to assess the order of magnitude of the received expression on the time scale, proportional to
value should be used to assess the order of magnitude of the received expression on the time scale, proportional to![]() .
.
In accordance with ideas of the kinetic theory of gases [14] , the characteristic space volume per particle of gas medium ![]() is identified with a characteristic volume, which the particle covers during the time of free path
is identified with a characteristic volume, which the particle covers during the time of free path![]() . Then, during the time of free path
. Then, during the time of free path![]() ,
, ![]() particles in average experience a collision within the volume, proportional to
particles in average experience a collision within the volume, proportional to![]() ,
,![]() . That is, during the time between collisions
. That is, during the time between collisions![]() , only one particle in average
, only one particle in average ![]() experiences a collision within the space volume per one medium particle
experiences a collision within the space volume per one medium particle![]() . Then, during the time between collisions
. Then, during the time between collisions![]() ,
, ![]() particles in average experience a collision within the volume
particles in average experience a collision within the volume ![]() (
(![]() , i.e.,
, i.e.,![]() ). That is, during the time, proportional to
). That is, during the time, proportional to![]() , each of medium particles in average experiences one collision. The error of the estimation
, each of medium particles in average experiences one collision. The error of the estimation ![]() does not exceed the typical number of triple collisions in medium during the time, proportional to
does not exceed the typical number of triple collisions in medium during the time, proportional to ![]()
![]() . Competition of the fluctuation error
. Competition of the fluctuation error ![]() is insignificant,
is insignificant, ![]() [15] ,
[15] , ![]() for
for![]() . The number of binary collisions within the volume
. The number of binary collisions within the volume ![]() during the time, proportional to
during the time, proportional to![]() , equals
, equals![]() .
.
Let particles 1 and 2 are located so that at time ![]() the vector
the vector ![]() does not extend beyond the colli-
does not extend beyond the colli-
![]()
Figure 2. Graphic representation of a pair of particles.
sion cylinder![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , Figure 3. The volume of the collision cylinder
, Figure 3. The volume of the collision cylinder ![]()
![]() equals to the average volume per particle of gas medium
equals to the average volume per particle of gas medium![]() . Let at the time
. Let at the time![]() ,
, ![]() , particles 1 and 2, having collided, leave the domain of their interaction
, particles 1 and 2, having collided, leave the domain of their interaction![]() ,
,![]() . At the time
. At the time ![]() the second term on the right hand side of Equation (3.1) describes a triple collision between particles 1, 2, and 3. During the collision time
the second term on the right hand side of Equation (3.1) describes a triple collision between particles 1, 2, and 3. During the collision time![]() , the order of the second term on the right hand side of Equation (3.1) will not exceed
, the order of the second term on the right hand side of Equation (3.1) will not exceed![]() . In accordance with Equation (3.2), as time of motion of particles 1 and 2 in
. In accordance with Equation (3.2), as time of motion of particles 1 and 2 in ![]() - space grows, contribution of the second term on the right hand side of Equation (3.1) increases monotonically. The probability that particle 1 will experience a collision with particle 3 becomes of the order of unity on the length of
- space grows, contribution of the second term on the right hand side of Equation (3.1) increases monotonically. The probability that particle 1 will experience a collision with particle 3 becomes of the order of unity on the length of![]() . Monotonic increase (3.2) of the second term on the right hand side of Equation (3.1) contradicts the ideas of the kinetic theory of gases on a free path of particle. Indeed, particle 1 has already experienced collision with particle 2 at the time
. Monotonic increase (3.2) of the second term on the right hand side of Equation (3.1) contradicts the ideas of the kinetic theory of gases on a free path of particle. Indeed, particle 1 has already experienced collision with particle 2 at the time ![]() at the boundary of the collisions cylinder
at the boundary of the collisions cylinder![]() . Therefore, the rectilinear motion of particle 1 within the cylinder
. Therefore, the rectilinear motion of particle 1 within the cylinder ![]() must not be interrupted on the length of
must not be interrupted on the length of ![]()
![]() . That is, the possibility of collision between particle 1 and particle 3 contradicts the above evaluated number of collisions
. That is, the possibility of collision between particle 1 and particle 3 contradicts the above evaluated number of collisions ![]() within the cylinder
within the cylinder![]() . As a result, monotonic increase (3.2) of the second term on the right hand side of Equation (3.1) contradicts also the above evaluated number of collisions
. As a result, monotonic increase (3.2) of the second term on the right hand side of Equation (3.1) contradicts also the above evaluated number of collisions ![]() within the volume
within the volume![]() . Indeed, in accordance with the estimation (3.2), the magnitude of
. Indeed, in accordance with the estimation (3.2), the magnitude of ![]() reaches
reaches ![]() that far exceeds the error
that far exceeds the error ![]() of the characteristic number of collisions (
of the characteristic number of collisions (![]() ,
,![]() ). Thus, the assumption that a particle may be present at all phase space locations with equal probabilities sets too high estimation of the second term on the right hand side of Equation (3.1). Estimation of the second term on the right side of Equation (3.1) requires a more accurate evaluation of the order of magnitude of the
). Thus, the assumption that a particle may be present at all phase space locations with equal probabilities sets too high estimation of the second term on the right hand side of Equation (3.1). Estimation of the second term on the right side of Equation (3.1) requires a more accurate evaluation of the order of magnitude of the ![]() function. The aforesaid estimations are fully applicable to the third term on the right hand side of Equation (3.1). Let the
function. The aforesaid estimations are fully applicable to the third term on the right hand side of Equation (3.1). Let the ![]() function describes particles 1 and 2 located within the collision cylinder
function describes particles 1 and 2 located within the collision cylinder![]() . Then, based on the estimation of the number of collisions
. Then, based on the estimation of the number of collisions ![]() within the cylinder
within the cylinder ![]() during the time, proportional to
during the time, proportional to![]() , we have :
, we have :
![]() (3.3)
(3.3)
Equation (3.3) has a clear physical meaning. It asserts that a pair of flying-apart particles, that is, of particles that have already left the domain of their interaction ![]() and are located within the cylindrical volume
and are located within the cylindrical volume![]() , travels undergoing no collisions with third particle 3. Note that the ideas of the kinetic theory of gases on the free path of particle are valid for an arbitrary gas particle at every time moment. That is why, partial distribution functions
, travels undergoing no collisions with third particle 3. Note that the ideas of the kinetic theory of gases on the free path of particle are valid for an arbitrary gas particle at every time moment. That is why, partial distribution functions![]() , themselves rather than fluctuations of these functions must correspond to these ideas.
, themselves rather than fluctuations of these functions must correspond to these ideas.
Let particles 1 and 2 are located so that at time ![]() the vector
the vector ![]() does not extend beyond the collision cylinder
does not extend beyond the collision cylinder![]() ,
, ![]() ,
, ![]() , Figure 3. The volume of collision cylinder
, Figure 3. The volume of collision cylinder ![]()
![]() equals to the average volume per particle of gas medium
equals to the average volume per particle of gas medium![]() . Let at the time
. Let at the time![]() ,
, ![]() , particles 1 and 2 reach the domain of their interaction
, particles 1 and 2 reach the domain of their interaction![]() ,
,![]() . At the time
. At the time ![]() the second term on the right hand side of Equation (3.1) describes a triple collision between particles 1, 2, and 3. During the collision time
the second term on the right hand side of Equation (3.1) describes a triple collision between particles 1, 2, and 3. During the collision time![]() , the order of the second term on the right hand side of Equation (3.1) will not exceed
, the order of the second term on the right hand side of Equation (3.1) will not exceed![]() . In accordance with Equation (3.2), as time of motion of particles 1 and 2 in
. In accordance with Equation (3.2), as time of motion of particles 1 and 2 in ![]() -space grows, contribution of the second term on the right hand side of Equation (3.1) increases monotonically. The probability that particle 1 will experience a collision with particle 3 becomes of the order of unity on the length of
-space grows, contribution of the second term on the right hand side of Equation (3.1) increases monotonically. The probability that particle 1 will experience a collision with particle 3 becomes of the order of unity on the length of![]() .
.
![]()
Figure 3. The interaction domain of a pair of particles C0, the collision cylinders C− and C+.
Monotonic increase (3.2) of the second term on the right hand side of Equation (3.1) contradicts the ideas of the kinetic theory of gases on a free path of particle. Indeed, particle 1 will experience collision with particle 2 at the time ![]() at the boundary of the collision cylinder
at the boundary of the collision cylinder![]() . Therefore, the rectilinear motion of the particle 1 within the cylinder
. Therefore, the rectilinear motion of the particle 1 within the cylinder ![]() must not be interrupted on the length
must not be interrupted on the length ![]()
![]() . As a result, the possibility of collision between particle 1 and particle 3 contradicts both the above estimated number of collisions
. As a result, the possibility of collision between particle 1 and particle 3 contradicts both the above estimated number of collisions ![]() within the cylinder C− and the number of collisions N4 within the volume V. Thus, the assumption that a particle may be present at all phase space locations with equal probabilities sets too high estimation of the second term on the right hand side of Equation (3.1). Evaluation of the second term on the right side of Equation (3.1) requires a more accurate estimation of the order of magnitude of the
within the cylinder C− and the number of collisions N4 within the volume V. Thus, the assumption that a particle may be present at all phase space locations with equal probabilities sets too high estimation of the second term on the right hand side of Equation (3.1). Evaluation of the second term on the right side of Equation (3.1) requires a more accurate estimation of the order of magnitude of the ![]() function. The aforesaid estimations are fully applicable to the third term on the right hand side of Equation (3.1). Let the
function. The aforesaid estimations are fully applicable to the third term on the right hand side of Equation (3.1). Let the ![]() function describes particles 1 and 2 located within the collision cylinder
function describes particles 1 and 2 located within the collision cylinder![]() . Then, based on the estimation of the number of collisions
. Then, based on the estimation of the number of collisions ![]() within the cylinder
within the cylinder ![]() during the time, proportional to
during the time, proportional to![]() , we have:
, we have:
![]() (3.4)
(3.4)
Equation (3.4) has a clear physical meaning. It asserts that a pair of drawing together particles, that is, of particles that have not yet reached the domain of their interaction ![]() and are located within the cylindrical volume
and are located within the cylindrical volume![]() , travels undergoing no collisions with third particle 3.
, travels undergoing no collisions with third particle 3.
Let particles 1 and 2 are located so that at time ![]() the vector
the vector ![]() does not extend beyond the domain of their interaction
does not extend beyond the domain of their interaction![]() ,
, ![]() ,
, ![]() , Figure 3. Let distribution function
, Figure 3. Let distribution function ![]() describes particles 1 and 2 located within the interaction domain
describes particles 1 and 2 located within the interaction domain![]() . The evolution of the
. The evolution of the ![]() function occurs at the times, proportional to
function occurs at the times, proportional to![]() . The second equation of the hierarchy (2.1) on the initial
. The second equation of the hierarchy (2.1) on the initial ![]() -scale has the form (2.2b), in which
-scale has the form (2.2b), in which ![]() can be replaced by
can be replaced by![]() . Let
. Let ![]() equals the
equals the ![]() function within the collision cylinder
function within the collision cylinder![]() , and the
, and the ![]() function within the collision cylinder
function within the collision cylinder![]() , and the function
, and the function ![]() within the interaction domain
within the interaction domain![]() . Then:
. Then:
![]() (3.5)
(3.5)
![]()
![]()
![]()
here,
![]() (3.6)
(3.6)
Generally, any medium particle forms a pair with every other particle. A medium therefore contains ![]() pairs of particles. All these pairs are described by the
pairs of particles. All these pairs are described by the ![]() function, which obeys the second equation of the BBGKY hierarchy (2.1). If a single particle 2, which either flies away from (Figure 2(a)) or approaches (Figure 2(b)) some particle 1, is selected as a partner of this particle, this pair is described by the
function, which obeys the second equation of the BBGKY hierarchy (2.1). If a single particle 2, which either flies away from (Figure 2(a)) or approaches (Figure 2(b)) some particle 1, is selected as a partner of this particle, this pair is described by the ![]() function that obeys Equation (3.5). Note that Equation (3.5) is valid for an arbitrary gas particle rather than some particular particle 1 (Figure 2). Generally, a medium contains
function that obeys Equation (3.5). Note that Equation (3.5) is valid for an arbitrary gas particle rather than some particular particle 1 (Figure 2). Generally, a medium contains ![]() pairs of approaching particles, and
pairs of approaching particles, and ![]() pairs of diverging particles. For this reason, Equation (3.5) is capable of describing the gas as a whole. Heuristic derivation of Equation (3.5) was given in [3] . In [11] , Equation (3.5) was derived in terms of conditional probabilities. In accordance with [11] , the
pairs of diverging particles. For this reason, Equation (3.5) is capable of describing the gas as a whole. Heuristic derivation of Equation (3.5) was given in [3] . In [11] , Equation (3.5) was derived in terms of conditional probabilities. In accordance with [11] , the ![]() distribution function is limited by the condition that the third particle is not located within the collision cylinders
distribution function is limited by the condition that the third particle is not located within the collision cylinders ![]() and
and![]() , Figure 3. Earlier, the formalism of conditional probabilities was used in [16] in deriving the Boltzmann equation for a gas consisting of rigid spheres.
, Figure 3. Earlier, the formalism of conditional probabilities was used in [16] in deriving the Boltzmann equation for a gas consisting of rigid spheres.
Expand the dimensionless two-particle distribution function in a perturbation theory series in terms of the virial parameter![]() :
:
![]() (3.7)
(3.7)
Let us substitute Equation (3.7) into the dimensionless Equation (3.5). Equating the multipliers at equal degrees of![]() , let us specify the equation for
, let us specify the equation for![]() . Let us omit the superscript of
. Let us omit the superscript of ![]() and go back to the dimensional quantities. Recasting the two-particle distribution function in variables
and go back to the dimensional quantities. Recasting the two-particle distribution function in variables![]() ,
, ![]() ,
, ![]() ,
, ![]() , one obtains:
, one obtains:
![]() (3.8)
(3.8)
Integrating Equation (3.8) with respect to ![]() over the cylindrical volumes
over the cylindrical volumes ![]() and
and ![]() yields
yields
![]() (3.9a)
(3.9a)
![]() (3.9b)
(3.9b)
where
![]() (3.10a)
(3.10a)
![]() (3.10b)
(3.10b)
Equation (3.8) allows putting on the trajectory ![]() in the 12-dimensional phase space both the first and the second terms on the right-hand side of Equation (3.9b):
in the 12-dimensional phase space both the first and the second terms on the right-hand side of Equation (3.9b):
![]() (3.11)
(3.11)
Let us recast Equation (3.11) in the dimensionless form. It turned out that ![]() is characteristic scale of variation of the
is characteristic scale of variation of the ![]() pair function with time along the trajectory of a center of mass of a pair. Let us op-
pair function with time along the trajectory of a center of mass of a pair. Let us op-
erate with ![]() directly on Equation (3.10b). Then, a weak dependence on
directly on Equation (3.10b). Then, a weak dependence on ![]() -scale with time
-scale with time
along the trajectory of a center of mass of a pair of the ![]() function on the left-hand side of Equation (3.10b) defines a weak dependence on
function on the left-hand side of Equation (3.10b) defines a weak dependence on ![]() -scale of the function
-scale of the function![]() ,
, ![]() , on the right side of Equation (3.10b). Function
, on the right side of Equation (3.10b). Function ![]() B (3.9а) pertains to a pair of particles escaping from the domain of their interaction
B (3.9а) pertains to a pair of particles escaping from the domain of their interaction![]() . In accordance with (2.5) and (2.6), express
. In accordance with (2.5) and (2.6), express ![]() in terms of the two- particle distribution function at the entrance to domain
in terms of the two- particle distribution function at the entrance to domain![]() . Let the series (3.7) be taken into account. Time averaging Equation (3.9a) along the trajectory of a center of mass of a pair with regard for Equations (2.5) and (2.6) yields
. Let the series (3.7) be taken into account. Time averaging Equation (3.9a) along the trajectory of a center of mass of a pair with regard for Equations (2.5) and (2.6) yields
![]() (3.12)
(3.12)
В (3.12)![]() . In deriving Equation (3.12), we took into account that, according to Equation (3.8),
. In deriving Equation (3.12), we took into account that, according to Equation (3.8), ![]() is conserved along the trajectory of a pair in the 12-dimensional phase space
is conserved along the trajectory of a pair in the 12-dimensional phase space
![]() (3.13)
(3.13)
The first term in the right hand side of Equation (3.12) contains information, which is excessive for the kinetic stage of gas description. This is information about mutual disposition of particles in the pair contained in the ![]() dependence on
dependence on ![]() and
and![]() . According to [17] , in order to proceed to the kinetic stage, we replace this function by its average value:
. According to [17] , in order to proceed to the kinetic stage, we replace this function by its average value:
![]() (3.14)
(3.14)
The replacement (3.14), being substituted in Equation (3.12), makes this equation irreversible.
Expanding the left hand side of Equation (3.12) into series in terms of ![]() gives
gives
![]() (3.15)
(3.15)
When writing the right hand side of Equation (3.15), we took into account that, according to Equation (3.13), function ![]() (likewise
(likewise![]() ) changes in time only little on the
) changes in time only little on the ![]() -scale along the trajectory of the center of mass of the pair, because it is represented by the
-scale along the trajectory of the center of mass of the pair, because it is represented by the ![]() function averaged over this trajectory. This does not necessary mean that functions
function averaged over this trajectory. This does not necessary mean that functions ![]() and
and ![]() insignificantly vary on the initial
insignificantly vary on the initial ![]() -scale with time and in space separately. Let
-scale with time and in space separately. Let
![]() (3.16)
(3.16)
The spatial integration in Equation (3.16) is implemented near point ![]() within the
within the ![]() region of a characteristic linear size
region of a characteristic linear size![]() ,
,![]() . Functions
. Functions ![]() and
and ![]() change only little in space on the initial scale. Since
change only little in space on the initial scale. Since ![]() and
and![]() , and, hence,
, and, hence, ![]() and
and ![]() change insignificantly in time along the trajectory of the center of mass of a pair on the initial scale, time variation of
change insignificantly in time along the trajectory of the center of mass of a pair on the initial scale, time variation of ![]() and
and ![]() on the initial scale is also insignificant.
on the initial scale is also insignificant.
Multiplying ![]() and
and ![]() by the number of possible selections of pairs from the set of
by the number of possible selections of pairs from the set of ![]() particles equal
particles equal ![]() (transmutations of particles do not lead to a new pair), we arrive at the pair distribution functions defined in [10]
(transmutations of particles do not lead to a new pair), we arrive at the pair distribution functions defined in [10]
![]() (3.17)
(3.17)
Let us average Equation (3.15) within the ![]() region. At the hydrodynamic stage of description, when the characteristic scale of changes in the distribution function
region. At the hydrodynamic stage of description, when the characteristic scale of changes in the distribution function![]() ,
, ![]() , the second term in the left hand side of Equation (3.15) is negligibly small as compared to the first term. As a result, we arrive at one of two equations, which has been derived in [10] heuristically:
, the second term in the left hand side of Equation (3.15) is negligibly small as compared to the first term. As a result, we arrive at one of two equations, which has been derived in [10] heuristically:
![]() (3.18)
(3.18)
Let![]() ,
, ![]() and
and ![]() are the spherical coordinates of vector
are the spherical coordinates of vector![]() . Integrating Equation (3.18) with respect to
. Integrating Equation (3.18) with respect to ![]() and
and ![]() yields
yields
![]() (3.19)
(3.19)
Equation for ![]() can be derived by analogy with derivation of Equation (3.19). In accordance with Equations (2.5) and (2.6), the
can be derived by analogy with derivation of Equation (3.19). In accordance with Equations (2.5) and (2.6), the ![]() function at the entrance to the interaction domain
function at the entrance to the interaction domain ![]() of a pair is expressed through the function at the exit from this domain:
of a pair is expressed through the function at the exit from this domain:
![]() (3.20)
(3.20)
where ![]() is the velocity of the relative motion of particles, which is acquired by these particles upon their collision, provided their parameters before collision have been
is the velocity of the relative motion of particles, which is acquired by these particles upon their collision, provided their parameters before collision have been![]() ,
, ![]() and
and![]() , Figure 1. Let the series (3.7) be taken into account. Substituting Equation (3.20) into Equation (3.9b) and time averaging along the trajectory of the center of mass of a pair yields
, Figure 1. Let the series (3.7) be taken into account. Substituting Equation (3.20) into Equation (3.9b) and time averaging along the trajectory of the center of mass of a pair yields
![]() (3.21)
(3.21)
Without performing the irreversible replacement in Equation (3.21), we integrate this equation with respect to ![]() and
and![]() . Then, averaging Equation (3.21) within the
. Then, averaging Equation (3.21) within the ![]() region near point
region near point ![]() and using definitions (3.16) and (3.17), we arrive at the second equation derived in [10] heuristically:
and using definitions (3.16) and (3.17), we arrive at the second equation derived in [10] heuristically:
![]() (3.22)
(3.22)
The solution to the closed set of Equations (3.19) and (3.22) discovers the basic property of the pair distribution functions. It shows that the distribution functions ![]() and
and ![]() do not change with time along the trajectory of the center of mass of a pair:
do not change with time along the trajectory of the center of mass of a pair:
![]() (3.23)
(3.23)
This means that particle collisions cannot influence the formation of hydrodynamic values constructed on the pair properties of![]() ,
,![]() . In other words, particle collisions cannot tune the distributions of all these hydrodynamic values to distributions of some other hydrodynamic values. That is, the set of hydrodynamic values constructed on the property
. In other words, particle collisions cannot tune the distributions of all these hydrodynamic values to distributions of some other hydrodynamic values. That is, the set of hydrodynamic values constructed on the property![]() ,
, ![]() ,
,
![]() (3.24)
(3.24)
is a set of principle hydrodynamic values. The relationship between the functions ![]() and
and ![]() is given in [5] . This relationship allows establishing a correspondence between the principal hydrodynamic values
is given in [5] . This relationship allows establishing a correspondence between the principal hydrodynamic values ![]() (2.21) and
(2.21) and ![]() (3.24).
(3.24).
4. Conclusions
The Navier-Stokes equations have been used with much success for more than one and a half century as a tool for very accurately describing stable incompressible flows, both stationary and non-stationary. However, in recent decades, the Navier-Stokes equations have been faced with insurmountable difficulties in interpreting flows, losing its stability. In accordance with the interpretation of [1] - [3] , the reason for their failure is the lack of the main hydrodynamic values used in constructing the equations of classic hydrodynamics.
Classic hydrodynamics equations are constructed for only three lower principle hydrodynamic values: the density of particles number, the hydrodynamic velocity, and the pressure. Higher principle hydrodynamic values are not used in the formation of classic hydrodynamics equations. The possibility of the formation of hydrodynamics equations with an arbitrary number of principle hydrodynamic values specified beforehand was found in [11] . The multimoment hydrodynamics equations were derived immediately from the equations for the pair distribution functions in [5] .
The distribution functions for pairs of drawing together and flying apart particles referred to as pair distribution functions are constructed in [10] , where the heuristic derivation of the equations for the pair distribution functions has been suggested. In [11] , the equations for the pair distribution functions are derived directly from the fundamental principles of the statistical mechanics. The Liouville equation was used in [11] as a base when deriving the equations for the pair distribution functions. There is an analogy between the derivation on these equations [11] and the Grad method [16] used in deriving the Boltzmann equation for a gas consisting of rigid spheres.
In [11] , equation for two-particle distribution function ![]() was derived in terms of conditional probabilities. In Section 2, the equation for
was derived in terms of conditional probabilities. In Section 2, the equation for ![]() is derived directly from the second equation of the BBGKY hierarchy within the frameworks of formalism of the multiscale method. Within the
is derived directly from the second equation of the BBGKY hierarchy within the frameworks of formalism of the multiscale method. Within the ![]() cylinder, the
cylinder, the ![]() distribution function describes pairs of particles which are diverging after collision with each other. These particles move further without collision with third particle. Within the
distribution function describes pairs of particles which are diverging after collision with each other. These particles move further without collision with third particle. Within the ![]() cylinder, the
cylinder, the ![]() distribution function describes pairs of particles, which are approaching each other before their collision. These particles also move without collision with third particle.
distribution function describes pairs of particles, which are approaching each other before their collision. These particles also move without collision with third particle.
The common ideology of the multiscale method is described in [12] . The multiscale method was used in [18] - [20] for the deriving the Boltzmann equation. Each of these formalisms interprets the ideology of some scales in its own way. In Sections 2 and 3, we don’t follow any of interpretations [18] [19] or [20] . Equations for the distribution functions are written separately at each scale. The ideas of the kinetic theory of gases on a free path are used when evaluating the order of terms in equations. Derived Equations (2.12) and (2.13) follow the evolution of the one-particle distribution function at the finest ![]() -scale. The transition to the kinetic scale leads to Equation (2.16) with the collision integral (2.17). The Boltzmann hypothesis of molecular chaos closes equation (2.16), allowing constructing classic hydrodynamics equations only with three lower principle hydrodynamic values. Equation (3.8) for the
-scale. The transition to the kinetic scale leads to Equation (2.16) with the collision integral (2.17). The Boltzmann hypothesis of molecular chaos closes equation (2.16), allowing constructing classic hydrodynamics equations only with three lower principle hydrodynamic values. Equation (3.8) for the ![]() function is used as a base when deriving equations for the pair distribution functions (3.18) and (3.22). Derived equations for the pair functions do not limit hydrodynamics equations in a number of principle hydrodynamic values.
function is used as a base when deriving equations for the pair distribution functions (3.18) and (3.22). Derived equations for the pair functions do not limit hydrodynamics equations in a number of principle hydrodynamic values.
References
- Lebed, I.V. and Umanskii, S.Y. (2007) The Appearance and Development of Turbulence in a Flow Past a Sphere: Problems and the Existing Approaches to Their Solution. Russian Journal of Physical Chemistry B, 1, 52-73. http://dx.doi.org/10.1134/S1990793107010071
- Lebed, I.V. and Umanskii, S.Y. (2012) On the Possibility of Improving Classic Hydrodynamics Equations by an In- crease in the Number of Hydrodynamic Values. Russian Journal of Physical Chemistry B, 6, 149-162. http://dx.doi.org/10.1134/S1990793112010204
- Lebed, I.V. (2013) About the Prospects for Passage to Instability. Open Journal of Fluid Dynamics, 3, 214-229. http://dx.doi.org/10.4236/ojfd.2013.33027
- Liboff, R.L. (1969) Introduction to the Theory of Kinetic Equations. Willey, New York.
- Lebed, I.V. (1996) Method of Two-Particle Distribution Functions. Hydrodynamic Equations. Chemical Physics Reports, 15, 861-883.
- Lebed, I.V. (1997) The Method of Pair Functions as Applied to the Problem of a Flow around a Quiescent Solid Sphere. Chemical Physics Reports, 16, 1263-1301.
- Lebed, I.V. (1998) About the Behavior of the Entropy of a Gas Flow Losing Its Stability. Chemical Physics Reports, 17, 411-439.
- Lebed, I.V. (2014) Multimoment Hydrodynamics in Problem on Flow around a Sphere: Entropy Interpretation of the Appearance and Development of Instability. Open Journal of Fluid Dynamics, 4, 163-206. http://dx.doi.org/10.4236/ojfd.2014.42015
- Lebed, I.V. (2014) Development of Instability in the Problem of Flow around a Sphere. Russian Journal of Physical Chemistry B, 8, 240-253. http://dx.doi.org/10.1134/S1990793114020171
- Lebed, I.V. (1990) Equations of Pair Distribution Functions. Chemical Physics Letters, 165, 226-228. http://dx.doi.org/10.1016/0009-2614(90)85433-D
- Lebed, I.V. (1995) Derivation of the Equations for Pair Distribution Functions. Chemical Physics Reports, 14, 599- 615.
- Van Dyke, M.D. (1964) Perturbation Methods in Fluid Mechanics. Academic Press, New York and London.
- Bogolyubov, N.N. (1946) The Problems of Dynamic Theory in Statistical Physics. Gostechizdat, Moscow-Leningrad.
- Ferziger, J.H. and Kaper, H.G. (1972) Mathematical Theory of Transport Processes in Gases. North-Holland Publishing Company, Amsterdam.
- Landau, L.D. and Lifshitz, E.M. (1976) Course of Theoretical Physics, Vol. 5: Statistical Physics, Part 1. Nauka, Moscow.
- Grad, H. (1958) Principles of the Kinetic Theory of Gases. Handbuch der Physik, 3/12, 205-294.
- Lebed, I.V. (2014) About Appearance of the Irreversibility. Open Journal of Fluid Dynamics, 4, 298-320. http://dx.doi.org/10.4236/ojfd.2014.43023
- Sandri, G. (1963) The Foundations of Nonequilibrium Statistical Mechanics. Annals of Physics, 24, 332-379, 380-418.
- Freeman, E.A. (1963) On a New Method in the Theory of Irreversible Processes. Journal of Mathematical Physics, 4, 410-427. http://dx.doi.org/10.1063/1.1703968
- Kogan, M.N. (1967) Rarefied Gas Dynamics. Nauka, Moscow.




 is reached; the ground axisymmetric stationary solution
is reached; the ground axisymmetric stationary solution  loses its stability. Nonstationary solution
loses its stability. Nonstationary solution 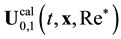 ensures the transition from the
ensures the transition from the 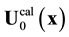 solution that loses its stability to the stable stationary nonaxisymmetric solution
solution that loses its stability to the stable stationary nonaxisymmetric solution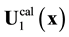 . The attainment of the second critical Reynolds number value
. The attainment of the second critical Reynolds number value 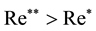 is accompanied by the loss of stability of the
is accompanied by the loss of stability of the 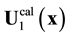 solution. Nonstationary solution
solution. Nonstationary solution 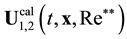 ensures the transition from the
ensures the transition from the 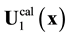 solution that loses its stability to the stable nonstationary limiting cycle
solution that loses its stability to the stable nonstationary limiting cycle . After attainment of the third critical Reynolds number value
. After attainment of the third critical Reynolds number value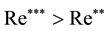 , the
, the  solution loses its stability. Nonstationary solution
solution loses its stability. Nonstationary solution 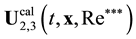 ensures the transition from the
ensures the transition from the 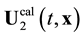 limiting cycle that loses its stability to the new stable position about which multiperiodic, that is, almost chaotic,
limiting cycle that loses its stability to the new stable position about which multiperiodic, that is, almost chaotic, 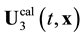 motion occurs.
motion occurs. and
and














































































































































































































































































































































































































































































































































































































