Open Journal of Fluid Dynamics
Vol.3 No.4(2013), Article ID:40448,10 pages DOI:10.4236/ojfd.2013.34038
Near Wake of a Horizontal Circular Cylinder in Stably Stratified Flows
Research Institute for Applied Mechanics, Kyushu University, Kasuga-shi, Japan
Email: ohya@riam.kyushu-u.ac.jp, Takanori@riam.kyushu-u.ac.jp, nagai@riam.kyushu-u.ac.jp
Copyright © 2013 Yuji Ohya et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 1, 2013; revised November 1, 2013; accepted November 8, 2013
Keywords: Stratified Flow; Circular Cylinder; Wake Pattern; Vortex Shedding; Lee Wave
ABSTRACT
The near wake of a circular cylinder in linearly stratified flows of finite depth was experimentally investigated by means of flow visualization and measurements of vortex shedding frequencies, at Reynolds numbers 3.5 × 103 - 1.2 × 104 and stratification parameters kd 0 - 2.0. The non-dimensional parameter kd is defined as kd = Nd/U, where N is the Brunt-Väisälä frequency, d, the diameter of the cylinder, and U, the approaching flow velocity. The study demonstrates that as kd increases from zero, the vortex shedding from a circular cylinder progressively strengthens, while the Strouhal number gradually becomes lower than that for homogeneous flow. This phenomenon can be explained by the effect of the increasingly stable stratification which enhances the two-dimensionality of the near-wake flow of the circular cylinder; the enhanced two-dimensionality of the flow strengthens the roll-up of the separated shear layer. Above a certain value of kd, however, vortex formation and shedding are strongly suppressed and the Strouhal number rises sharply. This observation is attributable to the development of stationary lee waves downstream of the circular cylinder because the lee waves strongly suppress vertical fluid motions.
1. Introduction
In stratified fluids with vertical gradients of density and/ or temperature, buoyancy effects become significant. For instance, the strength of stratification is a predominant factor for fluid motion, turbulence transport, and dispersion in the atmosphere and ocean. Accordingly, a large number of investigations have been conducted on stratified flow around terrain or objects on the Earth’s surface (e.g. Blumen [1]). Some of these investigations were conducted to improve understanding of meteorological phenomena such as lee waves and local winds (e.g. Snyder [2]). Other investigations have centered around issues of the atmospheric environment that require understanding of advection and dispersion of air pollutants. In contrast to the investigations on atmospheric flows, there exist few investigations on stratified flow around basic objects such as cylinders or spheres.
In stratified flow, the flow around an object is generally governed by the Reynolds number and other dimensionless stratification numbers (e.g. the Froude number). Honji [3-5] investigated two-dimensional flows around a circular cylinder placed horizontally in stratified flow for a range of Reynolds numbers less than approximately 800. With flow visualizations, Honji [3-5] determined the following properties of two-dimensional near wake flows. In stratified flow, fluid motions are suppressed in the direction of stratification. As a result, at low density stratification, Kármán-vortex-street wake-flow patterns are observed behind a horizontal circular cylinder placed perpendicular to the flow direction. However, with increasing stratification, the wake-flow pattern makes a gradual transition to that dominated by internal waves. When the stratification becomes sufficiently high, blocking occurs and upstream wakes emerge [6,7]. Furthermore, in a highly stratified fluid of finite depth, columnar disturbances emerge and propagate upstream of an object [8,9]. Boyer et al. [7] investigated the near-wake flows of a circular cylinder for Reynolds numbers less than 4000 and over a wide range of stratification. With a flow visualization experiment, the wake patterns of these investigated flows were classified in detail. Hwang and Lin [10] numerically computed stratified flows around a circular cylinder for Reynolds numbers less than 500. The results of their numerical computation showed suppressed vortex shedding with increasing density stratification, consistent with the experimental results above.
In more recent years, stratified wakes of tilted bluff bodies have been investigated by a number of authors (e.g. Boulanger [11,12], Meunier [13,14]). Meunier [13] reported in the study of stratified wake of a tilted cylinder, that the tendency of stabilization of the von Karman vortex street which can be seen with a moderate stratifycation is not efficient in a strongly stratified flow due to the presence of a second unstable mode characterized by tiled vortices. This leads to a discontinuity in the Strouhal number as a function of the Froude number which is related to the stratification through the Brunt-Väisälä frequency.
Besides a small number of recent studies on the tilted cylinder wakes, there have been only a limited number of results on the wakes of the cylinders in stratified flows, and almost no comprehensive publication on the near wakes of horizontal cylinder in stratified flows during last two decades.
In homogeneous flows, the effect of the Reynolds number is known to be large on the near wake flow of an object, particularly on the wake of a circular cylinder and a sphere. In contrast, the influence of stratification on the wake of an object is not yet well understood over a wide range of Reynolds numbers, particularly for high Reynolds numbers. Given this background, the present study investigates the influence of stratification on two-dimensional near wake flows around a circular cylinder with the use of a density-stratified wind tunnel. The density-stratified flow is generated with a Reynolds number in the range of 3.5 × 103 - 1.2 × 104. The near wake flow around a circular cylinder is investigated with a flow visualization technique and measurements of wake velocity fluctuations. Some of the phenomena observed in the current paper were previously reported as a letter [15]. The present paper will investigate the mechanisms of these phenomena.
2. Experimental Set-Up and Methodology
2.1. Generation and Evaluation of Density Stratification
Experiments were performed in a density-stratified wind tunnel of a closed-circuit type [16]. The test section of the wind tunnel was 0.4 m wide, 0.6 m high and 1.7 m long. Designed to generate predefined density-stratified flows, the wind tunnel, except for the contraction and test sections, was divided horizontally into six stories (Figure 1). A mixture of air and sulfur hexafluoride, SF6, was injected into each story from an external source to directly produce density stratification. Sulfur hexafluoride is a high-density gas with a molecular weight approximately 5 times that of air. Various types and strengths of vertical density gradients were produced in the test section
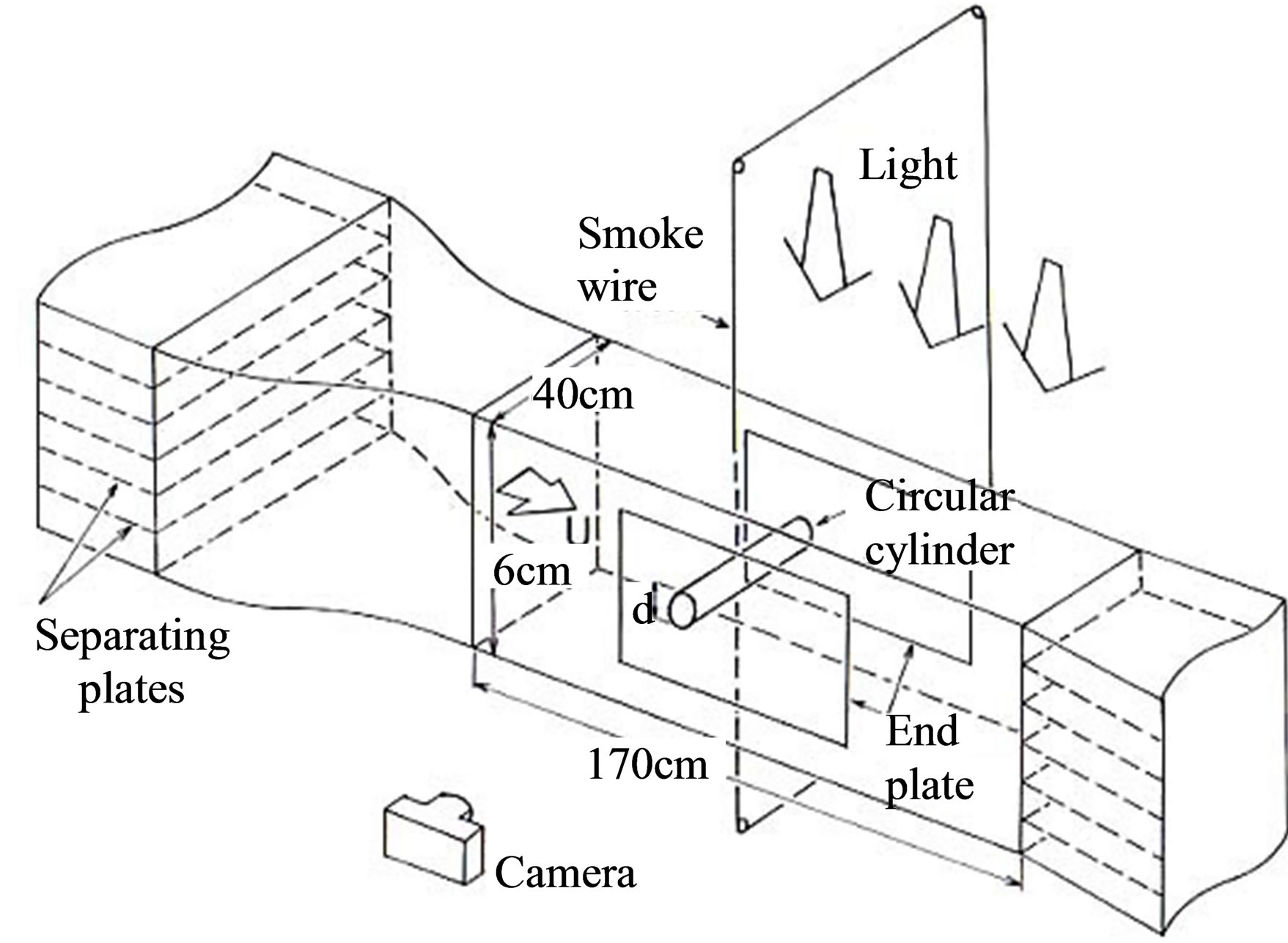
Figure 1. Test section of the density-stratified wind tunnel with a circular cylinder in place.
by appropriately adjusting the volume of SF6 injected into each story. The density of the gas mixture in the test section was indirectly measured with the use of an oxygen meter. To evaluate the volume fraction of oxygen, the gas mixture was sampled through a gas sampling tube placed upstream of the test section and sent to the oxygen meter. The volume fraction of oxygen is approximately 1/5 of a given volume of air. Thus, the volume fraction of oxygen evaluated by the oxygen meter allowed for the calculation of the volume fraction of the air, thus that of SF6 in the gas mixture. Finally, the molecular ratio of air to SF6 was used to evaluate the specific density of the gas mixture with respect to the air, ρ/ρa, at the location of the gas sampling.
2.2. Wind Velocity Control and Measurements
The wind in the test section was generated by 18 microfans, each driven by a micromotor; three microfans were mounted side by side on each story. The generated wind velocity, U, ranged from 0 to 1.2 m/s. In homogeneous flow (air only), an I-type hot-wire anemometer was deployed to measure low wind velocities with high accuracy. As for the wind velocity measurements in the stratified flow of the air-SF6 mixture, the smoke-tracer technique was adopted; that is, the visualized flow was video recorded and the transit time required for markers to pass between two reference points was analyzed to determine the wind velocity.
2.3. Test Models and Measurement of Velocity Fluctuations in the Wake
The models used in the present study were circular cylinders with diameters, d = 5, 7.5, 10 and 13 cm and two rectangular cylinders. The spanwise length of each of the cylinders was 30 cm. For both of the rectangular cylinders, the long side of the rectangular cross-section, d, was 10 cm. The symbol d is chosen for both the circular and rectangular cylinders because it represents the vertical height in both cases and will simplify the notation used in later analysis (see below and Section 5.1). The ratio of the short side to the long side of each rectangular cylinder, b/d, was 0.1 and 0.6, where b is the short side of the rectangular cross-section. All the cylinders were mounted in the test section so that their axes were horizontal and perpendicular to the flow direction. The rectangular cylinders were mounted with the long side of the rectangular cross-section facing the on-coming flow. To ensure the two-dimensionality of the flow, a 30 × 50 cm plate was attached to each end of the cylinders (models), and the plates were placed 5 cm away from the side walls (Figure 1).
The velocity fluctuations in the wake of a cylinder were measured by an I-type hot-wire anemometer at the outer edge of the wake behind the cylinder. Spectral analyses were performed on these data with an FFT analyzer. Finally, spanwise correlations of velocity fluctuations in the wake of the cylinder were evaluated using multiple I-type hot-wires deployed simultaneously in the spanwise direction (y-direction).
2.4. Flow Field Visualization and Flow Settings
The smoke-wire technique was adopted to visualize the flow field around a cylinder (Figure 1). A mixture of liquid paraffin and iron powder was used to prolong the duration of the smoke release. To illuminate the visualized flows, three 1 kW projectors were installed above the test section of the wind tunnel. The visualized flow was photographed by a Nikon F3 Camera (lens: 55 mm; exposure time: 1/125 sec; f-stop: 1.2; ASA400 black and white film) and video-taped simultaneously.
In the present study, the non-dimensional parameter, kd, is adopted to quantify the density stratification. The parameter kd is the inverse of the Froude number and defined as kd = Nd/U where N is the Brunt-Väisälä frequency and N2 = −(g/ρ0)/(dρdz). The variables g and ρ0 are the acceleration of gravity and the reference density, respectively. The reference density, ρ0, was set to the density value measured at the installation position of the circular cylinder, z = 30 cm above the floor of the wind tunnel. The Reynolds number is defined as Re = ρ0Ud/μ. The coefficient of viscosity, μ, for a mixture of air and SF6 with a volume ratio as high as 1:1, is 0.181 × 10−4 Pa·s (20˚C, 1 atm), approximately the same as that for air. In the present study, experiments with density-stratified flow were conducted mostly at U = 0.7 m/s, in some cases, U = 0.3, 0.5, and 0.76 m/s. For homogeneous flow, the wind velocity was set to U = 0.83 m/s, yielding Reynolds numbers over the range of Re = 3.5 × 103 - 1.2 × 104. The range of stratification parameter kd, varied from 0 to 2.0.
3. Experimental Results
3.1. Characteristics of Stratified Flow
Airflow with various vertical gradients of density was generated in the wind tunnel (Figure 2). Over this range of the vertical gradient of density, the generated density profiles were approximately linear. Figure 2 also suggests little change in the vertical gradient over the course of the flow visualization experiments, which lasted a few minutes. Finally, the vertical profile of the mean approach velocity, U, was nearly uniform in the all the stratified flows (not shown).
3.2. Flow Field Visualization
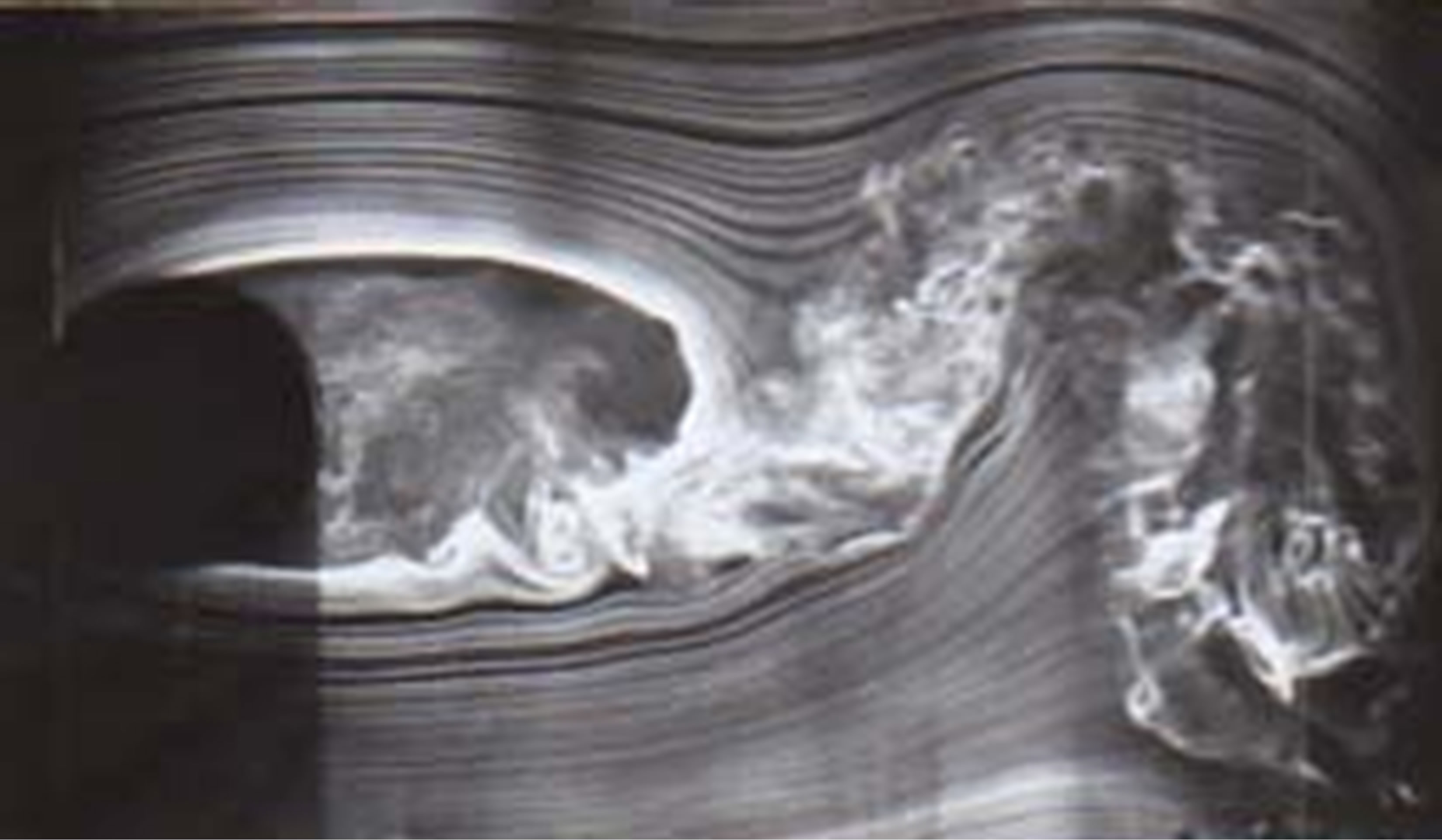
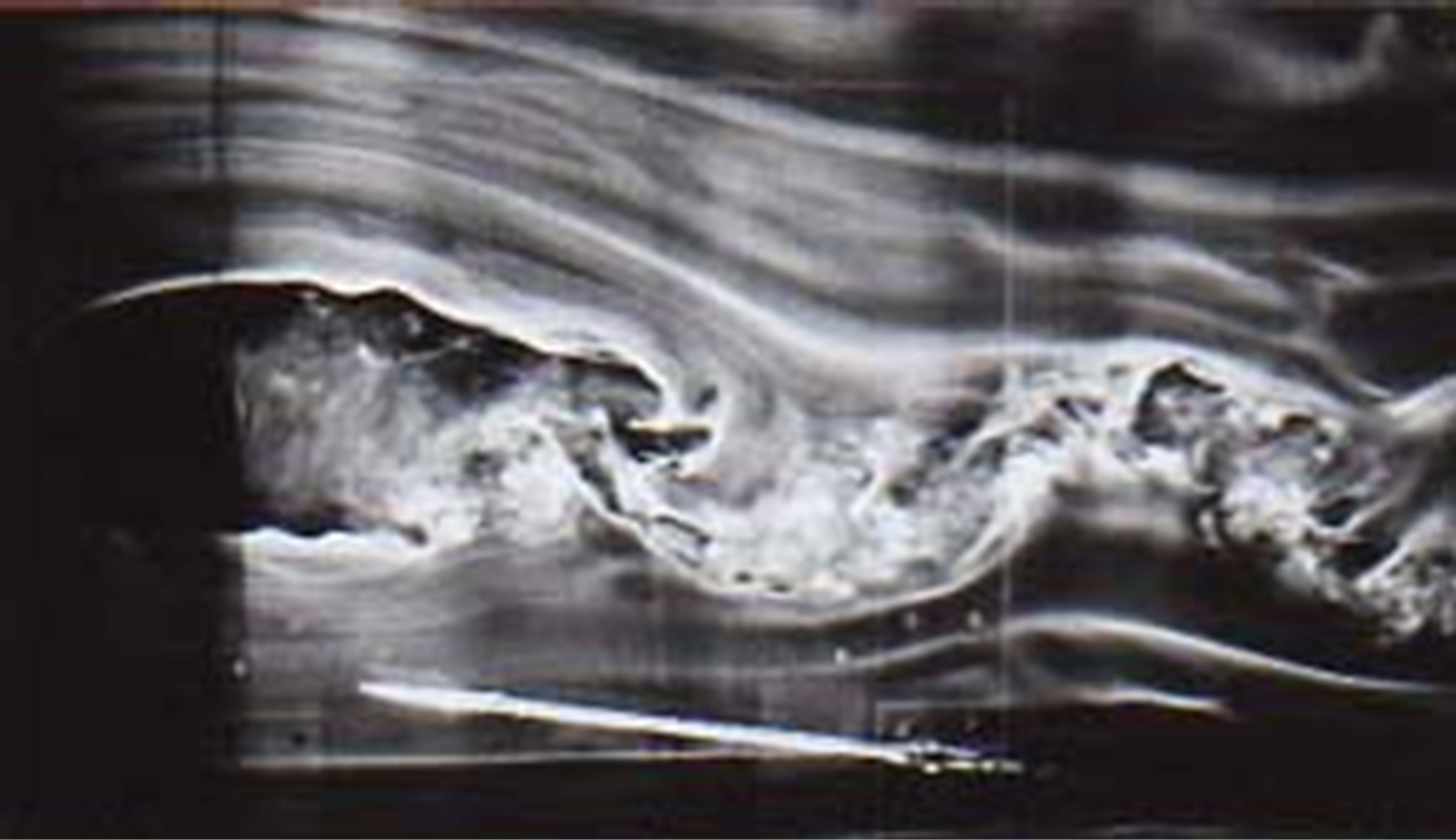
Flow around a circular cylinder (d = 10 cm) was observed in a stratified wind field that had a nearly uniform vertical profile of wind velocity and a linear vertical profile of density as in Figure 2. With the flow visualization technique, change in the near-wake flow pattern was examined with respect to the stratification parameter, kd. Figure 3 illustrates instantaneous flow patterns that are representative for various values of kd. The experiment was repeated a number of times for each condition, and the observed flow pattern was consistent and stable in the series of experiments. In Figure 3, vortex formation is observed behind the cylinder due to the roll up of the separated shear layer of the cylinder. Furthermore, with increasing values of kd, the vortex formation occurs closer to the rear side of the cylinder, and the strength of the vortex formation and shedding increases. In particular, the vortex formation and shedding are significantly enhanced at kd = 0.513 (Figure 3(c)) with respect to the homogeneous case. The flow pattern around the circular cylinder suddenly changes in the proximity of kd = 0.52 (Figure 3(d)). At this stratification, strong roll-up of the shear layers that have separated from the cylinder is no longer observed, and vortex formation in the wake is highly suppressed. With a further increase in the value of
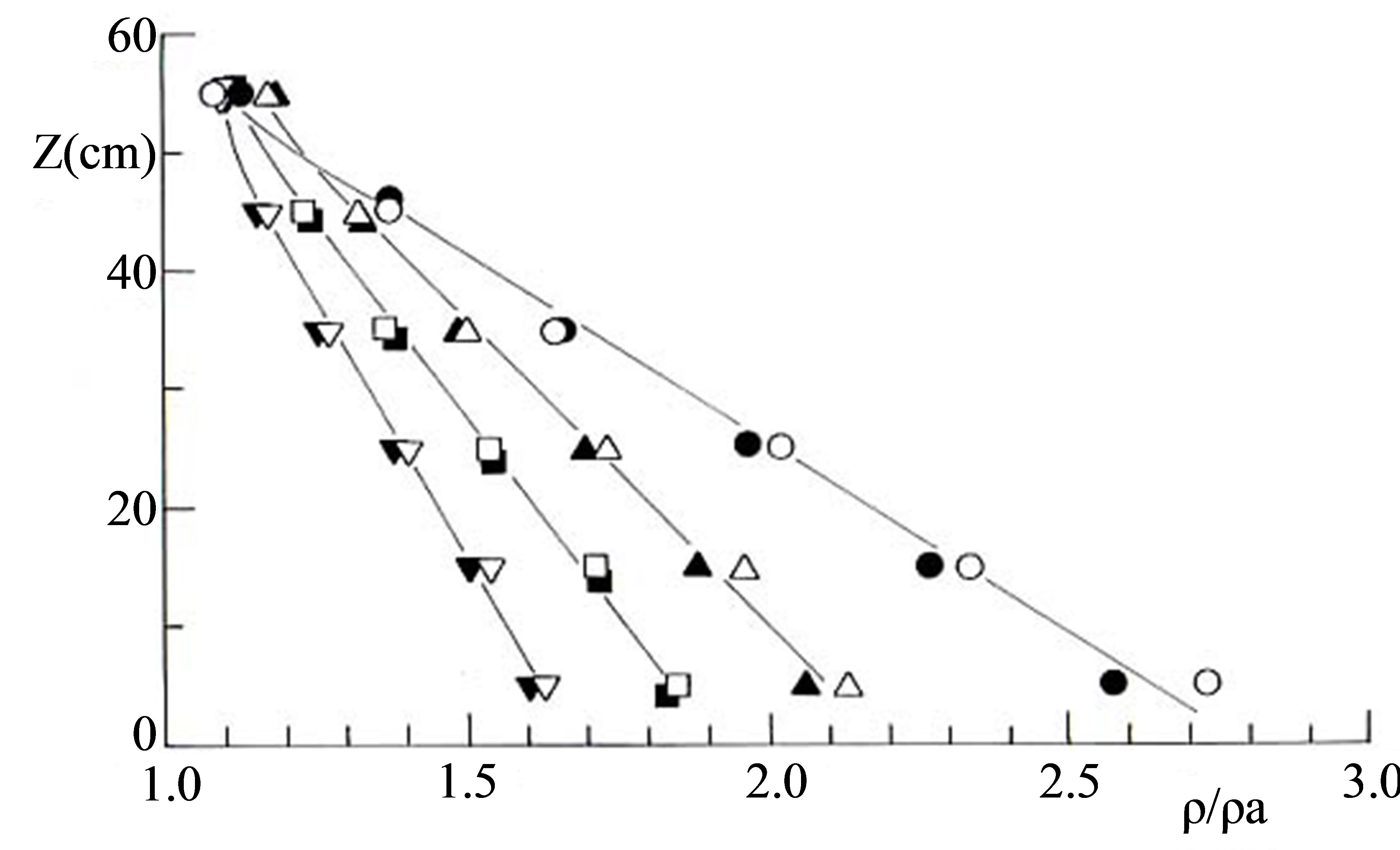
Figure 2. Example vertical profiles of the specific density, ρ/ρa at U = 0.7 m/s before (open symbols) and after (closed symbols) a flow visualization experiment.
 (a)
(a)  (b)
(b)  (c)
(c)
 (d)
(d)  (e)
(e)  (f)
(f)
Figure 3. Instantaneous flow patterns of the near-wake of a circular cylinder (d = 10 cm) in density-stratified flows. (a) kd = 0 (homogeneous flow), U = 0.83 m/s, Re = 5800, K = 0; (b) kd = 0.402, U = 0.7 m/s, Re = 7700, K = 0.77; (c) kd = 0.513, U = 0.7 m/s, Re = 8100, K = 0.98; (d) kd = 0.521, U = 0.7 m/s, Re = 8600, K = 1.0; (e) kd = 0.570, U = 0.5 m/s, Re = 5600, K = 1.09; (f) kd = 1.45, U = 0.3 m/s, Re = 3500, K = 2.77.
kd, the development of stationary lee-waves becomes evident downstream of the circular cylinder (Figure 3(f); U = 0.3 m/s); that is, the pattern of the near-wake flow has shifted from a vortex flow pattern to an internal-wave flow pattern.
3.3. Measurement of the Strouhal Number
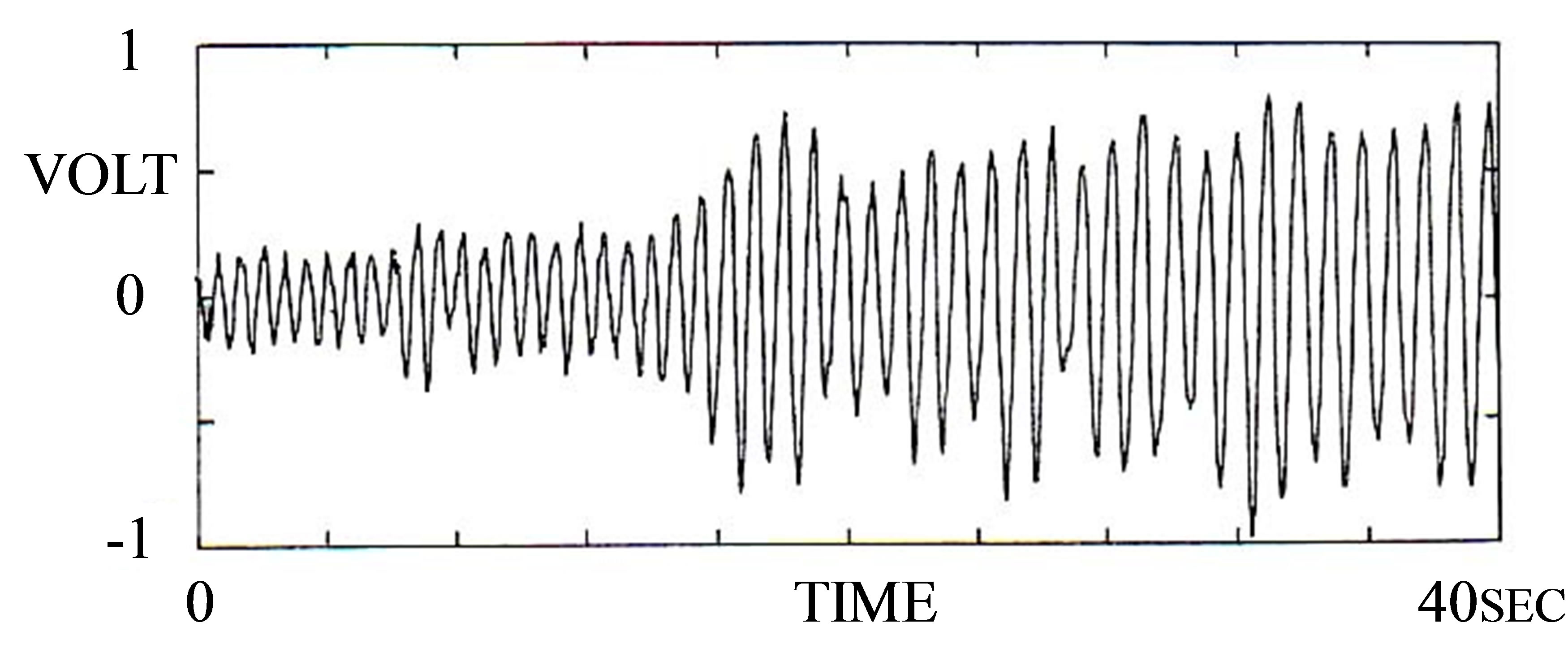
Concurrently with the flow visualization experiments, fluctuating wind velocity measurements were made at the outer edge of the wake of the circular cylinder. From the peak frequency of the wake velocity fluctuations, fv, the Strouhal number, St(=fv d/U) was evaluated for homogeneous and density-stratified flows (Figure 4). Because of the blockage effect (17%), the St value for homogeneous flow (kd = 0) is slightly higher than the typical value reported in the literature (St ≒ 0.21). With increasing kd, the value of St decreases gradually and becomes approximately 73% of that in homogeneous flow at kd = 0.513. With further increases in kd, the value of St increases steeply to a large value in response to the change in the flow pattern. This sudden change of the Strouhal number can be illustrated by the following example. A density-stratified flow with a large density stratification (large kd) was initially generated, and the density stratification was progressively reduced (smaller kd). Specifically, during an experiment with a constant wind speed, the value of kd was nudged gradually by adjusting the volume ratio of the two gasses in the gas mixture. Figure 5(a) shows the temporal change of the velocity fluctuations in the wake of a circular cylinder with d = 13 cm, and is characterized by a sudden increase of the magnitude of the velocity fluctuation. The accompanying change in the predominant frequency of the vortex shedding is shown in Figure 5(b), that is, the wake-flow pattern suddenly switches to that of low-frequency vortex shedding. The changes observed in this example are consistent with changes that would be expected in the transition between two flow regimes.
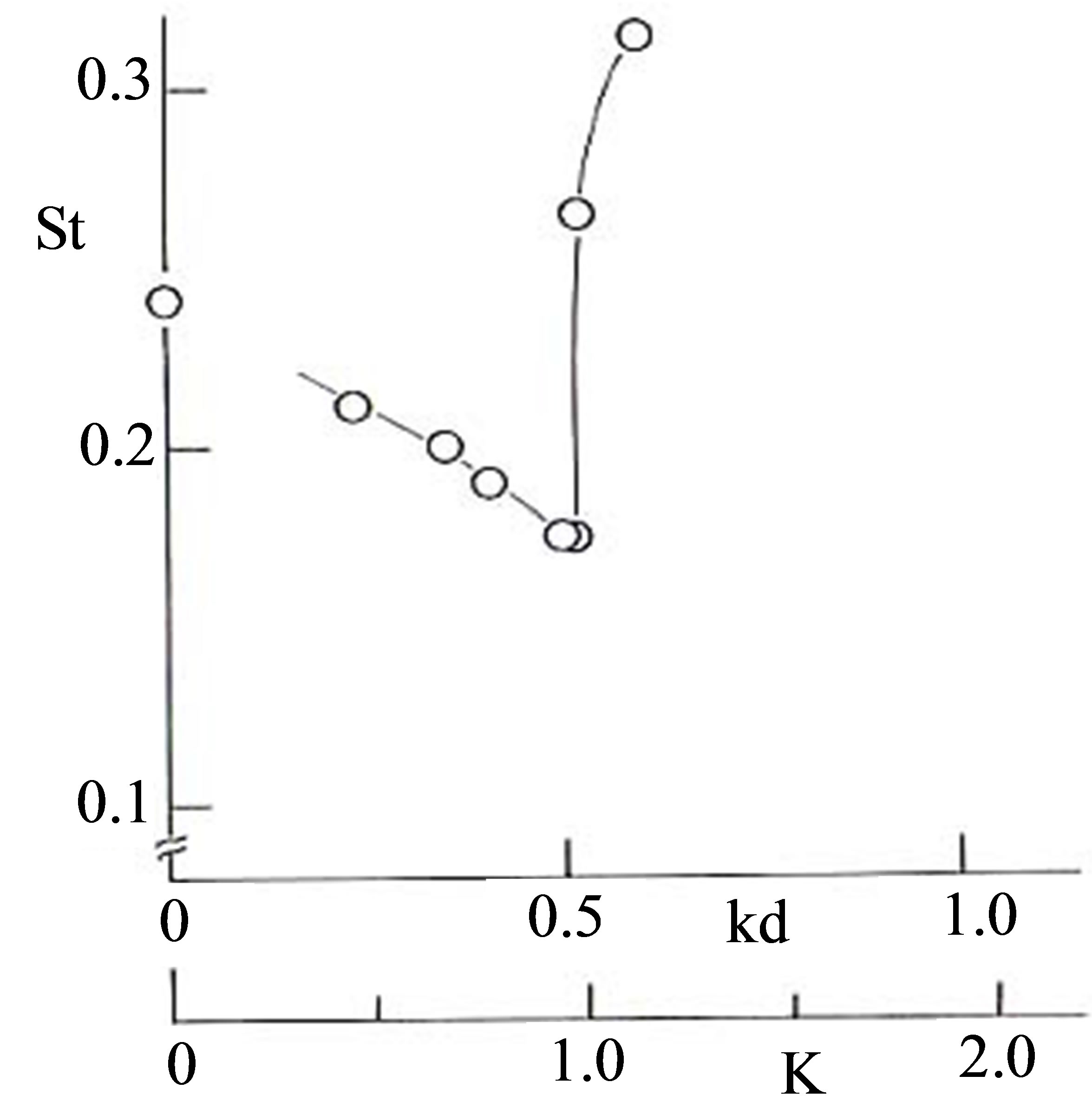
Figure 4. Relationship between the Strouhal number, St, and the stability parameters, kd and K (refer to Section 4 for the definition of K). U = 0.7 m/s, d = 10 cm (circular cylinder), Re = 5 × 103 - 9 × 103. The value of St at kd = 0 was observed in homogeneous flow (U = 0.83 m/s, Re = 5800).
 (a)
(a) 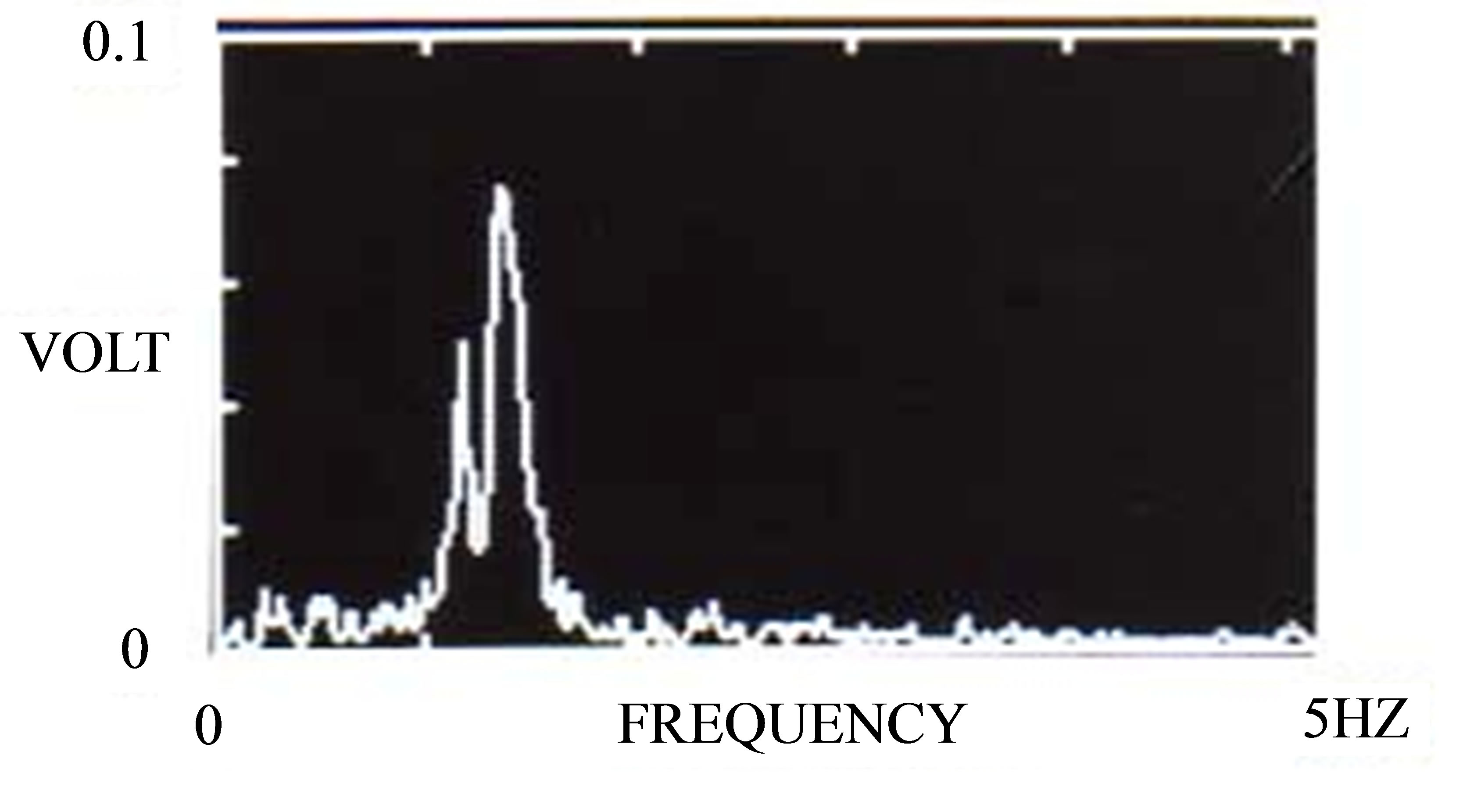 (b)
(b)
Figure 5. Sudden change in the flow around a circular cylinder at the critical stratification, (kd)cr; d = 13 cm (circular cylinder), U = 0.76 m/s, Re = 1.1 × 104, kd = 0.635, K = 0.93. (a) Temporal fluctuations of flow velocity in the wake of the cylinder as measured in voltage; (b) Power spectrum showing the shift in the predominant frequency of vortex shedding. The predominant frequency shifted from fv = 1.44 Hz (right peak) in the first part of the time series in (a) to fv = 1.04 Hz (left peak) in the second part of the time series in (a).
3.4. Summary of Experimental Results and Discussion
Figure 3 shows the transition of the wake pattern with increasing stability: (b,c)→(d,e)→(f). Initially, the nearwake pattern is characterized by highly-turbulent vortices (b and c). With increasing stratification, the turbulent near-wake becomes narrow (d and e) and finally, turbulent mixing occurs in isolated regions downstream of the cylinder (f). A similar three-regime transition of the cylinder wake pattern was observed in the salt water experiment of Boyer et al. [7]. They refer to the isolated regions of turbulent mixing similar to those in (f) as “isolated mixed regions”. In their experiment, wakes were generated behind cylinders in stably stratified water-tank flow at a Reynolds number up to 4000, which was smaller than the range of Reynolds numbers from our wind tunnel experiment (3.5 × 103 - 1.2 × 104). Because only limited experimental results are reported in Boyer et al. for the range of Reynolds number between 2000 and 4000, the wake flow transition is not clear in this range. However, the results from Boyer et al. and our experiment suggest that the transition of the cylinder wake pattern occurs in stratified flows with increasing stratification with high Reynolds numbers above approximately 400.
A further examination of the changes in the wake pattern in the present experiment (Section 3.3) reveals two flow regimes. First, with increasing kd (increasing stability) up to a critical value, the vortex formation behind the circular cylinder is enhanced and the Strouhal number, St, decreases gradually. The corresponding critical value of kd will be referred to as (kd)cr hereafter. Second, the strength of vortex formation behind the circular cylinder reaches its maximum at kd ≒ (kd)cr. With further increases in kd, vortex formation is sharply suppressed, and vortex formation becomes weak. Furthermore, this transition is accompanied by a sharp increase in St. The rapid change in the flow pattern at kd ≒ (kd)cr will be referred as the critical phenomenon below. In the following sections, the generation mechanisms of the phenomena in these two flow regimes will be discussed. In the present experimental set-up, stably stratified flows were produced in the flow channel bounded by solid horizontal top and bottom walls. Thus, characteristics of stratified flows of finite depth are first summarized in the following section.
4. Internal Gravity Waves in Stratified Flows of Finite Depth
In this section, stratified flow of finite depth, H, is considered in a flow channel bounded by solid horizontal top and bottom walls. No wave energy penetration is allowed into the walls, and nonviscous flow with no density dispersion is assumed. For this flow, two non-dimensional numbers are relevant: kd (=Nd/U) (or its inverse, the Froude number, Fd(=U/Nd) and K(=NH/πU) (or the blockage ratio, d/H). kd is defined with the characteristic length of an object while Fd is defined in terms of the finite depth, H. According to linear theory, discrete vertical modes exist for the internal gravity wave that arises in stratified flow of finite depth, and the vertical modes depend on the strength of the density stratification [8,17]. The dispersion relation for the nth vertical mode (wavelength in the vertical direction = 2 H/n) can be expressed as:
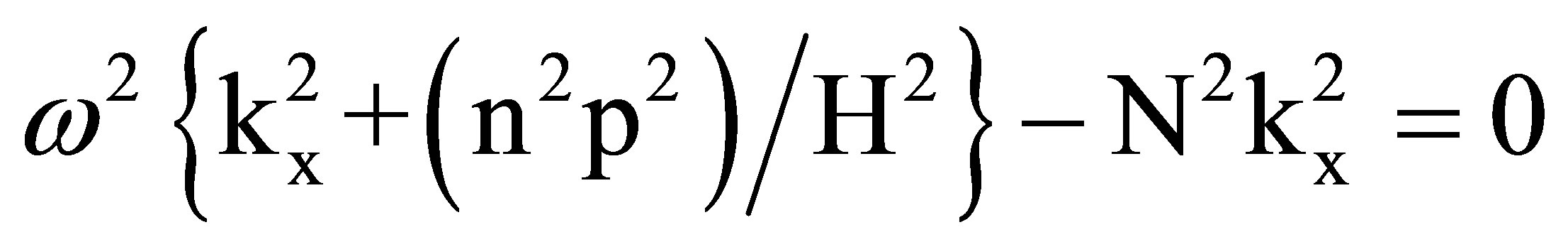 (1)
(1)
where ω is the angular frequency and kx is the wavenumber in the x-direction. The phase velocity, Cp, and group velocity, Cg, of the internal gravity wave can be expressed as:
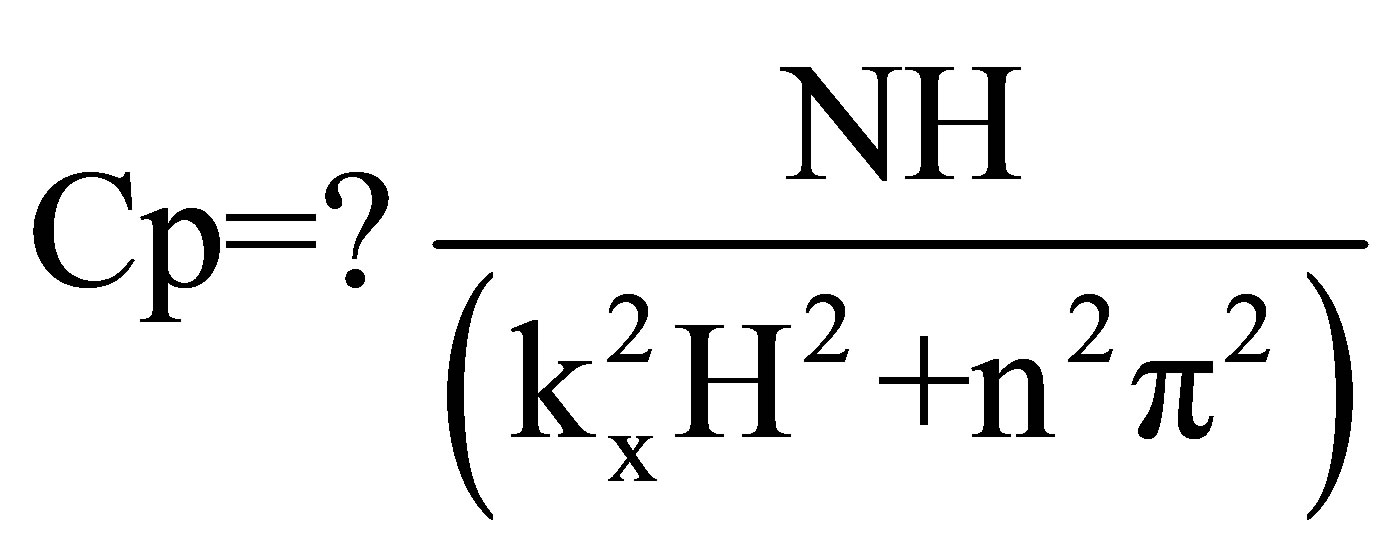 (2)
(2)
and
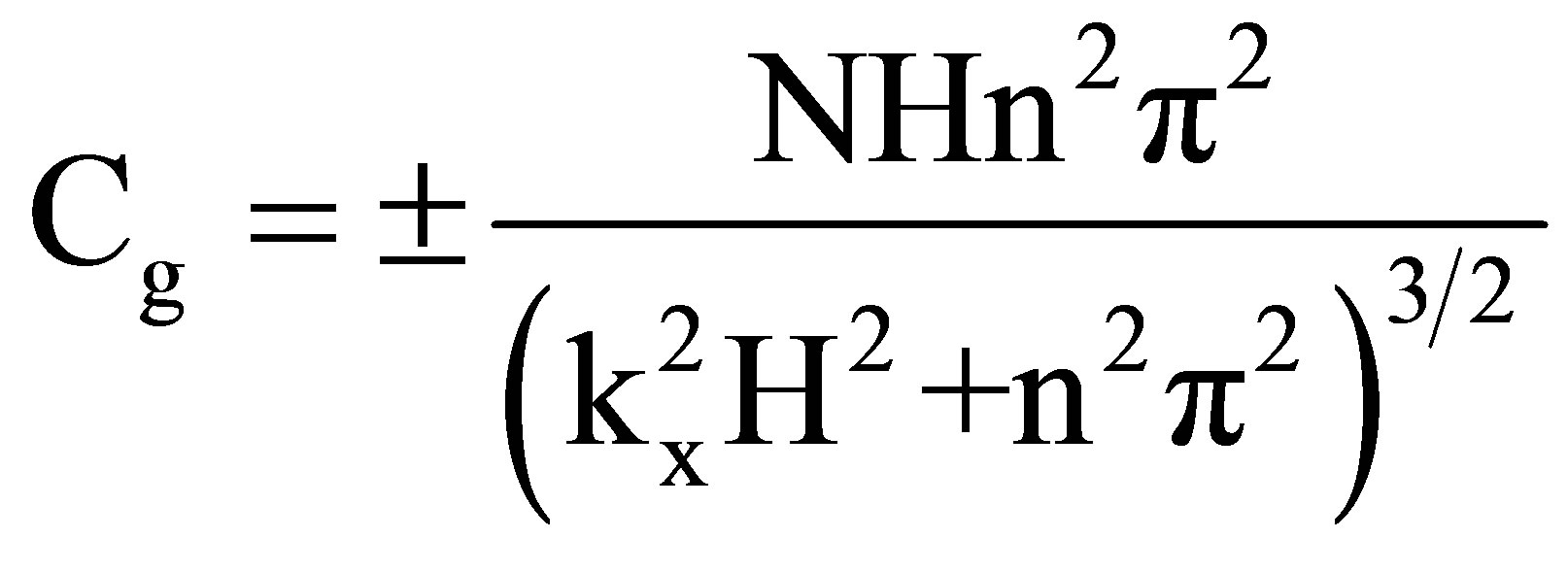 (3)
(3)
respectively.
For kx → 0, the values of Cp and Cg attain their maxima and Cn = Cp = Cg = ±NH/nπ where Cn is the phase velocity of the nth mode. For flow with approach velocity, U and Cn > U, that is, in terms of K and kd:
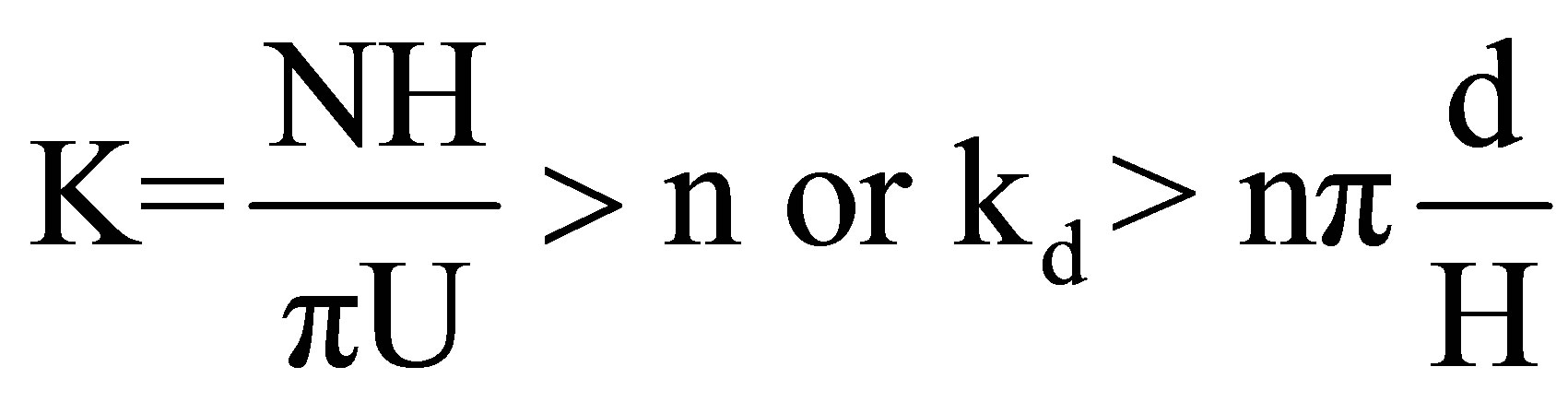 (4)
(4)
a columnar disturbance at the nth mode propagates upstream of the object at
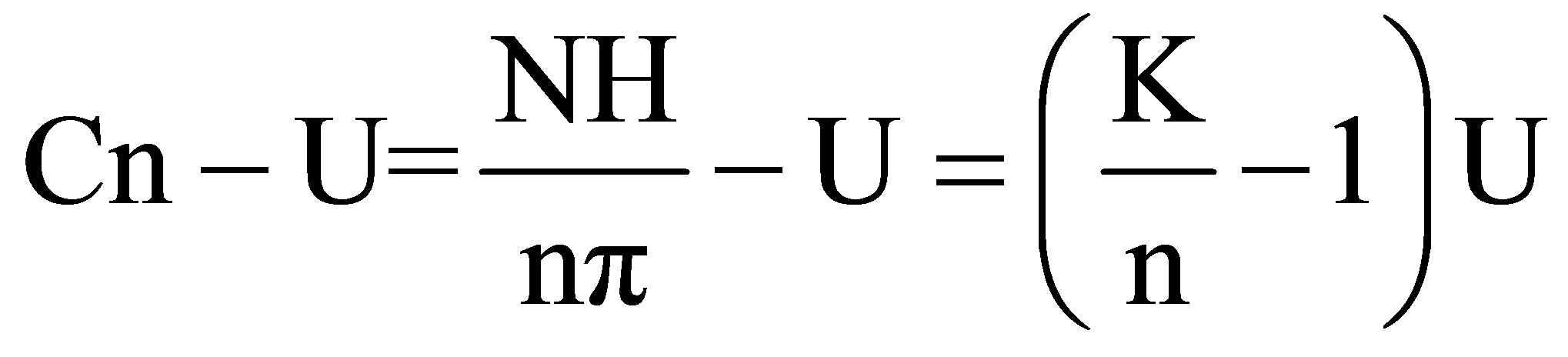 (5)
(5)
For kx ≠ 0, stationary waves develop only when U = Cp. Because Equations (2) and (3) yield Cp/Cg > 1, the group velocity, Cg, of the stationary wave that develops at U = Cp is characterized by Cg < U and the stationary wave can be present only downstream of the obstacle. The relationship U = Cp leads to,
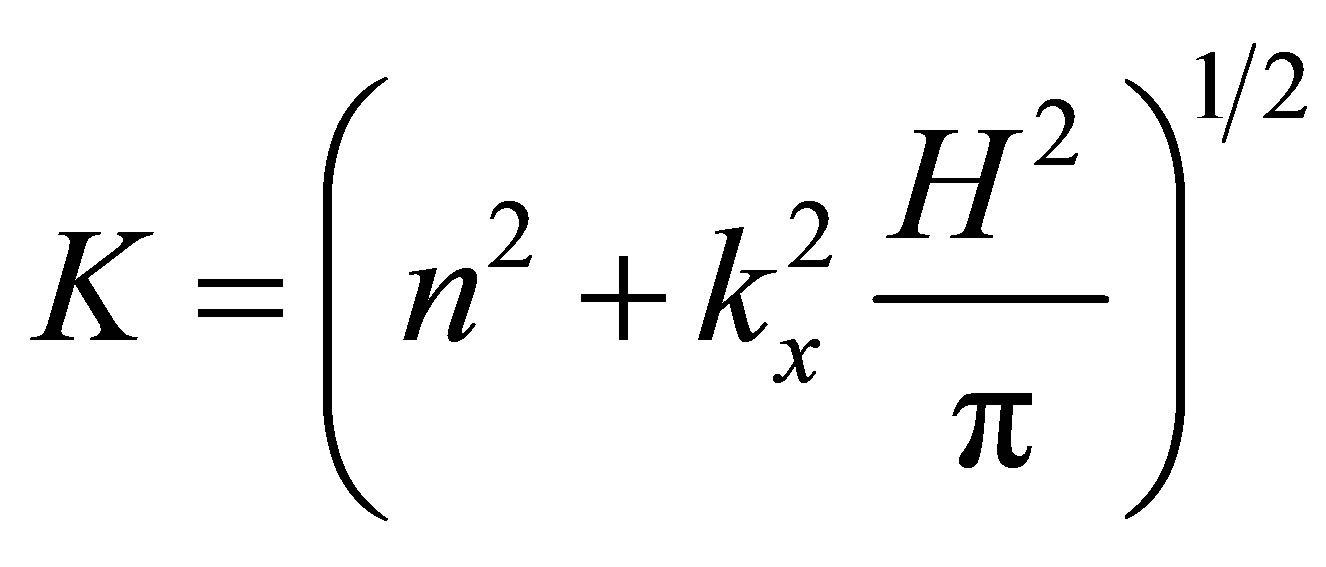 (6)
(6)
A comparison of Equations (4) and (6) suggests that columnar disturbances can develop whenever stationary lee waves are present. Furthermore, Equation (6) implies that both stationary lee waves and columnar disturbances develop with kx → 0, i.e. K ≒ n, therefore, starting at K ≒ 1. The wavelength of the stationary lee waves, λ, can be expressed with K as
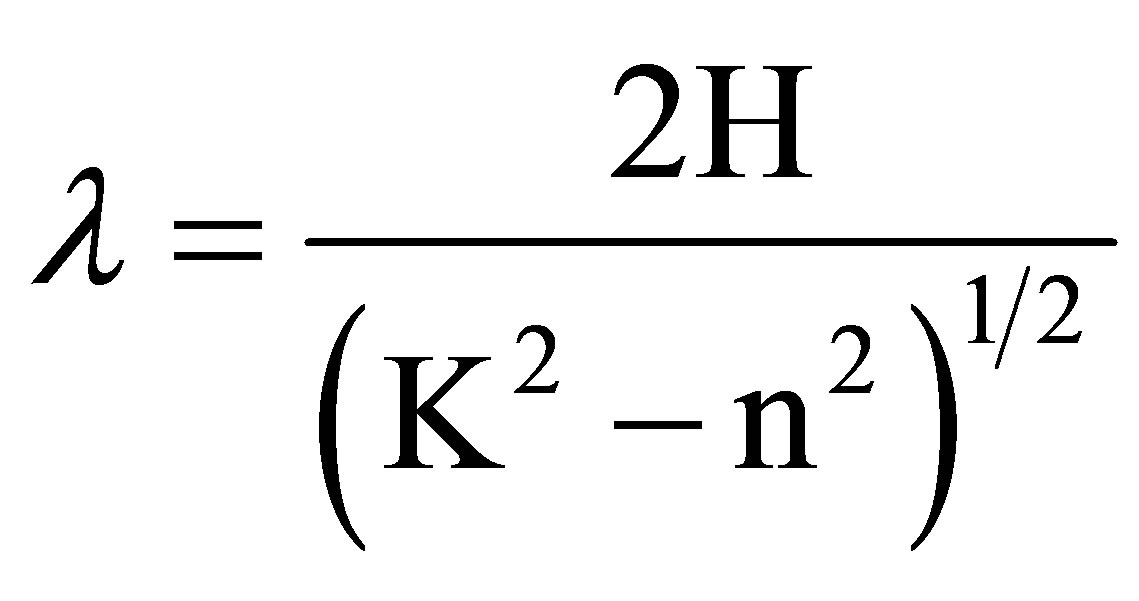 (7)
(7)
5. Abrupt Change in the Flow Pattern (Critical Phenomenon)
5.1. Critical Phenomenon around a Non-Circular Cylindrical Object
To investigate if the critical phenomenon at the critical stratification, kd ≒ (kd)cr, is unique to flow around a circular cylinder, additional experiments were performed with two rectangular cylinders (Section 2.3). The long side of the rectangular cross-section of both cylinders (d = 10 cm) was facing the on-coming flow, and this length was identical to the diameter of the circular cylinder (d = 10 cm) for which the near wake flow was investigated in Section 3. As with the experiment with the circular cylinder, the flow around the square cylinders was investigated for various degrees of stratification, kd, and flow visualization experiments were conducted. In addition, the fluctuating velocity in the near-wake was measured to evaluate the peak frequency, fv. As in the flow around the circular cylinder of d = 10 cm (Figure 4), a sudden change in the flow pattern and a sharp increase in the value of St are observed in the proximity of kd = 0.52 or K = 1 (Figures 6 and 7). When kd exceeds (kd)cr, the pattern of the near-wake flow behind the rectangular cylinder changes and vortex formation is suddenly suppressed (change from Figures 6(a) to (b)). The present investigation suggests that the critical phenomenon in the proximity of (kd)cr is not unique to the near-wake flow behind a circular cylinder. The critical phenomenon occurs at a similar value of (kd)cr behind a rectangular cylinder that has the same vertical dimension as the circular cylinder.
5.2. Cases with Circular Cylinders of Various Diameters, d, and Test Sections with Various Heights
The critical stratification, (kd)cr, for near-wake flows is investigated behind circular cylinders of three additional diameters, d = 5, 7.5, 13 cm, in the test section of height H = 60 cm. The results are summarized together with those from the experiment with the two rectangular cylinders (Section 5.1) in Figure 8. For an object with a certain diameter d (or a height d facing the on-coming flow), the critical phenomenon occurs at a similar value of kd, independent of the Reynolds number. Furthermore, the emergence of the critical phenomenon coincides with the lower limit of kd at which stationary lee waves are predicted to occur by the linear theory (Figure 9).
 (a)
(a) (b)
(b)  (c)
(c)
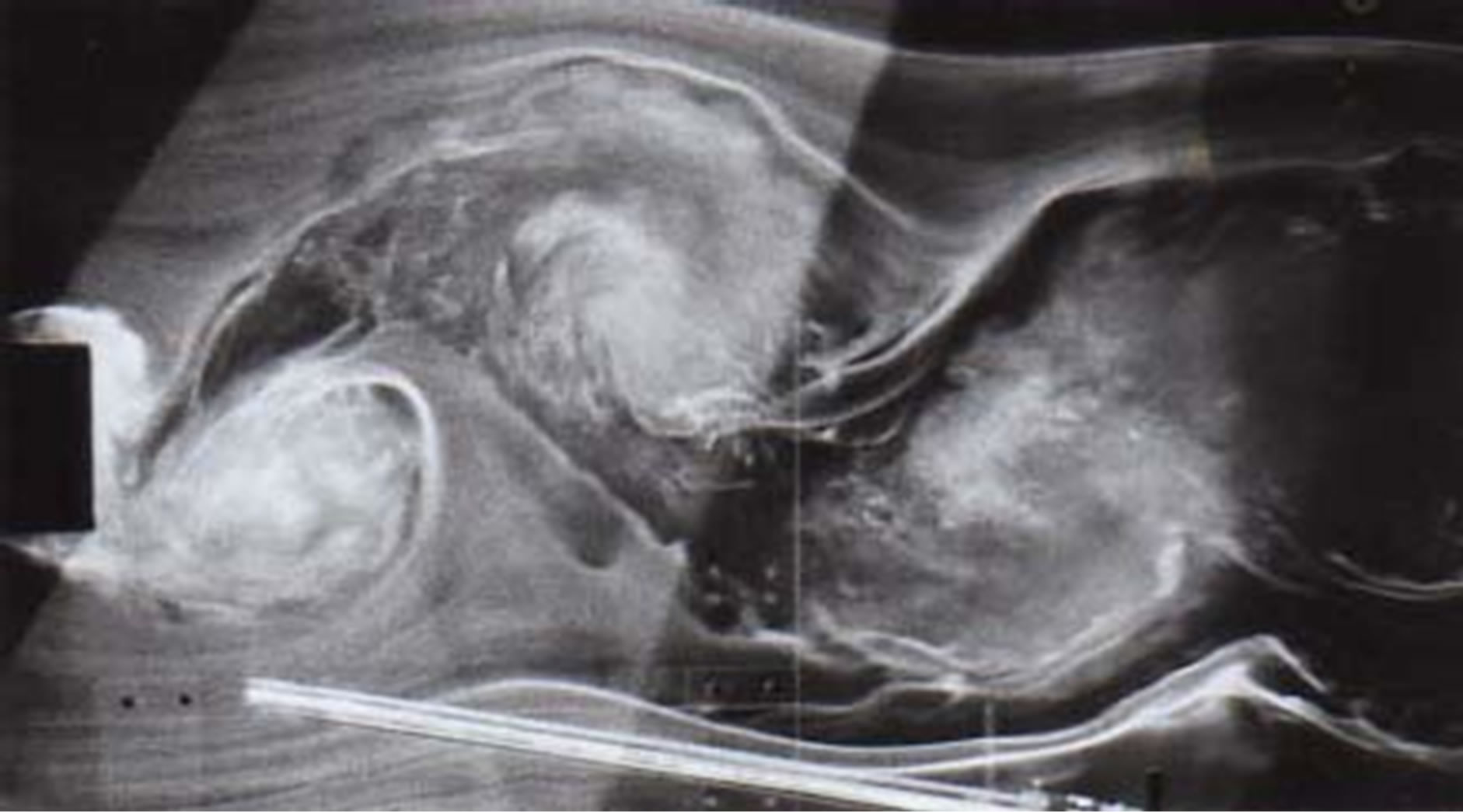
Figure 6. Instantaneous flow patterns around a rectangular cylinder of size b/d = 0.6 (ratio of short side to long side; long side was deployed vertically). D = 10 cm. (a) kd = 0.488, U = 0.7 m/s, Re = 8400, K = 0.93; (b) kd = 0.568, U = 0.7 m/s, Re = 8400, K = 1.08; (c) kd = 0.860, U = 0.5 m/s, Re = 5900, K = 1.64.
To further investigate the dependency of (kd)cr on d/H (or K), the height of the text section, H, was modified to H = 46.3 cm, and near-wakes behind a circular cylinder of d = 7.5 cm (d/H = 0.162) were studied. The value of (kd)cr observed for this case is approximately 0.52, which falls on the predicted lower limit for the occurrence of stationary lee waves (Figure 9). The present result suggests 1) the value of (kd)cr depends on d/H and not on the value of H itself, and 2) a close link exists between the critical phenomenon for near-wakes of horizontal objects in stratified flows and the occurrence of stationary lee waves.

Figure 7. Relationship between the Strouhal number, St, and the stability parameters, kd and K. d = 10 cm (d: side of the rectangular cylinder perpendicular to the streamwise direction). ○: b/d = 0.1, △: b/d = 0.6, Re = 6× 103 - 104.
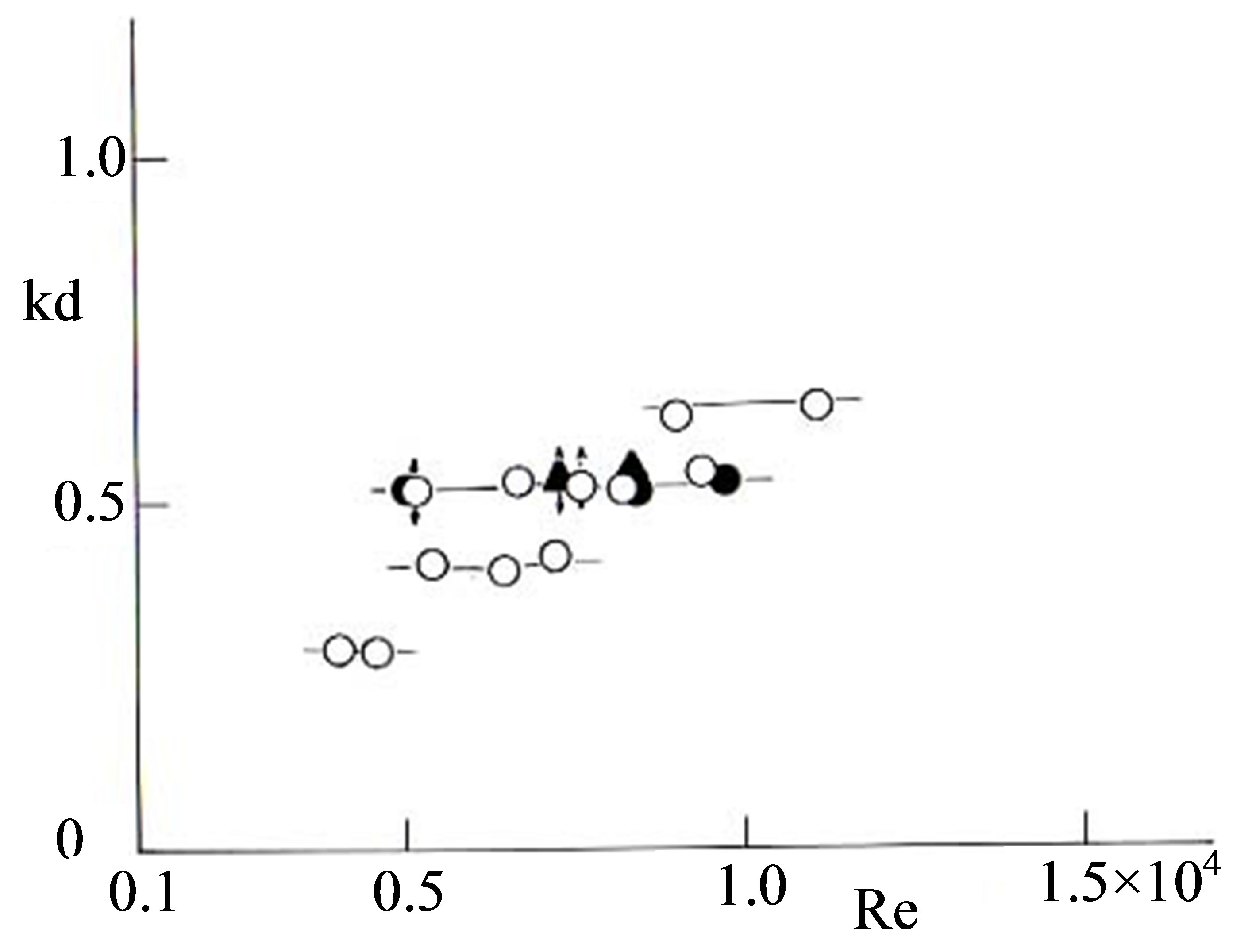
Figure 8. Relationship between the critical stratification, (kd)cr, and the Reynolds number, Re, for near-wake flows behind circular cylinders of 4 different diameters (○: from top to bottom, d = 13, 10, 7.5, 5 cm) and two rectangular cylinders (˜: b/d = 0.1, d = 10 cm; p: b/d = 0.6, d = 10 cm). The Reynolds number variations are due to variations in the wind speed, U, in the range of 0.5 - 0.8 m/s.
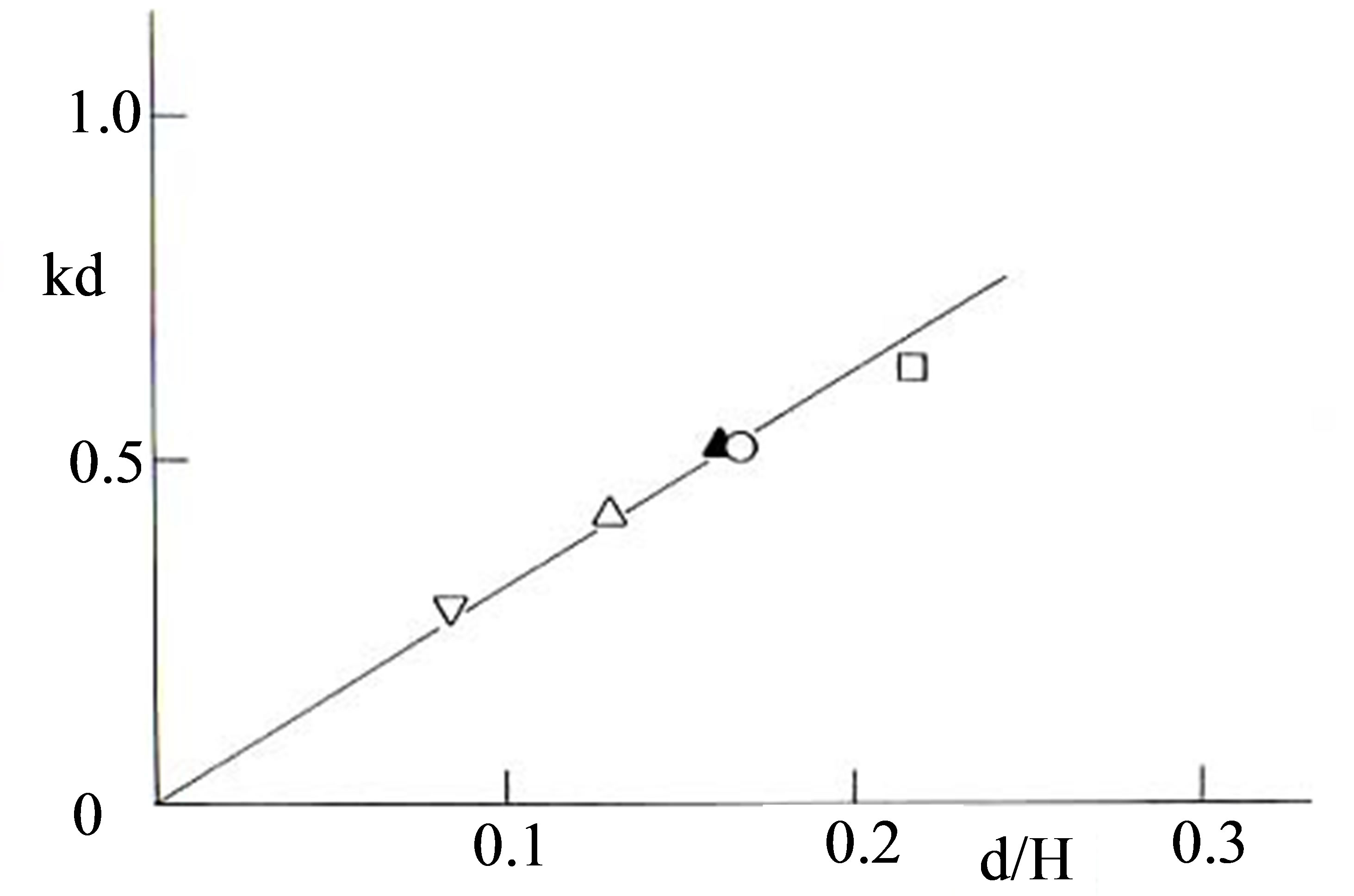
Figure 9. Relationship between the critical stratification, (kd)cr, and the blockage ratio, d/H for circular cylinders of 4 different diameters: s: d = 5 cm, r, p: d = 7.5 cm, ™: d = 10 cm, £: d = 13 cm, H = 60 cm except for p (H = 46.3 cm). The straight line, i.e. kd = π(d/H), indicates the lower limit of kd at which first-order mode stationary lee waves can develop (development of stationary lee waves is possible at kd > π(d/H) or K > 1). The predictive relationship, kd = π(d/H), is based on the linear theory (n = 1 in Equation (4)).
5.3. Development of Stationary Lee Waves and Critical Phenomenon
As elucidated in Section 4, the linear theory predicts that stationary lee waves develop when the non-dimensional parameter K exceeds 1. K is defined in terms of the finite depth of the stratified flow, H. The wavelength of the lee wave at K = 2.77 (kd = 1.45) in Figure 3(f), when normalized by H, becomes λ*(=λ/H) ≒ 0.87. This value coincides roughly with λ* = 0.78 as predicted by the linear theory for the first-order mode stationary lee wave. At a large value of K as in this case, the presence of stationary lee waves becomes evident, and the wavelength of the lee wave can be approximated by the linear theory. At K = 1.64, an undulating lee wave with a long wavelength is observed across the entire near-wake behind the rectangular cylinder with dimensions b/d = 0.6 (Figure 6(c)). At K = 1.09, a lee wave is present in the upper portion of the near-wake behind the circular cylinder (Figure 3(e)). However, with the value of K approaching 1, the wavelength of the lee wave deviates away from that predicted by the linear theory (Figure 10). In the proximity of K = 1, the lee waves are not easily distinguishable (Figure 3(d)). For this case, the wavelength of the lee wave is estimated to be λ* ≒ 1.83 from the wave undulation in the upper portion of the near-wake behind the circular cylinder.
The wavelength of lee waves observed in the present study deviated significantly from the predicted values at low values of K. However, a stationary lee wave initially developed in the proximity of K = 1 as predicted by the linear theory. When the stationary lee wave is present, vertical motions of fluid particles are highly suppressed downstream of the object creating the lee wave. Hence,
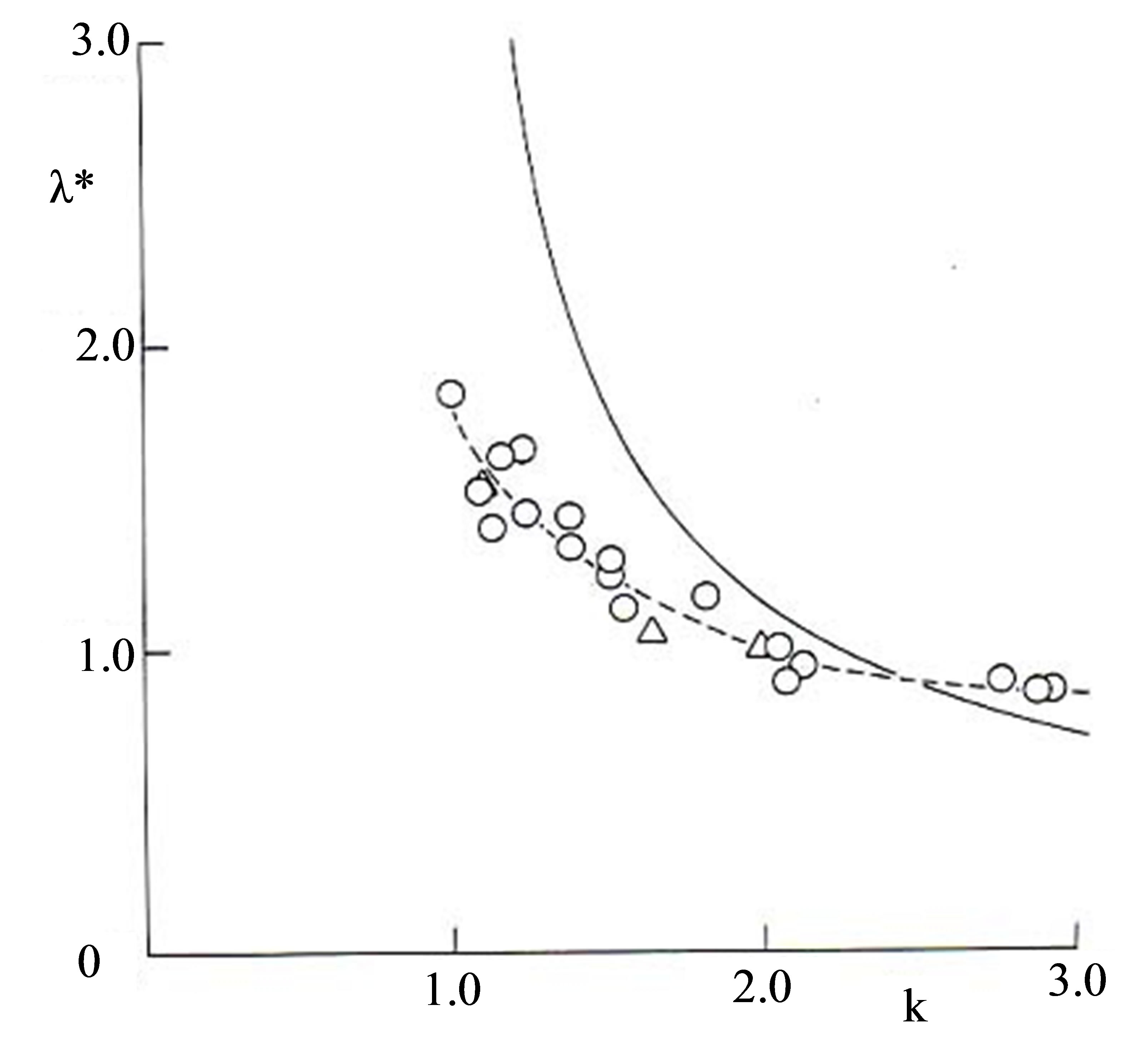
Figure 10. Relationship between the wavelength of lee waves, λ*(=λ/H), and the stratification parameter K. The solid line indicates the relationship based on the linear theory (λ* = 2/(K2 − 1)1/2). ™: circular cylinders, r: rectangular cylinders.
vertical motions are highly suppressed in the vortex formation region behind the object, thus large and strong vortices cannot roll up and widen the wake. Therefore, in the proximity of K = 1, the wake pattern changes sharply to that characterized by weak vortex formation concurrent with the development of stationary lee waves.
6. Intensification of Vortex Formation
6.1. Non-Circular Cylindrical Bluff Bodies
As discussed in Section 3, the vortex formation behind a circular cylinder is intensified with increasing stratification between kd = 0 (homogeneous flow) and (kd)cr. The intensification of vortex formation with increasing stability was also examined for the near-wake flows of noncircular cylindrical bluff bodies. Generally, the Strouhal number, St, is small for the wake behind a bluff body that is conducive to vigorous vortex formation. Therefore, the value of St is negatively correlated to the formation of strong vortices. The decreasing trends of St between kd = 0 and (kd)cr for the wakes behind the rectangular cylinders of b/d = 0.1, 0.6 (Figure 7) are smaller than those for the wakes behind the circular cylinders (Figure 4). In particular, the corresponding slope for the wake behind the rectangular cylinder of b/d = 0.6 is small. The flow visualization experiments also confirmed that enhancement of vortex formation behind the rectangular cylinder of b/d = 0.6 was not as evident as that behind the circular cylinders.
6.2. Spanwise Correlation of Fluctuating u-Velocities in Near-Wake Flows
Behaviors of the spanwise correlation of the fluctuating u-velocities were investigated in the near-wakes of circular (d = 5, 10 cm) and rectangular (b/d = 0.6) cylinders. The investigations were made in homogeneous flow and stratified flow at kd slightly less than (kd)cr. For the near-wakes behind the circular cylinders, the correlation of the fluctuating u-velocities is significantly higher in stratified flow at kd ≒ (kd)cr than that in homogeneous flow (Figure 11). In contrast, with kd approaching (kd)cr, the correlation for the wake of the rectangular cylinder is nearly the same as that for homogenous flow. This result is attributable to the highly two-dimensional nature of the near-wake flow around the rectangular cylinder as will be discussed in the next subsection.
6.3. Dependency of Vortex Formation Enhancement on the Shape of the Bluff Body
As discussed earlier, enhancement of vortex formation with increasing kd from kd = 0 to kd = (kd)cr is prominent particularly in the near-wake of a circular cylinder. Recent studies on the three-dimensional structure of the
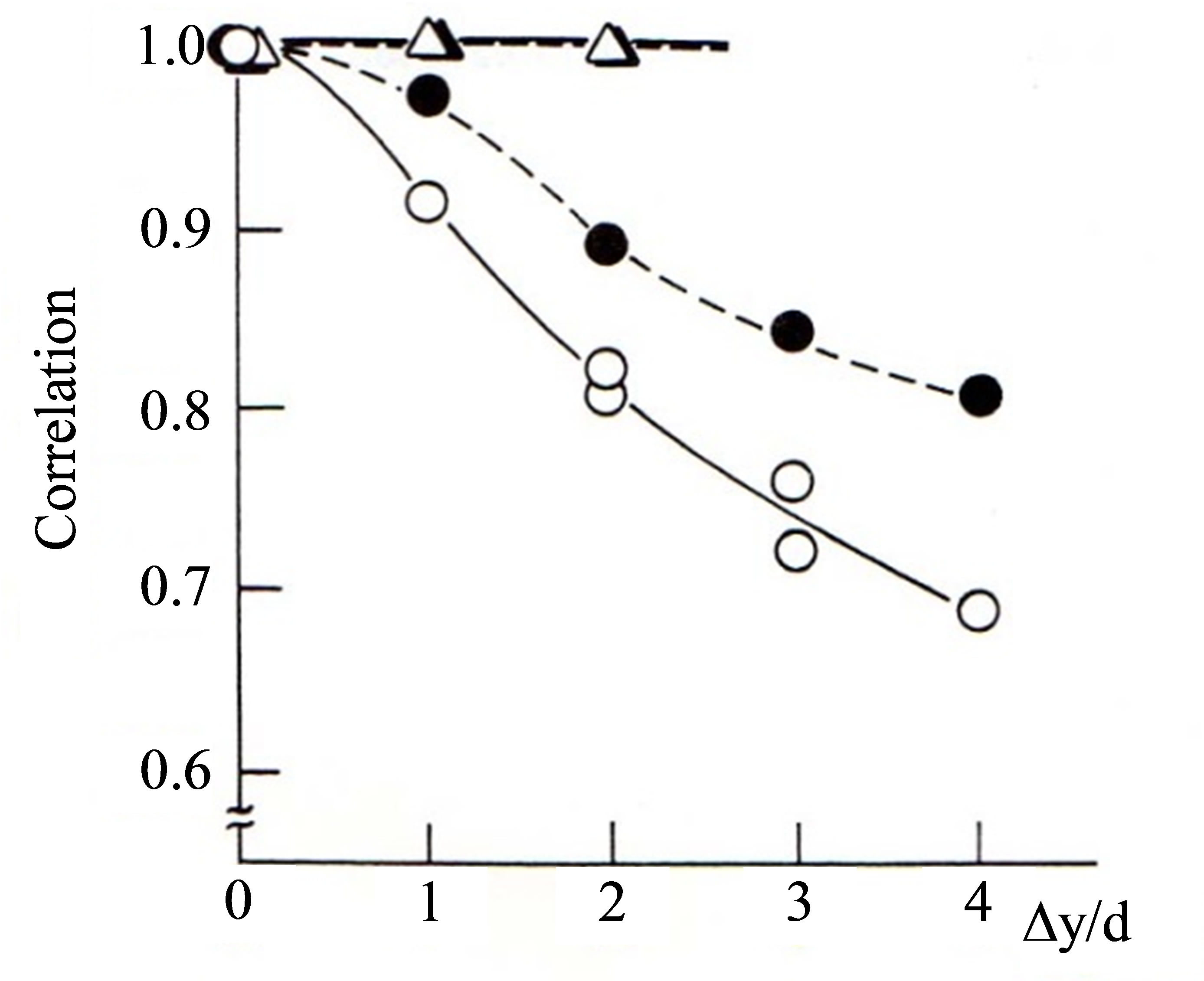
Figure 11. Relationship between the spanwise correlation of the fluctuating velocity, u, and the normalized spanwise separation distance, Δy/d. ™: circular cylinder (d = 5 cm) in homogeneous flow, ˜: circular cylinder (d = 5 cm) in stratified flow of kd = 0.27 (≒ (kd)cr), r: rectangular cylinder (b/d = 0.6, d = 10 cm) in homogeneous flow, p: rectangular cylinder (b/d = 0.6, d = 10 cm) in stratified flow of kd = 0.49 (≒(kd)cr).
near-wake flow behind circular cylinders (e.g., Yokoi and Kamemoto [18]) have revealed that the boundary layer separation from a circular cylinder is a three-dimensional phenomenon and that the separated shear layer rolls up in a non-two-dimensional manner. However, it is speculated that stable stratification suppresses the vertical velocity disturbance in the wake of a circular cylinder and causes the roll-up of the separated sheer layer to be more two-dimensional than it would be in homogeneous flow. Consistent with this speculation, Figure 11 shows that the value of spanwise u-velocity correlation in the wake of a circular cylinder increases due to the effect of stable stratification. The increasing two-dimensionality of the near-wake flow likely enhances vortex formation similar to the enhancement observed in the near-wake flows of a vibrating circular cylinder and a circular cylinder in a periodically fluctuating flow. The increased spanwise alignment is likely the cause of the enhanced vortex formation in a two-dimensional flow. In contrast to a circular cylinder, the geometry of a rectangular cylinder naturally forces the separation of the shear layer to be aligned in the span-wise direction resulting in a wake flow that is highly two-dimensional. As a result, the effect of stratification on the strength of vortex formation is small in the near-wake of a rectangular cylinder.
7. Conclusions
Near wakes behind horizontal circular and square cylinders were investigated in linearly density-stratified flows of varying stabilities. Experiments were performed with a nearly uniform approach velocity at relatively high Reynolds numbers, Re = 3.5 × 103 - 1.2 × 104. Flow visualization experiments and measurements of the velocity fluctuation frequencies in the near-wake led to the following conclusions:
1) With increasing values of kd(=Nd/U), i.e., increasing stratification, vortex formation and shedding behind a circular cylinder are gradually enhanced with respect to those in homogeneous flow, and the Strouhal number decreases. These observations can likely be explained by the effect of increasing stratification which enhances the two-dimensionality of the near wake flow behind a circular cylinder. The enhanced two-dimensionality of the flow strengthens the roll-up of the separated shear layer.
2) The strength of vortex formation and shedding reaches its maximum at kd ≒ (kd)cr, and is suddenly suppressed when kd exceeds (kd)cr. This critical phenomenon is accompanied by a sudden change in the flow pattern, that is, only weak vortex formation occurs downstream of the obstacle and the Strouhal number increases sharply. In terms of the stratification parameter K(=NH/πU) which includes the depth of stratified flow, H, the critical phenomenon occurs close to K = 1 for all sizes of circular and rectangular cylinders investigated. The linear theory predicts that lee waves will develop for K > 1. Thus, in this critical phenomenon, the emergence of a stationary lee wave suppresses the vertical fluid motions of the vortices formed behind an object and causes a sudden change in the flow pattern.
3) With further increase of kd, the wake flow pattern transitions to one dominated by internal waves.
8. Acknowledgements
The author wishes to acknowledge Kenichiro Sugitani for his extensive assistance with the present experiments.
REFERENCES
- W. Blumen, “Atmospheric Processes over Complex Terrain (Meteorological Monographs),” American Meteor Society, Vol. 23, No. 45, 1990, pp. 1-323.
- W. H. Snyder, “Fluid Modeling of Pollutant Transport and Diffusion in Stably Stratified Flows over Complex Terrain,” Annual Review of Fluid Mechanics, Vol. 17, 1985, pp. 239-266.
- H. Honji, “Stratified Flow Experiments,” Nagare, Vol. 6, 1987, pp. 276-284.
- H. Honji, “Vortex Street in the Stratified Fluids,” Reports of Research Institute for Applied Mechanics, No. 60, 1984, pp. 393-401.
- H. Honji, “Vortex Motions in the Stratified Wake Flows,” Fluid Dynamics Research, Vol. 3, No. 1-4, 1988, pp. 425-430. http://dx.doi.org/10.1016/0169-5983(88)90104-9
- J. T. Lin and Y. H. Pao, “Wakes in Stratified Fluids,” Annual Review of Fluid Mechanics, Vol. 11, 1979, pp. 317-338. http://dx.doi.org/10.1146/annurev.fl.11.010179.001533
- D. L. Boyer, P. A. Davies, H. J. S. Fernando and X. Zhang, “Linearly Stratified Flow Past a Horizontal Circular Cylinder,” Philosophical Transactions of the Royal Society of London. Series A, Vol. 328, 1989, pp. 501-528. http://dx.doi.org/10.1098/rsta.1989.0049
- S. N. Wei, T. W. Kao and H. P. Pao, “Experimental Study of Upstream Influence in the Two-Dimensional Flow of a Stratified Fluid over an Obstacle,” Geophysical fluid Dynamics, Vol. 6, No. 4, 1975, pp. 315-336. http://dx.doi.org/10.1080/03091927509365802
- H. Hanazaki, “Upstream and Advancing Columnar Disturbances in Two-Dimensional Stratified Flow of Finite Depth,” Physics of Fluids A, Vol. 1, No. 12, 1989, pp. 1976-1987.
- R. R. Hwang and S. H. Lin, “On Laminar Wakes behind a Circular Cylinder in Stratified Fluids,” Transactions of the ASME, Journal of Fluids Engineering, Vol. 114, No. 1, 1992, pp. 20-28. http://dx.doi.org/10.1115/1.2909993
- N. Boulanger, P. Meunier and S. Le Dizes, “Structure of a Stratified Tilted Vortex,” Journal of Fluid Mechanics, Vol. 583, 2007, pp. 443-458. http://dx.doi.org/10.1017/S0022112007006416
- N. Boulanger, P. Meunier and S. Le Dizes, “Tilt-Induced Instability of a Stratified Vortex,” Journal of Fluid Mechanics, Vol. 596, 2008, pp. 1-20. http://dx.doi.org/10.1017/S0022112007009263
- P. Meunier, “Stratified Wake of a Tilted Cylinder. Part 1. Suppression of a von Karman Vortex Street,” Journal of Fluid Mechanics, Vol. 699, 2012, pp. 174-197. http://dx.doi.org/10.1017/jfm.2012.92
- P. Meunier, “Stratified Wake of a Tilted Cylinder. Part 2. Lee Internal Waves,” Journal of Fluid Mechanics, Vol. 699, 2012, pp. 198-215. http://dx.doi.org/10.1017/jfm.2012.123
- Y. Ohya and Y. Nakamura, “Near Wakes of a Circular Cylinder in Stratified Flows,” Physics of Fluids A, Vol. 2-4, No. 4, 1990, pp. 481-483.
- Y. Ohya, S. Ozono and Y. Nakamura, “A Wind Tunnel for Studying Density-Stratified Flows,” Atmospheric Environment, Vol. 28, No. 11, 1994, pp. 1895-1900. http://dx.doi.org/10.1016/1352-2310(94)90329-8
- M. Funakoshi and M. Oikawa, “Non-Linear Waves in Stratified Flow,” Nagare, Vol. 8, 1989, pp. 311-335.
- Y. Yokoi and K. Kamemoto, “Initial Stage of a ThreeDimensional Vortex Structure Existing in a Two-Dimensional Boundary Layer Separation Flow: Observation of Laminar Boundary Layer Separation over a Circular Cylinder by Flow Visualization,” JSME International Journal. Ser. 2, Fluids Engineering, Heat Transfer, Power, Combustion, Thermophysical Properties, Vol. 35-II, No. 2, 1992, pp. 189-195.

