Open Journal of Fluid Dynamics
Vol.3 No.3(2013), Article ID:37055,10 pages DOI:10.4236/ojfd.2013.33028
MHD Mass Transfer Flow past a Vertical Porous Plate Embedded in a Porous Medium in a Slip Flow Regime with Thermal Radiation and Chemical Reaction
Department of Mathematics, Gauhati University, Guwahati, India
Email: saheel_nazib@yahoo.com, kishoredas969@yahoo.in
Copyright © 2013 Nazibuddin Ahmed, Kishor Kumar Das. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 25, 2013; revised August 23, 2013; accepted September 7, 2013
Keywords: Porous Medium; Slip Flow; Rarefaction; Viscous Drag; Free Convection
ABSTRACT
This problem presents the effects of thermal radiation and chemical reaction on MHD unsteady mass transfer flow past a semi-infinite vertical porous plate embedded in a porous medium in a slip flow regime with variable suction. A magnetic field of uniform strength is assumed to be applied transversely to the direction of the main flow. Perturbation technique is applied to transform the non-linear coupled governing partial differential equations in dimensionless form into a system of ordinary differential equations. The resulting equations are solved analytically and the solutions for the velocity, temperature and concentration fields are obtained. The effects of various flow parameters on velocity, temperature and concentration fields are presented graphically. For different values of the flow parameters involved in the problem, the numerical calculations for the Nusselt number, Sherwood number and skin-friction co-efficient at the plate are performed in tabulated form. It is seen that chemical reaction causes the velocity field and concentration field to decrease and the chemical reaction decreases the rate of viscous drag at the plate.
1. Introduction
In recent years, free convective flow and heat transfer problems in the presence of magnetic field through a porous medium have attracted the attention of a number of scholars because of their possible application in many branches of science and technology such as fiber and granular insulation, geothermal system, etc. In engineering science, it finds its application in MHD pumps, MHD bearing, MHD power generators, etc. The phenomena of heat and mass transfer are also very common in theory of stellar structure and observable effects are detectable on the solar structure.
Analytical solutions of the problem of convective flows, which arise in the fluids due to interaction of the force of gravity and density differences caused by simultaneous diffusion of thermal energy and chemical species, have been presented by many authors due to application of such problems in Geophysics and Engineering. Some of them are Bejan and Khair [1], Trevisan and Bejan [2], Acharya et al. [3], Rapits and Kafousias [4], and Das et al. [5]. The study through porous medium has got its importance because of its occurrence in movement of water. Investigations of such problems also have importance in purification process, petroleum technology and in the field of agricultural engineering. Study of flow problems through porous medium is heavily based on Darcy’s experimental law [6]. Wooding [7] and Brinkman [8,9] have modified Darcy’s law, which are used by many authors on study of convective flow in porous media. Recently Chaudhary and Jain [10] have studied the combined heat and mass transfer effects on MHD free convective flow through porous medium.
The study of the effect of chemical reaction on heat and mass transfer in a flow is of great practical importance to the engineers and scientists because of its universal occurrence of many branches of science and technology. In processes such as drying, distribution of temperature and moisture over agricultural fields, energy transfer in a wet cooling tower and flow in a cooler heat and mass transfer occur simultaneously. Possible applications of this type of flow can be found in many Industries. Many investigations have studied the effect of chemical reaction in different convective heat and mass transfer flows. Chambre and Young [11] have presented a first order chemical reaction in the neighbourhood of horizontal plate. Muthucumaraswamy [12] has presented heat and mass transfer effects on a continuously moving isothermal vertical surface with uniform suction by taking in to account the homogeneous chemical reaction of first order. Muthucumaraswamy and Meenakshisundaram [13] investigated theoretical study of chemical reaction effects on vertical oscillating plate with variable temperature and mass diffusion.
Radiation is a process of heat transfer through electromagnetic waves. Radiative convective flows are encountered in countless industrial and environmental process. For example, heating and cooling chambers, fossil fuel combustion energy processes, evaporation from large open water reservoirs, astrophysical flows etc. Radiative heat and mass transfer play an important role in space related technology. The effect of radiation on various convective flows under different conditions have been studied by many researchers including Hussain and Thakar [14], Ahmed and Sarmah [15], Rajesh and Varma [16], Pal and Mondal [17], Samad and Rahman [18], S. Karthikeyan et al. [19], Das et al. [20] and Pal et al. [21].
At the macroscopic level, it is accepted that the boundary condition for a viscous fluid at a solid wall is one of “no slip”. While no-slip boundary condition has been proven experimentally to be accurate for a number of macroscopic flows, it remains an assumption that is based on physical principles. In fact nearly two hundred years ago, Navier’s [22] proposes a general boundary condition that incorporates the possibility of fluid slip at a solid boundary. Navier’s proposed condition assumes that the fluid slip velocity at a solid surface is proportional to the shear stress at the surface. The mathematical form of the Navier’s proposed condition on slip velocity as emphasized by Goldstein [23] is  where
where
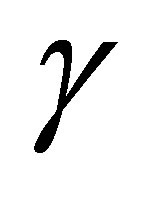 being the slip coefficient, v the slip velocity and y the normal coordinate. The fluid slippage phenomena at solid boundaries appear in many applications such as in micro-channels or nano channels and in applications where a thin film of light oil is attached to the moving plates or when the surface is coated with special coating such as thick monolayer of hydrophobic octadecyltrichorosilane. Due to practical applications of the fluid slippage phenomemenon at solid boundaries, several scholar have carried out their research work in that literature, the names of whom (Yu & Amed [24], Waltanebe et al. [25], Jain and Sharma [26], Khaled and Vafai [27] and Poonia and Chaudhary [28]) are worth meaning.
being the slip coefficient, v the slip velocity and y the normal coordinate. The fluid slippage phenomena at solid boundaries appear in many applications such as in micro-channels or nano channels and in applications where a thin film of light oil is attached to the moving plates or when the surface is coated with special coating such as thick monolayer of hydrophobic octadecyltrichorosilane. Due to practical applications of the fluid slippage phenomemenon at solid boundaries, several scholar have carried out their research work in that literature, the names of whom (Yu & Amed [24], Waltanebe et al. [25], Jain and Sharma [26], Khaled and Vafai [27] and Poonia and Chaudhary [28]) are worth meaning.
The present work is concerned with the effect of thermal radiation and chemical reaction on magneto-hydrodynamic convective mass transfer flow of an unsteady viscous incompressible eclectically conducting fluid past a semi-infinite vertical permeable plate embedded in a porous medium in slip flow regime. In this paper, we have generalized the work done by Karthikeyan et al. [19] by considering mass transfer with chemical reaction effect. The classical model for radiation effect introduced by Cogley et al. [29] is used. Perturbation technique is applied to convert the governing non-linear partial differential equations in to a system of ordinary differential equations which are solved analytically.
2. Mathematical Analysis
We consider a two-dimensional unsteady flow of a laminar, incompressible, electrically conducting and heat absorbing fluid past a semi-infinite vertical porous plate embedded in a uniform porous medium. We introduce the coordinate system 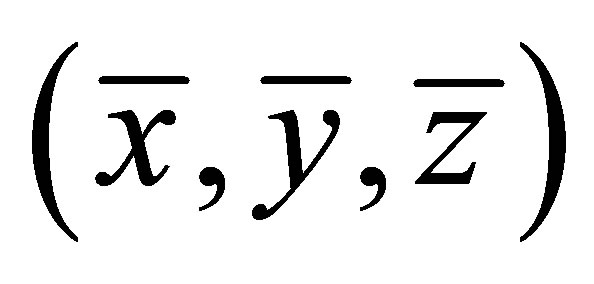 with X axis is chosen along the plate , Y axis perpendicular to it and directed in the fluid region and Z axis along the width of the plate as shown in the Figure 1. A uniform magnetic field of strength
with X axis is chosen along the plate , Y axis perpendicular to it and directed in the fluid region and Z axis along the width of the plate as shown in the Figure 1. A uniform magnetic field of strength 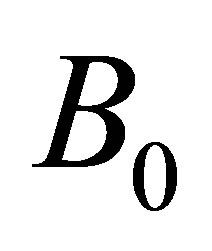 in the presence of radiation is imposed transversely in the direction of Y axis. The induced magnetic field is neglected under the assumption that the magnetic Reynolds number is small. It is assumed that there is no applied voltage which implies the absence of any electrical field. The radiative heat flux in the X direction is considered negligible in comparison to that in Y direction. The governing equations for this study are based on the conservation of mass, linear momentum, energy and species concentration. Taking in to consideration the assumptions made above, these equations in Cartesian frame of reference are given by Equation of continuity:
in the presence of radiation is imposed transversely in the direction of Y axis. The induced magnetic field is neglected under the assumption that the magnetic Reynolds number is small. It is assumed that there is no applied voltage which implies the absence of any electrical field. The radiative heat flux in the X direction is considered negligible in comparison to that in Y direction. The governing equations for this study are based on the conservation of mass, linear momentum, energy and species concentration. Taking in to consideration the assumptions made above, these equations in Cartesian frame of reference are given by Equation of continuity:
 (1)
(1)
Momentum equation:
 (2)
(2)
Energy equation
 (3)
(3)
Species continuity equation:

Figure 1. Physical model of the problem.
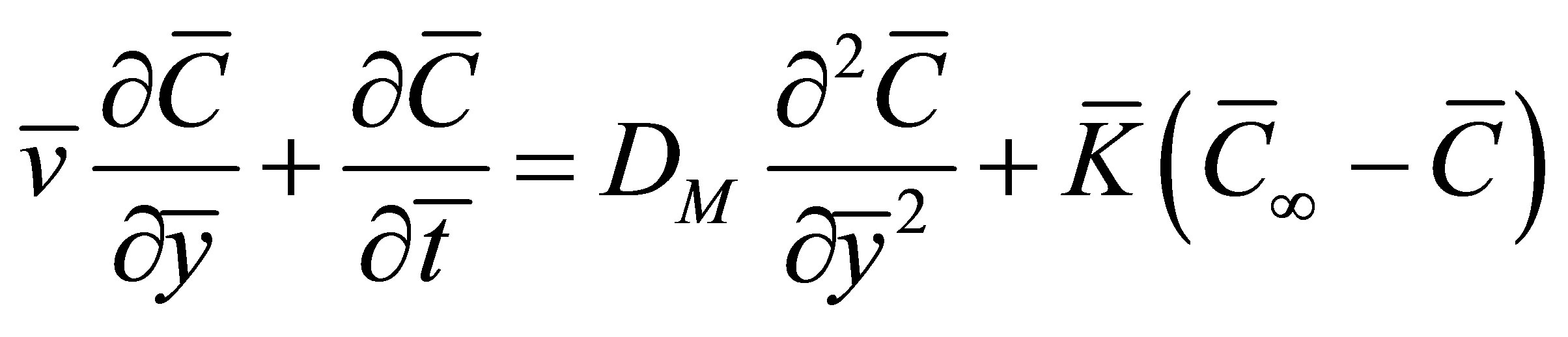 (4)
(4)
where  and
and 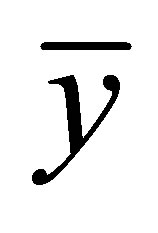 are the dimensional distances along and perpendicular to the plate respectively.
are the dimensional distances along and perpendicular to the plate respectively. 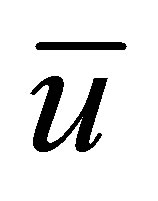 and
and  are the components of the dimensional velocities along
are the components of the dimensional velocities along  and
and 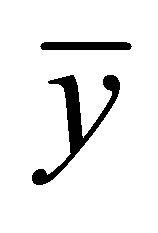 respectively.
respectively. 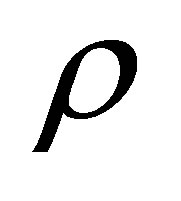 is the density of the medium, g is the acceleration due to gravity,
is the density of the medium, g is the acceleration due to gravity,  is the kinematic viscosity,
is the kinematic viscosity,  is the fluid electrical conductivity,
is the fluid electrical conductivity,  is the permeability of the porous medium,
is the permeability of the porous medium,  is first order chemical reaction,
is first order chemical reaction, 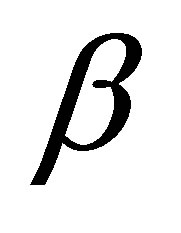 is the coefficient of thermal expansion,
is the coefficient of thermal expansion, 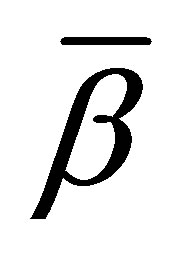 is the coefficient of mass expansion.
is the coefficient of mass expansion. 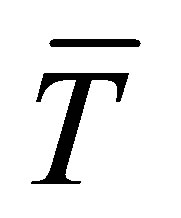 is the dimensional temperature of the fluid near the plate,
is the dimensional temperature of the fluid near the plate,  is the dimensional free stream temperature,
is the dimensional free stream temperature,  is the dimensional concentration of the fluid near the plate,
is the dimensional concentration of the fluid near the plate, 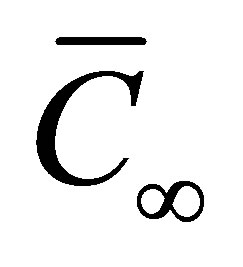 is the dimensional free stream concentration, k is constant pressure,
is the dimensional free stream concentration, k is constant pressure,  is the radiative heat flux and
is the radiative heat flux and  is the dimensional heat absorption coefficient.
is the dimensional heat absorption coefficient.
Cogley et al. [29] showed that, in the optically thin limit for a non-gray gas near equilibrium, the radiative heat flux is represented by the following form:
 (5)
(5)
where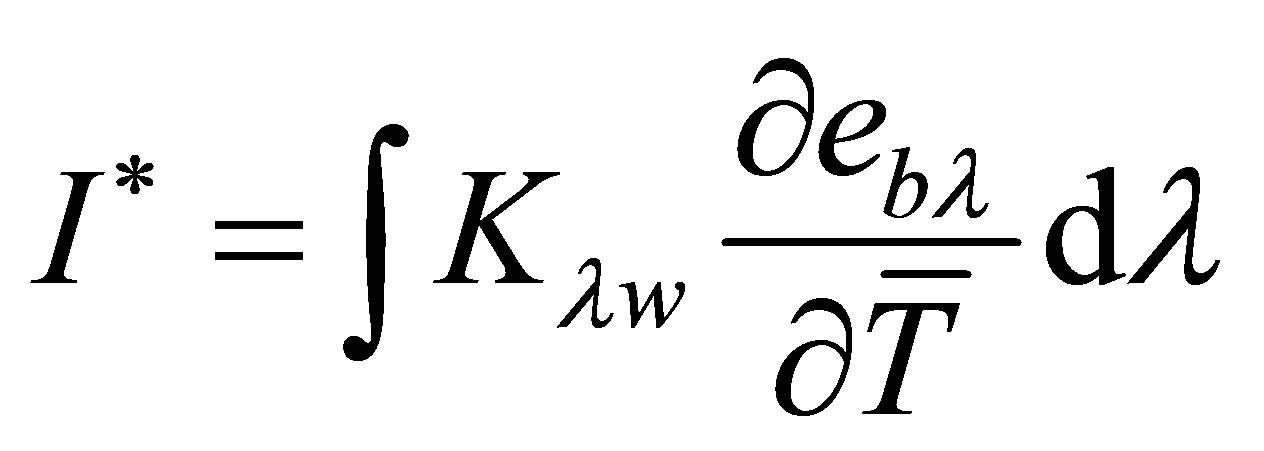 ,
, 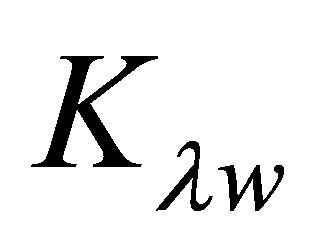 is the absorption coefficient at the wall and
is the absorption coefficient at the wall and 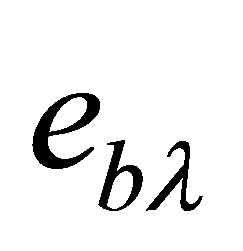 is the Planck’s function.
is the Planck’s function.
Under the assumption, the appropriate boundary conditions for velocity involving slip flow, temperature and concentration fields are given by
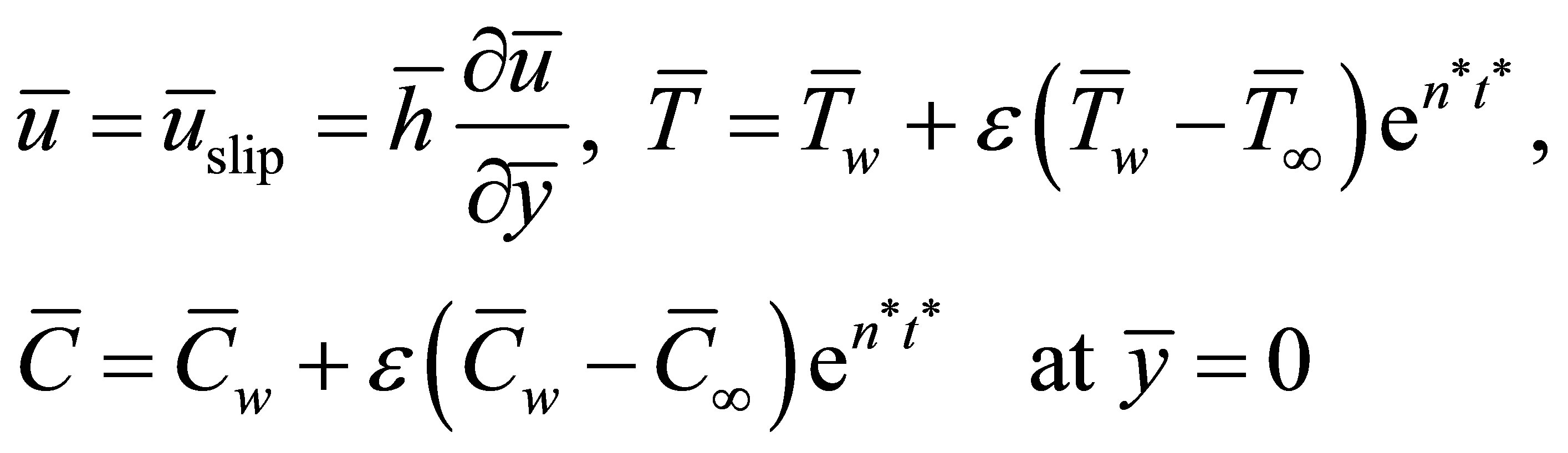 (6)
(6)
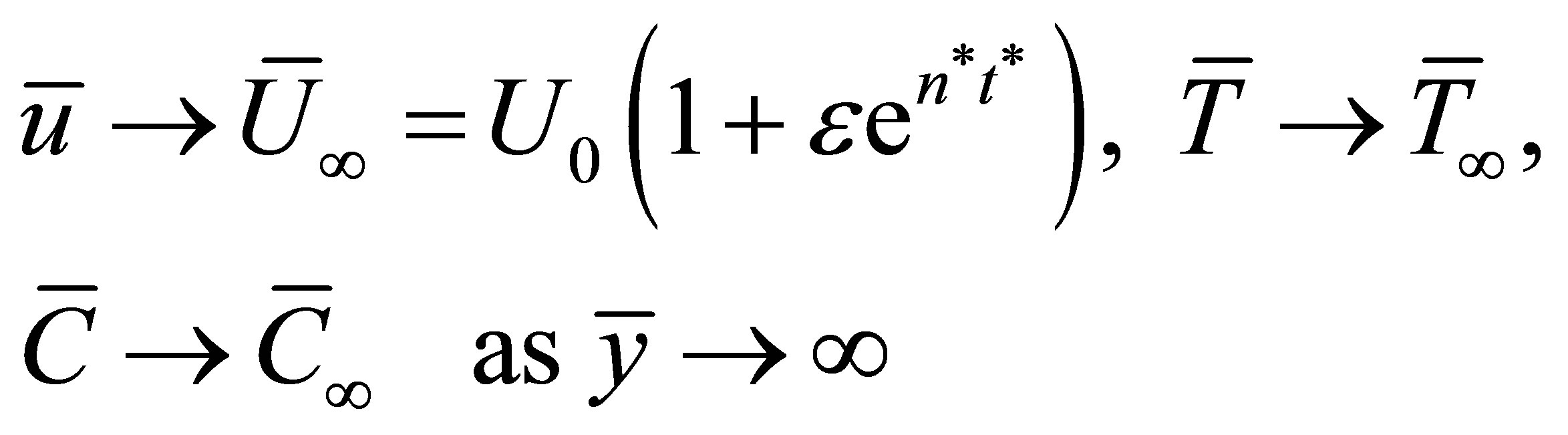 (7)
(7)
where  and
and 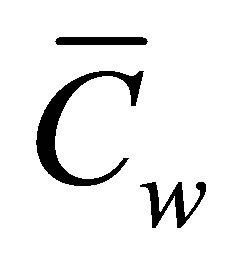 are the dimensional temperature and species concentration at the wall respectively and
are the dimensional temperature and species concentration at the wall respectively and  is the characteristic dimension of the flow fluid. Science the suction velocity normal to the plate is a function of time only, it can be taken in the exponential form as
is the characteristic dimension of the flow fluid. Science the suction velocity normal to the plate is a function of time only, it can be taken in the exponential form as
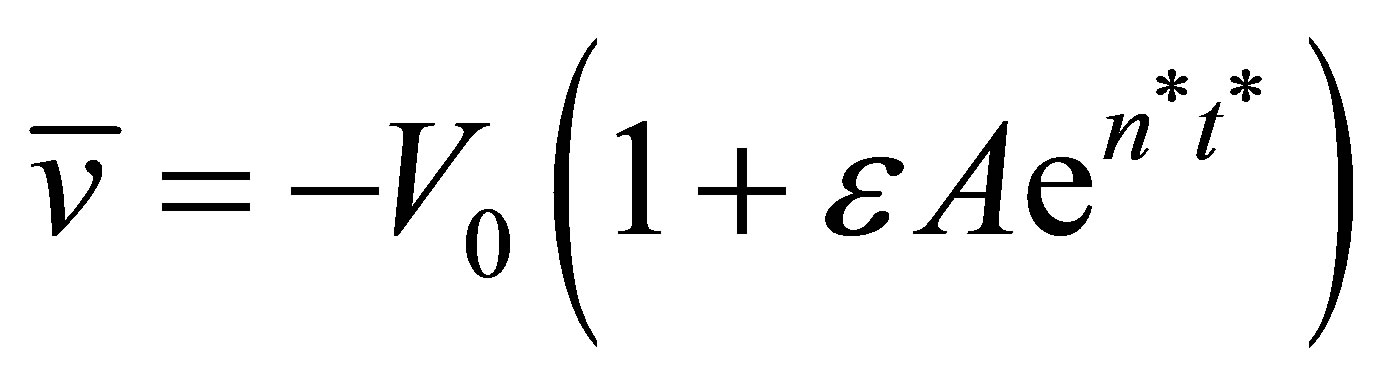 (8)
(8)
where A is a real positive constant, 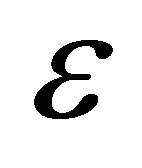 and
and 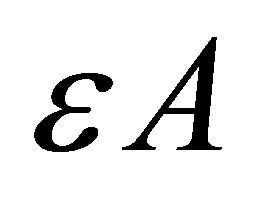 are small quantities less than unity and
are small quantities less than unity and 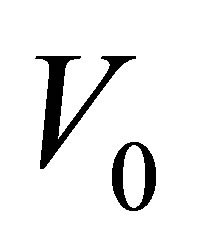 is a scale of suction velocity which is a non-zero positive constant.
is a scale of suction velocity which is a non-zero positive constant.
Outside the boundary layer, Equation (2) gives
 (9)
(9)
Now we introduce the dimensionless variables as follows
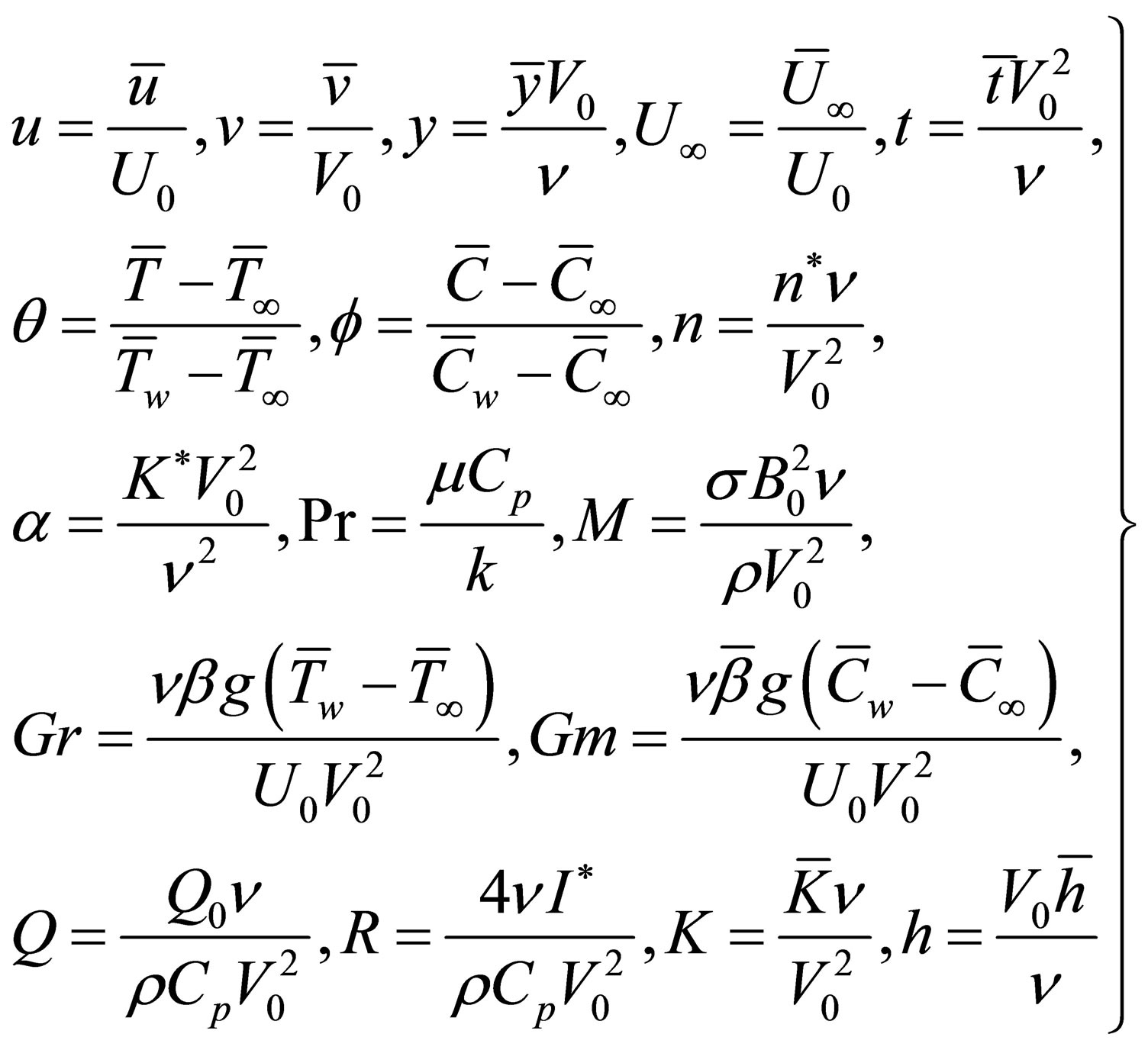 (10)
(10)
where Pr is the Prandtl number, M is the magnetic field parameter, 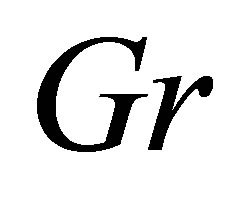 is Grashof number for heat transfer,
is Grashof number for heat transfer,  is the Grashof number for mass transfer, Q is the heat source parameter,
is the Grashof number for mass transfer, Q is the heat source parameter,  is the permeability parameter,
is the permeability parameter,  is the non dimensional temperature,
is the non dimensional temperature,  is the non dimensional concentration, R is radiation parameter, h is the rarefaction parameter and K is the chemical reaction parameter.
is the non dimensional concentration, R is radiation parameter, h is the rarefaction parameter and K is the chemical reaction parameter.
In view of Equations (8) to (10) the governing Equations (2), (3) and (4) reduce the following non-dimensional form:
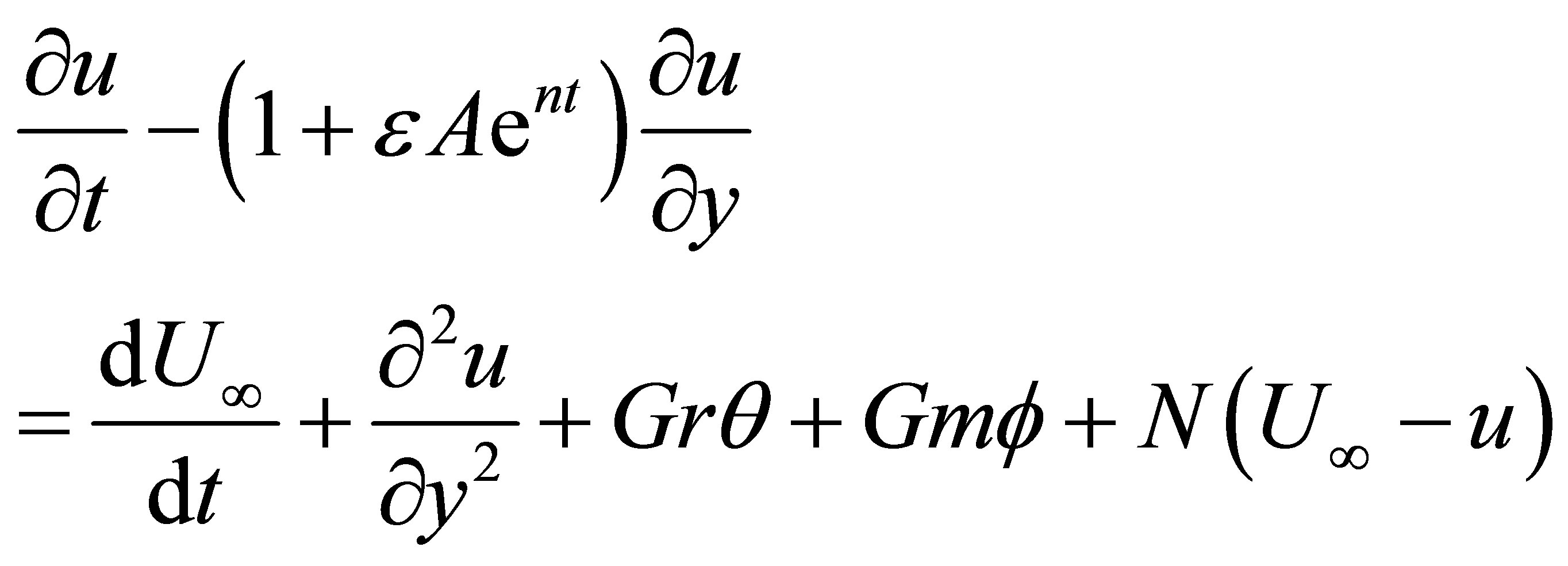 (11)
(11)
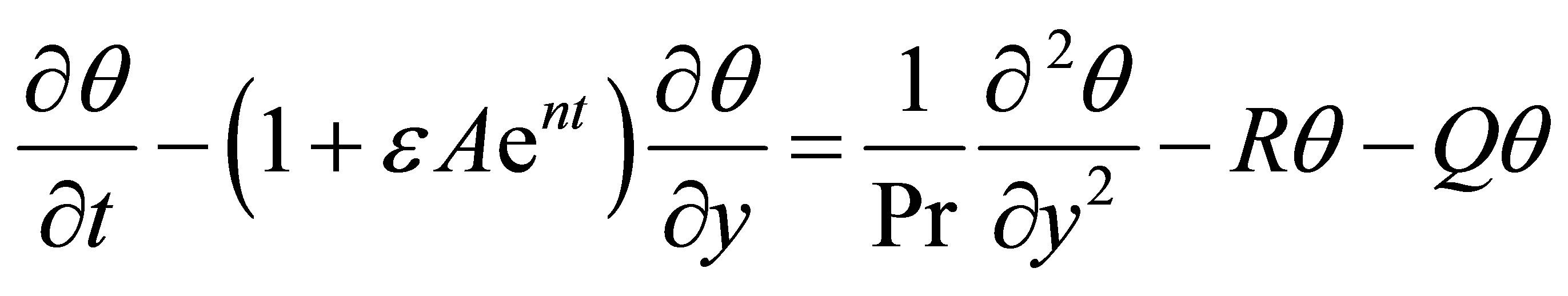 (12)
(12)
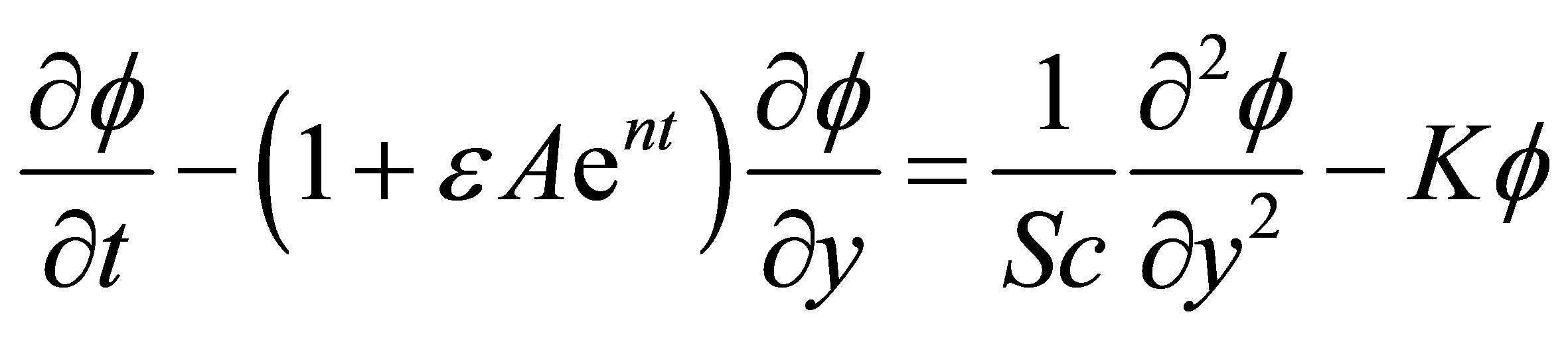 (13)
(13)
where 
The boundary conditions (6) and (7) in the dimensionless form can be written as
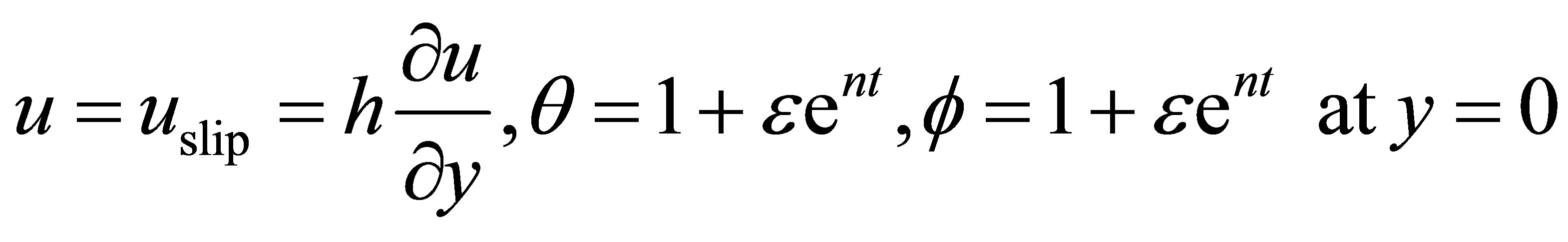 (14)
(14)
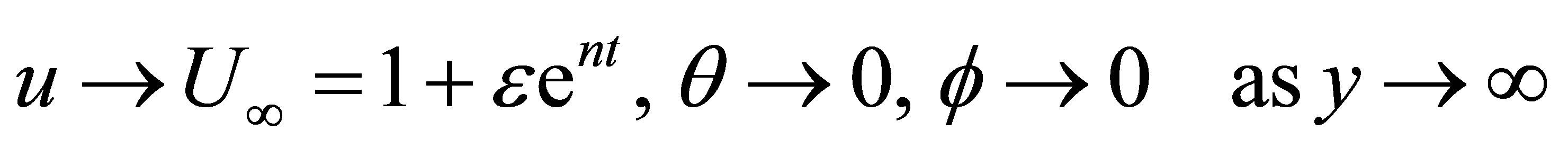 (15)
(15)
3. Solution of the Problem
Equations (11) to (13) are coupled non-linear partial differential equations and these can be solved in closed form. However, these equations can be reduced to a set of ordinary differential equations, which can be solved analytically. These can be done by representing the velocity, temperature and concentration of the fluid in the neighbourhood of the plate as
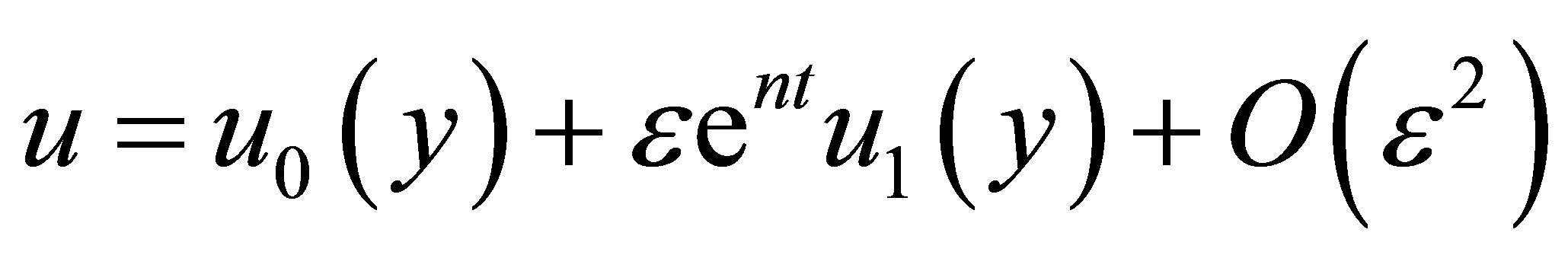 (16)
(16)
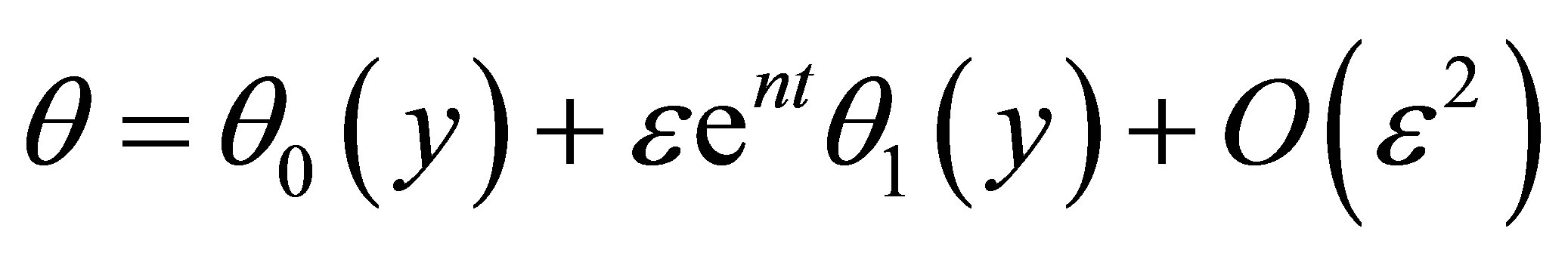 (17)
(17)
 (18)
(18)
Substituting (16) to (18) in Equations (11) to (13) and equating the harmonic and non harmonic terms and neglecting the coefficient of 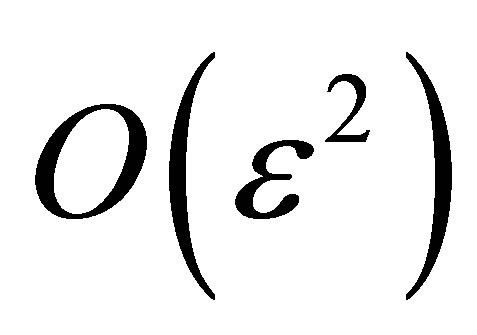 we get the following pairs of equations for
we get the following pairs of equations for  and
and .
.
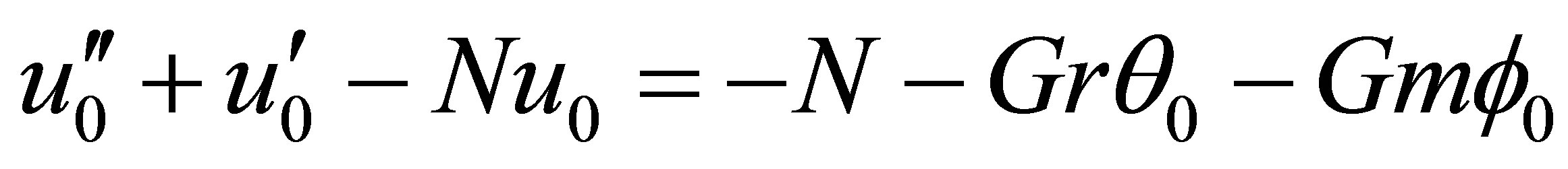 (19)
(19)
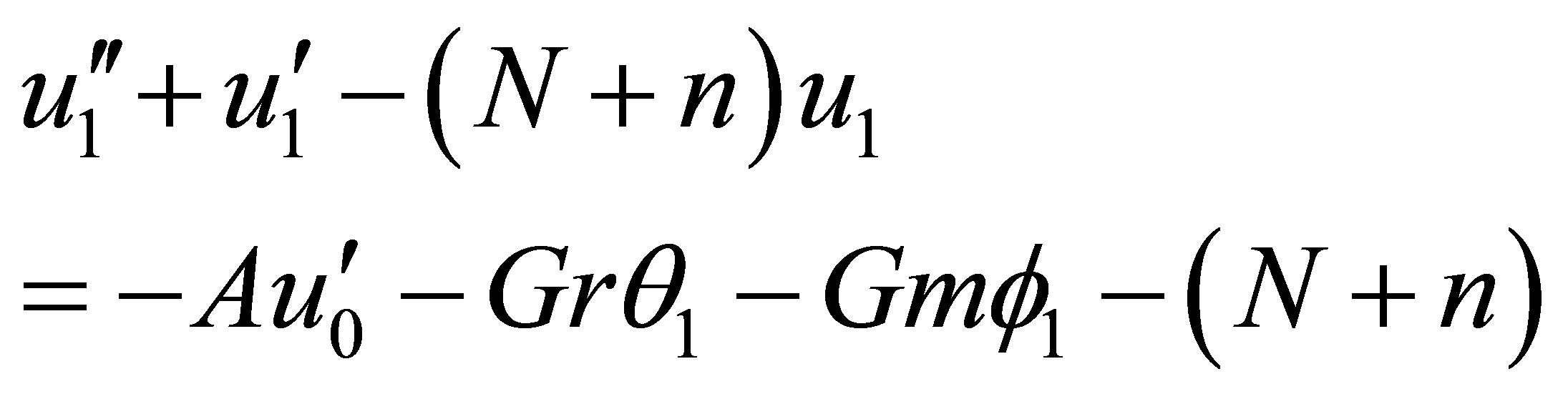 (20)
(20)
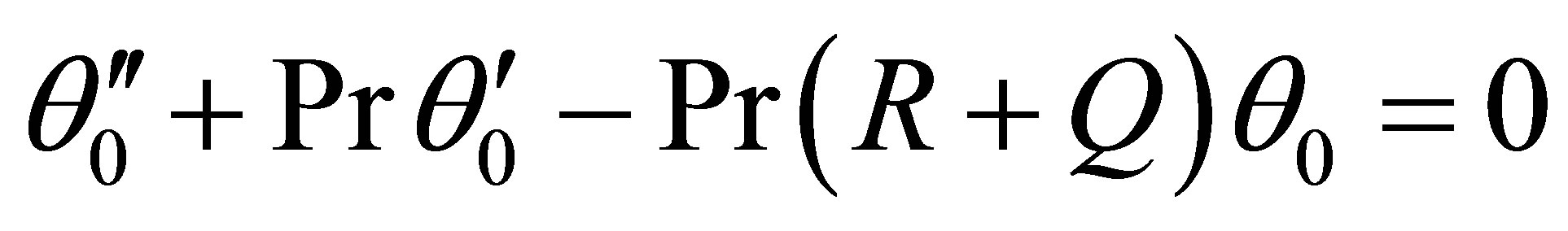 (21)
(21)
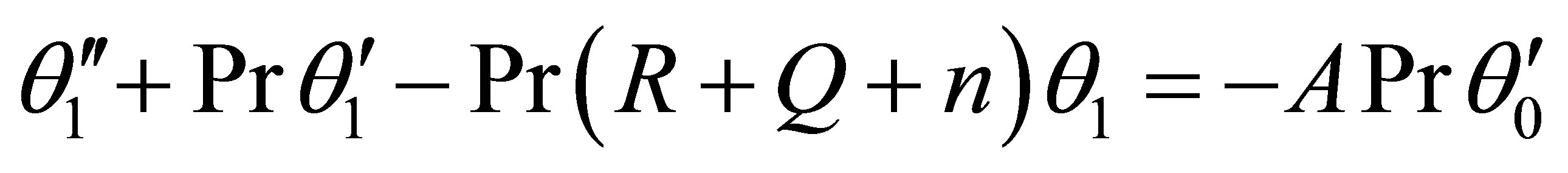 (22)
(22)
 (23)
(23)
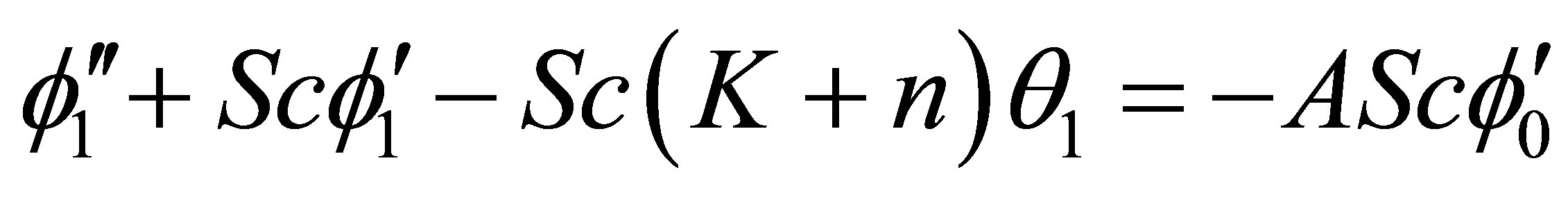 (24)
(24)
where the primes denote the differentiation with respect to y The corresponding boundary conditions can be written as
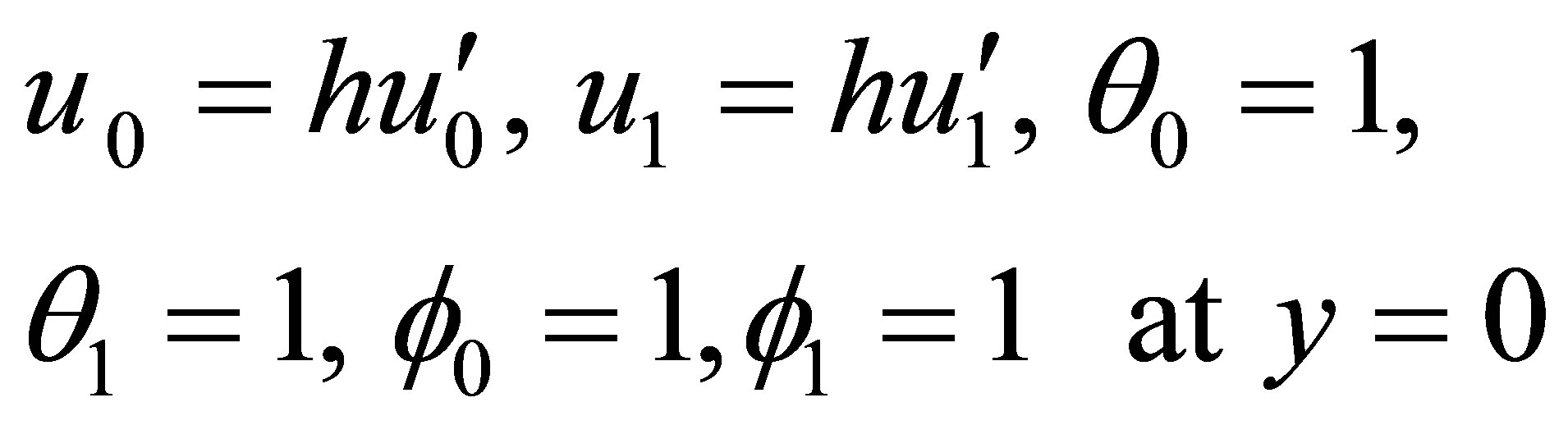 (25)
(25)
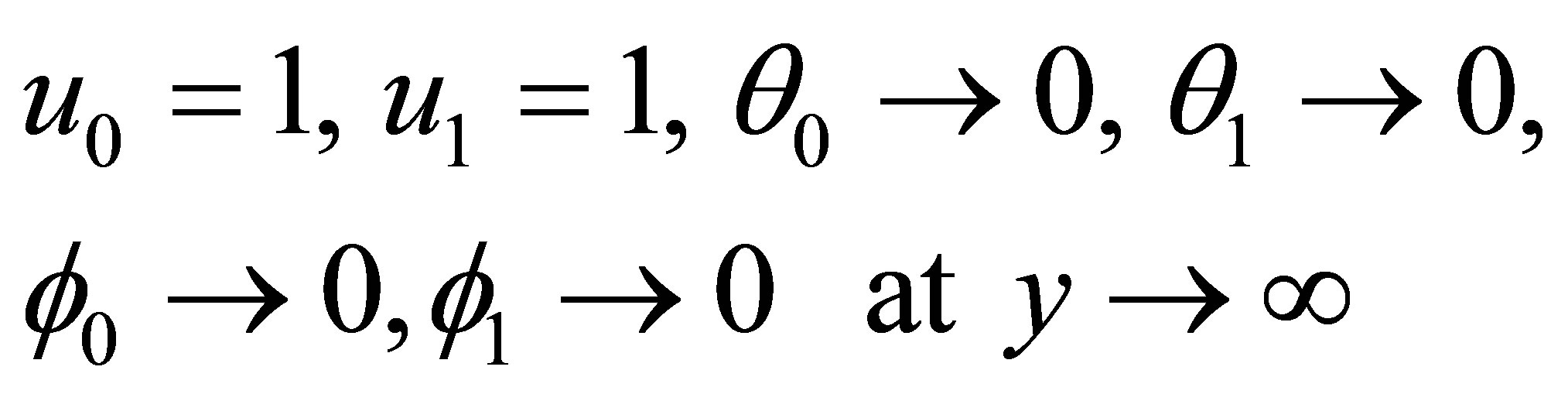 (26)
(26)
The solutions of Equations (18) to (23) which satisfy the boundary conditions (24) and (25) are given by
 (27)
(27)
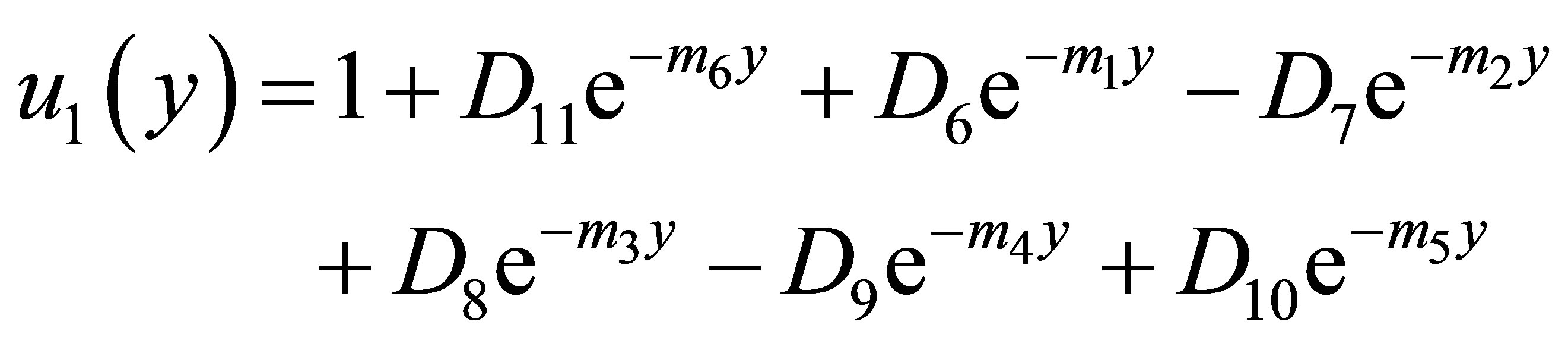 (28)
(28)
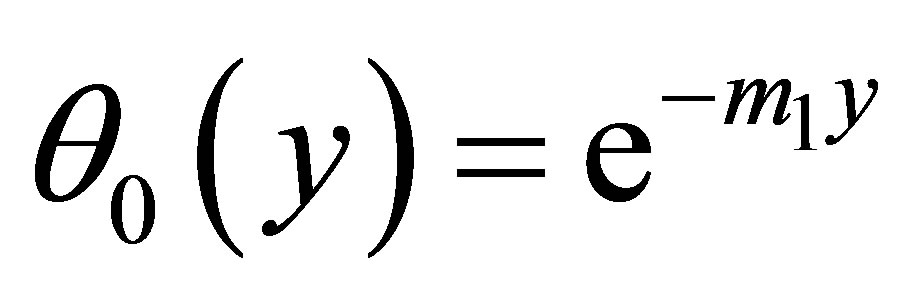 (29)
(29)
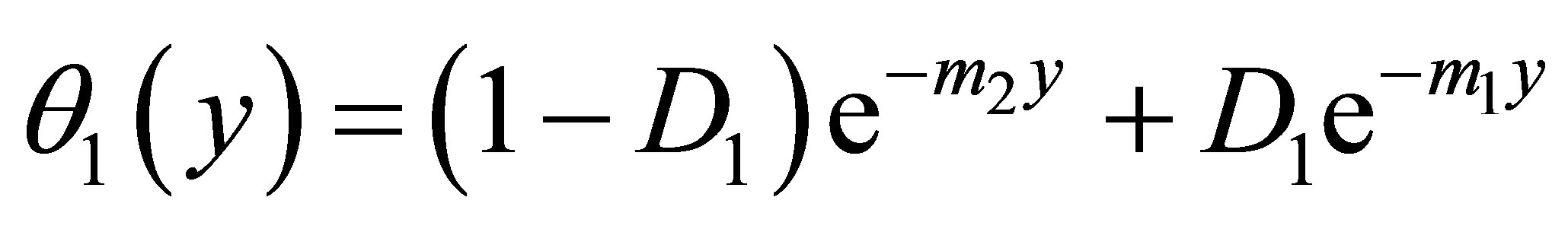 (30)
(30)
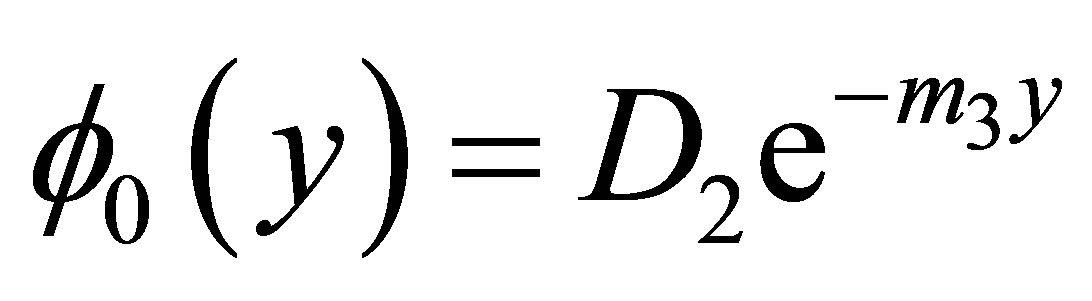 (31)
(31)
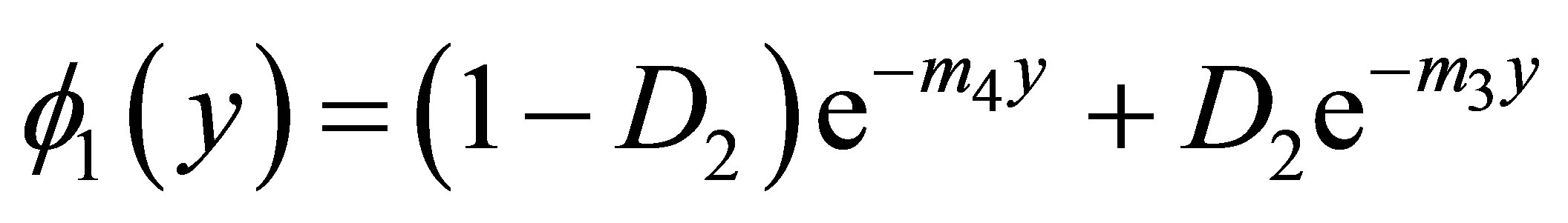 (32)
(32)
where,
 ,
,
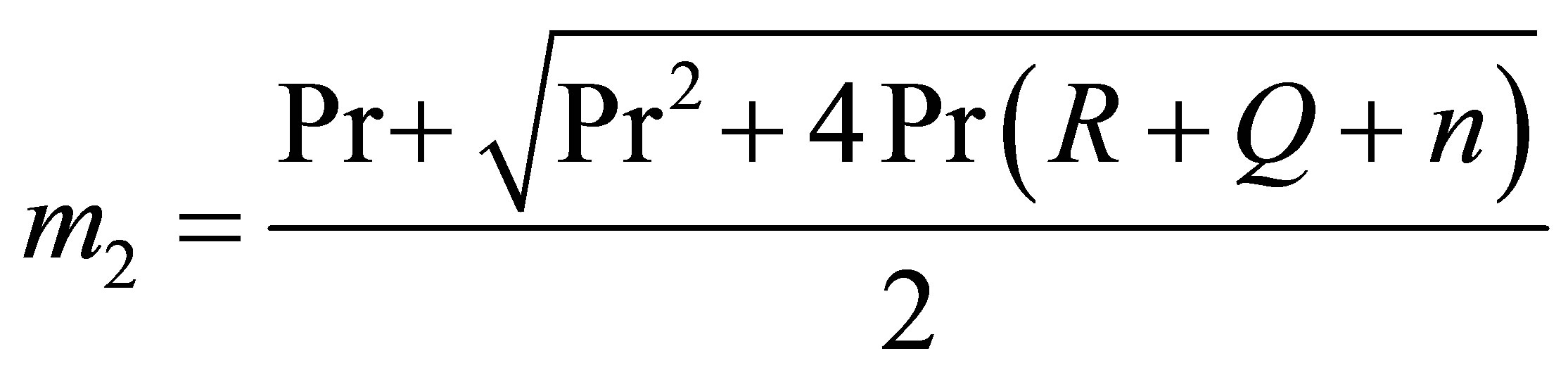 ,
,
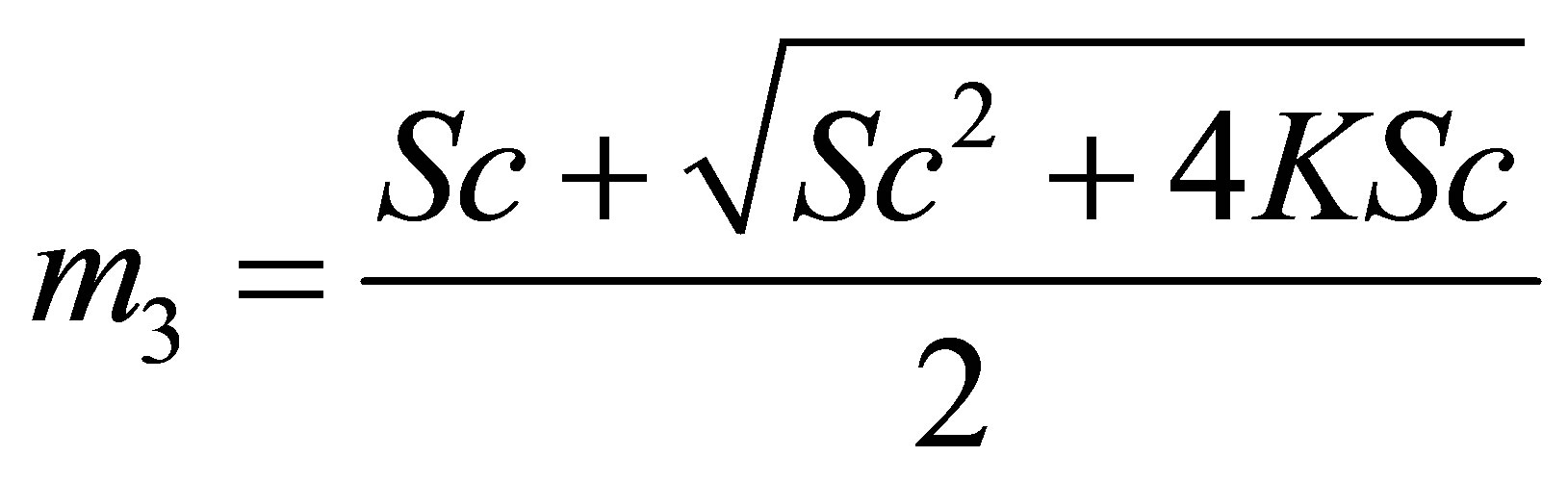 ,
,
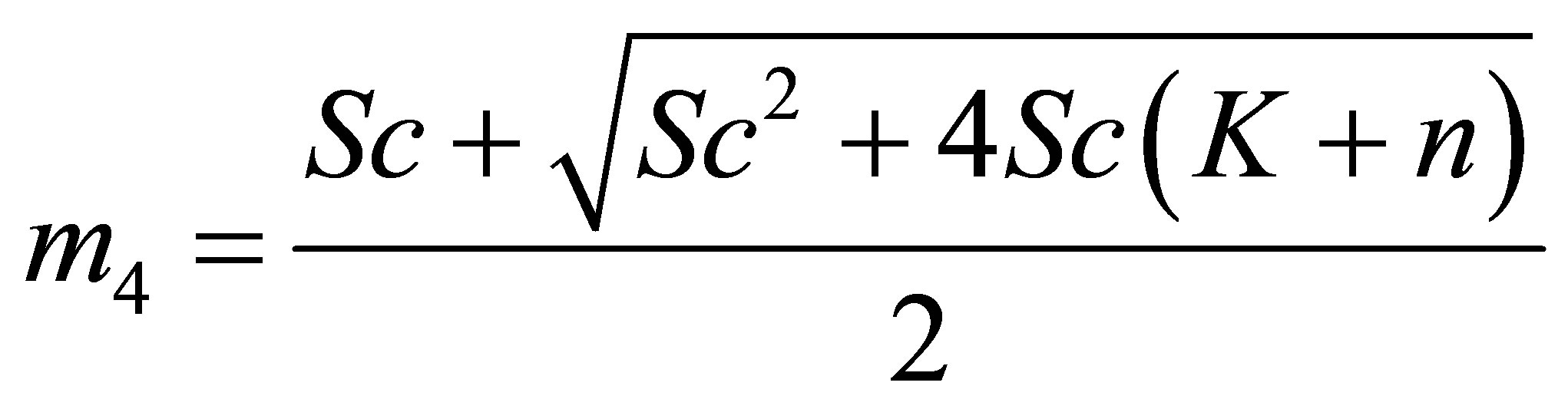 ,
,
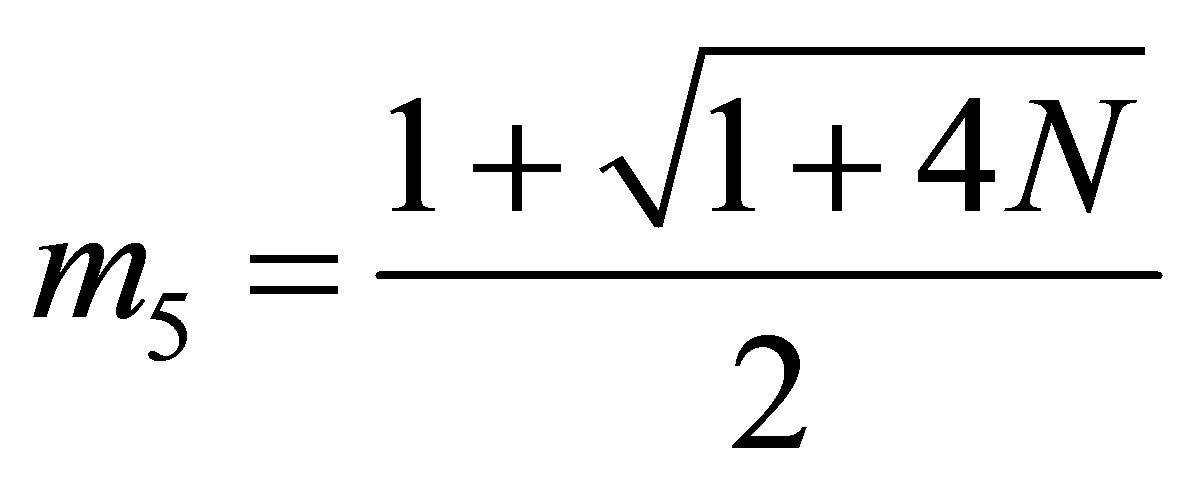 ,
,
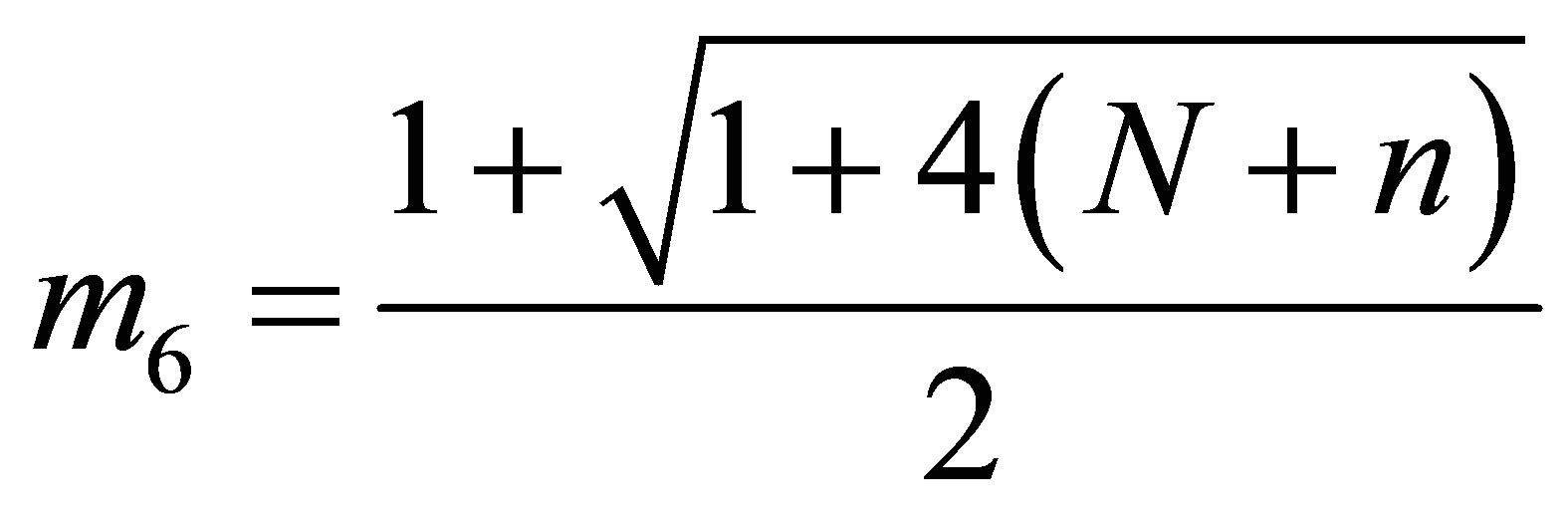
 ,
,
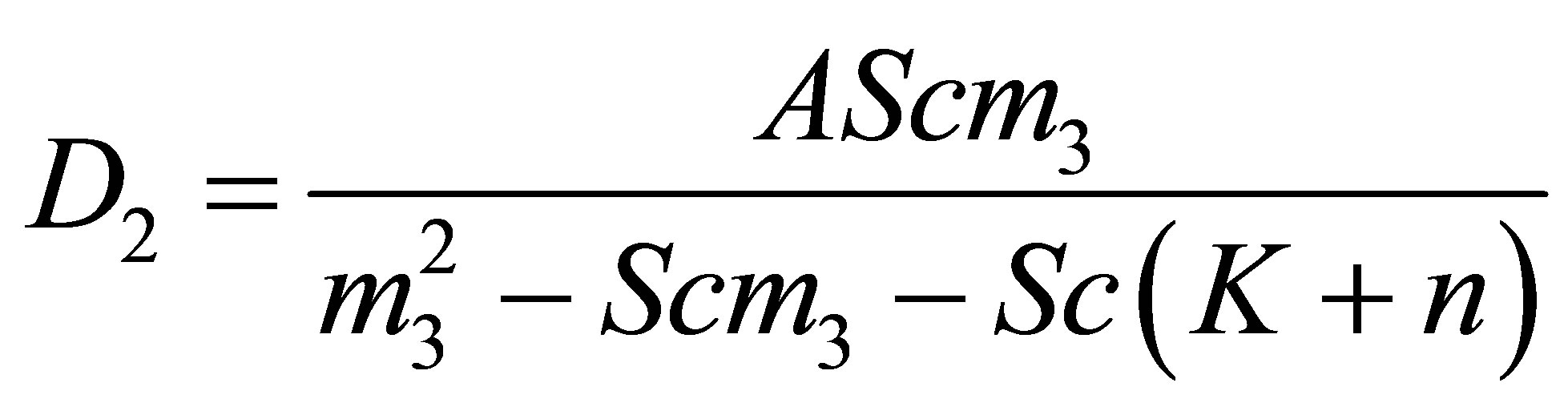 ,
,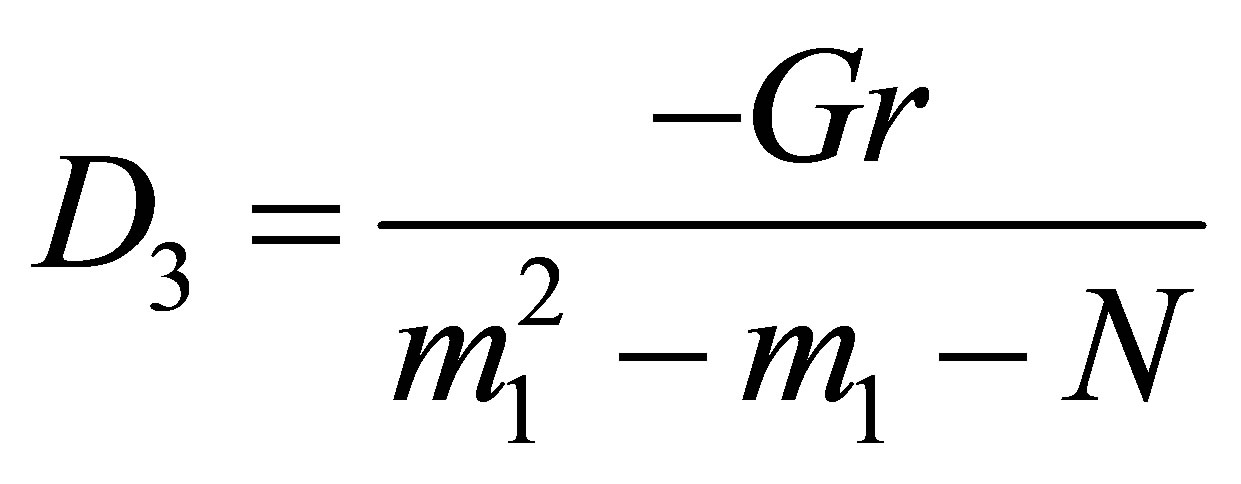 ’
’
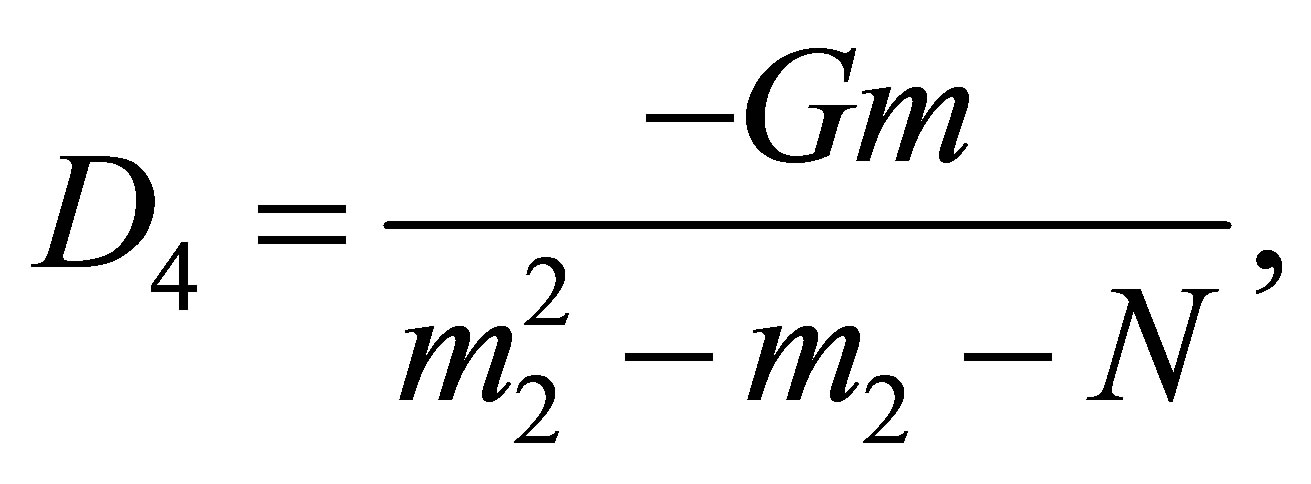
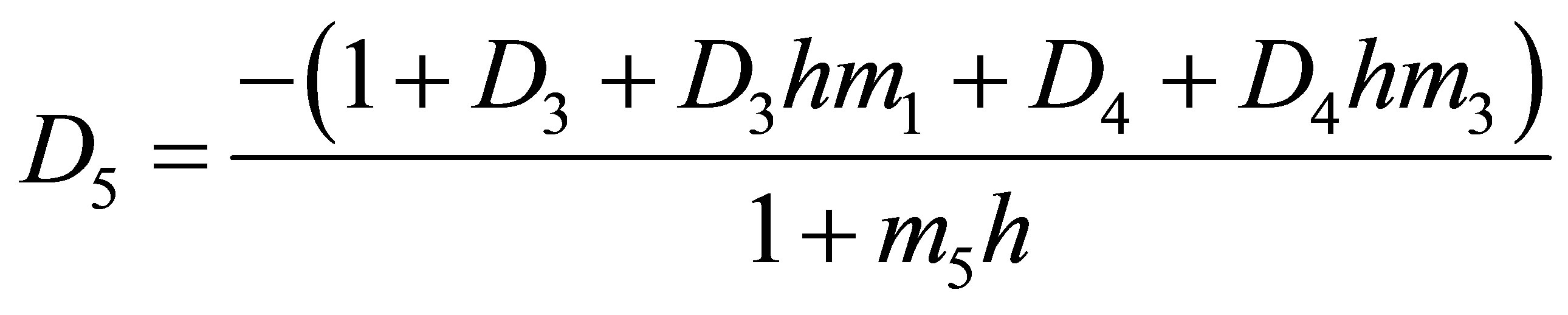 ,
,
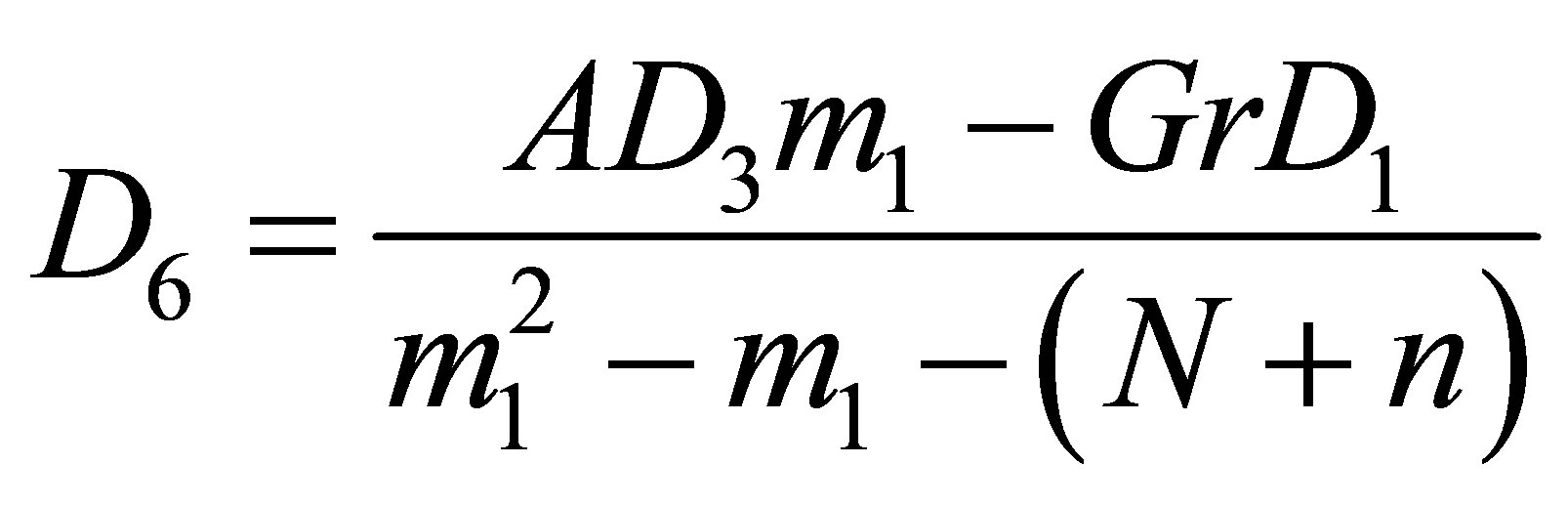 ,
,
 ,
,
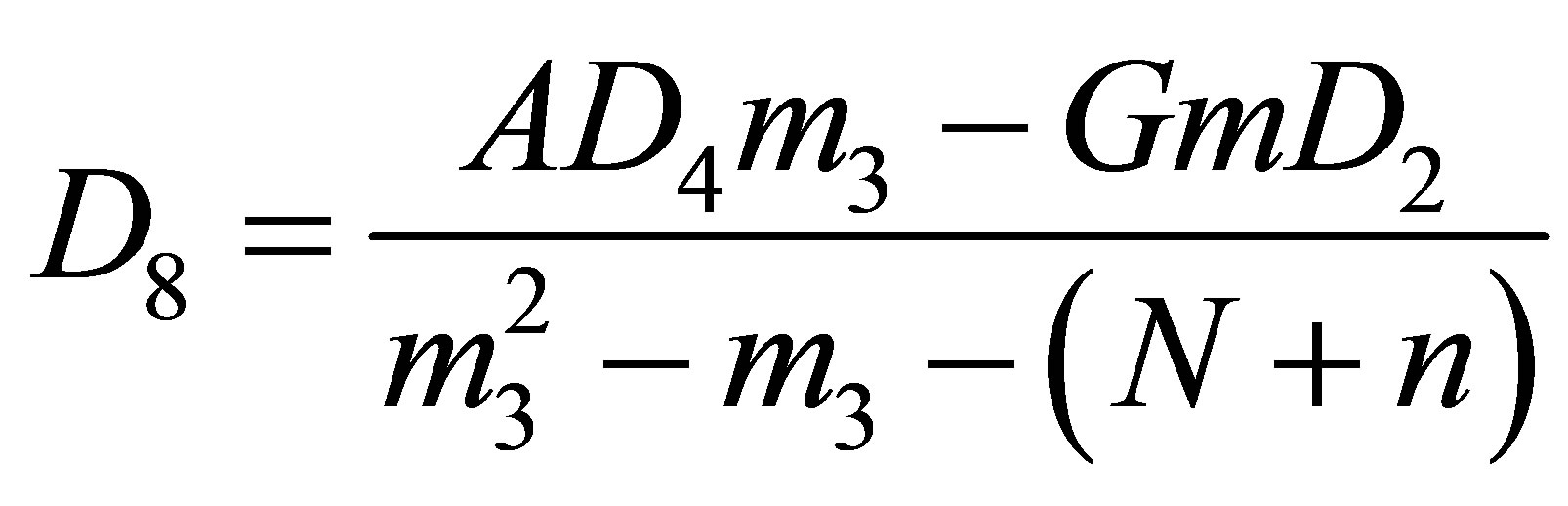 ,
,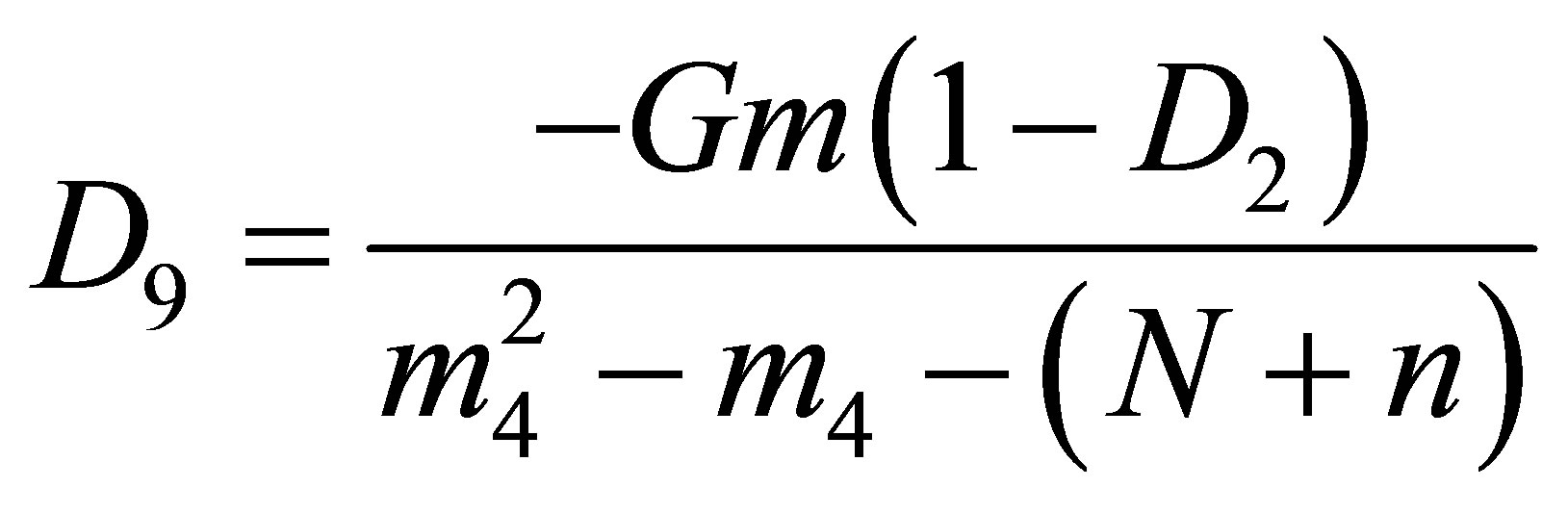 ,
,
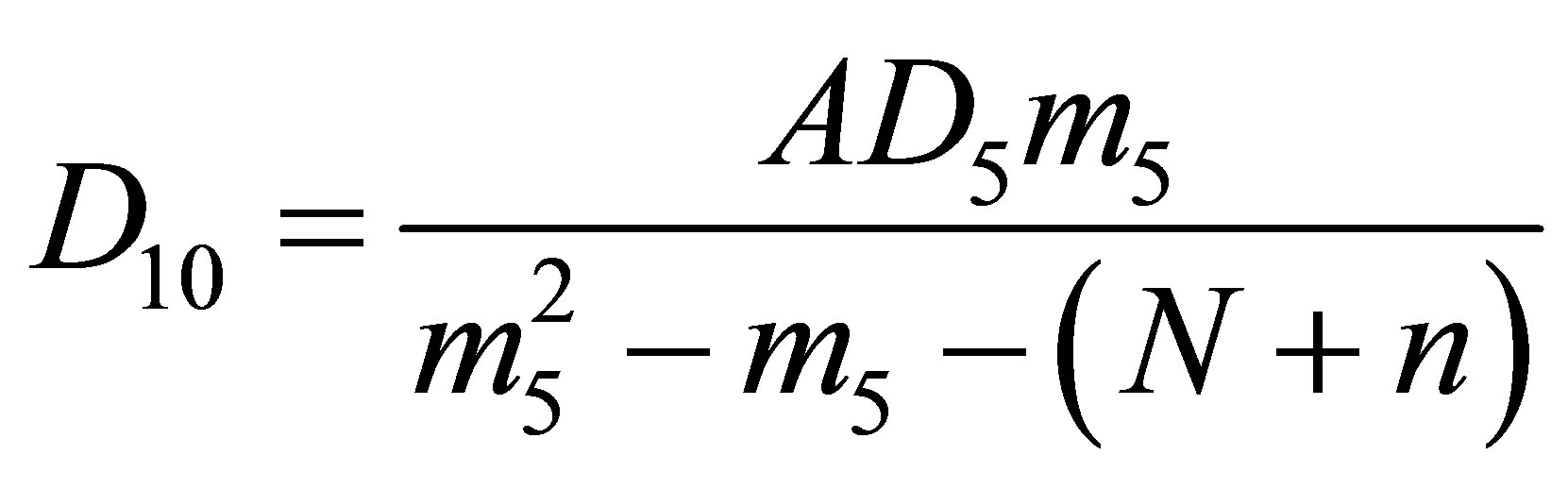 ,
,

Substituting equations (27)-(32) in Equations (16)- (18), we obtain the velocity, temperature and concentration distributions in the boundary layer as follows:
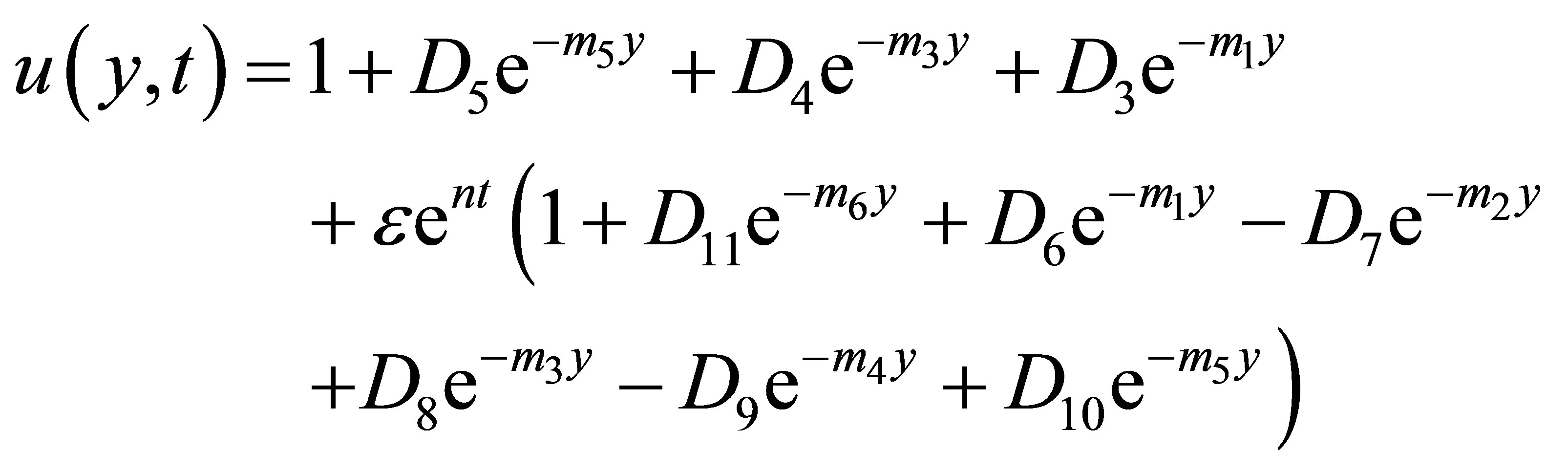 (33)
(33)
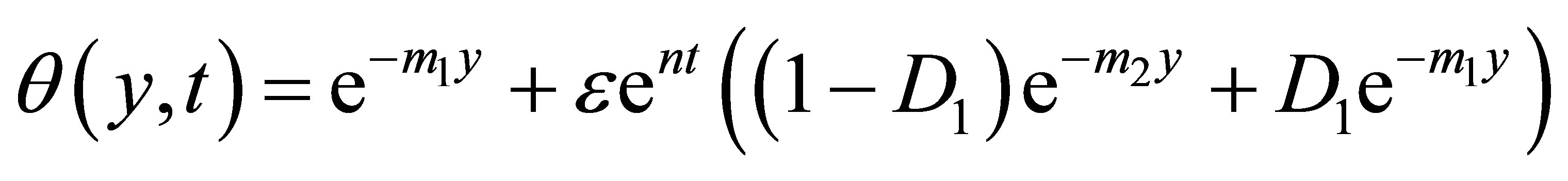 (34)
(34)
 (35)
(35)
4. Skin Friction
The non dimensional skin friction at the plate is given by:
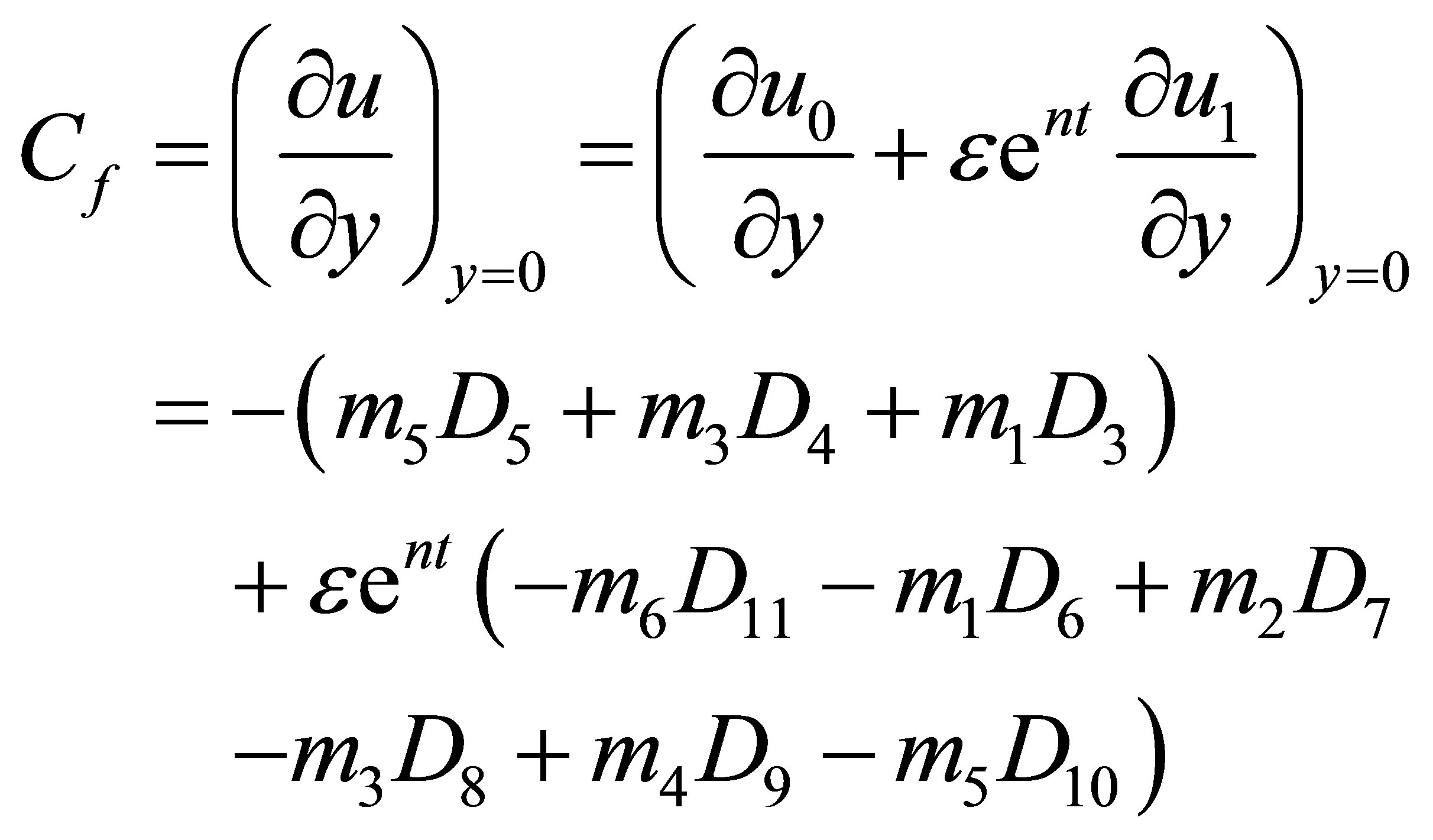 (36)
(36)
5. Nusselt Number
The non-dimensional form of the rate of heat transfer in terms of Nusselt number at the plate is given by:
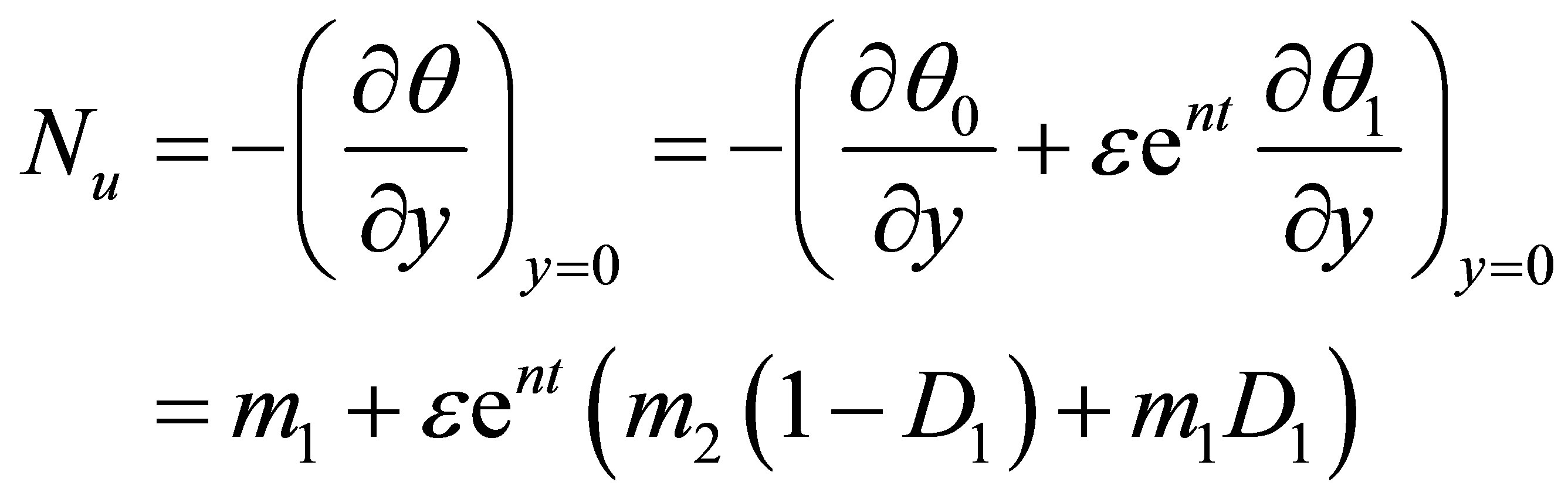 (37)
(37)
6. Sherwood Number
The non-dimensional form of the rate of mass transfer in terms of Sherwood number at the plate is given by:
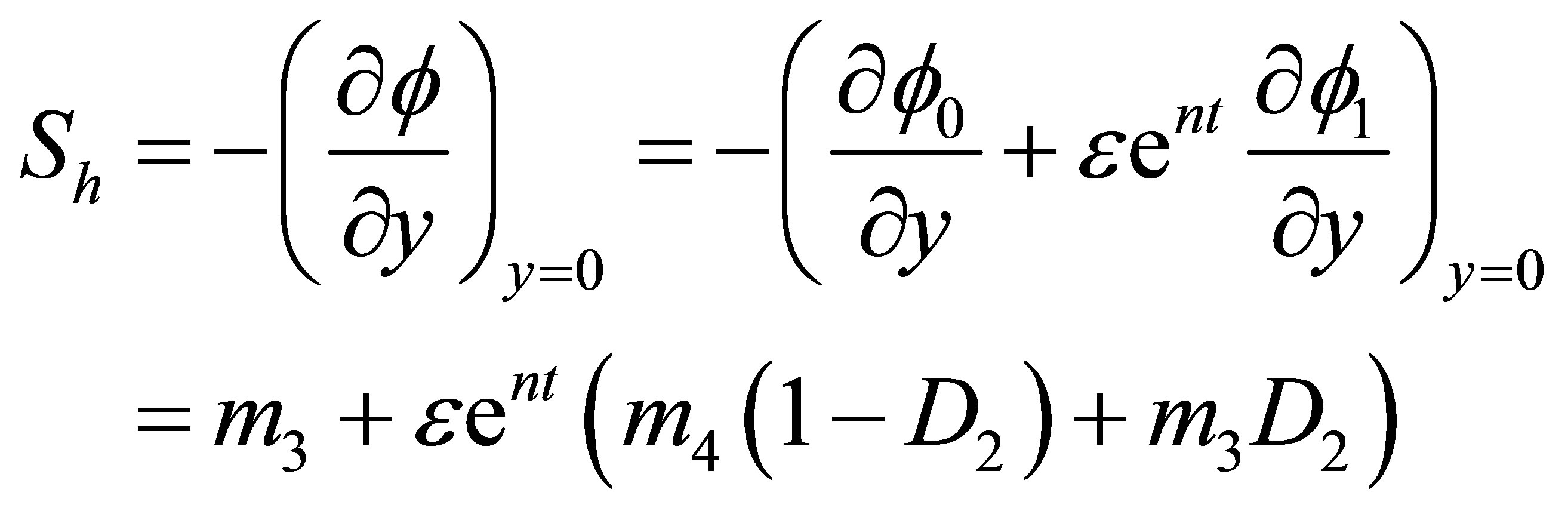 (38)
(38)
7. Results and Discussion
In order to get physical insight in to the problem, we have carried out numerical calculations for non-dimensional velocity field, temperature field, concentration field, co-efficient of skin friction 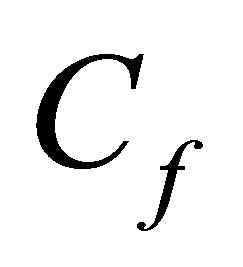 at the plate, the rate of heat transfer
at the plate, the rate of heat transfer  and the rate of mass transfer in terms of Sherwood number
and the rate of mass transfer in terms of Sherwood number  by assigning specific values to the different values to the parameters involved in the problem, viz., Magnetic parameter M, Chemical reaction parameter K, Radiation parameter R, Grashof number for heat transfer
by assigning specific values to the different values to the parameters involved in the problem, viz., Magnetic parameter M, Chemical reaction parameter K, Radiation parameter R, Grashof number for heat transfer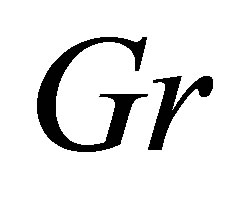 , Grashof number for mass transfer
, Grashof number for mass transfer , permeability parameter
, permeability parameter , heat source parameter Q and rarefaction parameter h. Throughout our investigation the value of Prandtl number Pr is kept constant at 0.71 which corresponding to air at
, heat source parameter Q and rarefaction parameter h. Throughout our investigation the value of Prandtl number Pr is kept constant at 0.71 which corresponding to air at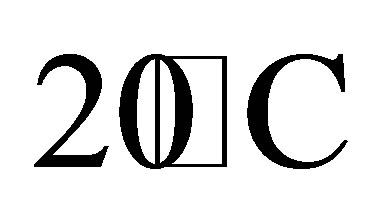 . The Schmidt number Sc are taken in such a way that they represent the diffusing chemical species of common interest in air (for example
. The Schmidt number Sc are taken in such a way that they represent the diffusing chemical species of common interest in air (for example  for He, Sc = 0.30 for
for He, Sc = 0.30 for 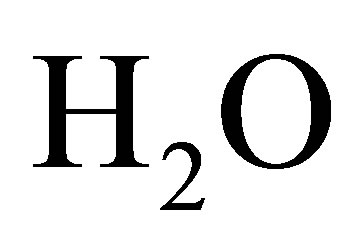 and
and 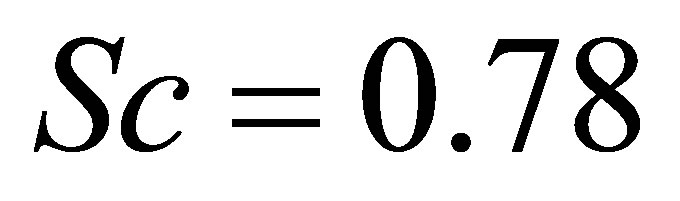 for
for ), time t = 1, n = 0.1, A = 1 and the values of other parameters are chosen arbitrarily. The numerical results are demonstrated through different graphs and table and their results are interpreted physically.
), time t = 1, n = 0.1, A = 1 and the values of other parameters are chosen arbitrarily. The numerical results are demonstrated through different graphs and table and their results are interpreted physically.
Figure 2 plots the velocity profiles against the spanwise coordinate y for different magnetic parameters. This illustrates that velocity decreases as the existence of magnetic field becomes stronger. This conclusion agrees with the fact that the magnetic field exerts retarding force on the free-convection flow.
Figure 3 illustrates the effect of radiation on the velocity. It is seen from this figure that there is a steady increase in the velocity with the increase in radiation parameter R. The increase in this parameter R leads to increase the boundary layer thickness and to reduce the

Figure 2. Velocity u versus y, under the effect of M, for R = 2, K = 1, Q = 1, h = 0.3, ε = 0.2, Sc = 0.6, Gr = 6, Gm = 4, α = 1.

Figure 3. Velocity u versus y, under the effect of R, for M = 3, K = 1, Q = 1, h = 0.3, ε = 0.2, Sc = 0.6, Gr = 6, Gm = 4, α = 1.
heat transfer rate in the presence of thermal buoyancy force.
The change of velocity profile due to different chemical reaction parameters is plotted in Figure 4. This figure shows that the fluid motion is retarded on account of chemical reaction. This shows that the consumption of chemical species leads to fall in the concentration field which in turn diminishes the buoyancy effects due to concentration gradients. Consequently, the flow field is decelerated.
Figure 5 depicted the effect of heat source parameter on velocity field. It is seen from this figure that the heat source parameter Q leads the fluid motion to retard.
Figure 6 indicates the fact that an increase in Schmidt number Sc decelerates the fluid flow. In other words, mass diffusivity causes the fluid velocity to increase.
It is observed from Figure 7 that an increase in Grashof number for heat transfer leads to a rise in the values of velocity u due to enhancement in buoyancy force.
The plot of velocity profile for different values of Grashof number for mass transfer is given in Figure 8. It is observed that velocity increases for the increasing values of Grashof number for mass transfer.
The change in velocity profile due to different perme-
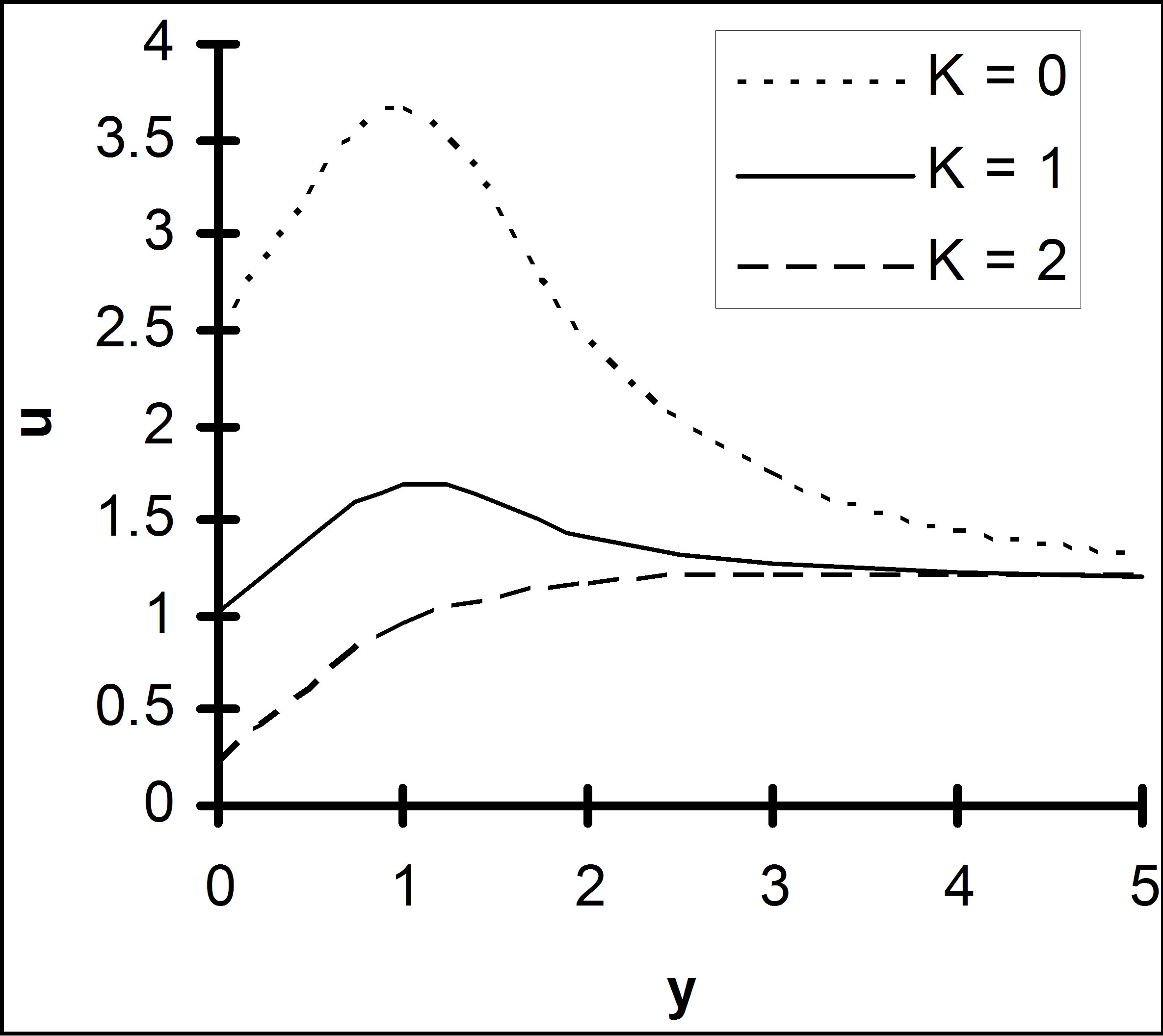
Figure 4. Velocity u versus y, under the effect K, for R = 2, M = 3, Q = 1, h = 0.3, ε = 0.2, Sc = 0.6, Gr = 6, Gm = 4, α = 1.
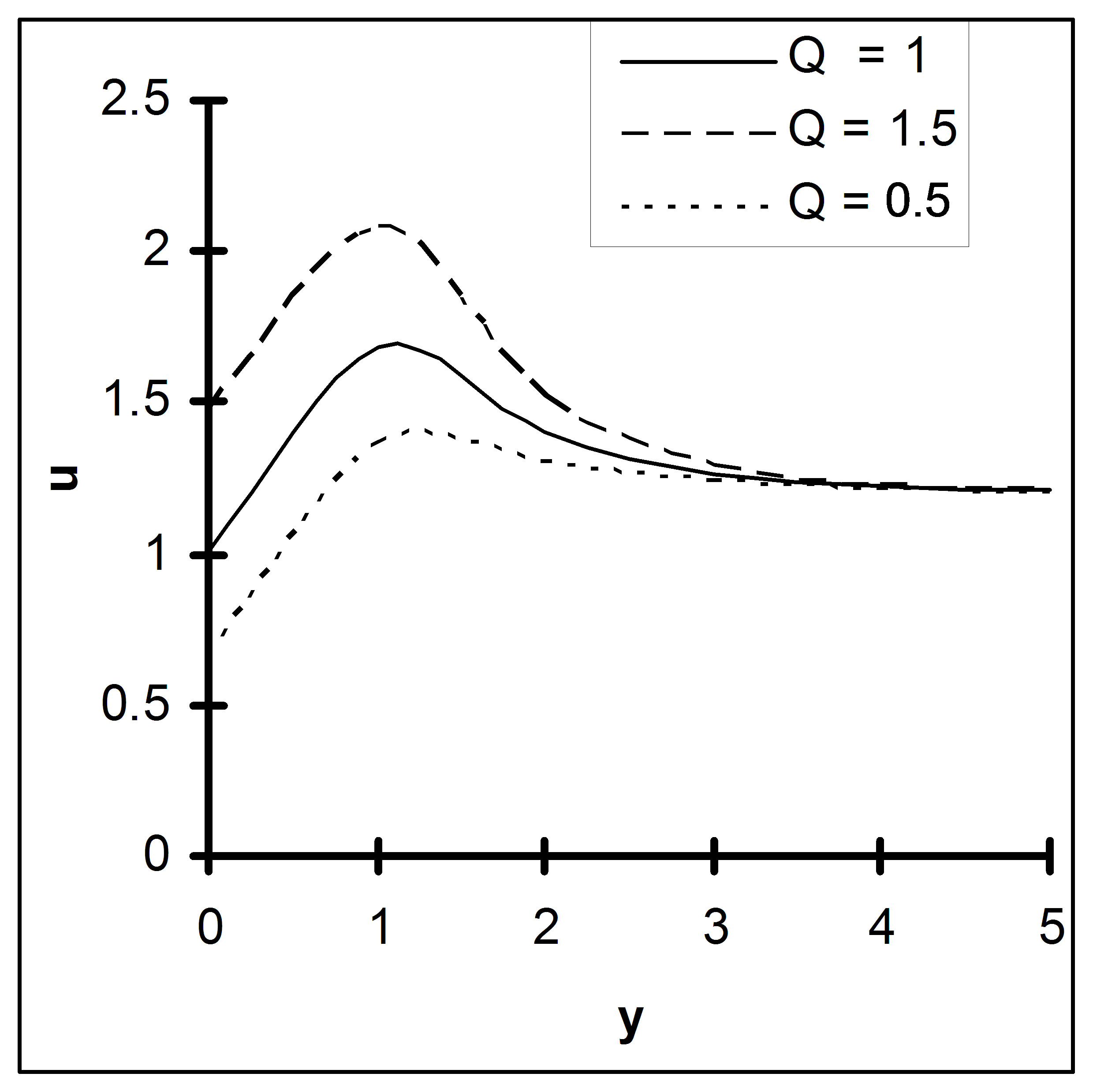
Figure 5. Velocity u versus y, under the effect Q, for R = 2, M = 3, K = 1, h = 0.3, ε = 0.2, Sc = 0.6, Gr = 6, Gm = 4, α = 1.
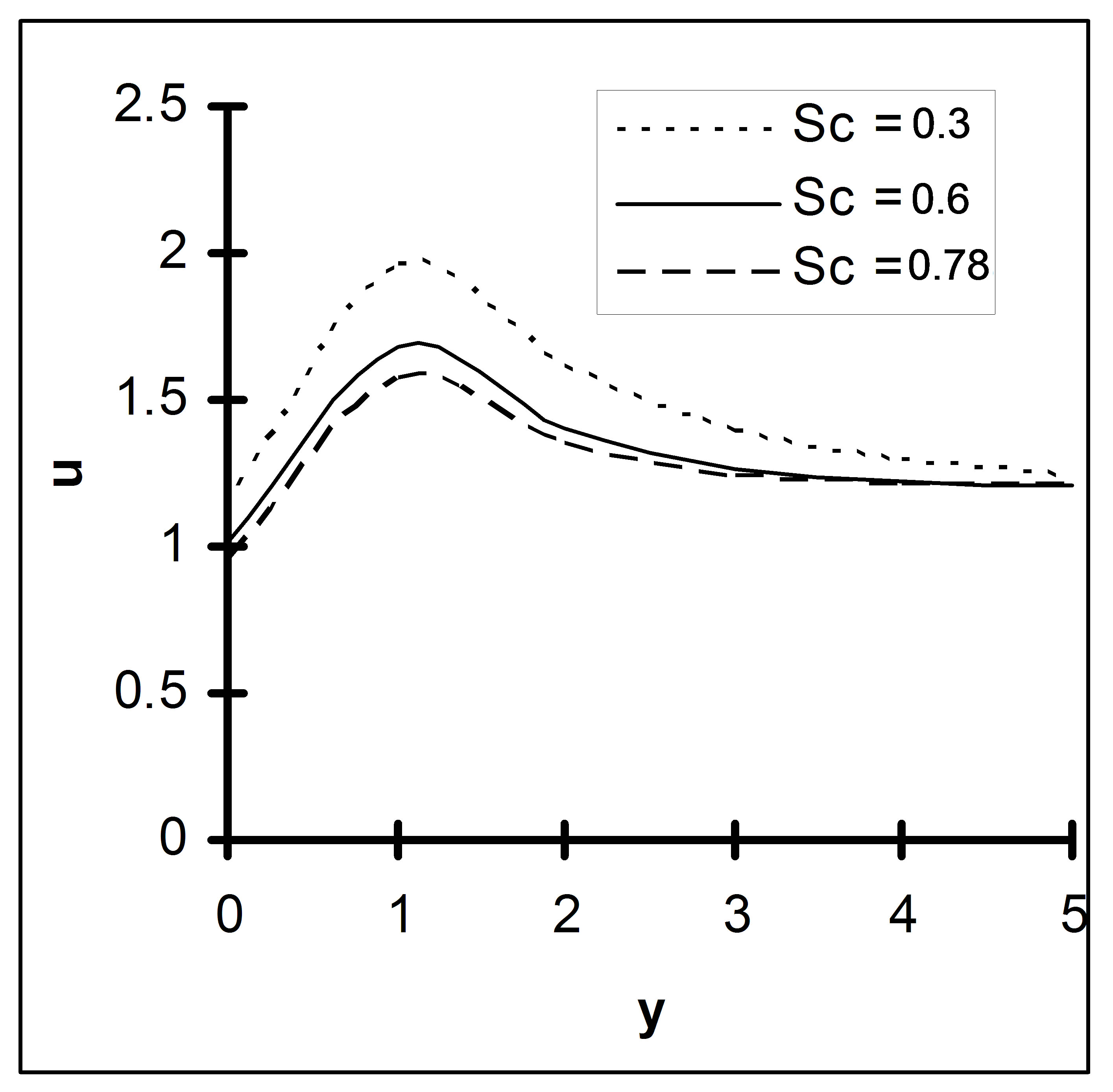
Figure 6. Velocity u versus y, under the effect Sc, for R = 2, M = 3, Q = 1, h = 0.3, ε = 0.2, K = 1, Gr = 6, Gm = 4, α = 1.

Figure 7. Velocity u versus y, under the effect of Gr, for R = 2, M = 3, K = 1, Q = 1, h = 0.3, ε = 0.2, Gm = 4, α = 1.
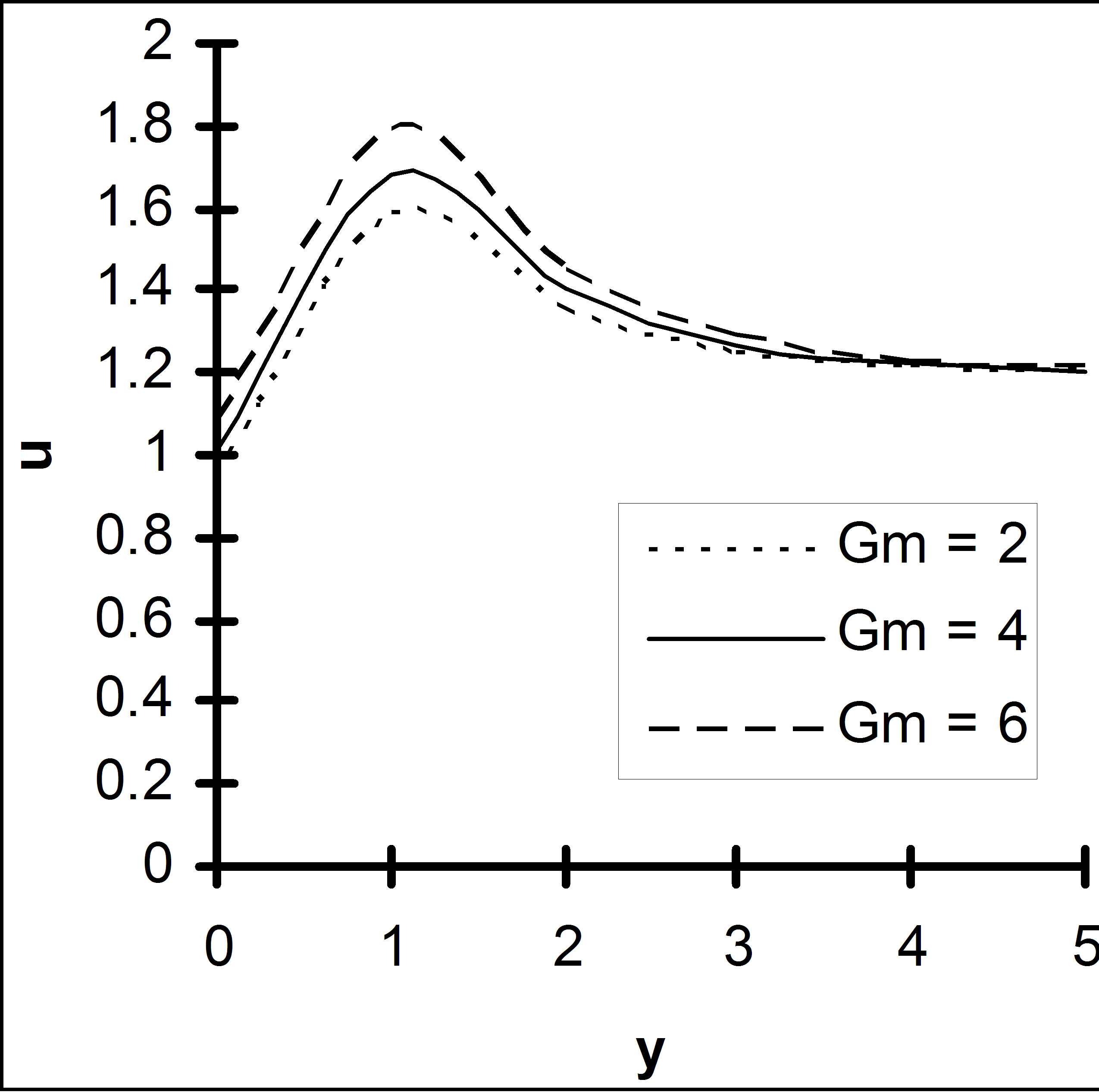
Figure 8. Velocity u versus y, under the effect of Gm, for R = 2, M = 3, K = 1, Q = 1, h = 0.3, ε = 0.2, Gr = 6, α = 1.
ability of porous medium is plotted in Figure 9. Here it is seen that due to increase of porosity of the medium fluid motion is accelerated. Moreover Figures 10 and 11 displays that the velocity u increases as  and rarefaction parameter h are increased indicating the fact that slips at the surface accelerates the fluid motion.
and rarefaction parameter h are increased indicating the fact that slips at the surface accelerates the fluid motion.
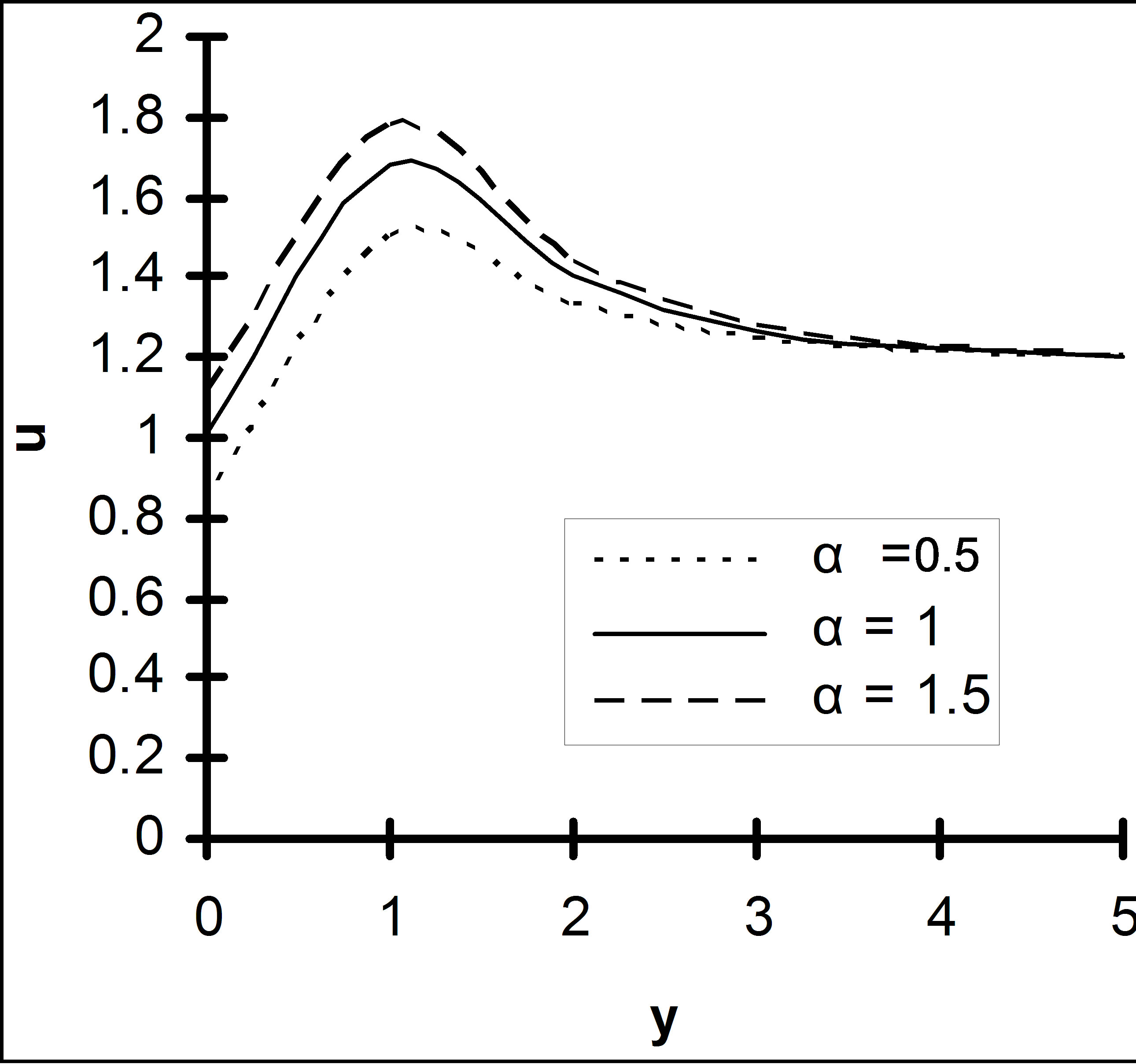
Figure 9. Velocity u versus y, under the effect of α, for R = 2, M = 3, K = 1, Q = 1, h = 0.3, ε = 0.2, Gr = 6, Gm = 4.
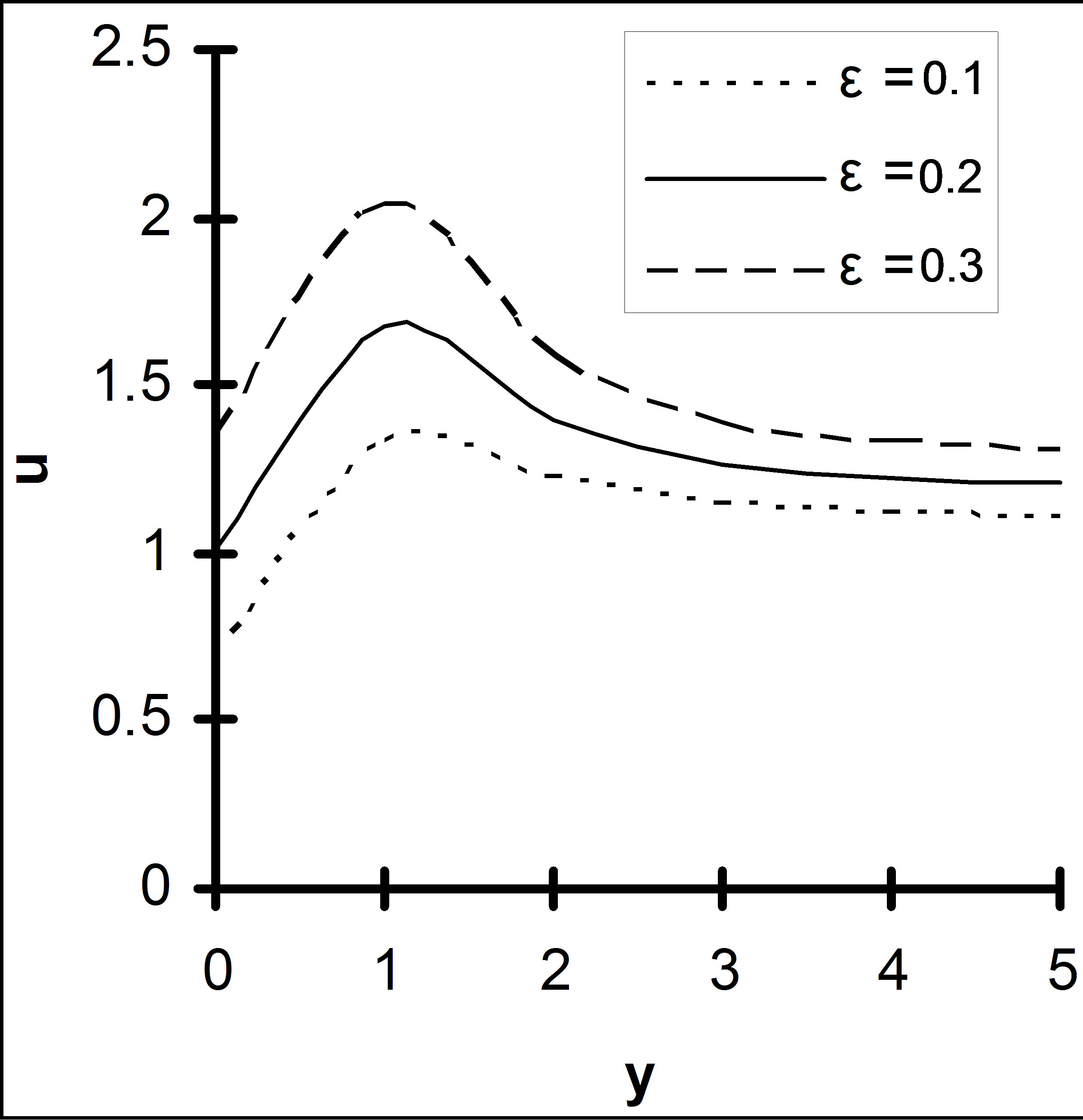
Figure 10. Velocity u versus y, under the effect of ε, for R = 2, M = 3, K = 1, Q = 1, h = 0.3, Gm = 4, Gr = 6, α = 1.
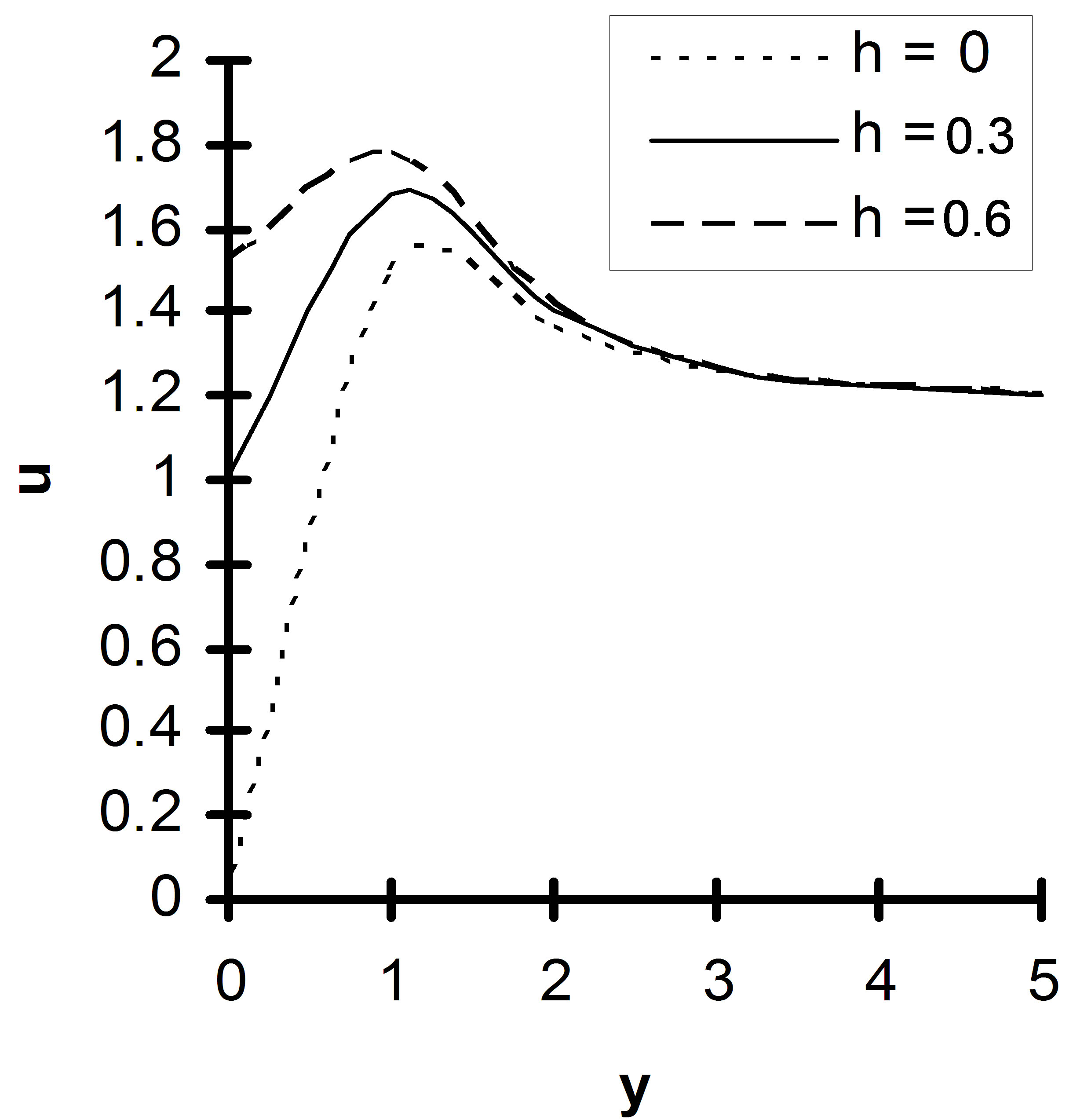
Figure 11. Velocity u versus y, under the effect of h, for R = 2, M = 3, K = 1, Q = 1, ε = 0.2, Gm = 4, Sc = 0.6, Gr = 6, α = 1.
The effects of Radiation parameter R, heat source parameter Q and 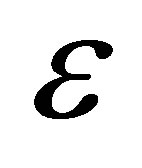 on temperature field against y are displayed in Figures 12-14.
on temperature field against y are displayed in Figures 12-14.
It is observed from Figure 12 that the temperature  decreases as the radiation parameter R increases. This result qualitatively agrees with expectation, since the
decreases as the radiation parameter R increases. This result qualitatively agrees with expectation, since the
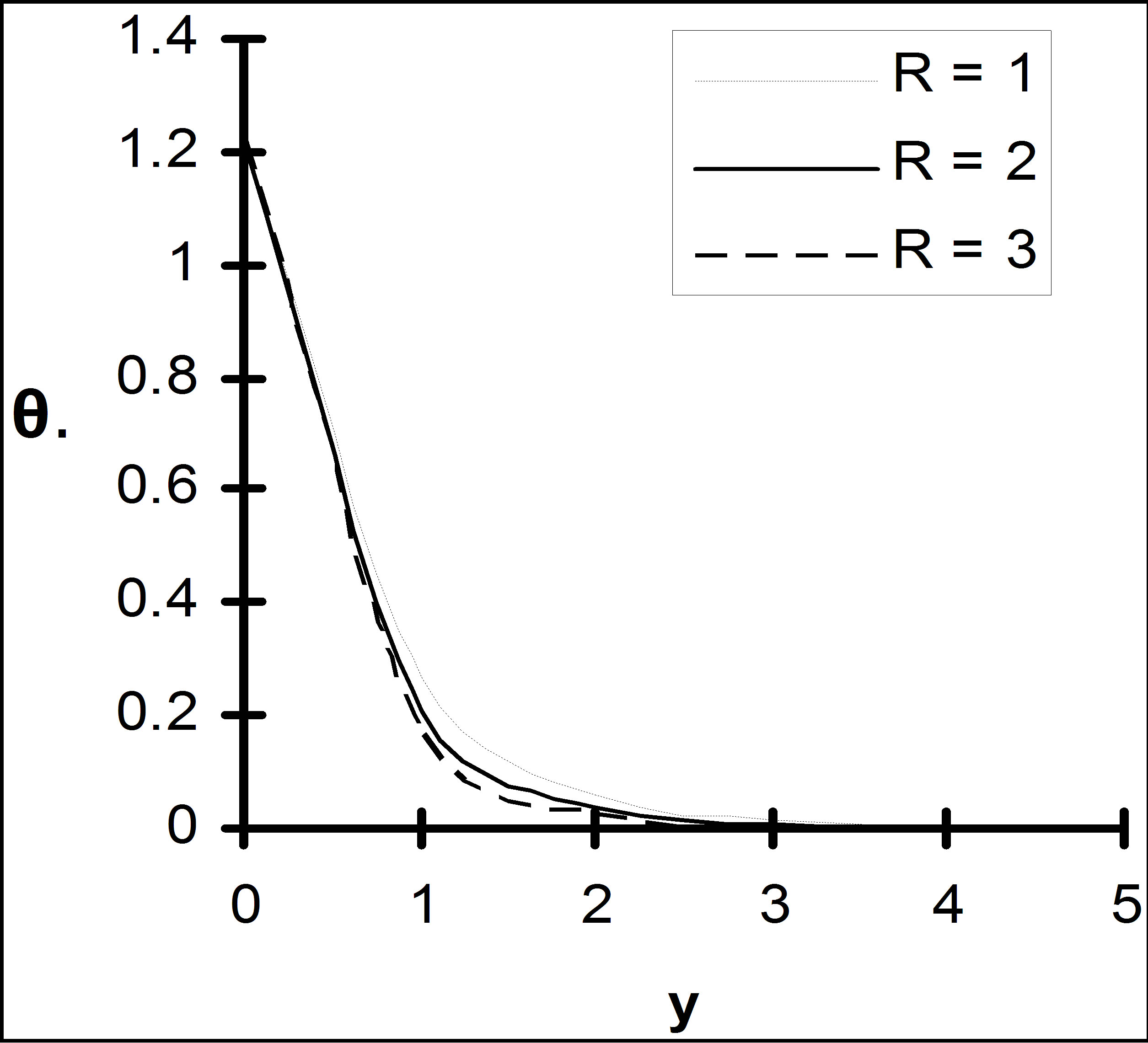
Figure 12. Temperature for different radiation parameter R with Q = 1, ε = 0.2.
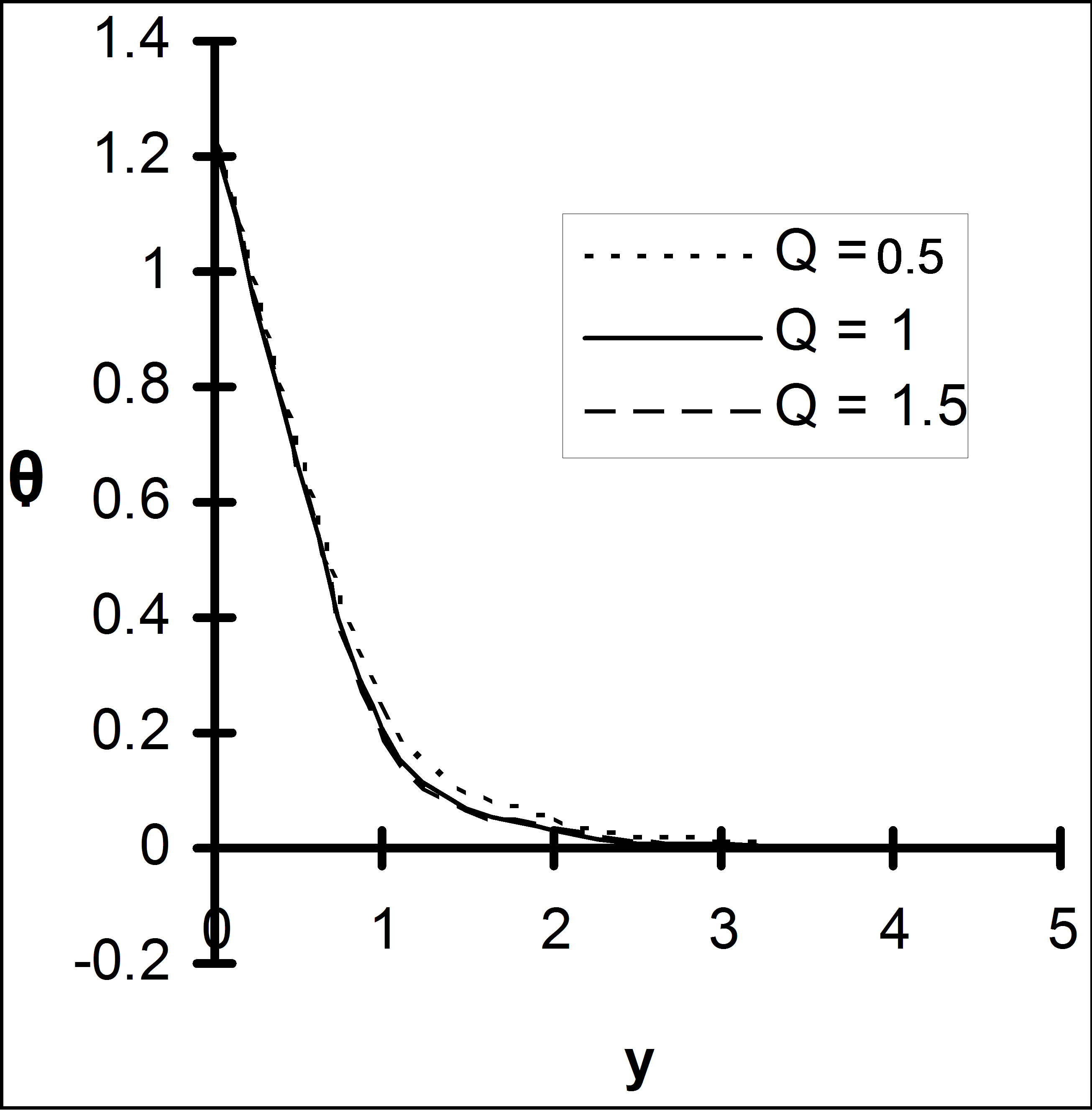
Figure 13. Temperature for different heat source parameters Q with R = 2, ε = 0.2.

Figure 14. Temperature for different radiation parameter ε with Q = 1, R = 2.
effect of radiation is to decrease the rate of energy transport to the fluid, thereby decreasing the temperature of the fluid.
It is seen from Figure 13 that increases in the heat source parameter decreases the temperature profile.
Moreover from Figure 14 it reveals that the temperature increases as 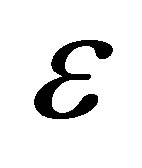 increases.
increases.
Figures 15-17 exhibit the variation of species concen-
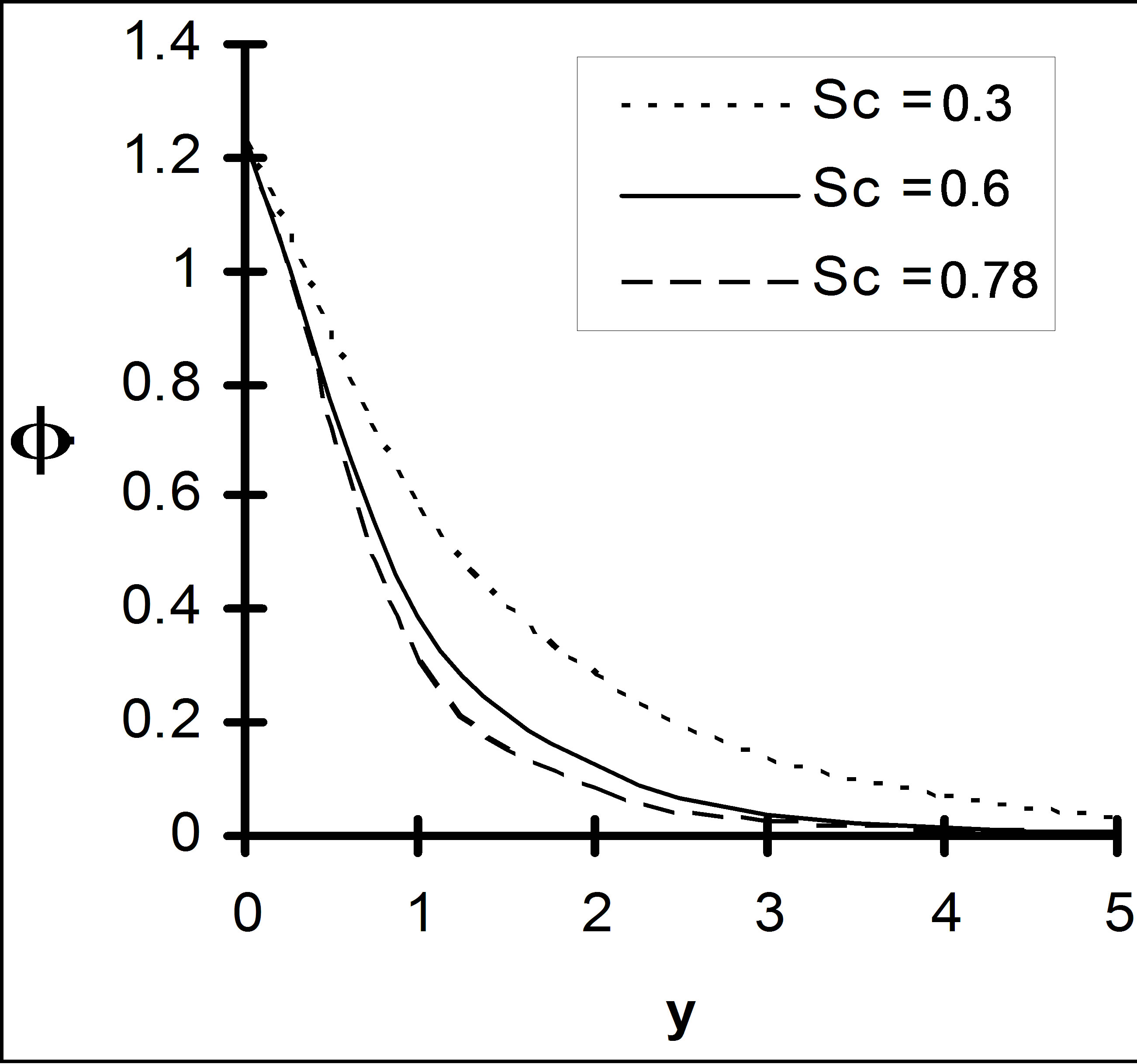
Figure 15. Concentration profile for different Sc with Q = 1, ε = 0.2, K = 1.
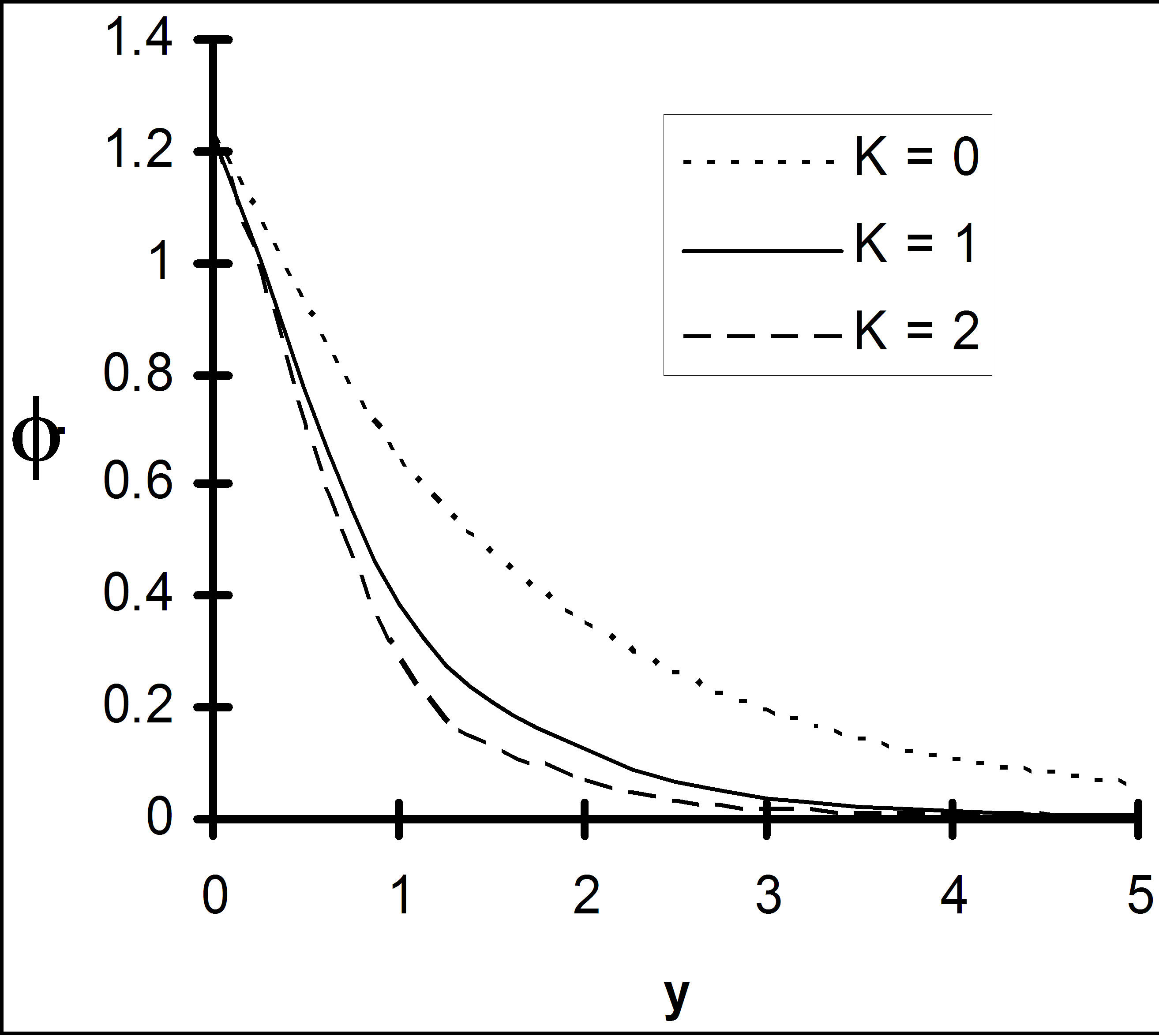
Figure 16. Concentration profile for different K with Q = 1, ε = 0.2, Sc = 0.6.
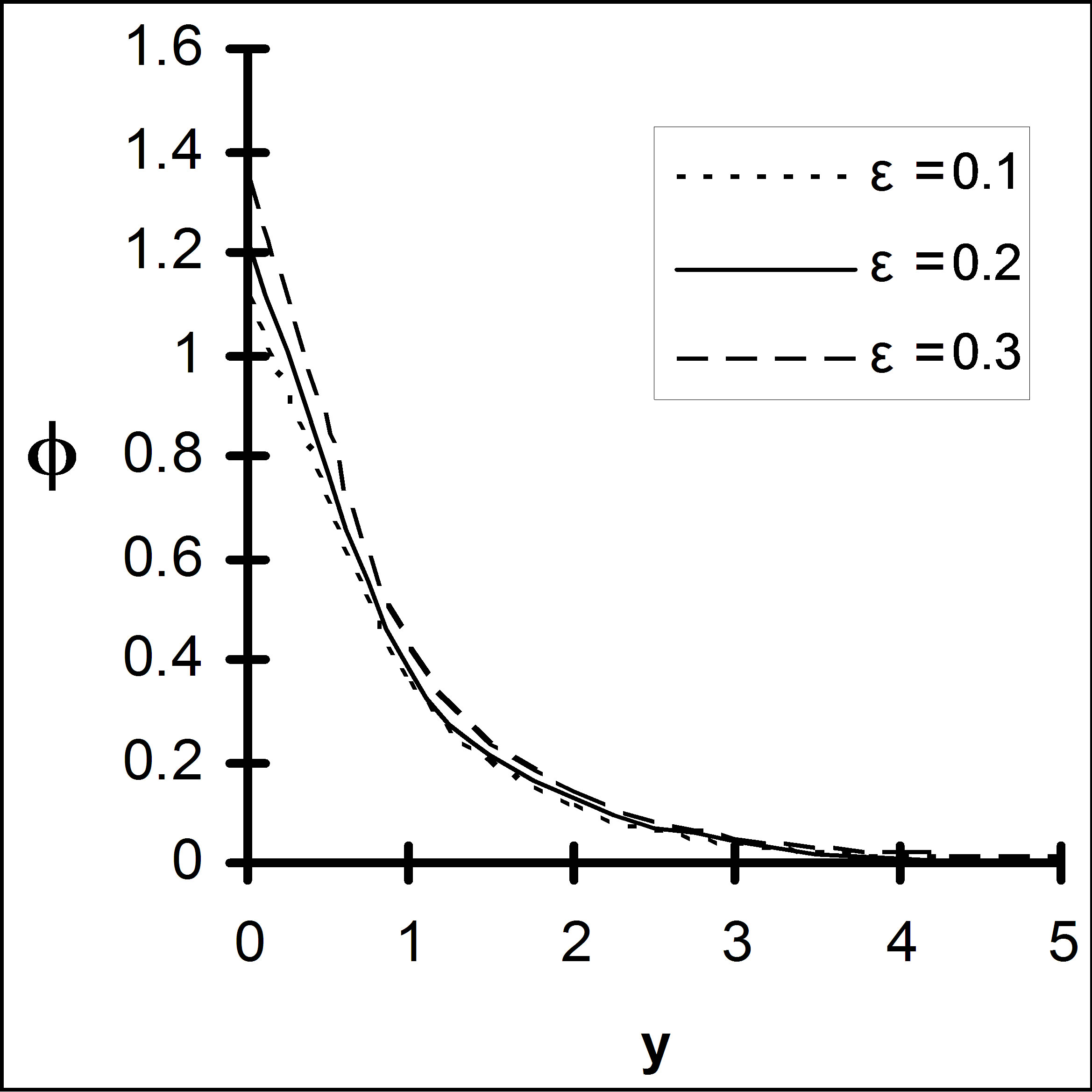
Figure 17. Concentration profile for different with ε, Q = 1, K = 1, Sc = 0.6.
tration against spanwise co-ordinate y under the influence of chemical reaction parameter K, Schmidt number Sc and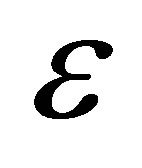 . It is seen from Figure 15 that the concentration level of the fluid drops due to increasing Schmidt number indicating the fact that the mass diffusivity raises the concentration level steadily. Further it is observed from Figures 15 and 16 that concentration falls under the effect of chemical reaction parameter K whereas it rises due to the effect of
. It is seen from Figure 15 that the concentration level of the fluid drops due to increasing Schmidt number indicating the fact that the mass diffusivity raises the concentration level steadily. Further it is observed from Figures 15 and 16 that concentration falls under the effect of chemical reaction parameter K whereas it rises due to the effect of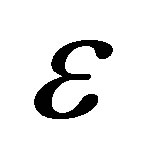 .
.
The numerical values for skin-friction, Nusselt number and Sherwood number are computed for various values of the parameters M, Sc, K, α, Q, h, Gr, R and Gm. These results are presented in table 1. It is seen from this table that the effect of increasing values of M, Sc and K is to decrease skin-friction coefficient whereas increasing values α, Q, Gr, Gm, h and R increases skin-friction coefficient.
It is observed from the Table 1 that there is no effect of M, Sc, K, α, h, Gr and Gm is seen on Nusselt number. But Nusselt number decreases with increase in Q and R.
Similarly, no effect of M, R, α, h, Gr and Gm is seen on Sherwood number whereas it is decrease with the increasing values of Sc and K respectively.
8. Conclusions
Our investigation of the problem setup leads to the following conclusions:
• The fluid velocity decreases as the existence of the magnetic field parameter becomes stronger.
• The fluid velocity is decelerated in the region adjacent to the plate, due to the effects of Schmidt number as well as chemical reaction.
• The fluid velocity is accelerated under the effects of thermal radiation, Grashof number for heat and mass transfer, heat source parameter,  , rear fraction parameter h and porosity of the medium.
, rear fraction parameter h and porosity of the medium.
• There is a steady drop in temperature for high radiation and chemical reaction.
• The mass diffusivity raises the concentration level steadily, i.e., the concentration level of the fluid, falls due to increasing Schmidt number.
• Increase in chemical reaction decreases the temperature whereas temperature increases as 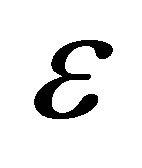 increases.
increases.
• The viscous drag at the plate in the direction of the buoyancy force may be successfully inhibited on application of strong magnetic field in operation.
• An increase in Grashof number for heat and mass transfer, thermal radiation, heat source parameter, rear fraction, 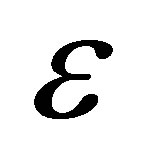 and porosity of the medium results in a growth in the drag force and it falls under the effects of chemical reaction and Schmidt number.
and porosity of the medium results in a growth in the drag force and it falls under the effects of chemical reaction and Schmidt number.
• The rate of heat transfer (from the plate to the fluid) decreases due to the effects of thermal radiation and heat source parameter.
The mass flux from the plate to the fluid is reduced under the influence of Schmidt number and chemical reaction.
9. Acknowledgements
The author is highly thankful to CSIR-HRDG for funding this research work under Research Grant-in-aid No.
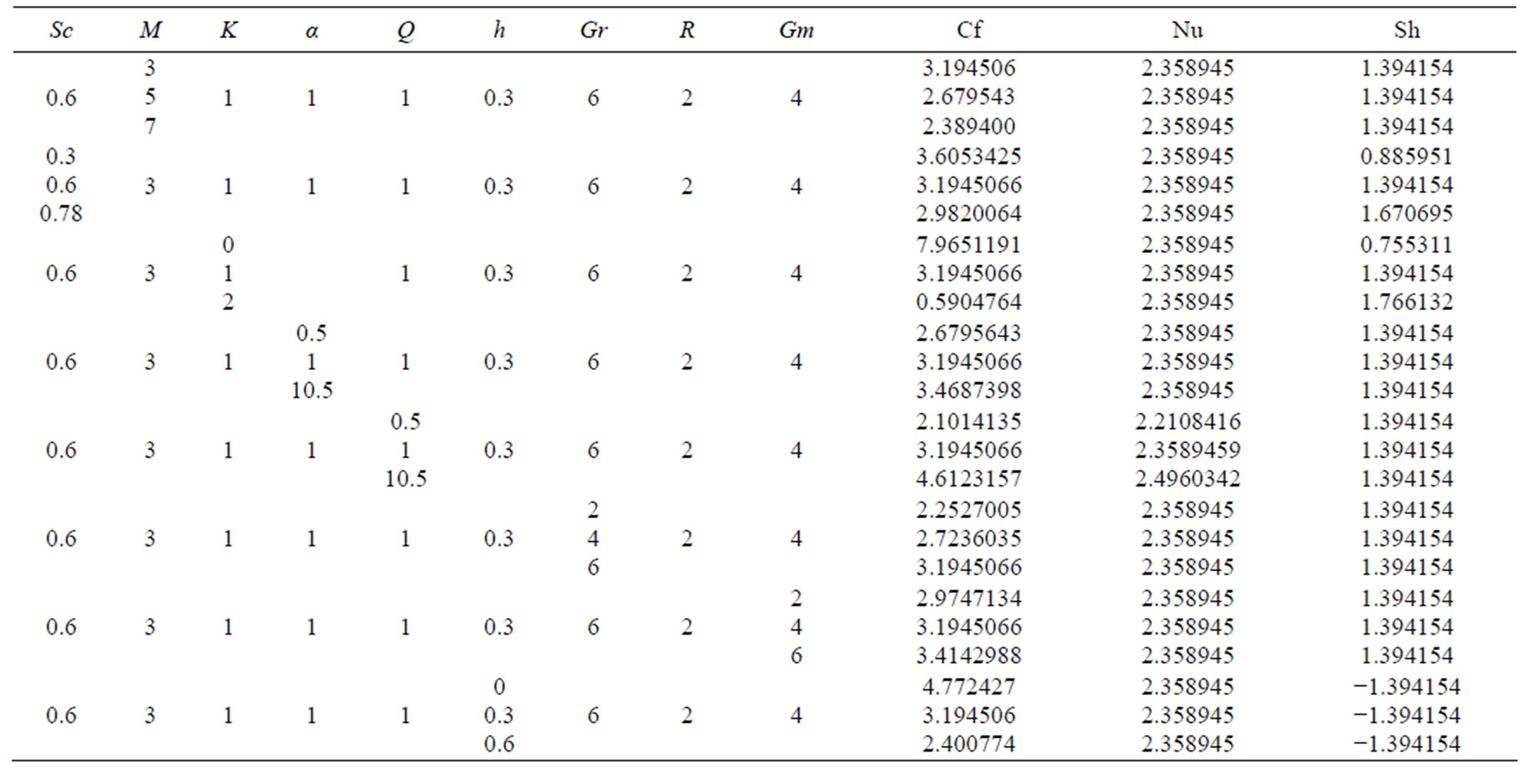
Table 1. Skin friction, Nusselt number and Sherwood number for various values of M, R, Gr, Gm, Sc, K, α with Pr = 0.7, n = 0.1, A = 1, ε = 0.2.
25(0209)/12/EMR-II.
REFERENCES
- A. Bejan and K. R. Khair, “Heat and Mass Transfer in Porous Medium,” International Journal of Heat and Mass Transfer, Vol. 28, No. 5, 1985. 902-918.
- O. V. Trevisan and A. Bejan, “Natural Convection with Combined Heat and Mass Transfer Buoyancy Effects in a Porous Medium,” Heat and Mass Transfer, Vol. 28, No. 8, 1985, pp. 1597-1611. doi:10.1016/0017-9310(85)90261-3
- M. Acharya, G. C. Das and L. P. Singh, “Magnetic Field Effects on the Free Convection and Mass Transfer Flow through Porous Medium with Constant Suction and Constant Heat Flux,” Indian Journal Pure Applied Mathematics, Vol. 31, No. 1, 2000, pp. 1-18.
- A. Rapits and N. Kafousias, “Magneto Hydrodynamics Free Convective Flow and Mass Transfer through a Porous Medium Bounded by an Infinite Vertical Porous Plate with constant Heat Flux,” Canadian Journal of Physics, Vol. 60, No. 12, 1982, pp. 1724-1729.
- U. N. Das, N. Ahmed and D. Sharma, “Three-Dimensional Free Convective MHD Flow and Heat Transfer through Porous Medium,” FJAM, Vol. 4, No. 3, 2000, pp. 357- 369.
- H. P. G. Darcy, “Lee Fort Airs Publication La Villede Dijan Victor Dalonat,” Paris, Vol. 1, 1857, p. 41.
- R. Wooding, “Steady State Free Thermal Convection of Liquid in a Saturated Permeable Medium,” Journal of Fluid Mechanics, Vol. 2, No. 3, 1957, pp. 273-285. doi:10.1017/S0022112057000129
- H. C. Brickmam, “A Calculation of the Viscous Force Exerted by a Flowing Fluid on a Dense Swarm of Particles,” Applied Sciences Research, Vol. A1, 1947, pp. 27- 34.
- H. C. Brickman, “On the Permeability of Media Consisting of Closely Packed Porous Particles,” Applied Sciences Research, Vol. A1, 1947, pp. 81-86.
- R. C. Chaudhary and A. Jain, “Combined Heat and Mass Transfer Effects on MHD Free Convection Flow Past an Oscillating Plate Embedded in Porous Medium,” Romanian Journal of Physics, Vol. 52, No. 5-7, 2007, pp. 505- 524.
- P. L. Chambre and J. D. Young, “On the Diffusion of a Chemically Reactive Species in a Laminar Boundary Layer Flow,” Physics of Fluids, Vol. 1, No. 1, 1958, pp. 48-54. doi:10.1063/1.1724336
- R. Muthucumaraswamy, “Effects of a Chemical on a Moving Isothermal Surface with Suction,” Acta Mechanica, Vol. 155, No. 1-2, 2002, pp. 65-70. doi:10.1007/BF01170840
- R. Muthucumaraswamy and S. Meenakshisundaram, “Theroretical Study of Chemical Reaction Effects on Vertical Oscillating Plate with Variable Temperature,” Theoretical and Applied Mechanics, Vol. 33, No. 3, 2006, pp. 245- 257.
- M. A. Hussain and H. S. Takhar, “Radiation Effect on Mixed Convection along a Vertical Plate in Presence of Heat Generation or Absorption,” Journal of Heat Transfer, Vol. 31, No. 4, 1996, pp. 243-248.
- N. Ahmed and H. K. Sarmah, “The Radiation Effect on a Transient MHD Flow Mass Transfer Past an Impulsively Fixed Infinite Vertical Plate,” International Journal of Applied Mathematics and Mechanics, Vol. 5, No. 5, 2009, pp. 87-98.
- V. Rajesh and S. V. K. Varma, “Radiation Effects on MHD Flow through a Porous Medium with Variable Temperature and Mass Diffusion,” International Journal of Applied Mathematics and Mechanics, Vol. 6, No. 11, 2010, pp. 39-57.
- D. Pal and H. Mondal, “Radiation Effects on Combined Convection over a Vertical Flat Plate Embedded in a Porous Medium of Variable Porosity,” Meccanica, Vol. 44, No. 2, 2009, pp. 133-144. doi:10.1007/s11012-008-9156-0
- A. M. D. Samad and M. M. Rahman, “Thermal Radiation Interaction with Unsteady MHD Flow past a Vertical Porous plate immersed in a porous medium, Journal of Naval Architecture and Marine Engineering, Vol. 3, No. 1, 2006, pp. 7-14.
- S. Karthikeyan, S. Sivasankaran and S. Rajan, “Thermal Radiation Effects on MHD Convective Flow over a Vertical Porous Plate Embedded in a Porous Medium by Perturbation Technique,” Proceedings of International Conference on Fluid Dynamics and Its Applications, Bangalore, 20-22 July 2010, pp. 484-491.
- S. Das, M. Jana and R. N. Jana, “Radiation Effect on Natural Convection near a Vertical Plate Embedded in Porous Medium with Ramped Wall Temperature,” Open Journal of Fluid Dynamics, Vol. 1, No. 1, 2011, pp. 1-11.
- D. Pal and B. Talukdar, “Perturbation Analysis of Unsteady Magnetohydrodynamic Convective Heat and Mass Transfer in a Boundary Layer Slip Flow past a Vertical Permeable Plate with Thermal Radiation Chemical Reaction,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 7, 2010, pp. 1813-1830.
- C. L. M. H. Navier, “Memoire Surles du Movement des,” Mem Acad. Sci. Inst. France, Vol. 1, No. 6, 1823, pp. 414-416.
- S. Yu and T. A. Ahem, “Slip Flow Heat Transfer in Rectangular Micro Channel,” International Journal of Heat and Mass Transfer, Vol. 44, No. 22, 2002, pp. 4225-4234. doi:10.1016/S0017-9310(01)00075-8
- S. Goldstein, “Modern Development in Fluid Dynamics,” Vol. 2, Dover, New York, 1965, p. 676.
- K. Watannebe and Y. H. Mizunuma, “Slip of Newtonian Fluids at Solid Boundary,” JSME International Journal Series B, Vol. 41, No. 3, 1998, p. 525.
- S. R. Jain and P. K. Sharma, “Effect of Viscous Heating on Flow past a Vertical Plate in Slip-Flow Regime without Periodic Temperature Variations,” Journal of Rajasthan Academy of Physical Sciences, Vol. 5, No. 4, 2006, pp. 383-398.
- A. R. A. Khaled and K. Vafai, “The Effect of the Slip Condition on Stokes and Couette Flows Due to an Oscillating Wall, Exact Solutions,” International Journal of Non-Linear Mechanics, Vol. 39, No. 5, 2004, pp. 759-809. doi:10.1016/S0020-7462(03)00043-X
- H. Poonia and R. C. Chaudhary, “The Influence of Radiative Heat Transfer on MHD Osciallating Flow in a Planner Channel with Slip Condition,” International Journal of Energy & Technology, Vol. 4, No. 2, 2012, pp. 1-7.
- A. C. L. Cogley, W. G. Vincenti and E. S. Giles, “Differential Approximation for Radiative Heat Transfer in a NonGrey Gas near Equilibrium,” American Institute of Aeronautics and Astronautics, Vol. 6, No. 3, 1968, pp. 551- 553. doi:10.2514/3.4538

