Open Journal of Applied Sciences
Vol.09 No.05(2019), Article ID:92741,6 pages
10.4236/ojapps.2019.95034
An NC Algorithm for Sorting Real Numbers in Operations
Yijie Han, Sneha Mishra, Md Usman Gani Syed
School of Computing and Engineering, University of Missouri at Kansas City, Kansas City, MO, USA

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 8, 2019; Accepted: May 27, 2019; Published: May 30, 2019
ABSTRACT
We apply the recent important result of serial sorting of n real numbers in time to the design of a parallel algorithm for sorting real numbers in time and operations. This is the first NC algorithm known to take operations for sorting real numbers.
Keywords:
Parallel Algorithms, Sorting, Sort Real Numbers, Complexity

1. Introduction
It is known widely that serial comparison sorting takes time for sorting n numbers [1] . Although integer sorting can outperform the lower bound for sorting n integers [2] [3], these algorithms generally do not apply to the problem of sorting real numbers. It has been known that n integers can be sorted in time and linear space [2] [3] . The time bound remains for sorting real numbers ever since. Only very recently Han showed that real numbers can be converted to integers for the sorting purpose in time [4], thus enabling the serial sorting of real numbers in time.
Parallel sorting algorithms for sorting real numbers run on the PRAM (Parallel Random Access Machine) model are known [5] [6] . The AKS sorting network [5] can be transformed into an EREW (Exclusive Read Exclusive Write) PRAM algorithm with time and operations. Cole’s parallel merge sort [6] sorts n numbers in time using n processors on the EREW PRAM. On the CRCW (Concurrent Read Concurrent Write) PRAM Cole showed [7] that his parallel merge sort can run in time using p processors. Also see [7] .
There are also parallel algorithms for integer sorting [8] [9] [10] [11] . In the case of integer sorting, the operation bound can be improved to below . In particular, [10] presents a CRCW PRAM integer sorting algorithm with time and operations and [11] presents an EREW PRAM integer sorting algorithm with time and operations.
For sorting real numbers, the previous best serial algorithm sorts in time. It was also known that for comparison sorting, is the tight lower bound. Thus if we use comparison sorting to sort real numbers, then in serial algorithms, we cannot avoid the time bound and in parallel algorithms, we cannot avoid the operation bound. In the past, no other sorting methods are known to sort real number in less than time and comparison sorting remained the norm for sorting real numbers.
However, the situation is recently changed completely as Han found a way to convert real numbers to integers for sorting purpose and he showed that real numbers can be sorted in time [4] . This result enables us to move further to improve the operation bound of parallel algorithms for sorting real numbers to below , as in the past, all parallel algorithms for sorting real numbers have an operation bound at least .
In this paper, we will apply the time serial real number sorting algorithm [4] to the design of an NC algorithm with time and
operations on the CREW (Concurrent Read Exclusive Write)
PRAM. NC stands for Nick’s Class [12] . NC algorithms are parallel algorithms with polylog time and polynomial operations. Algorithm in [4] is an inherently serial algorithm without much parallelism within it. Here, we use it in the design
of an NC algorithm with time and operations. This is the first NC algorithm for sorting real numbers with operations.
The computation model used for designing our algorithm is the CREW PRAM. On this model, in one step, any processor can read/write any memory cell. Concurrent read of one memory cell by multiple processors in one step is allowed and concurrent write of one memory cell by multiple processors in one step is prohibited. Parallel algorithms can be measured with their time complexity and the number of processors used. They can also be measured with time complexity and operation complexity which is the time processor product. The operation complexity (Tpp, with Tp time using p processors) of a parallel algorithm is often compared with the time T1 of the best serial algorithm. In general, . When , the parallel algorithm is said to be an operation optimal algorithm.
The main contribution of this paper is the demonstration of the existence of an NC parallel algorithm with operations for sorting real numbers. All previous parallel algorithms for sorting real numbers have at least operations. The algorithm presented in this paper is derived from Han’s time serial algorithm [4] for sorting real numbers by applying parallel algorithm design techniques. These parallel algorithm design techniques are specially tuned for the derivation of our parallel algorithm.
The remaining part of this paper is organized as follows. In Section 2 we present our NC algorithm for sorting real numbers with time and
operations. In Section 3, we present a running example of our algorithm and conclude our paper with the Main Theorem.
2. The Algorithm
Consider an algorithm for sorting n real numbers. Suppose each of the n/m lists with m real numbers in each list has already been sorted, we are to merge these n/m lists into one sorted list. We will do k-way merge in each pass to merge every k-lists into 1 sorted list and there are passes to have all n/m lists merged into 1 sorted list.
For simplicity, let us break down n elements into lists with m elements in each list. We can do parallel sort on the individual list of m elements recursively. Now we pick every k-lists and have them merged together.
The k-way merging of sorted lists is done as follows. For each sorted list of m real numbers we pick every k2-th real number, i.e. we pick the 0th real number, the k2-th real number, the 2k2-th real number, the 3k2-th real number, and so on. Thus from each list Li we picked m/k2 real numbers and these m/k2 real numbers form a sorted list . and from these k lists we picked m/k real numbers they form sorted lists . We merge into one sorted list L' using Valiant’s merging algorithm [13] (its improved version is given by Kruskal in [14] with time complexity of and linear operations for merging two sorted lists of m elements each) in logk passes and time and operations in each pass. Thus the total time for merging is and the total operation is .
Now for each real number r in
and for any
, r knows the largest real number s in
that is smaller than r and smallest real number l in
that is larger than r. s and l are actually neighbors in
. There are k2 elements between s and l in Lj. r then uses binary search in
time to find the largest real number among these k2 real numbers that is smaller than r and the smallest real number that is larger than r. That is, r finds the exact insertion point of r in Lj. Because there are k-lists and there are m/k real numbers in L' thus the time for this binary search is  and the operation is
and the operation is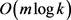 . The operation for all lists is
because there are n/m lists and every k-lists are merged in the k-way merge, we picked n/k2 real numbers and every one of them has to use k processors to check k-lists in the k-way merging. Because r is arbitrary picked and thus we know that every real number in L' knows its insertion point in every Lj. Let the real numbers in sorted order in L' be
. To merge
we need now to merge or sort all real numbers between the insertion points of ri and ri+1 in
. There are no more than k2 real numbers in Lj between the insertion points of ri and ri+1 and therefore the total number
of real numbers (call them a block) in
between the insertion points of ri and ri+1 is no more than k3 (i.e.
). When
we will combine multiple blocks together to reach k3 real numbers. We use the
serial sorting algorithm to sort them in
time. This represents
time and
operations in our parallel algorithm.
. The operation for all lists is
because there are n/m lists and every k-lists are merged in the k-way merge, we picked n/k2 real numbers and every one of them has to use k processors to check k-lists in the k-way merging. Because r is arbitrary picked and thus we know that every real number in L' knows its insertion point in every Lj. Let the real numbers in sorted order in L' be
. To merge
we need now to merge or sort all real numbers between the insertion points of ri and ri+1 in
. There are no more than k2 real numbers in Lj between the insertion points of ri and ri+1 and therefore the total number
of real numbers (call them a block) in
between the insertion points of ri and ri+1 is no more than k3 (i.e.
). When
we will combine multiple blocks together to reach k3 real numbers. We use the
serial sorting algorithm to sort them in
time. This represents
time and
operations in our parallel algorithm.
Thus the time for each stage is and the operation for each stage is . When we start with m as a constant then there are
stages and therefore the time of our algorithm is and the operation is .
Pick , we get time and operations.
3. Procedure
Step 1: Let’s say we have “m” sorted elements in each list, and we have a total of “n” elements to sort (Figure 1).
This implies that we have “n/m” lists to sort. To sort these blocks, we will apply k-way merging.
Step 2: Each stage of k-way merging is to merge every k sorted lists into 1 sorted list. This is repeatedly until all n/m lists are merged into one list (Figure 2).
Step 3: To merge k lists into 1 list, we need to pick the “0-th”, “k2-th”, “2k2-th”, “3k2-th”, … real numbers in each list Li to form a new list of m/k2 elements. This is shown as Figure 3.
Step 4: We merge into one sorted list L'. The elements of this new formed list L' then use binary search to find their exact insertion point in
Figure 1. n/m sorted lists of m elements each.
Figure 2. k-way merging of k lists.
Figure 3. Pick every k2-th element of each list.
. These insertion points then partition into m/k blocks with each block containing no more than k3 real numbers.
Step 5: When every one of these m/k blocks are sorted, we effectively merged into one sorted list L.
Main Theorem: n real numbers can be sorted in time and operations on the CREW PRAM.
Proof: The algorithm and its time complexity analysis are presented in Section 2. An example of the running of the algorithm is presented in Section 3. □
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Han, Y.J., Mishra, S. and Syed, M.U.G. (2019) An NC Algorithm for Sorting Real Numbers in
References
- 1. Corman, T.H., Leiserson, C.E., Rivest, R.L. and Stein, C. (2009) Introduction to Algorithms. Third Edition, The MIT Press.
- 2. Han, Y. (2015) A Linear Time Algorithm for Ordered Partition. International Workshop on Frontiers in Algorithmics (FAW'15), LNCS, 9130, 89-103. https://doi.org/10.1007/978-3-319-19647-3_9
- 3. Han, Y. (2004) Deterministic Sorting in O(nloglogn) Time and Linear Space. Journal of Algorithms, 50, 96-105. https://doi.org/10.1016/j.jalgor.2003.09.001
- 4. Han, Y. (2017) Sort Real Numbers in Time and Linear Space. In arXiv.org with paper id 1801.00776.
- 5. Ajtai, A., Komlós, J. and Szemerédi, E. (1983) An O(nlogn) Sorting Network. Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing, Boston, MA, 11-13 May 1983, 1-9. https://doi.org/10.1145/800061.808726
- 6. Cole, R. (1988) Parallel Merge Sort. SIAM Journal on Computing, 17, 770-785. https://doi.org/10.1137/0217049
- 7. Saxena, S., Chandra, P., Bhatt, P. and Prasad, V.C. (1994) On Parallel Prefix Computation. Parallel Processing Letters, 4, 429-436. https://doi.org/10.1142/S0129626494000399
- 8. Bhatt, P.C.P., Diks, K., Hagerup, T., Prasad, V.C., Radzik, T. and Saxena, S. (1991) Improved Deterministic Parallel Integer Sorting. Information and Computation, 94, 29-47. https://doi.org/10.1016/0890-5401(91)90031-V
- 9. Hagerup, T. (1987) Towards Optimal Parallel Bucket Sorting. Information and Computation, 73, 39-51. https://doi.org/10.1016/0890-5401(87)90062-9
- 10. Han, Y. and Shen, X. (1995) Conservative Algorithms for Parallel and Sequential Integer Sorting. International Computing and Combinatorics Conference, Lecture Notes in Computer Science, 959, 324-333. https://doi.org/10.1007/BFb0030847
- 11. Han, Y. and Shen, X. (2002) Parallel Integer Sorting Is More Efficient than Parallel Comparison Sorting on Exclusive Write PRAMs. Tenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA’99), Baltimore, Maryland, January 1999, 419-428. https://doi.org/10.1137/S0097539799352449
- 12. Cook, S.A. (1981) Towards a Complexity Theory of Synchronous Parallel Computation. L’Enseignement Mathématique, 27, 99-124.
- 13. Valiant, L.G. (1975) Parallelism in Comparison Problems. SIAM Journal on Computing, 4, 348-355. https://doi.org/10.1137/0204030
- 14. Kruskal, C.P. (1983) Searching, Merging, and Sorting in Parallel Computation. IEEE Transactions on Computers, C-32, 942-946. https://doi.org/10.1109/TC.1983.1676138




