Received 14 May 2016; accepted 26 July 2016; published 29 July 2016

ABSTRACT

The flexible wearable chair is like a light weight mobile exoskeleton that allows people to sit anywhere in any working position. The traditional chair is difficult to move to different working locations due to its large size, heavy weight (~5 - 7 kg) and rigid structure and thus, they are inappropriate for workplaces where enough space is not available. Flexible wearable chair has a gross weight of 3 kg as it utilizes light-weight aluminium alloy members. Unlike the traditional chair, it consists of kinematic pairs which enable taking halts between continuous movements at any working position and thus, it is capable of reducing the risk of the physical musculoskeletal disorder substantially among workers. The objective of this paper is to focus on the mechanical design and finite element analysis (FEA) of the mechanism using ANSYS^® software. In the present work, all the parts of the mechanism are designed under static load condition. The results of the analysis indicate that flexible wearable chair satisfies equilibrium and stability criterion and is capable of reducing fatigue during working in an assembly line/factory.

Keywords:

Assembly Line, Musculoskeletal Disorder (MSD), Flexible Wearable Chair, Equilibrium and Constraint Equations, Finite Element Analysis (FEA)

1. Introduction

Standing for some time is good for health, but only if you’ve not been forced to do it for hours. Excessive sitting is also dangerous as it badly affects the body’s metabolic rate, resulting in the risk of disease like high blood pressure, diabetes, cancer, depression, etc. In workstations, main concerned is to enhance the productivity but very less concerned is given to the effect of work fatigue on the worker’s body. Even though the workplace is ergonomically designed but, in fact, they are not successful in relieving worker fatigue since most of the time they have to work for hours in a particular posture. Till now in the present era of fast growing technology, workstations do not have a device which can provide comfort to the worker. It is evident that sloping/kneeling chair preserves lordosis and sacral slope with upright as well as slumped posture than a flat one; it results in less tissue strain which in turns lowers back pain. So why it is preferable to sit on a sloping chair than flat one [1] , this means flexible wearable chair provides better comfort than that of flat one for the same working posture.

Wearable chairs have a history of 37 years, in 1977, Darcy Robert Bonnet [2] invented a wearable chair which allowed users to sit on two legs, which was not obvious. But the design suggested by them has some demerits viz., it allows only one sitting position, irrespective to the user desire, also there is large stress on lower leg resulting from the reaction force imposed by the lower bar. The basic idea is that introducing internal hinges to the mechanism (structure when sitting) releases joint moment and providing these hinges coherent with human lower body joints helps in releasing severe joint stresses which occur during working. But the approach poses some ergonomic challenges, the biggest problem with such a design is ensuring that workers can move freely and after sitting, it is in stable equilibrium. It is well illustrated that how flexible wearable chair satisfies static equilibrium and stable configuration under loading.

According to Occupational Safety and Health Administration (OSHA) of US, MSDs are injuries and disorders of the soft tissues (muscles, tendons, ligaments, joints and cartilage) and nervous system and these are responsible for the ergonomic hazards in the developed and industrially developing countries. It becomes a challenging issue among ergonomists, industrial engineers and safety and health professionals all around the world. These ergonomic hazards lead to economic loss not only of the sufferer but also for the organization (large compensation and loss of productivity) and the society collectively thus ruining the manpower of a nation. Due to the hardcore physical work, workers in automotive assembly line/factories are subjected to various working postures, repetitive movements, vibrations and thermal gradients that can give rise to MSD [3] . The effect of workload on workers of an automotive industry in Malaysia shows that MSD is a major problem and needed to be controlled. Research data of other countries also show similar results. The study conducted by Anita et al. on a random sample of 255 workers of the median age of 24 years show that older age group is more susceptible to MSD than younger age groups. The prevalence of MSD among the automotive assembly line workers was 78.2% and now it is necessary to identify the body part/segment which undergoes severe stress cycle so that proper treatment has to be given during the incubation period of the muscular disorder. The prevalence of MSD at different body parts shown in Figure 1 (from Anita et al., 2014) indicates that the major stress area covers lower back to ankle, also 1 out of 4 persons is suffering from knee and ankle ache and 1 out of 2 suffering from lower back pain [4] . These data reflect the gravity of the situation and also give an indication to improve the design so that technology can be implemented in the industries.

The objective of the paper is to design and analyze a chair which can be adjusted as per work’s gesture and posture, minimize the load acting on the body parts and when needed, it can be portable from one place to another

place. MSD is burning issue which is faced by ergonomist in the present scenario and has to be relieved. Further, one can observe that implementing flexible wearable chair technology leads to easing muscle fatigue (MSD) and an increase in the productivity which makes it an integral part of workstations design.

2. Stability Criterion and Description of the Mechanism

There can be as many models for the proposed idea, but the successful model is one which competes with traditional chairs. Since for such structure, stability is of prime importance, in order to construct the most optimum model it is necessary to analyze all the parameters affecting stability and comfort. For a structure to be in static equilibrium the vectorial sum of all the forces and moment acting on it must be zero. A body satisfying the equilibrium equation, not necessarily to be stable (as stability is defined as a resistance to the disturbance of the body’s equilibrium), balance within muscle groups and alignment of the skeletal system affect body equilibrium and balance. Slight change in the body posture can affect the whole weight distribution. For a structure to be in stable equilibrium, the centre of mass of the body must fall within the base of support (BOS) (Figure 2). Under this condition, the reaction force at the base of support cancels the force of gravity and the torque produced by it. If the centre of mass is outside the base, the torque produced by the weight tends to topple the body [5] .

Base of support (BOS) is the supporting area beneath the body, it includes the points of contact with the supporting surface and the area between them; these points may be body parts (such as the feet), or extensions of body parts (such as crutches or other walking aids) (Figure 2).

The most important factors for achieving balance are the following [6] :

1) COG must fall within BOS i.e., one can stand at any posture till the line of gravity lies within the foot base;

2) Balancing is directly proportional to the size of the BOS i.e., larger the base of support, the body is more stable and in our mechanism BOS is user feet area plus the projected area of contact points of mechanism of both legs (cross-section of element E) with the ground;

3) Balancing is mass dependent, i.e., greater the mass body gets more balanced.

On careful investigating, one can notice that during vertically downward sitting knee bends forward and ensures that the projection of the centre of gravity of the body just falls within the BOS. Further, it can be noticed gradually downward sitting has an additional constraint that it has to move vertically downward like guide has to move in a slot. Installation of a flexible element between buttocks and ground can mimic the biomechanics of human sitting and transmit the whole body weight directly to the ground without the muscles pain (Figure 2(e) represents the flexible wearable chair and Figures 2(a)-(d) are from Egoyan and Moistsrapishvili, 2013). Figure 2(e) shows how BOS gets increased by attaching wearable mechanism and kinematic constraint that enforces COG to fall within BOS.

Flexible wearable chair consists of three beam elements AB, BC and CF (with a rectangular cross-section) which has to support the lower and upper leg, a flexible element (AE) between buttocks and ground for achieving various seating configurations and a locking mechanism. The flexible link is a cylindrical pair consisting of so many holes for various combinations of sitting positions and to lock the mechanism at desired working posture a pin has to be inserted into the mating holes and to be open manually for movement from one place to another. In the mechanism, two turning pairs are introduced between the beam elements AB, BC, and CF (Figure 4(b)). In order to follow the constraint of vertical sitting lower cylindrical link (DE) must be fixed at end “E” and co-axial with the upper hollow cylindrical rod (AD). An additional turning pair “A” is installed between beam AB and the upper hollow cylindrical rod AD, finally, the lower hollow cylindrical rod DE is attached to the bottom most

beam element CF. Both frames of the chair are connected by a wearable cover belt arrangement which has to be attached to the waist of the user. After introducing all these factors, the mechanism becomes completely constrained and it can be observed that flexible wearable chair is simply an inversion of four bar chain mechanism. The foam cushion is glued to the beam element for providing sitting comfort to the users and straps on the beam elements AB and BC are used to attach the flexible chair to the legs, Figure 3(a) shows a prototype of the flexible wearable chair without wearable cover belt arrangement.

3. Biomechanical Modelling

Figure 3(b) shows the schematics of the CAD model of the flexible wearable chair. For analyzing the model it is necessary to define various loads acting on the chair under lock condition, but the actual load distribution of the human body is quite complex therefore model is based on the following assumptions:

1) Loads are applied to the plane of bending i.e., 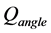is zero (is an angle between mechanical and anatomical axis) so that there is symmetric bending, also all-time COG of upper body part (A^#) pass through A.

2) Load distribution of thigh is linearly varying (UVL) (Figure 4(a)) and load is shared equally by both the legs.

3) The supporting surface has sufficient friction so that there is no sliding and the lowermost beam is fixed.

When the body adopts a sitting posture the weight of the body is distributed over the supporting surfaces. This distribution of weight depends on the mutual position of the surfaces. Table 1 and Table 2 (from Goossens, 1994) show the load distribution of human body parts [7] . In the following a model is presented to calculate the forces in perpendicular and parallel components, w.r.t the support surface.

In the model seated user/human is divided into links viz., lower legs (weight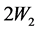), upper legs (weight) and upper body (weight 2P). These links (1, 2, 3 and 4) are joined by turning pairs (Figure 4(b)).

3.1. Load Distribution of Leg in Local Coordinate System

Making equilibrium of force in the vertical direction and moment about end B we have following equations:

(1)

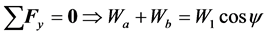. (2)

On solving (1) and (2) we get 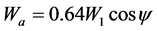and. Further and are the area under rectangular and triangular load distribution respectively, therefore maximum load intensities at end “A” are:

(3)

. (4)

Similarly for lower leg load distribution is given by:

and. (5)

Shear force at thigh and lower leg contact with beam are

and respectively. (6)

3.2. Equilibrium Equations in Local Coordinate System

As we know that a system of rigid bodies is statically determinant and stable if a number of independent equilibrium equations () are equal to the number of unknown (). Since for planar bodies we have three independent equilibrium equation for each body part so if is the bodies in a system than, further number of unknown is given by the relation; where is number of fixed supports, is number of hinged support and is number of simply supports [8] .

In this system, there are 4 body parts () which form 12 independent equilibrium equations. Also, there are two fixed one () and three hinged support () therefore number of unknowns are 12 thus system becomes statically determinant and stable. Considering equilibrium of flexible wearable chair (Figure 5):

(a) For beam element AB

(7)

(8)

(9)

(b) For beam element BC

(10)

(11)

(12)

(c) For beam element CF

(13)

(14)

(15)

(d) For rod assembly AE

(16)

(17)

. (18)

3.3. Buckling Criterion for Column “AE”

The column can be modelled as single stepped cantilever column fixed at end “E” (Figure 6). EI₃ and EI₄ are flexural rigidity for upper and lower portion of the column, respectively. Approximating deflection curve (red colour curve) by the equation

. (19)

Bending moment at any cross-section of column is given by:

(20)

where

The system will shift from stable equilibrium to unstable one if strain energy of the system due to bending () becomes less than work-done due to the compressive force (). The transverse force acting on hinge A is not considered in the analysis since it does not affect critical buckling load or corresponding transcendental relation. Following from [9] , the critical buckling load can be found from the equation:

.

The strain energy of bending is given by

(21)

Work done by compressive force (P) is given by

. (22)

Equating Equations ((21) and (22)) we get

(23)

where

4. Results and Discussion

The finite element method is a numerical method for solving problems of engineering and mathematical physics, ANSYS^® software is based on the fundamentals of FEA. For analyzing the problem biomechanical model is created in ANSYS^® software, but to get numerical output it is necessary to assign some feasible values for the dimension of various links of the flexible wearable chair.

At the location of the internal hinge (A, B and C) moment is zero; displacements are same but have an independent rotation. In general linear constraint equation in ANSYS^® can be defined as follows:

where = Constant term, = Coefficient of i^th displacement [10] .

For defining internal hinge at “A”, firstly two nodes viz., 1 and 2 are defined at “A” and then insert following constraint equation:; and. A Similar expression can be developed for internal hinges B and C.

4.1. Input Data for Analysis

Links dimension: Majumder J. [11] carried study on 147 Indian male within the age group of 18 - 65 years using Shapiro-Wilk test, results indicates that at a significance level of 0.271, 95^th percentile of population weight falls within 78.3 ± 10.5 kg. Considering some safety factor, the mechanism is designed for extreme weight of 100 kg with following functional length of 5^th percentile of selected population as mentioned in Table 3 (from Majumder, 2014) (which can be further extended for 95^th percentile of population by attaching extendable beam element).

4.2. Analysis Results

Since the mechanism has one degree of freedom, a relation exists between ψ and Ø which is given by and for prototype of the flexible wearable chair (see Figure 3(a)) equation reduces to. Another equation is needed for determining particular configuration (i.e., ψ and Ø) which is given by and at any given configuration it reduces to ; where length and angles are in mm and degree respectively. At any sitting position various loads are given by P = 304.11 N; and and by solving above two simultaneous equations one can get ψ and Ø. Thereafter intensity of distributed load and shear force on beam AB and BC can be determined from Equations ((3)-(6)). Prerequisites for the design of flexible wearable chair it is necessary to analyse the bending moment, buckling instability and deformation feature acting on various elements of chair, which are as follow.

4.2.1. Stress Analysis

For the design of structure it is important to find out the critical section and critical section can be found out by

the point of the maximum absolute bending moment. For different sitting positions absolute value of internal joint reactions and moment can be computed by solving simultaneous Equations ((7)-(18)) using MATLAB^® and results are plotted in Figure 8. The result shows that joint moment decreases continuously with increasing angle Ø whereas joint moment first increases with increasing Ø reaches its maximum () at 5^th locking position (Ø = 37.43˚) and then decreases with further increase in Ø. Finite element model of flexible wearable chair consists of 100 beam elements on member AB, BC, AD, AE and 50 elements on CF, it is seen that result converges to actual one on such meshing but elements fewer than this affects the distribution of bending moment along the members. Figure 7 shows the bending moment diagram of beam elements of structure in LCS using ANSYS^® for 1^st and 5^th position respectively. It can be seen that for 5^th sitting position maximum absolute bending moment occurs at E with a magnitude of 31.26 N-m, which validates the result obtained from Figure 8(a). Also, it can be noticed that out of beam AB and BC maximum bending

moment occurs on beam AB and it increases as Ø decreases (Figure 7) and reaches its maximum value of 5.294 N-m. As bending moment is independent of cross-sectional geometry so it can be used to design the beam elements. Flexural stress acting on the critical section of beam AB is given by Euler-Bernoulli equation as

4.2.2. Material Selection and Beam Dimensions

Mechanism can be portable if it is light weight, for this one have to choose high specific strength material. Additional to this considering hollow section further reduces weight and making beam/column stiffer. As most of the load is carried by column AE and it increases with Ø (see Figure 8(b)), which in turn increases the possibility of penetration of column via locking pin if an appropriate material is not selected. Considering all these aspects and material availability, proposed material for column AE is 6061-T6 aluminium alloy and pure aluminium for the beam elements. It is obvious that increasing the beam depth has more effect on the reduction of

flexural stress than an increase in beam width, for ergonomic consider-

ation minimum beam width (B) should be 60 mm. As the thickness (h) of rectangular cross-section increases flexural stress diminishes, but the major concerned is given to a weight reduction of the mechanism so it is not feasible to adopt a much thicker section. Internal hinges which are formed on 60 mm beam width exerts contact stress which tends to deform thin aluminium beam. A wooden block of length 50 mm are fitted at the end “A” of beam AB to get reed from this problem and a thickness, h = 1.5 mm is suitable for beams. The depth of beam affects the stresses induced on beam AB, as aluminium has much higher yield strength so it is unnecessary to go beyond w = 40 mm. The cross-sectional geometry of 63 × 37.4 × 1.5 mm³ is chosen for beam elements and with this geometry maximum stress induced is 5.3 MPa which is far-far less than the yield strength of aluminium.

4.2.3. Buckling Analysis

The flexible wearable chair gives relief to the user due to rods which directly transmit maximum body load to the ground, but users are in a trouble if there is a failure of these rods under static loading. Slenderness ratio of the rod assembly varies nearly in between 67.36 to 103 so buckling is a preferable mode of failure rather than crushing. Support conditions play a crucial role in the computation of critical buckling load, in the analysis top most point “A” of the rod assembly which is a hinge joint (free to move in the x-y plane) and a lowermost point “E” is fixed one. There can be a different choice of the section of column design, a hollow circular section of 6061-T6 material is considered, but for minimizing weight one have to choose the thickness of a column such that it doesn’t tear due to bearing pressure exerted by steel pin and no local buckling takes place. For buckling analysis column has been meshed with tetrahedron shaped element in ANSYS^®. For the configuration Ø = 57.92˚ firstly starting from coarse meshing with 19,789 nodes and 9857 elements large deviation is observed from modelling results, on mesh refinement to medium mesh with 21,478 nodes and 10,698 elements results converges to modelling predictions and further refinement doesn’t alter the accuracy. Similarly, for other configuration medium meshing results in the convergence of results within the desired accuracy.

Mathematical model doesn’t take the effect of holes, pin connection and increase in the value of the second moment of inertia I₄ of the column DE with decreasing Ø (due to insertion of rod AD inside DE), so it becomes necessary to consider such effects and analyzing critical buckling load predicted by mathematical model (Equation (23)) and actual model (from ANSYS^®). Figure 9 shows variation of Critical buckling load with Ø for two different combinations of external diameter of column AD and DE at three column thickness. Variation of critical buckling load predicted by ANSYS^® and mathematical model is shown by Figure 9(a) & Figure 9(b) and Figure 9(c) & Figure 9(d) respectively. It can be seen that irrespective of thickness buckling strength of column increases with decreasing Ø since with increase in Ø column length increases and become more prone to buckle. For d = 16 mm, D = 20 mm at Ø = 28.89˚ column strength reduces by 400N with a reduction of column thickness of 0.5 mm but as Ø increases this difference also decrease and reaches a value of 100N at Ø = 57.92˚. Similarly for d = 20 mm, D = 25 mm buckling strength reduces by 500N with a reduction of thickness from 2 mm to 1.5 mm but it reduces by 850N with a further reduction in column thickness from 1.5 mm to 1 mm. An error encountered due to practical aspect is nearly 4% - 5%, which, is a good agreement of results and mathematical method can be used for prediction of failure behaviour of the column.

Compressive load on the column increases with Ø and attains maximum load of 431N at Ø = 57.92˚ (Figure 8(b)), considering the worst case when user transfers whole body weight to one chair frame, which results in

column load of 862N. Actual buckling load at this configuration for d = 16 mm, D = 20 mm at different thickness t = 1 mm, 1.5 mm and 2 mm are 578.44N, 686.51N and 989.93N respectively, which indicates that column buckles for thickness less than 2 mm and one should consider 2 mm thickness including some safety margin. But for another column dimension d = 20 mm, D = 25 mm with t = 1 mm, 1.5 mm and 2 mm critical buckling load is given by 1204.9N, 1404N and 1800.6N respectively, these loads are higher than the critical buckling load at any thickness and one can select 1 mm column thickness. At locking position excessive bearing pressure exerted by pin and with such smaller column thickness pin can easily penetrate/tear leads to failure of the structure. After considering all these issues external diameter chosen for column AD and DE are 20 mm and 25 mm respectively with column thickness of 1.5 mm.

4.2.4. Deformation Analysis and Static Stability Issues

For deformation analysis, it is necessary to predefine various dimensions of the chair and a chosen dimension should be quite stiff. Due to the load distribution of the thigh, lower leg and body forces acting on the chair in locking position various stresses get induced in the chair and deflection analysis become important to judge the deformability of the chair frame. Results show that top most point A, undergo a net maximum deflection of 0.497 mm and point B undergo a deflection of 0.407 mm in x-y plane relative to the undeformed configuration of the chair. These deflections are very small which ensures that chair remains quite stiff in use. One can point out that contact points E and F are modelled as a fixed one under the assumption of sufficient friction between the shoe and ground. Sliding force increases as the inclination of lower leg with horizontal decreases (see Figure 8(b)) and reaches its maximum value of 50.349N at Ø = 28.89˚. This sliding force can fall user in trouble if sufficient friction doesn’t exist at the interface. Commonly used shoes material is rubber and its approximate coefficient of static friction with dry concrete, wood, wet concrete and mud are 1, 0.7, 0.9 and 0.45 respectively. For various “Ø” normal force on the interface remains 490.5N and minimum frictional resistance is for the shoe-mud interface which is equal to 220.725N (=0.45 × 490.5) before sliding takes place, which in turns 4.38 times of applied force. Thus, friction prevents sliding and takes care of user at various sitting positions.

5. Conclusion

Finite element method is used for verifying and further analysis of the biomechanical model; results from modelling successfully predict critical buckling load and deformation characteristics of the flexible wearable chair. Various dimensional and stress analysis had been performed on ANSYS^® software, the design was modified at each step to finalize the product dimensions. It is found that stress and deformations under loading condition are within the permissible value and structure will be stable under prescribed dimensions of beam and column. To test the model predictions, the results were successfully applied to fabricate the flexible wearable chair by using pure aluminium and its alloy 6061-T6. It is found that the gross weight of the mechanism for both legs is 3 kg and prototype fulfills the criterion of lightweight, reduces the risk of MSD and portable as per user requirement. A flexible wearable chair is a marvellous invention and hopefully, it will minimize the risk of MSD and leads to the increase in productivity of the industry by reducing worker’s fatigue.

6. Future Scope

The choice of material was limited due to its availability. In the future, carbon-fiber-reinforced polymer (CFRP) can be used to further minimize the weight and increase the strength of the structure. In present work, no attention is given to locking mechanism so different locking mechanisms can be used to involve providing better and smoothing functioning of the chair. The sensor can be attached to the body for locking of the mechanism by itself as per user needs. This chair is capable of relieving fatigue of lower body parts and needed further modification so that upper body parts are also free from MSD. The portability of the chair can be improved by converting it into a foldable flexible wearable chair.

Cite this paper

Ashutosh Bijalwan,Anadi Misra, (2016) Design and Structural Analysis of Flexible Wearable Chair Using Finite Element Method. Open Journal of Applied Sciences,06,465-477. doi: 10.4236/ojapps.2016.67047

References

Nomenclature

COG = Centre of gravity;

B = Width of beam in mm;

d = External diameter of column AD;

D = External diameter of column DE;

e = Eccentricity between beam element CE and column;

l= Length of rod assembly at any locked/working position;

LCS = Local co-ordinate system (x-axis is along the beam and y-axis is orthogonal to it);

= Vectorial summation of all the forces along the beam;

= Vectorial summation of all the forces perpendicular to the beam;

= Vectorial summation of all couple at i^th joint along z direction;

t = Thickness of column “AE” in mm;

W = Depth of beam in mm;

= Uniformly distributed load (UDL) with load intensity,;

= Triangular load (UVL) with extreme load intensity,;

Z = Section modulus;

Ø = Inclination of lower leg/beam element BC with horizontal;

= Inclination of human thigh/beam element AB with horizontal.

NOTES

^*Corresponding author.