Received 18 November 2015; accepted 27 December 2015; published 30 December 2015

ABSTRACT

The evaluation problem with three-parameter interval grey number (T-PIGN) widely exists in real world. To select effective evaluation indicators of the problem, this paper puts forward evaluation index system selection principle of T-PIGN based on distance entropy model, and gives out evaluation index system selection judgment criterion of T-PIGN. Furthermore, for the redundancy of evaluation index system with T-PIGN, a selection method of evaluation index system with T-PIGN is proposed. Finally, the applicability of the proposed method is verified by concrete examples.

Keywords:

Evaluation Indicators Selection, Three-Parameter Interval Grey Number, Grey Distance Entropy

1. Introduction

The comprehensiveness and proper simplification of evaluation index system is an important and key step in multiple attributes evaluation problem. Although, there are many influencing factors on the evaluation effectiveness of evaluation objects, the evaluation index is not the more the better. The key problem of evaluation is whether the selected index is proper and reasonable. The omission of important index and the overlap of index information will make the evaluation result distorted, and too many evaluation indexes will increase the unnecessary workload and difficulty of the quantitatively calculation. Therefore, scientifically establishing the evaluation index system is an important part of the evaluation problem. There are a lot of achievements in this aspect [1] -[5] . According to the methods and properties, the index selection method can be divided into qualitative method, quantitative method and comprehensive method [6] . Zhang et al. put forward a simple and feasible method that directly applies the basic principle of principle component and combines qualitative analysis with quantitative analysis to screen the economic index [7] . Li Chongming and Ding Lieyun gave a method to turn a system into a graph and formulated a model to select system core by using the cluster analysis and grey correlative analysis [8] . Li Yuanyuan, Yun Jun and Zhang Chaoyang proposed an indicator selection method based on attribute significance of rough set [9] [10] . These achievements provide technical support for constructing evaluation index system scientifically at different angles.

In reality, evaluation index with three-parameter interval grey number (T-PIGN) exists widely, and there are many scholars studying this problem. Li et al. proposed a risky evaluation approach based on prospect theory to solve the multi-criteria evaluation problem with T-PIGN [11] . Wang Jiefang and Liu Sifeng proposed the definition of relative superiority degree between T-PIGN and the real numbers, and gave two types of algebraic expression [12] . Wang et al. put forward a multi-index grey-target evaluation method based on grey lational entropy to solve the multi-index evaluation problems with T-PIGN [13] . However, there are fewer researches that involved in the selection of existing evaluation index system with T-PIGN. Therefore, this paper attempts to construct distance entropy model of T-PIGN based on the information entropy theory, and to provide a method to select the evaluation index system with T-PIGN.

2. Grey Distance Entropy Model Based on Three-Parameter Interval Grey Number

2.1. Three-Parameter Interval Grey Number

Definition 1: 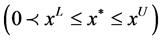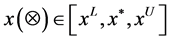is called the T-PIGN, where 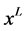and 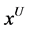are the lower and upper bounds; 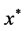is the center of gravity, namely the most possible data point.

Define the operation of T-PIGN, which is similar to the operation properties of the interval grey number.

Let

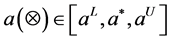and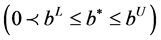

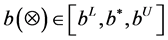
be the T-PIGN, we define:

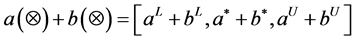
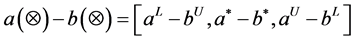
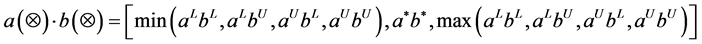
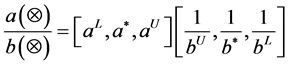
2.2. Three-Parameter Interval Grey Number Distance Entropy

Information entropy is an important concept in information theory, applied to measure the disorder degree of system. For a specific system, if the system is very random, chaotic and without order, the information entropy of the system will be large. Conversely, if a system is determinate, and obeys some order, the information entropy of the system will be small. Shannon proposed the information entropy equation [14] :

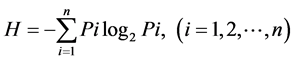
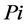denotes the occurrence probability of a random event i, and n denotes the number of random events.

Be similar to the operation of information entropy, the T-PIGN distance entropy can be defined [15] . To express conveniently, let, , where, , , , ,.

Definition 2: and are T-PIGN, let

(1)

be the distance entropy of and. The grey distance entropy is not the measure of distance, but the measure of approaching degree between and, that is to say the T-PIGN distance entropy can represent the information close degree of two T-PIGN.

Theorem: The closer and, the larger grey distance entropy; the farther and, the smaller. When, is the maximum;.

Proof:

Let

,

,

,

,

Thus, we can obtain that:.

The derivationof is that:.

Let, we can get that:.

Because, when, , is the maximum, and

.

Similarly, when, is the maximum; when, is the maximum.

Therefore, when, and, the distance entropy is the maximum.

In the same way, the theorem that the farther and, the smaller can be proved.

Meanwhile, the properties of grey distance entropy can be got:

1) It has the nonnegative, that is. Omit the process of proof;

2) It has the extremum, that is. The proof process is similar to theorem;

3) It has the symmetry, that is.

Proof:

Therefore, we can obtain that.

3. Selection Method of Evaluation Indicators with Three-Parameter Interval Grey Number

3.1. Selection Principle of Evaluation Indicators with Three-Parameter Interval Grey Number

Let be the scheme set of three-parameter multi-attribute evaluation problems, and be the index set. The index value is . Then the evaluation sample matrix X is given as follows:

.

In the multi-attribute evaluation problems, if the difference of index value of the same index in all schemes is small, the impact of the index on the evaluation distinguishing degree is small. Conversely, it shows that the impact of the index on the evaluation distinguishing degree is great. Therefore, considering from this angle, the index that has greater difference degree should be retained. By the definition and theorem of the T-PIGN distance entropy, we know that is inversely proportion to the approaching degree between and. So the difference degree of each index can be represented as the T-PIGN distance entropy. Let represent the difference degree of the index in the scheme and other schemes, is defined as follows:

(2)

And let

(3)

Because has the symmetry and is the result of repeated summation, let

(4)

expresses the sum of grey distance entropy of the index in all schemes.

If the grey distance entropy of the index in all schemes is larger, the impact of the index on the evaluation is smaller; Conversely, if the grey distance entropy of the index in all schemes is smaller, the impact of the index on the evaluation is greater. Therefore, considering from the angle of evaluation, the smaller the grey distance entropy of the index, the greater the difference degree of the index, and the index should be retained in the index selection process. The basic idea of this paper is to find and delete redundant indexes by comparing the grey distance entropy of the indexes, and establish the index system more succinctly and reasonably.

3.2. Selection Judgment Criterion of Evaluation Index System with Three-Parameter Interval Grey Number

Obtain the sum vector of grey distance entropy among the schemes under each index by calculating T-PIGN distance entropy, let sum vector, and calculate its variance, and sort the index according to the sum of grey distance entropy. If, we can obtain. And then remove the index which has the biggest distance grey entropy, the number of original index set decreases from s to, the weight of the removed index is assigned to the rest of indexes according to the original index weight proportion.

In the new evaluation sample matrix, because the grey distance entropy sum among the schemes under each index is constant, calculate the variance of surplus index grey distance entropy directly, and it is denoted as.

Compare the relative error between and expressed as, if (is the set value, the

greater, the greater the selection degree), it shows that rejecting this index has great impact on the whole index system, so this index should not be rejected, index selection is finished, evaluation index system at this time is optimal; if, it shows that rejecting this index has small impact on the whole index system, within the acceptable extent, this index can be rejected, continue the selection of index system. Repeating the above process until the relative error of adjacent variances is greater than the set value, index selection can be finished.

4. Example Analysis

Evaluation and selection of cadres is a multi-factors evaluation problem. A unit made 6 assessment index in the cadre assessment and selection: ideology and morality (), work attitude (), work style (), educational level (), leadership () and development ability (). Scoring for the index through the mass discussion (range from 0 to 100), and identifying 5 candidates according to the statistical result. The index value of each candidate is T-PIGN, the index weight is, data comes from [16] , and taking.

First, establish the evaluation matrix X.

Calculate the grey distance entropy of 5 candidates by using Equation (1), and the result is shown in Table 1.

Based on Table 1, we can obtain the results as follows by using Equation (4).

;

;

;

;

;

.

Thus, , and its variance. According to the theorem of T-PIGN distance entropy, the influence degree sorting of the index for the candidates is. Reject the index that has the smallest effect on the whole index system, the weight of remaining indexes is

Because the sum of grey distance entropy of each index is constant, the distance entropy is

, and its variance is, the relative error is

, therefore, continue to select the index system.

According to, we can obtain the influence degree sorting of the index for the candidates is . Reject the index that has the smallest effect on the whole index system, the remaining indexes weight is, , , , the distance entropy is, its variance is, the relative error is

, continue to select the index system.

According to, we can obtain the influence degree sorting of the index for the candidates is

. Reject the index that has the smallest effect on the whole index system, the remaining indexes weight is, , , the distance entropy is , its variance is, the relative error is

. It shows that the index should not be reject, and the index selection is fi-

nished. The optimal evaluation index system is.

Sort the 5 candidates in the original evaluation index system and the optimal evaluation index system through the index system selection, and then get the sorting of candidates by calculating the relative closeness. The result is shown in Table 2.

According to Table 2, we can get that the ranking in original evaluation index system and the optimal evaluation index system through the index system selection is the same, and the influence degree of index and is small so that they can be rejected. In addition, we also find that the distinguishing degree of relative closeness is significantly increased after selecting the evaluation index. Therefore, this index system selection method can be used to solve the evaluation problem. The index system after processing is not only comprehensive but also compendious.

5. Conclusions

This paper establishes T-PIGN distance entropy model that can be applied to the selection of evaluation index system with T-PIGN. The selection degree is related to the set value, the greater is, the greater the selection degree will be. According to the different actual situation, whether there is a certain value still needs further study. In this paper, the value of is 10%.

In order to further verify the effectiveness and applicability of the index system selection method, this paper applies this method in [17] and [18] . Finally, the optimal evaluation index system has the same result with the original evaluation index system, that is to say the index system selection method is correct.

Acknowledgements

The authors are grateful to anonymous referees for their helpful and constructive comments on this paper. This work was supported by the Soft-science Foundation of Henan Province (142400410727) and the Innovation Scientists and Technicians Troop Construction Projects of Henan Province (094100510013).

Cite this paper

FanlinMeng,NaWang,BingjunLi, (2015) Selection Method of Evaluation Indicators with Three-Parameter Interval Grey Number. Open Journal of Applied Sciences,05,833-840. doi: 10.4236/ojapps.2015.512080

References

NOTES

^*Corresponding author.