Received 24 September 2015; accepted 27 October 2015; published 30 October 2015

ABSTRACT

In this paper, the notions of integral 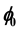-stability of ordinary impulsive differential equations are introduced. The definition of integral 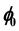-stability depends significantly on the fixed time impulses. Sufficient conditions for integral 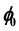-stability are obtained by using comparison principle and piecewise continuous cone valued Lyapunov functions. A new comparison lemma, connecting the solutions of given impulsive differential system to the solution of a vector valued impulsive differential system is also established.

Keywords:

Integral 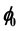-Stability, Cone Valued Lyapunov Functions, Impulsive Differential Equations, Fixed Time Impulses

1. Introduction

Impulsive differential equations have been developed in modeling impulsive problems in physics, population dynamics, ecology, biological systems, industrial robotics, optimal control, bio-technology and so forth. In view of the vast applications, the fundamental and qualitative properties i.e. stability, boundedness etc. of such equations are studied extensively in past decades. Several types of stability have been defined and established in literature by academicians for impulsive ordinary differential equations. Various techniques such as scalar valued piecewise continuous Lyapunov functions, vector valued piecewise continuous Lyapunov functions, Rajumikhin method, comparison principle etc. have been employed to establish stability results.

To the best of our knowledge, the concept of integral stability and 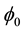-stability were introduced for ordinary differential equations by Lakshmikantham in 1969 [1] and by Akpan in 1992 [2] respectively. Later, these stabilities were developed in [3] and [4] by Akpan, Soliman and Abdalla but for ordinary differential equations. In 2010, Integral stability was established for impulsive functional differential equations by Hristova. Motivated by these works, in this paper, we introduce and establish integral 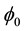-stability for impulsive ordinary differential equations:

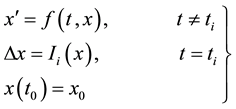(1)

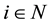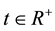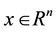
where, , , , , 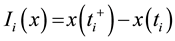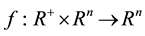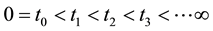and 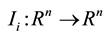are a sequence of instantaneous impulse operators and have been used to depict abrupt changes such as shocks, harvesting, natural disasters etc. and K is a cone defined in Section 2.

The paper is organized as follows:

In Section 2, some preliminaries notes and definitions are given. In Section 3, a new comparison lemma, connecting the solutions of given impulsive ordinary differential system to the solution of a vector valued impulsive differential system is worked out. This lemma plays an important role in establishing the main results of the paper. Sufficient conditions for integral 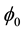-stability are obtained by employing comparison principle and piecewise continuous cone valued Lyapunov functions.

2. Preliminaries

Let 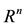denote the n-dimensional Euclidean space with any convenient norm and the scalar product, , ,.

For any, , we will write iff for all

Let be the solution of system (1), having discontinuities of the first type (left continuous) at the moments when they meet the hyper planes.

Together with system (1), let us consider, its perturbed IDS:

(2)

where, ,.

Let, so that the trivial solution of (1) and (2) exists.

Let us define the following:

Definition 1. A proper subset K of is called a cone if (i) (ii) (iii) (iv) (v), where and are interior and closure of respectively. denotes the boundary of.

Definition 2. The set is called the adjoint cone if it satisfies the properties (i)-(v) of definition 1.

The set iff for some.

Definition 3. A function is said to be quasi monotone relative to the cone if for each and imply that there exists such that and.

Consider the following sets:

.

Definition 4. A function is said to belong to class if:

1. is a continuous function in;

2. is Lipschitz continuous relative to cone K, in its second argument;

3. For each, and exist.

And for we define derivative of the function along the trajectory of the system (1) by.

Now referring [5] , let us define the following:

Definition 5. Let The function is said to be -weakly decrescent, if there exists a and a function such that the inequality implies that.

Definition 6. Let The function is said to be -strongly decrescent, if there exists a and a function such that the inequality implies that.

Throughout in the paper it was assumed that.

Let us consider the following comparison impulsive differential systems (referring [3] for Ordinary differential systems)

(3)

and

(4)

along with its perturbed system

(5)

where is quasi monotone non decreasing in its second argument and is quasi monotone non decreasing satisfying, , , , , , and are to be chosen later such that .

Definition 7. The zero solution of (1) is said to be -stable, if for every and for any there exists a positive function, which is continuous in for each such that the inequality implies that, where and is the maximal solution of (1) relative to the cone k.

Definition 8. The zero solution of (1) is said to be integrally stable, if for every and for any there exists a positive function, which is continuous in for each such that for any solution of perturbed system (2) , the inequality holds provided that and for every, the perturbations and of RHS of (2) satisfy

.

Definition 9. The trivial solution of (1) is said to be integrally -stable, if for every and for any there exists a positive function, which is continuous in for each such that for any solution of perturbed system (2) and for, the inequality holds provided that

(6)

and, for every, the perturbations and of RHS of (2) satisfy

. (7)

3. Main Results

Lemma 1: Consider the comparison system (3) and assume that

(i) where is quasi monotone non decreasing in its second argument;

(ii) such that and satisfies

(iii) such that for

Let be the maximal solution of (3) existing on J. Then for any solution of (1) existing on J, we have provided that.

Proof: Let be the solution of (1) existing for such that.

Define for such that. Then for small, we have

,

where M is the Lipschitz constant in.

Therefore we have

Also and.

Then by theorem (1.4.3) in [6] , we observe the desired inequality

for all.

Theorem 1: Let us assume the following:

1. Let and

2. There exist such that

(i) is -weakly decrescent

(ii) For the inequality

holds for all

where monotone non decreasing in its second argument

(iii) for all where is monotone non decreasing, satisfying

3. For any number there exists such that

(iv) for where

(v) For the inequality

holds for any

where is monotone non decreasing in its second argument.

(vi) for

where,

4. The system (3) and (4) have solutions, for any initial point.

5. For any initial point, the system (1) has solution.

Let the zero solution of (3) be -stable, and scalar IDE (4) is integrally -stable, then the system (1) will be integrally -stable.

Proof: Since is -weakly decrescent, therefore there exists a and a function such that the inequality implies that

(8)

where.

Let be a fixed time. Choose a number such that.

As, there exist Lipschitz constants and of and respectively. Let.

As the zero solution of (3) is -stable, therefore for every and for any there exists a positive function for each such that the inequality implies that

, (9)

where is the maximal solution of (3)

As, there exists and hence such that

. (10)

Again in view of the fact that the perturbations in (5), depend only on t and system (4) is -integrally stable, there exists a function, continuous in for each (take in particular) such that for every solution of perturbed system (5), the inequality

(11)

holds provided that and for every, the perturbation terms and satisfy

. (12)

Since, let us choose such that and where is a function satisfying.

Select, such that the inequalities

and hold (13)

Let be the solution of (2). Now we will prove that if the inequalities (6) and (7) are satisfied then

(14)

If possible let this be false. Therefore there exists a point such that

(15)

Case 1: Let for any. Then the solution is continuous at. Therefore

In this case first we note that.

For if, then by the choice of we get which is a contradiction to (15).

Now let us consider the interval

Subcase 1.1: Let there exists such that and

If is the maximal solution of (3) with, then in view of the assumptions (ii) and (iii) of theorem, using lemma 1, we obtain

(16)

where is a solution of (1), starting at.

As is chosen therefore we have and by using (8) and then (10), we get

Now by virtue of (9) gives:

(17)

Now from inequality (13) and condition (iv) of theorem, we get

(18)

Let us define the function, by

Now, for and, , in view of (v) of theorem and lipschitz condition on and, we have

(19)

Again for such that, by using condition (vi) of theorem and Lipschitz conditions on and, we get

(20)

For the impulsive differential system (5) which is the perturbed system of (4), set the perturbations on RHS of (5) as

Therefore (19) and (20) can be written as

and

.

If we consider the comparison system (5) with maximal solution, through the point where, using (19), (20) and lemma 1, we get

where H is the interval of existence of maximal solution

(21)

Now by using the inequality (7) for in the interval and from the choice of,

(22)

Let us choose a point such that.

Now let us define a continuous function given by

and the sequence of numbers.

We see that if (7) holds then from (22), for every

(23)

let be the maximal solution of (5), through the point where the perturbations terms are defined by and. Note that here we have.

From inequalities (17) and (18) we see, i.e.

(24)

and hence from (11), we get

for. (25)

Now from the choice of, inequalities (21), (25) and condition (iv) of statement of theorem, we get

which yields, a contradiction and therefore the inequality (14) is valid for.

Subcase 1.2: Let there exist a point for some such that and.

Choose satisfying with Now if we take in place of and repeat the proof of subcase 1.1 we arrive at contradiction that assures the validity of (14).

Case 2: If for some then from (15),

and

.

Let us select such that

Now by adopting the procedure as in case 1, we get the inequalities (21) and (25). Then by using these inequalities along with the conditions (iv) and (vi) of the statement of theorem, we have

and that again is a contradiction .Therefore inequality (14) is valid.

Thus in all the cases, validity of (14) proves that system (1) is integrally -stable.

4. Conclusion

Results in [1] [4] [7] have been exploited and extended to establish the new type of stability i.e. integral -stability for the impulsive differential systems. Sufficient conditions are obtained by employing comparison principle and piecewise continuous cone valued Lyapunov functions.

Cite this paper

AnjuSood,Sanjay K.Srivastava, (2015) Integral Φ₀-Stability of Impulsive Differential Equations. Open Journal of Applied Sciences,05,651-660. doi: 10.4236/ojapps.2015.510064

References