American Journal of Analytical Chemistry
Vol.05 No.14(2014), Article ID:51012,14 pages
10.4236/ajac.2014.514106
Preparation, Characterization and Statistical Studies of the Physicochemical Results of Series of “B” Carbonated Calcium Hydroxyapatites Containing Mg2+ and 
S. Ben Abdelkader, F. Bel Hadj Yahia, I. Khattech
Applied Thermodynamics Laboratory, Chemistry Department, Faculty of Sciences, Tunis, Tunisia
Email: faouziarockh1@Gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 21 August 2014; revised 6 October 2014; accepted 21 October 2014

ABSTRACT
In this study, series of hydroxyapatites containing Mg2+ and 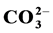 are prepared by the precipitation method with independently varying concentrations of
are prepared by the precipitation method with independently varying concentrations of 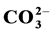 and Mg2+. All the compounds are characterized by infrared spectra (IR); powder X-ray diffraction (PXRD) and elemental analysis. The physical analysis results show that the prepared compounds are pure B-type carbonate apatite. The presence of Mg2+ and
and Mg2+. All the compounds are characterized by infrared spectra (IR); powder X-ray diffraction (PXRD) and elemental analysis. The physical analysis results show that the prepared compounds are pure B-type carbonate apatite. The presence of Mg2+ and 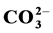 in the apatite cause the following effects on its physical properties: a decrease in a-dimension but no changes in c-dimension and a decrease in crystallinity as shown in XDR patterns and IR spectra. The results of the chemical analysis allow us to predict the predominant substitution mechanisms for the
in the apatite cause the following effects on its physical properties: a decrease in a-dimension but no changes in c-dimension and a decrease in crystallinity as shown in XDR patterns and IR spectra. The results of the chemical analysis allow us to predict the predominant substitution mechanisms for the 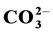 and the Mg2+ incorporations in the calcium hydroxyapatites and to calculate their relative contributions x, y and z.
and the Mg2+ incorporations in the calcium hydroxyapatites and to calculate their relative contributions x, y and z. 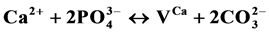 (II);
(II); 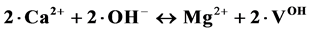 2. (IV);
2. (IV); 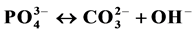 (V). Statistical studies of the results “multiple linear regression, analysis of variance (ANOVA) and t-test of the regression coefficients” allow us to determine and to test the mathematical model proposed. Finally, the present study makes it possible to write the general formula for these compounds.
(V). Statistical studies of the results “multiple linear regression, analysis of variance (ANOVA) and t-test of the regression coefficients” allow us to determine and to test the mathematical model proposed. Finally, the present study makes it possible to write the general formula for these compounds.
Keywords:
B-Type Carbonated Calcium Hydroxyapatite Containing Magnesium “B” CO3Mg-HAps, Substitution Mechanism(s), Multiple Linear Regression, F-Test (ANOVA), t-Test of the Coefficients

1. Introduction
A number of studies have reported that the incorporation of magnesium in hydroxyapatites Ca10(PO4)6(OH)2 is limited [1] - [3] . Previously, it has been shown that the magnesium can disturb the crystallization of apatites when its concentration in the solution is sufficient to be a major competitor for calcium [4] . But when the molar ratio of Mg/Ca is higher than 0.1, another phase is observed, the whitlockite [3] [5] - [7] . The co-substitution of a second ionic species like the carbonate ion can increase the insertion of magnesium in the lattice and prevent the decomposition while stabilizing the structure [8] [9] .
On the other hand, it is now well established that the biological minerals are best described as carbonated apatites rather than as a hydroxyapatite [2] [10] - [12] . The carbonate presents at 3% - 6% in biological apatites, mostly substitutes for the phosphate ion in the crystal structure and has a significant influence on the incorporation of other foreign ions into the apatite lattice. Magnesium is one of the most abundant trace ions present in the biological hard tissues and in dental enamel, its content approximately being 0.1% - 0.4%. In dentin, the magnesium content is up to 1.1%, while in bone, it is found at 0.6% [13] - [15] . Thusly, Magnesium has been the subject of many studies. To understand the role of magnesium on biological apatites, the works using synthetic carbonated apatites are very helpful.
Previous studies suggest that the magnesium is incorporated into or onto the carbonated apatites during their formation [16] - [24] . Some of these works demonstrate the role of the carbonate concentration, the pH of preparation, and the magnesium content incorporated into the apatites at similar quantities to those found in biological apatites [16] [17] [23] . Other works report the effect of the magnesium on the parameters of the lattice of apatites prepared by precipitation or high-temperature synthesis [4] [25] . Legeros et al. [22] noted an increase in the dissolution rates, of carbonate-containing apatites when the magnesium was incorporated. Some studies have investigated the phase’s composition after heat-treatment of the magnesium/carbonate co-substituted in the hydroxyapatite [16] [23] [24] .
Despite numerous investigations, the mechanism(s) by which the carbonate and the magnesium are incorporated in the apatite lattice are not yet known. Indications are found in the literature about the mechanisms by
which 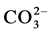 and alkalimetal M+ are incorporated in the apatite lattice [26] - [28] . In these works, De Maeyer
and alkalimetal M+ are incorporated in the apatite lattice [26] - [28] . In these works, De Maeyer
and Verbeeck suggest that six fundamental substitution mechanisms can contribute theoretically for these substitutions .
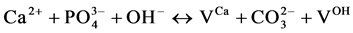 (I)
(I)
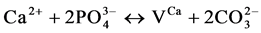 (II)
(II)
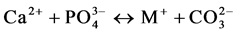 (III)
(III)
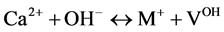 (IV)
(IV)
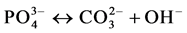 (V)
(V)
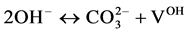 (VI)
(VI)
where VX stands for a vacancy in the X-sublattice. The contributions of each of these mechanisms should be estimated on the basis of a thorough physicochemical studies of the samples.
The present study tries to find the mechanism(s) which contribute to the incorporation of magnesium and carbonate in the apatites lattice. For this purpose, series of “B” carbonated calcium hydroxyapatites containing
magnesium are prepared by the precipitation method. In the first series, the concentration of the  solution
solution
is Cc = 0.00 M while the Mg2+ concentration CMg is 0.00, 1.7, 6.8 and 13.6 mM. For the second, the same procedure is remade with Cc = 0.025 M in the hydrolysis solution and for the third, Cc is equal to 0.05 M. The chemical and physical characteristics of the samples prepared are determined and an attempt is made to deduce the fundamental substitution mechanisms which determine their stoichiometry. Finally, statistical studies of the experiment results allow us to find the relationship between the different variables and to verify the proposed mechanisms by which 
2. Methods and Materials
2.1. Preparation of “B” Type Carbonated Hydroxyapatites Containing Magnesium
The method of preparation used in this work is inspired from the method used in reference [23] but it is slightly modified. The apaties are prepared by dropping 200 mL of a phosphate solution (NH4)2HPO4 (0.18 M) into 200 mL of a calcium solution Ca(NO3)·4H2O (0.44 M) under reflux at 87˚C. To the calcium solution is added 20 mL of a magnesium solution Mg(NO3)2·6H2O containing different concentrations: CMg (0.00; 1.7; 6.8 and 13.6) mM. The same procedure is remade by adding to the phosphate solution 5 mL of a carbonate solution NH4HCO3 (1 M). A third set of preparations is performed by adding 10 mL from the above carbonate solution. The pH is maintained at 9.0 during the precipitation by adding an ammonia concentrated solution (28% weight). The precipitation is carried out over 3 h. Then, the system is refluxed for an additional duration of 2 h. The samples are filtered, thoroughly washed with hot distilled water and dried overnight at 120˚C.
2.2. Physical Analysis
The powdered samples are identified by X-ray diffraction and by infra red spectroscopy. Infrared spectra of the samples dispersed in KBr tablets are recorded using a Shimadzu Fourier transform infrared spectrophotometer in the range of 4000 - 400 cm−1. Then, the samples are analyzed by X-ray diffraction (XRD) using a Philips diffractometer using Cu Ka radiation. The samples are scanned in the 2θ range of 20˚ - 60˚. The “a and c” parameters of the lattice of the hexagonal unit cell are calculated using “wincell” refinement program.
2.3. Chemical Analysis
The samples are analyzed for Ca, PO4, CO3 and Mg. The calcium content of the precipitates is determined by a complexometric titration with the ethylenediaminetetraacetic acid [29] , the magnesium by atomic absorption, the carbonate content is determined by coulometrically method and the phosphorus content by spectrophotometrie of the phosphomolybdate complex [30] .
3. Results
3.1. Results of Physical Analysis
The IR Spectra of some representative samples (Mg4, Mg8 and Mg12) are shown in Figure 1. The spectra contain the characteristic bands of the phosphate group 
Figure 1. IR spectra of some representative samples.
spectra of the samples (Mg8 and Mg12) are displayed typical absorption bands of 




The X-ray diffraction patterns of some representative samples are shown in Figure 2. The X-ray diffraction powder patterns of the compounds show only one crystal phase. The peaks are sharp, well resolved and characteristic of the hexagonal apatite phase. No extraneous peaks attributable to other phases than apatite could be found in the diffractograms. The increase of the level of 
The Table 1 contains the values of the lattice parameters “a” and “c” obtained for the different compounds.
From this table, we can see that simultaneous incorporation of two elements “CO3 and Mg” results in an decrease of the “a” parameter. This contraction is attributed to the simultaneous effects of the 
Figure 2. X-ray diffraction patterns of some representative samples.
Table 1. “a” and “c” Lattice parameters of “B” CO3Mg-Haps.
3.2. Chemical Results
The results of the chemical analysis of the samples in Weight % are summarized in Table 2. This table also gives the hydroxide content of the samples calculated on the basis of the electroneutrality condition and the total mass balance ∑ % obtained from the equation:

With MX the atomic or ionic mass of X. ∑ % value is lower than 100% indicating that the samples of the present study still contain some water after drying at 120˚C.
The results of the chemical and physical analysis (Table 2) allow us to calculate the number of each ion X per unit cell, nx according to the following equation:

The results of these calculations are summarized in Table 3. The errors in Table 4 are estimated by the means of error propagation theory.
Table 2. Chemical Composition (weight percent) and Total Mass Balance ∑ % of the hydroxyapatites obtained by precipitation in solutions containing Cc (M) CO3 and CMg (mM) Mg.
Table 3. Unit cell compositions of NaCO3 Aaps calculated on the basis of the chemical composition and using Equation (2).
Table 4. Multiple linear regression analysis of Yi = 
4. Statistical Analysis of the Physicochemical Results
4.1. Influence of the Experimental Conditions on the Composition of the Synthetic Apatites
To know the influence of the experimental conditions on the incorporation of 


From the Figure 3(a) and Figure 4(a), it is seen that 

To estimate the simultaneous influence of the experimental conditions on 

The mathematical model is described by the equation:

The method of least squares (O.L.S.) allows us to establish the predicted equation

that is most suitable to the data. On the other hand, this method allows us to calculate the estimated standard errors of the coefficients
4.2. Influence of the Incorporation of 
In attempts to disentangle and to measure the effects of the insertion of 

Figure 3. (a) 

Figure 4. (a) 
Table 5. Multiple linear regression analysis of Yi = nMg/nP molar ratio (Table 3) as a function of the concentration of carbonate Cc/M and magnesium CMg/mM in the solution. (a) Regression statistic; (b) Coefficients; (c) Analysis of variance.
tent of Ca2+ of the solid, we use the multiple linear regression on two X-variables where, X1 = 
Table 6. Multiple linear regression analysis of the estimated Yi = nCa2+ on X1,i = nMg2+, X2,i = 
Table 7. Multiple linear regression analysis of the estimated Yi = OH− on X1, i = nMg2+ and X2,i = 
4.3. The Determination of the Relationship between Y = c/a Crystallographic Parameters Ratio and 

To estimate the influence of the incorporation of carbonate on the lattice parameters “a” and “c” in presence of magnesium, we plot c/a crystallographic parameters ratio (Table 1) as a function of molar ratio 
Given that the shape of the curve obtained in Figure 5 is a polynomial, we construct a multiple linear regression on Yi = c/a as a function of three X-variables where, X1 = 



Least square [33] allows calculating the regression and correlation coefficients regression of the predicted
equation

These estimated rgression coefficients 

where n is sample size, m is number of parameters and (n − m − 1) is degree of freedom.
On the other hand, this method allows us to calculate the standard errors of the coefficients 

The analysis of variance (ANOVA) shows that F-test = 2018.9 is higher than criterion F(5%; 3; 8) = 4.07.
Table 8. Multiple linear regression analysis of Yi= c/a ratio of the lattice parameters of Mg-CO3 HAps (Table 1) on: X1i = 


Figure 5. c/a parameters ratio as a function of 
5. Determination of the General Formula of the Unit Cell of the Synthetic “B” CO3Mg-HAps
The relative composition (Table 3) and the results of the physical analysis demonstrate that the samples are pure “B” type carbonated apatites containing Mg2+ ions. Thus, mechanisms I, II, III and V could be account in the incorporation of 

Moreover, the study carried out previously (paragraph 4.1) show that the 
Many works [27] [28] have demonstrated that mechanism I and/or II are the main mechanisms for the incorporation of CO3. Otherwise, according the reference [27] , the contribution of mechanism I seems to be hardly influenced by the alkali metal which is not our case. Therefore, we consider that mechanism II contribute to the insertion of CO3 ions in the lattice of the solid.
Table 7 show that the variation of nOH− depends on the increase of 
Then the fundamental substitution mechanisms for the incorporation of 



where VOH stands for a vacancy in the OH− sub lattice. If x, y and z are the contributions of mechanisms II, 2.IV and V respectively, thus,




and 
and the generic formula has the following expression:
The values of x, y and z the contribution of mechanisms II, 2.IV and V respectively are calculated from the data (Table 3) and the following equations. Then statistical studies are conducted to verify the accuracy of the proposed formula. The results of these calculations are summarized in Tables 9-11.
Table 9. The values of x, y and z the contributions of the mechanisms II, 2.IV and V respectively calculated from Equations (10)-(14).
Table 10. Multiple linear regression analysis of the estimated Yi = nCa2+ the molar content of the solid “B” Mg-CO3 HAps (Table 3) on X1,i = x- and X2,i = y the contribution of mechanisms II and 2.IV (Table 9). (a) Regression statistic; (b) Coefficients; (c) Analysis of variance.
Table 11. Multiple linear regression analysis of the estimated Yi = nOH− the molar content of the solid “B” Mg-CO3 HAps (Table 3) on X1,i = z and X2,i = z the contribution of mechanisms II and V (Table 9). (a) Regression statistic; (b) Coefficients; (c) Analysis of variance.
6. Discussion
From Table 1,, we can see that simultaneous incorporation of two elements “CO3 and Mg” results in an decrease of the “a” parameter. This contraction is attributed to the simultaneous effects of the 
In Table 2 and Table 3, it is seen that the concentration of the 




Figure 3 and Figure 4, show that nCO3/nP the molar ratio increases with the increasing of the concentration of 

and 
Equations (9) and (10) show that the concentration of the 


To know the relationship between the variation of Ca2+ and OH− with the increasing of 


From the intercepts of the following equations it can seen that, within experimental error, a carbonate and magnesium-free apatite (nCO3 = 0, nMg = 0) contains 10 Ca2+ and 2 OH− ions per unit cell Equations (11) and (12). These results are in agreement with those in literature [24] - [26] [34] [35] .
As shown in Figure 5, there is a correlation of the unit cell parameters of the apatites with their chemical compositions. Indeed, the changes in the unit cell parameter “a” of the compounds are attributed to the additive effects of the substitution in the lattice of either carbonate and magnesium [2] [34] [35] . The solid line of best fit for these series of compounds in Figure 5 extrapolates to a ratio c/a very close to that in hydroxyapatite. This result is similary to these obtained previously [34] [35] . The application of multiple linear regression to Yi = c/a
on 

95% level:

To verify the general formula proposed, We apply the multiple linear regression to Yi = nCa2+ on X1i = x and X2i = y (the contributions of the mechanisms II and IV). Similar treatment is realized for Yi = nOH− on X1i = z and X2i = y (the contributions of the mechanisms V and IV) Table 10 and Table 11. The results of these calculations show that the predicted equations at 95% level are:


7. Conclusion
The theoretical calculations of the present study indicate unambiguously that the mechanisms II, III and V contribute to the incorporation of Mg and Ca in the lattice of apatite. This corroborates in more definite way our assumptions obtained from the experimental data and allows us to propose for these compounds the general formula:
References
- Kreidler, E.R. and Hummel, F.A. (1970) The Crystal Chemistry of Apatite: Structure: Fields of Fluor- and Chlorapatite. American Mineralogist, 55, 170.
- Legeros, R.Z. (1984) Tooth Enamel IV. In: Fearnhead, R.W. and Sugas, S., Eds., Elsevier, Amsterdam, 32-36.
- Ben Abdelkader, S., Khattech, I., Rey, C. and Jemal, M. (2001) Synthése, Caractérisation et Thermochimie d’Apatites Calco-Magnésiennes Hydroxylées et Fluorées. Thermochimica Acta, 376, 25-36. http://dx.doi.org/10.1016/S0040-6031(01)00565-2
- Terpstra, R.A. and Driessens, F.C.M. (1986) Magnesium in Tooth Enamel and Synthetic Apatites. Calcified Tissue International, 39, 348-354. http://dx.doi.org/10.1007/BF02555203
- Hayek, E. and Newsely, H. (1958) Über die Existenz von Tricalciumphosphat in wäBriger Lösung. Mn. Chem., 89, 88.
- Rowles, S.L. (1968) Crystallographic Study of Biological Apatites. Bulletin de la Société Chimique de France, 1797.
- Hamad, M. and Heughebaert, J.C. (1987) Study of Apatite and Whitlockite Formation at 100˚C in the System CaO- MgO-P2O5-H2O. J. Chim. Phys., 84, 985.
- Vignoles, M., Bonel, G. and Young, R.A. (1987) Occurrence of Nitrogenous Species in Precipitated B-Type Carbonated Hydroxyapatites. Calcified Tissue International, 40, 64-70. http://dx.doi.org/10.1007/BF02555707
- Vignoles, M., Bonel, G., Holcomb, D.W. and Young, R.A. (1988) Influence of Preparation Conditions on the Composition of Type B Carbonated Hydroxyapatite and on the Localization of the Carbonate Ions. Calcified Tissue International, 43, 33.
- Young, R.A. and Spooner, S. (1969) Neutron Diffraction Studies of Human Tooth Enamel. Archives of Oral Biology, 15, 47-63. http://dx.doi.org/10.1016/0003-9969(70)90144-5
- Bigi, A., Foresti, E., Gregorini, R., Ripamonti, A., Roveri, N. and Shah, J.S. (1992) The Role of Magnesium on the Structure of Biological Apatites. Calcified Tissue International, 50, 439-444. http://dx.doi.org/10.1007/BF00296775
- Holden, J.L., Clement, J.G. and Phakey, P.P. (1995) Age and Temperature Related Changes to the Ultrastructure and Composition of Human Bone Mineral. Journal of Bone and Mineral Research, 10, 1400-1409. http://dx.doi.org/10.1002/jbmr.5650100918
- Robinson, C., Weatherell, J.A. and Hallsworth, A.S. (1981) Distribution of Magnesium in Mature Human Enamel. Caries Research, 15, 70-77. http://dx.doi.org/10.1159/000260502
- Steinfort, J., Driessens, F.C.M., Heijligers, H.J.M. and Bertseen, W. (1991) The Distribution of Magnesium in Developing Rat Incisor Dentin. Journal of Dental Research, 70, 187-191. http://dx.doi.org/10.1177/00220345910700030601
- Tsuboi, S., Nakagi, H., Ishiguro, K., Kondo, K., Mukai, M., Robinson, C. and Weatherell, J.A. (1994) Magnesium Distribution in Human Bone. Calcified Tissue International, 54, 34-37. http://dx.doi.org/10.1007/BF00316287
- Bigi, A., Marchetti, F., Ripamonti, A., Roveri, N. and Foresti, E. (1981) Magnesium and Strontium Interaction with Carbonate-Containing Hydroxyapatite in Aqueous Medium. Journal of Inorganic Biochemistry, 15, 317-327. http://dx.doi.org/10.1016/S0162-0134(00)80235-4
- Featherstone, J.D.B., Mayer, I., Driessens, F.C.M., Verbeeck, R.M.H. and Heijligers, H.J. (1983) Synthetic Apatites Containing Na, Mg, and CO3 and Their Comparison with Tooth Enamel Mineral. Calcified Tissue International, 35, 169-171. http://dx.doi.org/10.1007/BF02405026
- Apfelbaum, F., Mayer, I. and Featherstone, J.D.B. (1991) The Role of
and
and
Ions in the Transformation of Synthetic Apatites to β-Ca3(PO4)2. Journal of Inorganic Biochemistry, 38, 1-8.
 Ions in the Transformation of Synthetic Apatites to
β-Ca3(PO4)2.
Journal of Inorganic Biochemistry, 38, 1-8.
http://dx.doi.org/10.1016/0162-0134(90)85001-D
Ions in the Transformation of Synthetic Apatites to
β-Ca3(PO4)2.
Journal of Inorganic Biochemistry, 38, 1-8.
http://dx.doi.org/10.1016/0162-0134(90)85001-D - Aoba, T., Moreno, E.C. and Shimoda, S. (1992) Competitive Adsorption of Magnesium and Calcium Ions onto Synthetic and Biological Apatites. Calcified Tissue International, 51, 143-150. http://dx.doi.org/10.1007/BF00298503
- Okazaki, M. and Legeros, R.Z. (1992) Crystallographic and Chemical Properties of Mg-Containing Apatites before and after Suspension in Solutions. Magnesium Research, 5, 103-108.
- Zhou, J.M., Zhang, X.D., Chen, J.Y., Zeng, S.X. and De Groot, K. (1993) High Temperature Characteristics of Synthetic Hydroxyapatite. Journal of Materials Science: Materials in Medicine, 4, 83-85. http://dx.doi.org/10.1007/BF00122983
- Legeros, R.Z., Kijkowska, R., Bautista, C. and Legeros, J.P. (1995) Synergistic Effects of Magnesium and Carbonate on Properties of Biological and Synthetic Apatites. Connective Tissue Research, 333, 203.
- Mayer, I., Schlam, R. and Featherstone, J.D.B. (1997) Magnesium-Containing Carbonate Apatites. Journal of Inorganic Biochemistry, 66, 1-6. http://dx.doi.org/10.1016/S0162-0134(96)00145-6
- Gibson, I.R. and Bonfield, W. (2002) Preparation and Characterization of Magnesium/Carbonate Co-Substituted Hydroxyapatites. Journal of Materials Science: Materials in Medicine, 13, 685-693. http://dx.doi.org/10.1023/A:1015793927364
- Baravell, S.S., Bigi, A., Ripamonti, A., Roveri, N. and Foresti, E. (1984) Thermal Behavior of Bone and Synthetic Hydroxyapatites Submitted to Magnesium Interaction in Aqueous Medium. Journal of Inorganic Biochemistry, 20, 1-12. http://dx.doi.org/10.1016/0162-0134(84)80001-X
- De Maeyer, E.A.P. and Verbeeck, R.M.H. (1993) Possible Substitution Mechanisms for Sodium and Carbonate in Calciumhydroxyapatite. Bulletin des Sociétés Chimiques Belges, 102, 601-609. http://dx.doi.org/10.1002/bscb.19931020907
- De Maeyer, E.A.P., Verbeeck, R.M.H. and Pieters, I.Y. (1996) Influence of the Solution Composition on the Stoichiometry of Na+- and of K+-Containing Carbonated Apatites Obtained by the Hydrolysis of Monetite. Journal of Crystal Growth, 169, 539-547. http://dx.doi.org/10.1016/S0022-0248(96)00424-1
- De Maeyer, E.A.P., Verbeeck, R.M.H. and Pieters, I.Y. (1996) Effect of K+ on the Stoichiometry of Carbonated Hydroxyapatite Obtained by the Hydrolysis of Monetite. Inorganic Chemistry, 35, 857-863. http://dx.doi.org/10.1021/ic950916k
- Charlot, G. (1966) Les Méthodes de la Chimie Analytique. Masson, Paris.
- Gee, A. and Deitz, V.R. (1953) Determination of Phosphate by Differential Spectrophotometry. Analytical Chemistry, 25, 1320-1324. http://dx.doi.org/10.1021/ac60081a006
- Legeros, R.Z. (1991) Calcium Phosphates in Oral Biology and Medicine. Monographs in Oral Science, 15, 89-95.
- Snedecor, G.W. and Cochran, W.G. (1980) Statistical Methods. 7th Edition, The Iowa State University Press, Ames.
- Borcard, D. (2009) Regression Multiple. Université de Montréal, Montréal. http://biol09.biol.umontreal.ca/BIO2042/Regr_mult.pdf
- Bel Hadj Yahia, F. and Jemal, M. (2010) Synthesis, Structural Analysis and Thermochemistry of B-Type Carbonate Apatites. Thermochimica Acta, 505, 22-32. http://dx.doi.org/10.1016/j.tca.2010.03.017
- Rockh B. Hadj Yahia, F. and Khattech, I. (2014) Statistical Studies of the Physicochemical Analytic Results of a Series of Synthetic Calcium Hydroxyapatite Containing Carbonate and Sodium. American Journal of Analytical Chemistry, 5, 343-357.










 and
and  and
and  Ions in the Transformation of Synthetic Apatites to β-Ca3(PO4)2.
Journal of Inorganic Biochemistry, 38, 1-8.
Ions in the Transformation of Synthetic Apatites to β-Ca3(PO4)2.
Journal of Inorganic Biochemistry, 38, 1-8.