Modeling and Numerical Simulation of Material Science
Vol.3 No.4(2013), Article ID:37919,3 pages DOI:10.4236/mnsms.2013.34022
Numerical Simulation of Stress-Strain State for Nonhomogeneous Shell-Type Structures Based on the Finite Element Method
1Oles Honchar Dnepropetrovsk National University, Dnepropetrovsk, Ukraine
2Institute of Technical Mechanics of National Academy of Sciences Ukraine and State Space Agency Ukraine, Dnepropetrovsk, Ukraine
Email: hudramovich@i.ua
Copyright © 2013 Eteri L. Hart et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 4, 2013; revised August 15, 2013; accepted September 1, 2013
Keywords: Projective-iterative version; Finite element method; Shell-type structures; Opening; Elastoplastic deformation
ABSTRACT
Projective-iterative version of finite element method has developed for numerical simulation of the stress-strain state of nonhomogeneous shell-type structures (shells with openings). Plastic deformation of the material is taken into account when using the method of elastic solutions that reduce the solution of elastoplastic problems to solution of elastic problems. Developed PIV’s significant savings of computer calculation has been compared with the calculation on a fine mesh of traditional FEM. Designed scheme allows analysis of the mutual influence of openings. Analysis of the transformation zone of plastic deformation is developed. For definiteness, the cylindrical shell structures with several rectangular openings are considered.
1. Introduction
Structures in the form of nonhomogeneous shells are common in the priority areas of modern technology (aviation, space technology, oil and gas industry). The main manifestation of nonhomogeneity is the presence of openings of different shapes.
Openings characterize the design features and damage defects that appear in various cases of exploitation or in manufacturing processes. They reduce to concentration of stresses [1,2].
High load levels lead to plastic deformation. This fact is taken into account when using the methods of elastic solutions that reduce the solution of elastoplastic problems to solution of elastic problems [3].
The fields of stresses and strains that arise near openings’ edges have the mutual influence on each other. This influence depends on the openings’ shapes, dimensions, quantities, and spacings. Plastic deformation appreciably changes the pattern of this interaction. Transformation of above-mentioned fields near the openings cause changes to the process of exhausting the carrying capacity.
The plastic deformation zones, stress distributions and loads that correspond to the start of merging and further transformation in the course of loading make it possible to predict load-carrying ability of shell-type structures with openings.
Let us consider shell-type structures in view of cylindrical shell with rectangular openings.
2. Features of Used Solution Methods
The numerical finite element method (FEM) is an efficient method for solution of various complex problems of stress-strain state (SSS) and critical states (carrying capacity, stability) of various structures.
The projective-iterative versions (PIV) of FEM essentially reduces the needed for calculations performed by means of personal computers, which is of importance in simulation of complex nonlinear deformation of shelltype structures with openings of various types.
The theoretical foundations of PIV FEM in [4-8] and in series of works in mathematics problems are presented. The basic idea is as follows.
The problem of finding the minimum of the potential energy functional, defining the SSS of shell structures members is the conditional minimization problem
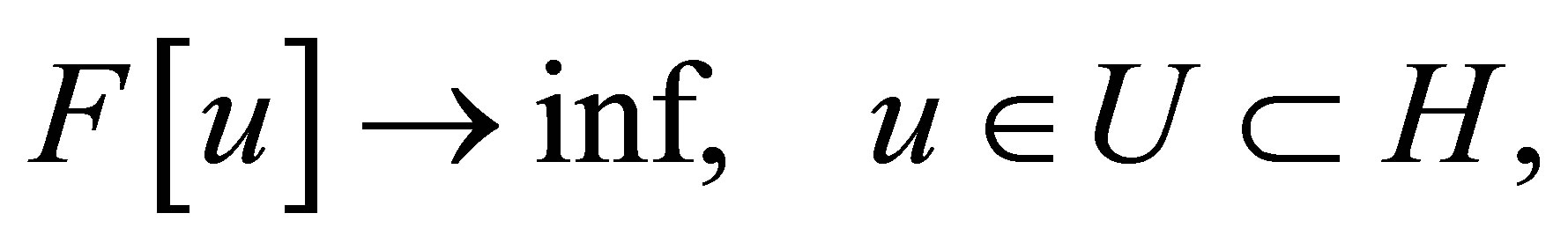 (1)
(1)
where 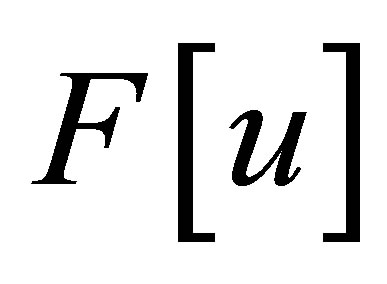 is the functional bounded on a set of cinematically possible displacements
is the functional bounded on a set of cinematically possible displacements  of the real Hilbert space
of the real Hilbert space .
.
The extremum problem Equation (1) is approximated, through the use of FEM, by a series of discrete extremum problems . Each of the problem is solved via some iterative process, but not completely. Starting from an arbitrary rather rough breakdown of the mesh, one constructs just a few approximations
. Each of the problem is solved via some iterative process, but not completely. Starting from an arbitrary rather rough breakdown of the mesh, one constructs just a few approximations  to the minimum point of the n-th multivariable function. The last approximation is interpolated into a finer finite element mesh and serves an initial approximation to the minimum point of the next function at the (n + 1)-th step of the PIV process that goes on until a present calculation accuracy is achieved.
to the minimum point of the n-th multivariable function. The last approximation is interpolated into a finer finite element mesh and serves an initial approximation to the minimum point of the next function at the (n + 1)-th step of the PIV process that goes on until a present calculation accuracy is achieved.
The PIV FEM models have been applied successfully of elastic boundary value problems, elastoplastic stressstrain state problems for plates with various openings, plane elastoplastic deformation problems for structured media containing assembles of pores, cracks, inclusions [2,8]. Use of this models provides a significant (dozensfold) saving in computation time in comparison to the conventional FEM.
For solution of elastoplastic problems we use the method of variable elastic parameters (VEP)—version of elastic solutions methods [3,8]. The method give construction of iterative process, in each approximation an elasticity problem with variable elasticity and shear modulus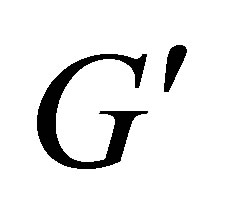 ,
, 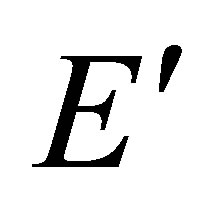 and Poisson’s ratio
and Poisson’s ratio 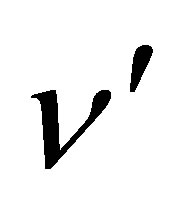 is solved. For deformation theory of plasticity we have for each approximation
is solved. For deformation theory of plasticity we have for each approximation
 ;
;
 ;
;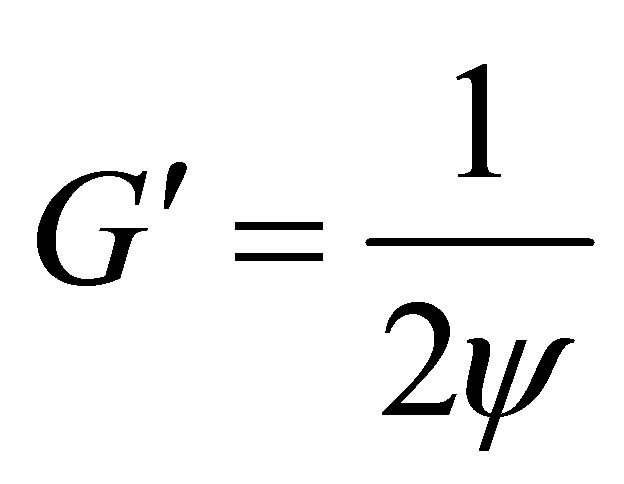 ;
;
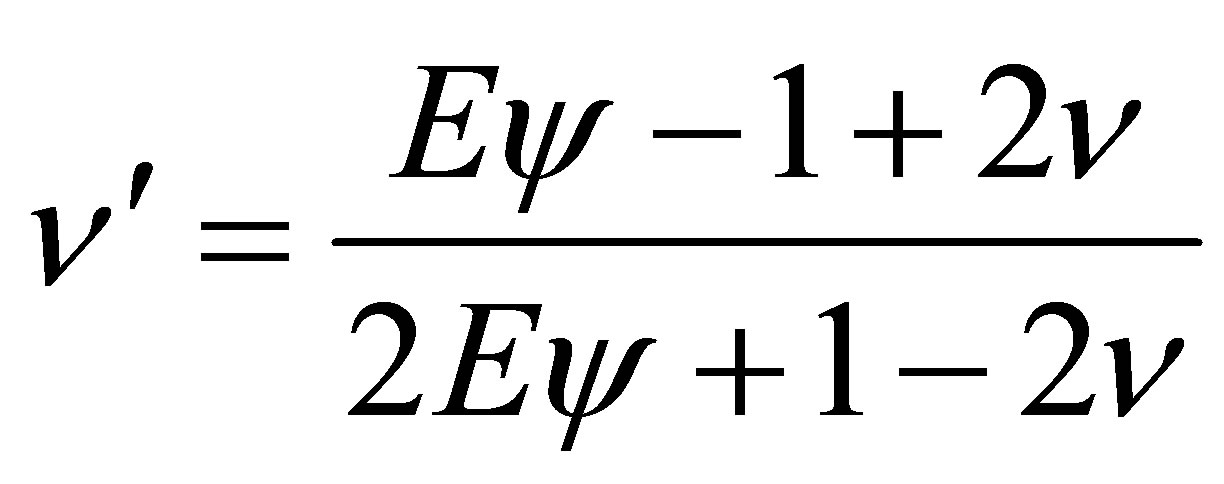 ;
;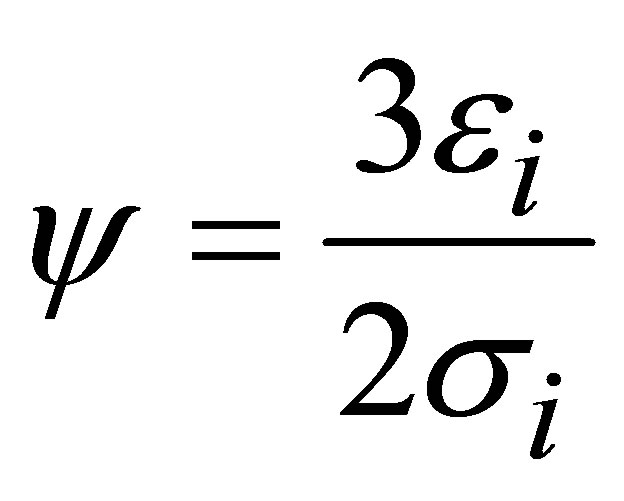 , (2)
, (2)
where  and
and 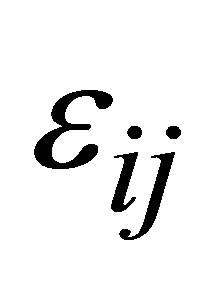 are the of stresses strains,
are the of stresses strains, 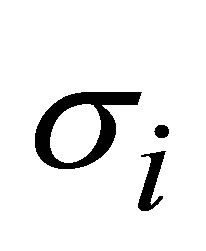 and
and 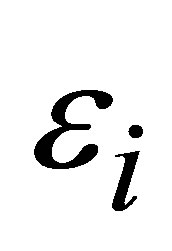 are the stress and strain intensities,
are the stress and strain intensities,  is the mean stress,
is the mean stress, 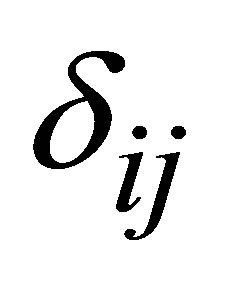 is the Kronecker delta.
is the Kronecker delta.
For a first approximation, we have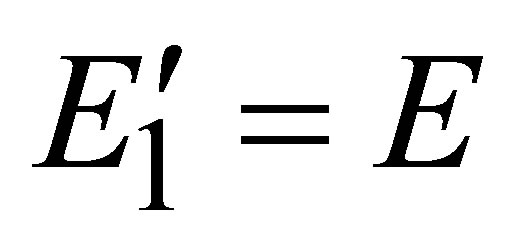 ,
,  and determine
and determine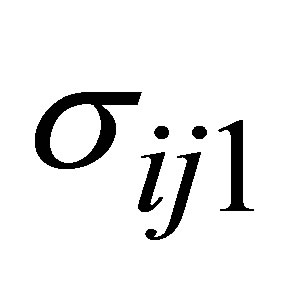 ,
, 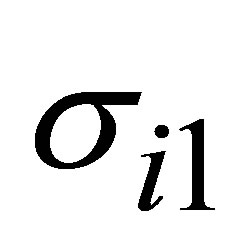 ,
,  ,
, . In a second approximation we have
. In a second approximation we have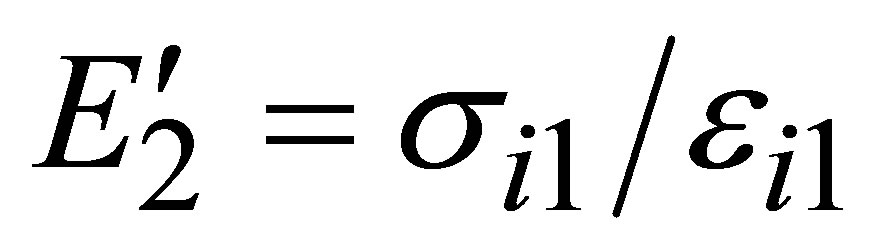 ,
, 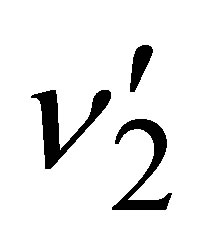 obtained from Equation (2) at
obtained from Equation (2) at 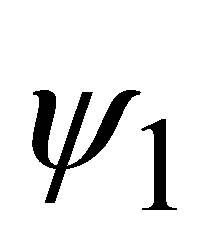 and so on. The process is run until two successive approximations coincide to within a given accuracy,
and so on. The process is run until two successive approximations coincide to within a given accuracy,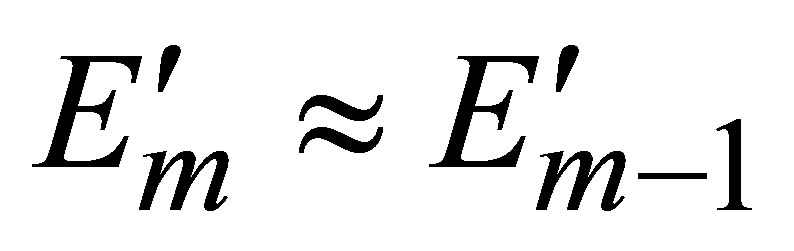 .
.
Corresponding schemes for the flow theory of plasticity may be constructed.
The corresponding minimized energy functional for shell with openings is written as [9]
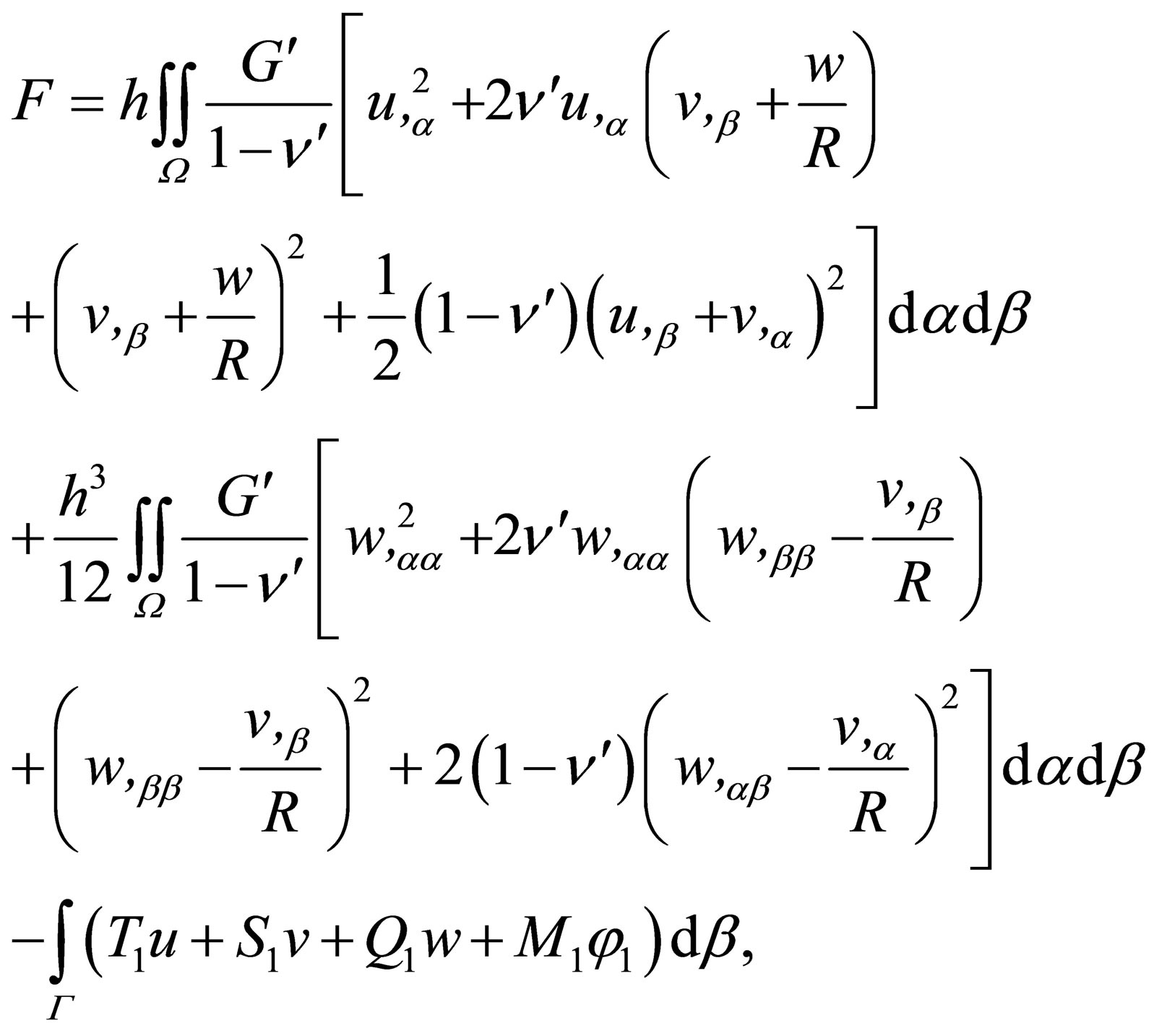 (3)
(3)
where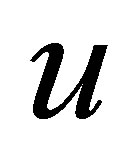 ,
, 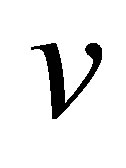 , and
, and 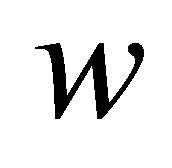 are the displacements of the middle surface,
are the displacements of the middle surface, 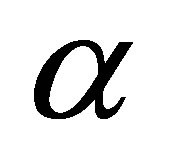 and
and —coordinates,
—coordinates,  is the shell thickness,
is the shell thickness,  is the sheet surface,
is the sheet surface, 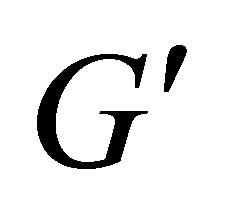 and
and 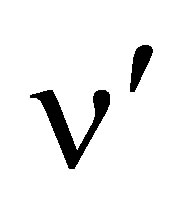 are the variable elastic parameters for each method VEP approximation,
are the variable elastic parameters for each method VEP approximation,  ,
, 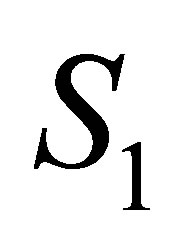 ,
, 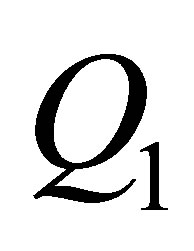 and
and  are the longitudinal, tangential, transverse force and bending moment, respectively which are applied to the shell edges
are the longitudinal, tangential, transverse force and bending moment, respectively which are applied to the shell edges , comma denotes differentiation in the coordinate. Stresses in the shell middle surface are given by
, comma denotes differentiation in the coordinate. Stresses in the shell middle surface are given by
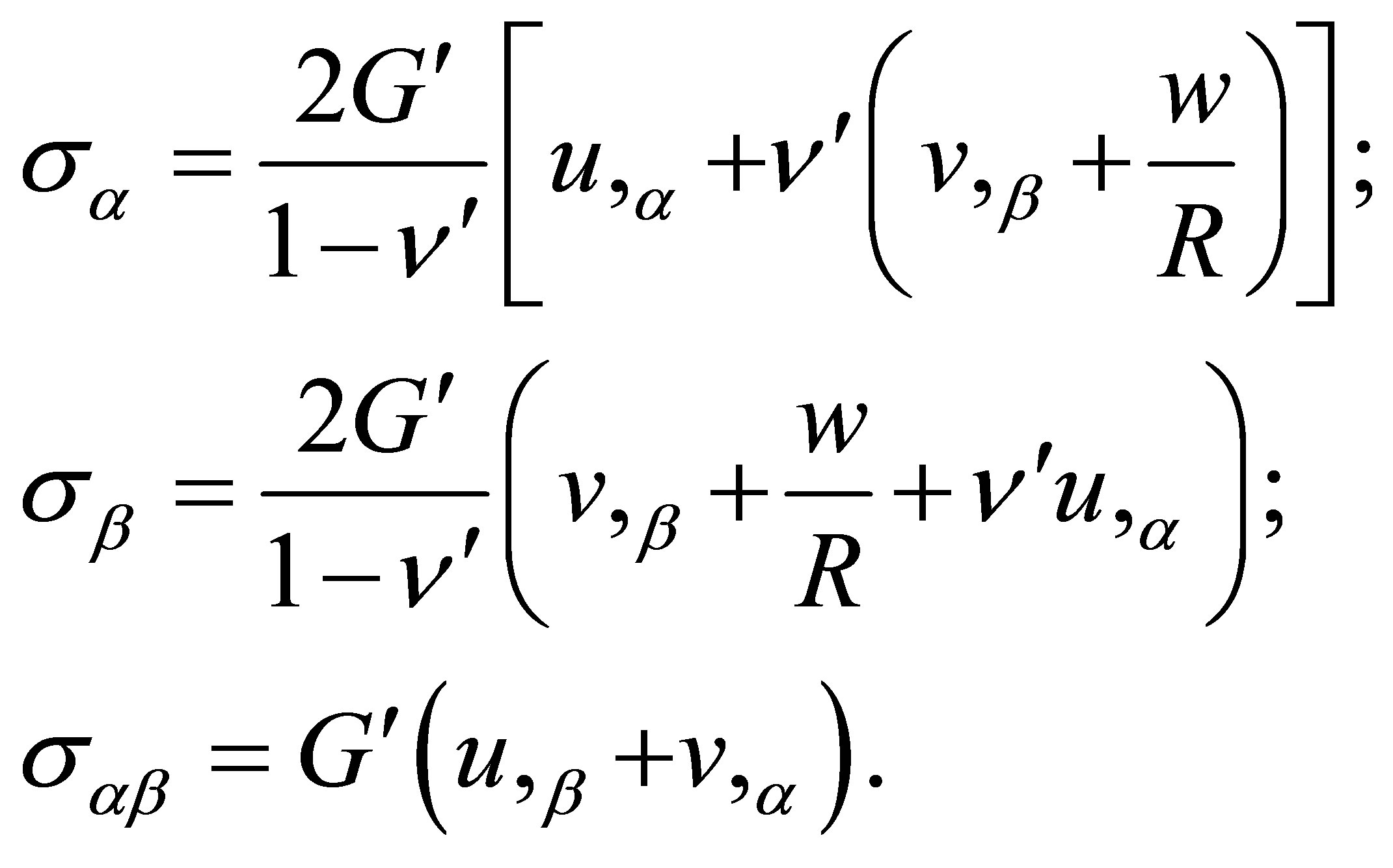 (4)
(4)
3. Results of Numerical Analysis
Founded on the PIV FEM procedure, a program in C++ language has been written for the stress-strain state analysis of cylindrical shell with three rectangular openings.
We calculated shells (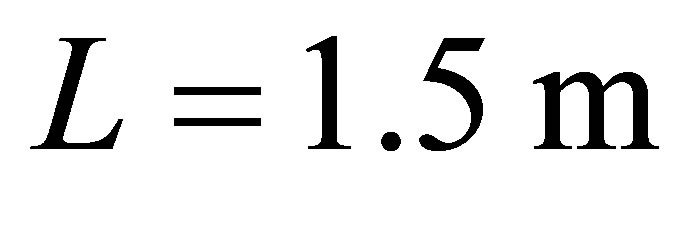 ,
,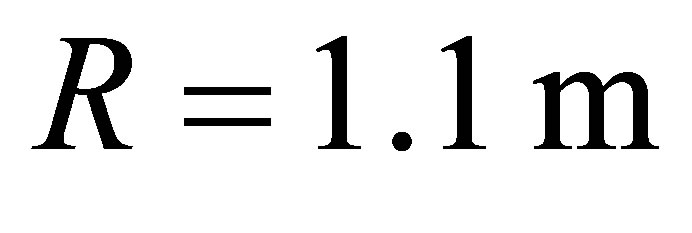 and
and ) of D16T aluminum alloy (Figure 1). The
) of D16T aluminum alloy (Figure 1). The
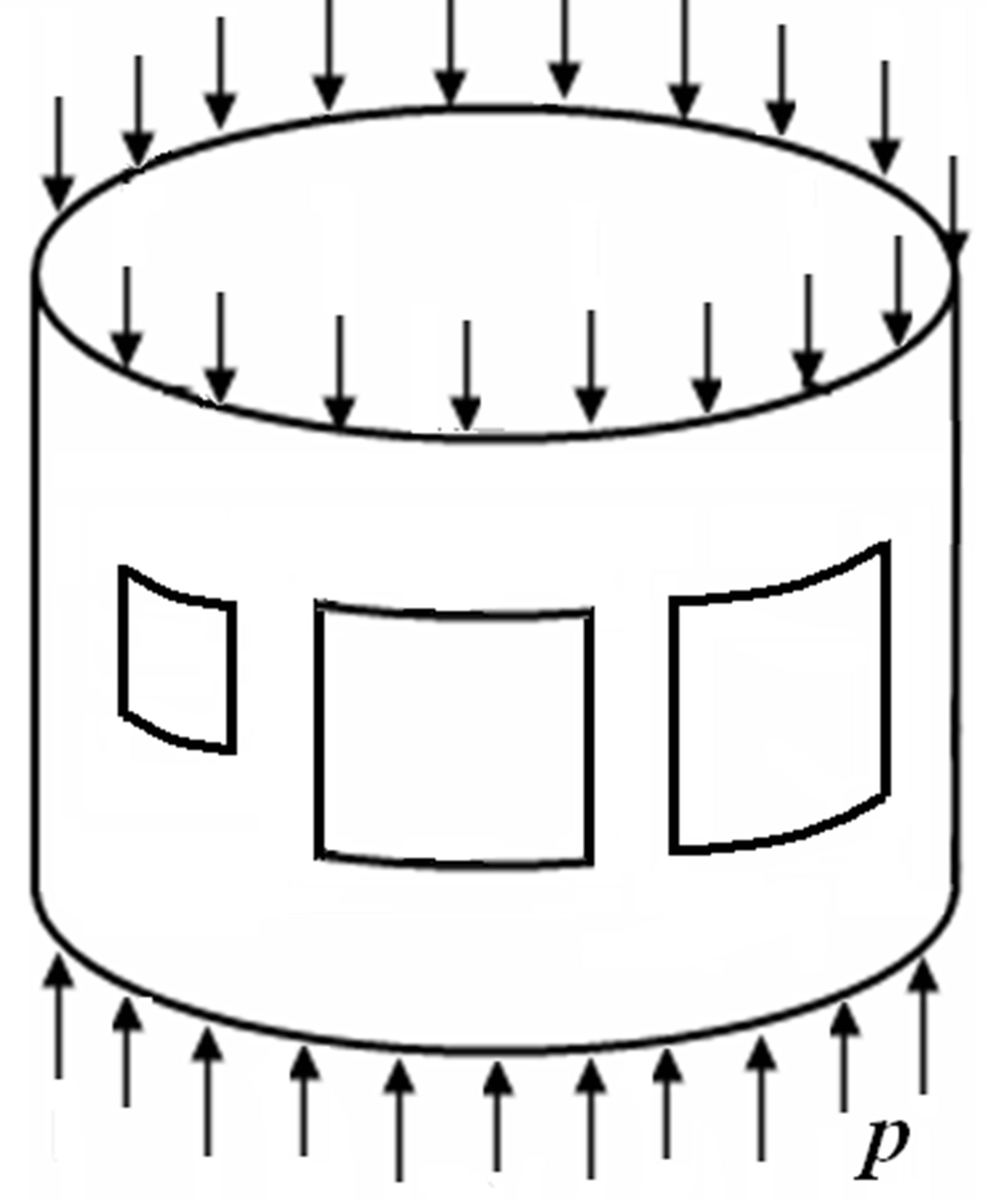
Figure 1. Scheme of shell structure and loading.
larger openings measures 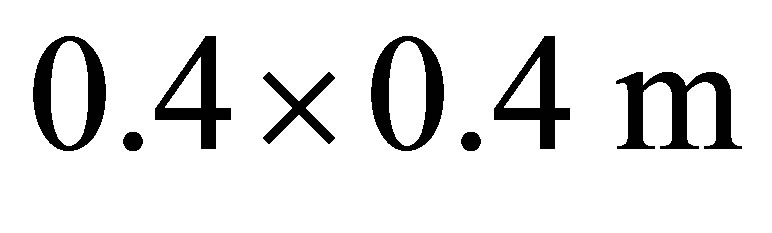 and the smaller one
and the smaller one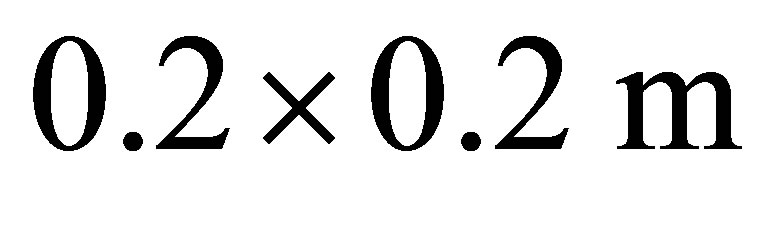 . Compressive loads
. Compressive loads 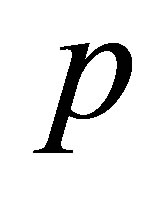 were varied from 55 to 100 MPa. The center-to-center distances:
were varied from 55 to 100 MPa. The center-to-center distances: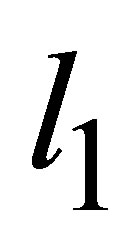 —between the small opening and the nearest larger opening,
—between the small opening and the nearest larger opening,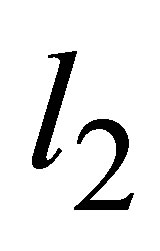 —between two larger openings were varied. The offset yield stress
—between two larger openings were varied. The offset yield stress  was taken 200 MPa.
was taken 200 MPa.
The PIV FEM has been implemented on eight double-folded FE meshes of rectangular Hermitian elements. The number 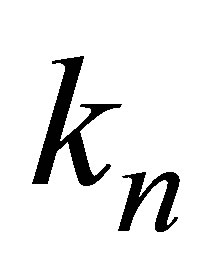 of approximations at the n-th step
of approximations at the n-th step 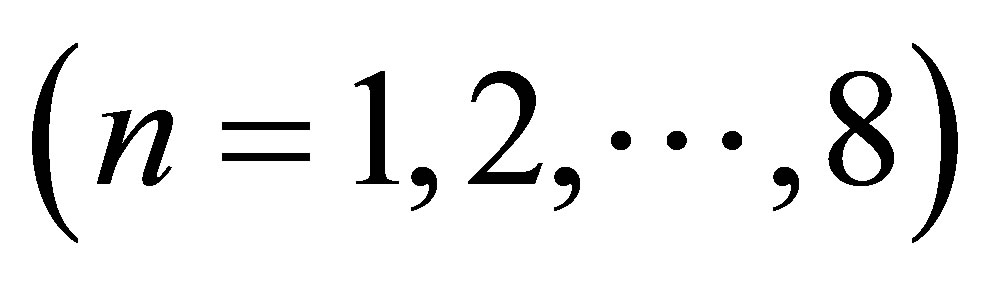 of the PIV process was chosen as the smallest integer k satisfying the condition
of the PIV process was chosen as the smallest integer k satisfying the condition
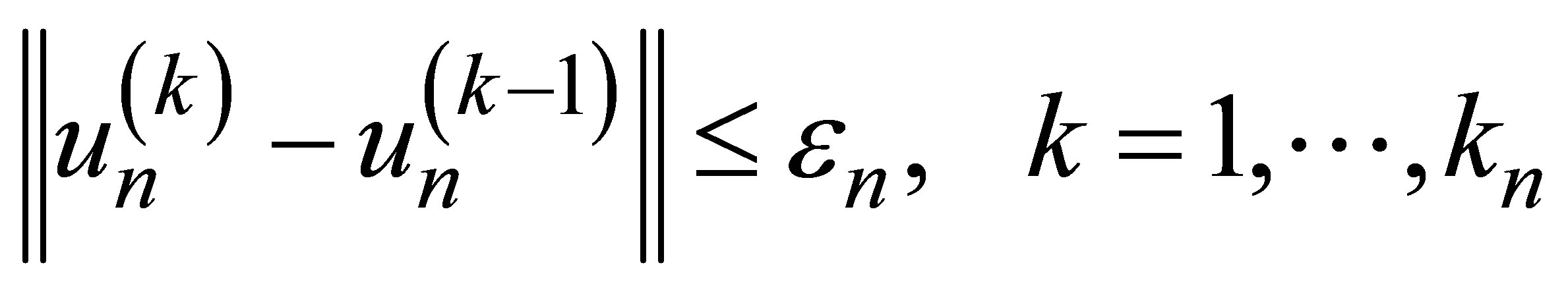 , (5)
, (5)
where 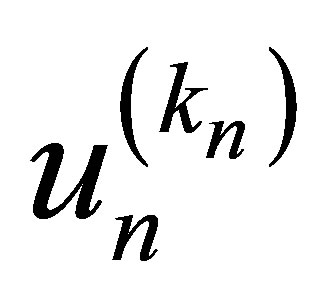 is the solution to the n-th finite-dimensional problems and
is the solution to the n-th finite-dimensional problems and  is the preset accuracy of computations on the n-th mesh.
is the preset accuracy of computations on the n-th mesh.
Let us consider some results of the numerical analysis.
By way of plane projections of the shell evolvent, Figure 2 shows how the plastic strain zones develop in a shell with openings:
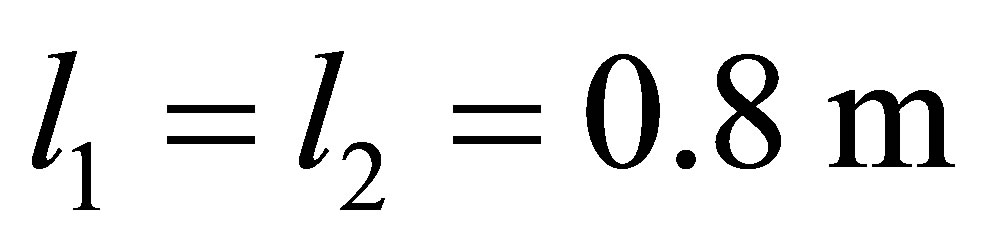 ,
, 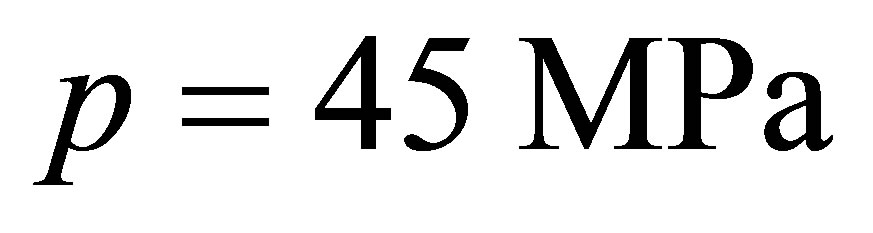
(Figure 2(a));
 ,
, 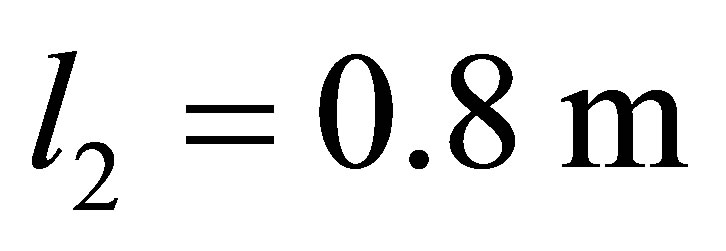 ,
, 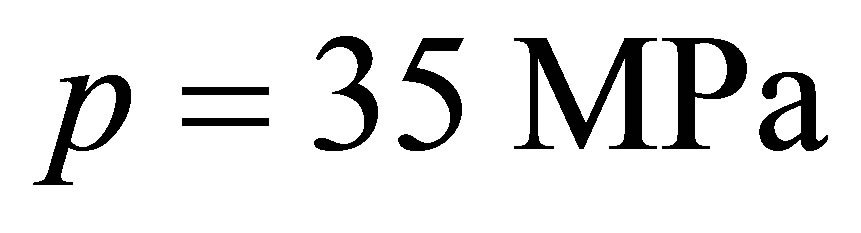
(Figure 2(b)).
These zones arise locally at the openings edges and at shell ends, merge as the load 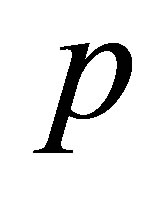 grow and
grow and  decreases. The variants of mutual influence of the openings will differ as the shell and openings parameters are changed.
decreases. The variants of mutual influence of the openings will differ as the shell and openings parameters are changed.
Using the computation program we can determine the loads whereby the plastic strain zones start merging to be become integral ones. The use PIV FEM models in these problems has provided a saving of computer time by a factor of 30 to 50 (depending on the class of problems) in comparison to the traditional FEM models (on a single mesh).
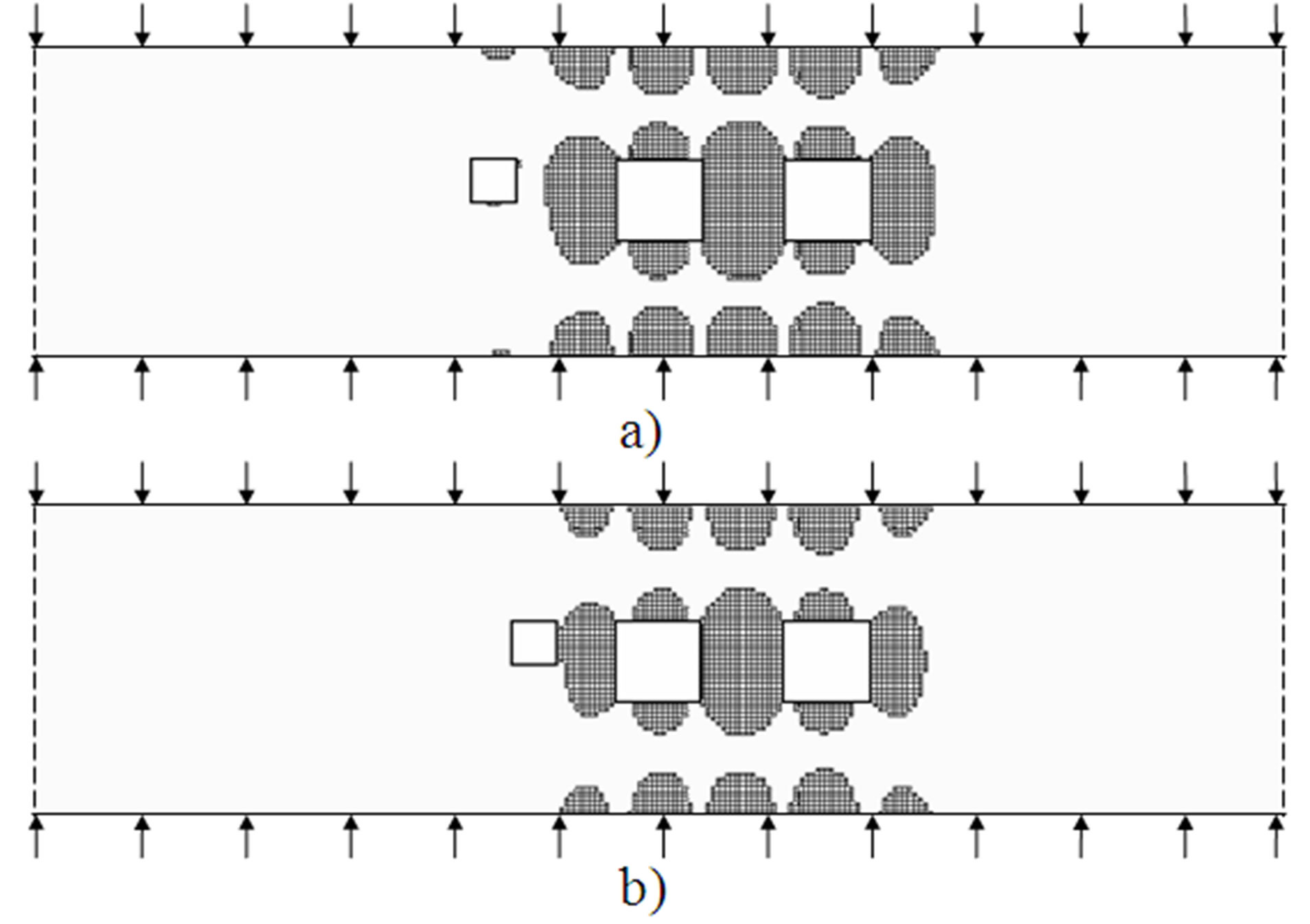
Figure 2. Distribution of plastic strain zones in a shell with openings.
The plastic strain zones affect on stiffness. The forma tion of the zones common for the openings considerably impairs the resistance of shall-type structures with openings to effective loads. This finding can be used in predicting their load-carrying capacity.
4. Conclusions
Founded on PIV, FEM models have significantly reduce the computation time (in comparison to the conventional FEM models). Therefore, methods of numerical simulation of strength for elastoplastic shell-type structures containing several rectangular openings are developed. The variation of openings parameters, quantities, and center-tocenter distances allows one to study the formation and transformation of plastic strain zones in the process of loading. Merging of the zones leads to a decrease in stiffness. This fact is used in predicting the load-carrying capacity.
The developed schemes for numerical simulation can be expended to the plate-shell structures members with openings of other shapes (circular, elliptical). This is partly done in [2,8].
REFERENCES
- V. S. Hudramovich, “Features of Nonlinear Deformation and Critical States of Shell Systems with Geometrical Imperfections,” Journal of Applied Mechanics, Vol. 42, No. 12, 2006, pp. 1323-1355.
- E. Hart and V. Hudramovich, “Applications of the Projective-Iterative Versions of FEM in Problems of Damage for Engineering Structures,” Proceedings of the 2th International Conference “Maintenance 2012”, Zenica, Bosnia and Herzegovina, 13-16 June 2012, pp. 157-163.
- A. A. Il’yushin, “Collected Works in 4 Volumes, Vol. 2: Plasticity (1946-1966),” Fizmatlit, Moscow, 2004.
- M. A. Krasnosel’skii, G. M. Vainikko and P. P. Zabreiko, “Approximate Solution of Operator Equations,” Nauka, Moscow, 1969.
- R. Kluge, “Ein Projektions-Iterationsverfahren bei Fixpunktproblemen und Gleichungen mit Monothonen Operatoren,” Monatsber. Dtsch. Akad. Wissenschaft, Vol. 11, No. 8-9, 1969, pp. 599-609.
- W. Hackbusch, “Multigrid Methods and Applications,” Springer, Berlin, 1985. http://dx.doi.org/10.1007/978-3-662-02427-0
- E. L. Hart, “Projection-Iterative Version of the Pointwise Relaxation Method,” Journal of Mathematical Sciences, Vol. 167, No. 1, 2010, pp. 76-88. http://dx.doi.org/10.1007/s10958-010-9903-3
- V. Hudramovich, E. Hart and S. Ryabokon, “Elastoplastic Deformation of Nonhomogeneous Plates,” Journal of Engineering Mathematics, Vol. 78, No. 1, 2013, pp. 181- 197. http://dx.doi.org/10.1007/s10665-010-9409-5
- V. V. Novozhilov, K. F. Chernych and E. I. Michailovskii, “Linear Theory of Thin Shells,” Politechnica, Leningrad, 1991.

