ABSTRACT

The lowest order mass for a KK graviton, as a non-zero product of two branes interacting via a situation similar to Steinhardt’s ekpyrotic universe is obtained, as to an alternative to the present dogma specifying that gravitons must be massless. The relative positions as to the branes give a dynamical picture as to how lowest order KK gravitons could be affected by contraction and then subsequent expansion. Initially we have bulk gravitons as a vacuum state. The massless condition is just one solution to a Stern Liuouville operator equation we discuss, which with a non-zero lowest order mass for a KK graviton permits modeling of gravitons via a dynamical Casmir effect which we generalize using Ruser and Duerrer’s 2007 work. In particular the blue spectrum for (massless gravitons), is revisited, with consequences for observational astrophysics.

Keywords:

Gravitons, Blue Spectrum, KK Theory, Casmir Effect

1. Introduction

We make use of work done by Ruser and Duerrer [1] which is essentially a re-do of the Steinhardt model of the ekpyrotic universe, with two branes, one of which is viewed to be stationary and the other is moving toward and away from the stationary brane.

The construction used, largely based upon the Ruser and Duerrer [1] article makes use of a set of differential equations based on the Sturm Liouville method which in the case of the zeroth order mass being zero have in usual parlance a zero value to lowest order KK graviton mass [1] . We will turn this idea on its head by having a non-zero graviton mass, zeroth order in the KK construction as to show how graviton mass, lowest order is affected by a Casmir plate treatment of graviton dynamic.

2. Setting up a Casmir Effect for Zeroth Order “Massive” KK Gravitons

What we will do is to examine the physics of what is mentioned via figure 1 as in their article as given in [1] the dynamics of the two branes with one stationary and the other moving, which influence a close form solution of the zeroth order graviton mass problem. Figure 1 in this case refers to a figure given in [1] which is not contained in this text.

Using Ruser and Duerrer [1] what we find is that there are two branes on the 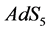space-time so that with one moving and one stationary, we can look at figure 1 as reproduced below which is part of the geometry used in the spatial decomposition of the differential operator acting upon the Fourier modes of the 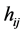operator [1] . As given by Ruser and Duerrer, [1] we have that

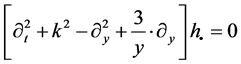(1)

Spatially, (1) can be, in its configuration as having

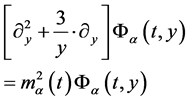(2)

What we will do, instead of looking at a Sturm Liouville operator, as was done in [1] is instead to look at an inner product treatment of the zeroth order mass as can be accessed in a KK decomposition of a graviton, and to consider though using

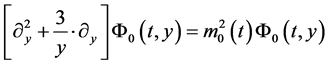(3)

Standard treatment of the problem represented in (3) is to use the RHS of (3) as set equal to zero. That allows for the “solution” to (3), namely 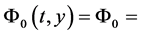constant with respect to space. Our substitution is given below:

An ansatz can be placed into the (3) results above, with, say,

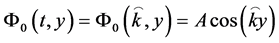(4)

Our next approximation is to keep the product 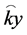real valued and do a power series expansion of (4) above. Also, we keep the following normalization intact from [1]

(5)

The right hand side is a Kroniker delta, and so it is equal to zero often. So we look at, then if we take an “inner product” procedure as to (4) above we have then the zeroth order mass for a graviton as written up as

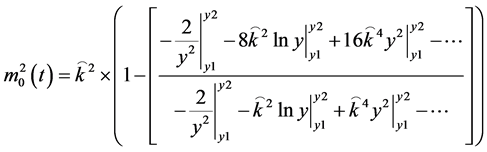(6)

The time dependence as to the above zeroth value comes from looking at if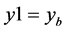, and 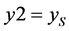are such with having, by figure 1 above, 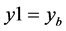moving 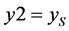not able to move, so that (6) definitely has a time dependence. The term 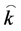is a term which can be fixed by requirements as to the initial conditions in (5) are met, and equal to 1 when 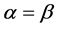and = 0. The end result is that the (6) is the zeroth order mass term which is not equal to 0.

3. Lessons from Gryzinski, as Far as Semi-Classical Derivation of a Usually Assumed Quantum Derivation of Inelastic Scattering in Atomic Hydrogen and Its Implications as to (3) and (6)

We will review the derivation of what is normally assumed to be a quantum result, with the startling implications that a cross section formula, normally quantum, does not need usual Hilbert space construction (usually Hilbert space means quantum mechanics). We will briefly review the Gryzinski result [2] [3] which came from something other than Hilbert space construction and then make our comparison with the likelihood of doing the same thing with respect to forming the zeroth order value of a graviton mass, as not equal to zero, by (3) above without mandating the existence of Hilbert spaces in the electroweak era. Gryzinski [2] [3] starts off with what is called an excitation cross section given by

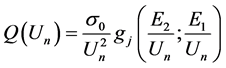(7)

where

(8)

and

(9)

and

(10)

with

(11)

The write up of (7) to (11) has, and being energy of level n, and being the energy of the bound electron, and being the energy of the incident electron. We refer the reader to [2] as to what the value of the Born approximation used as a comparison with (11) above. The result was that the Gryzinski’s approximation gives scattering cross sections lower than those of the Born approximation although the shape of the curves for cross sectional values are almost the same, with the difference between the Gryzinski approximation and the Born approximation in value closed in magnitude, with principal quantum numbers increased The net effect though is that having a Hilbert space, i.e. assuming that the presence of a Hilbert space implies the Quantum condition, is not always necessary for a typical quantum result. Now, how does that argument as to Hilbert spaces not being necessary for presumed quantum results relate to how to obtain (3)?

4. In Particular the Blue Spectrum for (Massless Gravitons), Is Revisited, if Gravitons Have a Slight Mass with Consequences for Observational Astrophysics

We refer to (3) and (6) as giving a non zero value of the zeroth order mass of a graviton in KK theory, and then try to refocus upon the more traditional 4 space definition of GW expansion in order to come up with normal modes. To do this, look at the mode equation in 4 space and its analogy to higher dimensions. In 4 space, the mode equation reads as

(12)

Usually, but if it is not equal to zero, then (12) has a more subtle meaning. Consider from Ruser and Duerrer [1] what (12) is turned into, in a more general setting. It gets exotic, namely

(13)

The obvious connection between the two (12) and (13) is that one will have if, then one observes

(14)

So, does one have, then, that.

We have, through (13) above outlined an application of Mach’s principle as far as the constant value of. Next will be describing how and why Mach’s principle can be applied to the gravitino. Note, Mishra [4] used a spin 3/2 particle, and we suggest this is in sync with using a Gravitino.

Mishra, and Mishra & Christian in [5] came up with a Fermionic particle description of the number of particles in the universe, and since gravitons have spin 2, we are lead to gravitinos of spin 3/2, a super partner description many times larger in mass than the super partner graviton. The Mistra approximation was for a fermionic treatment of kinetic energy as given by as a single particle distribution function, such that Mishra used [4] , where, and, with a variational parameter, and we have that kinetic energy KE is written as given by [4] [5] and [6]

(15)

This has a normalization such that

(16)

Furthermore, the potential energy is modeled via a Hartree-Fock approximation given by

(17)

These two were combined together by Mistra to reflect the self-gravitating fictitious particle Hamiltonian [4] [5]

(18)

So then a proper spatial averaging of the Hamiltonian will lead, for quantum energy of the universe given by [4] [5] and [6]

(19)

Note that the value m, is the mass of the fermionic particle, and that (26) when minimized leads to a minimum energy value of the variational parameter, which at the minimum energy has for which (26) becomes

(20)

The tie in with Mach’s principle comes as follows; i.e. Mishra sets a net radius value [4] [5] [6]

(21)

This spatial value is picked so that the potential energy of the system becomes equal to the total energy, and note that a total mass, M of the system is computed as follows, i.e. having a mass as given by Mistra, [4] then next assumes that then, there is due to this averaging a tie in, with M being the gravitational mass a linkage to inertial mass so as to write, using (28) and (29) a way to have inertial mass the same as gravitational mass via

(22)

This is for total mass M of the universe, and so if we wish to work with a subsystem as what we did with gravitinos, in the electroweak era, we will then change (31) to read instead as a sub set of this Mach’s principle, i.e. an electroweak version, i.e. a subset of the Mach’s principle

(23)

We shall outline the consequences of the Machian equation, of the sort given by (32) and from there say something about the limits, next of the Wheeler De Witt equation.

5. Machian Physics and the Linkage to the Wheeler De Witt Equation and the Limits of the Wheeler De Witt Equation

Barbour and Pfizer [7] write a very interesting and useful document and interpretation as far as Hamiltonian systems and general relativity. According to [7] , the dynamics of general relativity can be written up in terms of a constrained Hamiltonian “with the configuration space for pure gravity being given by the space of all Riemanian metrics on a 3 dimensional manifold of fixed but arbitrary topology. We call this topology and have that is the trajectory (of all paths) on. In their derivation the vacuum Einstein equations take the form of

(24)

This has a Hamiltonian constraint given by

(25)

And a momentum constraint given by

(26)

Here, is the Levi-Civita for a metric with a corresponding Ricci scalar and Ricci tensor with the terms associated with the De Witt metric [20] . As cited by [7] , if (25) and (26) are satisfied initially, then by (24), (25) and (26) are continually satisfied Now in what Barbor calls the Machian derivation of General relativity [7] [8] there is one constant linkage of his formalism with the Wheeler De Witt equation, which is that there is no formal time flow, i.e., that the Wheeler De Witt equation in its classical form as in [9] has NO time component added to it. Note that in [8] it is stated that there is no general flow of time, at best there are what Barbor called “time capsules” and that Quantum physics is a way of giving “high probability” to “time capsules”. What the author has proposed doing with the Machian perspective is to give a dynamical trajectory as to the Hamiltonian and momentum constraints given as (25) and (26). Needless to say though that what is attempted by (23) is to set up a precondition, independent of (25) and (26) as to set up a configuration for the set of (24), (25) and (26) via (23), and that we regard (24) as a precondition for fulfilling (25) and (26) which are then dynamically satisfied via (24). The idea is that (1) which forms as a byproduct of result of (23) is a precondition for then the formation of the WdW equation as we know it, which we accept as a time independent quantity [9] .

This construction of the WdW equation leads to the following question. If Barbor is right about there not being a “flow of time” as we think of it, can we interpret (1) and then (23) as a Machian set up of the WdW equations via (24), (25) and (26)? We submit that what is happening is that if there is no flow of time, that still there is a dynamical set up period, and a conservation of information flow as represented by the formation of as given in (21) and (22), with then (1), (24) to (26) as preconditions as to keeping the same value of during cosmological evolution, with the WdW equation forming after the setup of the initial which then remains constant.

6. How to Outline the Resulting Precondition for Constant Value for

In this note what we do is to organize the interrelationship of the formation of Planck’s constant with a necessary and sufficient condition for Quantum processes to form. In a word what we are seeing is that when Planck’s constant is being formed, as in the electrodynamic argument given in this paper, that a boundary condition created by Octonian space-time physics exists, which is a boundary of where orthodox QM does not apply and that then later we are applying QM with the formation of Planck’s constant after we enter in the regime after the formation of Planck’s constant. After the formation of Planck’s constant we then are in a position where the Machian relations between gravitinos and gravitons exist, which we claim is a necessary and sufficient condition for a no changing value of. What is done below is to summarize a very sophisticated interrelationship of formation of Planck’s constant, the zone of where Octonian geometry no longer holds as separated by a boundary from where Octonian geometry does hold as a necessary and sufficient condition for the onset of using this boundary between Octonionic and non Octonionic geometry as the necessary condition to use relic electromagnetic fields to construct Planck’s constant. Note that we are assuming very high electromagnetic fields during and before the electroweak regime [10] which allows, with the presence of a boundary between Octonionic and non Octonionic geometry Planck’s constant to form. We summarize our findings as to the results of our discussion in Table 1 as given below.

We have that the formation period for is our pre quantum regime.

This is incidentally the boundary region before the break down of Octonionic gravity, to our present cosmology. When we get to the present era, and the breakdown of Octonionic geometry, exemplified by spatial commutation relations equaling zero, is when QM applies. Before that regime, QM does not apply Furthermore, with the formation of a WdW cosmology, we then have confluence with Barbor’s dismissal of the flow of time, as given in [7] and [8] which is in adherence as to [9] in its treatment of the WdW equation as time independent.

7. Conclusion: Getting the Template as to Keeping Information Content Available for (32) Right

The Machian hypothesis [7] [10] and actually (9) are a way to address a serious issue. The issue is how to keep the consistency of physical law intact, in cosmological evolution. So far, using the template of gravitons and their superpartners, gravitinos, as information carriers, the author has provided a way to argue that Planck’s constant remains invariant as from the EW (electroweak era) to the present era. As one can deduce from physical evolution of the cosmos, time variance of Planck’s constant and time variation of the fine structure constant would lead to dramatically different cosmological events than what is deduced by observational astronomy. What we are arguing, using Mach’s principle is:

a) Physical law remains invariant in cosmological evolution due to the constant nature/magnitude of h bar, the fine structure constant, and G itself.

b) The linkage in information from a prior to the present universe can be thought of as far as the constancy of (19) concerning gravitinos. While we are aware that gravitinos have a short life time, we argue that (19) would have significant continuity at/before the big bang, and also that this is a way of answering the memory question as to how much cosmological memory is preserved from a prior to the present universe structures. Needless to say though there is a complete breakdown in causality before the formation of the gravitinos which is incidentally the pre-quantum regime of space-time, i.e. where Octonionic geometry predominates.

The main task the author sees is in experimental verification of the following identity. See (27) as below.

The motivation of using two types of Mach’s principle, one for the Gravitinos in the electroweak era, and then the 2nd modern day Mach’s principle, as organized by the author, is as seen in (27) as re-stated below [10] .

(27)

Once making the double Mach’s principle with (27) equal to a constant is done, with M = N times m, where N is the number of a particular particle species, and m is the net mass of the particle species, then an embedding of quantum mechanics using Mach’s principle as part of an embedding space can be ventured upon and investigated experimentally. Also, we will be then getting ready for the main prize, i.e. finding experimental constraints leading to Planck’s constant being invariant. That will do researchers a valuable service as to forming our view of a consistent cosmological evolution of our present cosmology from cycle to cycle. It also would allow for eventually understanding if entropy can also be stated in terms of gravitons alone in early universe models as was proposed by Kiefer & Starobinsky, et al. [11] . Finally, it would address if QM is embedded in a larger deterministic theory as advocated by t’ Hooft [12] , the end result would be in examining the following, in terms of values as influenced by massive gravitons. We can use this Machian relationship to understand the values as influenced by massive gravitons. As read from Hinterbichler [13] , if, and we look at a mass induced suppression factor put in of, then if

(28)

(29)

(30)

Here, we have that these values are solutions to the following equation, as given by [13] [14] , with D a dimensions value put in.

(31)

To understand the import of the above equations, and the influence of the Machian hypothesis, for GW and massive graviton signatures from the electroweak regime, set

(32)

And use the value of the radius of the universe, as given by , and rather than a super partner gravitino, use the If the values are understood, then we hope we can make sense out of the general uncertainty relationship given by [15]

(33)

The hope is to find tests of this generalized uncertainty due to values and to review [13] , i.e. to find experimentally falsifiable criteria to determine if Quantum mechanics is actually embedded within a semi classical super structure.

In doing this, we should keep in mind that what Corda brought up in [16] needs to be looked out, i.e. the interferometric tests of general relativity would be an outgrowth of such investigations.

Furthermore, [17] [18] should be kept in mind in terms of experimental constraints. Gravitational waves have been discovered, and it is opportune for us to keep [17] and [18] in mind when considering the applications of Equation (27) to whatever forms of data sets which may be achievable via experimental gravity.

Last but not least, the author has already had his own version of Equation (33), as seen in [19] . It remains to be seen if [19] is in line with the data sets we may be able to obtain, as well as fidelity with procedures which may allow the issues given in [20] [21] [22] [23] and [24] to be thoroughly looked at from an experimental stand point, as well as [25] for the mass of a graviton.

Finally it would be the gold standard, of determining if initial conditions can be ascertained by data sets to see if [12] , as given by t’ Hooft holds, i.e. the idea of deterministic conditions for quantum gravity. And possibly the constructions of [26] , and [27] as well, provided gravitons having a small pass are not experimentally ruled out.

Acknowledgements

Thanks to Dr. Corda to suggesting expansion of an initially very incomplete article. The main point of the Gryzinski derivation is that one does not need Hilbert space (usually associated with QM) to obtain what is thought to be a quantum physics result.

This work is supported in part by National Nature Science Foundation of China grant No. 11375279.

Cite this paper

Beckwith, A.W. (2017) Lowest Order Mass of KK Graviton Revisited and How It May Affect the Blue Spectrum for Gravitons. Journal of High Energy Physics, Gravitation and Cosmology, 3, 296-307. https://doi.org/10.4236/jhepgc.2017.32025

References