Received 29 October 2015; accepted 9 January 2016; published 12 January 2016

ABSTRACT

We initially look at a non-singular universe representation of time, and of comparing a general formula of a cosmological Potential energy as given by Padmanbhan, with Weinberg’s Quintessence Potential energy. Isolating a given time component which may serve as an introduction. We then compare this to when, and seeing what the time component then allows as far as available initial energy, the scale factor and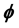, then finally admissible frequency, for Pre Planckian process generated Gravitational waves.

Keywords:

Gedanken Experiment, Quantum Bounce, Gravitational Waves, Cosmological Evolution

1. Introduction, Setting up for Calculation of Using the Results of Initial Time Step Value, Initial Energy as Due to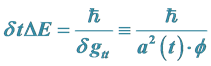

We follow what to expect from as given in [1] [2] for

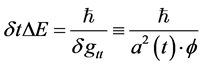(1)

as a way to quantify energy density when we have what is coming from Weinberg [3] on initial energy density and then from there to say something about initial time step and also potential energy as given by Padmanbhan [4] . Doing so will isolate out values of the Potential energy, as in [3] which will then be compared to [4] ’s potential energy value, which in turn gets a value of time, which we will set by first considering the following evolution equation. From [3]

(2)

Then, look at 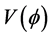from [3] as having the value of, if M is related to mass, with 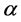a variable parameter

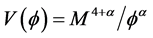(3)

So, then the 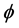is given by 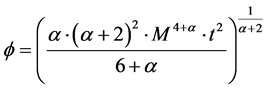[3]

(3)

And also look at Padmanabhan’s generalized inflaton potential [4] , of comparing Equation (2) with Equation (4) below

(4)

We have the Hubble parameter, if before Planck time, during Plank time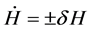

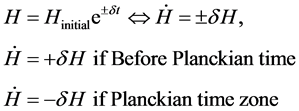(5)

Then, we could get the following variance in time,

(6)

2. Finding How to Use This Value of in Order to Estimate a Relic GW Frequency

If so, then, up to a point, in the Pre Plankian regime of space time, according to the signs on Equation (5) and Equation (6) and [1] [2] for the change in

(7)

We should keep in mind that delta times phi in the denominator of Equation (7) is a variation of the time component of the metric tensor as given by Giovannini in [5] with Equation (6) as a candidate for the scalar field.

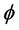
Set then, in early universe conditions, let us set, if we are considering gravitons, that we will set, say that the expression below would be for pre Planckian times, with t < 10⁻⁴⁴ seconds. The upshot would be that there would be a GW frequency, in many cases, as a result of pre Planckian physics of greater than or equal 10³² Hz, which would be red shifted down to about 10¹⁰ Hz, i.e. a 22 order of magnitude drop, in the present era. This is assuming, as well as we are assuming N ~ 10³⁷, as seen in [1] [2]

(8)

The M as given in this would correspond to the Mass value of the universe, which is roughly 3 × 10⁵⁵ g (where g is for grams.) [6] .

3. Marked Difference in Behaviour of Time, as given in Equation (6) Says Something about the Importance, of Pre Planckian Estimate for Relic Graviton Production

Note that time in Equation (6) remains finite but very small, as it came out less than 10 to the minus 44 power seconds, less than Planck time, with the parameter usually larger than 2. Time, in Equation (6) as estimate is actually negative, unless we have that we chose in Equation (5) the Pre Planckian option, which is saying that likely Planck time may not be the earliest sub division of time as we know it. This last point above will be important in our future research. As well as entropy production models due to discussions in [7] - [10] in terms of entropy generation in the Pre Planckian era.

4. Asking If This Frequency Matter Affects the Selection of Nonstandard Cosmologies? Yes, It Does. Here Is Why. Non Zero Initial Scale Factors May Imply Small Structures Initially which Have an Outsized Impact in Terms of Deviations from the Friedman-Walker Metric Cosmology

Equation (8) above has a minimum scale factor we can call which is extremely small, but not equal to zero. If we are assuming by [11] that there exits a nonzero minimum scale factor, we would be then introducing the notion of a quantum bounce, as introduced by [11] and loop quantum gravity. Theoretically, one could argue as given in [12] , by L.P. Grishchuk, in calculations which especially in his figure called “spectrum of relic gravitational waves” in [12] in ways which affirm the point being made in Equation (8) that there is a variation as given in [13] , i.e. an alternation from the Friedman Walker cosmology due to extremely small structure in early universe cosmology.

Furthermore, reference [14] raises a point made in the following quote about the consequentiality of small structure

“We develop a new, mathematically precise framework for treating the effects of nonlinear phenomena occurring on small scales in general relativity. Our approach is an adaptation of Burnett’s formulation of the ‘shortwave approximation’, which we generalize to analyze the effects of matter inhomogeneities as well as gravitational radiation. Our framework requires the metric to be close to a ‘background metric’, but allows arbitrarily large stress-energy fluctuations on small scales”.

[15] as a reference, adds more to the matter, and is a counter poise argument as to variations of the cosmology, which Wilkshire and others bring up as a counterpoise to [14] . In any case, the existence of a nonzero in radii initial radius may presage alterations in classical theories. Of Gravity.

Furthermore, there is another topic, to bring up, namely, the issues of the nature of determining if there is or not if there are conditions allowing for quantization in the genesis of GR, as given by [16] [17] in the quote that

“On the other hand, one can define Extended Theories of Gravity those semiclassical theories where the Lagrangian is modified, in respect to the standard Einstein-Hilbert gravitational Lagrangian, adding high-order terms in the curvature invariants (terms like…) or terms with scalar fields non minimally coupled to geometry (terms like)”, which allows for conditions giving more structure to the terms in the Pre Planckian possible quantization of GR we give as

(9)

In Equation (9), as given, in [18] , as written up by Beckwith,

“inputs into the terms, and may determine if the quote taken about the admissibility of adding in higher order terms in the curvature as alluded to in [16] above is accurate”, i.e. this is very important. Furthermore, if the bounce, with a nonzero initial scale factor means, also investigation into if say Loop quantum gravity and a nonsingular starting point, as a modification of Friedman-Walker cosmology is legitimate.

A good course starting for the experimental side to all of this, is to look at [17] , namely at the following quote

2.4 Stochastic searches Omni-directional gravitational wave background radiation could arise from fundamental processes in the early Universe, or from the superposition of a large number of signals with a point-like origin. Examples of the former include parametric amplification of gravitational vacuum fluctuations during the inflationary era, termination of inflation through axion decay or resonant preheating, Pre-Big Bang models inspired by string theory, and phase transitions in the early Universe.

i.e. the advantage of a correct rendering of Equation (8) we can understand if point sources are, initially an issue for relic GW, or some other initial configuration with say as given by [13] [14] enormous consequences to the formation of early structure.

5. BICEP 2 Issues, and the Continual Crisis over Its Results, How It Affects Our GW Frequency

[19] states, unequivocally that

We fit the single- and cross-frequency power spectra at frequencies ≥150 GHz to a lensed-ΛCDM model that includes dust and a possible contribution from inflationary gravitational waves (as parameterized by the tensor-to-scalar ratio r), using a prior on the frequency spectral behavior of polarized dust emission from previous/planck/analysis of other regions of the sky. We find strong evidence for dust and no statistically significant evidence for tensor modes. We probe various model variations and extensions

In the end, what we are looking for is to make sense of the following from [19] , i.e. “All the unified effort can do is put an upper limit on the likely size of the real signal”, as given in the search modes, stated in [19] , in addition to, as stated in [18] , that

An important, direct connection between the strain of relic gravitational waves and the inflaton field has been released by Dr. Corda [20] as far as the formula he derived for an inflaton and inputs of strain upon the inflaton field. This was given by Dr. Corda as [20]

(10)

Here, H is given as the evolving Hubble parameter, and represents the averaged amplitude of the perturbations of the RSBGWs, where RSBGWs is an abbreviation for relic stochastic background of gravitational waves (RSBGWs) which is proposed by the Pre-Big-Bang Theory. Below we work with an. amplitude, as compared to for a frequency range Corda gave as for when one has for the Hubble parameter when setting for a narrower frequency band width given. The upshot as claimed by Corda is for that range of GW that as a lower bound for the inflaton field. If so, then the inflaton field may have a different lower bound if, as an example one looks at, even if one looks at. The lower bound of the inflaton field becomes especially significant, if as an example inflaton fields are connected with initial entropy conditions which Beckwith picked as.

The upshot with the frequency, to this range, will affect the size of the initial scale factor, admissible to the perturbation of the term which is in turn affecting non linear contributions from a non zero radii initial starting point for the expansion of the universe.

End of quote from [18] .

6. Conclusions

We seek to avoid problems of measuring dust, which wrecked the Bicep2 results, as stated in the discussion above. Note the importance of Equation (10) above, which in turn is affected by which is what we very much wish to have. In short, refinement of measurements leads to, as given in [18] ,

(11)

Equation (11) may, with refinements of r = x, in the four dimensional Volume give the new HUP, in our problem, have impact upon GW generation and its relevance to Bicep 2, the search for validation of nonstandard cosmologies, and GW searches. Furthermore, as brought up in [18]

Note that also the value of a correct rendering of Equation (11) would be to ascertain the axial tilt as would be expected in early universe cosmology, and relic Gravitational waves, with greater precision than which showed up in the BICEP 2 results.

Refining (11), and understanding the exact particulars of input from relic frequency may allow us enough precision to avoid the Bicep 2 disaster.

Acknowledgements

This work is supported in part by National Nature Science Foundation of China grant No. 11375279.

Cite this paper

Andrew WalcottBeckwith, (2016) Gedanken Experiment for Energy, and Scale Factor, Based upon the Assumption of Quintessence and Idea of Quantum Bounce in Order to Isolate Admissible Frequency for Gravitational Waves in the Beginning of Cosmological Evolution. Journal of High Energy Physics, Gravitation and Cosmology,02,92-97. doi: 10.4236/jhepgc.2016.21010

References