Journal of Materials Science and Chemical Engineering
Vol.03 No.08(2015), Article ID:58905,6 pages
10.4236/msce.2015.38010
Creation of Bielectron of Dirac Cone: The Tachyon Solution in Magnetic Field
Lyubov E. Lokot
Institute of Semiconductor Physics, NAS of Ukraine, Kyiv, Ukraine
Email: llokot@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 June 2015; accepted 17 August 2015; published 20 August 2015
ABSTRACT
Schrödinger equation for pair of two massless Dirac particles when magnetic field is applied in Landau gauge is solved exactly. In this case, the separation of center of mass and relative motion is obtained. Landau quantization 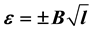 for pair of two Majorana fermions coupled via a Coulomb potential from massless chiral Dirac equation in cylindric coordinate is found. The root ambiguity in energy spectrum leads into Landau quantization for bielectron, when the states in which the one simultaneously exists are allowed. The tachyon solution with imaginary energy in Cooper problem
for pair of two Majorana fermions coupled via a Coulomb potential from massless chiral Dirac equation in cylindric coordinate is found. The root ambiguity in energy spectrum leads into Landau quantization for bielectron, when the states in which the one simultaneously exists are allowed. The tachyon solution with imaginary energy in Cooper problem 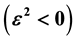 is found. The continuum symmetry of Dirac equation allows perfect pairing between electron Fermi spheres when magnetic field is applied in Landau gauge creating a Cooper pair.
is found. The continuum symmetry of Dirac equation allows perfect pairing between electron Fermi spheres when magnetic field is applied in Landau gauge creating a Cooper pair.
Keywords:
Bielectron, Dirac Cone, Tachyon, Magnetic Field, Graphene

1. Introduction
The graphene [1] - [3] presents a new state of matter of layered materials. The energy bands for graphite was found using “tight-binding” approximation by P.R. Wallace [4] . In the low-energy limit, the single-particle spectrum is Dirac cone similarly to the light cone in relativistic physics, where the light velocity is substituted by the Fermi velocity 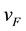 and describes by the massless Dirac equation.
and describes by the massless Dirac equation.
The graphene is the single graphite layer, i.e. two-dimensional graphite plane of thickness of single atom. The graphene lattice resembles a honeycomb lattice. The graphene lattice one can consider like into the composite of two triangular sublattices. In 1947, Wallace in “tight-binding” approximation consider a graphite which consist off the graphene blocks with taken into account the overlap only the nearest p-electrons.
The two-dimensional nature of graphene and the space and point symmetries of graphene acquire of the reason for the massless electron motion since lead into massless Dirac equation (Majorana fermions) [4] [5] . At low-energy limit, the single particle spectrum forms with p-electron carbon orbital and consist off completely occupation valence cone and completely empty conduction cone, which have cone like shape with single Dirac point. In Dirac point the existing an electron as well as a hole is proved. The state in Dirac cone is double degenerate with taken into account a spin.
The existing of the massless Dirac fermions in graphene was proved based on the unconventional quantum Hall effect. The reason of creation the integer Hall conductivity [6] - [9] is derived from Berry phase [10] [11] .
When the magnetic field is applied perpendicularly into graphene plane, the lowest (n = 0) Landau level has the energy 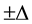 in two nonequivalent cones
in two nonequivalent cones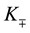 , correspondingly [12] . In the paper [12] , the Dirac mass via a splitting value is found when Zeeman coupling is absence. These properties of the lowest Landau level which distribute between particles and antiparticles in equal parts are base of the integer quantum Hall effect in graphene [12] . For
, correspondingly [12] . In the paper [12] , the Dirac mass via a splitting value is found when Zeeman coupling is absence. These properties of the lowest Landau level which distribute between particles and antiparticles in equal parts are base of the integer quantum Hall effect in graphene [12] . For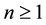 , all Landau levels are fourfold degenerate. For
, all Landau levels are fourfold degenerate. For  a states in both cones are twofold degenerate with energies
a states in both cones are twofold degenerate with energies 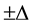 with taken into account a spin [12] .
with taken into account a spin [12] .
2. Solution of Massless Chiral Dirac Equation for Pair of Two Majorana Fermions Coupled via a Coulomb Potential in Magnetic Field in Landau Gauge
Calculation model of the graphene reflects continuum symmetry of QED2+1 including Lorentz group. SU(2) symmetry are shown to be found similar to chiral in the paper [12] . Hence is conserving quantum number of chirality.
The energy bands for graphene was found using “tight-binding” approximation in the papers [4] [12] .
Calculate the quantized Landau energy as well as the wave function of the Majorana particles in cylindrical coordinate in magnetic field in Landau gauge. Enter the production and annihilation operators as following:
 (1)
(1)
where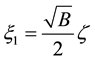 ,
, 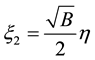 ,
, 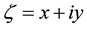 ,
, 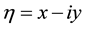 , which satisfies the commutator relation:
, which satisfies the commutator relation:
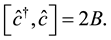 (2)
(2)
Hence for noninteracting Dirac particles we write the massless Dirac equation in the form:
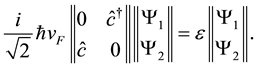 (3)
(3)
The Schrödinger equation for the reduced energy can be rewritten in the form:
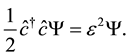 (4)
(4)
For graphene in vacuum the effective fine structure parameter



where 

When magnetic field is applied perpendicularly into graphene plane in z axis along field distribution. The
Figure 1. (Color online) Single-particle spectrum of graphene for massless Dirac fermions (Majorana fermions).
vector potential in the gauge [15] 



The Schrödinger Equation (6) with including the Coulomb potential Equation (5) one can rewritten in the form:

The solution Equation (7) with including the Coulomb potential Equation (5) can look for in the form:

Substituting the solution in Equation (7), one can find for the radial function the following equation

where




where




The solution of the Equation (10) can look for in the form:

To substitute the solution (11) in the Equation (10) it is necessarily to find as follows


Since


Substituting (12), (13), (14), (15) into the Equation (10) we find the equation for 

Hence for 

From the condition of finite of the wave function one can find the energy spectrum in the form:

where



where

Because the solution for the wave functions for the pair of two massless Dirac particles when magnetic field is applied in Landau gauge one can express via the product of the two identical wave functions one can conclude that in this case the separation of center of mass and relative motion is shown [16] .
Entering the production and annihilation operators as following (1) and solving Schrödinger equation one can derive the known for quantum electrodynamics (QED) solution-the root ambiguity in energy spectrum
where 

For graphene with strong Coulomb interaction the Bethe-Salpeter equation for the electron-hole bound state was solved and a tachyonic solution was found [19] .
Calculation model of the graphene reflects continuum symmetry of QED2+1 including Lorentz group. SU(2) symmetry are shown to be found similar chiral in the paper [12] . Hence is conserving quantum number of chirality. In the paper [20] the selection rules for the electron-radiation and for the electron-phonon interactions at all points in the Brillouin zone are derived based on irreducible representation of the crystallographic space groups as well as the symmetry properties of electrons and phonons. The each of these models are qualitatively different.
In the paper [21] a chiral superconductivity from electron-electron repulsive in doped graphene in the 
In the paper [22] a Magneto-Coulomb levels at a three-dimensional saddle point were found. The Schrödinger equation for the three-dimensional saddle surface geometry at the magnetic field is applied unconventionally was solved exactly in the paper [22] by reducing into one-dimensional Schrödinger equation.
In the paper [23] the exciton binding energy is scaled with the formed band gap when the magnetic field is applied and an exciton insulator transition in carbon nanotubes was not found and their THz application was predicted.
In the paper [24] in the UCoGe material the high-temperature superconductivity is connected with spin fluctuations and hence may be reduced by magnetic field is applied.
The exciton Wannier equation for graphene was solved in the papers [25] -[28] . A very large exciton binding energies were found. In the paper [25] a theoretical study the both the quantized energies of excitonic states and their wave functions in graphene is presented. An integral two-dimensional Schrödinger equation of the electron- hole pairing for a particles with electron-hole symmetry of reflection is exactly solved. The solutions of Schrö- dinger equation in momentum space in graphene by projection the two-dimensional space of momentum on the three-dimensional sphere are found exactly. We analytically solve an integral two-dimensional Schrödinger equation of the electron-hole pairing for particles with electron-hole symmetry of reflection. In single-layer graphene (SLG) the electron-hole pairing leads to the exciton insulator states. Quantized spectral series and light absorption rates of the excitonic states which distribute in valence cone are found exactly. If the electron and hole are separated, their energy is higher than if they are paired. The particle-hole symmetry of Dirac equation of layered materials allows perfect pairing between electron Fermi sphere and hole Fermi sphere in the valence cone and conduction cone and hence driving the Cooper instability.
3. Conclusion
Schrödinger equation for pair of two massless Dirac particles when magnetic field is applied in Landau gauge is solved exactly. Landau quantization 
potential from massless chiral Dirac equation in cylindric coordinate is found. In this case the separation of center of mass and relative motion is derived. The root ambiguity in energy spectrum leads into Landau quantization for bielectron, when the states in which the one simultaneously exists are allowed. The tachyon solution with imaginary energy in Cooper problem 
4. Mathematical Appendix
From a algebraic manipulation one can find a following recurrence relations:

where





From a algebraic manipulation one can find a following integrals and recurrence relations which connect theirs:







Cite this paper
Lyubov E.Lokot, (2015) Creation of Bielectron of Dirac Cone: The Tachyon Solution in Magnetic Field. Journal of Materials Science and Chemical Engineering,03,71-77. doi: 10.4236/msce.2015.38010
References
- 1. Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Katsnelson, M.I., Grigorieva, I.V., Dubonos, S.V. and Firsov, A.A. (2005) Two-Dimensional Gas of Massless Dirac Fermions in Grapheme. Nature, 438, 197-200.
http://dx.doi.org/10.1038/nature04233 - 2. Vasko, F.T. and Ryzhii, V. (2008) Photoconductivity of Intrinsic Grapheme. Physical Review B, 77, Article ID: 195433.
http://dx.doi.org/10.1103/PhysRevB.77.195433 - 3. Zhang, Y., Tan, Y.-W., Stormer, H.L. and Kim, P. (2005) Experimental Observation of the Quantum Hall Effect and Berry’s Phase in Graphene. Nature, 438, 201-204.
http://dx.doi.org/10.1038/nature04235 - 4. Wallace, P.R. (1947) The Band Theory of Graphite. Physical Review, 71, 622.
http://dx.doi.org/10.1103/PhysRev.71.622 - 5. Semenoff, G. (1984) Condensed-Matter Simulation of a Three-Dimensional Anomaly. Physical Review Letters, 53, 2449.
http://dx.doi.org/10.1103/PhysRevLett.53.2449 - 6. Zheng, Y. and Ando, T. (2002) Hall Conductivity of a Two-Dimensional Graphite System. Physical Review B, 65, 245420.
http://dx.doi.org/10.1103/PhysRevB.65.245420 - 7. Gusynin, V.P. and Sharapov, S.G. (2005) Unconventional Integer Quantum Hall Effect in Graphene. Physical Review Letters, 95, 146801.
http://dx.doi.org/10.1103/PhysRevLett.95.146801 - 8. Gusynin, V.P. and Sharapov, S.G. (2006) Transport of Dirac Quasiparticles in Graphene: Hall and Optical Conductivities. Physical Review B, 73, 245411.
http://dx.doi.org/10.1103/PhysRevB.73.245411 - 9. Peres, N.M.R., Guinea, F. and Castro Neto, A.H. (2006) Electronic Properties of Disordered Two-Dimensional Carbon. Physical Review B, 73, 125411.
http://dx.doi.org/10.1103/PhysRevB.73.125411 - 10. Berry, M.V. (1984) Quantal Phase Factors Accompanying Adiabatic Changes. Proceedings of the Royal Society of London A, 392, 45.
http://dx.doi.org/10.1098/rspa.1984.0023 - 11. Carmier, P. and Ullmo, D. (2008) Berry Phase in Graphene: Semiclassical Perspective. Physical Review B, 77, Article ID: 245413.
http://dx.doi.org/10.1103/PhysRevB.77.245413 - 12. Gusynin, V.P., Sharapov, S.G. and Carbotte, J.P. (2007) Ac Conductivity of Graphene: From Tight-Binding Model to 2 + 1-Dimensional Quantum Electrodynamics. International Journal of Modern Physics B, 21, 4611-4658.
http://dx.doi.org/10.1142/S0217979207038022 - 13. Alicea, J. and Fisher, M.P.A. (2006) Graphene Integer Quantum Hall Effect in the Ferromagnetic and Paramagnetic Regimes. Physical Review B, 74, Article ID: 075422.
http://dx.doi.org/10.1103/PhysRevB.74.075422 - 14. Novikov, D.S. (2007) Elastic Scattering Theory and Transport in Grapheme. Physical Review B, 76, Article ID: 245435.
http://dx.doi.org/10.1103/PhysRevB.76.245435 - 15. Landau, L.D. and Lifshitz, E.M. (1977) Quantum Mechanics. Non-Relativistic Theory. Pergamon, NewYork.
- 16. Lokot, L.E. (2015) Particle-Hole Pair States of Layered Materials. Physica E, 68, 176-183.
http://dx.doi.org/10.1016/j.physe.2014.12.022 - 17. McClure, J.W. (1956) Diamagnetism of Graphite. Physical Review, 104, 666-671.
http://dx.doi.org/10.1103/PhysRev.104.666 - 18. Berestetskii, V.B., Lifshitz, E.M. and Pitaevskii, L.P. (1989) Quantum Electrodynamics. Nauka, Moskow.
- 19. Gamayun, O.V., Gorbar, E.V. and Gusynin, V.P. (2009) Supercritical Coulomb Center and Excitonic Instability in Graphene. Physical Review B, 80, Article ID: 165429.
http://dx.doi.org/10.1103/PhysRevB.80.165429 - 20. Malard, L.M., Guimaraes, M.H.D., Mafra, D.L., Mazzoni, M.S.C. and Jorio, A. (2009) Group-Theory Analysis of Electrons and Phonons in N-Layer Graphene Systems. Physical Review B, 79, Article ID: 125426.
http://dx.doi.org/10.1103/PhysRevB.79.125426 - 21. Nandkishore, R., Levitov, L.S. and Chubukov, A.V. (2012) Chiral Superconductivity from Repulsive Interactions in Doped Graphene. Nature Physics, 8, 158-163.
http://dx.doi.org/10.1038/nphys2208 - 22. Rashba, E.I. and Edelshteyin, B.M. (1969) Magnetic Coulomb Levels Near the Saddle Points. JETP Letters, 9, 475- 480.
- 23. Hartmann, R.R., Shelykh, I.A. and Portnoi, M.E. (2011) Excitons in Narrow-Gap Carbon Nanotubes. Physical Review B, 84, Article ID: 035437.
http://dx.doi.org/10.1103/PhysRevB.84.035437 - 24. Julian, S. (2012) Viewpoint: Pairing with Spin Fluctuations. Physics, 5, 17.
http://dx.doi.org/10.1103/Physics.5.17 - 25. Lokot, L.E. (2015) Exciton Insulator States for Particle-Hole Pair in ZnO/(Zn,Mg)O Quantum Wells and for Dirac Cone. SSRG International Journal of Material Science and Engineering, 1, 1. arXiv: 1501.03696v2 [cond-mat.mes- hall].
- 26. Stroucken, T., Gronqvist, J.H. and Koch, S.W. (2011) Optical Response and Ground State of Graphene. Physical Review B, 84, Article ID: 205445.
http://dx.doi.org/10.1103/PhysRevB.84.205445 - 27. Gronqvist, J.H., Stroucken, T., Beghauser, G. and Koch, S.W. (2011) Excitons in Graphene and the Influence of the Dielectric Environment. arXiv:1107.5653v1 [cond-mat.mtrl-sci].
- 28. Malic, E., Winzer, T., Bobkin, E. and Knorr, A. (2011) Microscopic Theory of Absorption and Ultrafast Many-Particle Kinetics in Grapheme. Physical Review B, 84, Article ID: 205406.
http://dx.doi.org/10.1103/PhysRevB.84.205406


